Геометрия как быстро выучить что такое треугольник высота медиана биссектриса?
Высота значит точно то же, что и в обычном мире 🙂 То есть расстояние от вершины (она может быть любой) до той линии, на которой треугольник «стоит».
Медиана соединяет вершину с центром стороны напротив.
Биссектриса делит угол пополам, выходя из вершины «внутрь».
Высоты — из вершин к плоскости, на которой треугольник может «стоять». Тоесть под прямым углом сверху-вниз.
Медиана — делит сторону напротив угла пополам
Биссектриса — делит пополам сам угол
Медиана (геометрия) — это… Что такое Медиана (геометрия)?
- Медиана (геометрия)
-

Треугольник и его медианы.
Медиана треугольника ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
- Медианы треугольника пересекаются в одной точке, которая называется центроидом, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
- Из векторов, образующих медианы, можно составить треугольник.
- Формула медианы через стороны:

- поэтому сумма квадратов медиан произвольного треугольника всегда в 4/3 раза меньше суммы квадратов его сторон.
- Формула стороны через медианы:
 , где ma,mb,mc медианы к соответствующим сторонам треугольника, a,b,c — стороны треугольника.
, где ma,mb,mc медианы к соответствующим сторонам треугольника, a,b,c — стороны треугольника.
Медиана — это обезьяна, лазает по сторонам, делит их напополам.
См. также
Ссылки
Wikimedia Foundation. 2010.
- Медиальный
- Медиана (муниципалитет)
Смотреть что такое «Медиана (геометрия)» в других словарях:
Медиана треугольника — У этого термина существуют и другие значения, см. Медиана. Треугольник и его медианы. Медиана треугольника (лат. … Википедия
Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Клейн, Феликс — Феликс Клейн Дата рождения: 25 апреля 1849(1849 04 25 … Википедия
Клейн Ф. — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия
Клейн Феликс — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия
Феликс Клейн — Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия
Эрлангенская программа — Феликс Клейн Эрлангенская программа выступление 23 летнего немецкого математика Феликса Клейна в Эрлангенском университете (октябр … Википедия
Математическая статистика
— Математическая статистика наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на … ВикипедияПрямоугольный треугольник — Прямоугольный треугольник это треугольник, в котором один угол прямой (то есть составляет 90 градусов). Соотношения между сторонами и … Википедия
Теорема Аполлония — Зелёное + Голубое = Красное В планиметрии теорема Аполлония является формулой, выражающей длину медианы треугольника через … Википедия
Меридианы — урок. География, 5 класс.
Меридианы (от латинского слова meridianus — «полуденный») — воображаемые полуокружности, проходящие (соединяющие) через Северный и Южный полюсы.
Слово «меридиан» происходит от латинского слова «полуденный», поскольку направление всех меридианов совпадает с направлением тени от предметов в полдень.
Меридиан может быть проведён через любую точку земной поверхности. Меридианы — линии направления север–юг. Все точки, лежащие на одном меридиане, имеют одинаковую географическую долготу.
Меридианы имеют одинаковую длину — более \(20 000\) км.
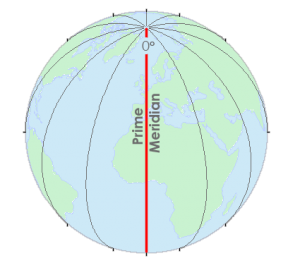
Гринвичский (нулевой, или начальный) меридиан — меридиан, от которого ведётся отсчёт географической долготы.
Для того чтобы вести отсчёт меридианам, учёные договорились, что нулевым (начальным) меридианом станет меридиан, проходящий через пригород Лондона Гринвич. Гринвич знаменит своей обсерваторией, одной из старейших в мире.
Гринвичская королевская обсерватория
Этот меридиан имеет \(3\) названия: нулевой, начальный и Гринвичский.
На глобусе нулевой меридиан, как и экватор, выделен жирной линией. Начальный меридиан и меридиан \(180°\) делят Землю на Западное и Восточное полушария.
К западу от начального меридиана до меридиана \(180°\) расположено Западное полушарие.
К востоку от нулевого меридиана до меридиана \(180°\) расположено Восточное полушарие.
Источники:
https://ru.wikipedia.org
http://lifeglobe.net
http://lanoonan.soulshineseries.com
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Определение. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Рис.1
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD.
Утверждение 1. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Доказательство. Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

Рис.2
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)


Поскольку отрезок BD является медианой, то

что и требовалось доказать.
Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.
Доказательство. Рассмотрим две любых медианы треугольника, например, медианы AD и CE, и обозначим точку их пересечения буквой O (рис. 3).

Рис.3
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Рис.4
Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Рис.5
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC. Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC. Следовательно,

откуда вытекает, что стороны ED и FG четырёхугольника FEDG равны и параллельны. Следовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополам (рис.6).

Рис.6
Таким образом,
| FO | = | OD | , | GO | = | OE | .
Следовательно,
| AF | = | FO | = | OD | , | CG | = | GO | = | OE | .
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1, считая от вершины треугольника.
Доказательство завершено.
Следствие. Все три медианы треугольника пересекаются в одной точке.
Доказательство. Рассмотрим медиану AD треугольника ABC и точку O, которая делит эту медиану в отношении 2 : 1, считая от вершины A (рис.7).

Рис.7
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение. Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Рис.8
Доказательство. Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна  площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).
площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Рис.9
Тогда


В силу утверждения 1,



что и требовалось доказать.
Утверждение 4. Длина медианы треугольника (рис. 10) вычисляется по формуле:


Рис.10
Доказательство. Воспользуемся теоремой косинусов, примененной к треугольникам DBC и ABD:


Складывая эти равенства, получим:


что и требовалось доказать.
Следствие. Длины медиан и длины сторон треугольника связаны формулой

Доказательство. В силу утверждения 4 справедливы равенства:

Складывая эти равенства, получим:


что и требовалось доказать.
Утверждение 5. В параллелограммепараллелограмме сумма квадратов диагоналей равна сумме квадратов сторон.
Доказательство. Рассмотрим рисунок 11.

Рис.11
Поскольку AO – медиана треугольника ABD, а DO – медиана треугольника ADC, то, в силу утверждения 4, справедливы равенства:

Следовательно,
d12 = 2a2 + 2b2 – d22,
d22 = 2a2 + 2b2 – d12.
Складывая эти равенства, получим



что и требовалось доказать.
Утверждение 6. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы (рис. 12).

Рис.12
Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B (рис. 13).

Рис.13
Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольникпрямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства:


что и требовалось доказать.
Следствие. Середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности (рис. 14).

Рис.14
Утверждение 7. Рассмотрим в пространстве или на плоскости декартову систему координат с началом в точке O и произвольный треугольник ABC. Если обозначить буквой M точку пересечения медиан этого треугольника (рис.15), то будет справедливо равенство



Рис.15
Доказательство. По свойствам векторов


Далее получаем


что и требовалось доказать.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Медиана треугольника abc: определение, основание, свойства, задачи
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
- BF – медиана, проведенная к стороне AC.
- AF = FC

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
- AO = 2OE
- BO = 2OF
- CO = 2OD
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

S1 = S2
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.

S1 = S2 = S3 = S4 = S5 = S6
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

- AC – самая длинная сторона, следовательно, медиана
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы ma, проведенную к стороне a, можно найти по формуле:

Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см2. Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:

Медиана (в геометрии) — это… Что такое Медиана (в геометрии)?
- Медиана (в геометрии)
- Медиана (от латинского mediana — средняя) в геометрии, отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны. Три М. треугольника пересекаются в одной точке, которую иногда называют «центром тяжести» треугольника, так как именно в этой точке находится центр тяжести однородной треугольной пластинки (а также центр тяжести системы трёх равных масс, помещенных в вершинах треугольника). Точка пересечения М. делит каждую из них в отношении 2 : 1 (считая от вершины к основанию).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Медиальный
- Медиана (в теории вероятностей)
Смотреть что такое «Медиана (в геометрии)» в других словарях:
Медиана — I Медиана (от латинского mediana средняя) в геометрии, отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны. Три М. треугольника пересекаются в одной точке, которую иногда называют «центром тяжести»… … Большая советская энциклопедия
Медиана — ж. 1. Прямая линия, проведенная от вершины треугольника к середине противоположной стороны (в геометрии). 2. Величина, находящаяся в середине ряда величин, расположенных в возрастающем или убывающем порядке (в статистике). Толковый словарь… … Современный толковый словарь русского языка Ефремовой
Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Клейн, Феликс — Феликс Клейн Дата рождения: 25 апреля 1849(1849 04 25 … Википедия
Клейн Ф. — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия
Клейн Феликс — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия
Феликс Клейн — Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия
Эрлангенская программа — Феликс Клейн Эрлангенская программа выступление 23 летнего немецкого математика Феликса Клейна в Эрлангенском университете (октябр … Википедия
Грамотность новобранцев — (призывников) степень владения навыками чтения и письма на родном языке, оцениваемая применительно к призывникам (рекрутам) в процессе их анкетирования в связи с призывом на военную службу по рекрутской (воинской) повинности. Уровень… … Википедия
Среднее геометрическое — Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально: Среднее геометрическое двух чисел также называется… … Википедия
Все формулы медианы треугольника
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

- Подробности
- Автор: Administrator

10 лучших наставников по геометрии около меридиана, ID
Он проявил ко мне много терпения, и я это очень ценю. Он даже помог мне запомнить все формулы geometry , которые действительно помогли мне на экзамене Geometry Common Core Regents. Он очень добр, поддерживает, вдохновляет и предан своим ученикам. Он научил меня множеству навыков для geometry , и это действительно помогло! Он помог мне пройти мой путь по сдаче экзамена на Риджентс, за что я очень благодарен.Филипп — потрясающий наставник! 🙂
Дайан К.
9 уроков геометрии
Он не преуспел в своем первом семестре Класс геометрии . Нам был нужен репетитор по математике, который мог бы помочь моему сыну в классе GA Recovery Geometry , чтобы сохранить его статус участия в баскетболе.Даниэль был тем человеком! В его профиле говорится: «Мне нравится преподавать алгебру и геометрии , помогая студентам приобретать навыки обучения и решения проблем». Мой сын может подтвердить это, и он очень доволен стилем преподавания Даниэля и очень быстро усвоил концепции и навыки Geometry .
Хизер Х.
2 урока геометрии
В первом семестре она получила четверку по экзамену Geometry , но что-то произошло во втором семестре, и мы увидели в Интернете, что она просто проваливала класс с 59%. Она отстала и просто не могла наверстать упущенное, и на любом уроке математики такая ситуация не исправит сама себя, поскольку каждая концепция основывается на следующей. К этому моменту ни мой муж, ни я не могли ей помочь, так как она попадала в проблемы, о которых мы просто не могли вспомнить (прошло много времени с класса Geometry !).
,Где центральный меридиан?
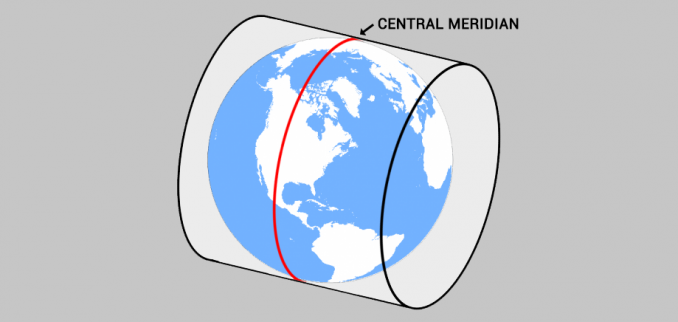
Автор: GIS Geography · Последнее обновление: 30 июля 2020 г.
Что такое центральный меридиан?
Центральный меридиан — это центральная линия долготы для проекционных систем.
Спроецированные системы координат часто используют его как точку отсчета для начала координат x.
Например, проекционные системы государственной плоскости и UTM используют центральный меридиан.
Вот несколько примеров центрального меридиана в системах координат.
Линии долготы проходят с севера на юг
Линии широты проходят с востока на запад и параллельны друг другу. В то время как линии долготы проходят с севера на юг и в конечном итоге сходятся на полюсах.
Например, нулевой меридиан — это линия долготы под углом 0 °. Все на этой линии имеет координату долготы 0 °.
Но нулевой меридиан (гринвичский меридиан) зависит от долготы 0 °. Точно так же, как экватор разделяет север и юг, гринвичский меридиан разделяет восток и запад.
Проекционные системы используют линии долготы как нулевой меридиан. Точно так же, как главный меридиан разделяется на восток и запад, центральные меридианы делают то же самое.
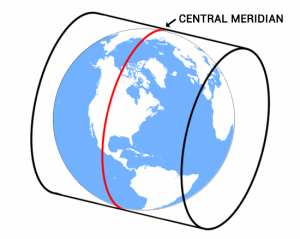
СистемаUTM использует центральный меридиан
Если вы переместитесь на 3 ° к востоку от нулевого меридиана, это будет центральный меридиан для зоны 31 UTM. Мы присваиваем всем X-координатам (восточным направлениям) на центральном меридиане значение 500 000 м.
Этот центральный меридиан — произвольное значение, удобное для избежания отрицательных координат восточного направления.Все значения восточного и западного направления от центрального меридиана будут положительными.
Каждая зона UTM имеет ширину 6 °. Таким образом, для зоны 31 UTM он находится в диапазоне от 0 ° до 6 ° восточной долготы. Тогда зона 32 UTM находится от 6 ° до 12 ° в.д. с центральным меридианом 9 ° в.д.
Поперечная проекция Меркатора берет цилиндр и кладет его на бок (поворачивает на 90 °). Затем цилиндр пересекает эллипсоид по двум маленьким окружностям, параллельным центральному меридиану.
Государственная плоская система координат использует центральный меридиан
В зависимости от размера и формы штата в системе координат штата (SPCS) используется 1 из 3 систем проецирования:
- Поперечный Меркатор
- Конформно-коническая форма Ламберта
- Hotine Oblique
Для зон, протяженных в направлении север-юг, используется поперечная проекция Меркатора.Как и в системе UTM, у нее есть центральный меридиан и два маленьких круга.
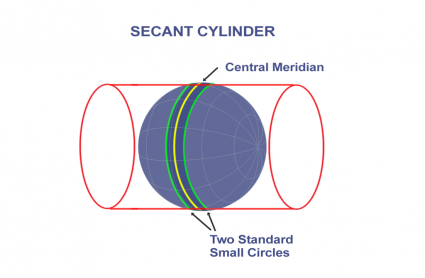
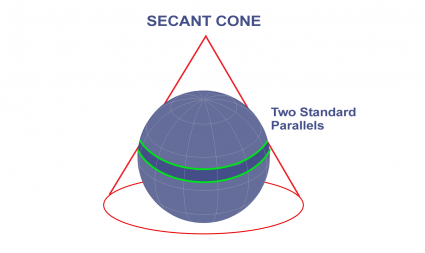
Если зона протяженная с востока на запад, SPCS использует проекцию конической формы Ламберта. Эта проекция использует секущий конус и имеет две стандартные параллели.
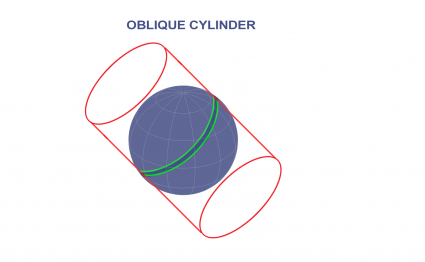
Когда зоны длинные в диагональном направлении, в проекции Hotine Oblique используется цилиндр, расположенный под углом к центральной линии.
Где центральный меридиан?
Центральный меридиан зависит от того, какую проекционную систему вы используете.
Например, каждая зона UTM использует центральный меридиан в качестве начала координат X (восточного направления).
Всему в центральном меридиане присвоено значение 500 000 м.
Это означает, что система UTM имеет 60 центральных меридианов для всех зон UTM.
UTM зон (Центральный меридиан)
| Зона UTM | Центральный меридиан | Протяженность зоны UTM |
|---|---|---|
| 1 | 177 ° з.д. | 180 ° W-174 ° W |
| 2 | 171 ° з.д. | 174 ° з.д.-168 ° з.д. |
| 3 | 165 ° з.д. | 168 ° з.д.-162 ° з.д. |
| 4 | 159 ° з.д. | 162 ° з.д.-156 ° з.д. |
| 5 | 153 ° з.д. | 156 ° Вт-150 ° Вт |
| 6 | 147 ° з.д. | 150 ° W-144 ° W |
| 7 | 141 ° з.д. | 144 ° з.д.-138 ° з.д. |
| 8 | 135 ° з.д. | 138 ° W-132 ° W |
| 9 | 129 ° з.д. | 132 ° з.д.-126 ° з.д. |
| 10 | 123 ° з.д. | 126 ° W-120 ° W |
| 11 | 117 ° з.д. | 120 ° W-114 ° W |
| 12 | 111 ° з.д. | 114 ° з.д.-108 ° з.д. |
| 13 | 105 ° з.д. | 108 ° з.д.-102 ° з.д. |
| 14 | 99 ° з.д. | 102 ° з.д.-96 ° з.д. |
| 15 | 93 ° з.д. | 96 ° W-90 ° W |
| 16 | 87 ° з.д. | 90 ° W-84 ° W |
| 17 | 81 ° з.д. | 84 ° з.д.-78 ° з.д. |
| 18 | 75 ° з.д. | 78 ° з.д.-72 ° з.д. |
| 19 | 69 ° з.д. | 72 ° W-66 ° W |
| 20 | 63 ° з.д. | 66 ° W-60 ° W |
| 21 | 57 ° з.д. | 60 ° W-54 ° W |
| 22 | 51 ° з.д. | 54 ° W-48 ° W |
| 23 | 45 ° з.д. | 48 ° W-42 ° W |
| 24 | 39 ° з.д. | 42 ° з.д.-36 ° з.д. |
| 25 | 33 ° з.д. | 36 ° з.д.-30 ° з.д. |
| 26 | 27 ° з.д. | 30 ° W-24 ° W |
| 27 | 21 ° з.д. | 24 ° W-18 ° W |
| 28 | 15 ° з.д. | 18 ° W-12 ° W |
| 29 | 9 ° з.д. | 12 ° W-6 ° W |
| 30 | 3 ° з.д. | 6 ° з.д.-0 ° |
| 31 | 3 ° в. Д. | 0 ° -6 ° в.д. |
| 32 | 9 ° в.д. | 6 ° в.д.-12 ° в.д. |
| 33 | 15 ° в.д. | 12 ° в.д.-18 ° в.д. |
| 34 | 21 ° в.д. | 18 ° в.д.-24 ° в.д. |
| 35 | 27 ° в.д. | 24 ° в.д.-30 ° в.д. |
| 36 | 33 ° в.д. | 30 ° в.д.-36 ° в.д. |
| 37 | 39 ° в.д. | 36 ° в.д.-42 ° в.д. |
| 38 | 45 ° в.д. | 42 ° в.д.-48 ° в.д. |
| 39 | 51 ° в.д. | 48 ° в.д.-54 ° в.д. |
| 40 | 57 ° в.д. | 54 ° в.д.-60 ° в.д. |
| 41 | 63 ° в.д. | 60 ° в.д.-66 ° в.д. |
| 42 | 69 ° в.д. | 66 ° в.д.-72 ° в.д. |
| 43 | 75 ° в.д. | 72 ° в.д.-78 ° в.д. |
| 44 | 81 ° в.д. | 78 ° в.д.-84 ° в.д. |
| 45 | 87 ° в.д. | 84 ° в.д.-90 ° в.д. |
| 46 | 93 ° в.д. | 90 ° в.д.-96 ° в.д. |
| 47 | 99 ° в.д. | 96 ° в.д.-102 ° в.д. |
| 48 | 105 ° в.д. | 102 ° в.д.-108 ° в.д. |
| 49 | 111 ° в.д. | 108 ° в.д.-114 ° в.д. |
| 50 | 117 ° в.д. | 114 ° в.д.-120 ° в.д. |
| 51 | 123 ° в.д. | 120 ° в.д.-126 ° в.д. |
| 52 | 129 ° в.д. | 126 ° в.д.-132 ° в.д. |
| 53 | 135 ° в.д. | 132 ° в.д.-138 ° в.д. |
| 54 | 141 ° в.д. | 138 ° в.д.-144 ° в.д. |
| 55 | 147 ° в.д. | 144 ° в.д.-150 ° в.д. |
| 56 | 153 ° в.д. | 150 ° в.д.-156 ° в.д. |
| 57 | 159 ° в.д. | 156 ° в.д.-162 ° в.д. |
| 58 | 165 ° в.д. | 162 ° в.д.-168 ° в.д. |
| 59 | 171 ° в.д. | 168 ° в.д.-174 ° в.д. |
| 60 | 177 ° в.д. | 174 ° в.д.-180 ° в.д. |
Медиана треугольника — математическое определение слова
Медиана треугольника — определение слова в математике — открытый справочник по математике Медиана треугольника — это отрезок присоединение к вершина до середины противоположной стороны.Следовательно, у треугольника три медианы. Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить форму треугольника. Обратите внимание, что все три медианы встречаются в одной точке.
Медиана треугольника — это отрезок от вершины треугольника к середина стороны, противоположной этой вершине.Поскольку есть три вершины, конечно, возможны три медианы. Один из увлекательных В них есть то, что независимо от формы треугольника, все три всегда пересекаются единственная точка. Эта точка называется центроидом треугольника.
Недвижимость
Медианы треугольника обладают некоторыми удивительными свойствами:- Тот факт, что три медианы всегда встречаются в одной точке, интересен сам по себе
- Каждая медиана делит треугольник на два меньших треугольника , имеющих одинаковую площадь
- Центроид (точка, где они встречаются) — это центр тяжести треугольника
- Три медианы делят треугольник на 6 меньших треугольников одинаковой площади, даже если они могут иметь разную форму.
Отрегулируйте треугольник выше, перетащив любую вершину. Убедите себя, что три медианы (серые линии) всегда пересекаются в одной точке. Вы также можете визуально оценить, что приведенные выше факты о местности соответствуют действительности.
Попробуй
- Сделайте из картона любой треугольник шириной около 12–24 дюймов. Сделайте его как можно скругленным и неправильным.
- Нарисуйте медиану на картонном треугольнике. Подойдет любой.
- В точке, где медиана пересекается со стороной треугольника, сделайте небольшое отверстие рядом с краем.Обвяжите его веревкой.
- Когда вы держите треугольник за веревку, средняя линия должна быть вертикальной — точно на одной линии с веревкой (см. Рисунок ниже).
- Почему?

Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Конгруэнтность и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Методы прохождения меридианов.
Короткий метод. В случае неподвижных или очень медленно движущихся судов допустимо использовать метод укороченного прохождения меридиана, который включает в себя расчет времени прохождения меридиана в текущей позиции DR.
Длинный метод. Для судов с хорошим ходом следует использовать длинный метод. Длинный метод включает в себя вычисление времени прохождения меридиана в текущем положении за час или около того до полудня, а затем построение нового положения DR для этого времени.Таким образом, время прохождения меридиана в новой позиции DR может быть рассчитано заранее.
Примечание. Поскольку в расчетах местоположения по меридианам используются часовой угол по Гринвичу и долгота, базовой линией для которых является гринвичский меридиан, в этих расчетах было бы целесообразно использовать среднее время по Гринвичу, а не универсальное время. Поскольку термины GMT и UT обычно считаются синонимами, потери точности не возникает.
Ссылки: Понимание прохождения меридиана, какова точка прохождения меридиана? Применение уравнения времени, метода длинного прохождения меридиана, местного часового угла и часового угла по Гринвичу, преобразование GMT в GHA, поясное время коррекции высоты,
Прохождение меридиана — короткий метод.
Как мы узнали из «Понимания прохождения меридианов», прохождение меридиана (mer. Pas.) Происходит, когда небесное тело пересекает меридиан долготы наблюдателя и в этот момент достигает своей наибольшей высоты над горизонтом наблюдателя.Мы также узнали, что если мы измеряем высоту Солнца при прохождении местного меридиана и используем результат вместе со склонением Солнца, мы можем вычислить нашу широту.
Короткий метод используется для неподвижных или очень медленно движущихся судов и включает в себя расчет времени прохождения меридиана в текущей позиции DR.
Правила расчета широты при прохождении меридиана. Следующие правила были полностью объяснены в разделе «Что такое меридианный проход», но их необходимо повторить здесь:
- Широта и склонение совпадают, но широта больше склонения: LAT = DEC + (90 o — ALT)
- Широта и склонение совпадают, но склонение больше широты: LAT = DEC — (90 o — ALT)
- Широта и склонение напротив названий: LAT = (90 o — ALT) — DEC
Краткое описание метода. Краткий метод включает в себя расчет времени прохождения местного меридиана в текущем географическом положении судна незадолго до полудня, а затем измерение высоты Солнца по мере приближения этого времени.
Схема шестиэтапной проформы для краткого метода прохождения меридиана . Эта простая в использовании шестиэтапная проформа может использоваться для расчета положения судна по методу сокращения меридианного прохода.
Предварительное планирование. По мере приближения полудня вычислите географическое положение вашего судна (DR или EP) и отметьте поясное время в этом месте.
- Шаг 1. Используя дневную страницу морского альманаха, найдите время прохождения меридиана (мер. Пас.) Для сегодняшней даты (по Гринвичу).
- Шаг 2. Преобразуйте время мер. па. от GMT до поясного времени. (Помните, что поясное время не будет соответствовать видимому времени Солнца, поэтому, несмотря на то, что мерп. Время приходится на видимый полдень, поясное время, вероятно, будет на несколько минут по обе стороны от него).
- Шаг 3. На ежедневной странице морского альманаха найдите склонение Солнца во время Мера.Па · с. (Обратите внимание, что при корректировке склонения с учетом приращения «d» необходимо следить за тем, чтобы проверять дневную страницу, чтобы увидеть, увеличивается или уменьшается склонение).
- Шаг 4 . Измерьте высоту нижней конечности Солнца в точке мер. па. и вычислите скорректированную высоту меридиана.
- Шаг 5. Вычислите широту судна по высоте меридиана и склонению Солнца, используя правила для Mer. Па · с. как объяснялось ранее.
- Шаг 6. Вычислите долготу судна, переведя разницу во времени между Mer. Па · с. и GMT.
Пример. Этот пример демонстрирует применение вышеупомянутого метода вычисления широты методом короткого прохождения меридиана.
Задача. Используйте метод короткого прохода по меридиану, чтобы вычислить положение судна в сценарии ниже, следуя шестиэтапной проформе выше.
Сценарий: Дата: 22 июня
Поясное время: 1140 (+4)
Зона: +4
Mer.Па .: 12 02
DR Позиция: 32 0 30’N. 61 0 55’W.
Скорость незначительна (рыболовные суда тянут сети).
Высота секстанта в Мер. Пас .: 80 o 55’.8
Ошибка индекса (I.E.): -0′.2
Ht. глаза: 2,5м.
Время наблюдения за палубой (DWT) на высоте меридиана: 16 ч 08 м 25,1 с
Deck Watch Error (DWE): быстро 5 секунд (-5)
Решение.
| Предварительное планирование. Дата: 22 июня. Поясное время: 1140 (+4). DR Pos: 32 0 30’N. 61 0 55’W |
| Шаг 1. Определите время Мер. Па · с. в Гринвиче. |
| Из ежедневной страницы морского альманаха за 22 июня, г. Mer. Па · с. по Гринвичу = 1202 GMT. |
| Шаг 2. Рассчитайте время Mer.Pas.at D.R. Позиция (DR Долгота = 61 0 55’W.)
Длинный: 61 o 55’W 4 x 61 o ÷ 60 = 4,066 ч = 4 ч 04 м 57,6 с 4 x 55 ’÷ 60 = 3,66 м = 0 ч 03 м 39,6 с = 4 ч 07 м 37,2 с (≈ 37 с )
Mer. Па · с. Гринвич = 12 ч 02 м 00 с (GMT) (со страницы дня) Long (61 o 55’W): = + 04 h 07 m 37 s (Longitude West, GMT Best (+)) Местный Мер. Пас (GMT) = 16 ч 09 м 37 с Зона (+4) = — 04 ч (+4 для GMT, но -4 для поясного времени). Поясное время Мер. Па · с. = 12 ч 09 м 37 с ≈ 1209 (ближайшая минута) |
| Шаг 3. Определить склонение во время местного Mer.Pas. Местный Мер. Па (по Гринвичу): 16 ч 09 м 37 с »16 ч 10 м декабрь вс (16 h ) = N23 o 25 ′.9 (с ежедневной страницы) (d = 0′.0) Коррекция d = 0′0 (из таблицы приращений) декабрь вс (16 ч 10 м GMT): = N23 o 25′.9 ( = N23 o .43) |
| Шаг 4. Вычислите высоту меридиана. Sext. Высота: 80 o 55’.8 I.E.: — 0’.2 Наблюдаемая высота: 80 o 55’.6 Отрыв (2,5 м): — 2’,8 Видимая высота: 80 o 52’,8 Коррекция высоты: + 15’.8 Истинная высота: 81 o 08’.6 (= 81 o .143) | |
| Шаг 5. Определите широту. DR Широта = 32 0 30’N. Склонение = N23 o . 43 (из шага 3) Высота = 81 o .143 (из шага 4) (Широта и дека одного полушария; Широта> Dec = правило 1) Следовательно, LAT = Dec + (90 o — ALT) — (правило 1) = 23 o . 43 + (90 o — 81 o .143) = 23 o . 43 + 8 o , 857 Следовательно, LAT = 32 o .287N = 32 o 17 ’13 ″ .2 N | |
| Шаг 6. Вычислите долготу (по DWT на высоте меридиана). DR Длинный = 61 0 55’W. Mer. Па .: 12 02
Время дежурства на палубе = 16 ч 08 м 25,1 с DWE: = -05 с GMT / UT: = 16 ч 08 м 20.1 с Мер Па: = 12 ч 02 м 00 с Разница во времени: = + 04 h 06 m 20,1 с (Западная долгота = GMT Best) 4 ч = 4 x 15 = 60 o 00 ’00” 06 м = 6 ÷ 4 = 1 o 30 ’00” 20,1 с = 20,1 ÷ 4 = 0 o 05 ’01 ″.5 = 61 o 35 ’01” .5 Следовательно, Long = 61 o 35 ’01 ″ .5 W |
Следовательно, наблюдаемая позиция в поясное время 12 ч 09 м (местный Мер Па)
= 32 o 17’13 ″ .2N. 61 o 35 ’01 ″ .5W.
(для сравнения DR Pos. На 11 h 40 m (поясное время) было 32 0 30’N.61 0 55’W.)
Где купить книги серии Astro Navigation Demystified:
Небесная навигация на Amazon.com
Celestial Navigation на Amazon.uk
Демистификация астронавигации на Amazon.com
Демистификация астронавигации на Amazon.uk
Применение математики в астронавигации на Amazon .com
Применение математики в астронавигации на Amazon .uk
Астрономия для астронавигации на Амазонке.com
Астрономия для астронавигации на Amazon.uk
Интернет: http://www.astronavigationdemystified.com
Нравится:
Нравится Загрузка …
.

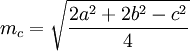
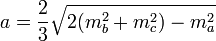 , где ma,mb,mc медианы к соответствующим сторонам треугольника, a,b,c — стороны треугольника.
, где ma,mb,mc медианы к соответствующим сторонам треугольника, a,b,c — стороны треугольника.