7 класс. Геометрия. Начальные геометрические сведения. Прямая, отрезок, луч, угол. — Измерение углов.
Комментарии преподавателяИз материала предыдущих уроков мы знаем, что угол – это два луча, выходящие из этой точки. На рисунке 1 изображен угол∠АОВ или , названный в честь лучей, которые из этой точки выходят.
Рис. 1. Угол АОВ
Любой неразвернутый угол имеет внешнюю и внутреннюю области. К примеру, точка М принадлежит внутренней области ∠АОВ.
На предыдущих уроках мы выяснили, что равными фигурами называются те, которые можно совместить наложением. Мы уже умеем сравнивать отрезки. В данный момент мы будем учиться сравнивать углы.
Мы рассмотрели, что в случае, когда один угол является частью другого угла, данные углы не равны. На рисунке 2 указано это соотношение.
Рис.
2. Измерение углов
Однако насколько угол ∠СОА больше угла ∠ВОС? В этом случае нам необходимо ввести эталонный угол и единицы измерения. Рассмотрим рисунок 3.
Рис. 3. Угол ∠АОВ – развернутый
В геометрии приняли развернутый угол за 180о градусов. Это значит, если поделить развернутый угол на 180 частей, то градусная мера одной части будет равна 1о. Таким образом, больший угол имеет большую градусную меру. Также можно вывести правило суммы градусных мер. К примеру, нам необходимо вычислить градусную меру угла ∠АОВ, а меры углов ∠ВОС и ∠СОА нам известны (см. рис. 2). В таком случае, ∠АОВ = ∠ВОС + ∠СОА. Градусную меру угла можно вычислить, к примеру, транспортиром. На рисунке 4 указаны углы, градусные меры которых равны 150о и 45о.
Рис. 4. Углы с указанными градусными мерами
Немаловажно уяснить, что углы могут измеряться в минутах и секундах.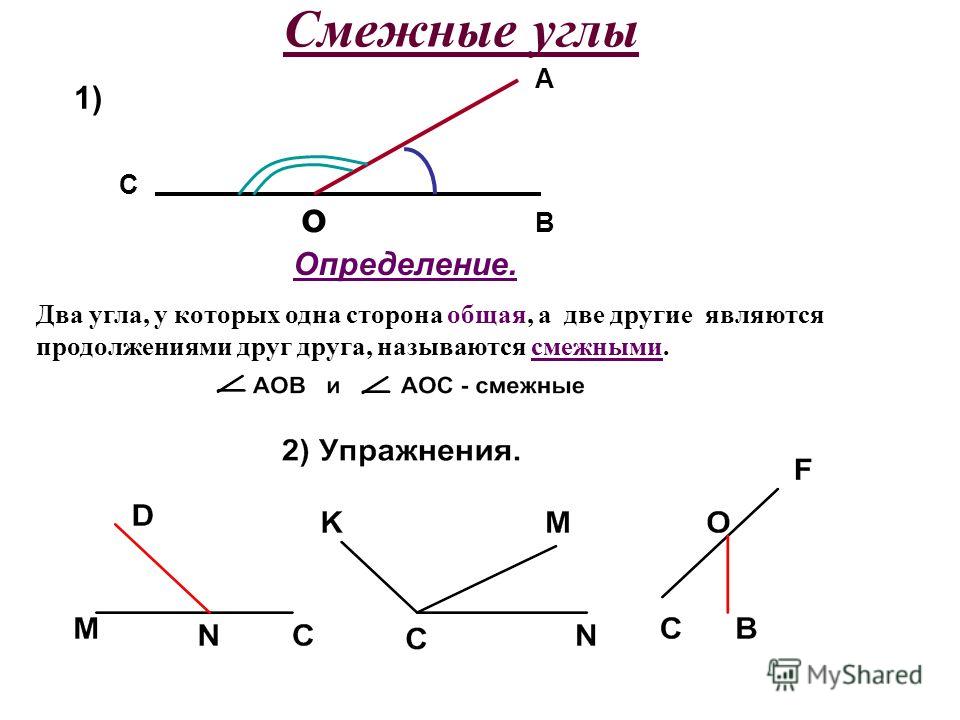
В зависимости от величины градусной меры, различают острые, тупые и прямые углы.
Рис. 5. Острый, прямой и тупой углы
|
Прямой ∠АОВ = 90о |
Острый 0 < ∠АОВ < 90o |
Тупой 90o < ∠АОВ < 180o |
Если градусная мера угла равна 90 градусов, то данный угол – прямой. В случае, если мера угла меньше 900, угол острый, а если больше – тупой.
Рассмотрим несколько задач, чтобы закрепить пройденный материал.
Пример 1:
На рисунке изображен угол ∠АОВ, который делится точкой Е на два угла. Найдите градусную меру данного угла, если ∠АОЕ = 44о, ∠ВОЕ = 77о.
Рассмотрите случай, когда ∠АОЕ = 12о37/, ∠ВОЕ = 108о25/
Решение:
Выполним пояснительный рисунок к задаче:
Рис.
6. Рисунок к примеру 1
По правилу суммы градусных мер углов, ∠АОВ = ∠ВОЕ + ∠ЕОА. Соответственно, подставим данные в условии значения и выполним подсчет.
1. ∠АОВ = ∠ВОЕ + ∠ЕОА = 44о + 77о = 121о.
2. ∠АОВ =∠ВОЕ + ∠ЕОА = 12о37/ + 108о25/ = 121о02/.
Ответ: 121о, 121о02/.
Пример 2:
На рисунке изображен угол ∠АОВ. Градусная мера данного угла составляет 78о. Луч ОС делит данный угол на 2 угла. Найдите градусную меру угла ∠ВОС, если угол ∠СОА на 18о меньше угла ∠ВОС.
Рис. 7. Рисунок к примеру 2
Решение:
Пусть градусная мера угла ∠ВОС равна хо, тогда мера угла ∠СОА равна (х-18)о. Поскольку их сумма будет равна 78о (по условию), составим и решим уравнение:
Х + (х – 18) = 78
2х – 18 = 78
2х = 96
х = 48
Ответ: ∠ВОС = 48о.
Пример 3:
Луч ОВ делит угол ∠АОС, градусная мера которого составляет 108о, на 2 части.
Найдите градусную меру угла ∠ВОА, если угол ∠ВОА в три раза больше угла ∠ВОС.
Рис. 8. Рисунок к примеру 3
Решение:
Решаем эту задачу подобно предыдущей. Пусть градусная мера угла ∠ВОС равна хо, тогда мера угла ∠ВОА равна (3х)о. Поскольку их сумма будет равна 108о (по условию), составим и решим уравнение:
Х + 3х = 108
4х = 108
х = 27
Соответственно, мера угла ∠ВОА равна (3х)о, то есть 81о.
Ответ: 81о.
Пример 4:
На рисунке изображен развернутый угол ∠АОD. Углы ∠ВОА и ∠СОD равны. Укажите, есть ли на рисунке еще равные углы?
Решение:
Выполним рисунок к задаче.
Рис. 9. Рисунок к примеру 4
Рассмотрим углы ∠АОС и ∠ВОD. Они состоят из равных между собой частей ∠ВОА и ∠СОD, а также общей части ∠ВОС.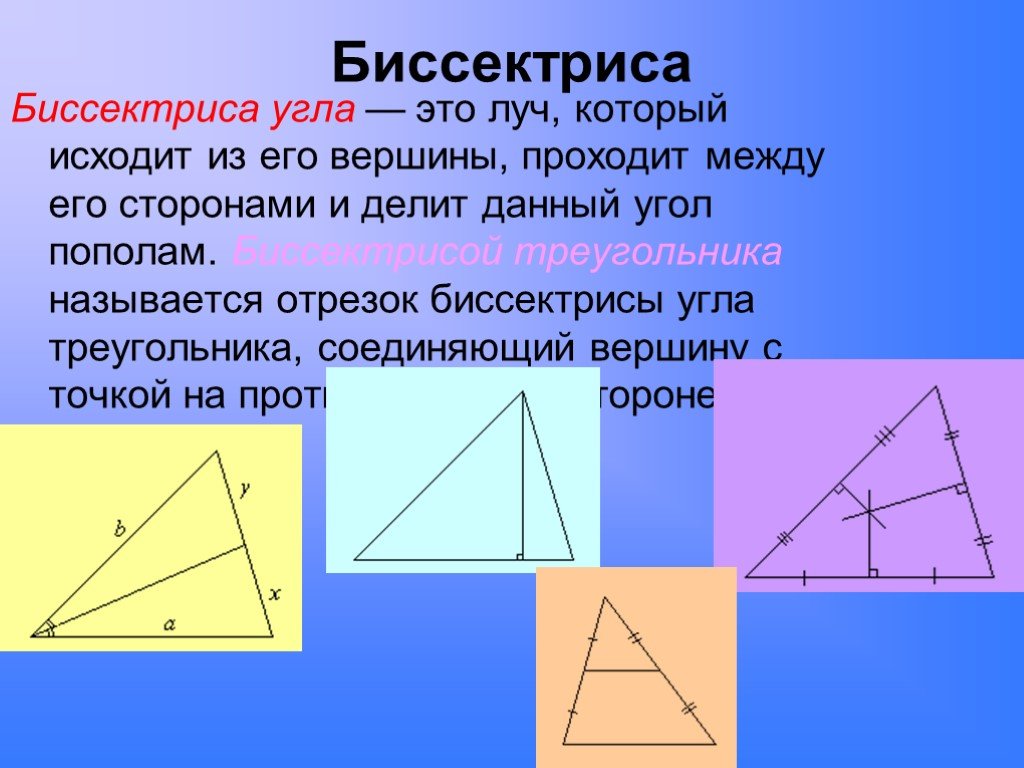
Выполним следующую запись:
Поскольку ∠ВОС – общий, а ∠АОС = ∠ВОD (по условию), то ∠АОС = ∠ВОD.
Ответ: ∠АОС = ∠ВОD.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/7-klass/nachalnye-geometricheskie-svedeniya/izmerenie-uglov
http://www.youtube.com/watch?v=rW2hWNeyco8
http://yuliaandreevna.ucoz.ru/izmerenie_otrezkov.jpg
http://klassnoedelo.ru/upload/iblock/0ff/0ff02026289ce10a139e5c7a81544908.jpg
http://5klass.net/datas/geometrija/Izmerenie-uglov-7-klass/0003-003-Izmerenie-uglov.jpg
http://5klass.net/datas/geometrija/Izmerenie-uglov-7-klass/0010-010-Vidy-uglov.jpg
http://u.5klass.net/zip/b16c483181631583c9663c9b68c8658d.zip
http://www.flconf.org/education/wp-content/uploads/2011/04/5107103-1886×2550-1-1024×757.jpg
http://cs1-26v4.vk-cdn.net/p15/f1c21f09bd9fad.mp3?extra=u96JCzuBb-XdruFah977CJD_izMWWpkY6XMumaQX91DaN6oYjpkhgbiIWHT_JgbeMV8sBTXjR7DNV22iBzUUOuBrsARIHPev
Читать онлайн «Геометрия.
7-9 класс», Александра Ведова – ЛитРес, страница 2Углы
Углы бывают четырех видов:
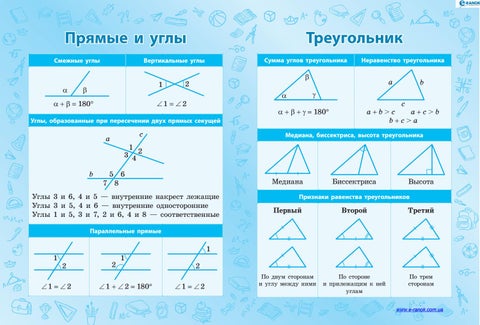
Углы на пересекающихся прямых
Углы, которые находятся напротив друг друга, называются вертикальными. Они равные.
Углы, которые находятся рядом и образуют прямую (или развернутый угол) называются смежными. В сумме они составляют 180 градусов.
Углы на двух параллельных прямых и секущей
Соответственные углы равны.
Внутренние накрест лежащие углы также равны
Внешние накрест лежащие углы также равны
Внутренние односторонние углы в сумме составляют 180 градусов
Внешние односторонние углы в сумме составляют 180 градусов
Градусная мера углов
Углы измеряются в градусах « о», минутах « ’», и секундах « ”»
До 9 класса достаточно знать о градусах. О минутах и секундах рассказывают в 10 классе на уроках Алгебры, в разделе «Тригонометрия».
Измерить градусную меру угла можно транспортиром :
Общие сведения о треугольниках
Общие сведения, которые касаются всех треугольников:
1.
Сумма углов в любом треугольнике равна ста восьмидесяти градусам
2.У любого треугольника есть средняя линия, длина которой равна половине основания.
Средняя линия (K M) – это отрезок, который соединяет середины сторон, т.е. K – середина AB, M – середина BC.
Значит AK=KB, CM=BM
а (основание для средней линии – это сторона, параллельная ей), т.е.
3.Кратчайшее расстояние от точки до прямой – перпендикуляр. Это понимание нужно для решений некоторых задач, где рисуя перпендикуляр то получается либо высота, либо прямоугольный треугольник , либо
4.Площадь треугольника где a – основание (сторона, на которую опущена сторона), – это высота, опущенная на сторону а.
где b – это основание, а
– это высота, опущенная на основание.
Т.е. площадь можно найти, используя половину произведения ЛЮБОЙ стороны и высоты, ОБЯЗАТЕЛЬНО опущенной именно на эту сторону.
5.Высота – это отрезок, концы которого соединяют вершину треугольника и противоположную сторону так, что сторона и отрезок образуют (прямой угол).
6.Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.
7.Биссектриса – это отрезок, исходящий из вершины на противоположную сторону и делящий угол пополам.
Виды и свойства треугольников.
Что такое треугольник, думаю, знают все: еще с начальной школы знаем, что такая фигура имеет три угла, три стороны и три вершины. Разберемся теперь, какие треугольники бывают.
В зависимости от углов:
остроугольные (все углы острые, меньше 90°)
тупоугольные (один из углов тупой, больше 90°)
прямоугольные (один из углов прямой, 90°)
В зависимости от сторон:
произвольный (все стороны и углы разные)
равнобедренный (две стороны равны)
равносторонний (три стороны равны)
В планиметрии рассматривают: прямоугольные, равнобедренные и равносторонние треугольники – они немного особенные и свойств у них много, которые надо знать.
У остроугольного нет особенностей.
У тупоугольного есть одна: три высоты будут пересекаться вне треугольника.
Прямоугольный:
Стороны, прилежащие к углу в 90°, называются катетами
Сторона, лежащая напротив угла в 90°, называется гипотенузой
Свойства:
Два острых угла дают в сумме 90°. (Сумма углов в треугольнике составляет 180°, в прямоугольном – один угол прямой, т.е. 90°, 180°-90°=90°, таким образом на два острых угла приходится только 90°.)
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
Равнобедренный:
Равные стороны называются боковыми, третья- основанием. Боковые стороны равны по определению.
Свойства:
Углы при основании равны.
В р/б треугольнике отрезок, проведенный из вершины к основанию, являющийся высотой (является перпендикуляром, опущена под 90°), также будет и медианой (делит сторону пополам), и биссектрисой (делит угол пополам).
Равносторонний:
Является всегда равнобедренным. Все стороны в равностороннем треугольнике равны.
Свойства:
Все углы равны, по 60°.
Все отрезки, проведенные из вершин к сторонам, являющиеся высотой, одновременно являются медианами и биссектрисами. Т.е. медиана, биссектриса и высота – это один и тот же отрезок.
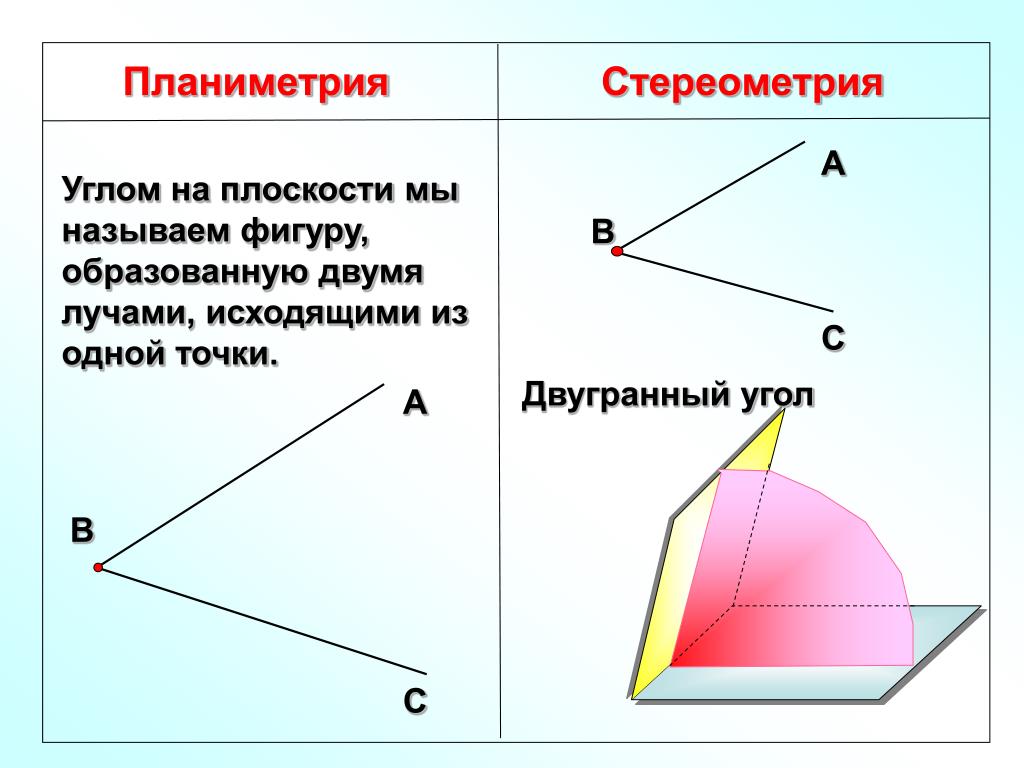
Что такое угол в геометрии
от Veerendra
Что такое угол в геометрии Угол Угол: Угол-это юнио общая начальная точка.
Когда два луча имеют общую начальную точку, образуется угол. Общая начальная точка называется вершиной угла, а два луча, образующие угол, называются плечами или сторонами угла. Угол обозначается символом «∠».
Углы, образованные лучами OA и OB, показаны на рисунке ниже и обозначены ∠BOA или ∠AOB
Для удобства угол ∠BOA или ∠AOB также может обозначаться просто как ∠O. Однако это невозможно сделать, если имеется более одного угла с одной и той же вершиной O. В таких случаях мы можем обозначать углы такими символами, как ∠1, ∠2, ∠3 и т.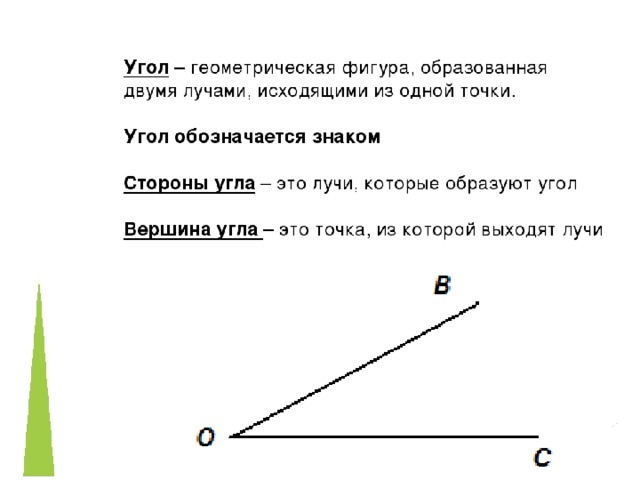
д.
Типы углов
Обозначение угла
Рассмотрим угол, как показано на рис.
Используя символ ∠, мы можем читать или записывать угол тремя способами:
(i) ∠1 (Присвоением номера)
(ii) ∠B (По его вершине)
(iii) ∠ABC или ∠CBA (По двум точкам на каждом луче/плече и вершине посередине)
Именование угол по двум точкам на его плечах и вершине более полезен, особенно когда два или более углов имеют общую вершину.
Образованы три угла, имеющие одну общую вершину B.
Это:
(i) ∠ABC или ∠CBA
(ii) ∠ABD или ∠DBA
(iii) ∠DBC или ∠CBD
Мы уже говорили, что любая фигура на плоскости делит плоскость на три части. Точно так же, когда мы рисуем угол на плоскости, он делит треугольник на три части.
Внутренняя часть угла: Внутренняя часть угла BAC представляет собой множество всех точек его плоскости, которые лежат по ту же сторону от AB, что и C, а также по ту же сторону от AC, что и B.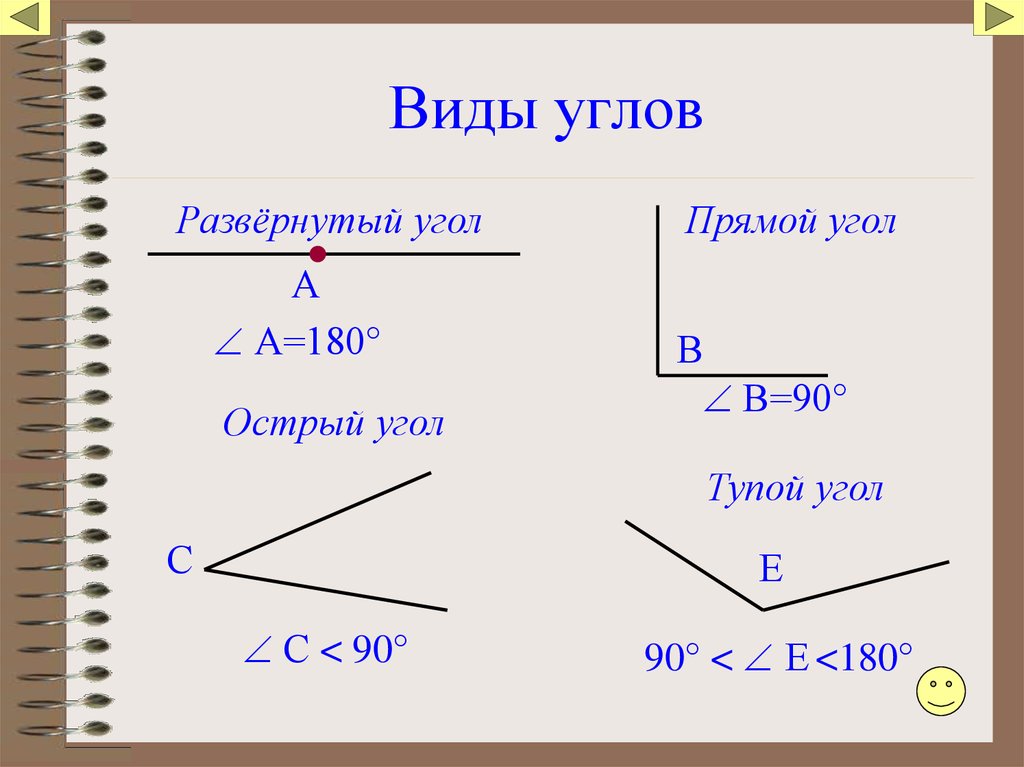
Внешность угла: Внешность угла BAC — это множество всех точек его плоскости, которые не лежат ни на угле, ни в его внутренней части.
Конгруэнтные углы: Два угла называются конгруэнтными, если копия одного из них может быть наложена на другой, чтобы покрыть его полностью и точно.
Если ∠BAC конгруэнтно ∠FEG, то мы пишем ∠BAC ≅ ∠FEG.
Смежные углы
Два угла на плоскости называются смежными, если они имеют
(i) общую вершину,
(ii) общее плечо и
(iii) два других необщих плеча на противоположных сторонах общего рукава.
На рисунке углы ∠AOB и ∠BOC смежные, так как имеют общую вершину O и общее плечо OB. Другие плечи OC и OA находятся по разные стороны от общего плеча OB. Теперь рассмотрим следующее:
Линейная пара: Если сумма ∠AOB и ∠BOC равна 180°, то мы говорим, что эти два смежных угла образуют линейную пару.
youtube.com/embed/DGKwdHMiqCg?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Величина угла Величина или величина угла зависит от раскрытия между его плечами. Это не зависит от длины рук. Два угла с разными отверстиями имеют разные величины.
Возьмем луч OA. Вращайте его по часовой стрелке вокруг вершины O и дойдите до точки B. Таким образом, OA становится начальным положением, а OB — конечным положением. В этом случае формируется ∠AOB. Вращение может быть как по часовой стрелке, так и против часовой стрелки.
Полный оборот делится на 360 равных частей, каждая из которых равна одному градусу. Таким образом, один полный оборот составляет 360°. Углы измеряются в градусах, обозначаемых °. Этот символ вставляется справа вверху от цифры, обозначающей открытие угла.
Пример: 30 градусов можно записать как 30°.
В рубрике: Математика С тегами: Смежные углы, Угол, Градусная мера угла, Внешний и внутренний угол, Величина угла
Классифицирующие углы в геометрии
Master 7 столбов школы успеха
Улучшение своих классов и снижение стресса
Прилегающие углы Поделитесь общей стороной и общей вершиной
. ABD и углы CBD являются смежными углами
Вертикальные углы – это углы, противоположные друг другу и имеющие общую вершину. Вертикальные углы равны.
Последовательные углы , также называемые Внутренние углы одной стороны , это внутренние углы, лежащие на одной стороне поперечной. Если пересекаемые прямые параллельны, а углы представляют собой линейную пару, то эти углы являются дополнительными.
Альтернативные внутренние углы находятся внутри пересекаемых линий и на противоположных сторонах поперечной.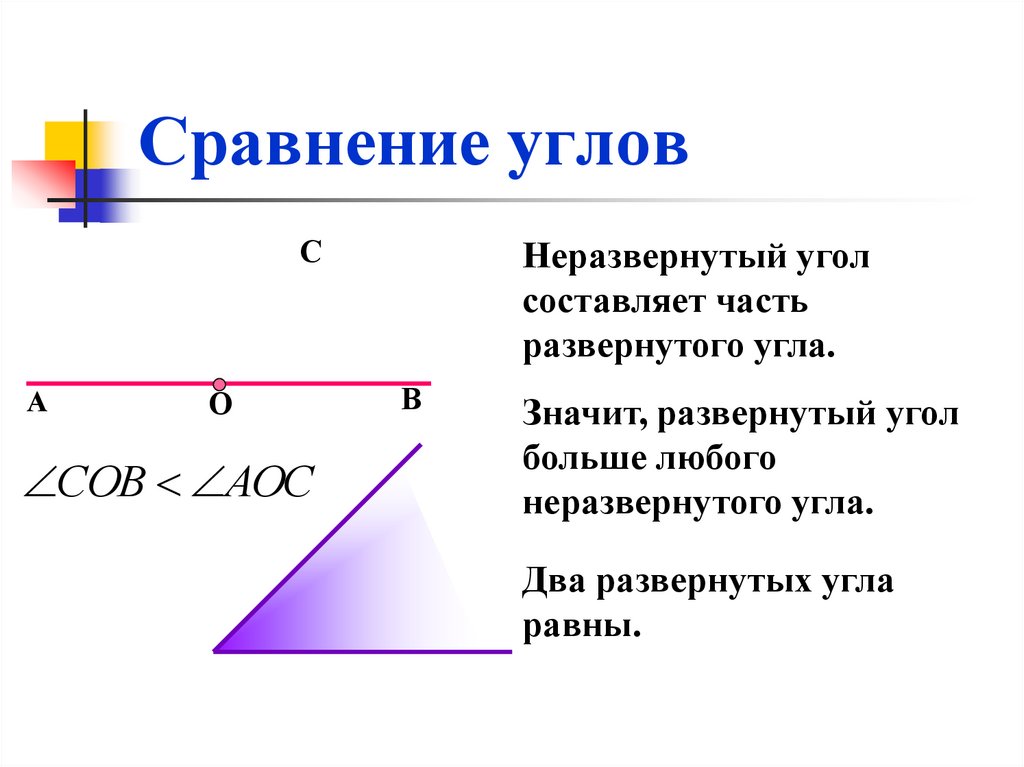
Эти углы равны.
Альтернативные внешние углы находятся вне пересекаемых линий и на противоположных сторонах поперечной. Эти углы равны.
Common Core Standard 7.G.4 Математика 7-го класса
Пары углов
∠A или ∠ABC
5 90 называется вершиной. Луч — это линия, имеющая начальную точку, но не имеющая конечной точки. Углы могут быть названы этой вершиной. Символ угла ∠ используется для математического обозначения угла. Обычный метод именования углов — использование трех точек. Две точки для лучей и одна для вершины.
Углы именования
Связанные участки …
Классификация углов/математическая планета
9018
Классифицирующие угловые игры
Основные классификации углов: острый угол, тупой угол, прямой угол, рефлекторный и прямой угол. 
Он думает об этом как о прямой линии. Тогда у вас есть угол, размер которого меньше 90 градусов, и это острый угол 90 250 90 251 . Тогда у вас есть угол , который больше 90, но меньше, чем прямой, и является тупо-острым. Итак, давайте обозначим их. Это первый номер 90 и это ваш опорный угол . Вы всегда должны быть знакомы с вашим углом 90 градусов , чтобы увидеть, есть ли у вас тот, который меньше. Значит, это острый угол. Этот больше, чем 90 градусов, и вы можете сделать набросок в L, если хотите, чтобы сравнить его. Тот больше, поэтому он тупой. А прямая это 180 градусов. Это два угла 90 градусов вместе взятые. Итак, это ваш прямой угол. Таким образом, вы всегда сравниваете с вашим углом 90 градусов или вашим прямым углом. Вот как классифицируются углы. Итак, давайте посмотрим на правила углов. Хорошо, острый угол — это угол, который меньше 90 градусов. Прямой угол равен 90 градусов. Ваш прямой угол является вашим исходным углом. Тогда у вас есть тупой угол, который больше 90 и прямой угол, равный 180 градусам.