Десятичные логарифмы и их свойства
ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ
ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»
Учитель Математики Высшей категории
Десятичные логарифмы и их свойства
За основание логарифмов часто принимают число 10. Логарифмы чисел по основанию 10 называются десятичными. Для обозначения десятичных логарифмов обычно используют знак lg, а не log; при этом число 10, указывающее основание, не пишут. Например, вместо log10105 пишут просто: lg 105; вместо log102 пишут lg 2 и т. д.
Десятичным лосарифмам присущи все те свойства, которыми обладают логарифмы при основании, большем 1. Например, десятичные логарифмы определены только для положительных чисел. Десятичные логарифмы чисел, больших 1, положительны, а чисел, меньших 1, отрицательны; из двух положительных чисел большему соответствует и больший десятичный логарифм и т. д. Но, кроме того, десятичные логарифмы обладают и рядом специфических свойств, которыми и объясняется, почему в качестве основания логарифмов удобно выбирать именно число 10.
Прежде чем рассмотреть эти свойства, введем следующее определение.
Целая часть десятичного логарифма числа а называется характеристикой, а дробная — мантиссой этого логарифма.
Характеристика десятичного логарифма числа а обозначается как [lg а], а мантисса как {lg а}.
Известно, например, что lg 2 ≈ 0,3010. Поэтому
[lg 2] = 0, {lg 2} ≈ 0,3010.
Известно* также, что lg 543,1 ≈ 2,7349. Следовательно,
[lg 543,1] = 2, {lg 543,1}≈ 0,7349.
* В дальнейшем мы научимся находить десятичные логарифмы положительных чисел по таблицам.
Точно так же из равенства lg 0,005 ≈ — 2,3010 заключаем, что
[lg 0,005] = — 3, {lg 0,005} = 0,6990.
Теперь перейдем к рассмотрению свойств десятичных логарифмов.
Свойство 1. Десятичный логарифм целого положительного числа, изображенного единицей с последующими нулями, есть целое положительное число, равное количеству нулей в записи данного числа.
Например, lg 1000 = 3,
lg 1 000000 = 6.
Вообще, если
то а = 10n и потому
lg a = lg 10n = n lg 10 = п.
Свойство 2. Десятичный логарифм положительной десятичной дроби, изображенной единицей с предшествующими нулями, равен — п, где п — число нулей в записи этого числа, считая и нуль целых.
Например, lg 0,01 = — 2,
lg 0,00001 = — 5.
Вообще, если
,
то a = 10—n и потому
lg a = lg 10—n = —n lg 10 = —п
Свойство 3. Характеристика десятичного логарифма положительного числа, большего 1, равна количеству цифр в целой части этого числа без одной.
Примеры. 1) Характеристика логарифма lg 75,631 равна 1.
Действительно, 10 < 75,631 < 100.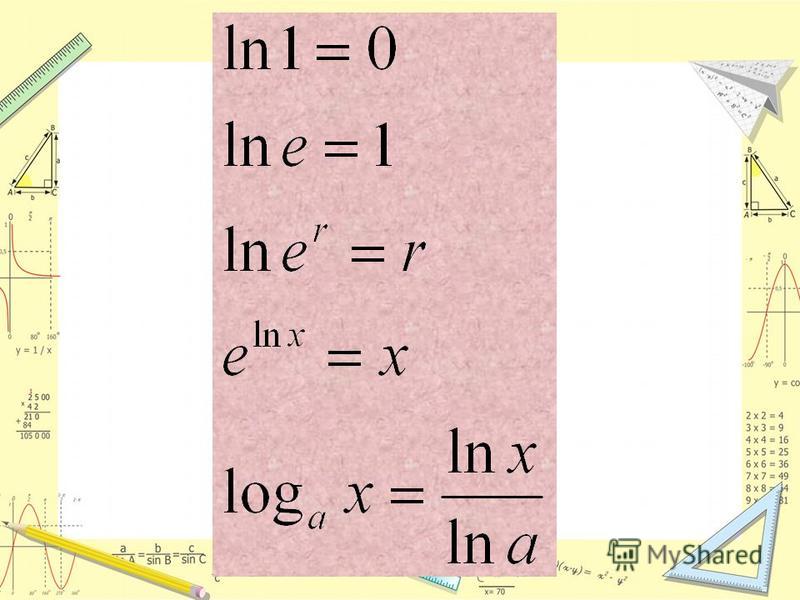
Поэтому
lg 10 < lg 75,631 < lg 100,
или
1 < lg 75,631 < 2.
Значит,
lg 75,631 = 1 + α,
где α — некоторая правильная положительная дробь. Но тогда
[lg 75,631] = 1,
что и требовалось доказать.
2) Характеристика логарифма lg 5673,1 равна 3. Действительно,
1000 < 5673,1 < 10 000. Поэтому
lg 1000 < lg 5673,1 < lg 10 000,
или
3 < lg 5673,l < 4.
Следовательно,
[lg 5673,1] = 3.
Вообще, если целая часть положительного числа а, большего единицы, содержит пцифр, то
10n —1 < а < 10n.
Поэтому
lg 10n —1 < lg а < lg 10n.,
или
n — 1 < lg a < n.
cледовательно,
[lg a] = n — 1.
Свойство 4. Характеристика десятичного логарифма положительной десятичной дроби, меньшей 1, равна — п, где п — число нулей в данной десятичной дроби перед первой значащей цифрой, считая и нуль целых.
Примеры. 1) Характеристика логарифма lg 0,0015 равна — 3.
Действительно,
0,001 < 0,0015 < 0,01.
Поэтому
lg 0,001 < lg 0,0015 < lg 0,01,
или
— 3 < lg 0,0015 < — 2.
Значит, lg 0,0015 = — 3 + α, где α — некоторая правильная положительная дробь. Но в таком случае
[lg 0,0015] = — 3.
2) Характеристика логарифма lg 0,6 равна — 1. Действительно.
0,1< 0,6 < 1.
Поэтому
lg 0,1 < lg 0,6< lg 1,
или
— 1 < lg 0,6 < 0.
Следовательно,
lg 0,6 = —1+ α,
где α — некоторая правильная положительная дробь.
Но в таком случае
[lg0,6] = —1.
Вообще, если первой значащей цифре правильной десятичной дроби α предшествуетп нулей (считая в том числе и нуль целых), то
или
— n < lg a < — (n — 1).
Следовательно,
[lg a ] = — n.
Свойство 5. При умножении числа на 10n десятичный логарифм его увеличивается на п.
Действительно, по теореме о логарифме произведения
lg (а • 10n) = lg a + lg 10n = lg a + п.
Например,
lg (579,13 • 100) = lg 579,13 + 2;
lg (16 • 1000) = lg 16 + 3.
Перенос запятой в положительной десятичной дроби на п знаков вправо равносилен умножению этой дроби на 10n. Поэтому при переносе запятой в положительной десятичной дроби на п знаков вправо десятичный логарифм увеличивается на п.
Свойство 6. При делении числа на 10n десятичный логарифм уменьшается на п.
Например,
lg 1,57/1000 = lg 1,57—3;
lg 0,63/100 = lg 0,63 — 2.
При переносе запятой в положительной десятичной дроби на п знаков влево десятичный логарифм уменьшается на п.
Например, lg 0,3567 = lg 35,67 — 2;
lg 0,00054 = lg 0,54 — 3.
Учащимся предлагается самостоятельно доказать эти утверждения.
Все доказанные до сих пор свойства десятичных логарифмов относились к их характеристике. Теперь обратимся к мантиссе десятичных логарифмов.
Свойство 7. Мантисса десятинного логарифма положительного числа не изменяется при умножении этого числа на 10n с любым целым показателем п.
Действительно, при любом целом п (как положительном, так и отрицательном)
lg (а • 10n) = lg a + lg 10n = lg a + п.
Но дробная часть числа не изменяется при прибавлении к нему целого числа.
Перенос запятой в десятичной дроби вправо или влево равносилен умножению этой дроби на степень числа 10 с целым показателем п (положительным или отрицательным). Поэтому при переносе запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не изменяется.
Например, {lg 0,0067} = {lg 0,67} = {lg 0,0000067}.
Упражнения
1. (У с т н о.) Найти десятичные логарифмы чисел:
1; 10; 100; 1000; 10 000;
0,1; 0,01; 0,001; 0,0001; 0,00001.
2. (У с т н о.) Найти характеристики десятичных логарифмов чисел:
2,00; 57,38; 632,70; 3402,99;
0,17; 0,99; 0,023; 0,0100; 0,0003.
3. Известно, что lg 2 ≈ 0,3010, lg 3 ≈ 0,4771.
Найдите характеристики и мантиссы следующих логарифмов:
a) lg 6; б) lg 15; в) lg 32; г) lg 30; д) 1/12.
свойства, формулы, основание, виды для школьников и студентов
Для любых a>0, a≠1 и b>0, x>0, y>0 выполняются следующие свойства логарифмов.
Именно это свойство логарифмов позволяет вычислять точные значения в отличае от других методов вычисления.
Неточность других методов вычисления основывается на неверной корреляции остаточного члена логарифмического равенства.
Наряду с этим каждое из свойств является индивидуальным, равно как каждый из его членов. Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.
Основное логарифмическое тождество
Основание a, возведенное в степень логарифма с основанием a, будет равно b.
alogab=b
Логарифм единицы
Логарифмический ноль. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.
Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли.
Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.
loga1=0
Логарифм числа, равного основанию
Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
logaa=1
Логарифм числа, обратного основанию
Если аргумент логарифма имеет значение обратное основанию, то значение логарифма будет равно -1.
loga1a=-1
Логарифм произведения двух положительных чисел
Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.
logax·y=logax+logay
Логарифм частного
Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.
logaxy=logax-logay
loga1y=-logay
Логарифм степени положительного числа
Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.
logaxn=nlogax
Логарифм корня числа
Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.
logaxn=logaxn
Основание логарифма в степени
loganx=logaxn, при n≠0
logax=logacxc
Формула перехода к новому основанию
logax=logbxlogba
logax=1logxa
Производная логарифма
Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.
При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов.
Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.
logax′=1xlna
Свойства логарифмов
Свойства логарифмов
|
Содержание: Эта страница соответствует § 4.3 (стр. 341) текста.
Предлагаемые проблемы из текста:
р. 345 #3, 7, 9, 11, 13, 25, 27, 33, 35, 45, 49, 53, 91
Смена базы
Свойства логарифмов
Смена базы
В то время как большинство научных калькуляторов имеют кнопки только для десятичного и натурального логарифмов, другие
логарифмы могут быть вычислены с помощью следующей формулы замены основания.
Сменная базовая формула
Пример 1 .
Оценить журнал 5 3. Формула изменения базы позволяет нам оценить это выражение, используя любой другой логарифм, поэтому мы решим эту задачу двумя способами, используя сначала натуральный логарифм, затем десятичный логарифм.
Натуральный логарифм:
десятичный логарифм:
Упражнение 1 :
Из логарифмического тождества 1 следует, что log 2 8 = 3.
(a) Используйте калькулятор и формулу изменения основания с натуральным логарифмом, чтобы проверить, что log 2 8 = 3,
(b) Используйте калькулятор и формулу изменения основания с десятичным логарифмом, чтобы убедиться, что log 2 8 = 3,
Ответить
Упражнение 2 :
Из логарифмического тождества 2 следует, что .
Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень.
Ответить
Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень.Вернуться к содержанию
Свойства логарифмов
| 1. журнал a (ув) = log a u + log a v | 1. ln (ув) = ln u + ln v |
| 2. log a (u/v) = log a u — log a v | 2. ln (u/v) = ln u — ln v |
| 3. лог a u n = n лог a u | 3. лн у н = н пер у |
Свойства слева справедливы для любого основания a.
Свойства справа являются переформулировкой общих свойств натурального логарифма.
Многие логарифмические выражения могут быть переписаны в расширенном или сокращенном виде с использованием трех указанных выше свойств.
Расширение — это разбиение сложного выражения на более простые компоненты.
Конденсация — это обратная сторона этого
процесс.
Пример 2 .
Расширение выражения.
переписать с использованием экспоненциальной записи недвижимость 3 собственность 1
Пример 3 .
Расширение выражения.
свойство 2 собственность 1 свойство 3
Пример 4 .
Сжатие выражения.
недвижимость 3 собственность 1 собственность 2
Распространенные ошибки
- Логарифмы разбивают произведения на суммы по свойству 1, но логарифм суммы нельзя переписать . За
Например, мы ничего не можем сделать с выражением ln(x 2 + 1).
- log u — log v равен log(u/v) по свойству 2, не равен log u/log v.
За
Например, мы ничего не можем сделать с выражением ln(x 2 + 1).Упражнение 3 :
(a) Разверните выражение . Ответ
(b) Сократите выражение 3 log x + 2 log y — (1/2) log z. Ответ
Вернуться к содержанию
|
Log-Base-10 — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Алгебра II Помощь » Математические отношения и основные графики » Логарифмы » Понимание логарифмов » Лог-база-10
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение: Чтобы исключить логарифм, основанный на десяти, нам нужно возвести обе части в степени, используя основание десяти.
Уравнение принимает следующий вид:
Десять и логарифмическая десятка отменяются, оставляя только степень в левой части. Превратите отрицательный показатель в дробь в правой части.
Разделить на два с обеих сторон, что аналогично умножению на половину с обеих сторон.
Упростите обе стороны.
Ответ:
Сообщить об ошибке
Каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, нам нужно будет переписать базу как , так как журнал по умолчанию имеет базу 10.
Перепишите выражение.
По логарифмическим правилам показатель степени можно опустить как коэффициент.
Ответ:
Сообщить об ошибке
Упростить Объяснение:
Одним из свойств журналов является возможность исключать термины на основе базы журнала.
Поскольку основание бревна равно 10, мы можем упростить 100 до 10 в квадрате.
Логарифмическая база 10 и 10 сокращаются, и в качестве ответа остается значение показателя степени, 2.
Сообщить об ошибке
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение:
По умолчанию логарифмический термин имеет основание 10. 1000 нужно будет переписать как основание 10.
Поднимите коэффициент логарифмического члена как степень.
В соответствии со свойством журнала:
Журнал на основе 10 и 10 внутри количества журнала будут отменены, останется только питание.
Ответ:
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
В журнале по умолчанию используется десятичная система счисления.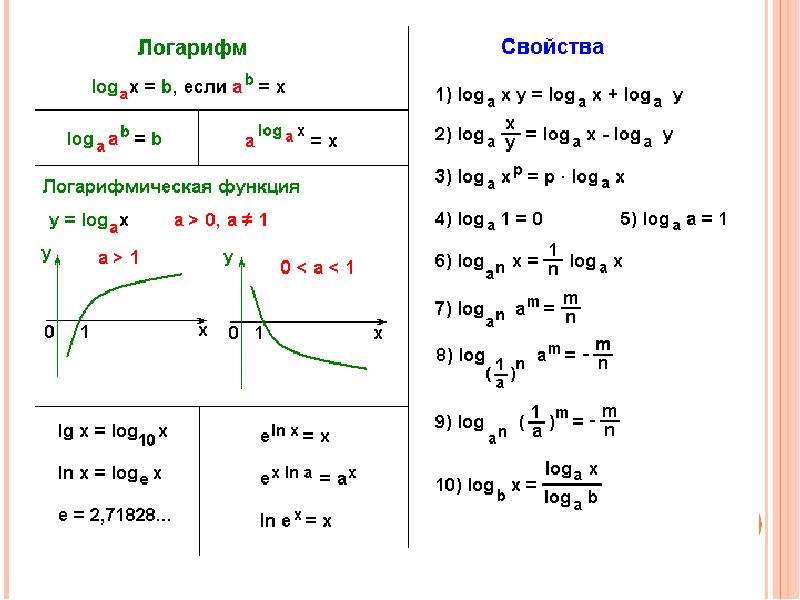
Это означает, что мы должны преобразовать 1000 в обычное основание 10.
Замените это значение внутри термина журнала.
Поскольку логарифмическая база 10 и десятка в определенной степени существуют, они оба аннулируются, оставляя только саму степень.
Ответ:
Отчет о ошибке
Решение:
Возможные ответы:
Правильный ответ:
8889. Объяснение:
Измените основание внутреннего члена или журнала на десятичное.
В соответствии со свойством журнала:
Журнал, основанный на десяти и десятках в степени, отменит, оставив только мощность.
Ответ:
Сообщить об ошибке
Оценка:
Возможные ответы:
Правильный ответ: 3
5
Перепишите журнал так, чтобы он был в самой простой форме.
Это можно разбить на добавление логов.
Ответ:
Отчет о ошибке
Решение уравнения:
Возможные ответы:
Правильный ответ:
. Правильный ответ:
89 . Объяснение:
Когда внутренние члены журнала разделены, мы можем просто переписать отдельные журналы, используя вычитание.
Обратите внимание, что журнал имеет основание по умолчанию десять, и мы можем переписать 1000 как десять в степени три.
Используйте это свойство, чтобы упростить второй член.
Ответ:
Сообщить об ошибке Объяснение:
Журнал по умолчанию имеет основание 10. Чтобы упростить этот журнал, нам нужно изменить основание 100 на основание 10.