Круг. Окружность. — Математика — Уроки
Круг. Окружность.
Задачи урока: расширить представление детей о круге и окружности, познакомить с понятиями: центр окружности, центр круга, радиус окружности, радиус круга.
l. Организационный момент.
2. Актуализация опорных знаний, умений и навыков
1.Задания для развития памяти и внимания.
Учитель показывает слайд 3 в течение нескольких секунд, затем закрывает и задает вопросы.
-Ребята, что вы увидели? Сколько штук? Какого цвета? (Круги, 3 штуки, красный, оранжевый, алый)
Учитель показывает рисунок в течение нескольких секунд, затем закрывает и задает вопросы.
– Из скольких кругов нарисован медвежонок?
2. Задание для развития логического мышления.
– Какой должен быть четвертый рисунок?(большой черный круг, 6 маленьких оранжевых кругов)
– Из какой фигуры нарисованы рисунки? (из кругов)
– Где вы встречались с кругом (колесо, руль и др.
)
– Тема нашего урока: “Круг и окружность”.
Знакомство с новым материалом
В Древней Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса!
Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500-3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму.
Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность.
Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания. Самым важным среди круглых тел был шар.
— А теперь давайте поближе познакомимся с окружностью и кругом.
Объяснение учителя.
Дан рисунок.
– Как вы думаете, который из этих рисунков круг, а который окружность?
Слушается ответ учеников. Затем учитель, демонстрируя, на альбомном листе маркером дает определение окружности.
Часть плоскости, находящаяся не внутри окружности вместе с этой окружностью, называется кругом.
У круга есть одна подруга
Известна всем ее наружность.
Она идет по краю круга
И называется….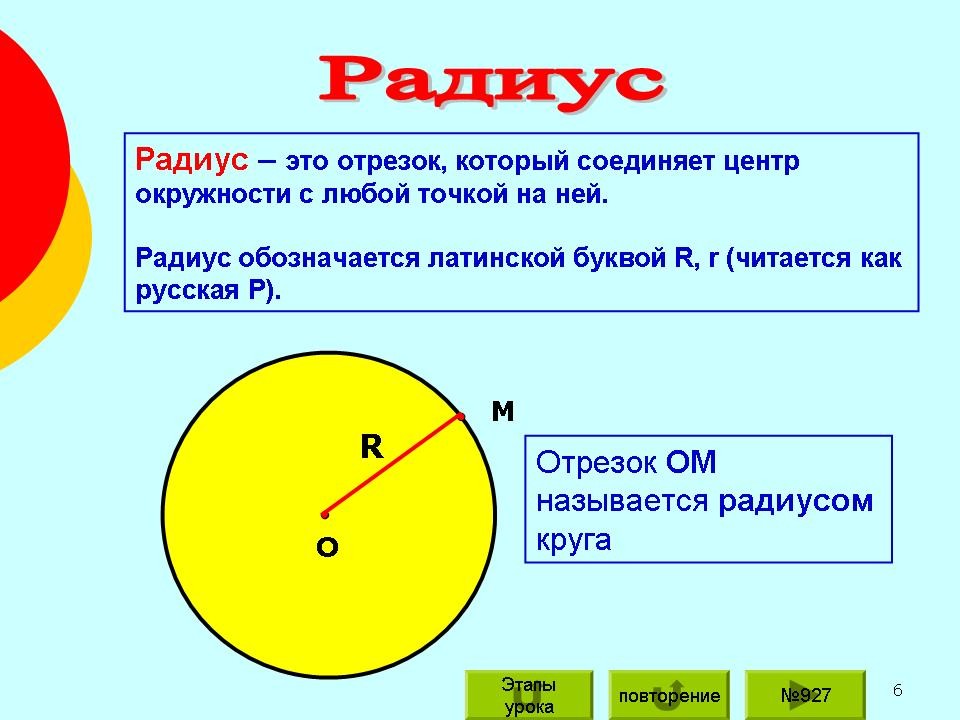
Окружность.
— А теперь смотрите, если я сверну круг пополам, то сгиб образует линию, которая разделяет круг на две равные части. Эта линия будет диаметром круга. Диаметр делит круг пополам. Если согнуть круг еще раз пополам, то получатся четыре равные части.
– Ребята, обратите внимание на линии сгиба, они пересеклись в одной точке, эта точка называется центром круга, а линии сгибов – диаметры, они пересекаются и точкой пересечения делятся пополам. Линия, соединяющая центр с краем круга называется радиусом. Обратите внимание, что длины диаметров равны. А что вы можете сказать о длинах радиусов? (Они тоже равны)
– Как начертить окружность определенного размера? (Ответы детей)
– Для этого существует инструмент, который называется циркуль.
(Показать инструмент)
– Ребята обратите внимание, как пишется слово “циркуль”.
Циркуль мой, циркач лихой,
Чертит круг одной ногой,
А другой проткнул бумагу,
Уцепился и – ни шагу.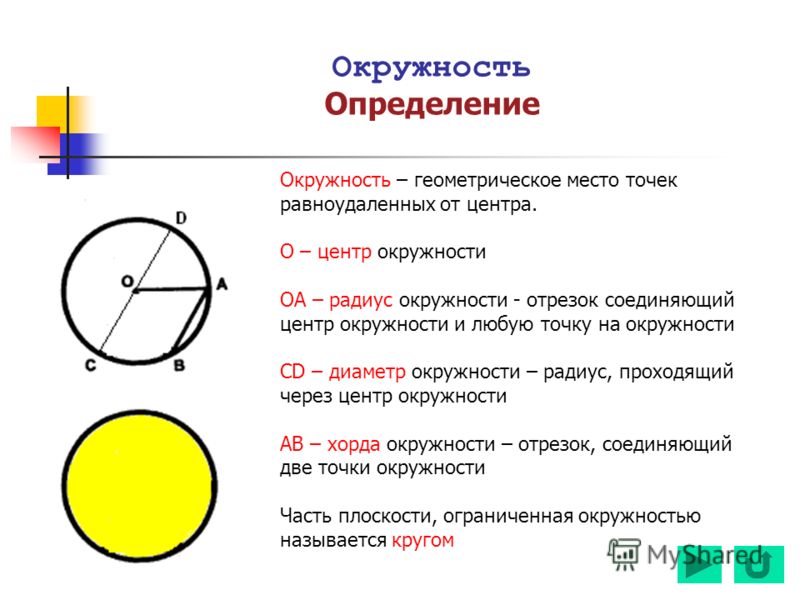
– У циркуля две ножки. На конце одной ножки игла, на конце другой грифель. Ножки циркуля двигаются. (Показываю на доске построение окружности). Для того чтобы начертить окружность надо отметить центр окружности, поставить в центр окружности ножку циркуля с иглой, взять циркуль за хвостик и провести окружность. Острый конец циркуля всегда должен оставаться в одной точке, а расстояние между ножками не должно меняться.
Прежде чем приступить к работе, я хочу обратить ваше внимание на правила безопасной работы циркулем. Ученики читают правила, а учитель выполняет демонстрации.
Правила безопасной работы циркулем.
1.Не держи циркуль концами вверх.
2. Не оставляй циркуль раскрытым.
3. Передавай циркуль закрытым, тупым концом вперед.
4. Работай аккуратно! Будь внимателен!
– Ребята, попробуйте начертить окружность в тетради.
(Я выполняю на доске).
– Сначала отметьте центр окружности. Обычно центр окружности обозначают буквой О.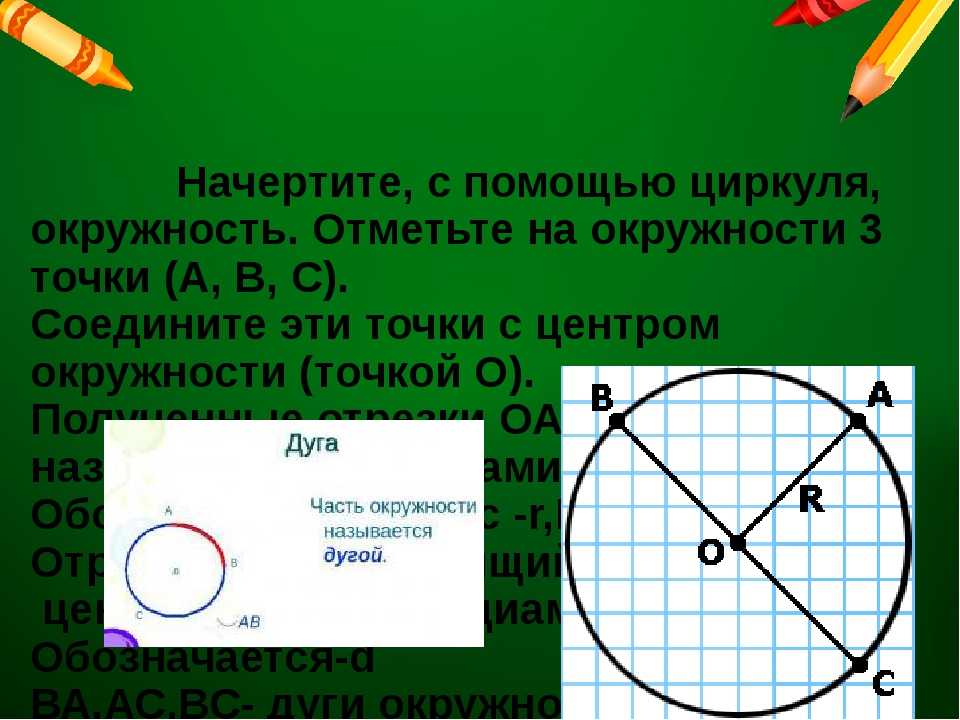
Теперь разведите циркуль на некоторое расстояние и начертите окружность. Вспомните, когда мы складывали круг из бумаги пополам, то говорили что линия сгиба это диаметр, он проходит через центр окружности. Давайте построим диаметр окружности. Теперь соединим центр окружности с любой ее точкой. Этот отрезок называется радиусом. Обратите внимание, что точка О делит диаметр на две части и каждая часть является радиусом окружности. Что можно сказать об отношении радиуса и диаметра? (Ответы детей).
– Диаметр состоит их двух радиусов.
Это отношение можно записать следующим образом.
d = 2r, где диаметр обозначается буквой d, радиус буквой r.
Из этого отношения также следует, что r = d : 2
Как вы думаете, сколько можно провести диаметров, радиусов? (Ответы детей).
– Теперь давайте подведем итоги проведенных опытов.
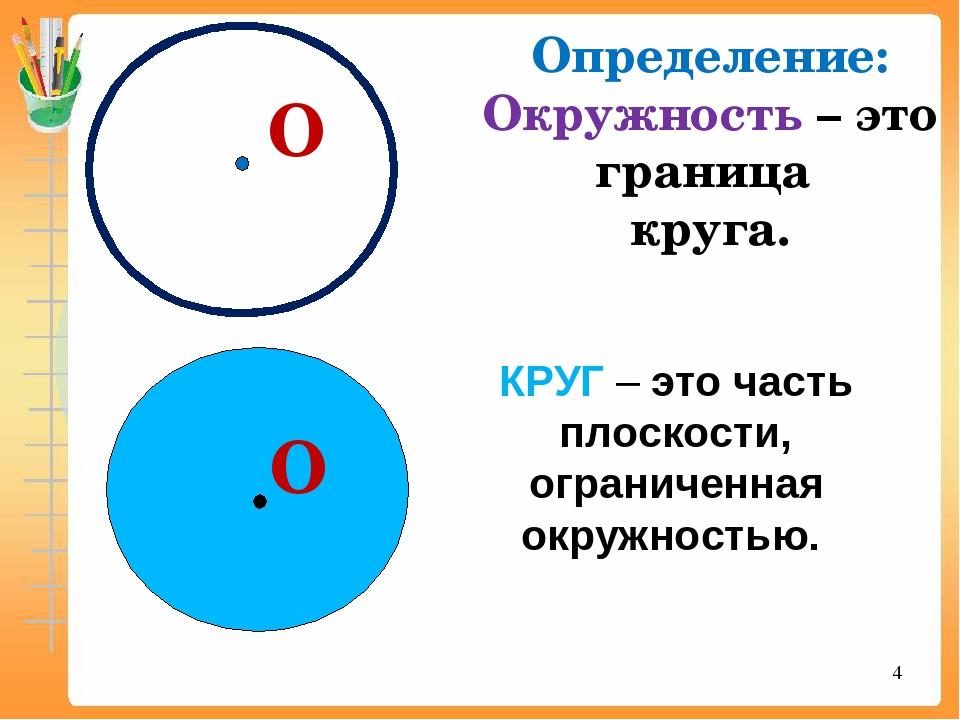
Окружность – замкнутая линия, все точки которой находятся на одинаковом расстоянии от данной точки.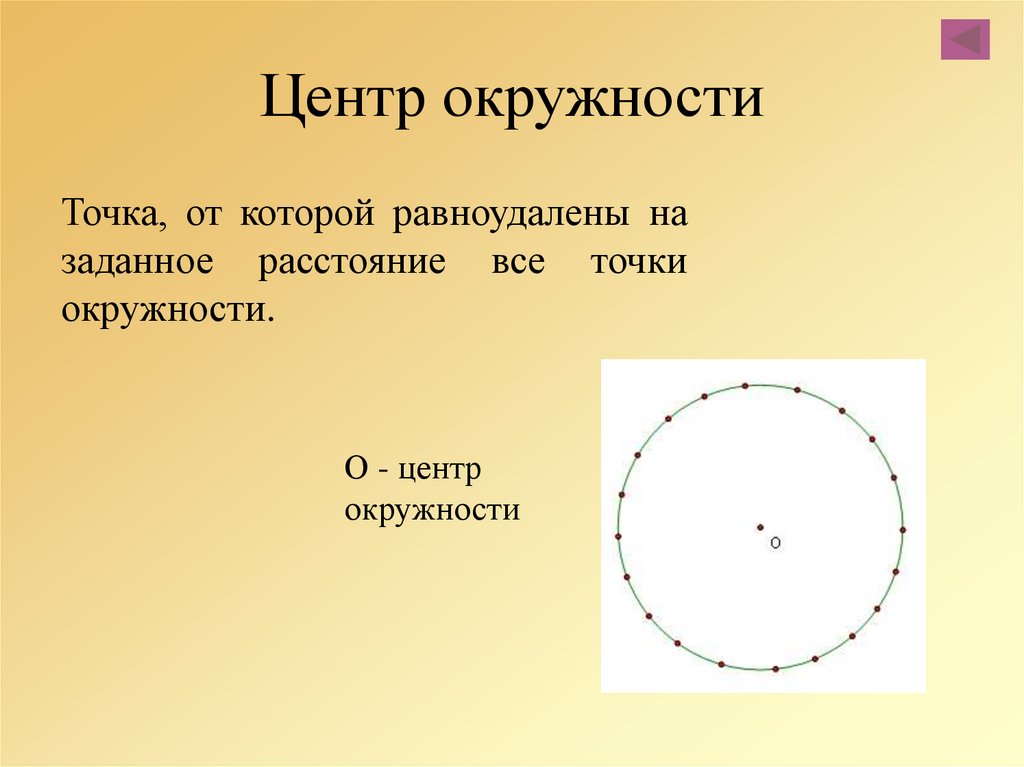
Эта точка называется центром окружности.
Круг – это часть плоскости, которая лежит внутри окружности (вместе с самой окружностью).
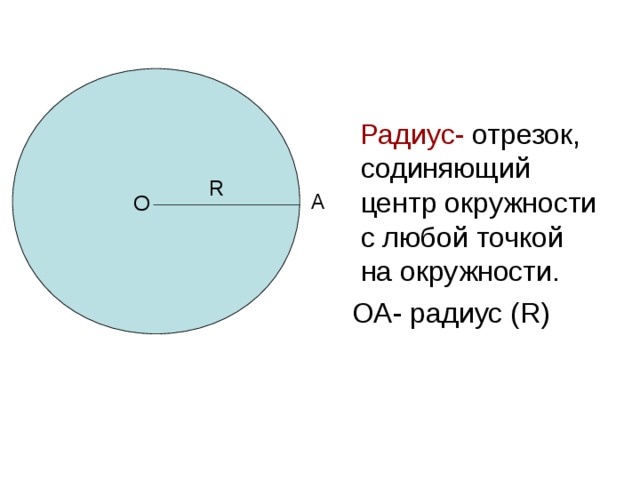
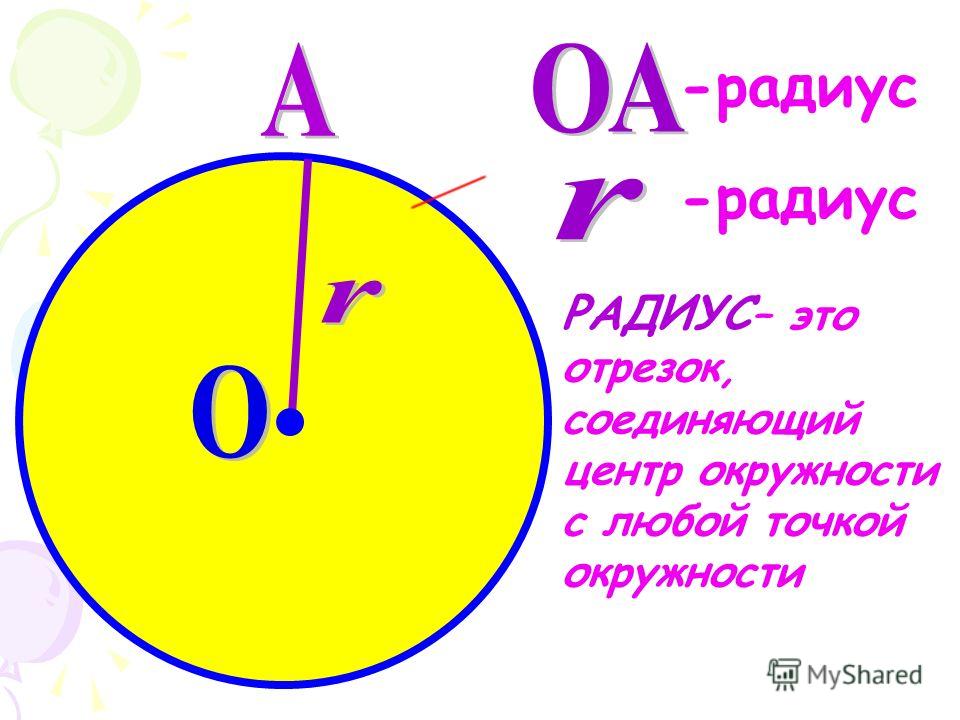
Радиус – отрезок, соединяющий центр окружности с точкой на окружности. Все радиусы окружности равны друг другу.
Диаметр – отрезок, соединяющий две точки окружности и проходящий через центр окружности. Все диаметры окружности равны друг другу.
“Радиус” (в переводе с латинского – луч) впервые встречается в “геометрии” французского ученого Рамуса, изданной в 1569 г, затем у Ф.Виета; термин “радиус” становится общепринятым лишь в конце XVII века.
Первичное закрепление
Задание 1: начертить окружность, радиус которой 2 см. Отметьте диаметр и радиус окружности. Найдите длину диаметра.
– Чтобы выполнить это задание понадобится линейка и циркуль.
– Ребята, как вы думаете, для чего нужна линейка? (Ответы детей).
– По линейке отмеряем 2 см. Это радиус окружности.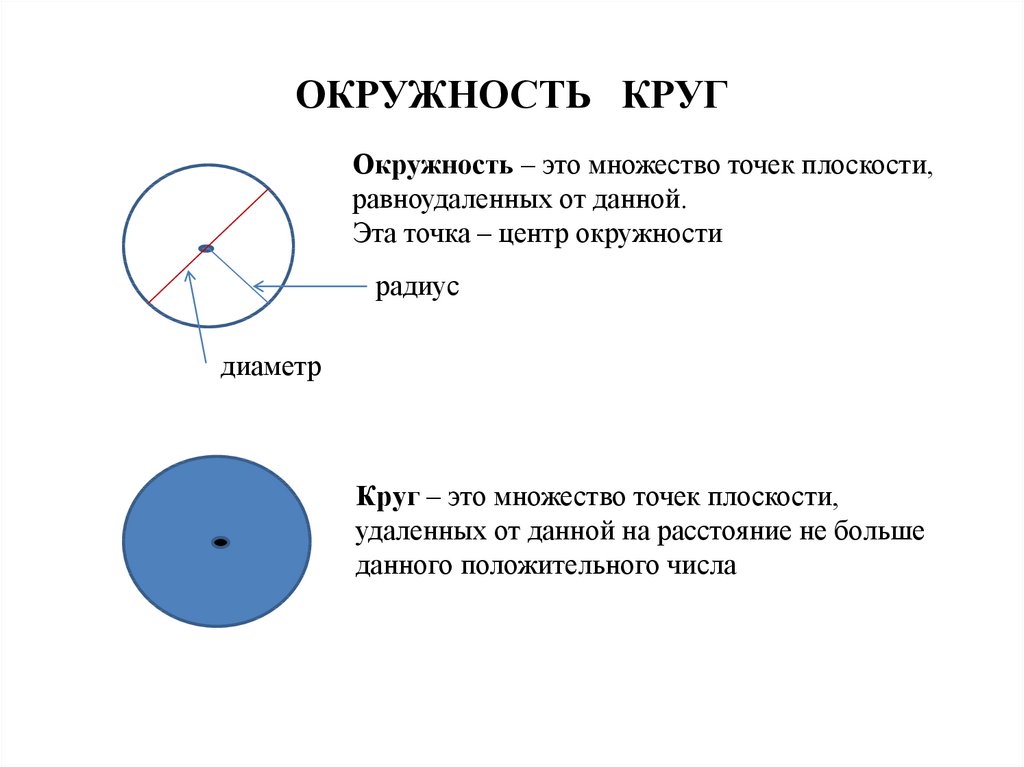
Теперь надо отметить центр окружности, обозначим его буквой О. Начертим окружность. Центр окружности соединим с любой точкой окружности, этот отрезок будет радиусом. Обозначим его буквой r. Теперь проведем диаметр.
– Ребята, как начертить диаметр? (Диаметр соединяет две точки окружности и проходит через ее центр)
— Какой буквой обозначается диаметр? (Диаметр обозначают буквой d)
Задание 2 (устно): Распределите слова на две группы “Окружность” и “Круг” Объясните свои действия.
Плоская тарелка, блин, резинка для волос, компакт-диск, покрышка для колес, обруч, кольцо.
Закрепление пройденного материала
Итог урока
Домашнее задание
Вариативная часть
Окружность или круг? Площадь круга
Репетиторы ❯ Математика ❯ Окружность или круг? Площадь круга
Автор: Владимир Л., онлайн репетитор по математике
●
05.
09.2011
●
Раздел: Математика
Окружность с центром О и радиусом R – это фигура, которая состоит из всех точек плоскости равноудалённых от точки О (центр окружности) на расстояние R.
Радиус окружности (расстояние R) – это отрезок, соединяющий центр окружности с любой точной на окружности. Все радиусы одной окружности равны.
Круг – это фигура на плоскости, ограниченная окружностью. Кругом с центром О и радиусом R называют фигуру, которая состоит из всех точек плоскости, удалённых от точки О этой плоскости на расстояние не больше, чем радиус R.
Т.е. окружность – это замкнутая линия, а круг – это плоская фигура, которая имеет площадь – часть поверхности, ограниченная замкнутым контуром данной фигуры. Мы можем вырезать из бумаги круг, а окружность не можем, потому что у неё нет площади, а есть только длина.
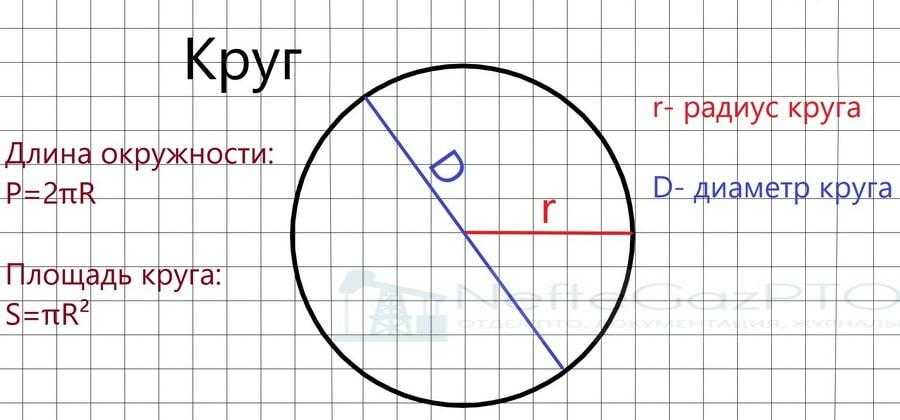
Как найти площадь круга?
Площадь круга равна произведению квадрата радиуса на число пи (3, 1415).
S = π R2
S – площадь круга;
R – радиус круга;
π = 3, 1415.
Сектор круга – пересечение круга и некоторого его центрального угла, то есть часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Площадь сектора
S = Ld · R/2 = (A · R2)/2
Где S – площадь сектора, R – радиус круга, Ld – длина дуги.
Если Вам необходима помощь при решении геометрических задач, Вы можете обратиться за помощью к онлайн репетитору по математике. Наш сайт предлагает школьникам реальную помощь при решении задач по математике, физике, химии. Решение задач на сайте происходит в режиме онлайн. Чтобы получить помощь, Вам не придётся ждать, наши репетиторы всегда на связи.
Во время занятий онлайн преподаватель решит задачу вместе с Вами и подробно объяснит все произведённые вычисления. Решив одну задачу с нашим онлайн репетитором, Вы сможете самостоятельно решать аналогичные.
Наши онлайн репетиторы могут проверить Ваше решение задач. Для этого Вам необходимо поместить на интерактивную классную доску свой вариант решения, и наши профессиональные педагоги по математике, физике и химии в реальном времени ответят на все Ваши вопросы, укажут на допущенные ошибки и при необходимости расскажут, что нужно исправить.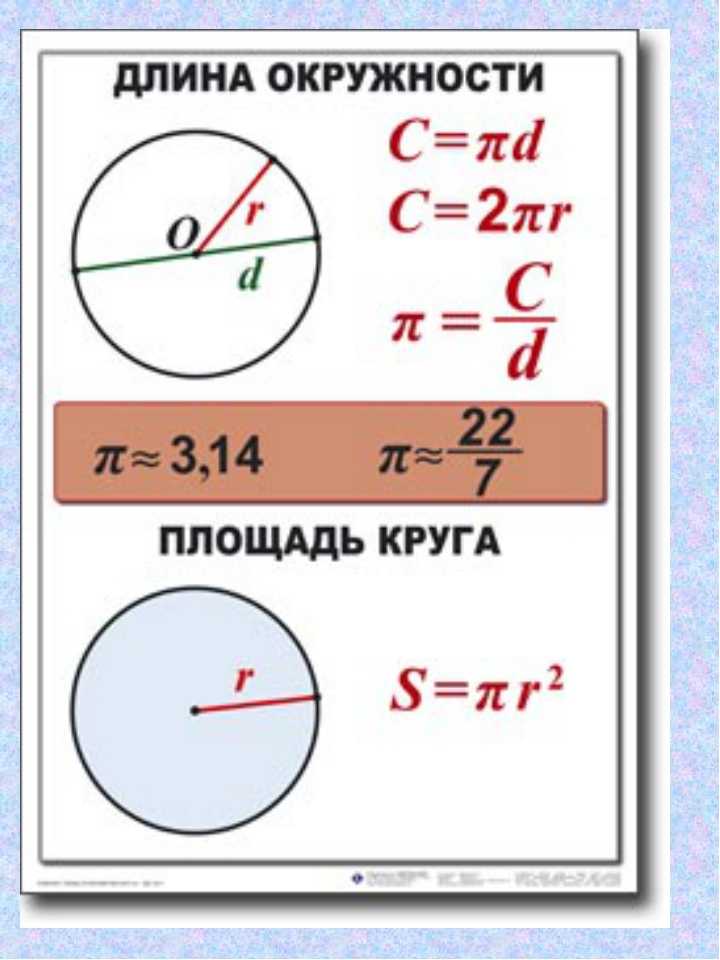
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Геометрия кругов
Определения и формулы радиуса окружности, диаметра окружности, длины окружности (периметра) окружности, площади окружности, хорды окружности, дуги и длины дуги окружности, сектора и площадь сектора круга
Просто прокрутите вниз или нажмите на то, что вы хотите, и я прокрутлю вниз для вас!
| радиус окружности | диаметр круга | длина окружности |
| площадь круга | хорда окружности | дуга окружности |
| длина дуги окружности | сектор круга | площадь сектора круга |
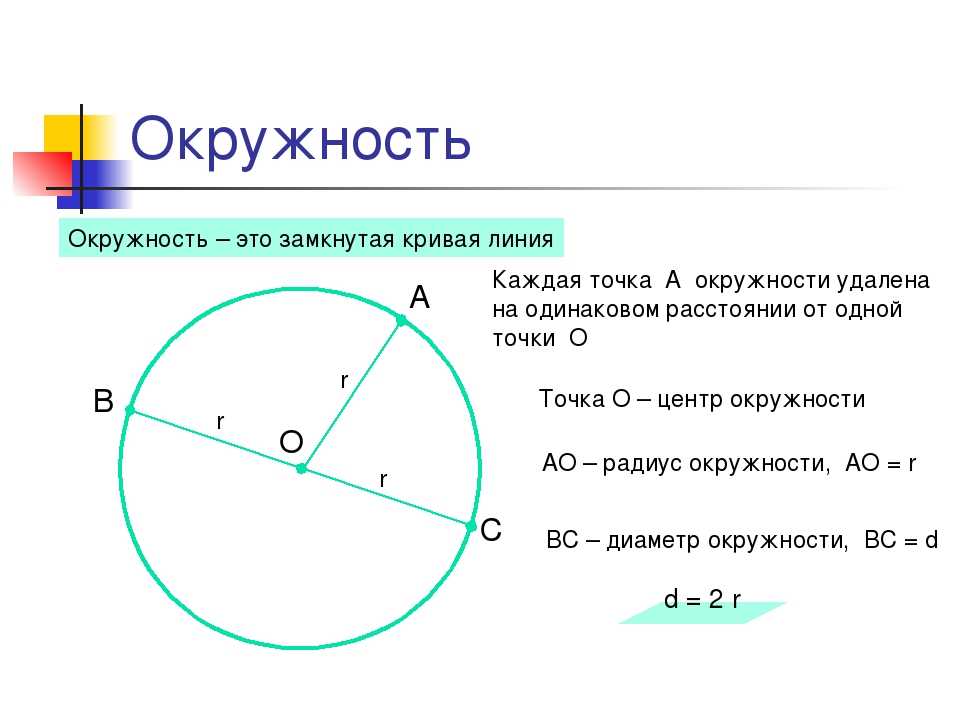
| Радиус окружности: | |
 | |
| Диаметр круга: | |
| Диаметр круга — это наибольшее расстояние поперек круга. (Диаметр проходит через центр круга. Это делает его самым длинным расстоянием.) | |
| Длина окружности (периметр круга): | |
| Длина окружности — это периметр — расстояние вокруг внешнего края. Окружность = | |
| Площадь круга: | |
Площадь = | |
.. | Хорда окружности: | |
| Хорда окружности — это отрезок, соединяющий одну точку на краю окружности с другой точкой на окружности. (Диаметр — это хорда — это просто самая длинная хорда!) | |
Радиус окружности – определение, теоремы и длина хорды окружности Формула
Когда вы двигаетесь относительно определенной точки, она образует окружность, только если вы движетесь по фиксированной траектории. Точка, которую вы берете в качестве ориентира, называется центром круга. Путь, по которому вы двигаетесь, образует окружность круга. Расстояние, которое остается неизменным при движении вокруг точки, называется радиусом окружности. Работать с кругами всегда было очень интересно.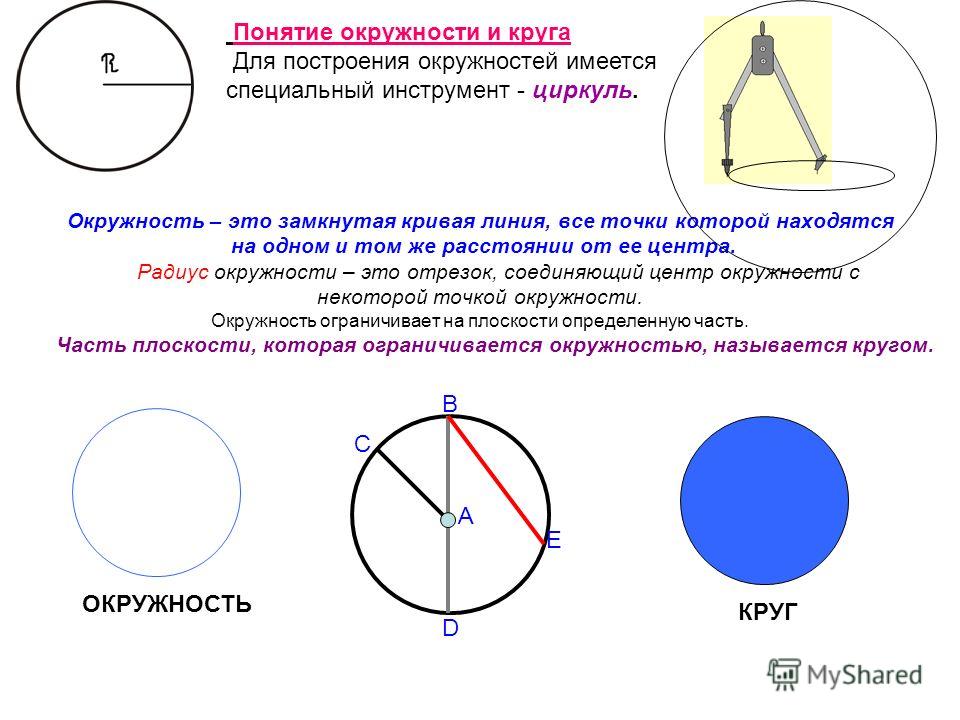
Это важная часть концепции математики для изучения.
Радиус окружности — это расстояние от центра окружности до любой точки на ее окружности. Обычно его обозначают буквами «R» или «r». Площадь и длина окружности также измеряются радиусом.
Радиус можно определить как меру расстояния от центра любого круглого объекта до его самого внешнего края или границы. Это не только измерение круга, но также и измерение сферы, полусферы, конуса с круглым основанием и цилиндра с круглым основанием.
Окружность может быть определена как геометрическое место точки, движущейся на плоскости таким образом, что ее расстояние от фиксированной точки всегда постоянно, и эта фиксированная точка известна как центр окружности, а расстояние между любой точкой окружности и ее центром есть радиус окружности.
Диаметр окружности — это длина линии, которая начинается от одной точки окружности до другой точки и проходит через центр окружности, и равна удвоенному радиусу окружности.
Обозначается буквой «d» или «D».Диаметр = 2 x Радиус
Или
Радиус = Диаметр/2.
Диаметр — это самая длинная хорда окружности.
Мы также можем выразить площадь и длину окружности через диаметр.
Здесь длина окружности = π (диаметр)
Площадь круга = π/4 (диаметр)2.
Определение радиуса окружности и хорды
Хорда — это отрезок, соединяющий две разные точки окружности, которые также могут проходить через центр окружности. Если хорда проходит через центр окружности, она называется диаметром. Радиусом окружности называется любой отрезок, соединяющий центр окружности с любой точкой на окружности. Хорда окружности — это отрезок, соединяющий любые две точки окружности.
Формула длины хорды окружности
Существуют две разные формулы для расчета длины хорды окружности.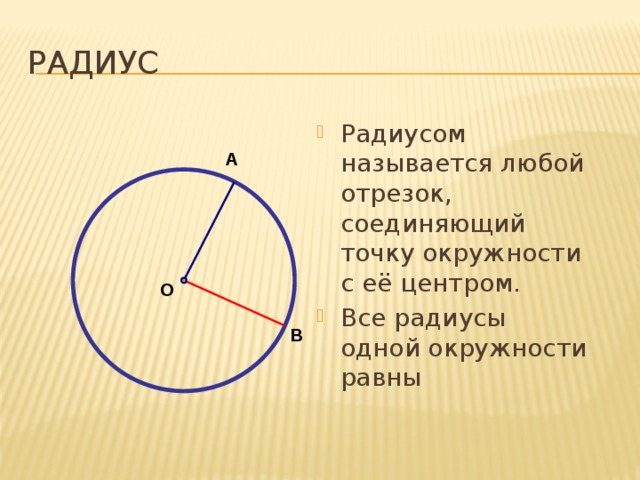
Формулы:
Длина хорды = 2 × √(r2 – d2). Эта формула используется при расчете с использованием перпендикуляра, проведенного из центра.
Для использования в тригонометрии длина хорды = 2 × r × sin(c/2), где r — радиус, d — диаметр, а c — центральный угол, образуемый хордой.
Что такое круг?
(Изображение будет загружено в ближайшее время)
На этой диаграмме показана окружность с центром в точке O и радиусом, одинаковым для всех точек окружности.
Определение радиуса окружности
Согласно классической геометрии радиус окружности определяется как равное расстояние, проведенное от центра до окружности окружности. Если мы удвоим это расстояние, то оно станет диаметром круга.
Определение связи между радиусом окружности и хордой
Хорда — это отрезок, соединяющий две разные точки окружности, которые также могут проходить через центр окружности.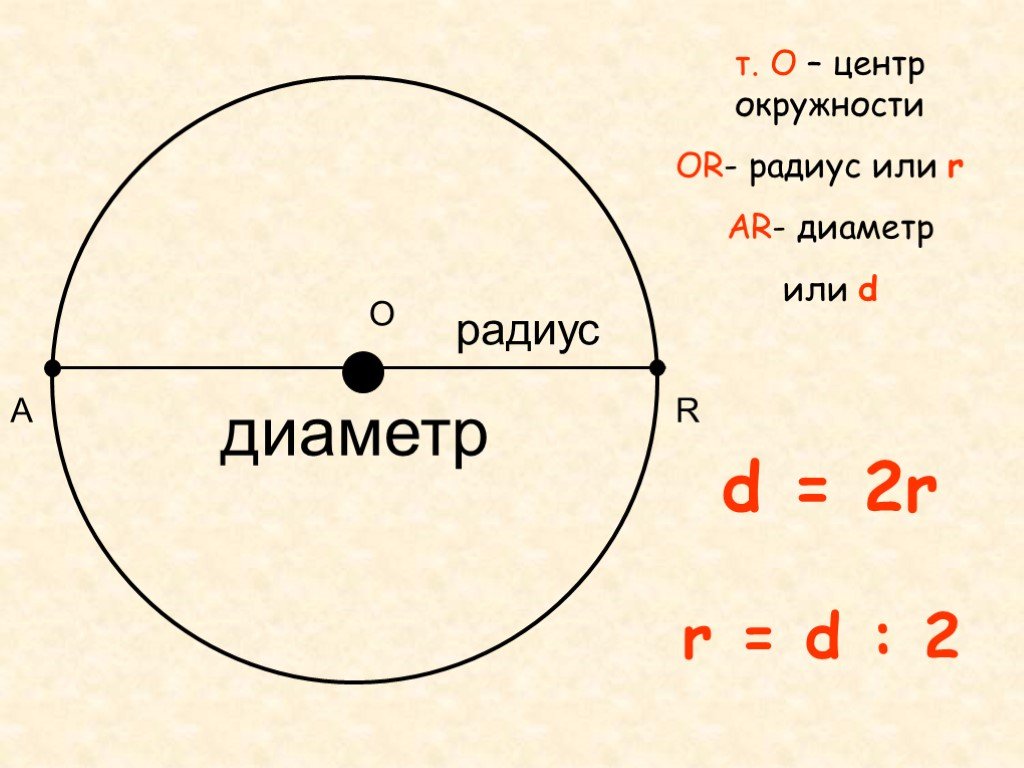
Если хорда проходит через центр окружности, то она становится диаметром.
Предположим, здесь мы рассматриваем d как диаметр, тогда радиус определяется как
d = r/2
Диаметр окружности – это самая длинная хорда.
Поясним понятие хорды с помощью схемы.
(Изображение будет загружено в ближайшее время)
На приведенной выше диаграмме показан отрезок прямой, который пересекает окружность в точках A и B.
AB является хордой окружности на приведенной выше диаграмме. Если этот AB проходит через центр в точке O, то он становится диаметром, который в два раза больше радиуса.
Хорда окружности Теоремы
Теорема 1:
Прямая, проведенная к хорде из центра, делит ее пополам под прямым углом.
(Изображение будет загружено в ближайшее время)
На приведенной выше диаграмме AB является хордой, а OC проведена из центра в точку C в точке AB.
Нам нужно доказать, если AC = BC
Решение:
Составьте треугольники, рисуя AO и OB.
Согласно заявлениям,
AO=OB
OC является общим для обоих треугольников, угол OCA = угол OCB = 90 градусов
Следовательно, два треугольника конгруэнтны друг другу.
Итак, AC = BC
Теорема 2:
Доказать, что прямая, делящая пополам хорду окружности, проведенная из центра, перпендикулярна хорде.
(Изображение будет загружено в ближайшее время)
На приведенной выше диаграмме
AC = CB
Нам нужно доказать, что OC перпендикулярна AB.
Образуйте два треугольника, соединив OA и OB
В двух треугольниках AOC и BOC
OA = OB
AC = BC
OC= OC (общий для обоих)
Следовательно, два треугольника равны другие по собственности SSS.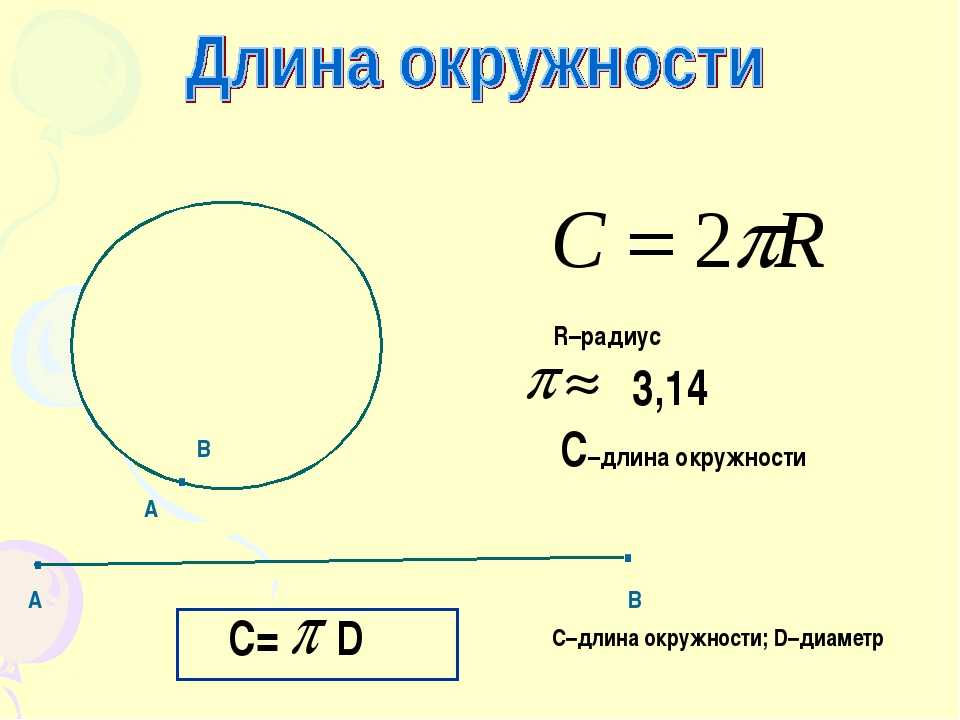
Согласно линейной паре
Угол 1 + угол 2 = 180
Кроме того, угол 1 = угол 2
Следовательно, угол 1 = угол 2 = 90 градусов
Отсюда доказано, что ОС перпендикулярна АВ.
Длина хорды окружности Формула
У нас есть две разные формулы для расчета длины хорды окружности. Ниже приведены упомянутые формулы.
Длина хорды = 2 × √(r2 – d2)
Эта формула используется при расчете с использованием перпендикуляра, проведенного из центра.
Если вы используете тригонометрию,
Длина хорды = 2 × r × sin(c/2)
Здесь r — радиус, d — диаметр, а c — центральный угол, образуемый хордой .
Что такое дуга и хорда окружности?
