Измерение углов транспортиром в докладе (5 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 239.
4.6
Средняя оценка: 4.6
Всего получено оценок: 239.
Измерение углов достаточно сложная тема математики 5 класса, поскольку эта фигура не имеет аналогов. Особую проблему представляет тема измерения углов, поскольку не всегда получается с первого раза разобраться с определением градусной меры.
Что такое угол?
Угол – это фигура, состоящая из двух лучей, имеющих начало в одной точке. Эта точка зовется вершиной угла. Величина угла показывает величину поворота оной стороны относительно другой. Наиболее ярким примером станут часы.
На сколько поворачивается минутная стрелка относительно другой? На какое-то количество минут. Так и геометрии, один луч поворачивается вокруг другого на какое-то количество градусов.
Изучение углов необходимо в физике, где колесо вращается вокруг оси; в строительстве, где у каждого строительного элемента есть вращательный момент и во многих других отраслях науки.
Углы есть практически во всех фигурах. Только круг без дополнительных построений не имеет в своем составе углов. Но стоит только провести радиус и углы сразу же появляются
Без углов нельзя себе представить треугольник, прямоугольник и прочие многоугольники. Это один из основных элементов геометрических фигур.
Углы существуют не только в плоскости, но и в пространстве. При пересечении двух плоскостей по прямой так же, как и при пересечении прямых образуется четыре угла. Чтобы найти величину такого угла придется построить плоский угол. Для этого необходимо в каждой плоскости провести перпендикуляр к одной точке, лежащей на линии пересечения плоскостей.
Угол между двумя перпендикулярами и будет равняться пространственному углу. Обратите внимание, угол между перпендикулярами в пространстве не всегда равняется 90 градусам.
Что такое градус?
Чтобы дать определение градуса нужно представить себе окружность и провести в ней радиус. Такими радиусами круг традиционно делят на 360 частей.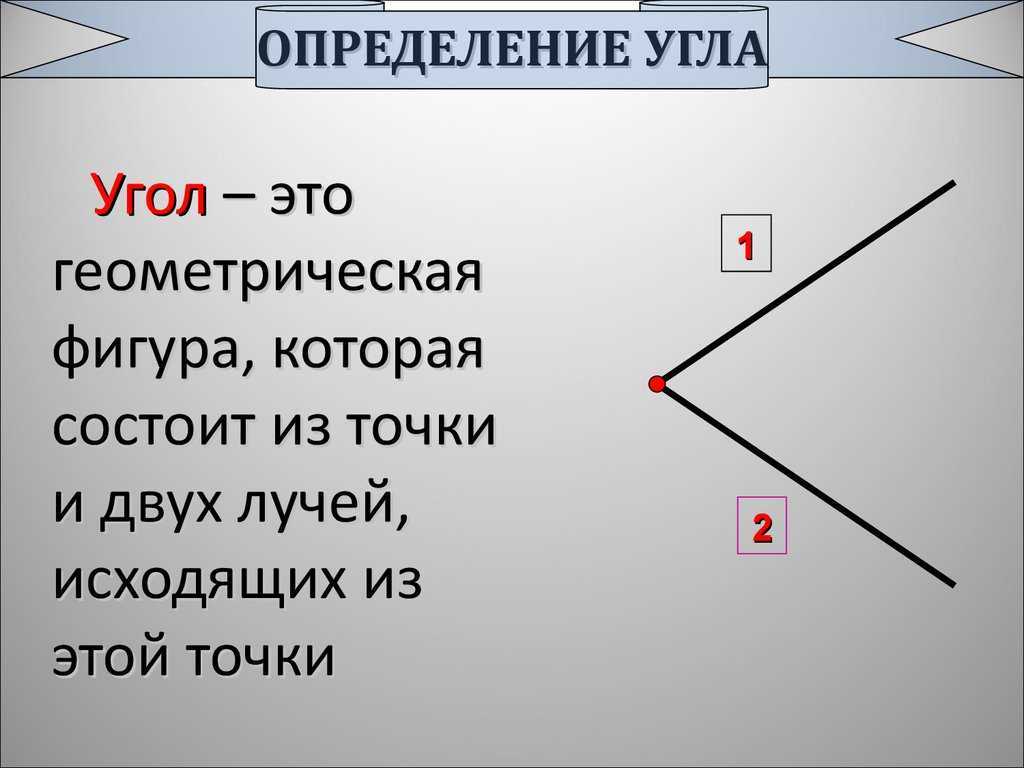
Почему на 360? Это традиция одной из цивилизаций древности. В современной математике было решено, что нет смысла делить круг на большее или меньшее количество частей.
К тому же, многие трактаты математики, таблицы, вроде таблиц Брадеса, и документы составлены согласно утверждению, что круг делится на 360 градусов. Поэтому нет смысла делить окружность на другое количество частей.
Измерение углов
Измерение углов производится с помощью транспортира. Производится совмещение нижнего луча с линейкой транспортира, тогда верхний луч угла укажет на размер фигуры.
Свойства измерения углов:
- Каждый угол имеет градусную меру, больше 0
- Развернутый угол представляет собой угол, две стороны которого лежат на одной прямой. Градусная мера развернутого угла равняется 180
- Если луч с началом в вершине угла, делит угол на две части, то изначальный угол равняется сумме двух малых углов.
Свойства углов гласят, что любой измеряемый угол не может иметь градусную меру меньше 0. Понятно, что никакая из измеряемых величин не может быть отрицательной. Но дело в том, что нулевой угол существует. Любой отрезок по факту можно назвать нулевым углом. Эффект нулевого угла возникает при наложении лучей или отрезков с началом в одной точке. Над вопросом признания существования нулевого угла в математике до сих пор ведутся научные споры и пишутся научные доклады.
Понятно, что никакая из измеряемых величин не может быть отрицательной. Но дело в том, что нулевой угол существует. Любой отрезок по факту можно назвать нулевым углом. Эффект нулевого угла возникает при наложении лучей или отрезков с началом в одной точке. Над вопросом признания существования нулевого угла в математике до сих пор ведутся научные споры и пишутся научные доклады.
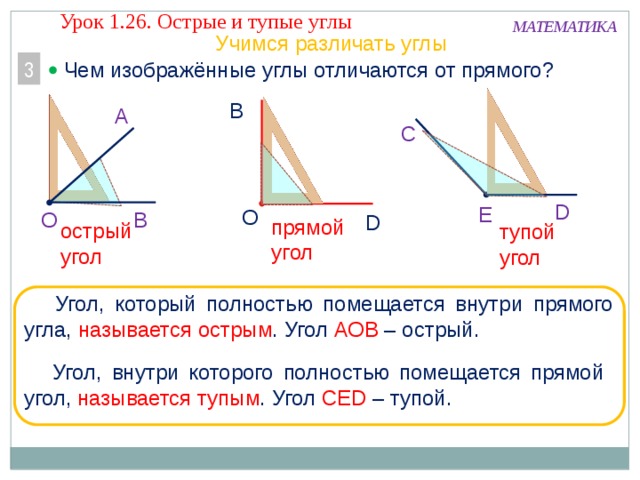
Что мы узнали?
Мы узнали, что такое угол, что это фигура, состоящая из двух лучей, имеющих начало в одной точке. Поговорили о единицах измерения этой фигуры и узнали свойства измерения углов.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.Ева Заворина
10/10
Арсений Санников
8/10
Арр Гор
7/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 239.
А какая ваша оценка?
Угол.
 Виды углов | Презентация к уроку по математике (1 класс):
Виды углов | Презентация к уроку по математике (1 класс):Опубликовано 21.09.2021 — 23:58 — Васильева Алёна Игоревна
Разновидности углов
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
«Угол. Виды углов»
Слайд 2
Вспомни! Какие бывают линии ? Начерти в тетради
Слайд 3
Назовём геометрические фигуры . .
Слайд 4
Угол Два луча, исходящие из одной точки, называются углом .
Слайд 5
Что такое угол? Как он получается? Начертите в тетради угол. Кто из моих помощников начертил угол ? Почему?
Слайд 6
Практическая работа Начертите разные углы Ребята, я помогу вам построить прямой угол 1. Возьмите угольник и карандаш. 2. Обведите угол, как у меня на рисунке.
Слайд 7
А я помогу построить тупой угол Возьмите линейку и карандаш. Проведите прямую линию А затем ещё одну, как у меня Приложите угольник. Что скажете?
Слайд 8
тупой больше …
Слайд 9
И я, ребята, вам помогу! Строим острый угол Возьмите линейку и карандаш.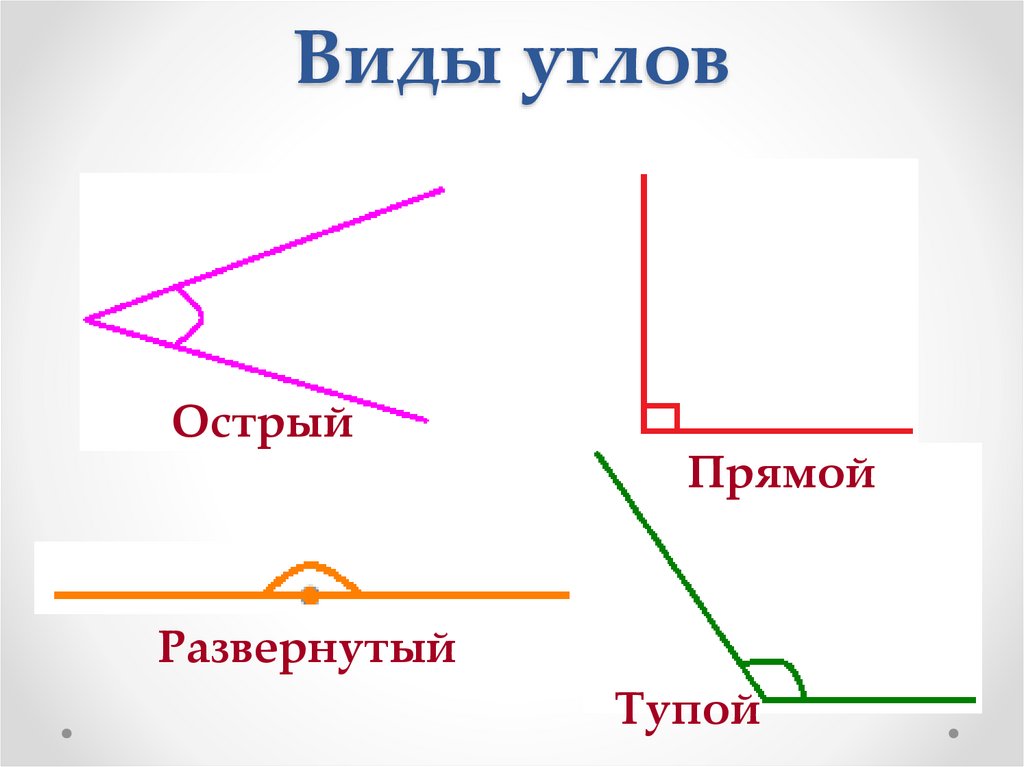 Проведите прямую линию А затем ещё одну, как у меня Приложите угольник. Что скажете?
Проведите прямую линию А затем ещё одну, как у меня Приложите угольник. Что скажете?
Слайд 10
Острый угол меньше прямого…
Слайд 11
Виды углов острый прямой тупой
Слайд 12
Подведение итогов. Что такое угол? Какие виды углов вам известны?
Слайд 13
Встретимся на следующем уроке! Вот и подошло к концу наше увлекательное путешествие в город Геометринск. Мои друзья прощаются с вами
По теме: методические разработки, презентации и конспекты
Фрагмент урока математики во 2 классе на тему: «Угол. Виды углов. Углы многоугольника.»
Вашему вниманию представлен фрагмент урока математики во 2 классе по программе «Перспективная начальная школа» по теме «Угол.Виды углов. Углы многоугольника». В данном фрагменте показан этап работы на…
Урок математики в 4-м классе по теме: «Математика в углу (угол, виды углов)»
Урок математики в 4-м классе по теме: «Математика в углу (угол, виды углов)» Цель: познакомить детей с понятиями «луч», закрепить знания о“сторонах угла”, “вершине угла”, понятиях “ос. ..
..
Математика в углу (угол, виды углов)
Урок математики в 4 классе по УМК «Начальная школа XXI века»к учебнику В.Н.Рудницкой, Т.В.Юдачевой «Математика»….
Презентация Угол. Прямой угол. Виды углов.
Презентация к уроку «Угол. Прямой угол. Виды углов.»…
МАТЕМАТИКА В УГЛУ (УГОЛ, ВИДЫ УГЛОВ)
Познакомить детей с понятиями “стороны угла”, “вершина угла”, “острый угол”, “тупой угол”, “прямой угол”. Учить находить прямой угол среди других углов. Закрепить знания о геометрических фигурах. Восп…
презентация к уроку математики в 3 классе по теме: «Угол. Виды углов. Сравнение углов»
Презентация составлена в соответствии с требованиями ФГОС и системы Л.В.Занкова…
Урок математики в 4-м классе по теме: «Математика в углу (угол, виды углов)»
Цель: познакомить детей с понятиями «луч», закрепить знания о“сторонах угла”, “вершине угла”, понятиях “острый угол”, “тупой угол”, “прямой угол”. Учить находить прямой угол среди других углов.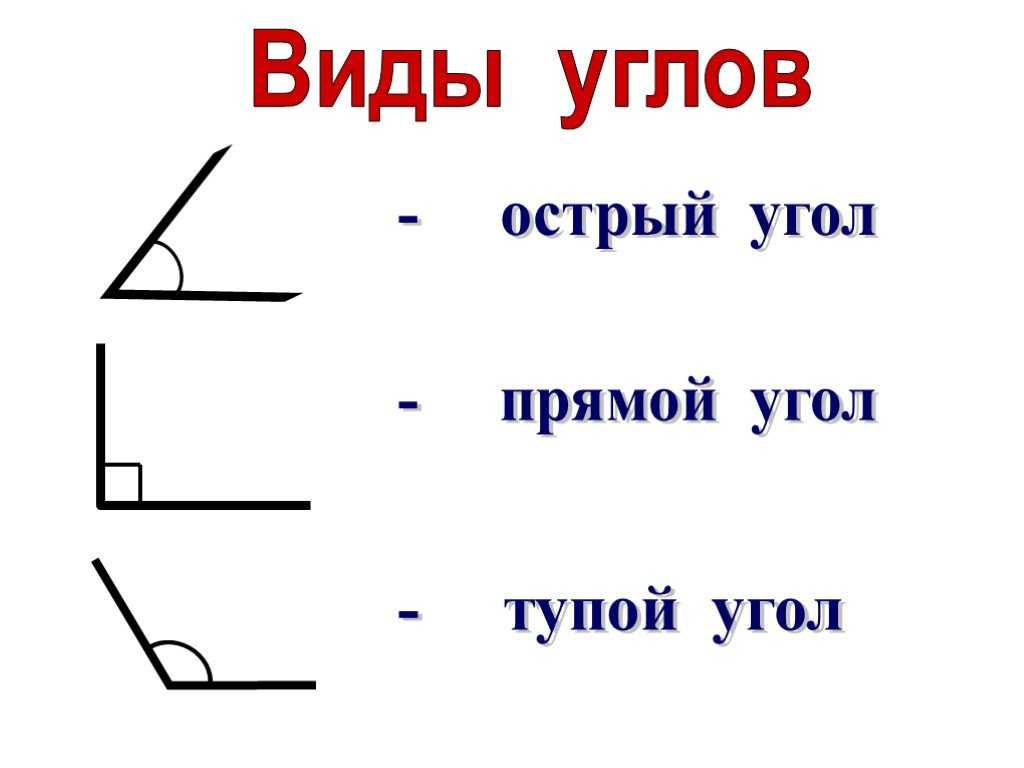 …
…
Поделиться:
Углы – Математика GCSE Revision – Повторная математика
Углы измеряются в градусах, пишется °. Максимальный угол составляет 360°. Это угол вокруг точки. Половина этого угла составляет угол на прямой, который равен 180°.
Взаимосвязанные углы
Прямые AB и CD параллельны друг другу (отсюда » на прямых).
a и d известны как вертикально противоположных углов. Вертикально противоположные углы равны. (b и c, e и h, f и g также вертикально противоположны).
g и c — соответствующих углов .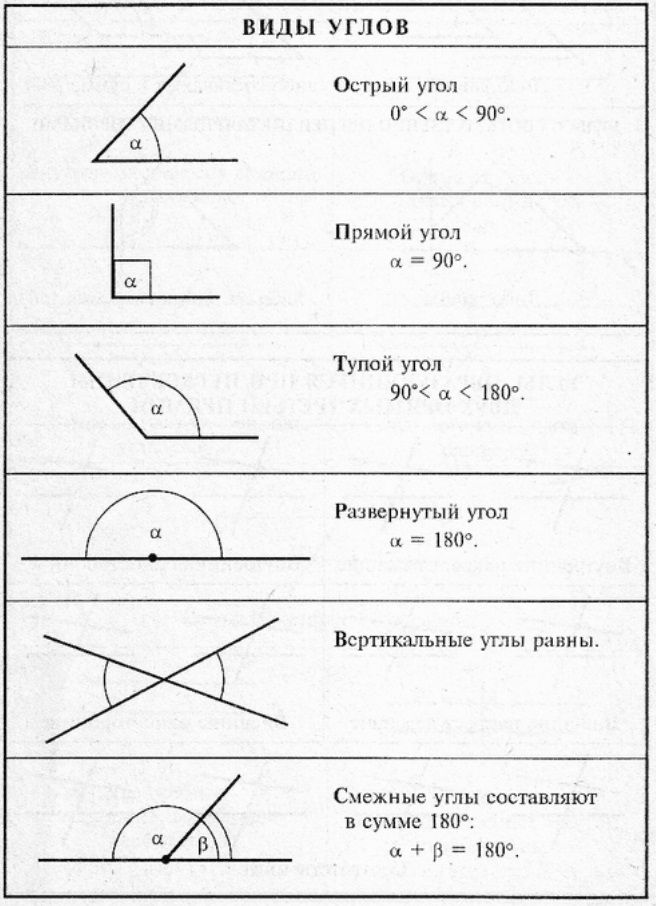 Соответствующие углы равны. (h и d, f и b, e и a также соответствуют).
Соответствующие углы равны. (h и d, f и b, e и a также соответствуют).
d и e альтернативные углы . Альтернативные углы равны. (c и f также чередуются). Альтернативные углы образуют форму «Z» и иногда называются «Z-углами».
a и b являются смежными углами . Смежные углы в сумме дают 180 градусов. (d и c, c и a, d и b, f и e, e и g, h и g, h и f также являются смежными).
d и f внутренние углы . В сумме они составляют 180 градусов (e и c также являются внутренними).
Любые два угла, сумма которых составляет 180 градусов, называются дополнительными углами .
Сумма углов треугольника
Используя некоторые из приведенных выше результатов, мы можем доказать, что сумма трех углов внутри любого треугольника всегда составляет 180 градусов.
Если у нас есть треугольник, вы всегда можете провести две параллельные линии следующим образом:
Теперь мы знаем, что альтернативных углов равны.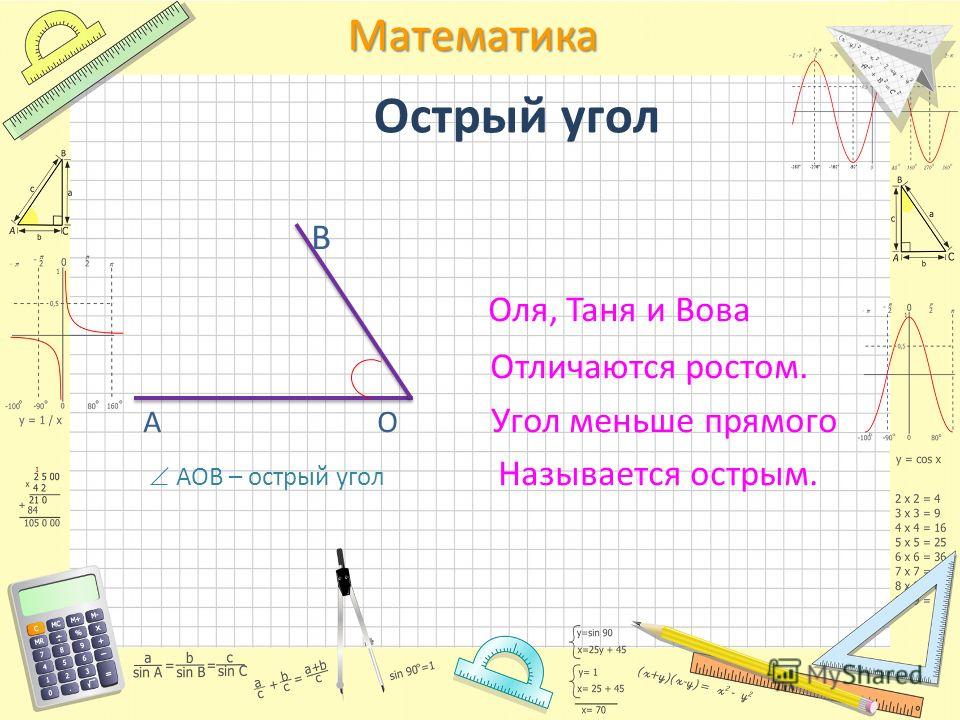 Следовательно, два угла, обозначенные х, равны. Кроме того, два угла, обозначенные y, равны.
Следовательно, два угла, обозначенные х, равны. Кроме того, два угла, обозначенные y, равны.
Мы знаем, что x, y и z вместе составляют 180 градусов, потому что вместе они представляют собой просто угол вокруг прямой. Таким образом, три угла треугольника должны составлять в сумме 180 градусов.
Сумма углов четырехугольника
Четырехугольник — фигура с 4 сторонами.
Теперь, когда мы знаем сумму углов треугольника, мы можем вычислить сумму углов четырехугольника.
Для любого четырехугольника можно провести диагональную линию, чтобы разделить его на два треугольника. Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.
Наружные уголки
Внешние углы фигуры — это углы, которые вы получите, если удлините стороны. Показаны внешние углы шестиугольника:
Многоугольник — это фигура с прямыми сторонами.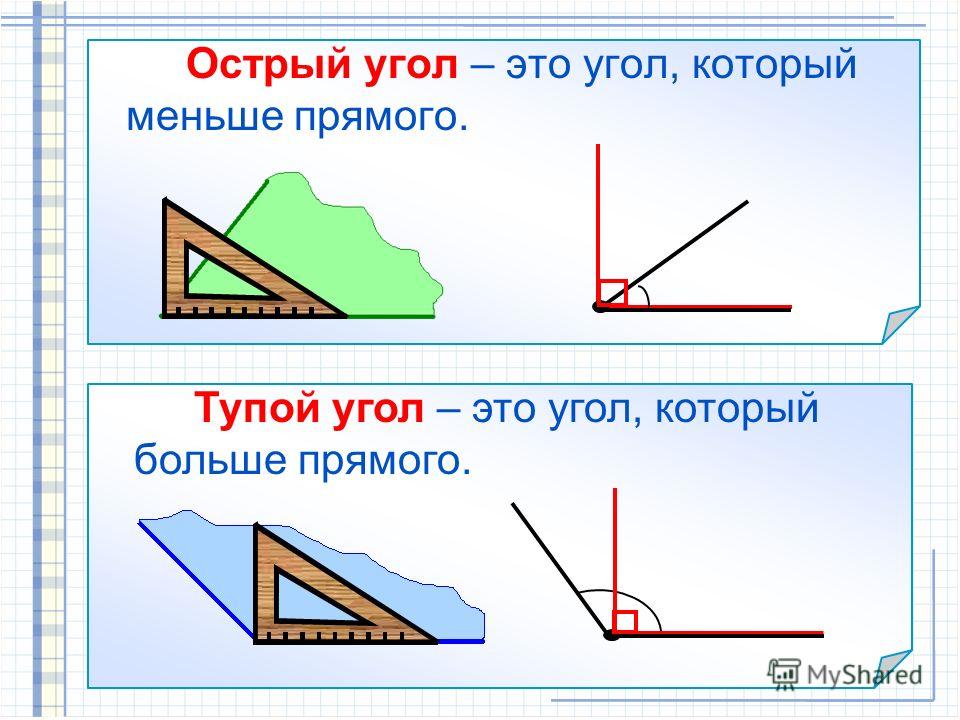
Следовательно, если у вас есть правильный многоугольник (другими словами, где все стороны имеют одинаковую длину и все углы одинаковы) , каждый из внешних углов будет иметь размер 360 ÷ количество сторон. Так, например, каждый из внешних углов шестиугольника равен 360/6 = 60°.
Внутренние углы
внутренних углов фигуры — это углы внутри нее. Если вы знаете размер внешнего угла, вы можете определить размер внутреннего угла рядом с ним, потому что они дадут в сумме 180 ° (поскольку вместе они составляют угол на прямой).
Внешний угол треугольника
Угол x — внешний угол треугольника:
Внешний угол треугольника равен сумме внутренних углов при двух других вершинах. Другими словами, x = a + b на диаграмме.
Доказательство:
- Углы треугольника в сумме составляют 180 градусов.
 Таким образом, a + b + y = 180, .
Таким образом, a + b + y = 180, . - Углы на прямой в сумме составляют 180 градусов. Итак, х + у = 180, .
- Поэтому у = 180 — х. Подставив это в первое уравнение, мы получим: a + b + 180 — x = 180. Следовательно, после перестановки a + b = x. Это мы и хотели доказать.
Как найти угол прямой
Все ресурсы по базовой геометрии
9Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 Следующая →
Справка по базовой геометрии » Плоская геометрия » Линии » Как найти угол прямой
Рассмотрите схему. Какое из этих условий , а не доказывает это ?
Возможные ответы:
и
Любое из этих утверждений может быть использовано для доказательства .
Правильный ответ:
Объяснение:
Если и , то , так как две прямые, параллельные одной и той же прямой, параллельны друг другу.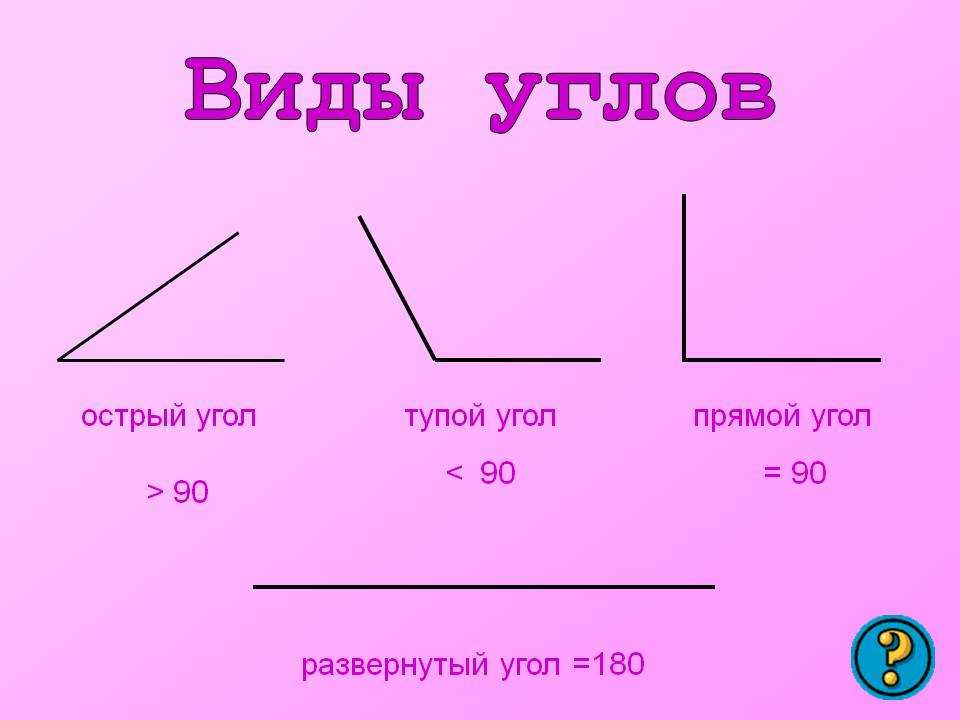
Если , то , так как два односторонних внутренних угла, образованных секущей, являются дополнительными.
Если , то , так как два альтернативных внутренних угла, образованных секущей , равны.
Однако, независимо от того, параллельны ли и ; это вертикальные углы, и по теореме о вертикальных углах они должны быть равны .
Сообщить об ошибке
У равнобедренного треугольника есть внутренний угол, равный . Чему равны два его других угла?
Этот треугольник не может существовать.
Правильный ответ:
Пояснение:
По теореме о равнобедренном треугольнике два внутренних угла должны быть равны. Однако, поскольку в треугольнике не может быть двух тупых внутренних углов, два недостающих угла должны быть равны. Поскольку общая мера угла треугольника , каждый из отсутствующих углов измеряет .
Поскольку общая мера угла треугольника , каждый из отсутствующих углов измеряет .
Сообщить об ошибке
Как бы вы классифицировали следующий угол?
Возможные ответы:
Скален
Острый
Прямой
Правый
Тупой
Правильный ответ:
Тупой
Объяснение:
Тупые углы больше .
Разнонаправленность — это обозначение треугольников, у которых один угол больше , но эта фигура не является треугольником.
Острые углы меньше , прямые углы равны , а прямые углы равны .
Следовательно, этот угол тупой.
Сообщить об ошибке
Что является мерой ?
Возможные ответы:
Правильный ответ:
Объяснение:
Когда две параллельные прямые пересекаются третьей прямой (называемой секущей), угол измеряется по определенной схеме.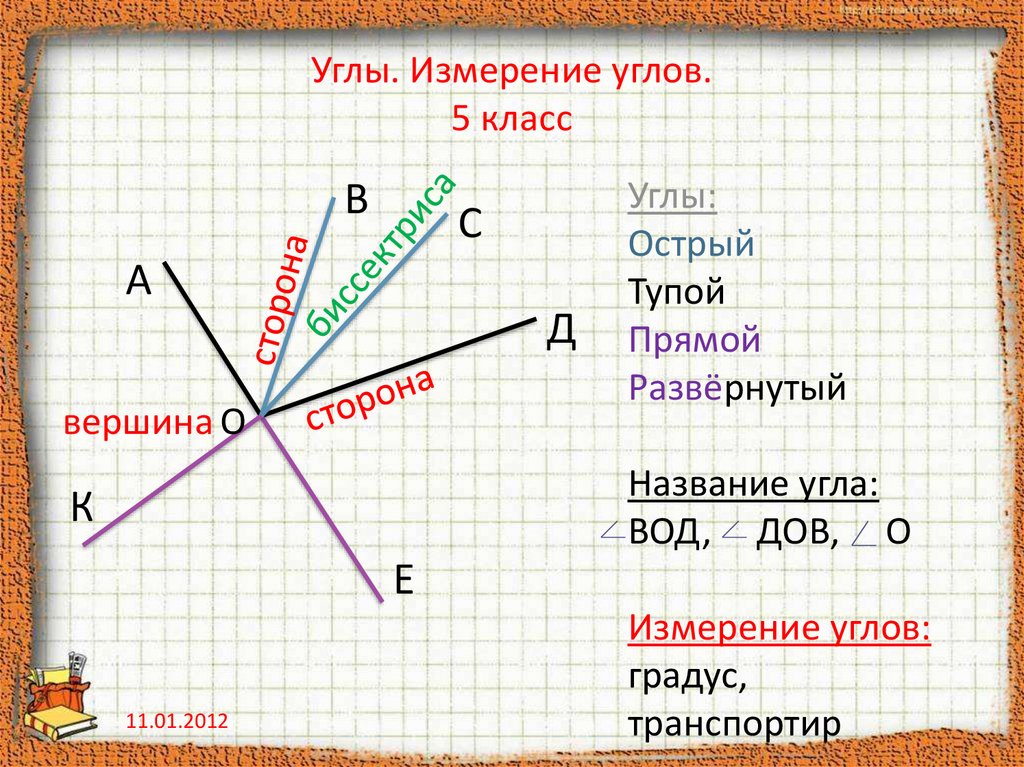 Пары углов внутри двух прямых и по разные стороны называются альтернативными внутренними углами. Альтернативные внутренние углы, такие как и , имеют одинаковую градусную меру. Следовательно, мера .
Пары углов внутри двух прямых и по разные стороны называются альтернативными внутренними углами. Альтернативные внутренние углы, такие как и , имеют одинаковую градусную меру. Следовательно, мера .
Сообщить об ошибке
Марк тренируется для бега по пересеченной местности и натыкается на новый холм для бега. Пробежав несколько метров, Марк оказывается на метровой высоте. Каков угол падения холма, когда он находится на высоте метров?
Возможные ответы:
То же самое, что угол наклона
не может быть определен
Правильный ответ:
Объяснение:
После прочтения вопроса у нас в голове остался этот пространственный образ Марка. После добавления данной информации изображение становится больше похоже на
Холм, по которому бежит Марк, можно увидеть в виде прямоугольного треугольника.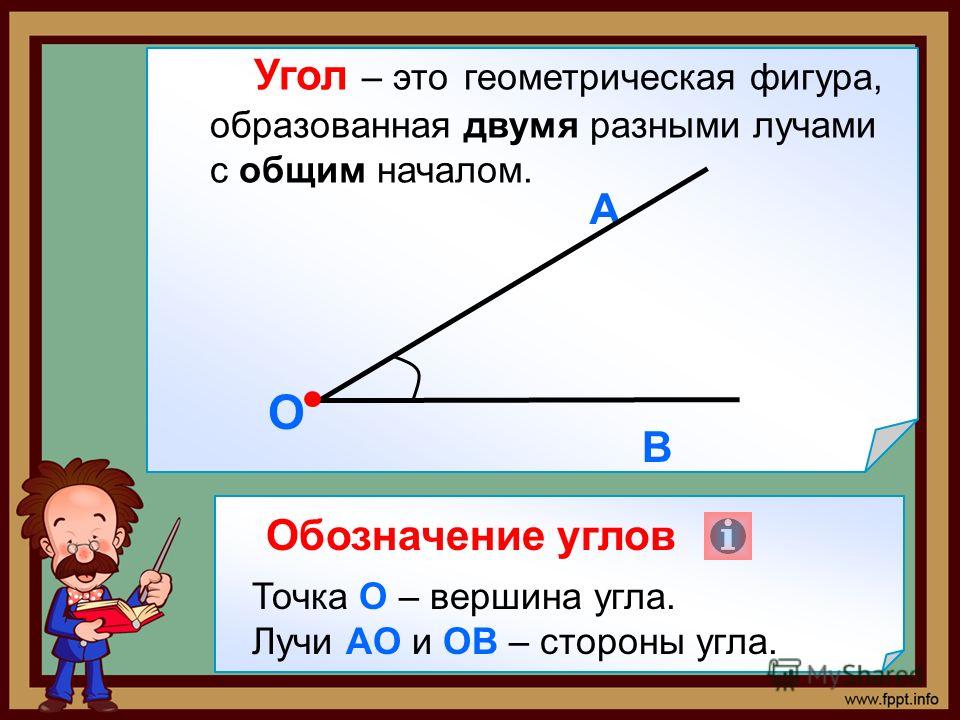 Эта проблема быстро превращается в проблему, требующую загадочного угла, учитывая, что даны две стороны треугольника. Чтобы найти угол наклона, мы должны обратиться к принципам касательной функции. Tan, Sin или Cos обычно используются, когда имеется угол и цель состоит в том, чтобы вычислить одну из сторон треугольника. В этом случае обстоятельства обратные.
Эта проблема быстро превращается в проблему, требующую загадочного угла, учитывая, что даны две стороны треугольника. Чтобы найти угол наклона, мы должны обратиться к принципам касательной функции. Tan, Sin или Cos обычно используются, когда имеется угол и цель состоит в том, чтобы вычислить одну из сторон треугольника. В этом случае обстоятельства обратные.
Вспомните «SOH CAH TOA». В этой задаче не дается никакой информации о гипотенузе, и мы не пытаемся вычислить гипотенузу. Поэтому у нас остается «ТОА». Если бы мы проверили, это сработало бы, потому что угол у ног Марка содержит информацию для противоположной стороны и соседней стороны.
Поскольку угол не задан, мы должны использовать принципы, лежащие в основе функции тангенса, при использовании дроби, состоящей из заданных сторон. Эта проблема будет решена с помощью arctan (иногда обозначается как ).
Сообщить об ошибке
Два угла являются дополнительными и имеют отношение 1:4. Какова величина меньшего угла?
Возможные ответы:
Правильный ответ:
Пояснение:
Поскольку углы смежные, их сумма равна 180 градусам.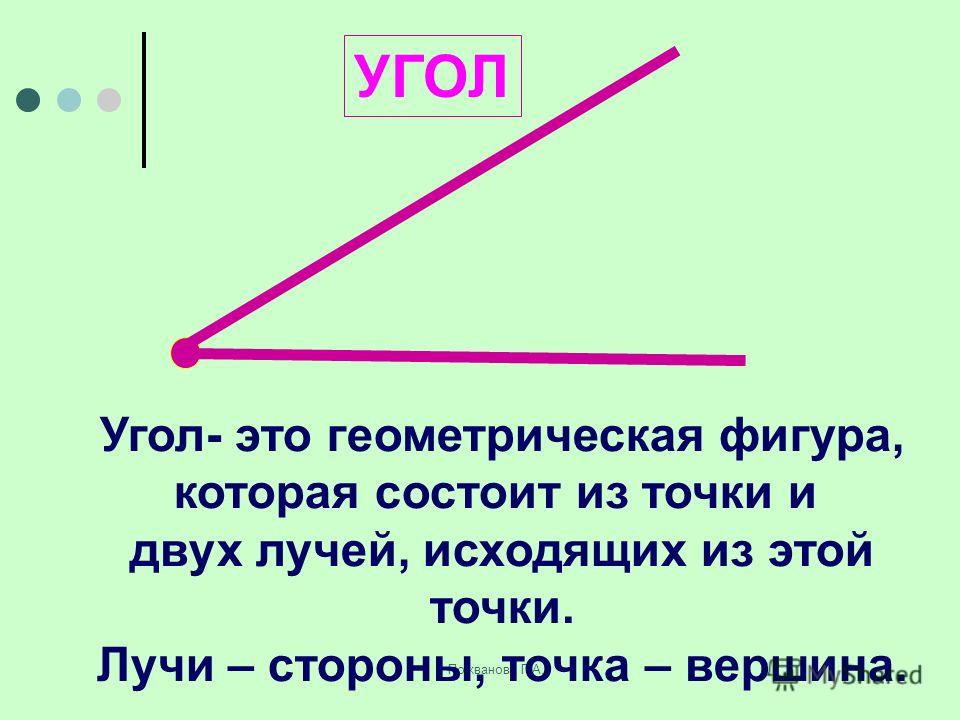 Поскольку они находятся в соотношении 1:4, можно записать следующее выражение:
Поскольку они находятся в соотношении 1:4, можно записать следующее выражение:
Сообщить об ошибке
AB и CD — две параллельные линии, пересекаемые линией EF. Если угол 1 равен , то чему равен угол 2?
Возможные ответы:
Правильный ответ:
Объяснение:
Углы равны. При пересечении двух параллельных прямых секущей соответствующие углы имеют одинаковую величину.
Сообщить об ошибке
Линии A и B на диаграмме ниже параллельны. Треугольник в нижней части рисунка равнобедренный.
Что такое градусная мера угла?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку A и B параллельны, а треугольник равнобедренный, мы можем использовать дополнительное правило для двух углов, и , которое в сумме даст . Составив для этого алгебраическое уравнение, получим . Решая для , получаем . При этом мы можем получить либо (для меньшего угла), либо (для большего угла — затем необходимо снова использовать дополнительное правило для внутреннего меньшего угла). В любом случае, мы находим, что внутренние углы при вершине равны 80 градусов каждый. Так как сумма углов внутри треугольника должна быть равна 180, мы можем составить уравнение как
Составив для этого алгебраическое уравнение, получим . Решая для , получаем . При этом мы можем получить либо (для меньшего угла), либо (для большего угла — затем необходимо снова использовать дополнительное правило для внутреннего меньшего угла). В любом случае, мы находим, что внутренние углы при вершине равны 80 градусов каждый. Так как сумма углов внутри треугольника должна быть равна 180, мы можем составить уравнение как
градуса.
Сообщить об ошибке
Рисунок выполнен не в масштабе.
На рисунке выше APB образует прямую линию. Если мера угла APC на восемьдесят один градус больше, чем мера угла DPB, а меры углов CPD и DPB равны, то какова мера угла CPB в градусах?
Возможные ответы:
40
33
114
50
66
Правильный ответ:
66
Пояснение:
Пусть х равно мере угла DPB. Поскольку мера угла APC на восемьдесят один градус больше, чем мера DPB, мы можем представить меру этого угла как x + 81. Кроме того, поскольку мера угла CPD равна мере угла DPB, мы можем представить мера CPD как x.
Поскольку мера угла APC на восемьдесят один градус больше, чем мера DPB, мы можем представить меру этого угла как x + 81. Кроме того, поскольку мера угла CPD равна мере угла DPB, мы можем представить мера CPD как x.
Поскольку APB — прямая линия, сумма углов DPB, APC и CPD должна быть равна 180; поэтому мы можем написать следующее уравнение, чтобы найти x:
x + (x + 81) + x = 180
Упростите, собрав x членов.
3x + 81 = 180
Вычесть 81 с обеих сторон.
3x = 99
Разделить на 3.
x = 33.
Это означает, что углы DPB и CPD равны 33 градусам. Исходный вопрос требует от нас найти меру угла CPB, которая равна сумме мер углов DPB и CPD.
мера КПБ = 33 + 33 = 66.
Ответ: 66.
Сообщить об ошибке
Половина меры дополнительного угла ABC равна удвоенной мере угла ABC. Чему равен в градусах дополнительный угол ABC?
Возможные ответы:
72
54
36
18
90
Правильный ответ:
54
Пояснение:
Пусть x равно мере угла ABC, y равно мере дополнения угла ABC, а z равно мере дополнения угла ABC.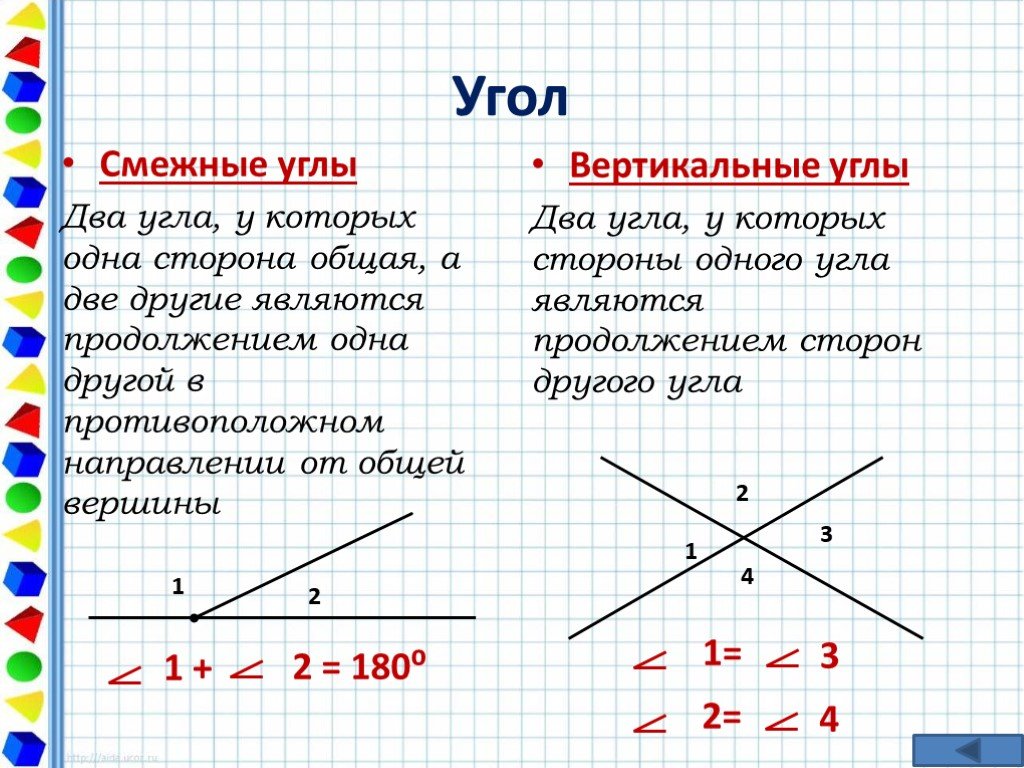
Так как x и y являются добавками, сумма их мер должна равняться 180. Другими словами, x + y = 180.
Нам говорят, что половина меры добавки равна удвоенной мере меры азбука. Мы могли бы написать это уравнение следующим образом:
(1/2)y = 2x.
Поскольку x + y = 180, мы можем найти y через x, вычитая x из обеих частей. Другими словами, y = 180 – x. Затем мы можем подставить это значение в уравнение (1/2)y = 2x, а затем найти x.
(1/2)(180-х) = 2х.
Умножьте обе части на 2, чтобы избавиться от дроби.
(180 – х) = 4х.
Добавьте x с обеих сторон.
180 = 5х.
Разделите обе стороны на 5.
x = 36.
Угол ABC равен 36 градусам. Однако исходный вопрос требует от нас найти меру дополнения ABC, которую мы ранее обозначили как z. Поскольку сумма меры угла и меры его дополнения равна 90, мы можем написать следующее уравнение:
x + z = 90.
Теперь мы можем подставить 36 в качестве значения x и найти z.

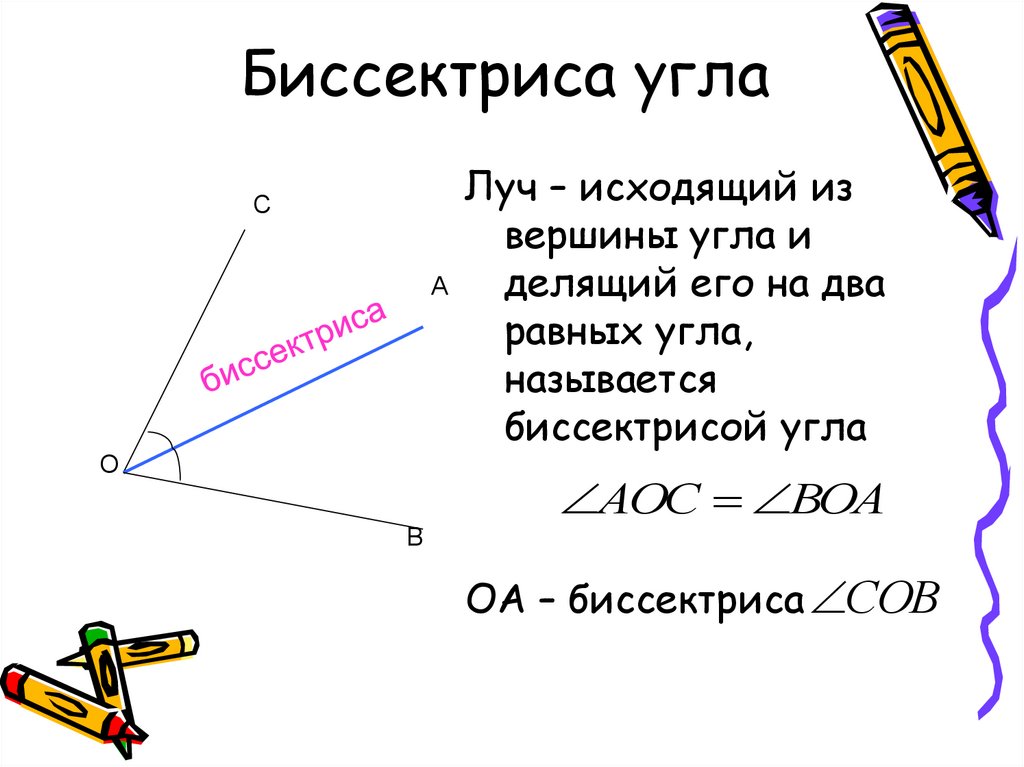 Таким образом, a + b + y = 180,
Таким образом, a + b + y = 180,