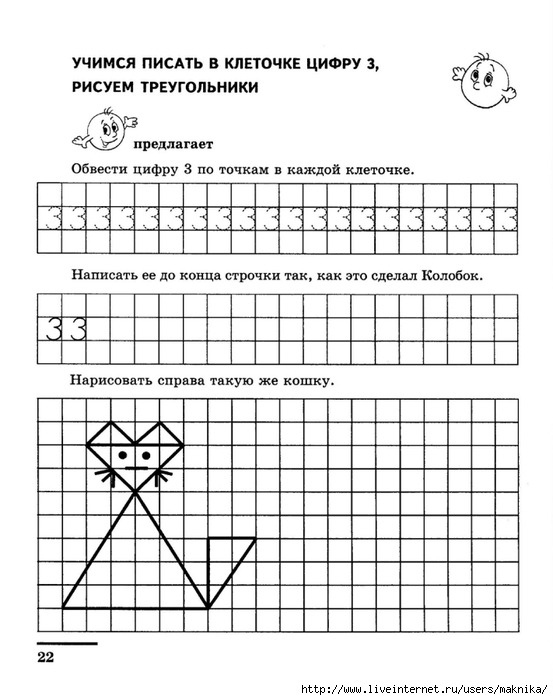
Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников
Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников — Элементы математического анализа)Поиск по сайту:
К. Л. САМАРОВ, С.С.САМАРОВА
Справочник по математике для школьников
Тематическое содержание
| ||
| Числовые последовательности | ||
Числовые последовательности. Способы задания числовых последовательностей Способы задания числовых последовательностей | ||
| Возрастающие и убывающие последовательности | ||
| Ограниченные и неограниченные последовательности | ||
| Пределы числовых последовательностей | ||
| Предел числовой последовательности | ||
| Свойства пределов числовых последовательностей | ||
| Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии | ||
| Примеры вычисления пределов последовательностей. Раскрытие неопределенностей | ||
| Число e. Второй замечательный предел | ||
Функции | ||
| Понятие функции. Область определения функции. Множество значений функции | ||
Понятие функции. Область определения функции. Множество значений функции Область определения функции. Множество значений функции | ||
| Примеры решения задач | ||
| Свойства функций. График функции | ||
| Ограниченные и неограниченные функции | ||
| Монотонные и строго монотонные функции | ||
| Четные и нечетные функции | ||
| Периодические и непериодические функции. Период функции | ||
| График функции. Свойства графиков четных, нечетных, периодических функций | ||
| Пределы функций | ||
| Предел функции | ||
| Свойства пределов функций | ||
| Раскрытие неопределенностей типа | ||
| Раскрытие неопределенностей типа | ||
| Первый замечательный предел | ||
Раскрытие неопределенностей типа . Второй замечательный предел Второй замечательный предел | ||
| Асимптоты графиков функций | ||
| Вертикальные асимптоты | ||
| Наклонные асимптоты | ||
| Горизонтальные асимптоты как частный случай наклонных асимптот | ||
| Поиск наклонных асимптот графиков функций | ||
Производная функции | ||
| Секущая графика функции. Касательная к графику функции. Производная функции. Геометрический смысл производной | ||
| Секущая графика функции. Уравнение секущей графика функции | ||
| Касательная к графику функции | ||
| Производная функции | ||
| Уравнение касательной к графику функции | ||
| Геометрический смысл производной | ||
Приращение аргумента и приращение функции. Производная как предел отношения приращений. Непрерывность функции Производная как предел отношения приращений. Непрерывность функции | ||
| Приращение аргумента и приращение функции. Производная как предел отношения приращений | ||
| Непрерывность функции | ||
| Правила вычисления производных. Таблица производных часто встречающихся функций. Таблица производных сложных функций | ||
| Правила вычисления производных | ||
| Таблица производных часто встречающихся функций | ||
| Таблица производных сложных функций | ||
| Примеры вычисления производных | ||
| Исследование поведения функций с помощью производной | ||
| Интервалы возрастания и убывания функции | ||
| Достаточные условия для возрастания и убывания функции | ||
| Экстремумы (максимумы и минимумы) функции | ||
«Подозрительные» на наличие экстремума точки функции. Теорема Ферма Теорема Ферма | ||
| Достаточные условия для существования экстремума функции | ||
| Пример исследования поведения функции | ||
| Исследование функции на выпуклость вверх и выпуклость вниз с помощью второй производной | ||
| Выпуклые вверх функции | ||
| Выпуклые вниз функции | ||
| Вторая производная функции | ||
| Достаточные условия выпуклости выпуклости вверх и выпуклости вниз | ||
| Точки перегиба | ||
| Необходимые условия для существования точки перегиба | ||
| Достаточные условия для существования точки перегиба | ||
| Построение графиков функций | ||
| Схема исследования поведения функций, применяемая для построения графиков функций | ||
| Примеры построения графиков функций | ||
| Наибольшее и наименьшее значения функции на отрезке | ||
| Наибольшее и наименьшее значения функции на множестве (основные определения) | ||
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса Теорема Вейерштрасса | ||
| Примеры решения задач | ||
Интегралы | ||
| Первообразная. Неопределенный интеграл. Правила интегрирования. Таблица интегралов. Примеры решения задач | ||
| Первообразная | ||
| Неопределенный интеграл | ||
| Правила интегрирования. Замена переменной в неопределенном интеграле | ||
| Таблица интегралов | ||
| Примеры решения задач | ||
| Определенный интеграл. Теорема Ньютона — Лейбница | ||
| Определенный интеграл как площадь криволинейной трапеции | ||
| Производная от определенного интеграла по верхнему пределу | ||
| Теорема Ньютона — Лейбница | ||
| Примеры решения задач | ||
| Геометрические приложения определенного интеграла | ||
| Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла | ||
| Примеры решения задач на вычисление площадей фигур на плоскости | ||
| Пример решения задачи на вычисление длины дуги кривой на плоскости | ||
| Вывод формул для объема пирамиды и для объема шара | ||
| Вывод формулы для площади сферы | ||
С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Множество. Элементы множества. 2-й класс
Цели:
- Ввести понятие «множество».
- Ввести понятие «элементы множества».
- Научить определять принадлежность элемента множеству.
Предварительная подготовка:
- Принести мяч.
- Принести картинки, на которых изображены предметы с общим названием (можно использовать карточки детского лото).

Ход урока
— Ребята, сегодня на уроке мы с вами узнаем, что такое «множество» и что называют «элементами множества»!
— У меня на доске нарисован мешок. Пока он пуст. Давайте соберем в него зверей, которых вы знаете.
Игра:
Учитель ходит с мячом по классу и кидает ученику мяч, а ученик должен быстро назвать какого-либо зверя.
-А теперь давайте всех названных зверей соберем в наш мешок.
Дети вспоминают, а учитель выписывает на доске всех названных в игре зверей (или использует карточки с магнитом).
— Много в мешке получилось зверей?
— Много.
— В математике такую группу предметов (или живых существ) с общим названием и собранных вместе называют «множеством». «Множество» от слова МНОГО. (Слайд 3,4)
— Попробуйте дать название множеству.
«Назови множество»:
Учитель показывает картинки с однородными предметами. Дети должны дать название этому множеству, например – рыбы, птицы, растения, книги.
Дети должны дать название этому множеству, например – рыбы, птицы, растения, книги.
— Это множество рыб. (Слайд 5)
— Это множество птиц. (Слайд 6)
— Давайте выполним задание №1 в тетради.
Задание №1. (Слайд 7)
Ученики должны назвать и подписать название предлагаемых множеств.
Множество: посуды, животных, обуви, игрушек, банных принадлежностей, предметов для рисования.
— Теперь давайте поиграем.
Игра «Назови множество» (Слайды 8,9,10)
Учитель перечисляет ряд предметов, а ученики придумывают название этому множеству.
— платье, брюки, шуба, юбка, кофта, куртка… — одежда.
(- шкаф, стул, стол, диван, тумбочка… — мебель.)
— береза, сосна, ель, тополь, дуб, ива… — деревья.
(- Москва, Одесса, Лондон, Париж, Санкт-Петербург… — города. )
)
— стрекоза, кузнечик, бабочка, муха, пчела… — насекомые.
После игры на доске появляется еще один мешок, в котором перечислены названия предметов, но нет общего названия. Его дети должны придумать сами. Например, сапоги, валенки, кроссовки, ботинки, тапочки.
— Это множество обуви.
— Все предметы из этого множества называют элементами этого множества. (Слайд 11,12)
— Выполним задание №2.
Задание №2.(Слайд 13)
При выполнении задания для каждой картинки следует проверить каждое предлагаемое слово.
— Можно сказать, что на лугу пасется стая коров?
— Нет
— А рой коров?
— Нет
— А букет коров?
-Нет
-Значит, для коров, пасущихся на лугу, подходит только слово «стадо».
Аналогично для остальных картинок перебираются возможные варианты, и выбирается подходящее слово.
— Итак, для некоторых групп предметов есть определенные слова, называющие эти группы, например, «стадо коров». Но сказать «рой коров» уже нельзя. Но зато любую группу предметов, собранных вместе, можно назвать «множеством»: множество коров, множество рыб, множество цветов.
Но сказать «рой коров» уже нельзя. Но зато любую группу предметов, собранных вместе, можно назвать «множеством»: множество коров, множество рыб, множество цветов.
— Сейчас снова будем играть. Для игры нам понадобятся ваши ладошки.
Игра «Найди лишнего» (Слайды 14,15,16)
Учитель называет какое-либо множество и начинает перечислять его элементы. Ученики должны хлопнуть в ладоши, если какой-либо названный предмет не является элементом заданного множества.
— Мы идем по парку и видим деревья: березу, дуб, розу (хлопок), тополь, сосну, ромашку (хлопок), ель, сирень (хлопок)…
— Мы заходим в магазин и покупаем овощи: помидоры, картошку, апельсины (хлопок), морковь, колбасу (хлопок), огурцы, свекла, яблоки (хлопок)…
— В спортивном зале мы видим спортивные принадлежности: мяч, лыжи, гантели, кресло (хлопок), теннисные ракетки, расческу (хлопок), коньки, стул (хлопок)…
— Выполняем задания в тетради.
Задание №3. (Слайд 17)
Ученики должны определить предмет, который мешает назвать множество остальных предметов.
— В клетке находится множество птиц, а кролик среди них является лишним.
Задание №4. (Слайд 18)
Аналогично предыдущему.
— Почему Незнайка вычеркнул круг?
— Потому что все остальные предметы с углами.
— А если оставить круг в начальном множестве, то какая другая фигура может быть лишней и почему?
— Лишним может быть прямоугольник, как серая фигура.
Задание №5. (Слайд 19)
Из заданного множества дети должны выделить элементы названных множеств: овощей и фруктов. Исследуется каждый предмет: если это овощ – подчеркивать одной чертой, если фрукт – двумя чертами. Предмет, не входящий ни в одно из названных множеств, подчеркивать не надо.
После этого следует перечислить все полученные множества вслух.
— Множество овощей: картошка, свекла, морковь, огурец, помидор, тыква.
— Множество фруктов: груша, яблоко, апельсин, лимон, ананас.
— Не подчеркнуты: масло, хлеб, колбаса, сыр, мяч.
Задание №6. (Слайд 20)
Главное в задании, чтобы ученик мог назвать выделенное им множество и перечислить его элементы.
— Множество музыкальных инструментов: труба, скрипка, гитара, гармошка, барабан.
— Множество спортивных принадлежностей: гантели, мяч, коньки, ракетка.
— Множество строительных инструментов: пила, пассатижи, отвертка.
— И снова играем. Здесь понадобятся ваши знания.
Игра «Продолжи ряд»:
Учитель перечисляет ряд предметов, а ученики, догадываясь о названии множества по перечисленным предметам, продолжают его своими элементами.
Обязательно в конце каждого этапа подвести итог: что же было перечислено, т.е. дать название множеству.
- сыроежка, мухомор, опенок…(подберезовик, подосиновик, лисичка) – это…множество грибов
- лиса, медведь, слон, бегемот…(волк, заяц, тигр, носорог) – это…множество зверей
- стрекоза, бабочка, кузнечик…(жук, комар, пчела, муха) – это…множество насекомых
- беретка, шляпа, панамка…(платок, кепка, шапка) – это…множество головных уборов
- щука, окунь, сом, плотва…(акула, карась, лещ) – это…множество рыб
Задание №7. (Слайд 21)
(Слайд 21)
Дети выполняют самостоятельно. Можно 1-2 учеников попросить озвучить свои ответы.
— Дорисовал тюльпан, т.к. это множество цветов.
— Ребята, назовите известные вам города (дети перечисляют названия городов).
— Можно городом назвать «Волгу»?
— Нет, это река.
— Можно ли назвать городом Россию?
— Нет, это страна.
Задание №8. (Слайд 22)
Выполняется самостоятельно.
Задание №9. (Слайд 23)
Ученики должны дать название каждому столбцу с тремя предметами (одежда, рыбы, деревья). После чего дуб должен быть вписан в столбец под названием «деревья», т.к. он является деревом.
Аналогично исследуются остальные предметы: окунь, лещ – «рыбы», юбка – «одежда».
ОДЕЖДА |
РЫБЫ |
ДЕРЕВЬЯ |
Шуба |
Щука |
Береза |
Брюки |
Акула |
Ель |
Рубашка |
Карась |
Сосна |
Юбка |
Окунь |
Дуб |
|
Лещ |
|
Итог урока:
— Итак, сегодня на уроке мы с вами познакомились с такими понятиями, как «множество» и «элементы множества». Научились определять множество, а также принадлежность элемента заданному множеству.
Научились определять множество, а также принадлежность элемента заданному множеству.
Карточки с заданиями (Слайды 24-30)
Учащимся раздаются карточки с заданиями в виде тестов на два варианта. Проверяется степень усвоения нового материала.
1 вариант:
2 вариант:
Домашнее задание: (Слайд 31)
№10.
Дети должны нарисовать любое множество предметов с общим названием и подписать название под картинкой.
Литература:
- Методические рекомендации для учителя, 2 класс, А.В.Горячев, К.И.Горина, Н.И.Суворова.
- Информатика в играх и задачах, 2 класс, часть 2. А.В.Горячев, К.И.Горина, Н.И.Суворова.
- Информатика тесты, 2 класс, О.Н.Крылова.
Элементы статистики
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.

Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Математика ЭДС
«Я даже не могу представить, какой была бы моя жизнь, если бы я не увидел красоту математики через ЭМП.»
Виви Романелли
Студент EMF
«Мой сын не может перестать говорить о математических идеях, которые он изучает. Он предпочитает использовать ЭДС вместо Minecraft!»
Нэн Розенберри
EMF Родительский
«Я только что начал изучать Calc 3 в Гарварде, и большая часть домашних заданий первых двух недель — это то, что я уже сделал в EMF, так что EMF определенно хорошо подготовил меня».
Томас Фергюсон
Выпускник EMF, бакалавриат Гарварда
«EMF — это способ взглянуть на все, что вы считали само собой разумеющимся в предыдущие годы, и проверить их, чтобы сделать их более подробными и полными. »
»
Ян Гонсалес
Студент EMF
«EMF предоставляет детям возможность математически расширить свои возможности. Чувство выполненного долга, которое получила наша дочь, укрепило ее уверенность в себе и подготовило ее ко всему, что встретится на ее пути».
Мэтт и Эми Кауфман
Родители EMF
«EMF расширил мою способность писать доказательства и мои математические навыки в целом. В нем есть одни из самых интересных математических концепций, которые я когда-либо видел.»
Альберт Ван
Студент EMF
«Теперь, когда я закончил EMF, я могу засвидетельствовать их заявление о том, что их ученики будут готовы к математическому анализу. Сейчас я примерно на полпути к изучению AP Calculus BC, и у меня нет никаких проблем с материалом.»
Александр Юэ
EMF Студент
«Мой сын приходит домой взволнованный, увидев, что будет дальше в EMF. Он абсолютно хочет преуспеть во всем теперь, когда он увидел, как весело учиться».
Венди Диаз
EMF Родитель
«Контент и педагогика самого высокого качества, и я рекомендую это безоговорочно.»
Почетный профессор Джеральд Р. Райзинг
Университет штата Нью-Йорк в Буффало
«Как мама, обучающаяся на дому, я могу сказать вам, что EMF — наша любимая учебная программа — сложная и интересная!»
Мишель Унгер
EMF Родитель
«EMF — сложная программа, но она окупается. Я научился подтверждать концепции и научился работать усерднее и по расписанию».
Андрей Чекмасов
EMF Студент
«Дни изучения математики путем повторения остались в прошлом. Хотя программа EMF предназначена для самостоятельного изучения, она дает ощущение индивидуального обучения с инструктором и по очень разумной цене. Как родитель, я даю EMF А+».
Хорхе Сардинас
Родитель EMF
«После ЭДС я не только понимаю, как пользоваться формулами, но и могу их доказать. Эта программа превратила меня из девушки, любившей математику, в настоящего математика.»
Эта программа превратила меня из девушки, любившей математику, в настоящего математика.»
Скайлар Гамберг
EMF Student
«EMF — курс для студентов, жаждущих математических знаний.»
Люк Фрид
EMF Студент
«Мой сын думал, что ему не нравится математика, пока он не начал изучать ЭМИ. Теперь это его самый любимый предмет. ЭМИ помогли ему обрести уверенность, развить дисциплину и побудить его младшую сестру ценить математическое мышление».
Пурнима Минакшисундарам
Родитель EMF
«Если вы хорошо разбираетесь в математике, но можете спать на уроках математики, потому что считаете их скучными, ЭМП — это круто, и они действительно не дадут вам заснуть».
Изабелла Йенг
Студент EMF
«До EMF моя дочь была разочарована тем, что ее уроки математики были недостаточно интересными, сложными или увлекательными. После EMF она полностью изменила свой взгляд на математику. Я уверен, что она не могла представить себе, что будет заниматься каким-либо другим курсом».
Я уверен, что она не могла представить себе, что будет заниматься каким-либо другим курсом».
Рэйчел Данциг
EMF Родитель
«EMF не только учит, но и вдохновляет. Используя идеи, которые я почерпнул из EMF, я смог показать своим ученикам, что математика — это действительно весело!»
Хоссейн Турджо
Студент EMF
«Мой сын не боится решать любую проблему, потому что с помощью ЭМП его научили думать и рассуждать над проблемой, а не полагаться на заученные формулы».
Карен Прайс
EMF Родитель
«EMF позволяет учащимся избежать ловушки убеждения, что математика — это не что иное, как задачи, которые нужно решать с помощью правил и калькулятора».
Корбин Диас
Студент EMF
«EMF намного интереснее, чем другие математические программы, и держит вас в напряжении. Мне нравится это, даже когда решение самых сложных задач занимает очень много времени.»
Имаан Нанджи
Студент EMF
«Наш сын, обучающийся на дому, активно пользуется образовательными онлайн-ресурсами. Недавно я попросил его выбрать свой любимый онлайн-курс. Он ответил: «Определенно EMF, с большим отрывом».
Недавно я попросил его выбрать свой любимый онлайн-курс. Он ответил: «Определенно EMF, с большим отрывом».
Арвиндер Освал
Родитель EMF
«EMF бросает вызов в хорошем смысле — как головоломка. Вы усердно работаете, совершенствуете свой ум и все равно получаете удовольствие!»
Грейс Хэнкок
EMF Student
«EMF учит очень сложным математическим понятиям, но презентация и наборы задач разработаны таким образом, чтобы дети средних классов могли изучать материал онлайн».
Максим Чекмасов, к.т.н.
EMF Родительский
«Я сдавал тренировочный тест для экзамена AMC8, рассчитанного на время, когда наткнулся на задачу, связанную с нестандартной математикой. Благодаря EMF я уже был знаком с этими идеями и решил задачу намного быстрее».
Пейтон Робертсон
EMF Student
«Нет никаких сомнений в том, что учебная программа «Элементы математики» дала мне навыки логического мышления и умственную основу, которые
вдохновил и позволил мне разработать систему головоломок Chocolate Fix».
Марк Энгельберг
Изобретатель логической игры ThinkFun’s Chocolate Fix
элементов математики | Издательство Принстонского университета
Elements of Mathematics отправляет читателей в увлекательное путешествие, которое начинается с элементарной математики, но, как показывает Джон Стиллвелл, этот предмет не так прост и прост, как можно было бы подумать. Не все темы, которые являются частью сегодняшней элементарной математики, всегда считались таковыми, и для того, чтобы определенные предметы стали «элементарными», должны были произойти великие математические достижения и открытия. Стиллвелл исследует элементарную математику с точки зрения, характерной для двадцать первого века, и описывает не только красоту и масштабы этой дисциплины, но и ее пределы.
От целых чисел Гаусса до логики высказываний Стиллвелл углубляется в арифметику, вычисления, алгебру, геометрию, исчисление, комбинаторику, вероятность и логику. Он обсуждает, как каждая область связана с более сложными темами для построения математики в целом. С помощью богатой коллекции основных принципов, ярких примеров и интересных задач Стиллвелл демонстрирует, что элементарная математика становится продвинутой с вмешательством бесконечности. Бесконечность наблюдалась на протяжении всей математической истории, но недавнее развитие «обратной математики» подтверждает, что бесконечность необходима для доказательства хорошо известных теорем, и помогает определить природу, контуры и границы элементарной математики.
С помощью богатой коллекции основных принципов, ярких примеров и интересных задач Стиллвелл демонстрирует, что элементарная математика становится продвинутой с вмешательством бесконечности. Бесконечность наблюдалась на протяжении всей математической истории, но недавнее развитие «обратной математики» подтверждает, что бесконечность необходима для доказательства хорошо известных теорем, и помогает определить природу, контуры и границы элементарной математики.
Elements of Mathematics дает читателям, от старшеклассников до профессиональных математиков, основные моменты элементарной математики и некоторые части математики за ее пределами.
Награды и признание
- Одна из 10 лучших книг по астрономии, физике и математике 2017 года по версии Forbes.com, выбранная GrrlScientist
Джон Стиллвелл — профессор математики в Университете Сан-Франциско. Он автор Обратная математика: доказательства изнутри наружу (Принстон).
«Отличное исследование элементарной математики, ее ограничений, того, как бесконечность усложняет вещи, и того, как различные разделы математики сочетаются друг с другом. » — Антонио Канджано, Math-Blog
» — Антонио Канджано, Math-Blog
«Стиллвелл… один из лучших современных авторов-математиков: он пишет ясно и увлекательно и прилагает больше усилий, чем другие, чтобы предоставить исторические детали и понять, как различные математические идеи связаны друг с другом… Черты, которые мы привыкли ожидать от Стиллвелла (включая, помимо прочего, превосходное письмо), присутствуют в [9].0187 Elements of Mathematics ]». — MAA Reviews
«Доступное чтение. . . . Стиллвелл раскрывает основы, предоставляя как исторические, так и практические перспективы от арифметики до бесконечности. арифметика, вычисления, алгебра, геометрия, исчисление и т. д. — и в каждой области Стилвеллу удается выделить основные идеи и связи с другими областями. Он мастер толкования, и тексту удается быть увлекательным и доступным, не разбавляя математику. Я определенно узнал много нового из книги!» — Брент Йорги, Не путешествовавший по математике
«За всю жизнь преподавания Стиллвелл выделил несколько прекрасных примеров из всей гаммы элементарной математики». — Mathematical Reviews Clippings
— Mathematical Reviews Clippings
«[A] замечательная книга… Я думаю, что [ Elements of Mathematics ] сама по себе станет современной классикой и справочником для всех, кто пытается изучить основные темы в любой из основные разделы математики». — Виктор Кац, 9 лет0187 Bulletin of the American Mathematical Society
» Elements of Mathematics — прекрасный… обзор области математики… Изложение ясное, краткое, систематизированное, диаграммы [и] иллюстрации превосходны. … Хотя некоторые обсуждения носят вводный или элементарный характер, они всегда ведут к более глубоким и сложным идеям… [Это] станет прекрасным базовым дополнением к книжным полкам большинства математиков». — Математическое танго
«Стиллвелл использует свои обширные и впечатляющие познания в области математики, чтобы провести читателя по каждой теме и перейти на более высокий уровень понимания и вопросов.» — Конвергенция
«[A] замечательная книга. .. Я думаю, что [ Elements of Mathematics ] сама по себе станет современной классикой и справочником для всех, кто пытается изучить основные темы в любой из основных областей. математики». — Виктор Кац, Бюллетень Американского математического общества
.. Я думаю, что [ Elements of Mathematics ] сама по себе станет современной классикой и справочником для всех, кто пытается изучить основные темы в любой из основных областей. математики». — Виктор Кац, Бюллетень Американского математического общества
«[ Элементы математики ] — это книга, которую должен прочитать каждый. Вам от этого станет лучше.» — Reuben Hersh, American Mathematical Monthly
«Читатели, знакомые с предыдущими книгами Стиллвелла… не удивятся, что эта великолепно оформленная книга содержит кристально чистую прозу, которая математически точна, исторически осведомлена, философски чувствительна и богата смыслом. новые повороты и освежающие идеи… Мне очень понравилась эта заставляющая задуматься и очень читабельная книга. Она особенно сильна (и особенно ясна) в отношении фундаментальных вопросов и того, как они теперь пронизывают всю математику и, к концу , я действительно проникся идеей попытаться чутко определить границу между элементарной и высшей математикой». — Ник Лорд, Mathematical Gazette
— Ник Лорд, Mathematical Gazette
«Эта превосходная книга определенно предназначена для математиков и попутчиков. —George Hacken, Computing Reviews
«Эта увлекательная книга Джона Стиллвелла, австралийского математика, получившего престижную премию Шовенэ, представляет собой тщательно структурированный и ясно написанный обзор множества «элементарных» математических тем, начиная с теория, вычислимость, алгебра, геометрия, исчисление, комбинаторика, вероятность и логика… Специалистам это понравится, в то время как остальные узнают много нового». —Forbes.com
«Последовательность математики демонстрируется в этом мастерском, прекрасно написанном синтезе. С помощью наводящих вопросов, ясных объяснений и увлекательных примеров и историй Джон Стиллвелл показывает, откуда взялись, казалось бы, отдельные разделы математики, как они переплетаются и почему скрытый объединяющий элемент является глубочайшей идеей из всех: бесконечностью». — Стивен Строгац, Корнельский университет, автор книги «Радость х»
— Стивен Строгац, Корнельский университет, автор книги «Радость х»
«Это прекрасно написанный обзор и экскурсия по элементарной математике, для неспециалистов. Книга отличается широтой охвата и точными деталями. Она станет классикой в этой области ». — Дэвид Брессоуд, Macalester College
«[A] сложная трактовка тем, обычно описываемых как элементарные». — Джон Аллен Паулос
13.1: Язык множеств и функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 242
- Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг
- Калифорнийский университет в Дэвисе
Всю математику можно рассматривать как изучение отношений между наборами объектов с помощью строгих рациональных рассуждений. Чаще всего закономерности в этих коллекциях и их отношения важнее, чем природа самих объектов. Сила математики во многом связана с выдвижением закономерностей на передний план и абстрагированием от «реальной» природы объектов. В математике наборы обычно называют множествами, а объекты — элементами множества. Функции являются наиболее распространенным типом отношений между множествами и их элементами, и основными объектами изучения в анализе являются функции, имеющие отношение к множеству действительных чисел. Поэтому важно развить хорошее понимание множеств и функций и знать словарь, используемый для определения множеств и функций и обсуждения их свойств.
Чаще всего закономерности в этих коллекциях и их отношения важнее, чем природа самих объектов. Сила математики во многом связана с выдвижением закономерностей на передний план и абстрагированием от «реальной» природы объектов. В математике наборы обычно называют множествами, а объекты — элементами множества. Функции являются наиболее распространенным типом отношений между множествами и их элементами, и основными объектами изучения в анализе являются функции, имеющие отношение к множеству действительных чисел. Поэтому важно развить хорошее понимание множеств и функций и знать словарь, используемый для определения множеств и функций и обсуждения их свойств.
Набор — это неупорядоченный набор различных объектов, которые мы называем его элементами. Множество \(A\) однозначно определяется своими элементами. Если объект а является элементом множества \(А\), мы пишем \(а \в А\) и говорим, что а принадлежит \(А\) или что \(А\) содержит а. Отрицание этого утверждения записывается как \(a \not\in A\), т. е. a не является элементом \(A.\) Обратите внимание, что оба утверждения не могут быть истинными одновременно
е. a не является элементом \(A.\) Обратите внимание, что оба утверждения не могут быть истинными одновременно
Если \(A \) и \(B\) — множества, они идентичны (это означает одно и то же множество), которые мы запишем как \(A = B\), если они имеют точно такие же элементы. Другими словами, \(A = B\) тогда и только тогда, когда для всех \(a \in A\) мы имеем \(a \in B\), а для всех \(b \in B\) мы имеем \(b \in A.\) Эквивалентно \(A \neq B\) тогда и только тогда, когда существует различие в их элементах: существует \(a \in A\) такое, что \(a \not\in B\) или существует \(b \in B\) такое, что \(b \not\in A.\)
Пример B.1.1. Начнем с простейших примеров множеств.
- Пустой набор (он же нулевой набор ) звучит так: набор без элементов. Обычно мы обозначаем его \(\emptyset\) или иногда \(\{~\}\). Пустое множество \(\emptyset\) однозначно определяется тем свойством, что для всех \(x\) мы имеем \(x \not\in \emptyset\).
 Ясно, что существует ровно одно пустое множество.
Ясно, что существует ровно одно пустое множество. - Далее идут синглтона . Синглтон — это множество, состоящее ровно из одного элемента. Если этот элемент равен \(x\), мы часто пишем синглтон, содержащий \(x\), как \(\{x\}\). В разговорном языке «одиночка \(x\)» на самом деле означает множество \(\{x\}\) и его всегда следует отличать от элемента \(x: x \neq \) {\(x\)} . Множество может быть элементом другого множества, но ни одно множество не является элементом самого себя (точнее, мы принимаем это как аксиому). Например, \(\{\{x\}\}\) — это синглтон, единственным элементом которого является синглтон \(\{x\}\). В частности, мы также имеем \(\{x\} \neq \{\{x\}\}.\)
- Одним из стандартных способов обозначения множеств является перечисление их элементов. Например, набор \(\{\alpha, \beta, \gamma\}\) содержит первые три строчные греческие буквы. Набор полностью определяется тем, что есть в списке. Порядок, в котором перечисляются элементы, значения не имеет.
 Таким образом, мы имеем \(\{\alpha, \gamma, \beta\} = \{\gamma, \beta, \alpha\} = \{\alpha, \beta, \gamma\},\) и т. д. Поскольку набор не может содержать один и тот же элемент дважды (элементы различны) единственное разумное значение чего-то вроде \(\{ \alpha, \beta, \alpha, \gamma\}\) состоит в том, что это то же самое, что и \(\{ \альфа, \бета, \гамма\}\). Поскольку \(x \neq \{x\}, \{x, \{x\}\}\) — множество из двух элементов. Что угодно можно рассматривать как элемент множества, и от элементов множества не требуется никакого отношения. Например, слово «яблоко», элемент уран и планета Плутон могут быть тремя элементами множества. Нет никаких ограничений на количество различных множеств, которым может принадлежать данный элемент, за исключением правила, согласно которому множество не может быть элементом самого себя.
Таким образом, мы имеем \(\{\alpha, \gamma, \beta\} = \{\gamma, \beta, \alpha\} = \{\alpha, \beta, \gamma\},\) и т. д. Поскольку набор не может содержать один и тот же элемент дважды (элементы различны) единственное разумное значение чего-то вроде \(\{ \alpha, \beta, \alpha, \gamma\}\) состоит в том, что это то же самое, что и \(\{ \альфа, \бета, \гамма\}\). Поскольку \(x \neq \{x\}, \{x, \{x\}\}\) — множество из двух элементов. Что угодно можно рассматривать как элемент множества, и от элементов множества не требуется никакого отношения. Например, слово «яблоко», элемент уран и планета Плутон могут быть тремя элементами множества. Нет никаких ограничений на количество различных множеств, которым может принадлежать данный элемент, за исключением правила, согласно которому множество не может быть элементом самого себя. - Количество элементов в наборе может быть бесконечным. Например, \(\mathbb{Z}, \mathbb{R},\) и \(\mathbb{C}\) обозначают множества всех целых, действительных и комплексных чисел соответственно.
 Не обязательно, чтобы мы могли перечислить все элементы.
Не обязательно, чтобы мы могли перечислить все элементы.
При введении нового набора (нового для целей данного обсуждения) крайне важно дать ему однозначное определение. Не требуется, чтобы из данного определения множества \(А\) было легко определить, каковы элементы \(А\) или даже сколько их, но должно быть ясно, что в принципе , на каждый вопрос вида «является ли \(x\) элементом \(A\)?» существует единственный и однозначный ответ. Существует несколько распространенных способов определения множеств. Вот несколько примеров.
Пример B.1.2.
1. Самый простой способ — это обобщение списочной нотации на бесконечные списки, которые можно описать шаблоном. Например, множество положительных целых чисел \(\mathbb{N} = \{1, 2, 3, \ldots \}.\) Список может быть двунаправленным, как и в наборе всех целых чисел \( \mathbb{Z} = \{\ldots , -2, -1, 0, 1, 2, \ldots \}.\)
Обратите внимание на использование тройных точек \(\ldots\) для обозначения продолжения списка .
2. Так называемая нотация построителя наборов дает больше возможностей для описания членства в наборе. Например, множество всех четных целых чисел, часто обозначаемое как \(2 \mathbb{Z}\), определяется как
\[2\mathbb{Z} = \{2a ~|~ a \in \mathbb{Z}\} .\]
Вместо вертикальной черты | часто используется двоеточие :, . Например, открытый интервал действительных чисел строго между \(0\) и \(1\) определяется как
\[(0, 1) = \{x \in \mathbb{R} : 0 < x < 1\}.\]
Определение B.2.1. Пусть \(A\) и \(B\) — множества. \(B\) является подмножеством \(A\), обозначаемым \(B \subset A\), тогда и только тогда, когда для всех \(b \in B\) мы имеем \(b \in A.\ ) Если \(B \subset A\) и \(B \neq A,\), мы говорим, что \(B\) есть правильное подмножество из \(A.\)
Если \(B \subset A\), то также говорят, что \(B\) содержится в \(A\) или что \(A\) содержит \ (B\), которое иногда обозначается как \(A \supset B.\) Отношение \(\subset\) называется включением . Если \(B\) является собственным подмножеством \(A\), то включение называется строгим. Чтобы подчеркнуть, что включение не обязательно строгое, можно использовать обозначение \(B \subseteq A\), но обратите внимание, что его математический смысл идентичен \(B \subset A.\). Строгое включение иногда обозначается \(B \subsetneq A\), но встречается реже.
Если \(B\) является собственным подмножеством \(A\), то включение называется строгим. Чтобы подчеркнуть, что включение не обязательно строгое, можно использовать обозначение \(B \subseteq A\), но обратите внимание, что его математический смысл идентичен \(B \subset A.\). Строгое включение иногда обозначается \(B \subsetneq A\), но встречается реже.
Пример B.2.2. Легко проверить следующие соотношения между множествами:
- Имеем \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C }\), и все эти включения являются строгими.
- Для любого множества \(A\) мы имеем \(\пустое множество\подмножество A\) и \(A \подмножество A.\)
- \((0, 1] \подмножество (0, 2). \)
- Для \(0 < a \leq b, [-a, a] \subset [-b, b].\) Включение является строгим, если \(a < b.\)
Помимо непосредственного построения множеств, множества можно также получить из других множеств с помощью ряда стандартных операций. Следующее определение вводит основные операции объединения , пересечения и разности множеств.
Следующее определение вводит основные операции объединения , пересечения и разности множеств.
Определение B.2.3 . Пусть \(A\) и \(B\) — множества. Тогда
- объединение \(A\) и \(B\), обозначаемое \(A \cup B\), определяется как \[A \cup B = \{x ~|~ x \ в A {\it{~или~}} x \in B\}.\]
- Пересечение точек \(A\) и \(B\), обозначаемое \(A \cap B\), определяется как \[A \cap B = \{x~ |~ x \in A {\it{~и~}} x \in B\}.\]
- Множество разностей \(B\) от \(A\), обозначаемое \(A \setminus B\), есть определяется как \[A \setminus B = \{x ~|~ x \in A {\it{~and~}} x \not\in B\}.\]
Часто контекст предоставляет «вселенную ‘ из всех возможных элементов, имеющих отношение к данному обсуждению. Предположим, мы дали такое множество «всех» элементов и назовем его \(U\). Затем 9c .\)
 \)
\)Чтобы ознакомиться с основными свойствами множеств и основными операциями над множествами, хорошим упражнением будет написание доказательств. для трех свойств, указанных в теореме.
Так называемое декартово произведение множеств — это мощный и вездесущий метод построения новых множеств из старых. 92 = \mathbb{R} \times \mathbb{R}\). Не случайно \(х\) и \(у\) в паре \((х, у)\) называют декартовыми координатами точки \((х, у)\) в самолет.
В этом разделе мы вводим два важных типа отношений: отношения порядка и отношения эквивалентности. Отношение \(R\) между элементами множества \(A\) и элементами множества \(B\) является подмножеством их декартова произведения: \(R \subset A \times B.\) Когда \(A = B\), мы также называем \(R\) просто отношением на \(A\).
Пусть \(A\) множество и \(R\) отношение на \(A\). Тогда
- \(R\) называется рефлексивным , если для всех \(a \in A, (a, a) \in R.
 \)
\) - \(R\) называется симметричным , если для все \(a, b \in A,\) если \((a, b) \in R\), то \((b, a) \in R.\)
- \(R\) называется антисимметричным , если для всех \(a, b \in A\) таких, что \((a, b) \in R\) и \((b, a) \in R, a = b.\)
- \( R\) называется транзитивным , если для всех \(a, b, c \in A\) таких \((a, b) \in R\) и \((b, c) \in R\), имеем \((a, c) \in R.\)
Определение B.3.1. . Пусть \(R\) — отношение на множестве \(A\). \(R\) является отношением порядка , если \(R\) является рефлексивным, антисимметричным и транзитивным . \(R\) является отношением эквивалентности, если \(R\) рефлексивно, симметрично и транзитивно.
Понятие подмножества является примером отношения порядка. Чтобы убедиться в этом, сначала определим степенное множество множества \(A\) как множество всех его подмножеств. Его часто обозначают \({\cal{P}}(A). \). Таким образом, для любого множества \(A, {\cal{P}}(A) = \{B : B \subset A\} .\) Отношение включения определяется как отношение \(R\) установкой
\). Таким образом, для любого множества \(A, {\cal{P}}(A) = \{B : B \subset A\} .\) Отношение включения определяется как отношение \(R\) установкой
\[R = \{(B, C) \in {\cal{P}}(A) \times {\cal{P}}(A)~ |~ B \subset C\}\]
Важные отношения, такие как отношение подмножества, имеют удобную нотацию вида \(a
Предложение B.3.2. Включение — это отношение порядка. В явном виде
- ( рефлексив ) Для всех \(B \in {\cal{P}}(A), B \subset B.\)
- ( антисимметричный ) Для всех \(B, C \in {\cal{P}}(A),\) , если \(B \subset C\) и \(C \subset B\), затем \(B = C.\)
- ( транзитивное ) Для всех \(B, C, D \in {\cal{P}}(A),\) если \(B \subset C\) и \(C \subset D,\) затем \(B \subset D.\)
В качестве упражнения напишите доказательство этого предложения.
Для любого отношения \(R \subset A \times B\), 9{-1} = \{(b, a) \in B \times A ~| ~(a, b) \in R\}.\]
Пусть \(A\) и \(B\) — множества. Функция с доменом \(A\) и кодоменом \(B\), обозначаемая \(f : A \rightarrow B\), является отношением между элементами \(A\) и \( B\), удовлетворяющие следующим свойствам: для всех \(a \in A,\) существует единственное \(b \in B\) такое, что \((a, b) \in f \). Символ, используемый для обозначения функции как отношения, представляет собой стрелку: \((a, b) \in f\) записывается как \(a \стрелка вправо b\) (часто также \(a \mapsto b\)). Нет необходимости и несколько громоздко напоминать себе, что функции представляют собой отношение особого рода и все время используется более удобное обозначение: \(f (a) = b.\) Если \(f\) равно функция, которую мы имеем, по определению, \(f (a) = b\) и \(f (a) = c\) влечет \(b = c\). Другими словами, для каждого \(a \in A\) существует ровно один \(b \in B\) такой, что \(f (a) = b. \) \(b\) называется изображение под \(f\) . Когда \(A\) и \(B\) являются наборами чисел, \(a\) иногда называют аргументом функции, а \(b = f (a)\) часто называют значение из \(f\) в \(a\).
\) \(b\) называется изображение под \(f\) . Когда \(A\) и \(B\) являются наборами чисел, \(a\) иногда называют аргументом функции, а \(b = f (a)\) часто называют значение из \(f\) в \(a\).
Требование существования образа \(b \in B\) для всех \(a \in A\) иногда ослабляется в том смысле, что областью определения функции является подмножество \ (иногда явно не указанное) (А\). Однако важно помнить, что функция не определена должным образом, если мы также не указали ее область определения.
Когда мы рассматриваем график функции, мы полагаемся на определение функции как отношения. График \(G\) функции \(f : A \rightarrow B\) — это подмножество \(A \times B\), определяемое формулой
\[G = \{(a, f (a)) ~|~ a \in A\}.\]
диапазон функции \(f : A \rightarrow B\), обозначаемый \(range (f ),\) или также \(f (A ),\) — это подмножество его области значений, состоящее из всех \(b \in B\), являющихся образом некоторого \(a \in A:\) 9{-1} (b) = \emptyset\) тогда и только тогда, когда \(b \in B \setminus range (f ). \)
\)
Функции различных видов широко распространены в математике, и был разработан большой словарный запас, некоторые из что избыточно. Термин карта часто используется в качестве альтернативы функции, а когда домен и кодовый домен совпадают, термин преобразование часто используется вместо функции. Существует большое количество терминов для функций в конкретном контексте со специальными свойствами. Три основных свойства даны в следующем определении.
Определение B.4.1. Пусть \(f : A \rightarrow B\) функция. Тогда мы называем \(f\)
- инъективным (\(f\) является инъекцией ), если \(f (a) = f (b)\) следует \(a = b\). Другими словами, никакие два элемента домена не имеют одинаковых изображений. Инъективную функцию также называют взаимно однозначной .
- сюръекция (\(f\) является сюръекцией ), если \(диапазон (f ) = B.\) Другими словами, каждый \(b \in B\) является образом хотя бы одного \ (а \в А\).
 Такая функция также называется на .
Такая функция также называется на . - биективно (\(f\) есть биекция ), если \(f\) одновременно инъективно и сюръективно, т. е. взаимно однозначно и на . Это означает, что f дает однозначное соответствие между всеми элементами \(A\) и всеми элементами \(B\).
Пусть \(f : A \rightarrow B\) и \(g : B \rightarrow C\) две функции, так что область определения \(f\) совпадает с областью определения \(g\). Тогда композиция ‘\(g\) после \(f\) ‘, обозначаемая \(g \circ f\) , представляет собой функцию \(g \circ f : A \rightarrow C,\), определяемую формулой \(a \mapsto g(f (a)).\) 9{-1} .\]
Докажите это предложение в качестве упражнения.
- Исайя Ланкхэм, математический факультет Калифорнийского университета в Дэвисе
- Бруно Нахтергаэле, математический факультет Калифорнийского университета в Дэвисе
- Энн Шиллинг, математический факультет Калифорнийского университета в Дэвисе
Версии этого учебника в твердом и мягком переплете доступны онлайн на сайте WorldScientific. com.
com.
Эта страница под названием 13.1: Язык множеств и функций распространяется по незаявленной лицензии, ее авторами, ремиксами и/или кураторами являются Исайя Лэнкхэм, Бруно Нахтергаэле и Энн Шиллинг.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг
- Показать страницу TOC
- нет
- Теги
- автортег:шиллинг
Расширение предметной области и идеальные элементы в математике† | Philosophia Mathematica
Abstract
Расширение предметной области в математике происходит всякий раз, когда данная математическая область расширяется, чтобы включить в нее новые элементы. Мандерс утверждает, что преимущества важных случаев расширения домена охватываются теоретико-модельными понятиями экзистенциального закрытия и завершения модели. Я утверждаю, что в конкретном случае расширения домена с помощью идеальных элементов предложенного Мандерсом объяснения недостаточно. Затем я разрабатываю и формализую другой подход к расширению домена, основанный на 9 методах Дедекинда.0433 Habilitationsrede , с которым сравнивается счет Мандерса. Я заканчиваю рассмотрением трех возможных подходов к расширениям с помощью идеальных элементов.
Мандерс утверждает, что преимущества важных случаев расширения домена охватываются теоретико-модельными понятиями экзистенциального закрытия и завершения модели. Я утверждаю, что в конкретном случае расширения домена с помощью идеальных элементов предложенного Мандерсом объяснения недостаточно. Затем я разрабатываю и формализую другой подход к расширению домена, основанный на 9 методах Дедекинда.0433 Habilitationsrede , с которым сравнивается счет Мандерса. Я заканчиваю рассмотрением трех возможных подходов к расширениям с помощью идеальных элементов.
1. ВВЕДЕНИЕ
В теории поля, алгебраической теории чисел и теории Галуа часто изучают числовые области вида |$\mathbb{Z}[\sqrt 2]$|, |$\mathbb{Q} [i]$|, |$\mathbb{R}(i)$|, и т. д. . Это числовые области, которые получаются из |$\mathbb{Z}$|, |$\mathbb{Q}$| и |$\mathbb{R}$| соответственно с помощью примыкающих новых элементов. Это означает, что новые элементы добавляются к старой структуре, а затем математик работает со структурой, которая получается, когда расширенная область закрывается в результате операций, которые уже были определены в старой области. Аналогичную процедуру можно провести и в геометрии. Там можно рассматривать проективную плоскость как полученную добавлением точек и линий в бесконечность к стандартной евклидовой плоскости, а затем замыканием структуры под, например, , , линейными преобразованиями. Исторически сложилось так, что некоторые успешные случаи таких расширений доменов стали называться расширениями через идеальных элементов (см. обсуждение идеальных элементов в трудах Дедекинда, а также Гаусса, Веронезе и других, содержащееся в [Cantù, 2013], резюмированное ниже в § 2).
Аналогичную процедуру можно провести и в геометрии. Там можно рассматривать проективную плоскость как полученную добавлением точек и линий в бесконечность к стандартной евклидовой плоскости, а затем замыканием структуры под, например, , , линейными преобразованиями. Исторически сложилось так, что некоторые успешные случаи таких расширений доменов стали называться расширениями через идеальных элементов (см. обсуждение идеальных элементов в трудах Дедекинда, а также Гаусса, Веронезе и других, содержащееся в [Cantù, 2013], резюмированное ниже в § 2).
Философское значение идеальных элементов и метода идеальных элементов в основном обсуждалось в контексте философии математики Гильберта [ср. Детлефсен, 1993; Халлетт, 1990; Стиллвелл, 2014]. В своей лекции 1919 г. «Роль идеальных сущностей» [Hilbert, 1992, с. 90–101] Гильберт характеризует метод идеальных элементов как состоящий в переходе от данной «системы», в которой решение определенных вопросов затруднено, к тот, где такие вопросы становятся простыми для решения ( оп. цит. ., стр. 90–91). Кроме того, новая система содержит подсистему, изоморфную старой системе. Таким образом, по крайней мере, согласно Гильберту, идеальные элементы вводятся для упрощения определенных математических задач, сохраняя при этом прежние условия, в которых эти проблемы возникли.
цит. ., стр. 90–91). Кроме того, новая система содержит подсистему, изоморфную старой системе. Таким образом, по крайней мере, согласно Гильберту, идеальные элементы вводятся для упрощения определенных математических задач, сохраняя при этом прежние условия, в которых эти проблемы возникли.
Однако помимо Гильберта другие математики, такие как Понселе (см., например, [Chemla, 2016]), Куммер и Дедекинд [Cantù, 2013], говорят об идеальных элементах; это говорит о том, что расширение домена с помощью идеальных элементов, возможно, понималось как математический метод еще до Гильберта. Помимо уже цитировавшейся трактовки идеальных элементов в контексте философии Гильберта, систематическое исследование того, что делает расширения предметной области успешными и, в частности, расширения предметных областей с помощью идеальных элементов, можно найти только в [Manders, 1989], где Мандерс делает набросок учетной записи для расширения домена. Мандерс утверждает, что работать с расширенными доменами продуктивно, поскольку они представляют собой экзистенциальное закрытие исходного домена. Другими словами, для того чтобы расширенный домен считался хорошим расширением домена, достаточно, чтобы он был экзистенциальным замыканием домена, который он расширяет.
Другими словами, для того чтобы расширенный домен считался хорошим расширением домена, достаточно, чтобы он был экзистенциальным замыканием домена, который он расширяет.
В этой статье, однако, я утверждаю, что если мы понимаем идеальные элементы как эвристические инструменты, дающие математику определенные прагматические или эпистемические преимущества, то предложенное Мандерсом объяснение плодотворности расширений предметной области может быть лишь частичным, поскольку оно не может объяснить некоторые исторически важные случаи расширения домена с помощью идеальных элементов. Затем я обращусь к другому подходу к расширению предметной области, вдохновленному Дедекиндом [1854], и буду отстаивать точку зрения, согласно которой при правильной интерпретации он может обеспечить основу для расширений предметной области, мотивируемых замыканием по свойствам и операциям. Учитывая исторический контекст, в котором была написана [Dedekind, 1854], в § 6 я исследую вопрос о том, как этот второй критерий поживает по отношению к параллельным разработкам в теории чисел. Я заключаю (§§7, 8), что сравнение между моделью Мандерса и моей оставляет нам три различных варианта философского подхода к расширению предметной области с помощью идеальных элементов в математике.
Я заключаю (§§7, 8), что сравнение между моделью Мандерса и моей оставляет нам три различных варианта философского подхода к расширению предметной области с помощью идеальных элементов в математике.
2. ИДЕАЛЬНЫЕ ЭЛЕМЕНТЫ
Cantù [2013] предлагает исторически обоснованную реконструкцию роли идеальных элементов в наборе инструментов математика. Она утверждает, что «идеальные», «воображаемые» математические объекты использовались математиками в своих доказательствах или построении теорий всякий раз, когда общепринятая математическая область не оправдывала их стремления к определенному упрощению или обобщению математики. Таким образом, введение идеальных элементов оправдано в глазах математика на основании следующего аргумента:
- Посылка (1)
Я, как математик, имею цель (|$G»$|) устранить исключения, разрешить прямые и обратные операции для удовлетворения свойств замыкания, а двойные преобразования между моделями для быть введены, когда это возможно.

- Посылка (2)
Цель (|$G»$|) поддерживается набором значений (|$V$|) и (|$V’$|) .
- Посылка (3)
Метод введения идеальных элементов является для меня как математика средством достижения (|$G»$|).
- Заключение (4)
Поэтому я должен (практически должен) ввести идеальные элементы. [Cantù, 2013, pp. 86, 88]
Значения, которые Канту признает поддерживающими цель математика, следующие:
(|$V$|) Значение |$V$|. Общность теории, , т. е. , отсутствие исключений — желательная ценность в математике [Cantù, 2013, p. 83];
(|$V’$|) Значение |$V’$| в качестве гарантии стоимости |$V$|. Общность желательна, потому что она увеличивает простоту [Cantù, 2013, p. 84].
Канту реконструирует этот аргумент на основе работ Гильберта, Дедекинда, Гаусса и Веронезе. Новые элементы идеальные или воображаемые и т. д. . потому что они могут обладать онтологическим, эпистемическим или прагматическим статусом, отличным от «реальных» элементов. Другими словами, они могут существовать в другом смысле; они могут быть менее эпистемически безопасными; или они могут использоваться иначе, чем настоящие элементы [Cantù, 2013, стр. 79–80].
д. . потому что они могут обладать онтологическим, эпистемическим или прагматическим статусом, отличным от «реальных» элементов. Другими словами, они могут существовать в другом смысле; они могут быть менее эпистемически безопасными; или они могут использоваться иначе, чем настоящие элементы [Cantù, 2013, стр. 79–80].
Приведенный выше аргумент призван защитить использование идеальных элементов в работах этих математиков, основанный на их собственных работах по этому вопросу. Канту, однако, не утверждает, что только этот аргумент оправдывает использование отдельными математиками идеальных элементов — она отмечает, однако, что некоторые математики используют приведенный выше аргумент для оправдания принятия идеальных элементов в своей практике. Этот аргумент не может объяснить, например, почему математик подписывается на (|$G»$|) или что происходит, когда (|$G»$|) противоречит другой математической цели. В зависимости от математика, эти вопросы отбиваются разными аргументами. 1
1
Остановившись, таким образом, на рабочем понятии идеальных элементов как эвристических инструментов, обладающих эпистемическими и/или прагматическими преимуществами, я теперь представляю первый из двух подходов к расширению предметной области с помощью идеальных элементов, рассматриваемых в этой статье.
3. СТРУКТУРА МАНДЕРСА
Мандерс [1989] предлагает использовать понятия экзистенциального замыкания и завершения модели из теории моделей, чтобы объяснить, почему некоторые исторические случаи расширения предметной области, включая некоторые важные случаи расширения посредством идеальных элементов, математически плодотворны. Прежде чем обрисовать предложение Мандерса, необходимо сделать несколько терминологических пояснений. Для остальной части бумаги, структура |$\mathcal{A}$| представляет собой упорядоченную пару, где первый элемент представляет собой набор отдельных лиц, который мы называем доменом |$A$|, а второй элемент представляет собой интерпретацию всех символов данного языка |$\mathcal {L}$| в |$\mathcal{A}$|. n$| в |$A$| [см., например ., Tent and Ziegler, 2012, с. 2]. Теперь пусть теория |$T$| быть набором предложений в |$\mathcal{L}$|. Если |$\mathcal{A}$| делает эти предложения истинными, мы говорим, что |$\mathcal{A}$| является моделью |$T$| [Тент и Циглер, 2012, с. 10]. Теперь мы можем сказать, в чем состоит экзистенциальное замыкание. Грубо говоря, экзистенциальное замыкание — это свойство, проявляемое структурой |$\mathcal{A}$|, рассматриваемой как модель данной теории |$T$|, или, что то же самое, как член класса |$K$| структур (класс всех и только тех структур, которые являются моделями |$T$|), всякий раз, когда |$\mathcal{A}$| содержит в своей области определения все решения уравнений и неравенств, которые могут быть выражены на языке |$\mathcal{A}$|. Этот язык должен быть языком первого порядка без символов отношения.
n$| в |$A$| [см., например ., Tent and Ziegler, 2012, с. 2]. Теперь пусть теория |$T$| быть набором предложений в |$\mathcal{L}$|. Если |$\mathcal{A}$| делает эти предложения истинными, мы говорим, что |$\mathcal{A}$| является моделью |$T$| [Тент и Циглер, 2012, с. 10]. Теперь мы можем сказать, в чем состоит экзистенциальное замыкание. Грубо говоря, экзистенциальное замыкание — это свойство, проявляемое структурой |$\mathcal{A}$|, рассматриваемой как модель данной теории |$T$|, или, что то же самое, как член класса |$K$| структур (класс всех и только тех структур, которые являются моделями |$T$|), всякий раз, когда |$\mathcal{A}$| содержит в своей области определения все решения уравнений и неравенств, которые могут быть выражены на языке |$\mathcal{A}$|. Этот язык должен быть языком первого порядка без символов отношения.
Согласно Мандерсу, при расширении домена посредством экзистенциального замыкания математик пытается сохранить три вещи: исходный домен объектов, который мы хотим расширить без изменения объектов, с которых мы начали; условия на указанные объекты, от которых мы не хотим отказываться, которые он называет «инвариантными условиями» (сокращенно «инварианты»), обозначаемые как |$\varphi(), \psi(), \dots$|; и свойства, которые порождаются этими условиями, предложения формы |$\forall \overline{x}\varphi(\overline{x})$|, где |$\varphi()$| сам является инвариантом. В то время как первое, а именно объекты, почти всегда сохраняются, от инвариантов и свойств, которые они порождают, иногда приходится отказываться, чтобы иметь место желаемое расширение. Мандерс утверждает, что этот (неформальный) процесс имеет формальный аналог в понятии экзистенциальной замкнутости:
В то время как первое, а именно объекты, почти всегда сохраняются, от инвариантов и свойств, которые они порождают, иногда приходится отказываться, чтобы иметь место желаемое расширение. Мандерс утверждает, что этот (неформальный) процесс имеет формальный аналог в понятии экзистенциальной замкнутости:
Цель Мандерса состоит в том, чтобы убедить своего читателя, что, используя экзистенциальное замыкание (и завершение модели, где это применимо) современной теории моделей для концептуализации исторических случаев расширения предметной области в математике, можно провести анализ того, что определяет выбор плодотворных теорий. в математике.
Дальнейшее утверждение Мандерса состоит в том, что если мы понимаем хорошие доменные расширения с точки зрения экзистенциальной замкнутости, то мы учитываем концептуальную унификацию, которую обеспечивают такие расширения ( там же. , с. 554). Так концептуальное единство следует из экзистенциальной замкнутости. Как только данная область экзистенциально замкнута, новая структура, рассматриваемая как модель старой теории, будет такова, что для определенных предложений они будут либо универсальными, либо не будут выполняться вообще (Мандерс называет это «выдавливанием среднего случая»). . Пример Мандерса состоит в том, что уравнения второй степени в некоторых случаях имеют решение только для действительных чисел, но как только это распространяется на комплексные числа, каждое уравнение второй степени имеет решение в расширенной области.
Как только данная область экзистенциально замкнута, новая структура, рассматриваемая как модель старой теории, будет такова, что для определенных предложений они будут либо универсальными, либо не будут выполняться вообще (Мандерс называет это «выдавливанием среднего случая»). . Пример Мандерса состоит в том, что уравнения второй степени в некоторых случаях имеют решение только для действительных чисел, но как только это распространяется на комплексные числа, каждое уравнение второй степени имеет решение в расширенной области.
Понятие экзистенциального замыкания весьма распространено в алгебре: мы можем говорить об экзистенциально замкнутой (э.к.) решетке, э.к. группа, э.к. поле. Тем не менее, говоря об э.к., нужно проявлять некоторую осторожность. структур, ибо само понятие всегда относится к классу структур. В случае полей, например, если |$K$| есть класс моделей теории поля, то э.к. структуры являются в точности алгебраически замкнутыми полями (см., напр. , [Ходжес, 1993, с. 362]). Если |$К$| с другой стороны, это класс моделей теории упорядоченных полей, то э.к. структуры — это реальные замкнутые поля, где алгебраически замкнутые и реально замкнутые поля не являются экстенсионально одним и тем же классом структур.
362]). Если |$К$| с другой стороны, это класс моделей теории упорядоченных полей, то э.к. структуры — это реальные замкнутые поля, где алгебраически замкнутые и реально замкнутые поля не являются экстенсионально одним и тем же классом структур.
Если экзистенциальная замкнутость в каком-то смысле довольно распространена, что делает ее примечательной для целей объяснения преимуществ доменных расширений? Короче говоря, экзистенциальная замкнутость может стать ступенькой к важной теоретико-модельной особенности некоторых теорий9.квантификатор 0433, исключение (или свойства, которые могут аппроксимировать преимущества, обеспечиваемые собственно исключением квантификатора). Теория |$T$| говорят, что квантор исключается всякий раз, когда для любой формулы |$\varphi$| на языке |$T$|, |$T$| доказывает, что |$\varphi$| эквивалентна бескванторной формуле. Исключение кванторов — важная теоретико-модельная особенность алгебраических теорий, поскольку она позволяет доказывать математически богатые результаты, такие как Nullstellensatz 9. 0434 . 3
0434 . 3
4. РАСШИРЕНИЯ ОБЛАСТИ И ИДЕАЛЬНЫЕ ЭЛЕМЕНТЫ
Цель Мандерса состоит в том, чтобы использовать случаи исторических расширений предметной области, которые оказываются экзистенциальными замыканиями ранее существовавших моделей 4 в качестве доказательства против утверждения, что плодотворность математических теорий является эмпирическим , исторический факт. Мандерс также предполагает, что экзистенциальная замкнутость — это формальное теоретико-модельное понятие, которое отражает (Гильбертовский) метод идеальных элементов. На первый взгляд, Мандерс рассматривает экзистенциальную замкнутость как достаточное условие успеха некоторых расширений предметной области — в частности, успешных расширений предметной области, которые Гильберт рассматривал бы как расширения посредством идеальных элементов. Меня интересует область применения этого объяснения.
Одним из примеров идеальных элементов Гильберта являются линии и точки, удаленные на бесконечность. Мандерс [1984] показывает, как при определенных условиях модели проективной геометрии являются экзистенциальными замыканиями евклидовой плоскости. Так что в этом смысле объяснение Мандерса верно в случае идеальных элементов в геометрии.
Мандерс [1984] показывает, как при определенных условиях модели проективной геометрии являются экзистенциальными замыканиями евклидовой плоскости. Так что в этом смысле объяснение Мандерса верно в случае идеальных элементов в геометрии.
А как насчет арифметики и алгебры? Позвольте мне начать с самого простого случая, а именно с комплексных чисел. Если мы рассмотрим поле комплексных чисел |$\mathbb{C}$| как структура в классе моделей теории полей, то, поскольку оно является алгебраически замкнутым полем, оно фактически экзистенциально замкнуто (это почти сразу следует из определений). Более того, теория алгебраически замкнутых полей является модельно-полной. Таким образом, схема Мандерса хорошо подходит для этого случая — и действительно, если мы оглянемся назад на то, как он ввел понятие экзистенциальной замкнутости, он в общем говорил обо всех тех случаях, в которых математическая область «закругляется» примыкающими корнями. Это ровно один из способов построения комплексных чисел, как |$\mathbb{R}(i)$|. Более того, его историческая дискуссия в [Manders, 1989] можно рассматривать как способ демонстрации того, как расширение вещественных чисел в комплексную систему счисления является одним из тех случаев расширения домена, которое обеспечивает концептуальное единство; можно рассматривать уравнения, которые раньше анализировались отдельно, как члены одного и того же класса уравнений.
Более того, его историческая дискуссия в [Manders, 1989] можно рассматривать как способ демонстрации того, как расширение вещественных чисел в комплексную систему счисления является одним из тех случаев расширения домена, которое обеспечивает концептуальное единство; можно рассматривать уравнения, которые раньше анализировались отдельно, как члены одного и того же класса уравнений.
4.1. Бесконечно малые как идеальные элементы
Следующий случай, который можно рассмотреть, — бесконечно малые. Хотя бесконечно малые числа явно не перечислены Гильбертом как один из канонических случаев идеальных элементов в его [1984], как и другие авторы, считает Канту, 5 . Я кратко проиллюстрирую, как современные авторы, такие как Робинсон [1996] и Голдблатт [1998], представляют преимущества работы в нестандартном анализе.
В своей работе [1996, с. 1–3] Робинсон пишет, что «смысл» предела более привлекателен, если он задан в терминах бесконечно малых величин — он проще. 6 Более того,
6 Более того,
Идеи Лейбница [то есть исчисление бесконечно малых] могут привести к плодотворный подход к классическому анализу и ко многим другим разделам математики. [|$\dots$|] Бесконечно малые числа имеют топологические обобщения, которые приводят к плодотворным приложениям. [Робинсон, 1996, с. 2, курсив добавлен]
Таким образом, бесконечно малые плодотворны; они ведут к упрощениям и обобщениям в математике.
Точно так же читаем в предисловии к [Goldblatt, 1998]:
Что предлагает нестандартный анализ для нашего понимания математики? [|$\dots$|] Новые определения знакомых понятий, часто более простые [|$\dots$|] Новые и содержательные (часто более простые) доказательства знакомых теорем. [Голдблатт, 19 лет98, с. vii]
Таким образом, по крайней мере некоторые математики, кажется, выступают в пользу бесконечно малых величин, потому что они допускают более четкие доказательства, более ясное выражение основополагающих понятий и новые результаты. Они утверждают, что работа с бесконечно малыми дает некоторые эпистемологические преимущества. Хотя приведенные выше цитаты не являются убедительным доказательством в этом отношении, кажется разумным допустить бесконечно малые под эгидой идеальных элементов, как их понимал Канту. 7
Они утверждают, что работа с бесконечно малыми дает некоторые эпистемологические преимущества. Хотя приведенные выше цитаты не являются убедительным доказательством в этом отношении, кажется разумным допустить бесконечно малые под эгидой идеальных элементов, как их понимал Канту. 7
Таким образом, предложение Мандерса, по-видимому, хорошо работает в нескольких случаях присоединения идеальных элементов, но не во всех. 8 Хотя это не подрывает его предложение экзистенциальной замкнутости как одного из достаточных условий для того, чтобы считать расширение предметной области хорошим или успешным, оно, похоже, предполагает, что его объяснение традиционных теоретических достоинств через теоретико-модельные более ограничено, чем может показаться с первого взгляда. Если присоединение бесконечно малых не является случаем экзистенциальной замкнутости, «плодотворность» и «упрощение», обеспечиваемые бесконечно малыми, остаются необъясненными в рамках Мандерса.
В следующем разделе я представлю альтернативную концептуализацию расширений предметной области и рассмотрю, может ли она объяснить статус бесконечно малых как идеальных элементов.
5. РАСШИРЕНИЕ ОБЛАСТИ В СООТВЕТСТВИИ С ДЕДЕКИНДОМ
В примечании к своей статье Мандерс мимоходом ссылается на альтернативный способ представления расширений домена для числовых доменов, называемый законом постоянства форм [Мандерс, 1989, с. 555]. Там он резюмирует содержание закона постоянства как требование, чтобы определенные универсальные свойства основных арифметических операций сохранялись в расширении математической области. Мандерс, кажется, быстро отвергает закон постоянства как недостаточно конкретный в определении того, какие свойства стоит сохранять в расширении домена. Чтобы оценить пределы закона постоянства как альтернативы мандерсовскому понятию успешного расширения домена, в этом разделе я (i) кратко обсужу происхождение этого закона, а затем (ii) представлю то, что, по-видимому, является точкой зрения Дедекинда. по закону постоянства. Затем это сформирует основу для альтернативного (полу)формального критерия хорошего расширения домена, с которым я сравню критерий Мандерса.
555]. Там он резюмирует содержание закона постоянства как требование, чтобы определенные универсальные свойства основных арифметических операций сохранялись в расширении математической области. Мандерс, кажется, быстро отвергает закон постоянства как недостаточно конкретный в определении того, какие свойства стоит сохранять в расширении домена. Чтобы оценить пределы закона постоянства как альтернативы мандерсовскому понятию успешного расширения домена, в этом разделе я (i) кратко обсужу происхождение этого закона, а затем (ii) представлю то, что, по-видимому, является точкой зрения Дедекинда. по закону постоянства. Затем это сформирует основу для альтернативного (полу)формального критерия хорошего расширения домена, с которым я сравню критерий Мандерса.
5.1. Закон постоянства форм
Закон постоянства, впервые введенный британским алгебраистом Джорджем Пикоком (1791–1858), гласит, что единственными алгебраическими законами, которые математик должен принимать, являются те, которые — в современных терминах — являются консервативными по отношению к определенным 9 результата элементарной арифметики. Пикок вводит упомянутый «закон» или «принцип» в контексте обоснования формальной алгебры как обобщения арифметики, где «формальная» алгебра обозначает часть алгебры, изучающую формы (уравнений). Гораздо более подробное обсуждение взглядов Пикока на математику и точную роль этого принципа в его философии математики можно найти в Detlefsen [2005, стр. 271–277]. Здесь я просто объясняю принцип в той мере, в какой это необходимо, чтобы дать некоторый контекст взглядам Дедекинда (которые будут рассмотрены в следующем подразделе).
Пикок вводит упомянутый «закон» или «принцип» в контексте обоснования формальной алгебры как обобщения арифметики, где «формальная» алгебра обозначает часть алгебры, изучающую формы (уравнений). Гораздо более подробное обсуждение взглядов Пикока на математику и точную роль этого принципа в его философии математики можно найти в Detlefsen [2005, стр. 271–277]. Здесь я просто объясняю принцип в той мере, в какой это необходимо, чтобы дать некоторый контекст взглядам Дедекинда (которые будут рассмотрены в следующем подразделе).
Сначала рассмотрим одну из собственных формулировок закона постоянства Пикока:
Вернемся снова к этому принципу или закону постоянства эквивалентных форм [|$\dots$|]. «Любая форма, алгебраически эквивалентная другой, выраженная в общих символах, должна быть истинной, что бы ни обозначали эти символы». Наоборот, если мы находим эквивалентную форму в арифметической алгебре или какой-либо другой второстепенной науке, когда символы являются общими по форме, хотя и специфичны по своей природе, то та же самая форма должна быть эквивалентной формой, когда символы являются общими по своей природе, а также по своей природе.
их форма. [Павлин, 1830, § 132, с. 104]
«Арифметическая алгебра» в приведенном выше отрывке — это просто арифметика, а «Символическая алгебра» — это алгебра. Пикок утверждает, что выражения элементарной арифметики, такие как |$5=5$| или |$5+5= 2\cdot 5$|, которые действительны только для арифметических величин, становятся законами символической алгебры, когда они выражены через символы, которые являются «общими по своей форме» (, т. Как поясняет приведенная ниже цитата, Пикок рассматривает арифметику и алгебру как связанные между собой более конкретную и более общую формулировки одной и той же науки, причем разница заключается в семантическом значении символов, используемых каждым из них в формулировке своих утверждений:0004 Но хотя наука арифметика или арифметическая алгебра не дает адекватного основания для науки символической алгебры, она неизбежно предлагает ее принципы или, скорее, ее закон комбинации; ибо, поскольку символическая алгебра, хотя и произвольна в авторитетности своих принципов, не произвольна в своем применении, будучи обязана включать в себя арифметическую алгебру, как и другие науки, очевидно, что их правила должны быть идентичны друг другу, поскольку насколько эти науки развиваются совместно: действительное различие между ними будет возникать из предположение или допущение, что символы в символической алгебре являются совершенно общими и неограниченными как по значению, так и по представлению, и что операции, которым они подлежат, также являются одинаково общими . Этот принцип грубо предписывает, что «символическая алгебра» по большей части представляет собой преобразование в переменных уже хорошо известных истин «арифметической алгебры». Так, например, если в арифметике (алгебре) обнаруживается, что |$+1-1=0, +2-2=0, +3-3=0, \cdots$|, то в символической алгебре можно просто утверждают общий символический принцип |$+a-a=0$|. Пикок, однако, признает, что некоторые законы (утверждения) его символической алгебры не могут быть таким образом «выведены» (или, используя собственную терминологию Пикока, «предложены») из арифметики. Поэтому необходимо предложить принципиальный способ руководства формированием новых принципов символической алгебры, и то, что предлагает Пикок, является более или менее критерием консервативности. Если некоторое утверждение в арифметике истинно, то в символическую алгебру нельзя принять другое утверждение, которое противоречило бы арифметическому. Закон Павлина, как Детлефсен [2005, с. Этот принцип [Dedekind’s, примечание автора ] аналогичен идеям Ома о том, как обобщить арифметические операции, и знаменитому «принципу постоянства», сформулированному Пикоком около 1830 г. , 1867]). Таким образом, в следующем подразделе я представляю аналогичные идеи Дедекинда о расширении домена, выраженные в [Dedekind, 1854]. Дедекинд Habilitationsrede [1854] главное утверждение состоит в том, что, как и в других науках, и в математике определения неизбежно выступают вначале в ограниченной форме, а их обобщение возникает только в ходе дальнейшего развития. Затем он сразу же делает замечание, которое озадачивает современного читателя и знакомо любому, кто знаком с принципом Пикока: ; напротив, они с неотвратимой необходимостью вытекают из прежних ограниченных определений, если применить следующий принцип: законы, вытекающие из исходных определений и характерные для обозначаемых ими понятий, следует рассматривать как общего действия . Обратите внимание, как Пикок спешит защищать алгебру как непроизвольное обобщение арифметики, так и Дедекинд защищает не только алгебру, но и любое расширенное математическое определение (или функцию). Однако расширение происходит несколько иначе: для Пикока расширение касается области действия определенных алгебраических утверждений; для Дедекинда расширение, по-видимому, состоит в расширении области объектов, подпадающих под определенное понятие (например, число). Существует также разница в области применения критерия Дедекинда и закона Пикока; поскольку Дедекинд, по-видимому, предлагает критерий (как предписывающий, так и описательный) для всех концептуальных расширений в математике, в то время как Пикок, по-видимому, сосредоточен на обобщении (где обобщение состоит в расширении области применения утверждения) арифметических Только. Утверждение о сходстве между Дедекиндом и Павлином подтверждается, есть еще один аспект размышлений Дедекинда, о котором стоит упомянуть, а именно его сосредоточенность на функциях, т. [7] Элементарная арифметика основана на образовании порядковых и количественных чисел; последовательный переход от одного члена последовательности положительных целых чисел к другому — первая и простейшая арифметическая операция; все остальные операции опираются на него. Если собрать в одно действие многократно повторяющееся выполнение этой элементарной операции, то придут к понятию сложения. Из этого понятия таким же образом образуется понятие умножения, а из умножения — понятие возведения в степень. Но определения, которые мы таким образом получаем для этих основных операций, уже недостаточны для дальнейшего развития арифметики, и это потому, что она предполагает, что числа, с которыми она учит нас оперировать, ограничены очень узкой областью. Этот отрывок показывает, как для Дедекинда соотносятся расширение домена и расширение операции, по крайней мере, в случае чисел: данный домен — это домен натуральных чисел, а данная операция — просто последующая. Из функции-преемника получаются другие прямые операции сложения и умножения, каждая из которых определяется как итерация ранее определенной функции. У нас уже есть определенный пример умножения. «Исходное определение» умножения как повторяющегося сложения должно быть изменено, чтобы его можно было определить и для отрицательных факторов, потому что нельзя повторять действие отрицательное число раз. Вместо этого левая дистрибутивность рассматривается как «общий закон», который должен сохраняться даже в расширенной области. Здесь важно отметить элемент неточности в рассуждениях Дедекинда, а именно то, что он, кажется, рассматривает одновременно два типа того, что можно назвать концептуальными расширениями в математике. С одной стороны, это введение новых операций (или функций, по названию его лекции) наряду с «цепочкой предыдущих». Это сродни расширению языка, который используется, чтобы «говорить» о предметной области, и вот пример того, как это должно работать. Если мы сохраним домен структуры |$\mathcal{A}$| фиксировано, мы можем добавить, скажем, символы отношения к языку, чтобы получить новую структуру |$\mathcal{A}’$| который также интерпретирует эти новые символы так же, как и старые. Как видно из цитаты, в тексте Дедекинда многое происходит. Следовательно, чтобы выявить точки сравнения с понятием расширения домена Мандерса, может быть полезно дать теоретико-модельную характеристику взглядов Дедекинда. Я предлагаю следующее: Условие (i) определения требует, чтобы |$\mathcal{A}$| быть вложенным в |$\mathcal{B}$|. Это обеспечивает сохранение функций среди особей исходной модели |$A$|, если языки |$\mathcal{L}$|, |$\mathcal{L}’$| включают функциональные символы, интерпретируемые в |$\mathcal{A}$| и |$\mathcal{B}$|. Условие (ii) направлено на то, чтобы зафиксировать правило Дедекинда о некоторых законах, которые следует рассматривать как «общедействительные». Ограничение положительности на |$\varphi$| мотивирован техническими проблемами, с которыми можно было бы столкнуться в противном случае, 12 , а также тем фактом, что уравнения, по-видимому, имеют привилегированный статус по сравнению с неравенствами. Для ясности, определение расширения Дедекинда само по себе не отвечает на вопрос, является ли данная математическая область хорошим расширением области другой области, согласно точке зрения, которую я приписываю Дедекинду. Выбор языков |$\mathcal{L},\,\mathcal{L}’$| также играет нетривиальную роль в этом смысле. Рассмотрим, например, следующий пример: пусть |$\mathbb{N},\,\mathbb{Z}$| — рассматриваемые модели с |$<\,\,\in\mathcal{L}$|. Тогда |$\mathbb{Z}$| не может быть расширением Дедекинда |$\mathbb{N}$|, потому что |$\mathbb{N}\vDash \forall x (x>0)$|, что неверно в |$\mathbb{Z }$|. В предыдущем разделе я представил размышления Дедекинда 1854 года как предлагающие концепцию расширения домена, родственную той, что лежит в основе принципа постоянства эквивалентных форм, и я предложил теоретико-модельную полуформализацию критерия. Это было сделано в попытке добиться прогресса в решении нормативного вопроса о том, что делает определенные доменные расширения «хорошими». В то же время работа в предыдущем разделе может оставить читателя в недоумении относительно исторический вопрос о том, действительно ли формализованный таким образом критерий соответствует отношению Дедекинда к новым системам счисления, разрабатываемым в середине 1850-х годов. Первый рассматриваемый случай — это случай кватернионов, или, в более общем смысле, так называемых гиперкомплексных чисел. Гиперкомплексное число традиционно представляет собой любое число, принадлежащее (унитальной) алгебре, построенной поверх действительных чисел. Существует несколько различных гиперкомплексных систем счисления, которые можно определить как векторные пространства над действительными числами; кватернионы и октонионы — системы счисления размерностей |$4$| и |$8$| соответственно, как следует из их названий. Это означает, что каждый кватернион может быть представлен четверкой действительных чисел, а каждый октонион может быть представлен восьмеркой (или восьмеркой). Дедекинд пишет о гиперкомплексных числах в двух статьях [1885; 1887]), и в обеих статьях его изложение состоит в том, что гиперкомплексные числа представляются в виде конечных сумм вида |$\Sigma\, \xi_{\iota}e_{\iota}$|, где |$e_{ \йота}$| является «главной единицей» ( Haupteinheit ) гиперкомплексных чисел (подумайте о |$i,j,k$| для кватернионов). Тогда операции между любыми двумя гиперкомплексными числами можно определить как операции над единицами, которые вместе образуют основа . Эти операции могут быть выражены в виде линейных преобразований, т. Если, с одной стороны, это поддерживает мою интерпретацию, согласно которой гиперкомплексные числа не являются настоящими новыми числами, то это также подрывает идею о том, что кватернионы считаются частным случаем гиперкомплексных чисел в этом отношении. Дедекинд считает их «достаточно новыми», чтобы считать их подлинными новыми числами. Итак, когда дело доходит до чисел, полученных путем присоединения новых мнимых единиц, кажется, что Дедекинд проводит линию в кватернионах с точки зрения того, что считается подлинными новыми числами. Ибо, если, с одной стороны, в его [1854] казалось, что и мнимые числа, и кватернионы являются числами, только еще не снабженными удовлетворительным объяснением того, как они получены, с другой стороны, эти системы счисления могут быть получены в грубой форме. Вторым случаем того, что можно было бы хотеть и ожидать от случая «хорошего расширения» для Дедекинда, являются собственные идеалы Дедекинда, или идеальные числа в более общем смысле. Впервые идеальные числа были введены Куммером в 1846 г. [Бордонья, 1996, с. 6; Эдвардс, 1980, с. 322] для решения конкретной проблемы уникальности факторизации для определенных числовых областей. Уникальная факторизация в случае натуральных (или даже целых) чисел довольно проста: для любого непростого натурального числа |$n$| существует однозначное разложение |$n$| в его простые множители, то есть в числа, которые сами по себе не могут быть записаны как произведение чего-либо, кроме самих себя и единицы. Хотя Куммер впервые заговорил об «идеальных числах» или «идеальных делителях» как о числах, существующих за пределами (вне) области действительных (, т. е. ., существующих в действительности) чисел, и как бы рассматривал их как дополнительные числа, подлежащие добавлению к уже существующим, позиция Дедекинда относительно статуса его идеалов (и соответствующих им идеальных чисел) не столь однозначна. Дедекинд представил свою теорию идеалов впервые в своих приложениях к Дирихле «Лекции по теории чисел» [1877; 1999], а затем в серии статей в Bulletin des Sciences Mathématiques et Astronomiques [Dedekind, 1876; 1877]. В своей формулировке теории Дедекинд приходит к «точному» определению идеального числа следующим образом. Отправной точкой является расширение конечной степени (в техническом смысле поля, которое можно рассматривать как одно- или двумерное векторное пространство над |$\mathbb{Q}$|) |$\Omega$ | |$\mathbb{Q}$|. Таким образом, идеал |$\mathfrak{a}$| состоит из всех целых чисел, содержащихся в |$\Omega$| и делится на целое число |$\mu$|; по этой причине мы будем говорить, что число |$\mu$|, хотя и не содержится в |$\Omega$|, равно идеальное число поля |$\Omega$| и соответствует идеалу |$\mathfrak{a}$|. Дедекинд останавливается перед тем, чтобы отождествить идеал, содержащий все числа, делящиеся на некоторый идеальный делитель, с самим идеальным делителем. Это различие может показаться аналогичным тому, которое Дедекинд проводит в случае действительных чисел и разрезов, где Дедекинд говорит, что каждому разрезу, не порожденному рациональным числом, соответствует иррациональное число, не говоря при этом, что разрез и число равны 9.0433 один и тот же  [Павлин, 1834, с. 195, курсив оригинала]
[Павлин, 1834, с. 195, курсив оригинала] 272], уже было как-то предвосхищено другими авторами, а также почти дословно цитируется в немецкоязычном контексте Ганкелем [1867, с. 11, 15]. 10 Таким образом, хотя мне не удалось найти прямых доказательств того, что Дедекинд читал труды Пикока, в идеях математиков об обобщении арифметики через алгебру и расширении функций и областей в математике, похоже, есть сходство. Дедекинд [1854] можно рассматривать как предложение критерия плодотворного расширения домена, сильно напоминающего принцип Пикока. Это также отмечает Феррейрос [Ferreirós, 2007, с. 219], который пишет:
272], уже было как-то предвосхищено другими авторами, а также почти дословно цитируется в немецкоязычном контексте Ганкелем [1867, с. 11, 15]. 10 Таким образом, хотя мне не удалось найти прямых доказательств того, что Дедекинд читал труды Пикока, в идеях математиков об обобщении арифметики через алгебру и расширении функций и областей в математике, похоже, есть сходство. Дедекинд [1854] можно рассматривать как предложение критерия плодотворного расширения домена, сильно напоминающего принцип Пикока. Это также отмечает Феррейрос [Ferreirós, 2007, с. 219], который пишет: Однако понимание протяженности Дедекиндом можно рассматривать как эквивалентное пониманию Пикока; ибо понятия определяются «характеристическими» законами, которые «вытекают из исходных определений» названных понятий. Так что, в конце концов, расширять понятие в дедекиндовском смысле (по крайней мере, в арифметическом) — это то же самое, что интерпретировать определенные специальные арифметические утверждения не только как относящиеся к ограниченной области, но как к более широкой и богатой. Это закон Пикока о постоянстве форм — закон, управляющий обобщением арифметических результатов на алгебру.
Однако понимание протяженности Дедекиндом можно рассматривать как эквивалентное пониманию Пикока; ибо понятия определяются «характеристическими» законами, которые «вытекают из исходных определений» названных понятий. Так что, в конце концов, расширять понятие в дедекиндовском смысле (по крайней мере, в арифметическом) — это то же самое, что интерпретировать определенные специальные арифметические утверждения не только как относящиеся к ограниченной области, но как к более широкой и богатой. Это закон Пикока о постоянстве форм — закон, управляющий обобщением арифметических результатов на алгебру. е. ., операций. То есть критерий Дедекинда, по-видимому, применим не только к расширенному домену и кодовому домену функций. Его интерес особенно очевиден в следующем отрывке, касающемся чисел и основных арифметических операций:
е. ., операций. То есть критерий Дедекинда, по-видимому, применим не только к расширенному домену и кодовому домену функций. Его интерес особенно очевиден в следующем отрывке, касающемся чисел и основных арифметических операций: То есть арифметика требует от нас при введении каждой из этих операций заново создавать всю существующую область чисел; или, точнее, она требует, чтобы косвенные, обратные операции вычитания, деления и т. п. были безусловно применимы. И это требование заставляет создавать новые классы чисел, так как при исходной последовательности натуральных чисел требование не может быть удовлетворено. Таким образом получают отрицательные, рациональные, иррациональные и, наконец, так называемые мнимые числа. Теперь, после того как числовая область была расширена таким образом, возникает необходимость заново определить операции [|$\dots$|]. [Дедекинд, 1854, § 7]
То есть арифметика требует от нас при введении каждой из этих операций заново создавать всю существующую область чисел; или, точнее, она требует, чтобы косвенные, обратные операции вычитания, деления и т. п. были безусловно применимы. И это требование заставляет создавать новые классы чисел, так как при исходной последовательности натуральных чисел требование не может быть удовлетворено. Таким образом получают отрицательные, рациональные, иррациональные и, наконец, так называемые мнимые числа. Теперь, после того как числовая область была расширена таким образом, возникает необходимость заново определить операции [|$\dots$|]. [Дедекинд, 1854, § 7] Когда все «прямые» операции определены, можно ввести обратные. Для сложения это вычитание. Однако для определения вычитания между двумя произвольными элементами области область должна быть расширена ( т. е. , понятие числа расширено) за счет включения и отрицательных чисел. Точно так же введение обратной операции умножения, а именно деления, вместе с требованием замыкания области определения новой операцией приводит к введению рациональных чисел. Эта итеративная конструкция (ввести новую операцию, затем новые числа, чтобы область была закрыта при указанной операции) доходит до мнимых чисел. Но с каждым раундом расширения числовой области старые операции также необходимо определять заново. 11 Дедекинд не говорит об этом эксплицитно, но кажется, что то, что позволяет остановить процесс, — это достижение достаточно богатой (числовой) области, которая также закрыта для всех определенных операций, взятых в их наиболее общем виде. Чтобы увидеть, как можно адаптировать «определение» операции к расширенной области, рассмотрим пример умножения Дедекинда:
Когда все «прямые» операции определены, можно ввести обратные. Для сложения это вычитание. Однако для определения вычитания между двумя произвольными элементами области область должна быть расширена ( т. е. , понятие числа расширено) за счет включения и отрицательных чисел. Точно так же введение обратной операции умножения, а именно деления, вместе с требованием замыкания области определения новой операцией приводит к введению рациональных чисел. Эта итеративная конструкция (ввести новую операцию, затем новые числа, чтобы область была закрыта при указанной операции) доходит до мнимых чисел. Но с каждым раундом расширения числовой области старые операции также необходимо определять заново. 11 Дедекинд не говорит об этом эксплицитно, но кажется, что то, что позволяет остановить процесс, — это достижение достаточно богатой (числовой) области, которая также закрыта для всех определенных операций, взятых в их наиболее общем виде. Чтобы увидеть, как можно адаптировать «определение» операции к расширенной области, рассмотрим пример умножения Дедекинда: Эта операция возникла из-за того, что многократное выполнение операции следующего более низкого ранга [Ordnung], а именно прибавление фиксированного положительного или отрицательного слагаемого (так называемого множимого), было собрано вместе в одно действие. Множитель, т. е. число, указывающее, как часто прибавление множимого следует рассматривать как повторяющееся, — следовательно, с самого начала обязательно является положительным целым числом; отрицательный множитель, согласно этому первому определению умножения, не имел бы абсолютно никакого смысла. Поэтому необходимо специальное определение, чтобы допустить и отрицательные множители и тем самым освободить операцию от начального ограничения; но такое определение предполагает a priori полный произвол, и только позже будет решено, принесет ли тогда это произвольно выбранное определение какую-либо реальную пользу арифметике; и даже если бы определение сбылось, это можно было бы назвать лишь удачной догадкой, счастливым совпадением — чего следует избегать научному методу.
Эта операция возникла из-за того, что многократное выполнение операции следующего более низкого ранга [Ordnung], а именно прибавление фиксированного положительного или отрицательного слагаемого (так называемого множимого), было собрано вместе в одно действие. Множитель, т. е. число, указывающее, как часто прибавление множимого следует рассматривать как повторяющееся, — следовательно, с самого начала обязательно является положительным целым числом; отрицательный множитель, согласно этому первому определению умножения, не имел бы абсолютно никакого смысла. Поэтому необходимо специальное определение, чтобы допустить и отрицательные множители и тем самым освободить операцию от начального ограничения; но такое определение предполагает a priori полный произвол, и только позже будет решено, принесет ли тогда это произвольно выбранное определение какую-либо реальную пользу арифметике; и даже если бы определение сбылось, это можно было бы назвать лишь удачной догадкой, счастливым совпадением — чего следует избегать научному методу. Поэтому давайте вместо этого применим наш общий принцип. Мы должны исследовать, какие законы управляют произведением, если множитель последовательно претерпевает те же самые общие изменения, которые привели к созданию последовательности отрицательных целых чисел из последовательности положительных целых чисел. Для этого достаточно определить изменение, которое претерпевает произведение, если произвести простейшую числовую операцию с множителем, а именно позволить ему перейти в следующее за ним число. Последовательным повторением этой операции мы получаем известную теорему сложения для множителя: чтобы умножить число на сумму, нужно умножить его на каждое слагаемое, а затем сложить эти частичные произведения вместе. Из этой теоремы немедленно следует теорема о вычитании для случая, когда уменьшаемое больше вычитаемого. Если теперь объявить этот закон справедливым вообще (то есть справедливым и тогда, когда разность, которую представляет множитель, отрицательна), то получится определение умножения с отрицательными множителями; и тогда, конечно, не случайно, что общий закон, которому подчиняется умножение, совершенно одинаков для обоих случаев.
Поэтому давайте вместо этого применим наш общий принцип. Мы должны исследовать, какие законы управляют произведением, если множитель последовательно претерпевает те же самые общие изменения, которые привели к созданию последовательности отрицательных целых чисел из последовательности положительных целых чисел. Для этого достаточно определить изменение, которое претерпевает произведение, если произвести простейшую числовую операцию с множителем, а именно позволить ему перейти в следующее за ним число. Последовательным повторением этой операции мы получаем известную теорему сложения для множителя: чтобы умножить число на сумму, нужно умножить его на каждое слагаемое, а затем сложить эти частичные произведения вместе. Из этой теоремы немедленно следует теорема о вычитании для случая, когда уменьшаемое больше вычитаемого. Если теперь объявить этот закон справедливым вообще (то есть справедливым и тогда, когда разность, которую представляет множитель, отрицательна), то получится определение умножения с отрицательными множителями; и тогда, конечно, не случайно, что общий закон, которому подчиняется умножение, совершенно одинаков для обоих случаев. [Дедекинд, 1854, § 8]
[Дедекинд, 1854, § 8] Если мы позволим |$N$| — множество всех натуральных чисел, то мы можем рассматривать как структуру |$\mathbb{N}$| натуральных чисел языка |$L=\{0, +\}$| и структура |$\mathbb{N}’$| натуральных чисел в языке |$L’=\{0, 1, +, \cdot\}$|. Домен, лежащий в основе обоих |$\mathbb{N}$| и |$\mathbb{N}’$| то же самое; в |$N$| не было добавлено никаких новых элементов. Тем не менее, между ними происходит расширение, которое включает только операции и константы. Второй тип расширения состоит в добавлении элементов к области функций или введении новых объектов в рамках старой концепции. Например, хотя первоначально определенное умножение может быть выполнено только между двумя положительными целыми числами, позже его можно переопределить, чтобы допустить также отрицательные целые числа в его области определения (и диапазоне). Это расширение можно проиллюстрировать следующим образом. |$\mathcal{L}$|-структура, с которой мы начинаем, это |$\mathbb{N}$|, где областью является просто |$N$|, а язык |$\mathcal{L}$ | содержит символ добавления «+», что |$\mathbb{N}$| интерпретируется как функция |$\{((m,n),m+n) : m,n\in N\}$|.
Если мы позволим |$N$| — множество всех натуральных чисел, то мы можем рассматривать как структуру |$\mathbb{N}$| натуральных чисел языка |$L=\{0, +\}$| и структура |$\mathbb{N}’$| натуральных чисел в языке |$L’=\{0, 1, +, \cdot\}$|. Домен, лежащий в основе обоих |$\mathbb{N}$| и |$\mathbb{N}’$| то же самое; в |$N$| не было добавлено никаких новых элементов. Тем не менее, между ними происходит расширение, которое включает только операции и константы. Второй тип расширения состоит в добавлении элементов к области функций или введении новых объектов в рамках старой концепции. Например, хотя первоначально определенное умножение может быть выполнено только между двумя положительными целыми числами, позже его можно переопределить, чтобы допустить также отрицательные целые числа в его области определения (и диапазоне). Это расширение можно проиллюстрировать следующим образом. |$\mathcal{L}$|-структура, с которой мы начинаем, это |$\mathbb{N}$|, где областью является просто |$N$|, а язык |$\mathcal{L}$ | содержит символ добавления «+», что |$\mathbb{N}$| интерпретируется как функция |$\{((m,n),m+n) : m,n\in N\}$|. Затем к |$N$| добавляют отрицательные целые числа, таким образом используя |$Z$| поскольку домен новой |$\mathcal{L}$|-структуры |$\mathbb{Z}$|, и, кроме того, |$`+$|’ теперь интерпретируется как |$\{((m,n ),m+n) : m,n\in Z\}\supseteq \{((m,n),m+n) : m,n\in N\}$|. Это второе изменение представляет собой более прямолинейный случай добавления элементов к общей области модели, а также к областям отдельных функций. Эти два (расширение языка по сравнению с расширением предметной области) в принципе представляют собой два различных вида расширения, однако Дедекинд, похоже, этого не замечает. Я полагаю, что причина, по которой Дедекинд не исследует два случая расширения по отдельности, заключается в том, что он не верит, что один может иметь место в отсутствие другого: если математик вводит новые элементы в рассматриваемую область, то он должен иметь возможность определить, как старые операции или функции применяются к новым объектам.
Затем к |$N$| добавляют отрицательные целые числа, таким образом используя |$Z$| поскольку домен новой |$\mathcal{L}$|-структуры |$\mathbb{Z}$|, и, кроме того, |$`+$|’ теперь интерпретируется как |$\{((m,n ),m+n) : m,n\in Z\}\supseteq \{((m,n),m+n) : m,n\in N\}$|. Это второе изменение представляет собой более прямолинейный случай добавления элементов к общей области модели, а также к областям отдельных функций. Эти два (расширение языка по сравнению с расширением предметной области) в принципе представляют собой два различных вида расширения, однако Дедекинд, похоже, этого не замечает. Я полагаю, что причина, по которой Дедекинд не исследует два случая расширения по отдельности, заключается в том, что он не верит, что один может иметь место в отсутствие другого: если математик вводит новые элементы в рассматриваемую область, то он должен иметь возможность определить, как старые операции или функции применяются к новым объектам. Сохранение уравнений — важная тема результатов универсальной алгебры, о чем свидетельствует поток исследований универсальной алгебры, состоящий в обобщениях и приложениях теоремы Биркгофа. 13 Более того, другие математики девятнадцатого века, такие как Ганкель [1867, стр. 26, 40–41] и Пикок [1834], неявно признают важность сохранения уравнений при расширении области значений и арифметических операций. Таким образом, ограничения на |$\varphi$| в формализации не должны рассматриваться как произвольные.
Сохранение уравнений — важная тема результатов универсальной алгебры, о чем свидетельствует поток исследований универсальной алгебры, состоящий в обобщениях и приложениях теоремы Биркгофа. 13 Более того, другие математики девятнадцатого века, такие как Ганкель [1867, стр. 26, 40–41] и Пикок [1834], неявно признают важность сохранения уравнений при расширении области значений и арифметических операций. Таким образом, ограничения на |$\varphi$| в формализации не должны рассматриваться как произвольные. Если исключить |$<$| из нашего языка, однако, проблемы не возникает и |$\mathbb{Z}$| можно считать расширением Дедекинда |$\mathbb{N}$|. Это означает, что понятие расширения Дедекинда все еще в некоторой степени зависит от контекста. Однако это также верно и для понятия Мандерса, поскольку экзистенциальное закрытие и завершение модели также чувствительны к языку.
Если исключить |$<$| из нашего языка, однако, проблемы не возникает и |$\mathbb{Z}$| можно считать расширением Дедекинда |$\mathbb{N}$|. Это означает, что понятие расширения Дедекинда все еще в некоторой степени зависит от контекста. Однако это также верно и для понятия Мандерса, поскольку экзистенциальное закрытие и завершение модели также чувствительны к языку. 6. РАСШИРЕНИЕ КОНЦЕПЦИИ ЧИСЛА
 Чтобы ответить на этот вопрос, я кратко напомню в этом разделе два таких теоретико-числовых развития и утверждаю, что в обоих случаях маловероятно, чтобы Дедекинд рассматривал их как расширения в смысле его [1854].
Чтобы ответить на этот вопрос, я кратко напомню в этом разделе два таких теоретико-числовых развития и утверждаю, что в обоих случаях маловероятно, чтобы Дедекинд рассматривал их как расширения в смысле его [1854]. 6.1. Кватернионы, октонионы и другие гиперкомплексные числа
 Проблема в том, что умножение в кватернионах некоммутативно, а в октонионах оно даже не может быть ассоциативным. Но коммутативность и ассоциативность умножения выражаются как универсальные позитивные высказывания того вида, который дедекиндовское расширение должно сохранять по определению. Отсюда ясно, что данное предложение, хотя и вдохновленное Дедекиндом, не может объяснить эти расширения как хорошие расширения.
Проблема в том, что умножение в кватернионах некоммутативно, а в октонионах оно даже не может быть ассоциативным. Но коммутативность и ассоциативность умножения выражаются как универсальные позитивные высказывания того вида, который дедекиндовское расширение должно сохранять по определению. Отсюда ясно, что данное предложение, хотя и вдохновленное Дедекиндом, не может объяснить эти расширения как хорошие расширения. {(s)}$| выведенные нами. Так что если мы хотим говорить о таких сложных величинах как о новых числах (что для меня нецелесообразно, так как в нашей высшей алгебре всегда возникают многозначные системы величин описанным здесь образом), то это можно сделать только, хотя и в совершенно иной форме. , и в самом деле бесконечно более слабый смысл, чем при введении мнимых чисел путем значительного обогащения поля действительных чисел, или также при введении гамильтоновых кватернионов, которые, хотя их полезность, по-видимому, ограничена очень малым полем, делают безусловным претензия на новизну по отношению к другим номерам. ([Дедекинд, 1885], в [Дедекинд, 1931, с. 16])
{(s)}$| выведенные нами. Так что если мы хотим говорить о таких сложных величинах как о новых числах (что для меня нецелесообразно, так как в нашей высшей алгебре всегда возникают многозначные системы величин описанным здесь образом), то это можно сделать только, хотя и в совершенно иной форме. , и в самом деле бесконечно более слабый смысл, чем при введении мнимых чисел путем значительного обогащения поля действительных чисел, или также при введении гамильтоновых кватернионов, которые, хотя их полезность, по-видимому, ограничена очень малым полем, делают безусловным претензия на новизну по отношению к другим номерам. ([Дедекинд, 1885], в [Дедекинд, 1931, с. 16]) Таким образом, у нас остается следующее: теория, вдохновленная Дедекиндом, правильно согласуется с различием между двумя случаями расширения — а именно, расширением области за счет расширения самого понятия числа (такими могут быть кватернионы) — и числовыми областями, полученными как уникальные расширения (с точностью до изоморфизма) натуральных чисел. Мое определение расширения Дедекинда адекватно описывает последний тип расширения домена как хорошее, но не включает гиперкомплексные числа, включая кватернионы, несмотря на то, что Дедекинд пишет в отрывке выше.
Таким образом, у нас остается следующее: теория, вдохновленная Дедекиндом, правильно согласуется с различием между двумя случаями расширения — а именно, расширением области за счет расширения самого понятия числа (такими могут быть кватернионы) — и числовыми областями, полученными как уникальные расширения (с точностью до изоморфизма) натуральных чисел. Мое определение расширения Дедекинда адекватно описывает последний тип расширения домена как хорошее, но не включает гиперкомплексные числа, включая кватернионы, несмотря на то, что Дедекинд пишет в отрывке выше. так же, как гиперкомплексные числа; так что можно было бы ожидать, что Дедекинд расценит все это либо как входящие, либо выходящие из категории «подлинных доменных расширений» (само собой разумеется, что-то должно быть подлинным доменным расширением, чтобы быть хорошим). При внимательном рассмотрении [Dedekind, 1854] можно сделать одно правдоподобное предположение, что, хотя и комплексные числа, и кватернионы являются подлинными расширениями области (поскольку в обоих случаях вводятся действительно новые числа), только комплексные числа получаются как замыкание уже принятой системы. числовая область (действительные числа) при некоторой обратной операции, а именно при возведении в степень. Поскольку определение расширения Дедекинда стремится уловить идею хорошего расширения домена, выраженную в [Dedekind, 1854], и эта идея состоит в том, что домены расширяются, чтобы закрыть их при операциях, это положительная черта определения расширения Дедекинда. что ему удовлетворяют комплексные числа как расширение действительных чисел, но не кватернионы, поскольку только комплексные числа вводятся как замыкание действительных чисел под квадратными корнями.
так же, как гиперкомплексные числа; так что можно было бы ожидать, что Дедекинд расценит все это либо как входящие, либо выходящие из категории «подлинных доменных расширений» (само собой разумеется, что-то должно быть подлинным доменным расширением, чтобы быть хорошим). При внимательном рассмотрении [Dedekind, 1854] можно сделать одно правдоподобное предположение, что, хотя и комплексные числа, и кватернионы являются подлинными расширениями области (поскольку в обоих случаях вводятся действительно новые числа), только комплексные числа получаются как замыкание уже принятой системы. числовая область (действительные числа) при некоторой обратной операции, а именно при возведении в степень. Поскольку определение расширения Дедекинда стремится уловить идею хорошего расширения домена, выраженную в [Dedekind, 1854], и эта идея состоит в том, что домены расширяются, чтобы закрыть их при операциях, это положительная черта определения расширения Дедекинда. что ему удовлетворяют комплексные числа как расширение действительных чисел, но не кватернионы, поскольку только комплексные числа вводятся как замыкание действительных чисел под квадратными корнями.
6.2. Идеалы Дедекинда и идеальные элементы
 В следующем подразделе я набросаю вторую версию дедекиндовской теории идеалов. На основе этого наброска я смогу затем решить вопрос о том, что это за расширение домена, если оно вообще такое. Для заинтересованных читателей [White, 2004] содержит подробное обсуждение различий между этими двумя версиями.
В следующем подразделе я набросаю вторую версию дедекиндовской теории идеалов. На основе этого наброска я смогу затем решить вопрос о том, что это за расширение домена, если оно вообще такое. Для заинтересованных читателей [White, 2004] содержит подробное обсуждение различий между этими двумя версиями. 6.2.1. Класс идеалов и «Строгое определение идеальных чисел» Дедекинда
 В этом поле идентифицируется подкольцо элементов, которые с точки зрения делимости ведут себя аналогично целым числам. Это кольцо целых чисел |$\mathfrak{o}$| поля |$\Omega$|. Проблема в том, что, как правило, уникальная факторизация не работает в |$\mathfrak{o}$|. Смысл введения идеальных делителей состоит в том, чтобы частично восстановить некоторые преимущества однозначной факторизации даже в тех случаях, когда она, строго говоря, не работает. В виде набора |$\mathfrak{o}$| не просто подкольцо |$\Omega$|; это тоже 9ч$| в |$\mathfrak{a}$| имеет вид |$b\alpha_1$| для некоторого |$b$|, и поэтому |$\alpha$| делится на |$\mu = \sqrt[h]{\alpha_1}$| и |$\mu$| — это «целое алгебраическое число», не принадлежащее к полю, с которого мы начали, |$\Omega$|. Таким образом, Дедекинд пишет:
В этом поле идентифицируется подкольцо элементов, которые с точки зрения делимости ведут себя аналогично целым числам. Это кольцо целых чисел |$\mathfrak{o}$| поля |$\Omega$|. Проблема в том, что, как правило, уникальная факторизация не работает в |$\mathfrak{o}$|. Смысл введения идеальных делителей состоит в том, чтобы частично восстановить некоторые преимущества однозначной факторизации даже в тех случаях, когда она, строго говоря, не работает. В виде набора |$\mathfrak{o}$| не просто подкольцо |$\Omega$|; это тоже 9ч$| в |$\mathfrak{a}$| имеет вид |$b\alpha_1$| для некоторого |$b$|, и поэтому |$\alpha$| делится на |$\mu = \sqrt[h]{\alpha_1}$| и |$\mu$| — это «целое алгебраическое число», не принадлежащее к полю, с которого мы начали, |$\Omega$|. Таким образом, Дедекинд пишет: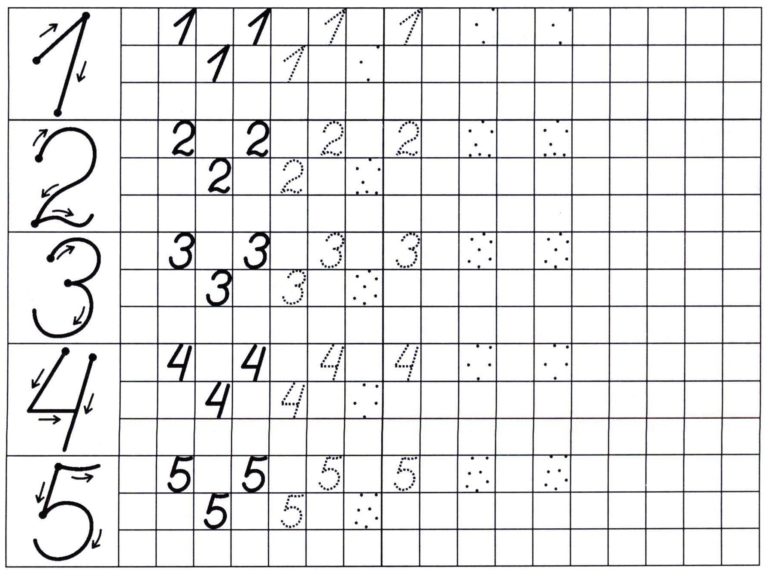 14 [1877, с. 246]
14 [1877, с. 246] Если посмотреть, как Дедекинд трактует целые и рациональные числа 16 видно, что эти шаги имеют общее то, что новые числа определяются как (упорядоченные) пары старых чисел, а арифметические операции над новыми числами определяются в терминах операций над старыми числами. Более того, Дедекинд, по-видимому, понимает вновь определенные числа как образующие новое целое, новую структуру (систему), обладающую определенными арифметическими свойствами (например, в случае целых чисел коммутативность сложения и законы дистрибутивности для сложения и дистрибутивности). умножение), которые справедливы и для натуральных чисел. Мне кажется, что в работе Дедекинда об идеалах не обнаруживается аналогичного интереса. Он не пытается показать, что существует какая-то глубокая преемственность между арифметическими свойствами натуральных чисел и арифметическими свойствами этих предполагаемых новых чисел (даже если можно сказать, что они порождены исследованием делимости и фундаментальной теоремой теории чисел).
Если посмотреть, как Дедекинд трактует целые и рациональные числа 16 видно, что эти шаги имеют общее то, что новые числа определяются как (упорядоченные) пары старых чисел, а арифметические операции над новыми числами определяются в терминах операций над старыми числами. Более того, Дедекинд, по-видимому, понимает вновь определенные числа как образующие новое целое, новую структуру (систему), обладающую определенными арифметическими свойствами (например, в случае целых чисел коммутативность сложения и законы дистрибутивности для сложения и дистрибутивности). умножение), которые справедливы и для натуральных чисел. Мне кажется, что в работе Дедекинда об идеалах не обнаруживается аналогичного интереса. Он не пытается показать, что существует какая-то глубокая преемственность между арифметическими свойствами натуральных чисел и арифметическими свойствами этих предполагаемых новых чисел (даже если можно сказать, что они порождены исследованием делимости и фундаментальной теоремой теории чисел). арифметика, и, следовательно, это то, что получается при попытке определить «делимость» в ее самой общей форме 9 .0433 т. е. ., расширяют делимость, в некотором смысле).
арифметика, и, следовательно, это то, что получается при попытке определить «делимость» в ее самой общей форме 9 .0433 т. е. ., расширяют делимость, в некотором смысле).
6.3. Являются ли идеалы и гиперкомплексы хорошими расширениями Дедекинда?
В изложении рассматриваемых идеалов Дедекинд явно дистанцируется от подхода Куммера к идеалам, который представляет их как несуществующие числа, индивидуализируемые только правилами делимости, заданными через громоздкие уравнения [Bordogna, 1996; Эдвардс, 1983].
Дедекинд, напротив, определяет идеалы как классы (комплексных) чисел. Он утверждает, что этих классов эквивалентности , а не , следует рассматривать как дополнение к числовому домену. Другими словами, он не считает себя расширителем домена.
Это соответствует тому, как расширения концепции числа представлены в Habilitation . Чтобы идеалы Дедекинда считались новыми числами, следует ожидать, что Дедекинд попытается доказать, что числовая область, расширенная за счет включения идеалов, по-прежнему сохраняет определенные «законы», которые были верны для той же области без идеалов. Но Дедекинд этого не делает. В частности, он не пытается доказать, что основные арифметические операции сохраняются в расширении.
Но Дедекинд этого не делает. В частности, он не пытается доказать, что основные арифметические операции сохраняются в расширении.
Аналогичным образом, такая забота, по-видимому, отсутствует в его трактовке гиперкомплексных чисел. Учитывая, что до сих пор в своих [1872] и [1888] Дедекинд гордо ссылается на [Dedekind, 1854] как на сценарий, цель которого одобряла сам Гаусс, маловероятно, что он не обратил бы внимания на расширение понятия числа, а именно, гиперкомплексные числа, что не согласуется с его описанием того, что ограничивает такие расширения.
Поэтому я придерживаюсь иной позиции, когда речь идет об идеалах и гиперкомплексных числах, а именно, что они не должны быть расширениями в смысле [Dedekind, 1854]. Есть две причины такой позиции. Во-первых, как уже упоминалось, оба случая ставят перед нами загадку: (предполагаемый) случай расширения, который, по-видимому, не удовлетворяет критерию Дедекинда для хорошего расширения. Во-вторых, я полагаю, что имеется достаточно текстовых свидетельств, чтобы предположить, что Дедекинд рассматривает эти два случая иначе, чем то, как он рассматривает целые числа (как расширение |$\mathbb{N}$|), рациональные и действительные числа. (Случай комплексных чисел не является проблемой, поскольку он является хорошим расширением предметной области в моем полуформальном представлении критерия Дедекинда 1854 года, а сам Дедекинд действительно рассматривает их как расширение действительных чисел). Я полагаю, что последние (целые числа, рациональные числа, действительные числа, комплексы) являются подлинными расширениями понятия числа для Дедекинда, в отличие от идеалов и гиперкомплексных чисел, и это также то, что предполагает моя полуформализация критерия Дедекинда.
(Случай комплексных чисел не является проблемой, поскольку он является хорошим расширением предметной области в моем полуформальном представлении критерия Дедекинда 1854 года, а сам Дедекинд действительно рассматривает их как расширение действительных чисел). Я полагаю, что последние (целые числа, рациональные числа, действительные числа, комплексы) являются подлинными расширениями понятия числа для Дедекинда, в отличие от идеалов и гиперкомплексных чисел, и это также то, что предполагает моя полуформализация критерия Дедекинда.
7. СРАВНЕНИЕ
Если рассмотреть критерий расширения Дедекинда, то интересующие Дедекинда случаи числовой области (расширения от |$\mathbb{N}$| до |$\mathbb{Z}$| все вплоть до |$\mathbb{C}$|) являются хорошими случаями расширения домена — если ограничить подписи, чтобы исключить порядок; в противном случае уже |$\mathbb{Z}$| как расширение |$\mathbb{N}$| не удовлетворяло бы условию (ii) в определении Дедекинда.
|$\mathbb{R}(i)$|, например, будет структурой, полученной как дополнение другой, а именно |$\mathbb{R}$|. Начинают с домена |$\mathbb{R}$|, добавляют один новый элемент, |$i$|, а затем добавляют также все подходящие алгебраические комбинации |$i$| со всеми элементами |$\mathbb{R}$|. Также кажется, что в процессе мы были консервативны в отношении |$\mathbb{R}$| как поле (но не как упорядоченное поле, учитывая, что |$\mathbb{R}$| линейно упорядочено, а |$\mathbb{R}(i)$| – нет). Таким образом, этот конкретный пример является расширением «хорошего случая» как для Мандерса, так и для Дедекинда. 9*\mathbb{R}$| также считается хорошим доменным расширением в рамках Дедекинда, в отличие от Мандерса. Это существенное различие, которое можно объяснить с точки зрения того, что пытаются зафиксировать две разные структуры. Использование Мандерсом экзистенциального замыкания предназначено для захвата случаев расширения предметной области, направленного на упрощение с точки зрения уменьшения сложности кванторов теории. Расширение Дедекинда, с другой стороны, предназначено для охвата случаев расширения предметной области, направленных на расширение данной концепции (9).0433 например ., сложения или числа) настолько, насколько позволяет сущность понятия. 17
Расширение Дедекинда, с другой стороны, предназначено для охвата случаев расширения предметной области, направленных на расширение данной концепции (9).0433 например ., сложения или числа) настолько, насколько позволяет сущность понятия. 17
В предыдущем разделе я затронул два известных случая предполагаемого расширения домена и пришел к выводу, что они, похоже, не подпадают под мою интерпретацию Дедекинда. Теперь мы кратко обратимся к вопросу о том, хорошо ли кватернионы и идеалы обрабатываются понятием Мандерса. Кватернионы (|$\mathbb{H}$|) не получаются как экзистенциальное замыкание |$\mathbb{C}$|, учитывая, что |$\mathbb{C}$| уже экзистенциально замкнуто и не изоморфно |$\mathbb{H}$|. В то же время не очевидно, что должен быть какой-то класс структур |$K$| над которым |$\mathbb{H}$| экзистенциально замкнут. Аналогично для идеалов, определенных над некоторым полем. Таким образом, без таких результатов нельзя окончательно решить, считаются ли кватернионы и идеалы хорошими расширениями предметной области для Мандерса. 18
18
В разделе 3 я объяснил, как Мандерс утверждает, что для любой теории, в которой каждое условие разрешимости имеет одно слабое дополнение, экзистенциальное замыкание приводит к упрощению и концептуальной унификации [Мандерс, 1989, стр. 554–556]. Мандерс разъясняет упрощение и унификацию с точки зрения формальных свойств теорий получаемых экзистенциально замкнутых моделей. Другими словами, Мандерс предполагает, что экзистенциальная замкнутость является достаточным условием для того, чтобы расширение домена считалось хорошим и плодотворным9.0801 19 , и он указывает, что несколько исторически важных случаев (комплексные числа, точки и линии в бесконечности) действительно являются случаями экзистенциальной замкнутости. Как таковые, они действительно являются средством частичного достижения цели (|$G»$|): с помощью таких результатов, как Nullstellensatz , они позволяют «вводить двойные преобразования между моделями», и в силу того, что Мандерс вызывает свойство «выжимание среднего регистра», они удаляют исключения.
Понятие Дедекинда, тем временем, фокусируется на сохранении определенных особенностей (теорем) теории, которые считаются существенными для задействованных понятий (например, сложения). Из-за этого расширение Дедекинда преследует цель (|$G»$|), позволяя прямым и обратным операциям удовлетворять свойствам замыкания. Это разделение цели (|$G»$|) предполагает возможность использования предложения Дедекинда и Мандерса для разработки дизъюнктивной характеристики исторических случаев идеальных элементов.
Тем не менее, существует принципиальное концептуальное различие между Дедекиндом, с одной стороны, и Мандерсом, с другой. Мандерс настаивает на том, что после факта расширения мы можем оказаться в состоянии отвергнуть свойства или факты, которые до расширения считались существенными для концепции, которую рассматриваемая структура должна представлять или моделировать (в некотором смысле). свободный смысл терминов). Как уже отмечалось в разделе 5, он даже ссылается на принцип постоянства эквивалентных форм Пикока, отмечая, что, несмотря на его prima facie правдоподобие, оно не может всегда оставаться верным. Это кажется непримиримым различием в том, как два противоположных лагеря — Мандерс, с одной стороны, Дедекинд, с другой — понимают цели и преимущества доменных расширений. Сохранение сущности функции является для Дедекинда критерием, который побуждает математика расширять свои функции и понятия так, а не иначе.
Это кажется непримиримым различием в том, как два противоположных лагеря — Мандерс, с одной стороны, Дедекинд, с другой — понимают цели и преимущества доменных расширений. Сохранение сущности функции является для Дедекинда критерием, который побуждает математика расширять свои функции и понятия так, а не иначе.
8. ЗАКЛЮЧЕНИЕ
В этой статье я начал с обзора идеальных элементов в математике, рассматриваемых как пример хороших расширений математических областей. Я считал [Мандерс, 1989] в качестве кандидата на теоретико-модельное объяснение гильбертовского метода идеальных элементов и его роли в развитии чистой математики.
Концепция расширения предметной области Мандерса, однако, оказалась недостаточно приспособленной для объяснения «идеальности» расширений предметной области, возникающих, когда математик стремится к замыканию посредством операций, или к упрощению и плодотворности иного рода, чем те, которые обеспечиваются устранением кванторов. Хотя верно то, что Мандерс стремится только предложить достаточное условие для успешного или хорошего расширения предметной области, количество и виды случаев, которые не демонстрируют теоретико-модельные характеристики, на которых он фокусируется, позволяют предположить, что объяснение Мандерса плодотворности расширений предметной области таково: в лучшем случае частично.
Хотя верно то, что Мандерс стремится только предложить достаточное условие для успешного или хорошего расширения предметной области, количество и виды случаев, которые не демонстрируют теоретико-модельные характеристики, на которых он фокусируется, позволяют предположить, что объяснение Мандерса плодотворности расширений предметной области таково: в лучшем случае частично.
В попытке пролить свет на связанные вопросы о том, как следует понимать приписывание теоретических достоинств, таких как простота и плодотворность, расширенным математическим областям (или сопутствующим теориям), и могут ли такие достоинства быть сведены к теоретико-модельным характеристикам рассматриваемых структур или теорий, как предлагает нам делать Мандерс, я использовал [Dedekind, 1854] в качестве основы для альтернативного теоретико-модельного критерия хороших расширений предметной области. Результат сравнения Дедекинда и Мандерса состоит в том, что они оба рассматривают комплексные числа как плодотворный случай расширения домена, но затем, кажется, расходятся во мнениях по большинству других случаев. Кватернионы и идеалы не так просто рассматривать в рамках модели Мандерса, но они и не кажутся тем расширением, которое его критерий призван зафиксировать в качестве хорошего случая расширения; они также не удовлетворяют определению расширения Дедекинда. Случай вещественных чисел с бесконечно малыми, с другой стороны, представляет собой хорошее расширение для Дедекинда, хотя и таким образом, что не раскрывает (эпистемологических) преимуществ работы с бесконечно малыми. Для Мандерса это невозможно. Для бесконечно малых тогда остается два следующих варианта: либо понимание идеальных элементов, предлагаемое формализацией Мандерса, слишком ограничительно, поскольку оно не учитывает роль идеальных элементов как «упростителей доказательства»; или, если принять предложение Мандерса за нормативное, бесконечно малые элементы, в конце концов, не являются идеальными элементами. Однако может быть и третий вариант, если более внимательно посмотреть на обсуждение идеальных элементов и расширений в начале статьи, а именно, может возникнуть желание провести различие между идеальными элементами, которые вводятся для округления области в смысле Мандерса или для упростить математику в стиле Мандерса и идеальные элементы, которые вводятся для обеспечения замыкания при определенных операциях.
Кватернионы и идеалы не так просто рассматривать в рамках модели Мандерса, но они и не кажутся тем расширением, которое его критерий призван зафиксировать в качестве хорошего случая расширения; они также не удовлетворяют определению расширения Дедекинда. Случай вещественных чисел с бесконечно малыми, с другой стороны, представляет собой хорошее расширение для Дедекинда, хотя и таким образом, что не раскрывает (эпистемологических) преимуществ работы с бесконечно малыми. Для Мандерса это невозможно. Для бесконечно малых тогда остается два следующих варианта: либо понимание идеальных элементов, предлагаемое формализацией Мандерса, слишком ограничительно, поскольку оно не учитывает роль идеальных элементов как «упростителей доказательства»; или, если принять предложение Мандерса за нормативное, бесконечно малые элементы, в конце концов, не являются идеальными элементами. Однако может быть и третий вариант, если более внимательно посмотреть на обсуждение идеальных элементов и расширений в начале статьи, а именно, может возникнуть желание провести различие между идеальными элементами, которые вводятся для округления области в смысле Мандерса или для упростить математику в стиле Мандерса и идеальные элементы, которые вводятся для обеспечения замыкания при определенных операциях. Согласно этому предположению, расширения Дедекинда — это расширения, которые включают в себя подлинное расширение домена объектов в домене и расширение, которое достигает закрытия при определенных операциях. Это решение соответствовало бы исторической дискуссии, выдвинутой Канту, подчеркивая при этом как сильные стороны, так и потенциальные ограничения использования концепций теории моделей для понимания расширения предметной области в математике.
Согласно этому предположению, расширения Дедекинда — это расширения, которые включают в себя подлинное расширение домена объектов в домене и расширение, которое достигает закрытия при определенных операциях. Это решение соответствовало бы исторической дискуссии, выдвинутой Канту, подчеркивая при этом как сильные стороны, так и потенциальные ограничения использования концепций теории моделей для понимания расширения предметной области в математике.
Footnotes
† Я хотел бы поблагодарить Арианну Бетти, Аннапаолу Джинамми, Луку Инкурвати, Джеффри Роберта Шаца, Хайна ван ден Берга и особенно Шона Уолша, а также двух анонимных рецензентов за их полезные комментарии к предыдущим проектам Эта бумага. Более ранние версии этой работы были представлены на различных семинарах и получили комментарии от их аудитории, в том числе на Восемнадцатом семинаре по математике Среднего Запада в Нотр-Даме (2017 г.) и Двенадцатой ежегодной Кембриджской конференции выпускников по философии математики и логики (2019 г. ).). Я особенно обязан Тиму Баттону как респонденту газеты в Кембридже.
).). Я особенно обязан Тиму Баттону как респонденту газеты в Кембридже.
Работа выполнена при поддержке Нидерландской организации научных исследований, проект № 277-20-007.
1 Более подробно возражения против аргумента (1)–(4) см. в [Cantù, 2013, pp. 89 ff.].
2 Экзистенциальная замкнутость в этой формулировке обусловлена [Hodges, 1993, p. 361].
Как оказалось, можно усилить определение экзистенциального замыкания, чтобы формула |$\varphi$| может быть любой экзистенциальной формулой, а не просто квантором существования, за которым следуют атомарные или отрицательные атомарные формулы. Это всего лишь следствие теоремы о дизъюнктивной нормальной форме для |$\exists_1$| формулы [Ходжес, 1993].
3 Nullstellensatz на самом деле — это название, данное нескольким теоремам современной алгебры, которые, однако, являются обобщениями Nullstellensatz Гильберта. Одна стандартная формулировка Гильберта Nullstellensatz выглядит следующим образом:
Предположим, что |$A$| — алгебраически замкнутое поле, |$I$| является идеалом в кольце многочленов |$A[x_0, \dots, x_{n-1}]$| и |$p(x_0, \dots, x_{n-1})$| является полиномом |$\in A[x_0, \dots, x_{n-1}]$| такое, что для всех |$\overline{a}\in A$| если |$q(\overline{a})= 0$| для всех |$q\in I$| тогда |$p(\overline{a})= 0$|.
k\in I$|. [Ходжес, 19 лет93, с. 366]
Nullstellensatz доказывается с помощью исключения кванторов, а его обобщение, называемое Strong Nullstellensatz , используется для установления определенных результатов в теории двойственности. [nLab, 2019]
4 Этот термин используется в нетехническом смысле, поскольку эти примеры на некоторое время предшествуют теории моделей.
5 За исключением, возможно, Веронезе, ср. [Cantù, 2013, стр. 94–95].
6 Вот полная цитата:
В основе фундаментальных понятий раздела математики, известного как анализ, лежит понятие предела. Производные и интегралы, сумма бесконечного ряда и непрерывность функции определяются в терминах пределов. Например, пусть |$f(x)$| — функция с действительным знаком, определенная для всех |$x$| в открытом интервале |$(0,1)$| и пусть |$x_0$| быть числом, принадлежащим этому интервалу. Тогда действительное число |$a$| является производной от |$f(x)$| в |$x_0$|, в символах 1.
1.1 |$f'(x_0) = (\frac{d f}{d x})_{x=x_0} = a$| если 1.1.2 |$\lim_{x\to x_0}\frac{f(x)- f(x_0)}{x-x_0} = a$|. Предположим, мы спросим хорошо подготовленного математика о значении 1.1.2. Тогда мы можем положиться на него, что, за исключением несущественных вариаций и терминологических различий (таких как использование некоторых топологических понятий), его объяснение будет таким:
Для любого положительного числа |$\epsilon$| существует положительное число |$\delta$| такое, что |$|\frac{f(x) — f(x_0)}{x-x_0}-a|<\epsilon$| для всех |$x$| в |$(0,1)$| для которого |$0<|x-x_0|<\delta$|.
Теперь спросим нашего математика, не согласится ли он со следующей более прямой интерпретацией 1.1.1 и 1.1.2.
Для любого |$x$| в интервале определения |$f(x)$| такое, что |$dx= x-x_0$| бесконечно близко к |$0$| но не равно |$0$|, отношение |$\frac{df}{dx}$|, где |$df = f(x)-f(x_0)$|, бесконечно близко к |$а$|. На этот вопрос мы можем ожидать ответа, что наше определение может быть проще [курсив добавлен] на вид, но совершенно неверно.
[|$\dots$|] [Робинсон, 19 лет96, pp. 1–2]
7 Хотя я не сомневаюсь, что бесконечно малые являются идеальными элементами, по крайней мере, в эпистемологическом смысле, я должен отметить, что нужно быть довольно либеральным в отношении того, что считается « удаление исключений», если кто-то хочет утверждать, что аргумент Канту (1)–(4) можно легко прочитать из цитат Робинсона и Голдблатта. Вот одна из возможных модификаций аргумента Канту: мы заменяем цель (|$G»$|) на цель (|$G»’$|) сделать формальную математику более понятной и максимально приближенной к наивная интуиция, а поддерживающие ценности (|$V$|) и (|$V’$|) со значениями (|$V»$|): простота понимания математической теории желательное значение в математике, и (|$V»’$|): желательна простота понимания, потому что это увеличивает плодотворность. Однако исторические сторонники исчисления бесконечно малых, возможно, апеллировали к этому аргументу именно так, как он представлен в [Cantù, 2013].
8 Здесь читатель может задаться вопросом, что произойдет, если вместо рассмотрения |$\mathbb{R}$| в качестве отправной точки расширения, как я только что сделал, мы рассматриваем случаи, когда |$\mathbb{R}$| является расширенным доменом — например, относительно |$\mathbb{Q}$|. Действительно, существует традиция рассматривать иррациональные числа как идеальные элементы относительно |$\mathbb{Q}$|, а случай |$\mathbb{R}$| как расширение |$\mathbb{Q}$| потенциально может быть проблематичным для аккаунта Мандерса; |$\mathbb{R}$| не является экзистенциальным замыканием |$\mathbb{Q}$| как поле. Поскольку алгебраическое замыкание и экзистенциальное замыкание сводятся к одному и тому же понятию для полей, это означает, что |$\mathbb{R}$| не является экзистенциальным замыканием |$\mathbb{Q}$|; поэтому проблематично приспособиться к структуре Мандерса. На это сторонник модели Мандерса для расширений с помощью идеальных элементов может дать два ответа. Во-первых, действительно, |$\mathbb{R}$| можно рассматривать как расширение |$\mathbb{Q}$| через идеальные элементы, но только если отойти от классической математической точки зрения. Во-вторых, этого следует ожидать, поскольку то, что делает действительные числа достойными внимания математика, — это их полнота, а полнота не может быть выражена в виде формулы первого порядка, в то время как экзистенциальное замыкание имеет дело только с сохранением формул первого порядка. . Можно принять эти два ответа как удовлетворительные, но обратите внимание, что они, по-видимому, приводят к тому, что объяснение Мандерса о расширении домена становится более ограничительным.
Во-вторых, этого следует ожидать, поскольку то, что делает действительные числа достойными внимания математика, — это их полнота, а полнота не может быть выражена в виде формулы первого порядка, в то время как экзистенциальное замыкание имеет дело только с сохранением формул первого порядка. . Можно принять эти два ответа как удовлетворительные, но обратите внимание, что они, по-видимому, приводят к тому, что объяснение Мандерса о расширении домена становится более ограничительным.
9 Как мы также увидим для Дедекинда, это ограничение того, какие законы арифметики должны сохраняться при расширениях, делает довольно нетривиальную работу в этих критериях для расширений.
10 На с. 11 one reads:
Der hierin enthaltene hodegetische Grundsatz kann als das Prinzip der Permanenz der formalen Gesetzen bezeichnet werden und besteht darin: Wenn zwei in allgemeinen Zeichen der arithmetica universalis ausgedrückte Formen einander gleich sind, so sollen sie einander auch gleich bleiben, wenn die Zeichen aufhören, einfachen Größen zu bezeichnen, und daher auch die Operationen einen irgend welchen anderen Inhalt bekommen.
Перевод автора: Содержащийся здесь вводный базовый принцип может быть назван принципом постоянства формальных законов и состоит в следующем: всякий раз, когда две формы, выраженные общими знаками arithmetica universalis , равны друг другу, они также должны остаются равными друг другу, когда знаки перестают обозначать простые величины, а потому и операции приобретают иное содержание [, т. е. ., значение].)
11 Обратите внимание, что Дедекинд, по-видимому, говорит, что в каждом раунде расширения, строго говоря, не просто добавляются новые элементы в числовую область или переопределяются операции, но вся числовая область «создается [ред] [|$\dots$|] заново’. Я нахожу правдоподобным, что здесь Дедекинд просто признает, что добавление чисел к старой области фактически является изменением концепции числа. Следовательно, добавление новых чисел приводит к полному переписыванию определения понятия числа, и в этом смысле ранее существовавшие числа также воссоздаются, как только новые числа появляются на месте. Это прочтение, по общему признанию, слабее, чем другие прочтения «креационизма» Дедекинда о числах, особенно в Was sind und was sollen die Zahlen и Stetigkeit und irrationale Zahlen ([1888; 1872] переведено в [Dedekind, 1963]), как представлено, , например ., в [Tait, 1996; Халлетт, 2019]. Тщательное обсуждение взаимосвязи между определениями и творчеством в работах Дедекинда выходит за рамки настоящей статьи.
Это прочтение, по общему признанию, слабее, чем другие прочтения «креационизма» Дедекинда о числах, особенно в Was sind und was sollen die Zahlen и Stetigkeit und irrationale Zahlen ([1888; 1872] переведено в [Dedekind, 1963]), как представлено, , например ., в [Tait, 1996; Халлетт, 2019]. Тщательное обсуждение взаимосвязи между определениями и творчеством в работах Дедекинда выходит за рамки настоящей статьи.
12 Рассмотрим, например, |$\mathbb{Z}$| как |$\mathcal{A}$|, |$\mathbb{Q}$| как |$\mathcal{B}$|. Если формализация должна отразить идею Дедекинда о хорошем расширении предметной области, то |$\mathbb{Q}$| должен оказаться таким для |$\mathbb{Z}$|. Для этого мое определение должно исключить например ., |$\forall x\, 2x\neq 1$| из класса предложений, которые нужно сохранить между |$\mathbb{Z}$| и |$\mathbb{Q}$|, и один из способов сделать это — исключить отношение(я) порядка из |$\varphi$|.
13 Теорема утверждает, что класс алгебр |$\mathcal{K}$| аксиоматизируемо по уравнениям тогда и только тогда, когда оно является многообразием — , т. е. , тогда и только тогда, когда оно удовлетворяет некоторым свойствам замыкания. Установить, что класс алгебр является многообразием, проще, чем явно дать аксиоматизацию класса алгебр, и знание того, что определенная структура определима уравнениями, чрезвычайно ценно.
е. , тогда и только тогда, когда оно удовлетворяет некоторым свойствам замыкания. Установить, что класс алгебр является многообразием, проще, чем явно дать аксиоматизацию класса алгебр, и знание того, что определенная структура определима уравнениями, чрезвычайно ценно.
14 Donc l’ideal |$\mathfrak{a}$| est composé de tous les nombres entiers contenus dans |$\Omega$| et divisibles par le nombre entier |$\mu$|; pour cette raison nous dirons que le nombre |$\mu$|, lors même qu’il n’est pas contenu dans |$\Omega$|, est un nombre idéal du corps |$\Omega$| , et qu’il соответствуют идеалу |$\mathfrak{a}$|.
15 Обсуждение взглядов Дедекинда на разрезы и действительные числа, а также на сопутствующие трудности см. в [Reck, 2020].
16 Dedekind предлагает конструкцию для каждого из них в Nachlass . Я смог получить доступ к его заметкам о целых числах благодаря Эммилу Хаффнер, но не тем, кто занимался «аналогичной конструкцией» рациональных чисел, и поэтому я полагаюсь на отчет Зига и Шлимма [2005] по этому вопросу.
17 Это замечание может подтолкнуть некоторых читателей к мысли, что случаи форсирования расширений в теории множеств относятся к тому типу расширений, которые должен быть в состоянии объяснить Дедекинд. У меня есть два ответа на этот вопрос. Во-первых, меня интересует дедекиндовское понятие расширения домена прежде всего в том случае, когда добавляемые элементы являются «идеальными элементами». Насколько мне известно, принудительное расширение не обсуждается в этих терминах в литературе. Во-вторых, более подходящим условием (ii) для понятия расширения, пытающегося охватить хорошие расширения теорий на языке теории множеств, было бы требование сохранения абсолютный , то есть |$\Delta_0$| понятия между исходной структурой и расширением.
18 Учитывая, что на первый взгляд гиперкомплексные числа и идеалы не попадают прямо в категорию хороших расширений предметной области ни в одной из рассмотренных здесь структур, можно задаться вопросом, является ли удовлетворительным объяснением расширения предметной области то, что подтверждает, что гиперкомплексные числа и идеалы являются хорошими расширениями предметной области.
Моя полуформализация предложения Дедекинда позволяет рассматривать коммутативность сложения и умножения как некоторые из законов, которые должно сохранять любое расширение числового понятия (или числовой области). Прямым следствием этого является то, что кватернионы, таким образом, не могут считаться случаем расширения Дедекинда. Более того, это согласуется с моим объяснением того, что должен фиксировать критерий Мандерса и что должен фиксировать критерий Дедекинда, что ни один из них не будет рассматривать идеалы и гиперкомплексные числа как хорошие расширения. Я полагаю, что достаточный критерий Мандерса охватывает случаи расширения области, мотивированные присоединением решений уравнений, выразимых, хотя и неразрешимых, в исходной области. Ясно, что гиперкомплексные числа и идеалы не являются такими вещами. Критерий Дедекинда, с другой стороны, должен охватывать случаи расширения области, происходящие от расширения области корректной определенности алгебраических операций 9. 0433 как можно больше . Я также хочу доказать, что введение идеалов не вызвано желанием «закрыть» область при выполнении некоторых операций — то есть функций — над исходной, ограниченной областью, что является своего рода расширением области, к которому я отношу идею Дедекинда. захватывать. Проблема, конечно, в том, что это делает оба описания (Мандерса и мое, основанное на Дедекинде) в некоторой степени нормативными, а не просто описательными.
0433 как можно больше . Я также хочу доказать, что введение идеалов не вызвано желанием «закрыть» область при выполнении некоторых операций — то есть функций — над исходной, ограниченной областью, что является своего рода расширением области, к которому я отношу идею Дедекинда. захватывать. Проблема, конечно, в том, что это делает оба описания (Мандерса и мое, основанное на Дедекинде) в некоторой степени нормативными, а не просто описательными.
19 Точнее, Мандерс предполагает, что для теорий, удовлетворяющих определенным свойствам, экзистенциальная замкнутость является достаточным условием для хорошего расширения области.
Список литературы
Bordogna,
F.
[
1996
]: ‘
Интерпретация идеала: встраивание идеальных чисел в математических программах Kummer, Dedekind и Klein
221 ‘9082.
Берлин
:
Институт истории науки имени Макса Планка
.
Cantù,
P.
[
2013
]: ‘
Аргументативный подход к идеальным элементам в математике
’, в
Абердейн
А.
и
Голубь,
И.Дж.
изд.,
Математический аргумент
, стр.
79
–
99
.
Логика, эпистемология и единство науки; 30
.
Спрингер
. дои.
орг/10.1007/978-94-007-6534-4_17
.
Чемла,
К.
[
2016
]: «
Ценность общности в историографии геометрии Мишеля Шаля
», в
Рено Чорле
K. C.
C.
и
Rabouin,
D.
Eds,
Оксфордский справочник общности в математике и науках
, стр.
47
—
89
2222222.Издательство Оксфордского университета
.
Дедекинд,
Р.
[
1854
]: ‘
О введении новых функций в математику
‘, in
Ewald,
W.
Источник в книге Абертиля 4:
Изд. Основы математики
, стр.
754
–
762
.
Издательство Оксфордского университета
.
Дедекинд,
Р.
[
1872
]:
Stetigkeit und Rationale Zahlen
.
Брауншвейг
:
Фридрих Виег и Зон
.
Dedekind,
R.
[
1876
]: ‘
Sur la théorie des nombres entiers algébriques
‘,
Bulletin des Sciences mathématiques et astronomiques (1)
11
,
278
–
288
.
Дедекинда,
R.
[
1877
]: ‘
Sur la théorie des nombres entiers algébriques
‘,
Bulletin des Sciences mathématiques et astronomiques (2)
1
,
17
—
41
,
69
—
92
,
144
—
164
,
207
222 –9,
207
222 –94
4
4
4
4
4924
4
—
,
—
9000,
210004922,—
.
Дедекинд,
R.
[
1885
]: ‘
Zur Theorie der aus |$n$| Haupteinheiten gebildeten komplexen Grössen
’,
Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen
,
141
–
159
.
Dedekind,
R.
[
1887
]: ‘
Erläuterungen zur Theorie der sogenannten allgemeinen komplexen Grössen
’,
Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen
,
1
–
7
.
Dedekind,
R.
[
1888
]:
Was sind und was sollen die Zahlen
.
Брауншвейг
:
Фридрих Виег и Зон
.
Дедекинд,
Р.
[
1931
]:
Gesammelte Mathematische Werke
, Vol.
2
.
Fricke
Robert
,
Noether
Emmy
и
Ore
Ø ystein
,.
Брауншвейг
:
Фридрих Виег и Зон
.
Дедекинд,
Р.
[
1963
]:
Очерки теории чисел
.
Нью-Йорк
:
Dover Publications
.
Detlefsen,
M.
[
1993
]: ‘
Hilbert’s formalism
‘,
Revue Internationale de Philosophie
47
,
285
–
304
.
Детлефсен,
М.
[
2005
]: ‘
Формализм
‘, в
Shapiro,
S.
Ed.,
Оксфордский справочник по математике и логике
, стр.
.
Издательство Оксфордского университета
.
Дирихле,
J.P.G.L.
и
Дедекинд
R.
[
1999
]:
Лекции по теории чисел
.
Провиденс, Род-Айленд
:
Амер. Мат. соц. и Лондонская математика. Соц
.
Эдвардс,
Х.М.
[
1980
]: ‘
The genesis of ideal theory
’,
Archive for History of Exact Sciences
23
,
321
–
378
.
Эдвардс,
Х.М.
[
1983
]: ‘
Dedekind’s Indecution of Ideations
’,
Бюллетень Лондонского математического общества
15
,
8
—
17
.
Ferreirós,
J.
[
2007
]:
Лабиринт мысли: история теории множеств и ее роль в современной математике
. 2-й об. изд..
Базель, Бостон
:
Биркхойзер
.
Goldblatt,
R.
[
1998
]:
Лекции о Гиперреалах
.
Нью-Йорк
:
Спрингер
.
Hallett,
M.
[
1990
]: ‘
Физиказм, редукционизм и Hilbert
’, в
Irvine,
22. 0822, стр.
0822, стр.
183
–
257
.
Спрингер
.
Hallett,
M.
[
2019
]: ‘
Фреге при создании
’, в
P.A
3 Ebert
3 и
Rossberg,
M.
Eds,
Эссе о основных законах Фреге арифметики
, с.0822 .
Издательство Оксфордского университета
.
Hankel,
H.
[
1867
]:
Теория Der Complecten Zahlensysteme insbesondere der gemeinen gemetrenhren zahlen und der hamilton’schen Quaternion Quaternion Quaternion Quaternion.
Лейпциг
:
Леопольд Фосс
.
Гильберт,
D.
[
1984
]: ‘
на Infinite
’, в
Benacerraf
P.
и
Putnam,
H.
EDS,
Философия математики
: 9000
. 2-е изд., с.
183
–
201
.
Издательство Кембриджского университета
.
Гильберт,
D.
[
1992
]: ‘
Die Rolle von Idealen Gebilden
’, в
Natur und Mathematisches Erkennen
, стр.
90
–
101
.
Роу
Дэвид
, изд.
Базель, Бостон
:
Биркхойзер
.
Hodges,
W.
[
1993
]:
Теория моделей. Энциклопедия математики и ее приложений
, Vol.
42
.
Издательство Кембриджского университета
.
Мандерс,
К.Л.
[
1984
]: ‘
Интерпретации и теория моделей классической геометрии
‘, в
Модели и наборы (AACHEN, 1983)
, с.
297
922 —, с.
297
22 —, с. 330
.
Конспект лекций по математике
;
1103
.
Спрингер
.
Мандерс,
К.Л.
[
1989
]: ‘
Domain extension and the philosophy of mathematics
’,
Journal of Philosophy
86
,
553
–
562
.
nLab [
2019
]: ‘
Nullstellensatz. Редакция 17
’. Доступно на http://ncatlab.org/nlab/revision/Nullstellensatz/17.
Павлина,
G.
[
1830
]:
Трактат по алгебре
.
Кембридж
:
Дж. и Дж.Дж. Дейтон
.
Peacock,
G.
[
1834
]: «
Отчет о недавнем прогрессе и текущем состоянии некоторых областей анализа
», в отчете Третьего собрания Британской ассоциации
90 для развития науки, стр.
185
–
352
.
Reck,
E.
[
2020
]: ‘
Вклады Дедекинда в основы математики
’, in
E ed. ,
,
The Stanford Encyclopedia of Philosophy
(
Winter
2020
ed.) Доступно на https://plato.stanford.edu/entries/dedekind-foundations/. Доступно
июнь
2021
.
Робинсон,
А.
[
1996
]:
Лекции о гиперреальности
.
Издательство Принстонского университета
.
Sieg,
W.
и
Schlimm
D.
[
2005
]: ‘
Анализ DeDekind number: Systems и Axioms
2 ‘,
. 0003 147
0003 147
,
121
–
170
.
Stillwell,
J.
[
2014
]: ‘
Ideal elements in Hilbert’s geometry
‘,
Perspectives on Science
22
,
35
–
55
.
Tait,
W.W.
[
1996
]: ‘
Фреге против Кантора и Дедекинда
’, в
Schirn,
M.
Ed.,
Frege: Важность и Legacy
, стр.
70
—
113
.
Берлин
:
Де Грюйтер
.
палатка,
К.
и
Ziegler
M.
[
2012
]:
Курс по теории модели
.
Конспект лекций по логике
;
40
.
Издательство Кембриджского университета
.
Белый,
D.
[
2004
]:
Аксиоматика, методология и теория идеалов Дедекинда.
Магистерская диссертация, Университет Карнеги-Меллона
.
© Автор [2021]. Опубликовано издательством Оксфордского университета.
Это статья в открытом доступе, распространяемая в соответствии с лицензией Creative Commons Attribution License (http://creativecommons. org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно цитируется.
org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно цитируется.
© Автор [2021]. Опубликовано издательством Оксфордского университета.
Наборы — типы, символы, свойства, примеры
Наборы в математике — это просто набор отдельных объектов, образующих группу. В наборе может быть любая группа предметов, будь то набор чисел, дней недели, видов транспорта и так далее. Каждый элемент множества называется элементом множества. Фигурные скобки используются при написании множества. Очень простой пример набора будет таким. Установите А = {1,2,3,4,5}. Существуют различные обозначения для представления элементов множества. Наборы обычно представляются с помощью формы списка или формы построителя наборов. Остановимся подробно на каждом из этих терминов.
1. Наборы определения 2.
Комплекты Представительство 3. Наборы символов 4. Типы наборов 5. Наборы формул 7. Набор свойств 8. Операции над множествами 9. Часто задаваемые вопросы о наборах
Наборы определения
В математике множество — это четко определенный набор объектов. Наборы именуются и представляются с заглавной буквы. В теории множеств элементами, из которых состоит множество, могут быть любые вещи: люди, буквы алфавита, числа, фигуры, переменные и т. д.
Наборы в математике Примеры
определено менее 10, тогда как совокупность умных учеников в классе не определена. Таким образом, набор четных натуральных чисел меньше 10 можно представить в виде множества A = {2, 4, 6, 8}. Давайте используем этот пример, чтобы понять основную терминологию, связанную с множествами в математике.
Элементы набора
Элементы, присутствующие в наборе, называются либо элементами, либо членами набора. Элементы множества заключены в фигурные скобки, разделенные запятыми. Для обозначения того, что элемент содержится в множестве, используется символ «∈». В приведенном выше примере 2 ∈ A. Если элемент не является членом множества, то он обозначается символом «∉». Здесь 3 ∉ A.
Кардинальное число набора
Кардинальное число, мощность или порядок набора обозначает общее количество элементов в наборе. Для натуральных четных чисел меньше 10 n(A) = 4. Наборы определяются как набор уникальных элементов. Одним из важных условий определения множества является то, что все элементы множества должны быть связаны друг с другом и иметь общее свойство. Например, если мы определим множество с элементами как названия месяцев в году, то мы можем сказать, что все элементы множества являются месяцами года.
Представление наборов
Для представления множеств используются различные нотации множеств. Они отличаются способом перечисления элементов. Для представления множеств используются три обозначения множеств:
Они отличаются способом перечисления элементов. Для представления множеств используются три обозначения множеств:
- Семантическая форма
- Форма реестра
- Набор сборщика форма
Семантическая форма
Семантическая нотация описывает оператор, показывающий, что является элементами множества. Например, набор А — это список первых пяти нечетных чисел.
Форма реестра
Наиболее распространенной формой, используемой для представления наборов, является запись реестра, в которой элементы наборов заключены в фигурные скобки, разделенные запятыми. Например, Set B = {2,4,6,8,10}, который представляет собой набор первых пяти четных чисел. В ростерной форме порядок элементов множества не имеет значения, например, множество первых пяти четных чисел также можно определить как {2,6,8,10,4}. Кроме того, если в наборе имеется бесконечный список элементов, то они определяются с помощью набора точек в конце последнего элемента. Например, бесконечные множества представлены как X = {1, 2, 3, 4, 5. ..}, где X — множество натуральных чисел. Чтобы подытожить нотацию формы реестра, пожалуйста, взгляните на примеры ниже.
..}, где X — множество натуральных чисел. Чтобы подытожить нотацию формы реестра, пожалуйста, взгляните на примеры ниже.
Обозначение множеств с конечным списком: множество A = {1, 2, 3, 4, 5} (первые пять натуральных чисел)
Обозначение наборов с бесконечным реестром: набор B = {5, 10, 15, 20 ….} (кратное 5)
Форма построителя набора
Нотация построителя набора имеет определенное правило или утверждение, которое конкретно описывает общее свойство всех элементов множества. Форма построителя набора использует в своем представлении вертикальную черту с текстом, описывающим характер элементов набора. Например, А = {к | k — четное число, k ≤ 20}. В заявлении говорится, что все элементы множества A являются четными числами, меньшими или равными 20. Иногда вместо «|» используется «:».
Визуальное представление множеств с помощью диаграммы Венна
Диаграмма Венна — это графическое представление множеств, где каждое множество представлено в виде круга. Элементы множества находятся внутри кругов. Иногда прямоугольник окружает круги, что представляет универсальный набор. Диаграмма Венна показывает, как данные наборы связаны друг с другом.
Элементы множества находятся внутри кругов. Иногда прямоугольник окружает круги, что представляет универсальный набор. Диаграмма Венна показывает, как данные наборы связаны друг с другом.
Наборы символов
Набор символов используется для определения элементов данного набора. В следующей таблице показаны некоторые из этих символов и их значение.
Символы Значение У Универсальный набор н(Х) Кардинальное число набора X б е А ‘b’ является элементом множества A а ∉ В ‘a’ не является элементом множества B {} Обозначает набор ∅ Нулевой или пустой набор А У Б Набор A Набор соединительных элементов B А ∩ В Набор пересечений A Набор B А ⊆ В Набор A является подмножеством набора B Б ⊇ А Набор B является надмножеством набора A
Типы наборов
Наборы подразделяются на разные типы. Некоторые из них являются одноэлементными, конечными, бесконечными, пустыми и т. д.
Некоторые из них являются одноэлементными, конечными, бесконечными, пустыми и т. д.
Одноэлементные наборы
Набор, состоящий только из одного элемента, называется одноэлементным набором или также называется единичным набором. Пример. Установите A = { k | k — целое число от 3 до 5}, то есть A = {4}.
Конечные множества
Как следует из названия, множество с конечным или счетным числом элементов называется конечным множеством. Пример. Установите B = {k | k — простое число меньше 20}, то есть B = {2,3,5,7,11,13,17,19}
Бесконечные множества
Множество с бесконечным числом элементов называется бесконечным множеством. Пример: Установите C = {кратное 3}.
Пустые или нулевые наборы
Набор, который не содержит ни одного элемента, называется пустым набором или нулевым набором. Пустое множество обозначается символом «∅». Читается как « фи ». Пример: Установите X = {}.
Равные множества
Если два множества содержат одни и те же элементы, то они называются равными множествами. Пример: А = {1,2,3} и В = {1,2,3}. Здесь множество A и множество B являются равными множествами. Это можно представить как A = B.
Пример: А = {1,2,3} и В = {1,2,3}. Здесь множество A и множество B являются равными множествами. Это можно представить как A = B.
Неравные множества
Если два множества имеют хотя бы один отличающийся элемент, то они являются неравными множествами. Пример: A = {1,2,3} и B = {2,3,4}. Здесь множество A и множество B являются неравными множествами. Это можно представить как A ≠ B.
Эквивалентные множества
Два множества называются эквивалентными множествами, если они имеют одинаковое количество элементов, хотя элементы разные. Пример: A = {1,2,3,4} и B = {a,b,c,d}. Здесь множество A и множество B являются эквивалентными множествами, поскольку n(A) = n(B)
Перекрывающиеся множества
Два множества называются перекрывающимися, если хотя бы один элемент из множества A присутствует в множестве B. Пример: A = {2,4,6} B = {4,8,10}. Здесь элемент 4 присутствует как в множестве A, так и в множестве B. Следовательно, множества A и B перекрываются.
Непересекающиеся множества
Два множества являются непересекающимися множествами, если в обоих множествах нет общих элементов. Пример: А = {1,2,3,4} В = {5,6,7,8}. Здесь множество A и множество B — непересекающиеся множества.
Подмножество и надмножество
Для двух множеств A и B, если каждый элемент множества A присутствует в множестве B, то множество A является подмножеством множества B(A ⊆ B), а B является надмножеством множества A(B ⊇ А).
Пример: А = {1,2,3} В = {1,2,3,4,5,6}
A ⊆ B, так как все элементы множества A присутствуют в множестве B.
B ⊇ A означает, что множество B является надмножеством множества A.
Универсальный набор
Универсальный набор — это совокупность всех элементов, относящихся к конкретному предмету. Универсальный набор обозначается буквой «У». Пример: Пусть U = {Список всех автотранспортных средств}. Здесь множество автомобилей является подмножеством этого универсального множества, множество велосипедов, поездов — все подмножества этого универсального множества.
Наборы мощности
Набор мощности — это набор всех подмножеств, которые может содержать набор. Пример: Установите A = {1,2,3}. Набор мощностей A = {{∅}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
Наборы формул
Множества находят свое применение в области алгебры, статистики и вероятностей. Ниже перечислены некоторые важные формулы набора.
Для любых двух перекрывающихся множеств A и B
- n(A U B) = n(A) + n(B) — n(A ∩ B)
- n (A ∩ B) = n(A) + n(B) — n(A U B)
- n(A) = n(A U B) + n(A ∩ B) — n(B)
- n(B) = n(A U B) + n(A ∩ B) — n(A)
- n(A — B) = n(A U B) — n(B)
- n(A — B) = n(A) — n(A ∩ B)
Для любых двух непересекающихся множеств A и B:
- n(A U B) = n(A) + n(B)
- А ∩ В = ∅
- n(A — B) = n(A)
Свойства наборов
Подобно числам, множества обладают такими свойствами, как ассоциативность, коммутативность и т. д. Существует шесть важных свойств множеств. Имея три множества A, B и C, свойства этих множеств следующие.
д. Существует шесть важных свойств множеств. Имея три множества A, B и C, свойства этих множеств следующие.
Собственность Пример Коммутативное имущество А У Б = Б У А
А ∩ В = В ∩ А Ассоциативное свойство (А ∩ В) ∩ С = А ∩ (В ∩ С)
(А У Б) У С = А У (Б У С) Распределительная собственность A U (B ∩ C) = (A U B) ∩ (A U C)
А ∩ (B U C) = (A ∩ B) U (A ∩ C) Идентификационное свойство А U ∅ = А
А ∩ U = А Дополнение Свойство А U А’ = U Идемпотентное свойство А ∩ А = А
А У А = А
Операции над множествами
Некоторые важные операции над множествами включают объединение, пересечение, разность, дополнение множества и декартово произведение множества. Краткое объяснение операций над множествами состоит в следующем.
Краткое объяснение операций над множествами состоит в следующем.
Объединение множеств
Объединение множеств, которое обозначается как A U B, перечисляет элементы множества A и множества B или элементы как множества A, так и множества B. Например, {1, 3} ∪ {1, 4 } = {1, 3, 4}
Пересечение множеств
Пересечение множеств, обозначаемое A ∩ B, перечисляет элементы, общие как для множества A, так и для множества B. Например, {1, 2} ∩ {2, 4} = {2}
Разность наборов
Разность наборов , которая обозначается буквами A — B, перечисляет элементы набора A, которых нет в наборе B. Например, A = {2, 3, 4} и B = {4, 5, 6}. А — В = {2, 3}.
Дополнение к множеству
Дополнение к множеству, которое обозначается A’, представляет собой множество всех элементов универсального множества, которые не присутствуют в множестве A. Другими словами, A’ обозначается как U — A, что представляет собой разность в элементах универсального множества и множества А.
Декартово произведение множеств
Декартово произведение двух множеств, обозначаемое A × B, является произведением двух непустых множеств, в котором получаются упорядоченные пары элементов. Например, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.
☛ Темы, связанные с наборами:
Ознакомьтесь с некоторыми интересными темами, связанными с наборами.
- Операции с множествами
- Диаграммы Венна
- Подмножество
- Обозначение реестра
- Универсальный набор
- Пересечение множеств
- Набор обозначений Builder
Часто задаваемые вопросы о наборах
Что такое множества в математике и примерах?
Наборы представляют собой набор отдельных элементов, заключенных в фигурные скобки и разделенных запятыми. Список элементов множества называется элементами множества. Примеры: коллекция фруктов, коллекция картинок. По-другому множества представляются следующим образом. Установите A = {a,b,c,d}. Здесь a,b,c,d — элементы множества A.
По-другому множества представляются следующим образом. Установите A = {a,b,c,d}. Здесь a,b,c,d — элементы множества A.
Какие существуют различные обозначения множеств для представления множеств?
Наборы могут быть представлены тремя способами. Представление множеств означает способ перечисления элементов множества. Они следующие.
- Семантическая запись: Элементы набора представлены одним оператором. Например, Set A — это количество дней в неделе.
- Roster Notation: эта форма представления наборов использует фигурные скобки для перечисления элементов набора. Например, установите A = {2,4,6,8,10}
- Обозначение построителя набора: форма построителя набора представляет элементы набора по общему правилу или свойству. Например, {х | x — простое число меньше 20}
Какие существуют типы наборов?
Наборы отличаются друг от друга в зависимости от присутствующих в них элементов. Исходя из этого, мы имеем следующие виды наборов. Это одноэлементные множества, конечные и бесконечные множества, пустые или нулевые множества, равные множества, неравные множества, эквивалентные множества, перекрывающиеся множества, непересекающиеся множества, подмножества, надмножества, степенные множества и универсальные множества.
Это одноэлементные множества, конечные и бесконечные множества, пустые или нулевые множества, равные множества, неравные множества, эквивалентные множества, перекрывающиеся множества, непересекающиеся множества, подмножества, надмножества, степенные множества и универсальные множества.
Каковы свойства множеств в теории множеств?
Различные свойства, связанные с множествами в математике:
- Переместительное свойство: A U B = B U A и A ∩ B = B ∩ A
- Ассоциативное свойство: (A ∩ B) ∩ C = A ∩ (B ∩ C) и (A U B) U C = A U (B U C)
- Распределительное свойство: A U (B ∩ C) = (A U B) ∩ (AU C) и A ∩ (B U C) = (A ∩ B) U (A ∩ C)
- Свойство идентичности: A U ∅ = A и A ∩ U = A
- Свойство дополнения: A U A’ = U
- Свойство идемпотента: A ∩ A = A и A U A = A
Что такое объединение наборов?
Объединение двух наборов A и B представляет собой элементы из обоих наборов A и B или оба вместе. Обозначается символом «У». Например, если установить A = {1,2,3} и установить B = {4,5,6}, то AUB = {1,2,3,4,5,6}. A U B читается как «союз B».
Например, если установить A = {1,2,3} и установить B = {4,5,6}, то AUB = {1,2,3,4,5,6}. A U B читается как «союз B».
Что такое пересечение множеств?
Пересечение двух множеств A и B — это элементы, общие для множества A и B. Оно обозначается символом ‘∩’. Например, если установить A = {1,2,3} и установить B = {3,4,5}, то A ∩ B = {3}. A ∩ B читается как «пересечение A B».
Что такое подмножества и надмножества?
Если каждый элемент множества A присутствует в множестве B, то множество B является надмножеством множества A, а множество A является подмножеством множества B.
Пример: А = {1,4,5} В = {1,2,3,4,5,6}
Поскольку все элементы множества A присутствуют в множестве B. ⇒ A ⊆ B и B ⊇ A.
Что такое универсальные множества?
Универсальный набор, обозначаемый буквой «U», представляет собой совокупность всех элементов, относящихся к определенному предмету.
Пример: Пусть U = {Список всех автотранспортных средств}. Здесь множество циклов является подмножеством этого универсального множества.
Что такое дополнение в наборах?
Дополнением множества, обозначаемого А’, является множество всех элементов универсального множества, не присутствующих в множестве А. Другими словами, А’ обозначается как U — А, что представляет собой разность элементы универсального множества и множества А.
Что такое Декартово произведение в множествах?
Декартово произведение двух множеств, обозначаемое A×B, есть произведение двух непустых множеств, при котором получаются упорядоченные пары элементов. Например, если A = {1,2} и B = {3,4}, то A×B = {(1,3), (1,4), (2,3), (2,4)} .
Какая польза от диаграммы Венна в множествах?
Диаграмма Венна — это графическое представление отношений между двумя или более множествами. Круги используются для представления наборов. Каждый круг представляет набор. Прямоугольник, окружающий круги, представляет универсальное множество.
Центр изучения дискретной математики
Наборы
Набор представляет собой неупорядоченный набор объектов.
Объекты набора называются элементами набора или членов . Обычно они указываются внутри фигурных скобок. Мы пишем $x \in A$, если $x$ является элементом (членом) множества $A$.
$\{1,2,3\}$ — множество из $3$ элементов. Это то же самое, что набор $\{1,3,2\}$ (порядок не имеет значения) и набор $\{1,1,2,3,3,3,3\}$ (повторение не имеет значения). иметь значение). Как правило, все объекты одинаковые (например, числа), но они не обязательно должны быть такими: $\{ 1, 3, \text{red}, \text{blue}, \text{John} \}$ множество.
Многоточие используется, когда шаблон понятен: $\{1,2,3,4,\ldots,50\}$ — множество всех целых чисел от $1$ до $50$ включительно.
Некоторые наборы мы используем много:
- $\mathbb{R}$ множество действительных чисел
- $\mathbb{N}$ — множество натуральных чисел
- $\mathbb{Z}$ — множество целых чисел
- $\mathbb{Q}$ — множество рациональных чисел
Возможно множество без элементов: $\{\}$. Это пустое множество , которое обычно обозначается как $\emptyset$. Это , а не , то же самое, что $\{\emptyset \}$, который представляет собой набор с одним элементом (который оказывается (пустым) набором).
Это пустое множество , которое обычно обозначается как $\emptyset$. Это , а не , то же самое, что $\{\emptyset \}$, который представляет собой набор с одним элементом (который оказывается (пустым) набором).
Количество различных элементов в множестве $S$ называется его мощностью и обозначается $|S|$. Если $|S|$ бесконечно (например, $\mathbb{Z}$), мы говорим, что множество бесконечно .
Одним из распространенных способов определения набора является нотация построителя набора . Вот два примера:
- $\mathbb{R} = \{ r \;|\; r \text{ действительное число} \}$
- $O = \{ х \;|\; x \text{ — нечетное целое число} \}$
Набор операций
Над наборами можно выполнять несколько операций.
- Union : Для двух множеств $A$ и $B$ объединение $A \cup B$ представляет собой множество всех элементов, которые находятся либо в $A$, либо в $B$.
 Например, если $A = \{ 1,3,5 \}$ и $B = \{ 2,3,6 \}$, то $A \cup B = \{ 1,2,3,4,5 ,6 \}$. Обратите внимание, что $A \cup B = \{ x \;|\; (x \in A) \lor (x \in B) \}$.
Например, если $A = \{ 1,3,5 \}$ и $B = \{ 2,3,6 \}$, то $A \cup B = \{ 1,2,3,4,5 ,6 \}$. Обратите внимание, что $A \cup B = \{ x \;|\; (x \in A) \lor (x \in B) \}$. - Пересечение : Для двух множеств $A$ и $B$ пересечение $A \cap B$ — это множество всех элементов, которые находятся как в $A$, так и в $B$. Например, если $A = \{ 1,2,3,4 \}$ и $B = \{ 3,4,5,6 \}$, то $A \cap B = \{ 3,4 \} $. Обратите внимание, что $A \cap B = \{ x \;|\; (x \in A) \land (x \in B) \}$. Мы говорим, что $A$ и $B$ являются непересекающимися , если $A \cap B = \emptyset$.
- Разность : Для двух множеств $A$ и $B$ разность $A \setminus B$ представляет собой множество всех элементов, которые находятся в $A$, но не в $B$. Например, если $A = \{ 1,2,3,4 \}$ и $B = \{ 3,4 \}$, то $A \setminus B = \{ 1,2 \}$. Обратите внимание, что $A \setminus B = \{ x \;|\; (x \in A) \land (x \notin B) \}$.
 $A \setminus B$ также обозначается как $A — B$.
$A \setminus B$ также обозначается как $A — B$. - Дополнение : для множества $A$ дополнение $\overline{A}$ — это множество всех элементов, число которых равно , а не , в $A$. Чтобы определить это, нам нужно некоторое определение вселенной всех возможных элементов $U$. Таким образом, мы можем рассматривать дополнение как частный случай разности множеств, где $\overline{A} = U \setminus A$. Например, если $U = \mathbb{Z}$ и $A = \{ x \;|\; x \text{ — нечетное целое число} \}$, тогда $\overline{A} = \{ x \;|\; x \text{ — четное число} \}$. Обратите внимание, что $\overline{A} = \{ x \;|\; х \не в А \}$.
- Декартово произведение : Для двух множеств $A$ и $B$ декартово произведение $A \times B$ представляет собой набор упорядоченных пар, где первый элемент находится в $A$, а второй элемент — в $B. $. Имеем $A \times B = \{ (a,b) \;|\; a \in A \land b \in B \}$.
 Например, если $A = \{ 1,2,3 \}$ и $B = \{ a,b \}$, то $A \times B = \{ (1,a),(1,b) ,(2,а),(2,б),(3,а),(3,б)\}$.
Например, если $A = \{ 1,2,3 \}$ и $B = \{ a,b \}$, то $A \times B = \{ (1,a),(1,b) ,(2,а),(2,б),(3,а),(3,б)\}$.
Подмножества
Набор $A$ является подмножеством множества $B$, если каждый элемент $A$ является элементом $B$. Мы пишем $A \subseteq B$. Другими словами, $A \subseteq B$ тогда и только тогда, когда $\forall x\;(x \in A \rightarrow x \in B)$.
Для любого набора S имеем:
- $\emptyset\subseteq S$
Доказательство: нужно показать, что $\forall x\;{(x \in \emptyset \rightarrow x \in S)}$. Поскольку $x \in \emptyset$ всегда ложно, импликация всегда истинна. Это пример тривиального или бессодержательного доказательства.
- $S \подмножество S$
Доказательство: нужно показать, что $\forall x\;{(x \in S \rightarrow x \in S)}$. Зафиксируйте элемент $x$. Мы должны показать, что $x \in S \rightarrow x \in S$. Эта импликация эквивалентна $x \in S \lor x \notin S$, что является тавтологией. Следовательно, по универсальному обобщению $S \subseteq S$.




ed. ,
,
The Stanford Encyclopedia of Philosophy
(
Winter
2020
ed.) Доступно на https://plato.stanford.edu/entries/dedekind-foundations/. Доступно
июнь
2021
.
Робинсон,
А.
[
1996
]:
Лекции о гиперреальности
.
Издательство Принстонского университета
.
Sieg,
W.
и
Schlimm
D.
[
2005
]: ‘
Анализ DeDekind number: Systems и Axioms
2 ‘,
. 0003 147
0003 147
,
121
–
170
.
Stillwell,
J.
[
2014
]: ‘
Ideal elements in Hilbert’s geometry
‘,
Perspectives on Science
22
,
35
–
55
.
Tait,
W.W.
[
1996
]: ‘
Фреге против Кантора и Дедекинда
’, в
Schirn,
M.
Ed.,
Frege: Важность и Legacy
, стр.
70
—
113
.
Берлин
:
Де Грюйтер
.
палатка,
К.
и
Ziegler
M.
[
2012
]:
Курс по теории модели
.
Конспект лекций по логике
;
40
.
Издательство Кембриджского университета
.
Белый,
D.
[
2004
]:
Аксиоматика, методология и теория идеалов Дедекинда.
Магистерская диссертация, Университет Карнеги-Меллона
.
© Автор [2021]. Опубликовано издательством Оксфордского университета.
Это статья в открытом доступе, распространяемая в соответствии с лицензией Creative Commons Attribution License (http://creativecommons. org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно цитируется.
org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно цитируется.
© Автор [2021]. Опубликовано издательством Оксфордского университета.
Наборы — типы, символы, свойства, примеры
Наборы в математике — это просто набор отдельных объектов, образующих группу. В наборе может быть любая группа предметов, будь то набор чисел, дней недели, видов транспорта и так далее. Каждый элемент множества называется элементом множества. Фигурные скобки используются при написании множества. Очень простой пример набора будет таким. Установите А = {1,2,3,4,5}. Существуют различные обозначения для представления элементов множества. Наборы обычно представляются с помощью формы списка или формы построителя наборов. Остановимся подробно на каждом из этих терминов.
| 1. | Наборы определения |
2. | Комплекты Представительство |
| 3. | Наборы символов |
| 4. | Типы наборов |
| 5. | Наборы формул |
| 7. | Набор свойств |
| 8. | Операции над множествами |
| 9. | Часто задаваемые вопросы о наборах |
Наборы определения
В математике множество — это четко определенный набор объектов. Наборы именуются и представляются с заглавной буквы. В теории множеств элементами, из которых состоит множество, могут быть любые вещи: люди, буквы алфавита, числа, фигуры, переменные и т. д.
Наборы в математике Примеры
определено менее 10, тогда как совокупность умных учеников в классе не определена. Таким образом, набор четных натуральных чисел меньше 10 можно представить в виде множества A = {2, 4, 6, 8}. Давайте используем этот пример, чтобы понять основную терминологию, связанную с множествами в математике.
Элементы набора
Элементы, присутствующие в наборе, называются либо элементами, либо членами набора. Элементы множества заключены в фигурные скобки, разделенные запятыми. Для обозначения того, что элемент содержится в множестве, используется символ «∈». В приведенном выше примере 2 ∈ A. Если элемент не является членом множества, то он обозначается символом «∉». Здесь 3 ∉ A.
Кардинальное число набора
Кардинальное число, мощность или порядок набора обозначает общее количество элементов в наборе. Для натуральных четных чисел меньше 10 n(A) = 4. Наборы определяются как набор уникальных элементов. Одним из важных условий определения множества является то, что все элементы множества должны быть связаны друг с другом и иметь общее свойство. Например, если мы определим множество с элементами как названия месяцев в году, то мы можем сказать, что все элементы множества являются месяцами года.
Представление наборов
Для представления множеств используются различные нотации множеств. Они отличаются способом перечисления элементов. Для представления множеств используются три обозначения множеств:
Они отличаются способом перечисления элементов. Для представления множеств используются три обозначения множеств:
- Семантическая форма
- Форма реестра
- Набор сборщика форма
Семантическая форма
Семантическая нотация описывает оператор, показывающий, что является элементами множества. Например, набор А — это список первых пяти нечетных чисел.
Форма реестра
Наиболее распространенной формой, используемой для представления наборов, является запись реестра, в которой элементы наборов заключены в фигурные скобки, разделенные запятыми. Например, Set B = {2,4,6,8,10}, который представляет собой набор первых пяти четных чисел. В ростерной форме порядок элементов множества не имеет значения, например, множество первых пяти четных чисел также можно определить как {2,6,8,10,4}. Кроме того, если в наборе имеется бесконечный список элементов, то они определяются с помощью набора точек в конце последнего элемента. Например, бесконечные множества представлены как X = {1, 2, 3, 4, 5. ..}, где X — множество натуральных чисел. Чтобы подытожить нотацию формы реестра, пожалуйста, взгляните на примеры ниже.
..}, где X — множество натуральных чисел. Чтобы подытожить нотацию формы реестра, пожалуйста, взгляните на примеры ниже.
Обозначение множеств с конечным списком: множество A = {1, 2, 3, 4, 5} (первые пять натуральных чисел)
Обозначение наборов с бесконечным реестром: набор B = {5, 10, 15, 20 ….} (кратное 5)
Форма построителя набора
Нотация построителя набора имеет определенное правило или утверждение, которое конкретно описывает общее свойство всех элементов множества. Форма построителя набора использует в своем представлении вертикальную черту с текстом, описывающим характер элементов набора. Например, А = {к | k — четное число, k ≤ 20}. В заявлении говорится, что все элементы множества A являются четными числами, меньшими или равными 20. Иногда вместо «|» используется «:».
Визуальное представление множеств с помощью диаграммы Венна
Диаграмма Венна — это графическое представление множеств, где каждое множество представлено в виде круга. Элементы множества находятся внутри кругов. Иногда прямоугольник окружает круги, что представляет универсальный набор. Диаграмма Венна показывает, как данные наборы связаны друг с другом.
Элементы множества находятся внутри кругов. Иногда прямоугольник окружает круги, что представляет универсальный набор. Диаграмма Венна показывает, как данные наборы связаны друг с другом.
Наборы символов
Набор символов используется для определения элементов данного набора. В следующей таблице показаны некоторые из этих символов и их значение.
| Символы | Значение |
|---|---|
| У | Универсальный набор |
| н(Х) | Кардинальное число набора X |
| б е А | ‘b’ является элементом множества A |
| а ∉ В | ‘a’ не является элементом множества B |
| {} | Обозначает набор |
| ∅ | Нулевой или пустой набор |
| А У Б | Набор A Набор соединительных элементов B |
| А ∩ В | Набор пересечений A Набор B |
| А ⊆ В | Набор A является подмножеством набора B |
| Б ⊇ А | Набор B является надмножеством набора A |
Типы наборов
Наборы подразделяются на разные типы. Некоторые из них являются одноэлементными, конечными, бесконечными, пустыми и т. д.
Некоторые из них являются одноэлементными, конечными, бесконечными, пустыми и т. д.
Одноэлементные наборы
Набор, состоящий только из одного элемента, называется одноэлементным набором или также называется единичным набором. Пример. Установите A = { k | k — целое число от 3 до 5}, то есть A = {4}.
Конечные множества
Как следует из названия, множество с конечным или счетным числом элементов называется конечным множеством. Пример. Установите B = {k | k — простое число меньше 20}, то есть B = {2,3,5,7,11,13,17,19}
Бесконечные множества
Множество с бесконечным числом элементов называется бесконечным множеством. Пример: Установите C = {кратное 3}.
Пустые или нулевые наборы
Набор, который не содержит ни одного элемента, называется пустым набором или нулевым набором. Пустое множество обозначается символом «∅». Читается как « фи ». Пример: Установите X = {}.
Равные множества
Если два множества содержат одни и те же элементы, то они называются равными множествами. Пример: А = {1,2,3} и В = {1,2,3}. Здесь множество A и множество B являются равными множествами. Это можно представить как A = B.
Пример: А = {1,2,3} и В = {1,2,3}. Здесь множество A и множество B являются равными множествами. Это можно представить как A = B.
Неравные множества
Если два множества имеют хотя бы один отличающийся элемент, то они являются неравными множествами. Пример: A = {1,2,3} и B = {2,3,4}. Здесь множество A и множество B являются неравными множествами. Это можно представить как A ≠ B.
Эквивалентные множества
Два множества называются эквивалентными множествами, если они имеют одинаковое количество элементов, хотя элементы разные. Пример: A = {1,2,3,4} и B = {a,b,c,d}. Здесь множество A и множество B являются эквивалентными множествами, поскольку n(A) = n(B)
Перекрывающиеся множества
Два множества называются перекрывающимися, если хотя бы один элемент из множества A присутствует в множестве B. Пример: A = {2,4,6} B = {4,8,10}. Здесь элемент 4 присутствует как в множестве A, так и в множестве B. Следовательно, множества A и B перекрываются.
Непересекающиеся множества
Два множества являются непересекающимися множествами, если в обоих множествах нет общих элементов. Пример: А = {1,2,3,4} В = {5,6,7,8}. Здесь множество A и множество B — непересекающиеся множества.
Подмножество и надмножество
Для двух множеств A и B, если каждый элемент множества A присутствует в множестве B, то множество A является подмножеством множества B(A ⊆ B), а B является надмножеством множества A(B ⊇ А).
Пример: А = {1,2,3} В = {1,2,3,4,5,6}
A ⊆ B, так как все элементы множества A присутствуют в множестве B.
B ⊇ A означает, что множество B является надмножеством множества A.
Универсальный набор
Универсальный набор — это совокупность всех элементов, относящихся к конкретному предмету. Универсальный набор обозначается буквой «У». Пример: Пусть U = {Список всех автотранспортных средств}. Здесь множество автомобилей является подмножеством этого универсального множества, множество велосипедов, поездов — все подмножества этого универсального множества.
Наборы мощности
Набор мощности — это набор всех подмножеств, которые может содержать набор. Пример: Установите A = {1,2,3}. Набор мощностей A = {{∅}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
Наборы формул
Множества находят свое применение в области алгебры, статистики и вероятностей. Ниже перечислены некоторые важные формулы набора.
Для любых двух перекрывающихся множеств A и B
- n(A U B) = n(A) + n(B) — n(A ∩ B)
- n (A ∩ B) = n(A) + n(B) — n(A U B)
- n(A) = n(A U B) + n(A ∩ B) — n(B)
- n(B) = n(A U B) + n(A ∩ B) — n(A)
- n(A — B) = n(A U B) — n(B)
- n(A — B) = n(A) — n(A ∩ B)
Для любых двух непересекающихся множеств A и B:
- n(A U B) = n(A) + n(B)
- А ∩ В = ∅
- n(A — B) = n(A)
Свойства наборов
Подобно числам, множества обладают такими свойствами, как ассоциативность, коммутативность и т. д. Существует шесть важных свойств множеств. Имея три множества A, B и C, свойства этих множеств следующие.
д. Существует шесть важных свойств множеств. Имея три множества A, B и C, свойства этих множеств следующие.
| Собственность | Пример |
|---|---|
| Коммутативное имущество | А У Б = Б У А А ∩ В = В ∩ А |
| Ассоциативное свойство | (А ∩ В) ∩ С = А ∩ (В ∩ С) (А У Б) У С = А У (Б У С) |
| Распределительная собственность | A U (B ∩ C) = (A U B) ∩ (A U C) А ∩ (B U C) = (A ∩ B) U (A ∩ C) |
| Идентификационное свойство | А U ∅ = А А ∩ U = А |
| Дополнение Свойство | А U А’ = U |
| Идемпотентное свойство | А ∩ А = А А У А = А |
Операции над множествами
Некоторые важные операции над множествами включают объединение, пересечение, разность, дополнение множества и декартово произведение множества. Краткое объяснение операций над множествами состоит в следующем.
Краткое объяснение операций над множествами состоит в следующем.
Объединение множеств
Объединение множеств, которое обозначается как A U B, перечисляет элементы множества A и множества B или элементы как множества A, так и множества B. Например, {1, 3} ∪ {1, 4 } = {1, 3, 4}
Пересечение множеств
Пересечение множеств, обозначаемое A ∩ B, перечисляет элементы, общие как для множества A, так и для множества B. Например, {1, 2} ∩ {2, 4} = {2}
Разность наборов
Разность наборов , которая обозначается буквами A — B, перечисляет элементы набора A, которых нет в наборе B. Например, A = {2, 3, 4} и B = {4, 5, 6}. А — В = {2, 3}.
Дополнение к множеству
Дополнение к множеству, которое обозначается A’, представляет собой множество всех элементов универсального множества, которые не присутствуют в множестве A. Другими словами, A’ обозначается как U — A, что представляет собой разность в элементах универсального множества и множества А.
Декартово произведение множеств
Декартово произведение двух множеств, обозначаемое A × B, является произведением двух непустых множеств, в котором получаются упорядоченные пары элементов. Например, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.
☛ Темы, связанные с наборами:
Ознакомьтесь с некоторыми интересными темами, связанными с наборами.
- Операции с множествами
- Диаграммы Венна
- Подмножество
- Обозначение реестра
- Универсальный набор
- Пересечение множеств
- Набор обозначений Builder
Часто задаваемые вопросы о наборах
Что такое множества в математике и примерах?
Наборы представляют собой набор отдельных элементов, заключенных в фигурные скобки и разделенных запятыми. Список элементов множества называется элементами множества. Примеры: коллекция фруктов, коллекция картинок. По-другому множества представляются следующим образом. Установите A = {a,b,c,d}. Здесь a,b,c,d — элементы множества A.
По-другому множества представляются следующим образом. Установите A = {a,b,c,d}. Здесь a,b,c,d — элементы множества A.
Какие существуют различные обозначения множеств для представления множеств?
Наборы могут быть представлены тремя способами. Представление множеств означает способ перечисления элементов множества. Они следующие.
- Семантическая запись: Элементы набора представлены одним оператором. Например, Set A — это количество дней в неделе.
- Roster Notation: эта форма представления наборов использует фигурные скобки для перечисления элементов набора. Например, установите A = {2,4,6,8,10}
- Обозначение построителя набора: форма построителя набора представляет элементы набора по общему правилу или свойству. Например, {х | x — простое число меньше 20}
Какие существуют типы наборов?
Наборы отличаются друг от друга в зависимости от присутствующих в них элементов. Исходя из этого, мы имеем следующие виды наборов. Это одноэлементные множества, конечные и бесконечные множества, пустые или нулевые множества, равные множества, неравные множества, эквивалентные множества, перекрывающиеся множества, непересекающиеся множества, подмножества, надмножества, степенные множества и универсальные множества.
Это одноэлементные множества, конечные и бесконечные множества, пустые или нулевые множества, равные множества, неравные множества, эквивалентные множества, перекрывающиеся множества, непересекающиеся множества, подмножества, надмножества, степенные множества и универсальные множества.
Каковы свойства множеств в теории множеств?
Различные свойства, связанные с множествами в математике:
- Переместительное свойство: A U B = B U A и A ∩ B = B ∩ A
- Ассоциативное свойство: (A ∩ B) ∩ C = A ∩ (B ∩ C) и (A U B) U C = A U (B U C)
- Распределительное свойство: A U (B ∩ C) = (A U B) ∩ (AU C) и A ∩ (B U C) = (A ∩ B) U (A ∩ C)
- Свойство идентичности: A U ∅ = A и A ∩ U = A
- Свойство дополнения: A U A’ = U
- Свойство идемпотента: A ∩ A = A и A U A = A
Что такое объединение наборов?
Объединение двух наборов A и B представляет собой элементы из обоих наборов A и B или оба вместе. Обозначается символом «У». Например, если установить A = {1,2,3} и установить B = {4,5,6}, то AUB = {1,2,3,4,5,6}. A U B читается как «союз B».
Например, если установить A = {1,2,3} и установить B = {4,5,6}, то AUB = {1,2,3,4,5,6}. A U B читается как «союз B».
Что такое пересечение множеств?
Пересечение двух множеств A и B — это элементы, общие для множества A и B. Оно обозначается символом ‘∩’. Например, если установить A = {1,2,3} и установить B = {3,4,5}, то A ∩ B = {3}. A ∩ B читается как «пересечение A B».
Что такое подмножества и надмножества?
Если каждый элемент множества A присутствует в множестве B, то множество B является надмножеством множества A, а множество A является подмножеством множества B.
Пример: А = {1,4,5} В = {1,2,3,4,5,6}
Поскольку все элементы множества A присутствуют в множестве B. ⇒ A ⊆ B и B ⊇ A.
Что такое универсальные множества?
Универсальный набор, обозначаемый буквой «U», представляет собой совокупность всех элементов, относящихся к определенному предмету.
Пример: Пусть U = {Список всех автотранспортных средств}. Здесь множество циклов является подмножеством этого универсального множества.
Что такое дополнение в наборах?
Дополнением множества, обозначаемого А’, является множество всех элементов универсального множества, не присутствующих в множестве А. Другими словами, А’ обозначается как U — А, что представляет собой разность элементы универсального множества и множества А.
Что такое Декартово произведение в множествах?
Декартово произведение двух множеств, обозначаемое A×B, есть произведение двух непустых множеств, при котором получаются упорядоченные пары элементов. Например, если A = {1,2} и B = {3,4}, то A×B = {(1,3), (1,4), (2,3), (2,4)} .
Какая польза от диаграммы Венна в множествах?
Диаграмма Венна — это графическое представление отношений между двумя или более множествами. Круги используются для представления наборов. Каждый круг представляет набор. Прямоугольник, окружающий круги, представляет универсальное множество.
Центр изучения дискретной математики
Наборы
Набор представляет собой неупорядоченный набор объектов.
Объекты набора называются элементами набора или членов . Обычно они указываются внутри фигурных скобок. Мы пишем $x \in A$, если $x$ является элементом (членом) множества $A$.
$\{1,2,3\}$ — множество из $3$ элементов. Это то же самое, что набор $\{1,3,2\}$ (порядок не имеет значения) и набор $\{1,1,2,3,3,3,3\}$ (повторение не имеет значения). иметь значение). Как правило, все объекты одинаковые (например, числа), но они не обязательно должны быть такими: $\{ 1, 3, \text{red}, \text{blue}, \text{John} \}$ множество.
Многоточие используется, когда шаблон понятен: $\{1,2,3,4,\ldots,50\}$ — множество всех целых чисел от $1$ до $50$ включительно.
Некоторые наборы мы используем много:
- $\mathbb{R}$ множество действительных чисел
- $\mathbb{N}$ — множество натуральных чисел
- $\mathbb{Z}$ — множество целых чисел
- $\mathbb{Q}$ — множество рациональных чисел
Возможно множество без элементов: $\{\}$. Это пустое множество , которое обычно обозначается как $\emptyset$. Это , а не , то же самое, что $\{\emptyset \}$, который представляет собой набор с одним элементом (который оказывается (пустым) набором).
Это пустое множество , которое обычно обозначается как $\emptyset$. Это , а не , то же самое, что $\{\emptyset \}$, который представляет собой набор с одним элементом (который оказывается (пустым) набором).
Количество различных элементов в множестве $S$ называется его мощностью и обозначается $|S|$. Если $|S|$ бесконечно (например, $\mathbb{Z}$), мы говорим, что множество бесконечно .
Одним из распространенных способов определения набора является нотация построителя набора . Вот два примера:
- $\mathbb{R} = \{ r \;|\; r \text{ действительное число} \}$
- $O = \{ х \;|\; x \text{ — нечетное целое число} \}$
Набор операций
Над наборами можно выполнять несколько операций.
- Union : Для двух множеств $A$ и $B$ объединение $A \cup B$ представляет собой множество всех элементов, которые находятся либо в $A$, либо в $B$.
 Например, если $A = \{ 1,3,5 \}$ и $B = \{ 2,3,6 \}$, то $A \cup B = \{ 1,2,3,4,5 ,6 \}$. Обратите внимание, что $A \cup B = \{ x \;|\; (x \in A) \lor (x \in B) \}$.
Например, если $A = \{ 1,3,5 \}$ и $B = \{ 2,3,6 \}$, то $A \cup B = \{ 1,2,3,4,5 ,6 \}$. Обратите внимание, что $A \cup B = \{ x \;|\; (x \in A) \lor (x \in B) \}$. - Пересечение : Для двух множеств $A$ и $B$ пересечение $A \cap B$ — это множество всех элементов, которые находятся как в $A$, так и в $B$. Например, если $A = \{ 1,2,3,4 \}$ и $B = \{ 3,4,5,6 \}$, то $A \cap B = \{ 3,4 \} $. Обратите внимание, что $A \cap B = \{ x \;|\; (x \in A) \land (x \in B) \}$. Мы говорим, что $A$ и $B$ являются непересекающимися , если $A \cap B = \emptyset$.
- Разность : Для двух множеств $A$ и $B$ разность $A \setminus B$ представляет собой множество всех элементов, которые находятся в $A$, но не в $B$. Например, если $A = \{ 1,2,3,4 \}$ и $B = \{ 3,4 \}$, то $A \setminus B = \{ 1,2 \}$. Обратите внимание, что $A \setminus B = \{ x \;|\; (x \in A) \land (x \notin B) \}$.
 $A \setminus B$ также обозначается как $A — B$.
$A \setminus B$ также обозначается как $A — B$. - Дополнение : для множества $A$ дополнение $\overline{A}$ — это множество всех элементов, число которых равно , а не , в $A$. Чтобы определить это, нам нужно некоторое определение вселенной всех возможных элементов $U$. Таким образом, мы можем рассматривать дополнение как частный случай разности множеств, где $\overline{A} = U \setminus A$. Например, если $U = \mathbb{Z}$ и $A = \{ x \;|\; x \text{ — нечетное целое число} \}$, тогда $\overline{A} = \{ x \;|\; x \text{ — четное число} \}$. Обратите внимание, что $\overline{A} = \{ x \;|\; х \не в А \}$.
- Декартово произведение : Для двух множеств $A$ и $B$ декартово произведение $A \times B$ представляет собой набор упорядоченных пар, где первый элемент находится в $A$, а второй элемент — в $B. $. Имеем $A \times B = \{ (a,b) \;|\; a \in A \land b \in B \}$.
 Например, если $A = \{ 1,2,3 \}$ и $B = \{ a,b \}$, то $A \times B = \{ (1,a),(1,b) ,(2,а),(2,б),(3,а),(3,б)\}$.
Например, если $A = \{ 1,2,3 \}$ и $B = \{ a,b \}$, то $A \times B = \{ (1,a),(1,b) ,(2,а),(2,б),(3,а),(3,б)\}$.
Подмножества
Набор $A$ является подмножеством множества $B$, если каждый элемент $A$ является элементом $B$. Мы пишем $A \subseteq B$. Другими словами, $A \subseteq B$ тогда и только тогда, когда $\forall x\;(x \in A \rightarrow x \in B)$.
Для любого набора S имеем:
- $\emptyset\subseteq S$
Доказательство: нужно показать, что $\forall x\;{(x \in \emptyset \rightarrow x \in S)}$. Поскольку $x \in \emptyset$ всегда ложно, импликация всегда истинна. Это пример тривиального или бессодержательного доказательства.
- $S \подмножество S$
Доказательство: нужно показать, что $\forall x\;{(x \in S \rightarrow x \in S)}$. Зафиксируйте элемент $x$. Мы должны показать, что $x \in S \rightarrow x \in S$. Эта импликация эквивалентна $x \in S \lor x \notin S$, что является тавтологией. Следовательно, по универсальному обобщению $S \subseteq S$.



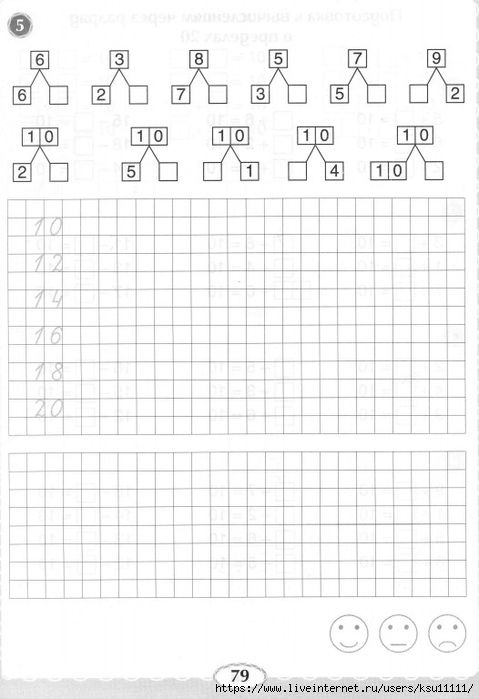 Ясно, что существует ровно одно пустое множество.
Ясно, что существует ровно одно пустое множество. Таким образом, мы имеем \(\{\alpha, \gamma, \beta\} = \{\gamma, \beta, \alpha\} = \{\alpha, \beta, \gamma\},\) и т. д. Поскольку набор не может содержать один и тот же элемент дважды (элементы различны) единственное разумное значение чего-то вроде \(\{ \alpha, \beta, \alpha, \gamma\}\) состоит в том, что это то же самое, что и \(\{ \альфа, \бета, \гамма\}\). Поскольку \(x \neq \{x\}, \{x, \{x\}\}\) — множество из двух элементов. Что угодно можно рассматривать как элемент множества, и от элементов множества не требуется никакого отношения. Например, слово «яблоко», элемент уран и планета Плутон могут быть тремя элементами множества. Нет никаких ограничений на количество различных множеств, которым может принадлежать данный элемент, за исключением правила, согласно которому множество не может быть элементом самого себя.
Таким образом, мы имеем \(\{\alpha, \gamma, \beta\} = \{\gamma, \beta, \alpha\} = \{\alpha, \beta, \gamma\},\) и т. д. Поскольку набор не может содержать один и тот же элемент дважды (элементы различны) единственное разумное значение чего-то вроде \(\{ \alpha, \beta, \alpha, \gamma\}\) состоит в том, что это то же самое, что и \(\{ \альфа, \бета, \гамма\}\). Поскольку \(x \neq \{x\}, \{x, \{x\}\}\) — множество из двух элементов. Что угодно можно рассматривать как элемент множества, и от элементов множества не требуется никакого отношения. Например, слово «яблоко», элемент уран и планета Плутон могут быть тремя элементами множества. Нет никаких ограничений на количество различных множеств, которым может принадлежать данный элемент, за исключением правила, согласно которому множество не может быть элементом самого себя. Не обязательно, чтобы мы могли перечислить все элементы.
Не обязательно, чтобы мы могли перечислить все элементы. \)
\) Такая функция также называется на .
Такая функция также называется на .
 их форма. [Павлин, 1830, § 132, с. 104]
их форма. [Павлин, 1830, § 132, с. 104]