Таблица математических знаков (символов): значения, распечатать
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Основные математические знаки и символы
Ниже представлена таблица с основными математическими символами и знаками: корень (√), больше (>), меньше (<), равенство (=) и др. Также приведено их краткое описание и примеры для лучшего понимания.
| Символ / знак | Название | Значение / описание | Пример |
| = | равно | равенство | е. 4 плюс 3 равно 7</nobr>» data-order=»<nobr>7 = 4 + 3,</nobr><br><nobr>т.е. 4 плюс 3 равно 7</nobr>»>7 = 4 + 3, |
| ≠ | не равно | неравенство | 7 ≠ 10, 7 не равно 10 |
| ≈ | приблизительно равно | приближенное равенство/округление | равно 0,36</nobr>» data-order=»<nobr>0,35765 ≈ 0,36,</nobr><br><nobr>0,35765 прибл. равно 0,36</nobr>»>0,35765 ≈ 0,36, |
| > | больше | A больше, чем B | 15 > 10, 15 больше 10 |
| < | меньше | A меньше, чем B | 6 < 8, 6 меньше 8 |
| ≥ | больше или равно | A больше или равно B | 10 ≥ 4, 10 больше или равно 4 |
| ≤ | меньше или равно | A меньше или равно B | 3 ≤ 7, 3 меньше или равно 7 |
| ( ) | круглые скобки | сначала считается выражение внутри скобок | 3 ⋅ (4 + 6) = 30 |
| [ ] | квадратные скобки | сначала считается выражение внутри скобок | [(1 + 3) ⋅ (2 + 4)] = 24 |
| + | плюс | знак сложения | 1 + 2 = 3 |
| − | минус | знак вычитания | 3 − 2 = 1 |
| ± | плюс-минус | выполняются оба действия: и сложение, и вычитание | 4 ± 6 = 10 или -2 |
| ± | минус-плюс | выполняются оба действия: и вычитание, и сложение | 5 ∓ 8 = -3 или 13 |
| * | звездочка | умножение | 3 * 3 = 9 |
| × | икс | умножение | 3 × 3 = 9 |
| ⋅ | точка | умножение | 3 ⋅ 3 = 9 |
| ÷ | обелюс | деление | 8 ÷ 2 = 4 |
| / | косая черта | деление | 8 / 2 = 4 |
| : | двоеточие | деление | 8 : 2 = 4 |
| — | горизонтальная линия | дробь (деление) | 1/2 |
| mod | modulo | остаток от деления | 7 mod 2 = 1, 7 : 2 = 3 (остаток 1) |
| » data-order=».»>. | точка | десятичный разделитель | 3.45 = 3 + 45/100 |
| , | запятая | десятичный разделитель | 6,12 = 6 + 12/100 |
| ab | степень | число А в степени B | 32 = 9 |
| a^b | циркумфлекс | число А в степени B | 4^3 = 64 |
| √a | квадратный корень | √a ⋅ √a = a | √16 = ±4 |
| 3√a | кубический корень | 3√a ⋅ 3√a ⋅ 3√a = a | 3√27 = 3 |
| n√a | корень n-й степени | n√8 = 2 для n=3 | |
| % | процент | 1% = 1/100 | 10% × 50 = 5 |
| ‰ | промилле | 1%</nobr>» data-order=»<nobr>1‰ = 1/1000 = 0.1%</nobr>»>1‰ = 1/1000 = 0.1% | 5‰ × 40 = 0.2 |
microexcel.ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Что такое математика — ИНФОРМАТ
Математика — царица всех наук
Гаусс Карл Фридрих
Математика — наука, исторически основанная на решении задач о количественных и пространственных соотношениях реального мира путём идеализации необходимых для этого свойств объектов и формализации этих задач.
Наука, занимающаяся изучением чисел, структур, пространств и преобразований.
Как правило, люди думают, что математика — это всего лишь арифметика, то есть изучение чисел и действий с их помощью, например, умножения и деления. На самом деле математика — это намного больше. Это способ описать мир и то, как одна его часть сочетается с другой. Взаимоотношения чисел выражаются в математических символах, которые описывают Вселенную, в которой мы живем. Любой нормальный ребенок может преуспевать в математике, потому что «ощущение числа» — это врожденная способность. Правда, для этого нужно приложить некоторые усилия и затратить немного времени.
Умение считать — это еще не все. Ребенку необходимо уметь хорошо выражать свои мысли, чтобы понимать задачи и устанавливать связи между фактами, которые хранятся в памяти. Для того чтобы выучить таблицу умножения, нужны память и речь. Именно поэтому некоторым людям с поврежденным мозгом трудно умножать, хотя другие виды счета не представляют для них сложности.
Для того чтобы хорошо знать геометрию и разбираться в форме и пространстве, требуются и другие виды мышления. С помощью математики мы решаем в жизни проблемы, например, делим шоколадку поровну или находим нужный размер ботинок. Благодаря знанию математики ребенок умеет копить карманные деньги и понимает, что можно купить и сколько денег тогда у него останется. Математика — это еще и способность отсчитать нужное количество семян и посеять их в горшочек, отмерять нужное количество муки для пирога или ткани на платье, понять счет футбольной игры и множество других повседневных дел. Везде: в банке, в магазине, дома, на работе — нам необходимо умение понимать числа, формы и меры и обращаться с ними. Числа — это только часть особого математического языка, а лучший способ выучить любой язык — это применять его. И начинать лучше с ранних лет.
О математике «умно»
Обычно идеализированные свойства исследуемых объектов и процессов формулируются в виде аксиом, затем по строгим правилам логического вывода из них выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное к математике положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе существует много различных определений математики.
Разделы математики
- Математический анализ.
- Алгебра.
- Аналитическая геометрия.
- Линейная алгебра и геометрия.

- Дискретная математика.
- Математическая логика.
- Дифференциальные уравнения.
- Дифференциальная геометрия.
- Топология.
- Функциональный анализ и интегральные уравнения.
- Теория функций комплексного переменного.
- Уравнения с частными производными.
- Теория вероятностей.
- Математическая статистика.
- Теория случайных процессов.
- Вариационное исчисление и методы оптимизации.
- Методы вычислений, то есть численные методы.
- Теория чисел.
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного математика — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. Пространство Rn, при n>3 является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях.
Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Видео-лекция Смирнова С.К. и Ященко И.В. «Что такое математика»:
Похожая информация:
Алексей Савватеев: зачем нам математика и почему ее должен знать каждый
Наверняка каждый задумывался в школе на уроках алгебры или геометрии, как эти предметы пригодятся нам в жизни. Математик Алексей Савватеев — о пользе науки и о том, почему математика — это не только сложно, но и красиво
Об эксперте: Алексей Савватеев — российский математик, популяризатор математики, доктор физико-математических наук, профессор МФТИ, профессор Адыгейского государственного университета, член-корреспондент РАН.
Алексей Савватеев | Почему математика может все? Ну, почти…
(Видео: РБК Тренды)
Математику нужно знать каждому?
Эта наука лежит в основе нашего мира, поэтому, я думаю, что положение любого человека в нем прямо пропорционально его пониманию математики.
Мое мнение: математика не нужна разве что поэтам, художникам, исполнителям песен — тем, кто имеет дело с вдохновением. Всем остальным людям, особенно если их жизнь связана с чем-то материальным, с окружающим миром и его законами, математические знания точно пригодятся. Дизайнер Артемий Лебедев считал, что математика ему не нужна совсем, но, когда мы с ним побеседовали, я его частично убедил в том, что даже в дизайнерском деле она может быть полезна.
Хороший вопрос: нужна ли математика в спорте? Я бы сказал, да. Например, марафонцам в беге на сверхдлинные дистанции или лыжникам важно понимать, укладываются ли они в график. Компьютера и калькулятора, понятно, под рукой нет, но в голове есть простая формула, которая поможет высчитать, укладывается ли спортсмен в отведенное время. Много математики в спортивном ориентировании — чего только стоит вычисление правильного градуса угла. Да и в футболе без базовых знаний математики не обойтись: важно ведь не просто послать мяч, а сделать это с умом, по правильной траектории.
Нужна ли сегодня фундаментальная математика?
Казалось бы, зачем в наш век современных технологий знать основы, которые закладывали Ферма, Ньютон, Лейбниц, Гаусс, Эйлер, нужно ли сегодня изучать их наследие? Ответ: конечно, нужно. Все современные алгоритмы имеют внутреннюю логику, не понимая которую вы не сможете ими пользоваться. Важно вникать в фундаментальную математику как в основу бытия. А из основы уже можно вытянуть любую ниточку.
Алексей Савватеев: «В этом смысле я категорический оппонент тех, кто считает, что в наш век все настолько быстро меняется, что предметные знания отходят на второй план, а важным становится только умение учиться, быстро осваивать новое. Но как вы научитесь учиться, если не знаете таблицу умножения?» (Фото: Unsplash)
Чем математика отличается от других наук?
Математика — очень сложная для постижения наука. Наверное, с ней может сравниться только физика, и то она все же уступает. Погружение в какую-либо науку я бы сравнил с такой ситуацией: ты поднимаешься по лестнице, открываешь дверь и выходишь на этаж с множеством других дверей. Это стандартный путь изучения любой дисциплины: ты устал, пока поднимался, но на финише ты собой доволен. Даже можешь открыть много смежных дверей в другие науки и все поймешь.
Наверное, с ней может сравниться только физика, и то она все же уступает. Погружение в какую-либо науку я бы сравнил с такой ситуацией: ты поднимаешься по лестнице, открываешь дверь и выходишь на этаж с множеством других дверей. Это стандартный путь изучения любой дисциплины: ты устал, пока поднимался, но на финише ты собой доволен. Даже можешь открыть много смежных дверей в другие науки и все поймешь.
Изучение математики — это когда ты долго поднимаешься по лестнице, хочешь выйти на этаж и понимаешь, что вместо открытого пространства там стены, а на них еще более крутые лестницы, по которым нужно карабкаться. Ты лезешь дальше, с огромным трудом достигаешь следующего этажа и думаешь, что здесь-то ты уже можешь говорить на одном языке с великими учеными — с Пуанкаре, Перельманом, но вокруг опять только стены и лестница. И так этаж за этажом. У тебя нет никакого раздолья, нет награды за твои труды. Что ты получаешь за свое стремление вверх? Пропуск к еще большим трудам. Вот так устроена математика. За это мы ее обожаем. Потому что она никогда не дает расслабляться.
За это мы ее обожаем. Потому что она никогда не дает расслабляться.
Из каких уровней состоит математика?
Первый этаж математики — это абстракция числа как такового. Это идея о том, что существуют отдельно взятые предметы, и мы можем посчитать, сколько их. Такова первая ступень математики, которую, конечно, проходят все. Хотя, если верить Аурэлю Фоссу — автору книги «Сущность математики», на земле до сих пор остались некие сумеречные народы, которые для счета птиц и чумов, к примеру, используют разные числительные. Они не понимают, как можно считать разные предметы, используя одну систему. Значит, эти народности еще не вышли на первый «этаж математики». А все цивилизованные народы давно на нем стоят.
Второй этаж математики обусловлен появлением неизвестных — x, y, z и других. Появляются такие задачи, для решения которых нужно обозначить хоть что-то за x и дальше «выкрутиться» через решение уравнения. В более сложных ситуациях возникают системы уравнений с двумя неизвестными, с тремя и так далее — когда вы занимаетесь большой наукой, будет столько неизвестных, сколько вам нужно. На втором этаже вы спокойно ориентируетесь с неизвестными, применяете формулы сокращенного умножения, разность квадратов, бином Ньютона. В принципе, взойти на этот этаж достаточно легко.
На втором этаже вы спокойно ориентируетесь с неизвестными, применяете формулы сокращенного умножения, разность квадратов, бином Ньютона. В принципе, взойти на этот этаж достаточно легко.
Третий этаж — это исследование операций над цифрами и буквами. Плюс, минус, умножить, разделить, возвести в степень; возникает абстрактное понятие группа, кольцо, поле, модуль и так далее. Этими абстрактными понятиями оперирует вся современная математика. Если вы смогли их освоить, то я вас поздравляю, можно идти на мехмат и пытаться хотя бы первые два года на нем учиться.
Так можно продолжать очень долго! Четвертый этаж — это гомологии и когомологии, с которыми я сейчас пытаюсь разобраться. А пятый этаж — это категории. Но в них я ничего не понимаю, и, наверное, еще долго не пойму. Дальше, говорят, возникают этажи, вход на которые открыт только гениальным филдсовским лауреатам.
Филдсовская премия (Fields Medal) — самая престижная международная премия и медаль в области математики. Вручается один раз в четыре года на каждом международном математическом конгрессе 2–4 молодым ученым не старше 40 лет (или достигших 40-летия в год вручения премии).
Вручается один раз в четыре года на каждом международном математическом конгрессе 2–4 молодым ученым не старше 40 лет (или достигших 40-летия в год вручения премии).
Приз и медаль названы в честь Джона Филдса, президента VII международного математического конгресса, проходившего в 1924 году в Торонто.
Математики сами надстраивают эти сложнейшие этажи один за другим. Фактически математика — это наука для тех, кто хочет всю жизнь думать и никогда не останавливаться ни на чем.
Зашита ли математика в стандарты красоты?
Я в это не верю. Мне кажется, что гениальная мелодия или картина — штучная вещь, а стандарта красоты вообще не может быть. Нам обычно все-таки нравится что-то непредсказуемое. То, что построено по каким-то формулам, не привлекает. Наоборот, настоящая красота рождается там, где нарушается конструкция.
Любой человек может сказать, что картина идеальна, потому что написана по правилам золотого сечения. Это уловка мозга — мы пытаемся постфактум объяснить то, что нам кажется красивым. На самом деле, истинная красота непредсказуема, немоделируема и нематематична. Так что золотое сечение переоценено. Но мне бы хотелось отметить, что оно играет ключевую роль при построении правильного пятиугольника циркулем и линейкой, а это важнее любых «народно-хозяйственных задач». Это очень круто и суперкрасиво.
На самом деле, истинная красота непредсказуема, немоделируема и нематематична. Так что золотое сечение переоценено. Но мне бы хотелось отметить, что оно играет ключевую роль при построении правильного пятиугольника циркулем и линейкой, а это важнее любых «народно-хозяйственных задач». Это очень круто и суперкрасиво.
Остались ли еще в математике нерешенные задачи?
Вы удивитесь, но они есть даже в школьной математике! Вот пример одной из них. Простое число делится только на себя и на единицу: 2, 3, 5, 7, 11, 13, 17, 19. Еще Евклид доказал, что это бесконечный ряд чисел, он никогда не кончится. В этом ряду есть такие пары простых чисел, например, 17 и 19, 101 и 103, 71 и 73 — которые стоят «через одно» друг от друга. Если вы заглянете далеко-далеко в натуральный ряд, то вы будете постоянно обнаруживать, что какие-то два числа, оба простые, стоят вот так — через одно друг за другом.
И науке не известно, кончатся ли такие близняшки или их соседство тоже будет бесконечным. Никто не знает, как не знали и при Евклиде. Открытая математическая проблема, казалось бы, доступная школьнику. Таких проблем, на вскидку, штук 30.
Никто не знает, как не знали и при Евклиде. Открытая математическая проблема, казалось бы, доступная школьнику. Таких проблем, на вскидку, штук 30.
Научные модели позволяют делать прогнозы?
Если грамотно ввести начальные данные, физические модели предскажут явление довольно точно. Но предсказательная сила уменьшается, если вмешиваются различные факторы — неожиданные или те, что мы и не собирались учитывать. Дальше, в таких науках как химия, биология, медицина с прогнозами все хуже. А к социуму вообще невозможно применить моделирование, потому что если вы ставите людей в некоторые условия, то они начинают себя вести выгодным образом. Прогностические модели в описании социума работают из рук вон плохо, но все равно не надо отчаиваться. Без них еще хуже.
Реально предсказать кризисное явление нельзя, и в этом, мне кажется, заключается красота нашего мира. Хотя некоторые говорят, как жаль, мы хотим, чтобы мир был полностью предсказуем. Я, например, этого не хочу, мне не интересно жить в предсказуемом мире.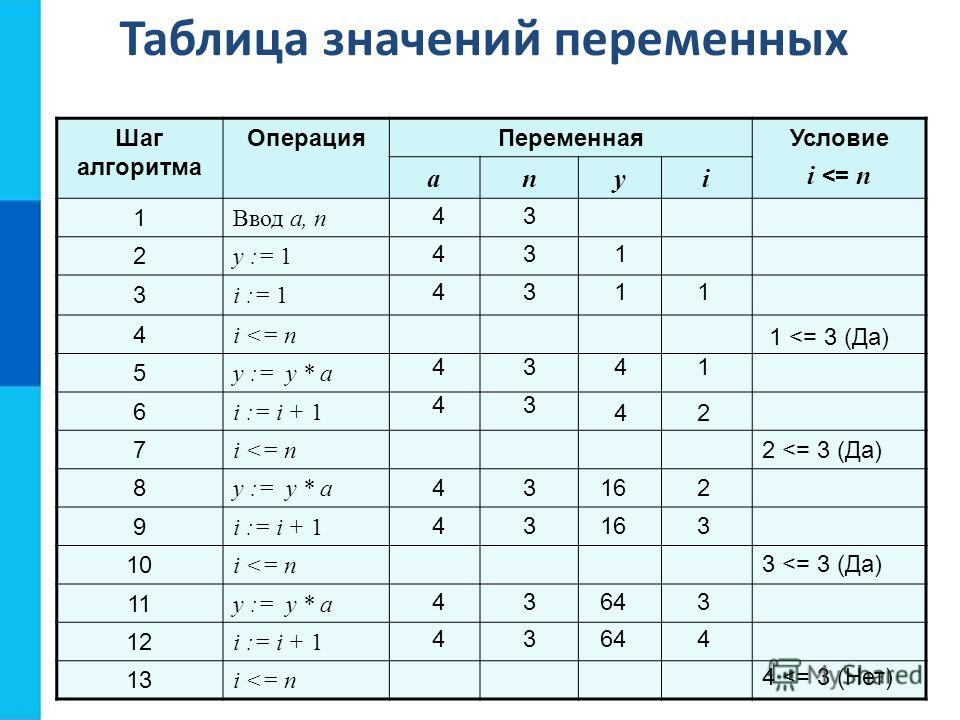 Мне интересно жить в мире, который не описывается математикой.
Мне интересно жить в мире, который не описывается математикой.
Математика — универсальный язык Вселенной?
Я бы сказал так: в широком смысле математика — это язык, на котором Бог общается с нами, передает свои законы посредством такого языка. В узком смысле, конечно, математика остается универсальным языком технической сферы и даже таких наук, как физика, химия и биология. Но то, что это универсальный язык общественных наук, я бы уже не сказал. Определенные закономерности социума математикой описываются, но их надо уметь правильно к социуму прикладывать. Даже знания законов спроса и предложения или теорий аукционов, транспортного моделирования не помогут решить реальные проблемы общества. Вам все равно придется вдумываться в предметную область, читать гуманитарные тексты, написанные в прошлом, и после этого вы сможете принести пользу со своими моделями.
То есть, когда речь идет не о законах природы, а о законах общества, математика имеет меньшее значение. И совсем нулевое значение она имеет в законах общения конкретных людей, индивидуальностей друг с другом. Если вы попытаетесь математику применить к общению со своим супругом, боюсь, вас ждет развод.
Если вы попытаетесь математику применить к общению со своим супругом, боюсь, вас ждет развод.
Что произойдет в математической сфере в ближайшие годы?
Математический прогноз на ближайшие 5–10 лет дать невозможно: наши горизонты планирования — это тысячи лет. Поэтому десятилетие тут играет незначительную роль. За это время можно успеть подкрутить какие-то гипотезы, начать что-то проверять. В чистой математике бывают прорывы — скажем, с 1975 по 2005 годы были сняты чуть ли не пять величайших математических загадок, включая Последнюю Теорему Ферма и гипотезу Пуанкаре. А вот в технической сфере ничего существенного не изобретали уже давно. Сейчас, по сути, допиливаются идеи, которые были высказаны в 50–60-е годы.
Мне кажется, технический прогресс приостановился. Сейчас он связан с интернетом, банковскими картами, шифрованием, кодированием — но все это тоже вещи не быстрые, не на ближайшие пять лет.
Что прочитать, чтобы вникнуть в основы математики?
Чтобы поднатореть в математике, нужно прочесть хотя бы какие-то вводные вещи, например, мою «Математику для гуманитариев» — книга есть в свободном доступе в интернете. За ней — «Что такое математика» Куранта и Роббинса. Можно читать Перельмана, но это, скорее, развлекаловка. Потом идет Иэн Стюарт «Величайшие математические задачи» — очень хорошая книга. Кто любит практику — «Кому нужна математика?» Райгородского. Под редакцией моего друга Николая Андреева вышла книга «Математическая составляющая», а недавно еще и новое издание — рекомендую. Уровень выше — математика для первого курса мехмата: «Введение в матанализ» Зорича, «Линейная алгебра и геометрия» Кострикина.
За ней — «Что такое математика» Куранта и Роббинса. Можно читать Перельмана, но это, скорее, развлекаловка. Потом идет Иэн Стюарт «Величайшие математические задачи» — очень хорошая книга. Кто любит практику — «Кому нужна математика?» Райгородского. Под редакцией моего друга Николая Андреева вышла книга «Математическая составляющая», а недавно еще и новое издание — рекомендую. Уровень выше — математика для первого курса мехмата: «Введение в матанализ» Зорича, «Линейная алгебра и геометрия» Кострикина.
Так что умнейте. А дальше — уже вперед, на все этажи забирайтесь, господа альпинисты!
Что такое среднее? Определение в математике и формула для расчета
Что такое среднее значение?
Среднее значение — это простое математическое среднее набора из двух или более чисел. Среднее значение для данного набора чисел может быть вычислено более чем одним способом, включая метод среднего арифметического, который использует сумму чисел в ряду, и метод среднего геометрического, который представляет собой среднее значение набора продуктов. Однако все основные методы вычисления простого среднего в большинстве случаев дают один и тот же приблизительный результат.
Однако все основные методы вычисления простого среднего в большинстве случаев дают один и тот же приблизительный результат.
Ключевые выводы
- Среднее значение — это среднее математическое значение набора из двух или более чисел.
- Среднее арифметическое и среднее геометрическое — это два типа средних значений, которые можно вычислить.
- Формула вычисления среднего арифметического состоит в том, чтобы сложить числа в наборе и разделить на общее количество чисел в наборе.
- Формула для вычисления среднего геометрического состоит в том, чтобы умножить все значения в наборе данных, затем извлечь корень из суммы, равной количеству значений в этом наборе данных.
- Среднее значение помогает вам оценить набор чисел, сообщая вам среднее значение, помогая контекстуализировать каждую точку данных.
Расчет среднего
Понимание среднего
Среднее значение — это статистический показатель, который можно использовать для оценки производительности с течением времени. Применительно к инвестированию среднее значение используется для понимания динамики цены акций компании в течение нескольких дней, месяцев или лет.
Применительно к инвестированию среднее значение используется для понимания динамики цены акций компании в течение нескольких дней, месяцев или лет.
Аналитик, который хочет измерить траекторию стоимости акций компании за последние, скажем, 10 дней, подытожит цену закрытия акций в каждый из 10 дней. Затем общая сумма будет разделена на количество дней, чтобы получить среднее арифметическое. Среднее геометрическое будет вычислено путем перемножения всех значений вместе. Затем извлекается корень n-й степени из общего произведения, в данном случае 10 -й корень, чтобы получить среднее значение.
Формулы для вычисления среднего арифметического и среднего геометрического
Расчеты как для среднего арифметического, так и для среднего геометрического довольно схожи. Расчетная сумма для одного не будет существенно отличаться от другого. Однако между этими двумя подходами есть тонкие различия, которые действительно приводят к разным числам.
Среднее арифметическое
Формула расчета среднего арифметического состоит в том, чтобы сложить все цифры и разделить на количество использованных цифр.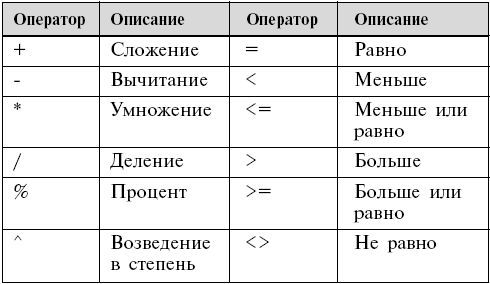 Например, среднее арифметическое чисел 4 и 9находится путем сложения 4 и 9, а затем деления на 2 (количество чисел, которые мы используем). Среднее арифметическое в этом примере равно 6,5.
Например, среднее арифметическое чисел 4 и 9находится путем сложения 4 и 9, а затем деления на 2 (количество чисел, которые мы используем). Среднее арифметическое в этом примере равно 6,5.
Среднее арифметическое
Плюсы
Легче считать.
Проще отслеживать и проверять результаты.
Его расчетное значение является конечным числом.
Более широко используется в алгебраических вычислениях.
Зачастую это самый быстрый способ расчета среднего значения.
Минусы
На него сильно влияют существенные выбросы или экстремальные числа за пределами набора данных.
Это не так полезно для искаженных дистрибутивов.
Это бесполезно при использовании данных временных рядов (или других рядов данных с различной основой).
Он одинаково взвешивает все элементы, уменьшая важность более важных точек данных.

Среднее геометрическое
Среднее геометрическое более сложно и использует более сложную формулу. Формула для расчета среднего геометрического заключается в перемножении всех значений в наборе данных. Затем возьмите корень суммы, равной количеству значений в этом наборе данных. Например, чтобы вычислить геометрическую величину значений 4 и 9, умножьте два числа вместе, чтобы получить 36. Затем извлеките квадратный корень (поскольку значений два). Среднее геометрическое в этом примере равно 6.Среднее геометрическое
Плюсы
Крайние выбросы с меньшей вероятностью повлияют на него.
Возвращает более точное измерение для более изменчивых наборов данных.
Учитывает влияние начисления процентов.
Более точен при использовании набора данных за длительный период времени (за счет начисления процентов).
Минусы
Его нельзя использовать, если какое-либо значение в наборе данных равно 0 или отрицательно.

Его формула более сложная и неудобная в использовании.
Его расчет непрозрачен и более труден для аудита.
Он менее распространен и используется не так часто, как другие методы.
Пример расчета среднего значения
Давайте применим это на практике, изучив цену акции за 10-дневный период. Представьте, что инвестор купил одну акцию за 148,01 доллара. Цена акции в течение следующих 10 дней также включена.
Изображение Сабрины Цзян © Investopedia, 2022
Среднее арифметическое составляет 0,67% и представляет собой просто общую сумму доходностей, деленную на 10. Однако среднее арифметическое доходностей является точным только при отсутствии волатильности, что практически невозможно на фондовом рынке.
В дополнение к среднему арифметическому и геометрическому среднее гармоническое рассчитывается путем деления числа наблюдений на обратную величину (на единицу больше значения) каждого числа в ряду.
Среднее геометрическое влияет на компаундирование и волатильность, что делает его лучшим показателем средней доходности. Поскольку невозможно извлечь корень из отрицательного значения, прибавьте единицу ко всем процентным доходам, чтобы сумма продукта дала положительное число. Возьмите 10 -й -й корень этого числа и не забудьте вычесть из единицы, чтобы получить число в процентах. Среднее геометрическое доходности инвестора за последние пять дней составляет 0,61%. Согласно математическому правилу, среднее геометрическое всегда будет меньше или равно среднему арифметическому.
Среднее арифметическое знак равно ( 0,0045 ) + 0,0121 + 0,0726 + . . . + 0,0043 + ( 0,0049 ) + 0,0376 10 знак равно 0,0067 знак равно 0,67 % \begin{align}\text{Среднее арифметическое} &= \tiny{\frac{(0,0045) + 0,0121 + 0,0726 + . .. + 0,0043 + (0,0049) + 0,0376} {10} } \\&= 0,0067 \\ &= 0,67\% \\\конец{выровнено}
Среднее арифметическое=10(0,0045)+0,0121+0,0726+…+0,0043+(0,0049)+0,0376=0,0067=0,67%
.. + 0,0043 + (0,0049) + 0,0376} {10} } \\&= 0,0067 \\ &= 0,67\% \\\конец{выровнено}
Среднее арифметическое=10(0,0045)+0,0121+0,0726+…+0,0043+(0,0049)+0,0376=0,0067=0,67%
Среднее геометрическое знак равно 0,9955 × 1.0121 × 1.0726 × . . . × 1.0043 × 0,9951 × 1.0376 10 − 1 знак равно 0,0061 знак равно 0,61 % \begin{align}\text{Среднее геометрическое} &= \tiny{\sqrt[10]{ 0,9955 \times 1,0121 \times 1,0726 \times … \times 1,0043 \times 0,9951 \times 1,0376 } — 1} \\& = 0,0061 \\&= 0,61\% \\\конец {выровнено}
Среднее геометрическое=100,9955×1,0121×1,0726×…×1,0043×0,9951×1,0376−1=0,0061=0,61%
Анализ таблицы показывает, почему среднее геометрическое дает лучшее значение. Когда к каждой цене акций применяется среднее арифметическое 0,67%, конечная стоимость составляет 152,63 доллара. Однако в последний день акции торговались по $157,32. Это означает, что среднее арифметическое доходности занижено.
С другой стороны, когда каждая из цен закрытия повышается на среднюю геометрическую доходность 0,61%, рассчитывается точная цена 157,32 доллара. В этом примере и, как это часто бывает во многих расчетах, среднее геометрическое является более точным отражением истинной доходности портфеля.
В этом примере и, как это часто бывает во многих расчетах, среднее геометрическое является более точным отражением истинной доходности портфеля.
Хотя среднее значение является хорошим инструментом для оценки эффективности компании или портфеля, его также следует использовать с другими фундаментальными и статистическими инструментами, чтобы получить более полную и полную картину исторических и будущих перспектив инвестиций.
Примеры случаев, когда средства важны при инвестировании
В бизнесе и инвестициях среднее значение широко используется для анализа производительности. Примеры ситуаций, в которых вы можете столкнуться со средним значением, включают:
- Определение того, торгуется ли акция выше или ниже своего среднего значения за определенный период времени.
- Оглядываясь назад, чтобы увидеть, как сравнительная торговая активность может определить будущие результаты. Например, наблюдение за средней нормой доходности для широких рынков во время предыдущих рецессий может помочь при принятии решений во время будущих экономических спадов.

- Проверка того, соответствует ли объем торгов или количество рыночных ордеров недавней рыночной активности.
- Анализ операционной деятельности компании. Например, некоторые финансовые коэффициенты, такие как количество дней продажи, требуют определения среднего остатка дебиторской задолженности для числителя.
- Количественная оценка макроэкономических данных, таких как средний уровень безработицы за определенный период времени, для определения общего состояния экономики.
Что такое среднее значение в математике?
В математике и статистике под средним понимается среднее значение набора значений. Среднее значение можно вычислить несколькими способами, включая простое среднее арифметическое (сложите числа и разделите сумму на количество наблюдений), среднее геометрическое и среднее гармоническое.
Как найти среднее значение?
Среднее значение — это характеристика набора данных, описывающая некоторое среднее значение. Чтобы найти среднее значение, вы можете вычислить его математически, используя один из нескольких методов, в зависимости от структуры данных и типа необходимого вам среднего значения. Во многих случаях вы также можете визуально определить среднее значение, построив график распределения данных. В нормальном распределении среднее значение, мода и медиана — это одно и то же значение, которое находится в центре графика.
Чтобы найти среднее значение, вы можете вычислить его математически, используя один из нескольких методов, в зависимости от структуры данных и типа необходимого вам среднего значения. Во многих случаях вы также можете визуально определить среднее значение, построив график распределения данных. В нормальном распределении среднее значение, мода и медиана — это одно и то же значение, которое находится в центре графика.
В чем разница между средним значением, медианой и модой?
Среднее значение — это среднее значение, которое появляется в наборе данных. Вместо этого медиана — это средняя точка выше (ниже), где находится 50% значений в данных. Мода относится к наиболее часто наблюдаемому значению в данных (тот, который встречается чаще всего).
Почему важно среднее значение?
Среднее значение — это ценный статистический показатель, который сообщает вам, каков ожидаемый результат при сравнении всех точек данных вместе. Хотя это не гарантирует будущих результатов, среднее значение помогает установить ожидания будущих результатов на основе того, что уже произошло.
Среднее равно среднему?
Среднее значение — это среднее математическое значение набора из двух или более чисел.
среднее | Определение, формула и факты
- Связанные темы:
- среднее арифметическое квадратичное среднее гармоническое среднее среднее геометрическое взвешенное среднее арифметическое
Просмотреть весь связанный контент →
означает , в математике количество, имеющее промежуточное значение между значениями крайних членов некоторого множества. Существует несколько видов средних, и метод расчета среднего зависит от известного или предполагаемого отношения, управляющего другими членами. Среднее арифметическое, обозначенное x , из набора N Числа x 1 , x 2 ,…, x N .
Среднее арифметическое (обычно синоним среднего) представляет собой точку, относительно которой балансируются числа. Например, если единичные массы размещены на прямой в точках с координатами x 1 , x 2 , …, x n , то среднее арифметическое является координатой центра тяжести системы. В статистике среднее арифметическое обычно используется как единственное значение, типичное для набора данных. Для системы частиц, имеющих неравные массы, центр тяжести определяется более общей средней, взвешенной средней арифметической. Если каждому числу ( x ) присвоить соответствующий положительный вес ( w ), взвешенное среднее арифметическое определяется как сумма их произведений ( w x ), деленное на сумму их весов. В этом случае
В статистике среднее арифметическое обычно используется как единственное значение, типичное для набора данных. Для системы частиц, имеющих неравные массы, центр тяжести определяется более общей средней, взвешенной средней арифметической. Если каждому числу ( x ) присвоить соответствующий положительный вес ( w ), взвешенное среднее арифметическое определяется как сумма их произведений ( w x ), деленное на сумму их весов. В этом случае
Средневзвешенное арифметическое также используется при статистическом анализе сгруппированных данных: каждое число x i является серединой интервала, и каждое соответствующее значение w i — количество точек данных в пределах этого интервала.
Для заданного набора данных можно определить множество возможных способов, в зависимости от того, какие характеристики данных представляют интерес. Например, пусть даны пять квадратов со сторонами 1, 1, 2, 5 и 7 см. Их средняя площадь составляет (1 2 + 1 2 + 2 2 + 5 2 + 7 2 )/5, или 16 квадратных см, площадь квадрата со стороной 4 см. Число 4 является средним квадратным (или среднеквадратичным) чисел 1, 1, 2, 5 и 7 и отличается от их среднего арифметического, которое составляет 3 1 / 5 . В общем, среднее квадратичное n чисел x 1 , x 2 , …, x n является их средним арифметическим квадратом не указывает, насколько широко данные разбросаны или разбросаны по среднему значению. Меры дисперсии обеспечиваются средними арифметическими и квадратичными N Различия x 1 — x , x 2 — x ,…, x N a N a . Среднеквадратичное значение дает стандартное отклонение x 1 , x 2 , …, x n .
Их средняя площадь составляет (1 2 + 1 2 + 2 2 + 5 2 + 7 2 )/5, или 16 квадратных см, площадь квадрата со стороной 4 см. Число 4 является средним квадратным (или среднеквадратичным) чисел 1, 1, 2, 5 и 7 и отличается от их среднего арифметического, которое составляет 3 1 / 5 . В общем, среднее квадратичное n чисел x 1 , x 2 , …, x n является их средним арифметическим квадратом не указывает, насколько широко данные разбросаны или разбросаны по среднему значению. Меры дисперсии обеспечиваются средними арифметическими и квадратичными N Различия x 1 — x , x 2 — x ,…, x N a N a . Среднеквадратичное значение дает стандартное отклонение x 1 , x 2 , …, x n .
Средние арифметические и квадратичные средние являются особыми случаями p = 1 и p = 2 p среднего в й степени, M p , определяется по формуле, где p может быть любым действительным числом, кроме нуля. Случай p = −1 также называется гармоническим средним. Взвешенные p x 2 находятся в арифметической прогрессии. Если H — это гармоническое среднее значение x 1 и x 2 , Числа x 1 , H , X 2 H , X 2 . Число G Такое, что x 1 , G , x 2 находятся в геометрическом прогрессе, определяется условием, которое x 1 / G9208 x x x x x x x x x x x / x x / x x / x x / = = x . х 2 или г 2 = x 1 x 2 ; следовательно, это г называется средним геометрическим от х 1 и х 2 . Среднее геометрическое значение N Числа x 1 , x 2 ,…, x N . Подпишитесь на Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
х 2 или г 2 = x 1 x 2 ; следовательно, это г называется средним геометрическим от х 1 и х 2 . Среднее геометрическое значение N Числа x 1 , x 2 ,…, x N . Подпишитесь на Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Все обсуждаемые средства являются частными случаями более общего среднего. Если f есть функция, имеющая обратную f −1 (функция, которая «отменяет» исходную функцию), число называется средним значением x 1 , x 2 , …, x n связанный с f . Когда f ( x ) = x p , обратное значение равно f −1 ( x ) = x 1/ p , а среднее значение равно p th-степенное среднее, M 1 902 Когда f ( x ) = ln x (натуральный логарифм), обратное значение равно f −1 ( x ) = e x , (экспоненциальная функция) а среднее значение является средним геометрическим.
Для получения информации о разработке различных определений среднего, см. Вероятность и статистика. Для получения дополнительной технической информации см. статистика и теория вероятностей.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном.
Что значит быть успешным в математике?
Посетите NAP.edu/10766, чтобы получить дополнительную информацию об этой книге, купить ее в печатном виде или загрузить в виде бесплатного PDF-файла.
« Предыдущая: Введение
Страница 8 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 9 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Наш анализ математики, которую необходимо изучить, наше чтение исследований в области когнитивной психологии и математического образования, наш опыт в качестве учащихся и преподавателей математики, а также наши профессиональные суждения привели нас к принятию комплексного взгляда на успешное изучение математики. Признавая, что ни один термин не охватывает полностью все аспекты опыта, компетентности, знаний и способностей в математике, мы выбрали 9 терминов. 0208 математические способности , чтобы выразить то, что, по нашему мнению, означает для любого человека успешное изучение математики.
0208 математические способности , чтобы выразить то, что, по нашему мнению, означает для любого человека успешное изучение математики.
Математическое мастерство состоит из пяти направлений: 3
Понимание: Понимание математических понятий, операций и отношений — знание того, что означают математические символы, диаграммы и процедуры.
Информатика: Выполнение математических операций, таких как сложение, вычитание, умножение и деление чисел гибко, точно, эффективно и надлежащим образом.
Применение: Способность математически формулировать проблемы и разрабатывать стратегии их решения с использованием надлежащих концепций и процедур.
Рассуждение: Использование логики для объяснения и обоснования решения проблемы или расширения от чего-то известного до чего-то еще неизвестного.

Вовлечение: Считать математику разумной, полезной и выполнимой — , если вы работаете над этим — и готовы выполнять работу.
Важнейшей особенностью математических знаний является то, что эти пять нитей переплетены и взаимозависимы. Другие взгляды на изучение математики
Страница 10 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
, как правило, подчеркивают только один аспект мастерства, ожидая, что другие аспекты будут развиваться как следствие. Например, некоторые люди, которые подчеркивали необходимость того, чтобы учащиеся овладевали вычислениями, предполагали, что за этим последует понимание. Другие, сосредотачиваясь на понимании учащимися понятий, предполагали, что навык будет развиваться естественным образом. Используя эти пять направлений, мы попытались дать более полное представление об успешном изучении математики.
Например, некоторые люди, которые подчеркивали необходимость того, чтобы учащиеся овладевали вычислениями, предполагали, что за этим последует понимание. Другие, сосредотачиваясь на понимании учащимися понятий, предполагали, что навык будет развиваться естественным образом. Используя эти пять направлений, мы попытались дать более полное представление об успешном изучении математики.
Главной идеей этой книги является то, что все учащиеся могут и должны достичь математических знаний. Точно так же, как все учащиеся могут стать опытными читателями, все могут стать опытными в школьной математике. Математические способности — это не то, чего учащиеся достигают только в восьмом или двенадцатом классе; они могут быть профессионалами независимо от их класса. Кроме того, математические способности больше не могут быть ограничены немногими избранными. Все молодые американцы должны научиться мыслить математически, если Соединенные Штаты хотят воспитать образованную рабочую силу и граждан, которых потребует завтрашний мир.
(1) Понимание: Понимание математических понятий, операций и отношений — знание того, что означают математические символы, диаграммы, процедуры.
Понимание относится к пониманию учащимся фундаментальных математических идей. Студенты с пониманием знают больше, чем отдельные факты и процедуры. Они знают, почему математическая идея важна и в каких контекстах она полезна. Кроме того, они знают о многих связях между математическими идеями. На самом деле степень понимания учащимися связана с богатством и масштабом связей, которые они установили.
Например, учащиеся, понимающие деление дробей, могут не только вычислять . Они также могут представить операцию в виде диаграммы и составить задачу для выполнения вычислений. (Если в рецепте требуется чашка сахара, а в наличии имеется 6 чашек сахара, сколько партий по рецепту можно приготовить из имеющегося сахара?)
разные ситуации. Если они понимают общий принцип, согласно которому порядок, в котором умножаются два числа, не имеет значения — например, 3 × 5 — это то же самое, что 5 × 3, — им придется выучить вдвое меньше «фактов о числах». Или если учащиеся понимают общий принцип, согласно которому умножение размеров трехмерного объекта на коэффициент n увеличивает свой
Или если учащиеся понимают общий принцип, согласно которому умножение размеров трехмерного объекта на коэффициент n увеличивает свой
Страница 11 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
объема с коэффициентом n 3 , они могут понять многие ситуации, в которых объекты любой формы пропорционально увеличиваются или уменьшаются. (Они могут понять, например, почему чашка на 16 унций, имеющая ту же форму, что и чашка на 8 унций, намного меньше, чем в два раза выше.)
Знание, полученное с пониманием, обеспечивает основу для запоминания или реконструкции математических фактов и методы для решения новых и незнакомых проблем и для получения новых знаний. Например, учащиеся, хорошо разбирающиеся в операциях с целыми числами, могут распространить эти понятия и процедуры на операции с десятичными числами.
Например, учащиеся, хорошо разбирающиеся в операциях с целыми числами, могут распространить эти понятия и процедуры на операции с десятичными числами.
Понимание также помогает учащимся избежать критических ошибок при решении задач, особенно масштабных. Любой ученик с хорошим чувством числа, который умножает 9,83 и 7,65 и получает за ответ 7 519,95, должен сразу увидеть, что что-то не так. Ответ не может быть больше, чем 10 раз по 8 или 80, так как одно число меньше 10, а другое меньше 8. Это рассуждение должно подсказать учащемуся, что десятичная точка поставлена не на место.
(2) Информатика: Выполнение математических действий, таких как сложение, вычитание, умножение и деление чисел гибко, точно, эффективно и надлежащим образом.
Информатика включает в себя свободное владение процедурами сложения, вычитания, умножения и деления в уме или с помощью бумаги и карандаша, а также знание того, когда и как правильно использовать эти процедуры. Хотя слово , вычисляющее , подразумевает арифметическую процедуру, в этом документе оно также относится к свободному владению процедурами из других разделов математики, таких как измерение (измерение длин), алгебра (решение уравнений), геометрия (построение подобных фигур) и статистика (графические данные). Свободное владение языком означает умение выполнять процедуру эффективно, точно и гибко.
Свободное владение языком означает умение выполнять процедуру эффективно, точно и гибко.
Ученики должны быстро и точно вычислять основные комбинации чисел (6+7, 17−9, 8×4 и т. д.). Они также должны стать точными и эффективными при работе с алгоритмами — пошаговыми процедурами сложения, вычитания, умножения и деления многозначных целых чисел, дробей и десятичных дробей, а также для выполнения других вычислений. Например, у всех учащихся должен быть понятный им алгоритм умножения 64 и 37, достаточно эффективный и достаточно общий, чтобы его можно было использовать с другими двузначными числами, и который можно расширить для использования с большими числами.
Использование калькуляторов не должно угрожать развитию вычислительных навыков учащихся. Наоборот, калькуляторы могут улучшить как понимание, так и
Page 12 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Какая сторона «математических войн» правильная? Реформы в 1980-х и 1990-х годах принижали значение вычислительных навыков, вместо этого подчеркивая, что учащиеся должны понимать и уметь использовать математику. В крайних случаях студенты должны были изобретать математику практически без посторонней помощи. Реакция на эти усилия привела к повышенному вниманию к запоминанию и вычислительным навыкам, и ожидалось, что учащиеся усвоят процедуры, представленные учителями или учебниками. Столкновение этих противоположных позиций получило название «математических войн». Какая позиция правильная? Ни один. Математические инструкции не могут быть эффективными, если они основаны на крайних позициях. Учащиеся становятся более опытными, когда понимают основные концепции математики, и они легче понимают концепции, если они имеют навыки вычислительных процедур. Американским учащимся нужно больше навыков и больше понимания, а также способность применять концепции для решения проблем, логически рассуждать и рассматривать математику как разумную, полезную и выполнимую. Все меньшее ведет к знанию, которое является хрупким, разрозненным и слабым. |
Страница 13 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
и вычисления. 4 Но, как и любое учебное пособие, калькуляторы и компьютеры можно использовать эффективно или не очень эффективно. Учителя должны научиться использовать эти инструменты — и учить студентов использовать их — таким образом, чтобы поддерживать и интегрировать нити мастерства.
Точность и эффективность процедур важны, но вычисления также способствуют пониманию. Работая с процедурами, достаточно общими для решения целого класса задач, такими как процедура сложения любых двух дробей, учащиеся получают представление о том, что математика предсказуема, хорошо структурирована и полна шаблонов.
Когда учащиеся просто запоминают процедуры, они могут не понять более глубоких идей, которые могут облегчить запоминание и применение того, что они изучают. Например, при вычитании многие дети вычитают меньшее число из большего в каждом столбце, независимо от того, где оно находится, поэтому распространены неправильные ответы, подобные следующим:
Например, при вычитании многие дети вычитают меньшее число из большего в каждом столбце, независимо от того, где оно находится, поэтому распространены неправильные ответы, подобные следующим:
Дети, которые учатся вычитать с пониманием, редко делают такого рода ошибка. 5
Развитие вычислительных навыков и развитие понимания часто рассматриваются как конкурирующие за внимание в школьной математике. Но противопоставление умения и понимания создает ложную дихотомию. Понимание облегчает усвоение навыков, а процедуры обучения могут укреплять и развивать математическое понимание.
(3) Применение: Способность математически формулировать проблемы и разрабатывать стратегии их решения с использованием соответствующих концепций и процедур.
Применение предполагает использование концептуальных и процедурных знаний для решения проблем. Понятие или процедура бесполезны, если учащиеся не понимают, когда и где их использовать, а также когда и где они неприменимы. В школе учащимся даются конкретные задачи для решения, но вне школы они сталкиваются с ситуациями, в которых одна из трудностей состоит в том, чтобы точно определить, в чем заключается проблема. Следовательно, учащиеся также должны уметь ставить проблемы, разрабатывать стратегии решения и выбирать наиболее полезную стратегию решения проблем. Им нужно знать, как представлять величины в уме или рисовать их на бумаге, и им нужно знать, как отличать известное и актуальное от неизвестного.
В школе учащимся даются конкретные задачи для решения, но вне школы они сталкиваются с ситуациями, в которых одна из трудностей состоит в том, чтобы точно определить, в чем заключается проблема. Следовательно, учащиеся также должны уметь ставить проблемы, разрабатывать стратегии решения и выбирать наиболее полезную стратегию решения проблем. Им нужно знать, как представлять величины в уме или рисовать их на бумаге, и им нужно знать, как отличать известное и актуальное от неизвестного.
Страница 14 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Рутинные проблемы всегда можно решить с помощью стандартных процедур. Например, большинство второклассников знают, что они должны добавить, чтобы ответить на следующий вопрос: «Если в микроавтобусе 12 учеников и еще 7 садятся, сколько учеников в автобусе?» Но для нестандартных задач учащиеся должны изобрести способ понять и решить проблему. Например, второклассникам можно задать следующий вопрос: «В микроавтобусе 7 мест, в каждом по 2-3 ученика. Если есть 19Студенты, сколько человек должно сесть по двое на одно место и сколько должно сесть по трое на одно место?» Чтобы найти ответ, они должны изобрести метод решения. Им необходимо понимать величины в задаче и их взаимосвязь, а также обладать вычислительными навыками, необходимыми для решения задачи.
Например, большинство второклассников знают, что они должны добавить, чтобы ответить на следующий вопрос: «Если в микроавтобусе 12 учеников и еще 7 садятся, сколько учеников в автобусе?» Но для нестандартных задач учащиеся должны изобрести способ понять и решить проблему. Например, второклассникам можно задать следующий вопрос: «В микроавтобусе 7 мест, в каждом по 2-3 ученика. Если есть 19Студенты, сколько человек должно сесть по двое на одно место и сколько должно сесть по трое на одно место?» Чтобы найти ответ, они должны изобрести метод решения. Им необходимо понимать величины в задаче и их взаимосвязь, а также обладать вычислительными навыками, необходимыми для решения задачи.
(4) Рассуждение: использование логики для обоснования решения проблемы или расширения от чего-то известного до чего-то еще неизвестного.
Рассуждение — это клей, скрепляющий математику. Думая о логических связях между понятиями и ситуациями, учащиеся могут перемещаться по элементам проблемы и видеть, как они сочетаются друг с другом. Например, если предоставить возможность изучить и обсудить четные и нечетные числа, четвероклассники могут объяснить, почему сумма любого четного и любого нечетного числа будет нечетной.
Например, если предоставить возможность изучить и обсудить четные и нечетные числа, четвероклассники могут объяснить, почему сумма любого четного и любого нечетного числа будет нечетной.
Один из лучших способов для учащихся улучшить свои рассуждения — объяснить или обосновать свои решения другим. Например, после того, как процедура сложения дробей была разработана, студентов иногда следует просить объяснить и обосновать эту процедуру, а не просто решать практические задачи. В процессе сообщения своих мыслей они оттачивают свои навыки рассуждения.
Рассуждения сильно взаимодействуют с другими элементами математических навыков, особенно когда учащиеся решают задачи. Когда учащиеся рассуждают о проблеме, они могут построить свое понимание, выполнить необходимые вычисления, применить свои знания, объяснить свои рассуждения другим и прийти к выводу, что математика разумна и выполнима.
(5) Вовлечение: Видеть в математике разумную, полезную и выполнимую задачу — , если вы работаете над ней — и готовность выполнять эту работу.
Занятия математикой — ключ к успеху. Наш взгляд на математическое мастерство выходит за рамки способности понимать, вычислять, применять и
Page 15 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Нужно ли учащимся учиться считать с помощью бумаги и карандаша теперь, когда доступны калькуляторы и компьютеры? Да. Широкая доступность калькуляторов значительно уменьшила потребность в выполнении сложных вычислений с помощью бумаги и карандаша. |
Страница 16 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
причина. Это включает в себя взаимодействие с математикой: учащиеся должны иметь личную приверженность идее, что математика имеет смысл и что, приложив разумные усилия, они могут изучить ее и использовать как в школе, так и за ее пределами. Учащиеся, хорошо разбирающиеся в математике, считают ее разумной, полезной и стоящей и считают, что их усилия по ее изучению окупаются; они считают себя эффективными учениками, исполнителями и пользователями математики.
Успех в изучении математики требует положительного отношения к предмету. Студенты, занимающиеся математикой, не верят, что есть какой-то таинственный «математический ген», диктующий успех. Они верят, что при достаточном усилии и опыте могут научиться. Если учащиеся должны эффективно изучать, делать и использовать математику, они не должны рассматривать ее как произвольный набор правил и процедур. Вместо этого им нужно видеть это как предмет, в котором вещи логически и разумно сочетаются друг с другом, и им нужно верить, что они способны понять это.
Вместо этого им нужно видеть это как предмет, в котором вещи логически и разумно сочетаются друг с другом, и им нужно верить, что они способны понять это.
Занятие математикой требует частых возможностей разобраться в ней, испытать на себе вознаграждение за ее осмысление и осознать преимущества настойчивости. По мере того, как учащиеся совершенствуют свои математические навыки, они становятся более уверенными в своей способности изучать математику и использовать ее. Чем больше математических понятий они понимают, тем более осмысленным становится весь предмет. Напротив, когда они думают, что математику нужно изучать, запоминая, а не осмысливая ее, они начинают терять уверенность в себе как в учениках. Учащиеся, хорошо разбирающиеся в математике, считают, что они могут решать проблемы, развивать понимание и изучать процедуры посредством тяжелой работы, и что получение математических знаний полезно для них.
Интеграция навыков Точно так же, как табуретка не может стоять на одной ножке или даже на двух, так и математическое мастерство не может стоять на одной или двух изолированных ветвях. Чтобы овладеть математическими способностями, учащиеся должны развивать все пять направлений в начальной и средней школе.
Чтобы овладеть математическими способностями, учащиеся должны развивать все пять направлений в начальной и средней школе.
В любой момент урока математики или раздела можно выделить одну или две нити. Но все нити должны в конечном итоге быть рассмотрены, чтобы связи между ними были усилены. Например, урок, основной целью которого является развитие у учащихся понимания математической концепции, может также основываться на решении задач и требовать ряда вычислений. Или студентов могут попросить рассуждать о недавно представленной идее, а не симулировать ее.0005
Страница 17 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
слой представлен с определением и примерами. Кроме того, в течение учебного года учащиеся должны иметь возможность сосредоточиться на различных направлениях в различных сочетаниях. Если учителя регулярно делают акцент только на одном или двух направлениях, игнорируя остальные, математика, которую изучают их ученики, скорее всего, будет неполной и хрупкой.
Развивать навыки по отдельности намного сложнее, чем изучать их вместе. На самом деле практически невозможно освоить какое-то одно из направлений в отдельности. Возможно, именно поэтому учащимся так трудно запомнить, например, все правила вычисления с дробями и десятичными знаками, если это все, что они изучают. Обращение ко всем аспектам мастерства делает знания более прочными, долговечными, более адаптируемыми, более полезными и более актуальными.
Интеграция навыков математики полностью соответствует типичному подходу учащихся к обучению. Например, по мере понимания ребенок лучше запоминает вычислительные процедуры и более гибко использует их для решения задач. В свою очередь, по мере того, как процедура становится более автоматической, ребенок может думать о других аспектах проблемы и может решать новые проблемы, что приводит к новому пониманию. В рамке на странице 18 дается дальнейшее описание интеграции направлений математических знаний.
Например, по мере понимания ребенок лучше запоминает вычислительные процедуры и более гибко использует их для решения задач. В свою очередь, по мере того, как процедура становится более автоматической, ребенок может думать о других аспектах проблемы и может решать новые проблемы, что приводит к новому пониманию. В рамке на странице 18 дается дальнейшее описание интеграции направлений математических знаний.
Современная школьная математика в США часто предполагает, что дети должны овладеть определенными навыками, прежде чем они смогут понять процедуры и применять их — как будто дети не могут сыграть мелодию, пока не освоят все гаммы. Но учащиеся могут вычислить, что в полосе длиной 5,5 фута находится лента длиной 5,5 фута, прежде чем их научат «переворачивать и умножать». Фактически, решение таких задач может помочь учащимся понять процедуру инвертирования и умножения. Они могли бы, например, заметить, что количество футов длины в 1 футе равно двум. Следовательно, умножение (обратное ) даст общее количество длин в футах в полосе в футах.
Точно так же, как симфонию нельзя услышать, последовательно слушая партии каждого инструмента, математических навыков нельзя достичь, изучая каждую из составляющих мастерства по отдельности. При обучении необходимо использовать естественную склонность детей использовать все пять направлений математического мастерства. (Во вставке на страницах 19–20 приведены примеры того, как навыки могут быть интегрированы в изучение решения пропорций.) Таким образом, учащиеся понимают и знают, как применять процедуры, которые от них часто требуется просто запомнить.
Страница 18 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Интеграция уровней мастерства в изучение числовых комбинаций Обучение сложению, вычитанию, умножению и делению однозначных чисел долгое время характеризовалось в Соединенных Штатах как «изучение основных фактов или числовых комбинаций», и от учащихся традиционно ожидалось, что они просто запомнят эти комбинации. Однако исследования показали, что учащиеся на самом деле проходят довольно четко определенную последовательность методов решения, когда учатся выполнять операции с однозначными числами. Это более глубокое понимание процесса обучения студентов демонстрирует, как четыре других уровня навыков — в дополнение к вычислениям — могут быть усилены за счет изучения числовых комбинаций. 6 Понимание Комбинации номеров связаны между собой. Связи между сложением и вычитанием, а также между умножением и делением можно использовать, чтобы облегчить учащимся изучение комбинаций чисел, связанных с вычитанием и делением. Например, 13–8 можно рассматривать как число, которое нужно прибавить к 8, чтобы получить 13. Многим учащимся легче выполнять вычитание таким способом наращивания, что связано с их знаниями о сложении. Применение Изучение комбинаций чисел можно рассматривать как деятельность по решению проблем. Учащиеся используют комбинации цифр, которые они знают, для создания комбинаций цифр, которые они не знают. Например, поскольку числа, кратные 5, относительно легко выучить, учащийся может использовать свои знания о 5×8, чтобы найти 6×8. Это (5×8)+8. Рассуждение Когда учащиеся рассказывают о том, как они вычислили определенную комбинацию чисел, у них есть возможность объяснить, как они это сделали. Объясняя свои решения, они демонстрируют и уточняют свое понимание соответствующих взаимосвязей. Примером может быть: «Я знаю, что 4×6 — это 24, потому что я знаю свои четверки. А 8х6 будет еще четыре группы по шесть. Итак, 8×6 — это 24 плюс 24, и это 48». Зацепление Когда они рассматривают отношения между числовыми комбинациями, учащиеся считают изучение числовых комбинаций разумным, а не просто изучением произвольных ассоциаций между числами. Они также узнают, что могут создавать комбинации чисел, если забудут их. У них есть ресурсы, чтобы учиться самостоятельно, и им не нужно полагаться на учителя, чтобы сказать им, есть ли у них правильный ответ. |
Страница 19 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Математическая подготовка в развитии пропорционального мышления Результаты национальных оценок показывают, что решение задач на пропорции, таких как «Если девочка может прочитать 3 страницы за 4 минуты, с такой скоростью, сколько страниц она прочитает за 10 минут?» часто трудно для американских восьмиклассников. Белинда получила правильный ответ (16 долларов), нарисовав на бумаге 24 круга, а затем вычеркнув три и написав 2 доллара. Она продолжала вычеркивать круги группами по три, отслеживая суммы в 2 доллара в столбце, а затем добавила столбец из 2 долларов. Деймон разделил 24 на 3, чтобы получить 8 долларов; затем он разделил 24 на 2 и получил 12 долларов. Не сумев примирить два своих ответа, он прибегнул к набору кубиков; он сформировал восемь групп по три кубика в каждой. |
Страница 20 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
| Ответ был 16 долларов, что объясняется тем, что, поскольку каждая упаковка из трех воздушных шаров стоит 2 доллара, а их было восемь, 2 × 8 = 16. Марти рассчитала стоимость одного шарика, разделив 2 доллара на 3 на своем калькуляторе. Она получила 0,6667, которую назвала «дурацкой цифрой». Она умножила этот результат на 24, чтобы получить 16. Способы, которыми эти дети решили задачу, показывают, что овладение пропорциональными рассуждениями требует объединения всех навыков. Все они решили задачу, но каждый ребенок использовал свою технику, некоторые более сложные, чем другие. Они не просто случайным образом производили операции над числами, как это начал делать Дэймон. Все они понимали, что отношения между воздушными шарами и долларами должны оставаться прежними, что иллюстрируют круги Белинды и столбец с двумя долларами. Свободное владение различными вычислительными процедурами, такими как счет, умножение и деление, помогло каждому учащемуся справиться с задачей. Этот пример показывает, как учащиеся могут использовать свои собственные навыки осмысления, чтобы начать работу в такой сложной области, как эта. По мере того, как они приобретают больше опыта в пропорциональных ситуациях, они могут продолжать разрабатывать и изучать более эффективные методы, не теряя связи с другими направлениями математического мастерства. |
Страница 21 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Развитие навыков в начальной и средней школеМатематические навыки нельзя охарактеризовать просто как имеющиеся или отсутствующие. Каждая важная математическая идея может быть понята на многих уровнях и разными способами. Очевидно, что понимание сложения у первоклассника не такое, как у математика или даже у среднего взрослого человека. Но первоклассник все еще может хорошо складывать однозначные числа, если его или ее мышление в этой области включает в себя все пять навыков.
Способность к математике развивается со временем. Таким образом, с каждым годом обучения в школе учащиеся должны становиться все более опытными как в старом, так и в новом содержании. Например, третьеклассники должны лучше уметь складывать целые числа, чем в первом классе. Но в каждом классе учащиеся должны быть в состоянии продемонстрировать математические способности в той или иной форме.
Но в каждом классе учащиеся должны быть в состоянии продемонстрировать математические способности в той или иной форме.
Исторически школьная политика в области математики в Соединенных Штатах основывалась на предположении, что только избранная группа учащихся должна овладеть математикой. Это предположение больше несостоятельно. Молодые люди, неспособные мыслить математически, лишены многих лучших возможностей, которые предлагает общество, и общество лишено их потенциального вклада.
Многие взрослые предполагают, что различия в успеваемости по математике отражают различия в врожденных способностях, а не различия в индивидуальных усилиях или возможностях учиться. Эти ожидания глубоко недооценивают возможности детей. Основные принципы, понятия и навыки математики доступны всем детям. Когда и родители, и учителя одинаково верят, что тяжелая работа окупается, и когда математика преподается и изучается с использованием всех навыков, успеваемость по математике улучшается для всех учащихся.
Тщательные исследования показали, что математическое знание — достижимая цель. В нескольких школах, разбросанных по всей стране, высокий процент учащихся из всех слоев общества добился высоких результатов по математике. Специальные мероприятия в некоторых школах с низкой успеваемостью дали значительный прогресс. Теперь стало известно больше о том, как дети изучают математику, и о том, какие виды обучения способствуют прогрессу.
Данные исследований показывают, что все учащиеся, за исключением очень небольшого числа, могут научиться грамотному чтению. Они могут учиться с разной скоростью и могут нуждаться в разном объеме и типах учебной поддержки, чтобы научиться хорошо читать, но все могут научиться читать. 9 То же самое относится к обучению и занятиям математикой.
Страница 22 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Что не так со старыми способами преподавания математики? Преподавание, сосредоточенное на одном направлении за раз — например, освоение вычислительных процедур с последующим решением задач — не помогло большинству учащихся достичь математических навыков. Результаты крупных национальных исследований, проводившихся десятилетиями, показывают, что учащиеся никогда не добивались особых успехов в развитии вычислительных навыков, выходящих за рамки целых чисел, и они были очень неудачны в применении полученных навыков. 10 Они также не продемонстрировали достаточного понимания математических концепций, используемых в вычислениях или решении задач. |
Как учителя могут развивать все направления математики, когда им уже так много нужно преподавать? Благодаря комплексному обучению математике учителя в конечном итоге сэкономят время. Они устранят необходимость повторять одно и то же содержание снова и снова, потому что учащиеся не усвоили его в первую очередь. Они не будут тратить так много времени на одно направление, откладывая другие направления до тех пор, пока ученики не будут «готовы». Скорее, пять нитей будут поддерживать друг друга, что сделает обучение более эффективным и продолжительным. |
Страница 23 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Успехи в классах учащихся из неблагополучных семей Данные исследований показывают, что учащиеся могут достичь хороших результатов, если математика преподается последовательным и комплексным образом. Например, крупномасштабное исследование 150 классных комнат для учащихся с первого по шестой классы, обслуживающих малообеспеченные семьи, продемонстрировало преимущества обучения математике. В одном наборе классов использовалась обычная учебная программа, ориентированная на вычисления. Другой набор подчеркивал концептуальное понимание и расширял круг математических тем, включенных в учебную программу, помимо арифметики. Учащиеся в последних классах успевали значительно лучше, чем в обычных классах. К концу двухгодичного обучения эти студенты не только лучше разбирались в продвинутых навыках, но и лучше владели вычислительными навыками. Аналогичные результаты были получены для чтения и письма. Распространенный миф в сфере образования состоит в том, что учащиеся в классах с высоким уровнем бедности не должны заниматься сложной академической работой до тех пор, пока они не овладеют базовыми навыками. Это исследование развеивает этот миф. Это показывает, что обучение, организованное вокруг всех направлений математического мастерства, особенно уместно и эффективно для учащихся из неблагополучных семей. |
Страница 8 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 9 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10. 17226/10434.
17226/10434.
×
Сохранить
Отменить
Страница 10 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 11 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 12 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 13 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 14 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 15 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 16 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 17 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 18 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 19 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 20 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
×
Сохранить
Отменить
Страница 21 Делиться Цитировать
Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий.

 Наука, занимающаяся изучением чисел, структур, пространств и преобразований.
Наука, занимающаяся изучением чисел, структур, пространств и преобразований.




 Оба слишком узкие. Когда люди отстаивают только одну область мастерства, они упускают из виду общую цель. Такое узкое отношение к математике вполне может быть одной из причин плохой успеваемости американских учащихся в национальных и международных оценках.
Оба слишком узкие. Когда люди отстаивают только одну область мастерства, они упускают из виду общую цель. Такое узкое отношение к математике вполне может быть одной из причин плохой успеваемости американских учащихся в национальных и международных оценках.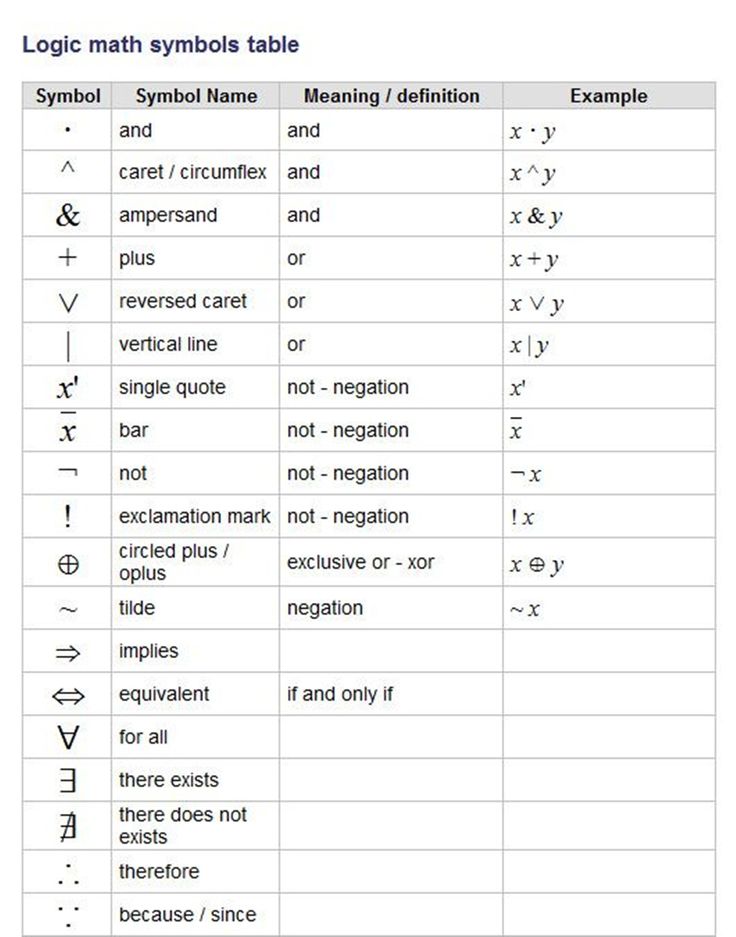 Но учащиеся должны понимать, что происходит в этих сложных вычислениях, и им все еще нужно научиться выполнять более простые вычисления с помощью карандаша и бумаги, потому что это помогает им развить математические навыки. Например, определенный уровень навыков работы с основными комбинациями чисел необходим для понимания процедур умножения двузначных чисел, а беглость вычислений часто необходима при решении задач по алгебре и объяснении их решений. Сколько учебного времени должно быть потрачено на сложные расчеты карандашом и бумагой, — это вопрос, который необходимо будет постоянно пересматривать в течение следующих десятилетий.
Но учащиеся должны понимать, что происходит в этих сложных вычислениях, и им все еще нужно научиться выполнять более простые вычисления с помощью карандаша и бумаги, потому что это помогает им развить математические навыки. Например, определенный уровень навыков работы с основными комбинациями чисел необходим для понимания процедур умножения двузначных чисел, а беглость вычислений часто необходима при решении задач по алгебре и объяснении их решений. Сколько учебного времени должно быть потрачено на сложные расчеты карандашом и бумагой, — это вопрос, который необходимо будет постоянно пересматривать в течение следующих десятилетий. Распознавание и использование этих связей может сделать изучение комбинаций чисел более легким и менее подверженным забыванию и ошибкам. Например, учащиеся быстро узнают, что 5 файлов cookie плюс 4 файла cookie на единицу больше, чем 4 файла cookie плюс 4 файла cookie. Студенты также узнают некоторые комбинации чисел раньше, чем другие. Например, они часто выучивают двойные числа (например, 6+6, 9+9) и суммирует до десяти (например, 7+3) раньше, чем другие комбинации чисел, и они могут использовать это знание для изучения других комбинаций чисел (например, 6+7 на единицу больше, чем 6+6; 8+5 можно разбивается на 8+2+3).
Распознавание и использование этих связей может сделать изучение комбинаций чисел более легким и менее подверженным забыванию и ошибкам. Например, учащиеся быстро узнают, что 5 файлов cookie плюс 4 файла cookie на единицу больше, чем 4 файла cookie плюс 4 файла cookie. Студенты также узнают некоторые комбинации чисел раньше, чем другие. Например, они часто выучивают двойные числа (например, 6+6, 9+9) и суммирует до десяти (например, 7+3) раньше, чем другие комбинации чисел, и они могут использовать это знание для изучения других комбинаций чисел (например, 6+7 на единицу больше, чем 6+6; 8+5 можно разбивается на 8+2+3).
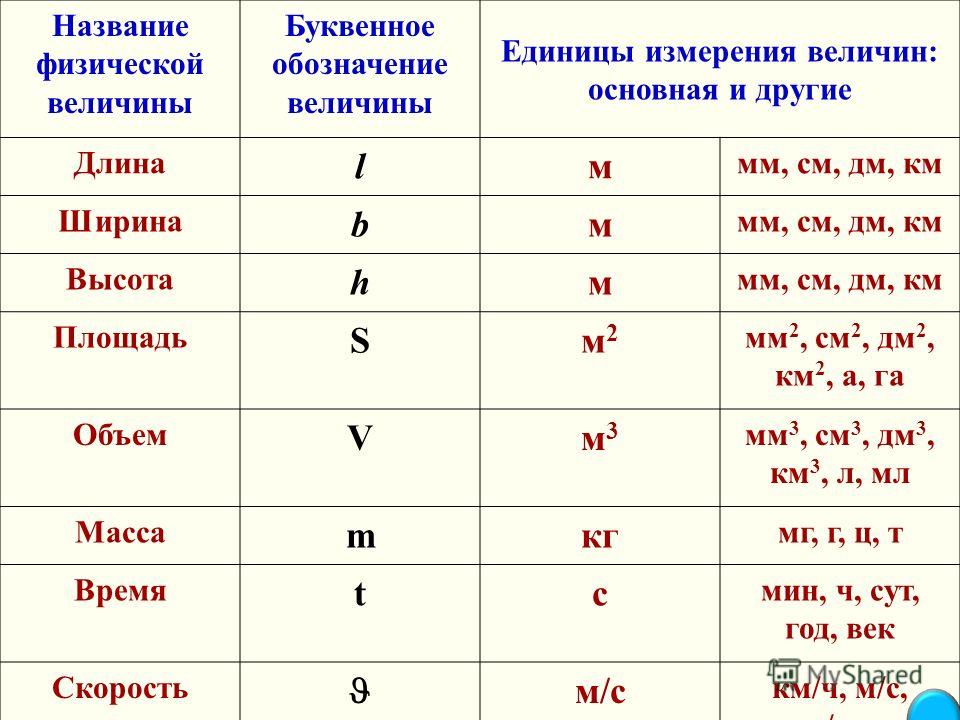 Они начинают считать себя способными использовать числа для решения практических задач.
Они начинают считать себя способными использовать числа для решения практических задач. Однако, когда учащимся предлагается исследовать пропорциональные ситуации в различных контекстах задач, они, естественно, используют все нити математических навыков. Кроме того, поощряя их интегрировать нити, пока они учатся решать пропорции, можно добиться более высоких результатов. 7 Чтобы проиллюстрировать, как учащиеся интегрируют навыки, рассмотрим работу нескольких пятиклассников, которым была задана следующая задача: в 3 за 2 доллара. Они решили вернуться в магазин и купить достаточно воздушных шаров для всех в классе. Сколько бы они заплатили за еще 24 воздушных шара?
Однако, когда учащимся предлагается исследовать пропорциональные ситуации в различных контекстах задач, они, естественно, используют все нити математических навыков. Кроме того, поощряя их интегрировать нити, пока они учатся решать пропорции, можно добиться более высоких результатов. 7 Чтобы проиллюстрировать, как учащиеся интегрируют навыки, рассмотрим работу нескольких пятиклассников, которым была задана следующая задача: в 3 за 2 доллара. Они решили вернуться в магазин и купить достаточно воздушных шаров для всех в классе. Сколько бы они заплатили за еще 24 воздушных шара?  Он объявил, что
Он объявил, что Позже Марти рассказывала своему старшему брату о том, как дети в ее классе по-разному решали задачу о воздушном шаре. Ее брат показал ей другой способ, используя эквивалентные дроби: 2 доллара за три шарика эквивалентны тому, сколько стоит 24 шарика? (То есть .) Он объяснил, что, поскольку вы умножаете 3 на 8, чтобы получить 24, вы должны умножить 2 на 8, чтобы получить недостающий числитель. Итак, ответ: 16 долларов.
Позже Марти рассказывала своему старшему брату о том, как дети в ее классе по-разному решали задачу о воздушном шаре. Ее брат показал ей другой способ, используя эквивалентные дроби: 2 доллара за три шарика эквивалентны тому, сколько стоит 24 шарика? (То есть .) Он объяснил, что, поскольку вы умножаете 3 на 8, чтобы получить 24, вы должны умножить 2 на 8, чтобы получить недостающий числитель. Итак, ответ: 16 долларов. Каждый ребенок также мог рассуждать о ситуации и объяснять другим, что он или она делает. Все они ожидали, что смогут разобраться в проблеме, и упорствовали, пока не пришли к решению, в котором были уверены, хотя Деймон начал с двух разных ответов, а Марти — с «дурацкой цифры».
Каждый ребенок также мог рассуждать о ситуации и объяснять другим, что он или она делает. Все они ожидали, что смогут разобраться в проблеме, и упорствовали, пока не пришли к решению, в котором были уверены, хотя Деймон начал с двух разных ответов, а Марти — с «дурацкой цифры».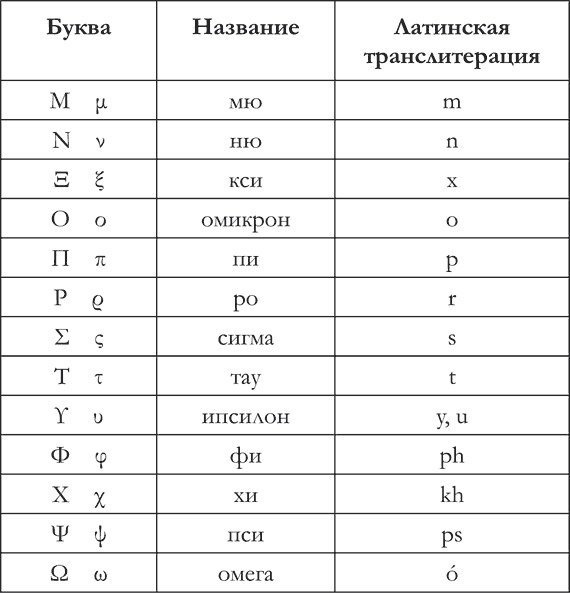
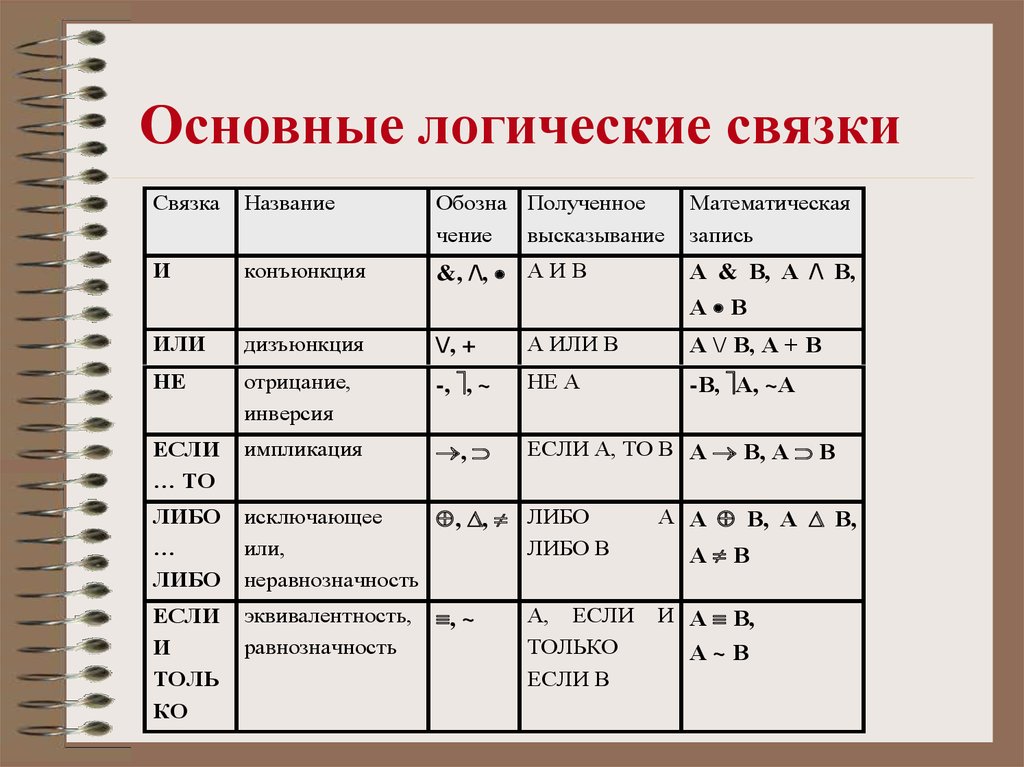 В последних классах учителя использовали несколько представлений математических идей для поддержки понимания, сосредоточивались на нестандартных задачах, чтобы укрепить применение понятий, подчеркивали несколько решений задач для развития беглости вычислений и проводили обсуждения в классе, требующие логических рассуждений, которые исследовали альтернативные решения или значения математические процедуры или результаты.
В последних классах учителя использовали несколько представлений математических идей для поддержки понимания, сосредоточивались на нестандартных задачах, чтобы укрепить применение понятий, подчеркивали несколько решений задач для развития беглости вычислений и проводили обсуждения в классе, требующие логических рассуждений, которые исследовали альтернативные решения или значения математические процедуры или результаты. 11
11