Как правильно решить задачу по математике: Как научить ребёнка самостоятельно решать задачи по математике

Как научить ребёнка самостоятельно решать задачи по математике

Как научить ребёнка решать задачи по математике? Таким вопросом задаются родители, чьи дети начинают ходить в школу. Многим ребятам бывает сложно не то чтобы решить саму задачу, но даже правильно понять ее условие. В этой статье рассказываем, как научить ребенка понимать и решать задачи по математике просто и с удовольствием, а родителям сберечь нервы. Ведь после рабочего дня  больше всего хочется отдохнуть, а не сидеть до ночи с ребенком над уроками.

Задачи бывают разные

Прежде чем перейти к практическим советам, как научить ребенка решать математику, рассмотрим, какие типы задач бывают:

Простые

Пожалуй, это самые любимые задачи детей и родителей. Решаются в одно действие (сложение, вычитание). Для их решения ребенку необходимо запомнить разницу между «+» и «-», понятиями «больше» и «меньше», «стало» и «осталось».

Например:

На тарелку, на которой лежало 5 яблок, положили еще 3 яблока. Сколько яблок стало на тарелке? (5+3 = 8)

С косвенным вопросом

Их уже любят меньше. Решение по-прежнему остается простым, но чтобы не ошибиться, важно правильно понять условие.

Например:

На одной тарелке 7 яблок. Это на 2 яблока больше, чем на другой тарелке. Сколько яблок на другой тарелке? (7 – 2 = 5)

Совет: В таких задачах перечитывайте условия несколько раз, пока ребенок не поймет.

Составные

Для их решения понадобится выполнить несколько действий, поэтому пригодится мини-план.

Например: В одной корзине 10 яиц, а в другой – на 3 яйца меньше. Сколько яиц в обеих корзинах? (10 – 3 = 7, 10 + 7 = 17)

Ребенку можно предложить задать следующие вопросы:

• Что нам нужно узнать? (Сколько всего яиц в двух корзинах).
• Что для этого нужно сделать? (Узнать, сколько яиц во второй корзине).
• Что нужно сделать после того, как мы это узнаем? (Посчитать яйца в обеих корзинах).

Простые задачи на умножение и деление

Например: Катя читала 4 книги, по 5 страниц в каждой книге. Сколько всего страниц прочитала Катя? (5 * 4 = 20)

Здесь ребенок должен понимать, каким образом он может получить ответ: сложить 5 + 5 + 5 + 5 или воспользоваться умножением 5 * 4. Второй способ предполагает понимание множителей и произведений (первый множитель показывает, какое число повторяется, а второй множитель показывает, сколько раз оно повторяется). В случае с делением – делимое, делитель частное.

Составные задачи на разные арифметические действия

Например: После того, как на 3 тарелки положили по 8 апельсинов, осталось еще 13 апельсинов. Сколько всего было апельсинов?

Здесь ребенку стоит предложить написать для себя краткое понятное условие, где будет видно, что дано, что ищем и с помощью каких действий вычислить.

Краткое условие:

Положили 8 апельсинов на 3 тарелки;

Осталось 13 апельсинов;

Сколько было — ?

Решаем задачу в два действия:

1. 8 * 3 = 24 (всего апельсинов положили)
2. 24 + 13 = 37 (ответ: было 37 апельсинов)

Есть еще задачи на движение, цену, количество, стоимость. Далее разберемся, как научить ребенка решать задачи по математике любой сложности.

Как научить ребенка решать задачи по математике просто и с удовольствием

Теперь давайте обобщим то, о чем говорили выше. Придерживаясь определенного алгоритма, ребенок быстрее освоит навык решения задач и будет пользоваться им на протяжении всей учебы.

Читаем условия внимательно

Сначала пусть ребенок прочитает задачу вслух сам. Затем спросите, что он понял. Если что-то понял не так, пусть прочтет еще раз. Спросите снова и при необходимости перечитайте условие вместе, делая паузы на непонятных моментах. Главное не нервничайте и позвольте ребенку спокойно разобраться в задаче самостоятельно. Особое внимание уделяйте задачам с косвенным вопросом, в них дети путаются чаще всего.

Описываем задачу своими словами

Можно выписать краткое условие, как мы делали в примерах выше, или составить наглядную схему. Визуальные образы воспринимаются мозгом лучше всего. Визуализация задачи на бумаге поможет ребенку быстро разобраться в условии и увидеть возможные решения уже на этом этапе.

Выбираем способ решения

Предыдущий шаг может помочь ребенку увидеть решение, но если нет, следует воспользоваться вспомогательными вопросами, как в примере с составной задачей про яйца.

⠀

Если и это способ не сработает, то попробуйте, например, разыграть сценку из подручных предметов или игрушек. Только не повторяйте один вопрос по несколько раз, это точно не работает, а только повышает напряжение у родителя и ребенка.

⠀

Каждая математическая задача строится по принципу «неизвестное получается из 2 известных». Но чтобы найти нужные числа, необходимо разложить условие на несколько простых действий и выбрать подходящий способ вычисления. Перед этим следует запомнить, какими способами можно находить неизвестное.

Решение тоже можно расписать подробно, чтобы лучше запомнить последовательность и затем использовать для других задач.

Формулируем ответ

Ребенок должен записать ответ четко и точно.  Если это «2 яблока», значит, никакой другой информации в ответе быть не должно. Самая часто встречающаяся ошибка – переносить в ответ те данные, которые были в условии.

⠀

Привыкая к правильным формулировкам, ребенок учится нести ответственность за свои действия и серьезно относится к полученному результату.

Закрепляем навыки

Правильно решив задачу один раз, ребенок сразу не станет гением в точных науках. Полученный результат следует закреплять, как говорится, повторение – мать учения. Можно, например, «поиграть» с задачей и поменять условия, попросив ребенка решить ее еще раз. Главное, чтобы он запомнил, как нужно рассуждать и какие действия выполнять для получения ответа. Благодаря регулярному закреплению ребенок научится правильно рассуждать при решении задач любой сложности.

Читайте также:

Математические игры для дошкольников: считаем, измеряем быстро и легко

Что еще поможет ребенку решать задачи

Конечно, мы не откроем секрет, если скажем, чтобы научить ребенка решать математику, сначала нужно научить его хорошо считать. Ниже несколько рекомендации, которые помогут сделать процесс решения задач легче и увлекательнее:

• Нужно научить ребенка решать простые примеры, выучить с ним таблицу умножения, освоить простые уравнения.
• Лучше подходить к обучению творчески. Детям младшего школьного возраста интереснее всего учиться в игровой форме. Например, можно менять условия задач, подставляя вместо обычных «Кать и Миш», любимых героев из книг и мультфильмов.

Математика в стихах: занимательные задачи для детей от 4 до 7 лет 

• Стоит параллельно развивать логическое мышление. Детям с развитым мышлением учеба дается легче. Пробуйте решать с ребенком не только математические задачи, но и логические. Это поможет ему быстрее находить несколько вариантов решения и уходить от шаблонного мышления.

Погрузиться в тему развития логического мышления:

Математическое мышление у ребенка: в чем польза и как его развить? 

Как развить креативное мышление у ребенка в домашних условиях? Методы ТРИЗ для детей от 5 лет

• Запишите ребенка на курс математики в онлайн-школу Kidskey. Все наши уроки проходят онлайн в игровой форме, после чего ребенку открывается домашнее задание, и он сразу закрепляет пройденный материал. А главное, что ему настолько нравится математика в Kidskey, что ваше присутствие во время урока абсолютно не обязательно. На занятии правильность ответов контролирует педагог, а домашнее задание – сама система.

Не уверены, подойдет ли онлайн-формат вашему ребенку? Попробуйте урок бесплатно. Нажимайте на кнопку ниже, и мы подберем для вас удобное время.

Как научить ребенка решать задачи по математике

03.05.2021

Решение задач – одна из неотъемлемых составляющих школьного процесса обучения. В начальных классах дети решают простенькие арифметические задачи, потом наступает пора задач по алгебре и геометрии, физике, химии, биологии.

Содержание:

• Почему важно научить школьника решать задачи?
• Пошаговый алгоритм действий
  • Шаг 1. Чтение условия
  • Шаг 2. Составление краткого описания
  • Шаг 3. Поиск алгоритма решения
  • Шаг 4. Запись ответа
• Какие навыки необходимы для решения задач

Почему важно научить школьника решать задачи?

Условия задач по разным предметам совершенно не похожи друг на друга, однако методы и приемы решения имеют много общего. И если ребенок не научится решать задачи по арифметике в младшей школе, он будет испытывать нарастающие сложности по мере перехода из класса в класс.

Проблемы с математическими задачами в младших классах – прямой путь к тому, что ребенок сопротивляется изучению точных наук в средней и старшей школе. Преподаватели и родители «записывают» таких учеников в гуманитарии и считают, что им «не дано» научиться решать задачи. А в учебниках написаны сухие формальные правила, которые никак не помогают и не мотивируют учащихся.

На самом деле, умение логически мыслить и решать задачи необходимо все ученикам, даже абсолютным гуманитариям. Без этого во взрослом возрасте невозможно решать даже простейшие бытовые вопросы – к примеру, посчитать количество стройматериалов для ремонта или пропорции ингредиентов при приготовлении блюд. А для программиста, инженера или управленца логическое и аналитическое мышление – неотъемлемая составляющая профессии.

Пошаговый алгоритм действий

Родителям необходимо ребенка учить решать задачи уже с первого класса, причем делать это надо в доброжелательной форме. Нельзя кричать, сердиться или решать задания вместо школьника, как бы вам этого не хотелось. Не ругайте ребенка за ошибки, ведь в процессе обучения они неизбежны, без этого невозможно научиться делать что-либо в принципе.

Функция родителей – объяснить условие задачи и алгоритм рассуждений, который позволяет получить ответ. Стоит сразу запастись терпением, просто не будет. Это кропотливая и длительная работа, за один раз даже самого талантливого ребенка невозможно научить решать задачи.

Шаг 1. Чтение условия

Умение читать условие и вникать в детали – обязательный навык для успешного решения задачи. Попросите ребенка прочитать условие вслух и задайте ему вопросы, чтобы убедиться в понимании текста. Если в задаче употребляются незнакомые понятия и формулировки, объясните их значения.

Особое внимание обратите на то, правильно ли ребенок понял вопрос. Зачастую сложности проистекают из того, что школьник путает математические понятия «больше в», «больше на» и прочие.

Шаг 2. Составление краткого описания

В школе детей учат составлять описание по определенным правилам, что вызывает у них сложности. Помимо того, что надо понять смысл задачи, школьник вынужден думать, как это записать в соответствии с требованиями учителя.

Значительно проще для ребенка нарисовать условие задачи. Графическая схема позволяет наглядно увидеть связи между элементами задачи и разобраться в условии.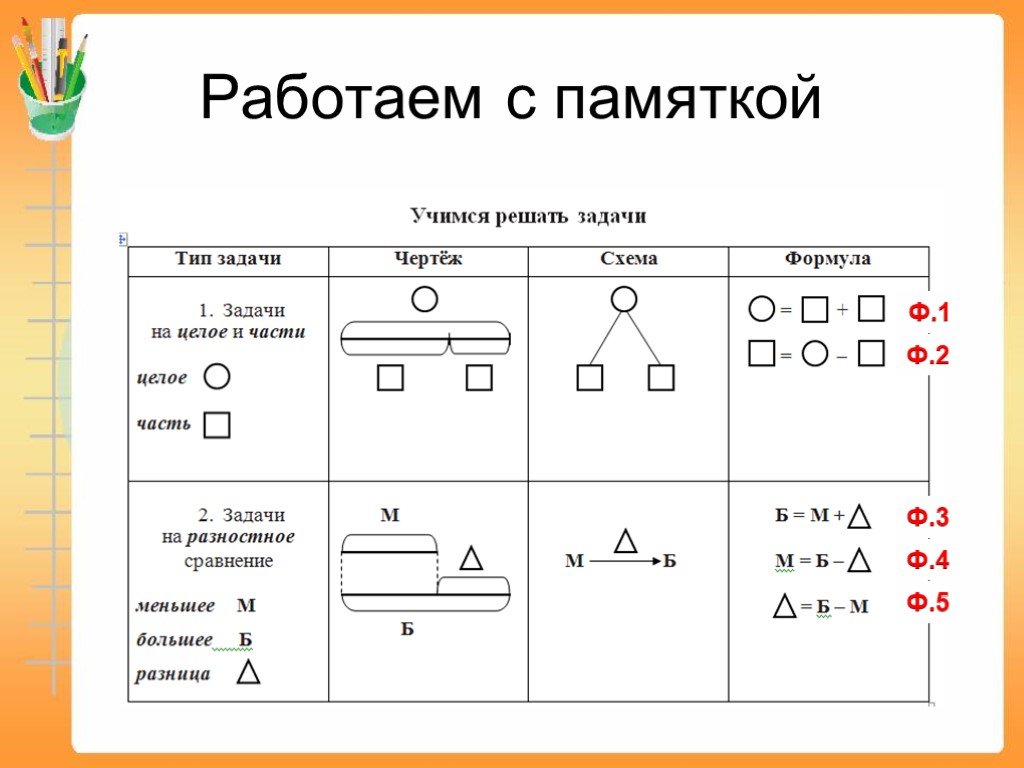

Очень часто алгоритм решения становится понятен ребенку уже на этом этапе.

Шаг 3. Поиск алгоритма решения

Наглядная графическая схема в большинстве случаев наталкивает школьника на правильный ход рассуждений. Но что делать, если этого не происходит? В этом случае попробуйте иллюстрировать задачу подручными предметами, разыграйте с ними сценку, задайте наводящие вопросы. Единого метода не существует, вам нужно будет найти подход к ребенку.

Схему решения нужно подробно записать и убедиться, что школьник понимает общий принцип. Тогда он сможет пользоваться в дальнейшем для аналогичных задач.

Шаг 4. Запись ответа

Ответ нужно формулировать полно и точно. Убедитесь, что ребенок отвечает именно на тот вопрос, который спрашивается в задаче. Если это не так, нужно вернуться на первый шаг и заново пройти всю цепочку.

Какие навыки необходимы для решения задач

Для нахождения ответа во многих задач нужно выполнить несколько действий. Убедитесь, что ребенок усвоил правила нахождения слагаемого, уменьшаемого, вычитаемого, множителя, делителя, делимого. Он должен уметь вычислять эти данные на «автомате».

Чтобы сохранить мотивацию, проявите творческий подход. К примеру, замените груши и яблоки любимыми лакомствами ребенка, а поезда и катера – космическими кораблями.

Развитая логика и аналитическое мышление – помощники в решении задач. Обязательно решайте с ребенком логические задания, разгадывайте головоломки и ребусы, учите его анализировать окружающие предметы и явления.

Решайте уравнения, упрощайте выражения с помощью программы «Пошаговое решение математических задач»

Алгебра

Раздел алгебры QuickMath позволяет вам манипулировать математическими выражениями всевозможными полезными способами. На данный момент QuickMath может расширять, разлагать или упрощать практически любое выражение, отменять общие множители внутри дробей, разбивать дроби на более мелкие («частичные») дроби и объединять две или более дробей вместе в одну дробь. На подходе более специализированные команды.

Что такое алгебра?

Термин «алгебра» используется для обозначения многих вещей в математике, но в этом разделе мы будем говорить только о том виде алгебры, с которым вы сталкиваетесь в старшей школе.

Алгебра — это раздел элементарной математики, в котором для обозначения неизвестных величин используются символы. В более общем смысле он состоит из решения уравнений или манипулирования выражениями, которые содержат символы (обычно буквы, такие как x, y или z), а также числа и функции. Хотя решение уравнений на самом деле является частью алгебры, это настолько обширная область, что для нее есть отдельный раздел в QuickMath.

Эта часть QuickMath имеет дело только с алгебраическими выражениями.

Это математические операторы, которые содержат буквы, цифры и функции, но не содержат знаков равенства. Вот несколько примеров простых алгебраических выражений:

х 2 -1 x 2 -2x+1 аб 2 +3а 3 б-5аб x 3 +1 1 а + б  +  1 а — б х 2 -1 х + 1

Расширить

Команда расширения используется в основном для перезаписи многочленов с умножением всех скобок и целых степеней и сбором всех подобных членов вместе. В расширенном разделе у вас также есть возможность расширения тригонометрических функций, расширения по модулю любого целого числа и оставления нетронутыми определенных частей выражения при расширении остальных.

Перейти на страницу Развернуть

Factor

Команда factor попытается переписать выражение как произведение меньших выражений. Он заботится о таких вещах, как удаление общих множителей, разложение на множители по парам, квадратичные трехчлены, разности двух квадратов, суммы и разности двух кубов и многое другое. Расширенный раздел включает в себя параметры факторизации тригонометрических функций, факторизации по модулю любого целого числа, факторизации поля целых чисел Гаусса (как раз то, что нужно для этих хитрых сумм квадратов) и даже расширения поля, в котором происходит факторизация, с вашими собственными расширениями.

Перейти на страницу Factor

Simplify

Упрощение, пожалуй, самая сложная из всех команд для описания. То, как упрощение выполняется в QuickMath, включает просмотр множества различных комбинаций преобразований выражения и выбор той, которая имеет наименьшее количество частей. Помимо прочего, команда «Упростить» позаботится об исключении общих множителей сверху и снизу дроби и сборе одинаковых членов. Расширенные параметры позволяют упростить тригонометрические функции или дать указание QuickMath прилагать больше усилий для поиска упрощенного выражения.

Перейти на страницу упрощения

Отмена

Команда отмены позволяет исключить общие множители в знаменателе и числителе любой дроби, встречающейся в выражении. Эта команда работает путем отмены наибольшего общего делителя знаменателя и числителя.

Перейти на страницу отмены

Частичные дроби

Команда дробей позволяет разделить рациональную функцию на сумму или разность дробей. Рациональная функция — это просто частное двух многочленов. Любую рациональную функцию можно представить в виде суммы дробей, где знаменатели дробей являются степенями множителей знаменателя исходного выражения. Эта команда особенно полезна, если вам нужно интегрировать рациональную функцию. Разбив его сначала на неполные дроби, интегрирование часто можно сделать намного проще.

Перейти на страницу «Частичные дроби»

«Соединить дроби»

Команда «Соединить дроби», по существу, выполняет обратную команду «Частичные дроби». Он перепишет ряд дробей, которые добавляются или вычитаются, как одна дробь. Знаменатель этой единственной дроби обычно будет наименьшим общим кратным знаменателей всех дробей, которые складываются или вычитаются. Любые общие множители в числителе и знаменателе ответа будут автоматически аннулированы.

Перейти на страницу объединения фракций

Понятие переписки часто встречается в повседневной жизни. Для Например, каждой книге в библиотеке соответствует количество страниц в книга. В качестве другого примера, каждому человеку соответствует дата рождения. К приведите третий пример, если температура воздуха регистрируется в течение всего сутки, то в каждый момент времени есть соответствующая температура.

Примеры соответствий, которые мы привели, включают два множества X и Y. В В нашем первом примере X обозначает набор книг в библиотеке, а Y — набор положительные целые числа. Каждой книге x в X соответствует натуральное число y, а именно количество страниц в книге. Во втором примере, если мы допустим X обозначим множество всех людей, а Y множество всех возможных дат, тогда каждому человеку x в X соответствует дата рождения y.

Иногда мы представляем соответствия диаграммами типа, показанного на рис. Рисунок 1.17, где множества X и Y представлены точками внутри областей в самолет. Изогнутая стрелка указывает, что элемент y из Y соответствует элемент x из X. Мы изобразили X и Y как разные множества. Однако X и Y могут имеют общие элементы. На самом деле мы часто имеем X = Y.

Наши примеры показывают, что каждому x в X соответствует один и только один у в Y; то есть y уникален для данного x. Однако один и тот же элемент Y может соответствуют разным элементам X. Например, две разные книги могут иметь одинаковое количество страниц, у двух разных людей может быть один и тот же день рождения, и скоро.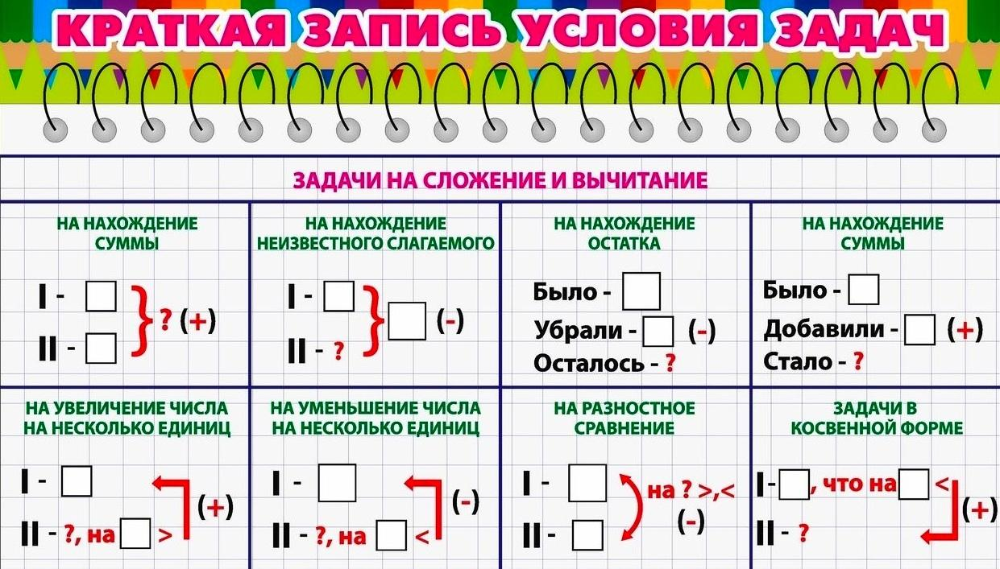

В большей части нашей работы X и Y будут наборами действительных чисел. Для иллюстрации пусть X и Y оба обозначают множество R действительных чисел, и каждому вещественному числу x соответствует назначьте его квадрат x ² . Таким образом, 3 мы приписываем 9, — 5 мы присваиваем 25, а скоро. Это дает нам соответствие от R до R. Все примеры соответствия, которые мы дали, являются функциями, как определено ниже.

Определение

Функция f из множества X в множество Y является соответствием, которое присваивает каждому элемент x из X уникальный элемент y из Y. Элемент y называется образом x при f и обозначается через f(x). Множество X называется областью определения функции. Диапазон функции состоит из всех изображений элементов X.

Ранее мы ввели обозначение f(x) для элемента Y, который соответствует х. Обычно это читается как «f of x». Мы также называем f(x) значением ф в х. В терминах графического представления, данного ранее, мы можем теперь нарисуйте схему, как на рис. 1.18. Изогнутые стрелки указывают на то, что элементы f(x), f(w), f(z) и f(a) из Y соответствуют элементам x, y, z и a из X. Повторим тот важный факт, что каждому х в X соответствует в точности одно изображение f(x) в Y; однако различные элементы X, такие как w и z на рисунке 1.18 может иметь такое же изображение в Y.

Начинающих учеников иногда смущают символы f и f(x). Помнить что f используется для представления функции. Его нет ни в X, ни в Y. Однако, f(x) является элементом Y, а именно элементом, который f сопоставляет x. Две функции Говорят, что f и g от X до Y равны, что записывается как

для каждого x в X. для каждого x в R. Найдите f(-6) и f(a), где a — любое действительное число. Что диапазон ф?

Решение Значения f (или изображений под f) можно найти, заменив x в уравнение f(x) = x ² . Таким образом:

Если T обозначает диапазон выключения, то по предыдущему определению T состоит из всех числа вида f(a), где a находится в R . Следовательно, T есть множество всех квадраты a ² , где a — действительное число. Так как квадрат любого действительного число неотрицательно. T содержится в множестве всех неотрицательных вещественных числа. Более того, каждое неотрицательное действительное число c является образом ниже f, так как . Следовательно, диапазон f — это набор всех неотрицательных действительных чисел.

Если функция определена, как в предыдущем примере, символ, используемый для переменная несущественна; то есть такие выражения, как:

и т. д., все определяют одну и ту же функцию. Это верно, потому что если a является любым число в области f, то то же самое изображение a ² получается без независимо от того, какое выражение используется.

Пример 2 Пусть X обозначает множество неотрицательных действительных чисел, а f функция от X до R определяется формулой для каждого x в X. Найдите f(4) и f (пи). Если b и c принадлежат X, найдите f(b + c) и f(b) + f(c).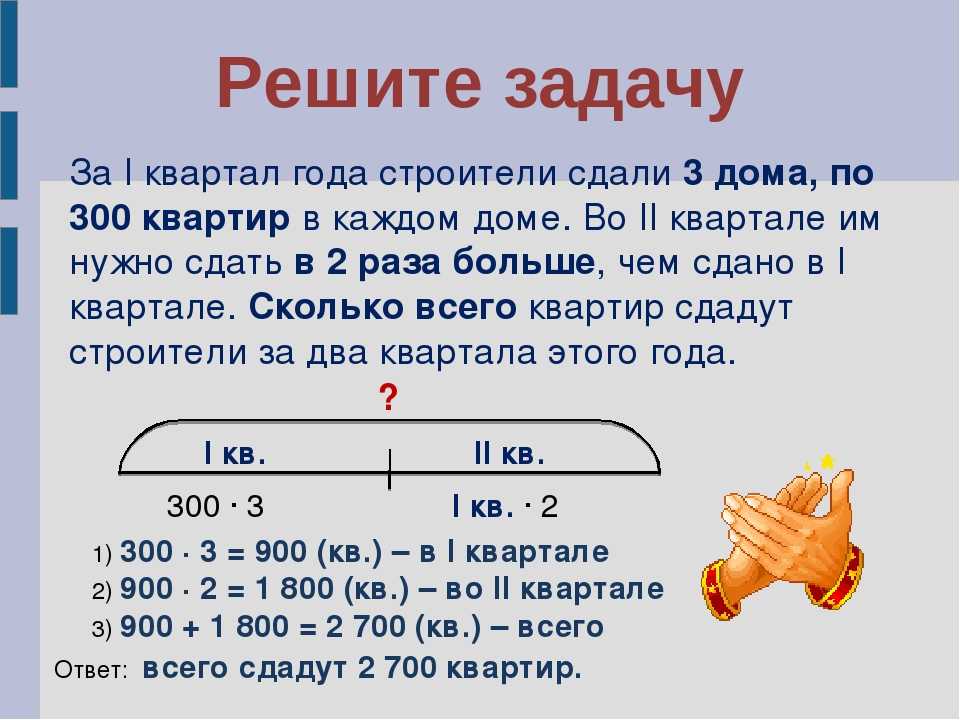

Решение Как и в примере 1, поиск изображений под f — это просто вопрос подставляя подходящее число вместо x в выражении для f(x). Таким образом:

Многие формулы, встречающиеся в математике и естественных науках, определяют функции. В качестве иллюстрации формула A = pi*r ² для площади A круга радиуса r присваивает каждому положительному вещественному числу r уникальное значение А. Это определяет функцию f, где f(r) = pi*r ² , и мы можем написать А = f(r). Буква r, обозначающая произвольное число из домена off, часто называют независимой переменной. Буква А, обозначающая число из диапазона off, называется зависимой переменной, так как ее значение зависит от номер, присвоенный тор. Когда две переменные r и A связаны таким образом, принято использовать фразу A является функцией r. Чтобы привести другой пример, если автомобиль движется с постоянной скоростью 50 миль в час, то расстояние d (мили), пройденное за время t (часы), определяется как d = 50t и, следовательно, расстояние d является функцией времени t.

Мы видели, что различные элементы области определения функции могут иметь такое же изображение. Если изображения всегда разные, то, как и в следующем определении, функция называется один к одному.
 

4 шага для решения даже самой сложной математической задачи

Математика — это область, в которой можно использовать несколько подходов для решения задачи. Этот упрощенный пошаговый подход поможет найти решение даже самой сложной математической задачи.

Нью-Дели, ОБНОВЛЕНО: 2 ноября 2018 г., 12:03 IST

Этот упрощенный метод может помочь каждому решить даже самую сложную математическую задачу и улучшить свои математические навыки, пока вы это делаете!

Есть несколько способов решения математических задач; однако упрощенный метод, который может помочь каждому решить даже самую сложную проблему, состоит из трех шагов.

Процесс таков:

1. Визуализация проблемы
2. Подход к этой проблеме
3. Наконец, решите задачу

Этот трехэтапный процесс, возможно, поможет вам улучшить свои математические навыки.

Вот четыре шага, которые помогут легко решить любые математические задачи:

реклама

1. Внимательно прочитайте, поймите и определите тип задачи

Определите категорию, к которой относится ваша математическая задача, прежде чем вы двигаться вперед, так как это поможет найти лучшее решение для ее решения.

Когда вы впервые начинаете изучать математику, проверьте тип задачи — будь то задача со словами, задача о дробях, квадратные уравнения или любая другая задача.

Определите категорию, к которой относится ваша математическая задача, прежде чем двигаться дальше, так как это поможет найти лучшее решение для ее решения.

Внимательно прочитать проблему и убедиться, что вы правильно ее поняли, чрезвычайно важно для принятия следующих мер.

2. Нарисуйте и просмотрите свою задачу

Возможно, вы также можете поискать закономерности или использовать графики для решения математической задачи.

После того, как вы поняли проблему, следующим шагом может быть ее рисование, так как это поможет вам двигаться вперед. Рисунок может быть простым в виде фигур или фигур с цифрами.

Здесь вы также можете искать закономерности или использовать графики. После того, как весь этот процесс понимания, чтения и рисования завершен, вам необходимо просмотреть анализ, который вы сделали на его основе.

Это поможет вам определить тип проблемы и способ ее решения.

3. Разработайте план ее решения

Сначала нужно выяснить формулу, которая потребуется для решения математической задачи.

Есть четыре простых шага, которые нужно пройти, чтобы разработать план ее решения. Шаги указаны ниже:

• Во-первых, нужно выяснить формулу, которая понадобится для решения задачи. Здесь вам нужно потратить некоторое время на просмотр понятий в ваших учебниках, которые помогут вам решить задачу
.

• Вам нужно записать свою потребность, чтобы получить ответ на вашу проблему. Для этого вам нужно составить пошаговый список того, что вам нужно для решения проблемы, а также помочь вам оставаться организованным

• В случае, если есть более простая задача, вы, вероятно, могли бы сначала поработать над ней, чтобы решить ее. Иногда формулы повторяются для решения обеих задач. Это даст вам еще немного времени для решения сложной задачи

• Вы можете сделать обоснованное предположение об ответе, чтобы попытаться получить оценку ответа, прежде чем начать его решать. Здесь вы можете указать количество и другие факторы, которые будут способствовать тому же. Наконец, просмотрите смету, а затем проверьте, не упустили ли вы что-нибудь

4. Решите задачу

Убедитесь, что все перечисленные вами шаги для решения математической задачи выполнены

объявление

Как только ваша стратегия и метод решения проблемы будут готовы, вы можете приступить к ее решению. Ниже приведены шаги:

• Убедитесь, что все шаги, перечисленные вами для решения проблемы, выполнены. Перепроверьте каждый из ваших ответов, чтобы убедиться, что точность идеальна

• Сравните ответ с оценками, которые вы указали после завершения каждого шага. Это позволит вам сэкономить время, если конечный результат не соответствует вашим ожиданиям. Также проверьте, внимательно ли вы выполнили все шаги

• Если в середине вы поймете, что ваш план не работает, вы всегда можете вернуться к этапу планирования и составить новый план. Иногда это происходит из-за распространенных ошибок, но вы должны научиться принимать это и быть готовым к плану Б, чтобы решить эту проблему

• После того, как вы правильно решили проблему, вы должны вернуться и посмотреть на процесс. Найдите минутку, чтобы подумать о проблеме и методе, с помощью которого вы ее решили. Это поможет в определении концепций, которые вам необходимо изучить во время практики.

реклама

— Статья Судханшу Синхала, управляющего директора Sinhal Classes Pvt.