Как считать вероятность в математике: Теория вероятностей на ЕГЭ по математике. Формулы, теория, решения

alexxlab / / Математике

Содержание

Расчёт вероятности получения положительной отметки при решении тестовых заданий по математике

  • Авторы
  • Руководители
  • Файлы работы
  • Наградные документы

Кокорев Е.Э. 1

1МБОУ «Плотавская СОШ»

Левшина О.Н. 1

1МБОУ «Плотавская СОШ»

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Расчёт вероятности получения положительной отметки

при решении тестовых заданий по математике

Высшее назначение математики…состоит в том,

чтобы находить скрытый порядок в хаосе, который нас окружает

Н. Винер

Введение

Однажды при подготовке к контрольной работе учитель математики задала на дом пять задач по геометрии. Четыре я решил, пятая же не получилась. Я понадеялся, что учитель спросит кого-либо другого, а если и меня, то попадется одна из четырех решенных мной задач. Но учитель вызвала именно меня и спросила как раз пятую задачу. Случайность! И на этот раз не очень-то приятная! Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться!

При решении самостоятельной или контрольной работы в тестовой форме, особенно по математике, информатике, физике большинство моих одноклассников надеются, что за работу можно будет получить хорошую оценку, выбирая правильные варианты ответов интуитивно, без теоретических знаний. Поэтому я решил оценить, насколько данный метод обеспечит положительную оценку, и как результаты моего исследования по теории вероятностей можно будет практически применить при тестировании.

 Актуальность

Тестирование в образовании – современный подход к оценке знаний учащихся. Тестовая форма контроля на сегодняшний день является самой востребованной: она используется на ГИА и ЕГЭ. А потому, чем раньше мы начнем приобщаться к такой форме проверки знаний, тем лучше будем подготовлены к итоговой аттестации и различного рода испытаниям в тестовой форме.

Гипотеза:

Вероятность угадать верные ответы при тестировании очень мала, а значит практически невозможно получить положительную оценку без подготовки.

Цель:

Определить вероятность получения положительной отметки при написании тестов по математике путем угадывания правильного ответа.

Для реализации цели были поставлены следующие 

задачи:

1) собрать, изучить и систематизировать материал о теории вероятностей, воспользовавшись различными источниками информации;

2) провести статистический эксперимент;

3) проанализировать результаты тестовых работ с применением теории вероятности.

Объект исследования: теория вероятности.

Предмет исследования: тесты по математике.

Методы исследования: анализ, синтез, сбор информации, анкетирование работа с литературой, эксперимент.

Практическая значимость данной работы состоит в том, что она нацелена помочь обучающимся осознать важность учения, так как согласно проведенному исследованию получить положительную отметку за тестовую работу путем угадывания мало вероятна.

Теоретическая часть

Глава 1. Теория вероятностей

История возникновения.

Теория вероятностей — раздел математики, изучающий случайность. Теория вероятностей используется в таких разделах математики как математическая статистика, теория случайных процессов, теория массового обслуживания. Она находит применение в физике, в анализе азартных игр, в страховании и в расчете пенсионных схем. На теории вероятностей основана разработка, применение и анализ вероятностных алгоритмов [1].

Как наука, теория вероятностей зародилась в середине XVII века с появлением азартных игр, таких как карты и кости, когда начали применять в них количественные подсчеты и прогнозирование шансов на успех. А зарождение теории вероятностей началось с того, что придворный французского короля, шевалье (кавалер) де Мерэ (1607-1648г. г. ), сам азартный игрок, обратился к французскому физику, математику и философу Блезу Паскалю (1623-1662г. г.) с вопросами к задаче об очках. (см. главы «Формулировки и основные понятия», «Примеры и решения практических задач на вероятность»). Паскаль обратился к математику Пьеру Ферма (1601-1665г. г.) и переписывался с ним по поводу этих задач. Они вдвоем установили некоторые основные положения теории вероятностей, в частности пришли к понятию математического ожидания и теоремам сложения и умножения вероятностей.

Другим толчком для развития теории вероятностей послужило страховое дело, а именно с конца XVII века на научной основе стало производиться страхование от несчастных случаев и стихийных бедствий. В XVI-XVII веках во всех странах Западной Европы получило распространение страхование судов и страхование от пожаров. В XVII веке были созданы многочисленные страховые компании и лотереи в Италии, Фландрии, Нидерландах. Затем методы теории вероятностей стали широко применять в демографии, например, при ведении статистики рождения и смерти.

Первооткрывателями теории вероятностей считаются французские ученые Б. Паскаль и П. Ферма и голландский ученый Х. Гюйгенс (1629-1695г. г.). Стала зарождаться новая наука, вырисовываться ее специфика и методология: определения, теоремы, методы. Также теория вероятностей связана с именами известных математиков: швейцарца Якоба Бернулли (1654-1705г.г.), француза П. С. Лапласа, англичанина А. Муавра (1667-1754г. г. ) и др. Вклад в развитие теории вероятностей внесли русские и советские ученые П. Л. Чебышев, А. А. Марков, А. М Ляпунов и многие другие [2].

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире.

Была создана современная теория вероятностей [3].

Основные понятия теории вероятностей

Основными понятиями в теории вероятностей являются испытание, событие и вероятность.

Испытание — это эксперимент, проводимый над объектом в комплексе определенных условий.

Событие — это случай или факт, который произошел или не произошел в результате испытания.

Вероятность — это численная мера степени объективной возможности наступления события.

Вероятностью события А называется отношение числа случаев наступления этого события к общему числу случаев:

, P(A

) – вероятность события A, m – число случаев наступления события А, n – общее число случаев, m , 0. Данное определение принято называть классическим определением вероятности. Оно применяется, когда теоретически удается выявить все равновозможные исходы испытания и определить благоприятствующие исследуемому испытанию исходы.

При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: достоверные, случайные, невозможные, равновероятные.

Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости. 

Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Событие V называют невозможным по отношению к некоторому испытанию, если в ходе этого испытания событие V не произойдет. 

Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.

Но встречаются случаи, когда без практики определить число благоприятных исходов невозможно. В таких случаях используется статистическое определение вероятности.

Статистическая вероятность (частота, относительная частота) –это отношение числа испытаний, в которых событие появилось к общему числу фактически произведенных испытаний. Определяется следующей формулой для события: P(A

) = , где n – общее число фактически проведенных испытаний, m – число появлений событий. Другими словами, статистическая вероятность – это вероятность события, рассчитанная опытным путем.

Формула Бернулли — это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула названа в честь выдающегося швейцарского математика Якоба Бернулли [4].

Теория вероятности в жизни

Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать, или спланировать. В разное время разными способами. В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [2]

Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Невозможно представить без теории вероятности жизнь брокеров на мировых рынках. Предсказывание денежного курса на денежных опционах дает возможность зарабатывать на данной теории серьезные деньги.

Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах.

Таким образом, теорию вероятностей нельзя не применять в нашей жизни. Она имеет разные области применения такие как: биологические и химические процессы, история, экономика, кораблестроение и машиностроение, медицина и большинство различной деятельности человека. Люди применяют её как сознательно, так и подсознательно, что проявляется в обычных повседневных фразах и действиях. Разумный человек должен стремиться мыслить, исходя из законов вероятностей. Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас [5].

Вероятностно–статистические методы играют важную роль в практической деятельности — это контроль качества продукции, техническая диагностика оборудования, технология производства, обеспечения надежности оборудования, организация массового обслуживания, военное дело (стрельба, бомбометание, тактика, теория боеприпасов), получение достоверных результатов измерений, астрономические наблюдения и многое другое.

Глава 2. Практическая часть

2.1 Исследование

Сейчас обучение в любом классе начинается с входного тестирования, сопровождается текущим контролем с помощью заданий в тестовой форме и заканчивается объективным тестированием учебных достижений.

Кроме того, тесты позволяют наладить самоконтроль — самую полезную для обучения и гуманную форму контроля знаний, а также организовать рейтинг — эффективное средство повышения учебной мотивации.

Мы провели социологический опрос среди учащихся 7-9 классов. В связи малой накаляемостью учащихся в классах нашей школы (5-6 учащихся – средняя накаляемость класса), в анкетировании принимали участие 15 человек. Учащимся предложили ответить на вопросы:

можно ли сдать тест, экзамен без подготовки методом угадывания?

можно ли угадать, например, 6 заданий из 10, таким образом, решив тестовое задание по математике без подготовки?

По первому вопросу из 15 респондентов 9 человек (60%) ответили «да», 6 человек ( 40%) ответили «нет», т. е. считают, что таким способом сдать экзамен или решить тест нельзя.

По второму вопросу результаты такие: 80% учащихся 7 класса считают, что можно угадать 6 заданий из 10, 8кл. — 60%, 9кл. — 33%.

Вывод: чем старше класс, тем меньше веры в случай. (Приложение 1)

2.2 Теоретический расчет успешного решения тестового задания

Определить вероятность угадывания верного ответа можно по формуле Бернулли.

Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании теста. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4).

Тогда p=1/4, а q=1-p=3/4.

Вероятность получения положительной оценки:

Р10(7)= С10 5 р5 q10-5 , где

= = 2 3 7 = 252

Р10(5)=252 = 0,0583991 0,058

То есть, вероятность благополучного исхода очень низкая, примерно 5,8%

Вывод: мало шансов решить тест или сдать экзамен на положительную оценку без подготовки. Из 10000 человек только 5- 6 могут получить положительную оценку.

2.3 Эксперимент: расчет вероятности получения положительной отметки по алгебре

Для подтверждения гипотезы исследования в 7-9 классах мы воспользовались материалами сайта «Контроль знаний» [6]. Учащимся предложили решить тесты по алгебре по следующим темам1:

Тест по алгебре 7 класс: Степень и её свойства (10 вопросов)2

Тест по алгебре 8 класс: «Решение неравенств с одной переменной» (10 вопросов)3.

Алгебра 9: Квадратный трехчлен(10 вопросов)4.

В каждом тесте 10 заданий с выбором ответа по алгебре. Один ответ из четырех верный. Чтобы получить положительную оценку необходимо правильно угадать 6 ответов (60%).

Результаты эксперимента показывают, что угадал 6 ответов только один ученик (Приложение 2).

Произведем расчеты по формуле.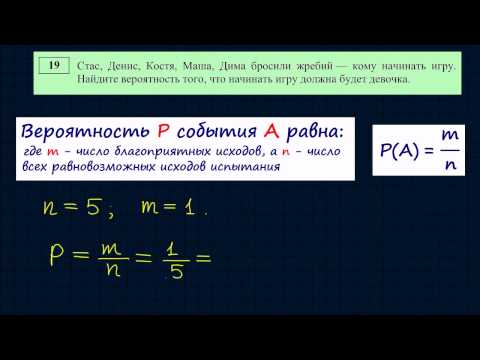

Пусть событие А– это правильно выбранный ответ из четырех предложенных в одном задании. Вероятность события Аопределена как отношение числа случаев, благоприятствующих этому событию (то есть правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда p = P(A)=1/4.

Вероятность противоположного события q = P(Ā)=1- p = 3/4.

Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 10, m = 6.

Вероятность получения положительной оценки:

Р10(6)= С10 6 р4 q10-6 , где

= = 10 3 7= 210

Р10(6) = 210 = 0,016222 0,02

Таким образом, максимальное количество правильно угаданных ответов

равно 4, что не позволяет ученику получить положительную отметку за тест по алгебре. Это же подтверждают теоретические вычисления – вероятность угадывания правильных ответов – достаточно мала, в данном случае только 0,02.. Процент правильно угаданных ответов — 13,3% (Приложение 2).

2.4 Эксперимент: расчет вероятности получения положительной отметки по геометрии

При повторном эксперименте учащимся предложили решить тесты по геометрии по следующим темам:

Геометрия 7 класс. Свойства параллельных прямых5.

Геометрия 8. Признаки подобия треугольников6

Геометрия 9. Треугольники7

В каждом тесте 12 заданий с выбором ответа по геометрии. Один ответ из четырех верный. Чтобы получить положительную оценку необходимо правильно угадать не менее 50% от всего теста, т.е. угадать не менее 6 ответов.

Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 12, m = 6.

Вероятность получения положительной оценки:

Р12(6)= С12 6 р6 q12-6 , где

= = 11 3 = 924

Р12(6) = 924 = 0,0401494 0,04. Вероятность угадывания правильных ответов выше, чем в первом эксперименте. Процент правильно угаданных ответов 17% (Приложение 3).

Вывод: данные теории вероятностей и результаты эксперимента показывают, что способом угадывания правильного ответа в тестовом задании по алгебре и геометрии получить положительную отметку почти невозможно.

Заключение

В результате проделанной работы, были достигнуты поставленные задачи:

была изучена научная литература по теме «Теория вероятностей» — это огромный раздел науки математики;

в ходе работы был проведен эксперимент, позволяющий определить вероятность успешного выполнения тестов по математике обучающимися 7-9 классов путем угадывания правильного ответа, применяя теорию вероятностей.

При проведении эксперимента наибольший процент правильно угаданных ответов был получен при написании тестовой работы по геометрии. Это, возможно, связано с тем, что обучающиеся использовали те знания, которые они получили на уроках и в повседневной жизни. Им было легче сориентироваться при выборе ответа, на уровне подсознания.

Таким образом, ранее выдвинутая гипотеза нашла свое подтверждение в проведенном исследовании. Полученные данные позволяют сделать вывод, что только планомерная, вдумчивая и добросовестная учеба в школе позволит учащимся успешно писать тестовые контрольные работы, хорошо подготовиться к участию в ГИА и успешно решить судьбоносную проблему при переходе на более высокий уровень обучения в ВУЗ.

С результатами данного исследования можно ознакомить будущих выпускников во время проведения классных часов, внеклассных мероприятий, с целью пропаганды подготовки их к экзаменам.

Вывод

Результаты практических экспериментов и их теоретическое обоснование подтверждают правильность выдвинутой гипотезы.

Литература

Савельева Р. Ю. Основы теории вероятностей и математической статистики [Электронный ресурс]. – Режим доступа: http://открытыйурок.рф/статьи/526665/ (дата обращения – 24.01.2018)

Гатауллина Л. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2012/01/07/teoriya-veroyatnosti-v-zhizni (дата обращения — 6.02.2018)

Кибзун А. И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами [Текст]: учебное пособие/А. И. Кибзун, Е. Р. Горяинова, А. В. Наумов, А. Н. Сиротин. – Москва: ФИЗМАТЛИТ, 2002. – 224 с.

Теория вероятностей и основные понятия теории [Электронный ресурс]. – Режим доступа: https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/ (дата обращения 24.01.2018) 

Вишня Ю. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder. com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018)

http://контрользнаний.рф/geometriya-7-test-za-ii-chetvert/

Приложение 1

Анкетирование

Можно ли сдать тест, экзамен без подготовки методом угадывания?

Рис. 1. Результаты анкетирования респондентов

Можно ли угадать, например, 6 заданий из 10, таким образом, решив тестовое задание по математике без подготовки?

Приложение 2

Результаты статистического эксперимента: выбор учащимися 7-9 классов правильного ответа в тесте по алгебре

Класс

К-во уч-ся

Количество угаданных ответов

0

1

2

3

4

5

6

7 и более

7

3

1

1

2

1

0

0

0

0

8

5

1

0

3

1

1

0

1

0

9

7

0

1

4

1

1

1

0

0

Всего

15

2

2

9

3

2

1

1

0

Выбор правильных ответов по алгебре

Приложение 3.

Результаты статистического эксперимента: выбор учащимися 7-9 классов правильного ответа в тесте по геометрии

Класс

К-во уч-ся

Количество угаданных ответов

0

1

2

3

4

5

6

7

8 и более

7

3

1

1

2

1

0

0

0

0

0

8

5

1

0

3

1

1

1

1

1

0

9

7

1

1

4

2

2

1

1

0

0

Всего

15

2

2

9

4

3

2

2

1

0

Выбор правильных ответов по геометрии

1 http://контроль-знаний. рф/

2 http://контроль-знаний.рф/stepen-i-eyo-svoystva/

3 http://контроль-знаний.рф/reshenie-neravenstv-s-odnoy-peremen/

4 http://контроль-знаний.рф/kvadratnyy-trekhchlen/

5 http://контроль-знаний.рф/svoystva-parallelnykh-pryamykh/

6 http://контроль-знаний.рф/priznaki-podobiya-treugolnikov/

7 https://testedu.ru/test/matematika/9-klass/treugolniki.html

Просмотров работы: 1087

Что такое теория вероятностей?

      1. Что такое теория вероятностей?
      2. Как рассчитать вероятность?
      3. Формула вероятности: примеры

     

    Теория вероятности – объемный и достаточно сложный раздел математики. Во время работы нам часто приходится сталкиваться с необходимостью определять эффективность и прогнозировать результаты, скажем для построения маркетинговых стратегий и других заданий. В статье изложена суть и основные формулы вероятности, которые помогут сориентироваться в этой математической отрасли и применять ее на практике.  

     

    Что такое теория вероятностей?

    Итогом проведенных исследований относительно влияния случайности и неопределенности на социальные, поведенческие и физические явления стал раздел математики, посвященный теории вероятностей. В количественном эквиваленте вероятность определяется числом от 0 до 1, где 0 означает окончательную невозможность события, а 1 – стопроцентную достоверность того, что событие произойдет. Чем больше это число будет приближаться к 1, тем большая вероятность наступления определенных событий. Вероятность также измеряется шкалой от 0 до 100%.

     

    Простым примером вероятности является жеребьевка: выпадения орла или решки одинаковые по степени вероятности, поскольку других исходов такого подбрасывания монеты не предусмотрено. На практике теория вероятностей используется для моделирования ситуаций, когда в одинаковых условиях вследствие одних и тех самых действий имеем разные результаты.

     

    Результат подбрасывания монеты является случайным. Случайные события нельзя полностью спрогнозировать, однако все они имеют длительные закономерности, которые мы можем описать и количественно оценить с помощью вероятности. 

     

    Рассмотрим три основные теории. 

     

    Одинаково вероятные результаты

    Нет никаких причин утверждать, что вероятность одного результата события имеет преимущество перед другими результатами. Представьте сосуд с одинаковыми шариками, которые тщательно перемешали. Игроку предлагают достать один из шариков, при этом вероятность выбора каждого из шариков будет одинаковой. Если заданная ситуация имеет количество результатов, равное n, то вероятность каждого результата составляет 100%. 

     

    Теория частоты

    Согласно с этой теорией, вероятность – это предел относительной частоты, с которой событие происходит в повторяющихся условиях. Утверждение «вероятность того, что А произойдет, равна р%» в этом случае означает следующее: если вы повторяете эксперимент снова и снова, независимо и в приблизительно одинаковых условиях, процент времени, когда А произойдет, приближается к р. Относительная частота рассчитывается исключительно после проведения опытов на основании фактически полученных данных. 

     

    Если ряд экспериментов проводится в неизменных условиях, то относительная частота обретает устойчивость, то есть варьируется в пределах незначительных отличий. Так, профессиональный лучник сделал 100 выстрелов и из них попал в мишень 90 раз. Его вероятность попадания в цель при определенных условиях составляет 0,9. Если за свою карьеру он сделал 10511 выстрелов, из которых попал в цель 9846 раз, относительная частота равна 9846/10511=0,9367. Этот показатель и будет учитываться для прогнозирования результата лучника в будущих соревнованиях. 

     

    Субъективная теория

    Такой тип вероятности применяется в процессе принятия решений с целью в дальнейшем прогнозировать поведение человека. Он не имеет статистической характеристики. В таком случае вероятностью является ступень проверки определенного утверждения. Например, целесообразность инвестирования средств в разные рисковые проекты, участие в лотерее, планирование запасов лекарств в медицинских заведениях и т.д. Субъективная вероятность определяется с помощью соответствующих местных экспертиз. 

     Читайте также: Как написать CV для поступления за границу?

    Как рассчитать вероятность?

    Если вам нужно применить теорию вероятностей на практике, можете воспользоваться следующим алгоритмом расчетов:

        1. Определите одно событие с одним результатом. Сначала необходимо определиться с вероятностью, которую вы хотите рассчитать. Например, вам нужно узнать вероятность того, что в бросании кубика выпадет двойка. 

        2. Узнайте общее количество сценариев, которые могут наступить. Во время первого шага вы определили событие. Если обратиться к примеру с бросанием игрального кубика, то общее количество сценариев равно шести, поскольку на кубике шесть чисел. Таким образом, выпадение двойки может иметь шесть разных сценариев.

        3. Поделите количество событий на количество возможных сценариев. Выпадение двойки во время первого бросания кубика – это одно событие. Выходит, что вероятность выпадения двойки составляет 1/6, а вероятность того, что двойка не выпадет, равна 5/6. В результате получаем 1/5 или 20% – шанс выпадения двойки во время первого броска. 

    А как рассчитать вероятность с несколькими случайными событиями? Ваши шаги следующие:

        1. Определите каждое из событий, с которыми вы будете работать. Скажем, вам нужно найти вероятность выпадения четверки на каждом из двух разных кубиков.

        2. Рассчитайте вероятность для каждого события отдельно. Она составит 1/6. Это позволит определить также вероятность одновременного выпадения четверки на двух кубиках.

        3. Перемножьте все вероятности. В нашем примере с кубиком 1/6×1/6 = 1/36 – шансы, что четверка выпадет на двух кубиках одновременно. 

    Рассмотрим это наглядно с помощью схемы:

    Если вам сложно разобраться с теорией вероятности самостоятельно, всегда можно обратиться к репетитору. Профессиональный педагог покажет, как эта теория работает для решения реальных жизненных и профессиональных заданий. Вы сможете не только открыть для себя этот полезный раздел математики, но и применить его в работе и практических ситуациях. Найти преподавателя поможет сервис BUKI, где быстро и результативно можно подобрать педагога под ваши потребности. 

     Читайте также: Свойства и формулы логарифмов

    Формула вероятности: примеры

    Классическая иллюстрация вероятности выглядит так:

    при условии, что . 

     

    Пример 1

    Эту формулу применяем в теореме сложения вероятностей. Например: в ящике находится 50 карточек, из них 15 имеют рисунки, а 8 – написанные на них слова. Остальные 27 без каких-либо изображений. После перемешивания с ящика вслепую достают карточку. Какая вероятность того, что вынутая карточка будет иметь изображение? 

    Р(С) = Р(А) + Р(В) = 15/50 + 8/50 = 23/50, или 0,46.

     

    Пример 2 – задачи на противоположные события.

    Есть два игральных кубика, которые бросают один раз. Нужно рассчитать вероятность того, что хотя бы один раз выпадет цифра 6. 

    Р(А+В) = Р(А) + Р(В) – Р(АВ), где А – это возможность такого выпадения на первом кубике, В – возможность выпадения на втором кубике. 

    1/6 + 1/6 – 1/36 = 11/36. 

     

    Пример 3

    Есть ящик с 6 желтыми и 4 зелеными кубиками. Необходимо определить вероятность доставания желтого кубика с другого раза при условии, что первым достали зеленый кубик. Имеем дело с условной вероятностью. Сначала определим: Дальше по формуле:

    Получаем:

     

    Пример 4

    Обратимся к теории умножения вероятностей. Имеем числа от 1 до 13. Известно, что выбранное из этой последовательности число парное. Необходимо найти вероятность того, что это число будет кратно 3.

    Формула вероятности будет иметь такой вид:

     

     Пример 5

    В магазине реализуется продукция трех фирм, и доля каждой составляет: 1-й фирмы – 50%, 2-й фирмы – 30%, 3-й фирмы – 20%. Для продукции каждой из фирм брак составляет: для 1-й фирмы – 2%, для 2-й фирмы – 3%, 3-й фирмы – 5%. Какая вероятность того, что наугад приобретенная в магазине единица продукции имеет хорошее качество?

    Далее, исходя из формулы полной вероятности

    имеем: P(A) = 5,0 ⋅ 98,0 + 3,0 ⋅ 97,0 + 2,0 ⋅ 95,0 = 0, 971.

    Читайте также: Геометрическая прогрессия: объяснение и формулы

Понимание математической вероятности — определение, формула и как ее найти

В этой статье

  1. Что такое Вероятность?

  2. Как измеряется вероятность?

  3. Как записывать вероятности

  4. Основные термины, которые вы должны знать

  5. Формула вероятности

  6. Как рассчитать вероятность с помощью формулы вероятности

  7. Теоремы о вероятности

  8. Типы вероятности

  9. Решения проблем с упражнениями

Что такое вероятность?

Вероятность – это изучение вероятности. Какова вероятность того, что завтра будет дождь? Каковы шансы, что вам выпадет карманная пара в игре в покер? Какова вероятность зарабатывать на жизнь концертирующим пианистом? На все эти вопросы может помочь ответить вероятность.

Как измеряется вероятность?

Мы измеряем вероятность по шкале от 0 до 1, где 0 и 1 представляют уверенность.

Вероятность 0 указывает на то, что событие определенно не произойдет, а вероятность 1 указывает на то, что событие обязательно произойдет.

Однако мало что в жизни происходит с уверенностью. Большинство событий и утверждений о мире связаны с некоторой степенью неопределенности или случайности. Вероятность неопределенных событий находится где-то между 0 и 1. Чем ближе вероятность к 0, тем меньше вероятность того, что это произойдет. Чем ближе вероятность к 1, тем больше вероятность того, что это произойдет.

Как записывать вероятности

Вот три вещи, которые нужно знать о выражении вероятностей:

1. Десятичные числа, проценты или дроби

Мы можем выражать вероятности, используя десятичные дроби, проценты или дроби.

Вы можете легко преобразовать вероятность из десятичной дроби в дробную, поместив десятичную дробь над ее разрядным значением (0,2 = 210=⅕\frac{2}{10} = ⅕102​=⅕ или 0,02 = 2100=150)\frac{2 {100} = \frac{1}{50})1002​=501​).

Вы можете преобразовать вероятность из десятичной дроби в проценты, умножив десятичную дробь на 100 (0,2 x 100 = 20%).

Примеры

2. Шанс

Вы можете использовать слово «шанс» как синоним слова «вероятность».

Примеры

Вероятность дождя завтра 40% = Вероятность дождя завтра 40%.

3. Шансы

Вы не можете использовать слово «шансы» как синоним слова «вероятность».

Шансы и вероятность — связанные понятия, но они разные. Мы рассчитываем шансы, взяв отношение двух вероятностей: вероятности того, что событие произойдет, и вероятности того, что оно не произойдет. Осторожно, не путайте вероятности с шансами.

Примеры

Основные термины, которые вы должны знать

Ниже приведены некоторые основные термины, которые вы должны знать, прежде чем работать с вероятностями.

1. Случайный эксперимент

Случайный эксперимент — это процесс, который вы можете повторять снова и снова, и вы не можете с уверенностью предсказать результат. Каждое повторение эксперимента должно происходить в одних и тех же условиях и иметь идентичный набор возможных результатов. Когда вы повторно запускаете случайный эксперимент, каждое повторение называется испытанием.

Пример

Бросание игральной кости или подбрасывание монеты — хорошие примеры случайных экспериментов. Бросание игральной кости — это процесс, который вы можете повторять снова и снова, как и подбрасывание монеты. Каждый раз, когда вы бросаете кубик, есть шесть возможных результатов, и результаты неопределенны — вы можете бросить 1, 2, 3, 4, 5 или 6. Каждый раз, когда вы подбрасываете монету, есть два возможных результата, и результаты неопределенны — вы можете перевернуть орел или решку.

2. Итоги

Исходы – это результаты случайного эксперимента. Результаты являются взаимоисключающими, то есть вы можете наблюдать только один результат за раз.

Пример

Есть шесть возможных исходов, когда вы бросаете кубик: 1, 2, 3, 4, 5 и 6. Эти исходы взаимоисключающие, потому что вы не можете выбросить 1 одновременно с 6. При каждом броске вы наблюдать только один из шести исходов.

3. Пространство для образцов

Выборочное пространство — это множество всех возможных результатов. Обычно мы обозначаем выборочное пространство, используя обозначение множества (т. е. фигурные скобки {}) или диаграмму Венна.

Пример

Пространство выборки при броске одной кости равно {1, 2, 3, 4, 5, 6}. Точно так же пример пространства при штрафном броске: {сделал, промахнулся}.

4. Благоприятные исходы

Благоприятные исходы — это исходы в выборочном пространстве, для которых вы вместе хотите рассчитать вероятность.

Пример

Если вы хотите рассчитать вероятность выпадения 2 при бросании игральной кости, есть только один благоприятный исход — 2. Если вы хотите рассчитать вероятность выпадения четного числа, есть три благоприятных исхода: 2, 4 и 6. Если вы хотите рассчитать вероятность выпадения числа меньше 6, есть пять благоприятных исходов: 1, 2, 3, 4 и 5.

5. Событие

Событие — это подмножество выборочного пространства, которому можно присвоить вероятность. Как и в случае с выборочными пространствами, мы часто обозначаем события, используя систему обозначений (например, фигурные скобки {}) или диаграмму Венна.

Примеры

В эксперименте, где вы бросаете кубик, «выпадение 5» — это событие, «выпадение четного числа» — это событие, «выпадение нечетного числа» — это событие и так далее.

При вытягивании карты из колоды игральных карт событием является:

Формула вероятности

В математике вероятности, которые проще всего рассчитать, связаны с экспериментами, в которых имеется ряд различных и равновероятных исходов.

В таких случаях вычислить вероятность событий несложно! Вы просто подсчитываете количество благоприятных исходов и делите его на общее количество возможных исходов.

Формула вероятности для равновероятных исходов

Вероятность события = количество благоприятных исходовОбщее количество возможных исходов\frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}}Общее количество возможных исходовКоличество благоприятных исходов​

Как оказалось, многие вероятностные ситуации предполагают равновероятные исходы, поэтому эта формула невероятно полезна для расчета вероятностей.

Как рассчитать вероятность с помощью формулы вероятности

Подбрасывание монеты, бросание игральных костей и вытягивание карт являются примерами случайных экспериментов, в которых возможные результаты равновероятны. Это означает, что мы можем применить формулу вероятности.

Ниже приведены несколько примеров и практических задач того, как можно применить уравнение вероятности к подбрасыванию монеты, бросанию игральной кости и извлечению карт из колоды.

Подбрасывание монеты

При подбрасывании монеты возможны два равновероятных исхода, поэтому пространство выборки (множество всех возможных исходов) равно:

S= {орел, решка} или {H, T}

Используя формулу вероятности, мы можем найти вероятность события «выпадение решки». Количество благоприятных исходов, связанных с этим событием, равно 1, а общее количество возможных исходов равно 2.

P(T) = Вероятность того, что монета выпадет решкой = Количество благоприятных исходовОбщее количество возможных исходов\frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}}Общее число возможных исходовКоличество благоприятных исходов = ½ или 0,5

То же самое касается определения вероятности выпадения орла.

P(H) = Вероятность того, что монета выпадет орлом = Количество благоприятных исходовОбщее количество возможных исходов\frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}}Общее число возможных исходовЧисло из Благоприятные исходы​ = ½ или 0,5

Используя формулу вероятности, посмотрите, сможете ли вы найти вероятность выпадения орла или решки при подбрасывании монеты. Прокрутите эту статью до конца, чтобы увидеть правильный ответ.

Игра в кости

При бросании игральной кости существует шесть равновероятных исходов, поэтому выборочное пространство равно:

S = {1, 2, 3, 4, 5, 6}

Используя формулу вероятности, найдем вероятность выпадения числа меньше 3. числа на кубике, которые меньше 3, равны 1 и 2, поэтому вероятность выпадения числа меньше 3 равна вероятности выпадения 1 или 2.

P(1 или 2) = Вероятность выпадения числа меньше 3 = Количество благоприятных исходовОбщее количество возможных исходов=26\frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}} = \frac{2}{6}Общее Количество Возможных ИсходовКоличество Благоприятных Исходов​=62​ = или 0,3333

Используя формулу вероятности, посмотрите, сможете ли вы найти вероятность выпадения нечетного числа. Прокрутите эту статью до конца, чтобы увидеть правильный ответ

. Игральные карты

Теперь давайте подумаем о вытягивании одной карты из колоды игральных карт. Вы с равной вероятностью вытянете любую карту из колоды; все возможные исходы равновероятны. В колоде 52 карты, так что в ячейке образца есть 52 возможных исхода.

Выпадение двойки червей

Какова вероятность выпадения двойки червей при данном пространстве выборки? Так как во всей колоде только одна двойка червей, количество благоприятных исходов равно 1.

Как мы уже определили, общее количество возможных исходов равно 52.

P(2♥) =Количество благоприятных исходовОбщее количество возможных исходов=152\frac{\text{Количество благоприятных исходов}}{\text{ Общее количество возможных исходов}} = \frac{1}{52}Общее число возможных исходовКоличество благоприятных исходов=521​ = 0,019

Вытягивание 2 любой масти

Как насчет вероятности выпадения двойки независимо от подходить? В данном случае в колоде четыре двойки, значит, благоприятных исходов 4.

P(2) = Количество благоприятных исходовОбщее количество возможных исходов=452\frac{\text{Количество благоприятных исходов}}{\text{Общее число возможных исходов}} = \frac{4}{52}Всего Количество возможных исходовКоличество благоприятных исходов=524=0,019

Вытягивание алмаза

Какова вероятность выпадения алмаза? Если вы посчитаете бриллианты в ячейке образца, вы увидите, что в колоде есть 13 карт, которые являются бриллиантами.

P(♦) = количество благоприятных исходов. Общее количество возможных исходов = 1352 \ frac {\ text {Количество благоприятных исходов}} {\ text {Общее число возможных исходов}} = \ frac {13} {52} Итого Количество возможных исходовКоличество благоприятных исходов=5213​= ¼ = 0,25

Вытягивание бубна или пики

Какова вероятность вытягивания бубна или пики? В колоде 13 бубнов и 13 пик. Таким образом, всего у этого события есть 26 благоприятных исходов.

P(♦ или ♠ ) = Количество благоприятных исходовОбщее количество возможных исходов=2652\frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}} = \frac{26}{52 } Общее количество возможных исходовКоличество благоприятных исходов=5226​= ½ = 0,5

Практические задачи

Чтобы проверить себя, посмотрите, сможете ли вы найти следующие вероятности, и прокрутите эту статью до конца, чтобы убедиться, что вы правы.

  • Какова вероятность вытянуть черную карту?

  • Какова вероятность того, что выпадет лицевая карта (валет, дама или король)?

  • Какова вероятность того, что выпадет пика, черва или бубна?

Теоремы о вероятности

Вы сможете применять формулу вероятности с большей легкостью и к более широкому кругу задач, если изучите следующие теоремы.

Правило сложения

Формула правила сложения:

P(A или B)=P(A) + P(B) — P(A и B)\text{P(A или B)} = \text{P(A) + P(B) — P (A и B)}P(A или B)=P(A) + P(B) — P(A и B)

Правило сложения гласит, что вероятность события A или события B равна вероятности события A плюс вероятность события B минус вероятность пересечения событий A и B.

Один из способов описать взаимосвязь между событиями — использовать термин «пересечение», один из четырех распространенных примеров операций над множествами.

Пересечение A и B состоит из исходов, которые входят как в Событие A, так и в Событие B. Пересечение двух событий обозначается словом «и» или символом ⋂.

Простой способ продемонстрировать правило сложения — вернуться к нашей колоде карт.

Колода карт Пример

Напомним, что пространство выборки:

Воспользуемся правилом сложения, чтобы найти вероятность того, что выпадет двойка или ромб. Правило сложения гласит:

P(2 или ♦)=P(2) + P(♦)−P(2 и ♦)\text{P(2 или} ♦) = \text{P(2) + P }(♦) — \text{P(2 и} ♦)P(2 или ♦)=P(2) + P(♦)−P(2 и ♦)

Мы уже нашли P(2) и P( ♦) выше. P(2) равнялось 4/52, а P(♦) равнялось 1352\frac{13}{52}5213​. Чтобы применить правило сложения, все, что нам нужно сделать, это найти пересечение двух событий P(2⋂♦).

Если вы посмотрите на выборочное пространство, вы увидите, что есть один результат, который является одновременно 2 и ромбом (двойка бубнов), поэтому P(2⋂♦)=152\frac{1}{52 }521​. Теперь, когда у нас есть P(2), P(♦) и пересечение P(2⋂♦), мы можем подставить каждую вероятность в формулу правила сложения.

P(2 или ♦)=452+1352−152=1652=0,308\text{P(2 или }♦) = \frac{4}{52} + \frac{13}{52} — \frac{ 1}{52} = \frac{16}{52} = 0,308P(2 или ♦)=524​+5213​−521​=5216​=0,308

Зачем нам нужно вычитать пересечение при использовании сложения правило?

Что ж, если мы вернемся к нашему уравнению вероятности, общее правило все еще применимо. Чтобы найти вероятность выпадения 2 или a♦, нам нужно подсчитать все благоприятные исходы (исходы, которые являются 2 или ♦) и разделить их на общее количество исходов.

Проблема в том, что если мы посчитаем все двойки (в колоде четыре двойки) и все ♦ (в колоде тринадцать бубнов), и если мы сложим эти два числа вместе (4+13 ), мы дважды считаем 2 бубна! Вычитание пересечения гарантирует, что мы не будем учитывать дважды ни один из благоприятных исходов.

Вы могли заметить, что выше мы уже рассчитывали подобные вероятности без использования правила сложения. Мы рассчитали вероятность выпадения 1 или 2, P(1 или 2), и мы рассчитали вероятность выпадения бубна или пики, P(♦ или ♠). В обоих этих случаях пересечение двух событий было равно нулю.

При броске кубика нет результатов, связанных с выпадением 1 и 2. Точно так же невозможно вытянуть карту из колоды, которая одновременно является бубном и пикой. Поскольку перекресток пуст, нам не нужно было беспокоиться о двойном учете результатов.

P(1 или 2)=P(1) + (P(2) + P(1 и 2) = P(1) + P(2)+0\text{P(1 или }2) = \ text{P(1) + (P(2) + P(1 и 2)} = \text{P(1) + P(2)} + 0P(1 или 2)=P(1) + (P( 2) + P(1 и 2)=P(1) + P(2)+0

Практические задачи

Посмотрите, сможете ли вы использовать правило сложения для расчета следующих вероятностей. Прокрутите вниз до конца этой статьи, чтобы убедиться, что вы правы.

Какова вероятность того, что из колоды вытащат короля или красную карту? Подсказка: вы ищете P (король или красное).

Какова вероятность вытянуть красную карту или пику?

Правило дополнения

Дополнением к событию А является то, что А не происходит. cAc.

Правило дополнения гласит, что вероятность события A и вероятность его дополнительного события A’ будут в сумме равны 1.

P(A) + P(A’)=1\text{P(A) + P(A’)} = 1P(A) + P(A’)=1

Мы можем проверить это с помощью нашего кубика. . Вероятность выпадения двойки плюс вероятность того, что двойка не выпадет, равна:

P(2) + P(2′) = P(2) + P(1, 3, 4, 5, 6) = 16+56\frac{1}{6} + \frac{5}{6}61 ​+65​ = 1

Интуитивно это должно иметь смысл. Дополнение события содержит все исходы, которых нет в исходном событии. Следовательно, вероятность P(A) + P(A’) на самом деле является вероятностью выбора результата из всего пространства выборки. Это вероятность выпадения любого из шести чисел на кубике. Шанс сделать это равен 1 или уверенности.

Условное правило

Условное правило можно применять, когда вы хотите найти вероятность того, что какое-то событие произойдет при условии (или при условии, что) другое событие также произошло. Обозначение условной вероятности — P(A|B). Это вероятность того, что событие А произойдет при условии, что произошло В.

Условное правило гласит, что P(A|B) равно вероятности пересечения A и B, деленной на вероятность B.

P(A|B) = P(A и B)P(B)\text{P(A|B) = }\frac{P(\text{A и B)}}{P(B)} P(A|B) = P(B)P(A и B)​

Аналогично, если мы ищем вероятность B при заданном A, условное правило будет выглядеть так. Обратите внимание, что числитель тот же, но знаменатель уравнения равен P(A) вместо P(B).

P(B|A) = P(A и B)P(A)\text{P(B|A) =}\frac{P(\text{A и B)}}{P(A)} P(B|A) = P(A)P(A и B)​

Пример карт

Вернемся к нашим картам. Какова вероятность того, что выпадет туз, если вы вытянули трефу? Это P(Туз|♣).

P(Туз|♣)=P(Туз и ♣)P(♣)=1521352=113=0,077\text{P(Туз|♣)}=\frac{\text{P(Туз и ♣)}} {\ text {P (♣)}} = \ frac {\ frac {1} {52}} {\ frac {13} {52}} = \ frac {1} {13} = 0,077 P(Ace|♣)=P(♣)P(Ace и ♣)​=5213​521​=131​=0,077

Туз и ♣” имеет только один благоприятный исход (туз треф, A♣). Следовательно, вероятность пересечения P(Туз и ♣) равна 152\frac{1}{52}521​. Вероятность P(♣) = 1352\frac{13}{52}5213​, а условная вероятность P(Ace|♣) равна 152\frac{1}{52}521​, деленное на 1352\frac{13} {52}5213​ или 113\frac{1}{13}131​.

Другой способ думать об этом таков. Если вы знаете, что вытянули трефу, пространство выборки, по сути, сократилось с 52 карт до 13. Вы знаете, что не выбрали ни одну из других мастей. Теперь у вас есть тринадцать возможных карт вместо первоначальных 52. Из этих тринадцати карт есть только один благоприятный исход — туз. Следовательно, P(Ace|♣) равно 113\frac{1}{13}131​.

Используйте условное правило, чтобы узнать, сможете ли вы найти вероятность вытягивания трефы при условии, что вы вытянули туз, P(♣|Туз). Осторожный! Это не то же самое, что P(Ace|♣). Прокрутите вниз до конца этой статьи, чтобы проверить свой ответ.

Правило умножения

Правило умножения — это перестановка условного правила. Правило гласит, что вероятность пересечения A и B, P(A и B), равна условной вероятности A при заданном B, P(A|B), умноженной на вероятность B, P(B) . Это просто перестановка условного правила для P(A|B).

P(A и B)=P(A|B) x P(B)\text{P(A и B)} = \text{P(A|B) x P(B)}P(A и B)=P(A|B) x P(B)

Поскольку P(B|A) = P(A и B)P(A)\text{P(B|A) = }\frac{P( \text{A и B)}}{P(A)}P(B|A) = P(A)P(A и B)​, мы также можем записать правило умножения в виде:

P(A и B)=P(B|A) x P(A)\text{P(A и B)} = \text{P(B|A) x P(A)}P(A и B)=P(B|A) x P(A)

Вы также можете ознакомиться с более подробной информацией о многих из этих основных правил ниже.

Типы вероятности

Последнее, что вам нужно знать, чтобы получить общее представление о вероятности, это то, что существуют разные подходы к изучению вероятностей. Когда мы применяли формулу вероятности, мы фактически использовали теоретическую или классическую вероятность. Однако бывают случаи, когда пространство выборки или вероятность результатов неизвестны. Если это так, мы можем подойти к вероятности несколько иначе.

Теоретическая вероятность

Теоретическая (или классическая) вероятность имеет дело с экспериментами с несколькими возможными исходами, которые все равновероятны. Теоретическая вероятность может быть применена к широкому кругу задач. Тем не менее, ее нельзя использовать в качестве общей теории вероятностей, потому что ее нельзя применять в случаях, когда у нас нет достаточной информации о пространстве выборки и вероятности результатов. Его нельзя использовать в тех случаях, когда вероятность наступления всех исходов не одинакова.

Частотная интерпретация вероятности

Частотная (или эмпирическая) интерпретация вероятности использует фактические испытания и наблюдения для оценки вероятностей. В экспериментальной вероятности человек начинает без предварительных убеждений о вероятности результатов. Скорее, чтобы оценить вероятности, они повторяют эксперименты снова и снова, присваивая вероятности событиям на основе относительной частоты, с которой они наблюдают определенные результаты.

В качестве упрощенного примера предположим, что человек выполняет сто штрафных бросков, и он делает 75. В этом случае частотник оценит, что вероятность того, что этот человек сделает штрафной бросок, составляет 75/100 или 0,75. Чем больше испытаний проводится, тем точнее считаются оценки.

Байесовская интерпретация вероятности

Байесовские (или субъективные) интерпретации вероятности включают индивидуальные представления о вероятности. С байесовской точки зрения вероятность — это разумное ожидание человека относительно вероятности события.

Это может показаться совершенно ненаучным подходом к вероятности. По сути, это говорит о том, что вероятности — это то, чем люди верят в них. Однако байесовцы утверждают, что субъективные представления о вероятности можно подвергнуть проверке и что, если люди строят свои убеждения рационально, субъективная вероятность соответствует основным правилам вероятности и может обновляться по мере появления новой информации и свидетельств о событиях.

Решения задач упражнения

Подбрасывание монеты

Вероятность выпадения орла или решки при подбрасывании монеты:

= P(H или T)=Количество благоприятных исходовОбщее количество возможных исходов=22\text{P(H или T)} = \frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов }}= \frac{2}{2}P(H или T)=общее количество возможных исходовКоличество благоприятных исходов=22​ = 1

Бросание игральной кости

Вероятность выпадения нечетного числа:

= P(НЕЧЕТНОЕ)=Количество благоприятных исходовОбщее количество возможных исходов=36\text{P(НЕЧЕТНОЕ)} = \frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}}= \ frac{3}{6}P(ODD)=Общее Количество Возможных ИсходовКоличество Благоприятных Исходов = 63​= 0,5

Вытягивание карты

Задача 1

Вероятность вытянуть черную карту:

= P(черный)=Количество благоприятных исходовОбщее количество возможных исходов=2652\text{P(черный)}= \frac{\text{Количество благоприятных исходов}}{\text{Общее количество возможных исходов}} = \ frac{26}{52}P(Black)=Общее Количество Возможных ИсходовКоличество Благоприятных Исходов = 5226​ = 0,5

Задача 2

Вероятность вытянуть лицевую карту (валет, дама или король):

= P(лицевая карта)=количество благоприятных исходовОбщее количество возможных исходов=1252\text{P(лицевая карта)}= \frac{\text{количество благоприятных исходов}}{\text{общее количество возможных исходов}} = \frac{12}{52}P(Face Card)=Общее Количество Возможных ИсходовКоличество Благоприятных Исходов = 5212​ = 0,231

Задача 3

Вероятность выпадения пики, червы или бубна:

= P(♠ или ♥ или ♦)=Количество Благоприятных ИсходовОбщее Количество Возможных Исходов=3952\text{P(♠ или ♥ или ♦)}= \frac{\text{Число благоприятных исходов}}{\text{Общее количество возможных исходов}} = \frac{39}{52}P(♠ или ♥ или ♦) = Общее количество возможных исходовКоличество благоприятных исходов=5239​ = ¾ =0,75

Применение правила сложения к взятию карты

Задача 1

Вероятность вытягивания короля или красной карты:

=P(Король или Красная)=\text{P(Король или Красная)} =P(Король или Красный)

=P(Король)+P(Красный)−P(Король⋂Красный)=\text{P(Король)} + \text{P(Красный)} — \text{P(Король} ⋂ \ text{Красный)} =P(Король)+P(Красный)−P(Король⋂Красный)

=452+2652−252=\frac{4}{52} + \frac{26}{52} — \frac{2}{52} =524​+5226​−522​

=2852=\ frac{28}{52}=5228​

= 0,538

Задача 2

Вероятность вытянуть красную карту или пику:

=P(Красный или ♠)=\text{P(Красный или }♠) =P(Красный или ♠)

=P(Красный) + P(♠)−P(Красный⋂♠)= \text{P( Красный) + P}(♠) — \text{P(Красный} ⋂ ♠) =P(Красный) + P(♠)−P(Красный⋂♠)

=2652+1352−0= \frac{26} {52} + \frac{13}{52} — 0 =5226​+5213​−0

=3952= \frac{39}{52}=5239​

Обратите внимание, что вероятность пересечения P(Red ⋂ ♠) здесь равна 0. Это потому, что нет красных карточек, которые также являются ♠s. Невозможно нарисовать красную лопату!

Применение условного правила к извлечению карты

P(Туз|♣)=P(Туз и ♣)P(♣)=152452=14=0,25\text{P(Туз|♣)}=\frac{\text{P(Туз и ♣)}} {\ text {P (♣)}} = \ frac {\ frac {1} {52}} {\ frac {4} {52}} = \ frac {1} {4} = 0,25P (туз | ♣) =P(♣)P(Туз и ♣)​=524​521​=41​=0,25

Узнайте об отмеченных наградами курсах Outlier For-Credit

Outlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа.

Ознакомьтесь с этими связанными курсами:

Введение в статистику

Изучите курс

Введение в статистику

Как данные описывают наш мир.

Обзор курса

Введение в микроэкономику

Знакомство с курсом

Введение в микроэкономику

Почему маленькие решения имеют большое значение.

Изучить курс

Введение в макроэкономику

Изучить курс

Введение в макроэкономику

Как деньги движут нашим миром.

Изучить курс

Введение в психологию

Изучить курс

Введение в психологию

Наука о разуме.

Обзорный курс

3.2: Комбинирование вероятностей с «И» и «Или»

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    22318
    • Макси Иниго, Дженнифер Джеймсон, Кэтрин Козак, Майя Ланзетта и Ким Сониро Community College 9
      • 9000 Community College

    Многие вероятности в реальной жизни предполагают более одного исхода. Если мы возьмем одну карту из колоды, мы можем захотеть узнать вероятность того, что она либо красная, либо валет. Если мы посмотрим на группу студентов, мы можем захотеть узнать вероятность того, что у одного из них каштановые волосы и голубые глаза. Когда мы объединяем два исхода, чтобы сделать одно событие, мы связываем исходы словом «и» или словом «или». Очень важно по вероятности обратить внимание на слова «и» и «или», если они встречаются в задаче. Слово «и» ограничивает поле возможных исходов только теми исходами, которые одновременно удовлетворяют более чем одному событию. Слово «или» расширяет поле возможных исходов до тех, которые удовлетворяют одному или нескольким событиям.

    Пример \(\PageIndex{1}\): подсчет учащихся

    Предположим, учитель хочет узнать вероятность того, что один ученик в его классе из 30 учеников изучает либо искусство, либо английский язык. Она просит класс поднять руки, если они берут искусство, и насчитала 13 рук. Затем она просит класс поднять руки, если они изучают английский язык и насчитали 21 руку. Затем учитель вычисляет

    \[P(\text{искусство или английский}) = \dfrac{13+21}{30} = \dfrac{33}{30} \nonumber \]

    Учитель знает, что это неправильно, потому что вероятности должны быть между нулем и единицей включительно. Подумав об этом, она вспоминает, что девять студентов изучают и искусство, и английский язык. Эти ученики поднимали руки каждый раз, когда она считала, поэтому учитель считал их дважды. Когда мы вычисляем вероятности, мы должны быть осторожны, чтобы учитывать каждый результат только один раз.

    Рисунок \(\PageIndex{1}\): College Classroom (Colwell, 2013)

    Взаимоисключающие события

    Эксперимент состоит в извлечении одной карты из хорошо перетасованной колоды из 52 карт. Рассмотреть события E : карта красная, F : карта пятерка и G : карта пиковая. Карта может быть и красной, и пятеркой одновременно, но карта не может быть и красной, и пиковой одновременно. Было бы легко случайно дважды по ошибке сосчитать красную пятерку. Дважды пересчитать красную пику невозможно.

    Определение: Взаимоисключающие

    Два события являются взаимоисключающими , если у них нет общих исходов.

    Пример \(\PageIndex{2}\): Взаимоисключающее использование игральных костей

    Подбрасываются две игральные кости, и записываются разные события. Пусть события E , F и G будут следующими:

    • E = {сумма равна пяти} = {(1, 4), (2, 3), (3, 2) , (4, 1)}
    • F = {оба числа четные} = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), ( 6, 2), (6, 4), (6, 6)}
    • G = {оба числа меньше пяти} = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2) , (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4,1), (4, 2), ( 4, 3), (4,4)}
    1. Являются ли события E и F взаимоисключающими?

    Да. E и F исключают друг друга, потому что у них нет общих результатов. Невозможно сложить два четных числа, чтобы получить в сумме пять.

    1. Являются ли события E и G взаимоисключающими?

    № E и G не исключают друг друга, поскольку имеют некоторые общие результаты. Все пары (1, 4), (2, 3), (3, 2) и (4, 1) имеют суммы 5, и оба числа меньше пяти.

    1. Являются ли события F и G взаимоисключающими?

    № F и G не исключают друг друга, поскольку имеют некоторые общие результаты. Все пары (2, 2), (2, 4), (4, 2) и (4, 4) содержат два четных числа, меньших пяти.

    Правило сложения для вероятностей «ИЛИ»

    Правило сложения для вероятностей используется, когда события связаны словом «или». Помните нашего учителя в примере \(\PageIndex{1}\) в начале раздела? Она хотела узнать вероятность того, что ее ученики изучают искусство или английский язык. Ее проблема заключалась в том, что некоторых учеников она считала дважды. Ей нужно было прибавить количество студентов, изучающих искусство, к количеству студентов, изучающих английский язык, а затем вычесть количество студентов, которое она подсчитала дважды. Разделив результат на общее количество учеников, она найдет искомую вероятность. Расчет следующий:

    \[ \begin{align*} P(\text{art or English}) &= \dfrac{\# \text{ с изображением + } \# \text{ с использованием английского — } \# \text{ с обоими }}{\text{общее количество учащихся}} \\[4pt] &= \dfrac{13+21-9}{30} \\[4pt] &= \dfrac{25}{30} \приблизительно {0,833 } \end{align*} \nonumber \]

    Вероятность того, что студент изучает искусство или английский язык, составляет 0,833 или 83,3%.

    Когда мы вычисляем вероятность составных событий, связанных словом «или», мы должны быть осторожны, чтобы не посчитать одно и то же дважды. Если нам нужна вероятность вытянуть красную карточку или пятерку, мы не можем считать красные пятерки дважды. Если нам нужна вероятность того, что человек светловолосый или голубоглазый, мы не можем посчитать голубоглазых блондинов дважды. Правило сложения для вероятностей прибавляет количество светловолосых людей к количеству голубоглазых, а затем вычитает количество людей, которое мы подсчитали дважды.

    Правило сложения для вероятностей «ИЛИ»

    Если A и B являются любыми событиями, то

    \[P(A\, \text{or}\, B) = P(A) + P(B ) – Р(А\,\текст{и}\,В). \nonumber \]

    Если A и B являются взаимоисключающими событиями, то \(P(A \,\text{and}\, B) = 0\), поэтому тогда

    \[P(A \ , \text{или}\, В) = Р(А) + Р(В). \nonumber \]

    Пример \(\PageIndex{3}\): Дополнительное правило для взятия карт

    Одна карта вытягивается из хорошо перетасованной колоды из 52 карт. Найти вероятность того, что карта трефовая или фигурная.

    Решение

    Есть 13 трефовых карт, 12 лицевых карт (J, Q, K каждой масти) и 3 лицевых карты треф.

    \[ \begin{align*} P(\text{трефа или лицевая карта}) &= P(\text{клуб}) + P(\text{лицевая карта}) — P(\text{трефа и лицо карта}) \\[4pt] &= \dfrac{13}{52} + \dfrac{12}{52} — \dfrac{3}{52} \\[4pt] &= \dfrac{22}{52 } = \dfrac{11}{26} \ приблизительно {0,423} \end{align*} \nonumber \]

    Вероятность того, что карта является трефовой или лицевой, составляет приблизительно 0,423 или 42,3%.

    Пример \(\PageIndex{4}\): правило сложения для подбрасывания монеты и броска игральной кости

    Эксперимент состоит из подбрасывания монеты и последующего броска игральной кости. Найдите вероятность того, что монета выпадет решкой вверх или число равно пяти.

    Решение

    Пусть H представляет решку вверх, а T представляет решку вверх. Пример пространства для этого эксперимента S = {h2, h3, h4, h5, H5, H6, T1, T2, T3, T4, T5, T6}.

    • Монета может выпасть решкой вверх шестью способами: {h2, h3, h4, h5, H5, H6}.
    • Кубик может выпасть на пятерке двумя способами: {H5, T5}.
    • Существует один способ выпадения монеты орлом вверх и выпадения кубика на пятерке {H5}.

    \[ \begin{align*} P(\text{головы или пять}) &= P(\text{головы}) + P(\text{пять}) — P(\text{обе головы и пять} ) \\[4pt] &= \dfrac{6}{12} + \dfrac{2}{12} — \dfrac{1}{12} \\[4pt] &= \dfrac{7}{12} = \примерно {0,583} \end{align*} \nonumber \]

    Вероятность того, что монета выпадет решкой вверх или выпадет пять, составляет примерно 0,583 или 58,3%.

    Пример \(\PageIndex{5}\): Дополнительное правило для оценки удовлетворенности покупателей автомобилей

    Было опрошено 250 человек, недавно купивших автомобиль, и результаты сведены в следующую таблицу.

    Таблица \(\PageIndex{2}\): Удовлетворенность покупателей автомобилей
    х 10 х 10 х 10 х 10
    х 10 х 10 х 10 х 10
    х 10 х 10 х 10 х 10
    х 10 х 10 х 10 х 10

    Найдите вероятность того, что человек купил новую машину или остался ею не доволен.

    Решение

    \[\begin{align*} P(\text{новая машина или не устраивает}) &= P(\text{новая машина}) + P(\text{не устраивает}) — P(\ text{новая машина и не устраивает}) \\[4pt] &= \dfrac{120}{250} + \dfrac{75}{250} — \dfrac{28}{250} = \dfrac{167}{250 } \приблизительно 0,668 \end{align*} \nonumber \]

    Вероятность того, что человек купил новую машину или осталась недовольна, составляет примерно 0,668 или 66,8%.

    Независимые события

    Иногда нам нужно рассчитать вероятности составных событий, связанных словом «и». У нас есть два метода на выбор: независимые события или условные вероятности (раздел 3.3). Многократный подбрасывание монеты или бросание игральной кости — это независимые события. Каждый раз, когда вы подбрасываете правильную монету, вероятность выпадения решки равна ½. Неважно, что произошло в последний раз, когда вы подбрасывали монету. Это похоже на игру в кости. Если в прошлый раз вы выбросили двойную шестерку, это не меняет вероятности того, что в этот раз выпадет двойная шестерка. Вытягивание двух карт без замены не является самостоятельным событием. Когда вы берете первую карту и откладываете ее в сторону, вероятность второй карты теперь составляет 51 карту, а не 52 карты.

    Определение: Независимые события

    Два события являются независимыми событиями , если возникновение одного события не влияет на вероятность возникновения другого события.

    Правило умножения для вероятностей «И»: независимые события

    Если события A и B являются независимыми событиями, то \( P(\text{A и B}) = P(A) \cdot P(B )\).

    Пример \(\PageIndex{6}\): независимые события для подбрасывания монет

    Предположим, что справедливая монета подбрасывается четыре раза. Какова вероятность того, что все четыре броска выпадут орлом вверх?

    Решение

    Подбрасывание монеты является независимым событием. Информация о том, что в первом испытании была подброшена голова, не меняет вероятность того, что выпадет решка во втором испытании.

    \(P(\text{четыре решки подряд}) = P(\text{1-я решка и 2-я решка и 3-я решка и 4-я решка})\)

    \( = P(\text{1-я решка}) ) \cdot P(\text{2-й орел}) \cdot P(\text{3-й орел}) \cdot P(\text{4-й орел})\)

    \( = \dfrac{1}{2} \ cdot \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}\)

    \( = \dfrac{1}{16}\)

    Вероятность того, что все четыре броска выпадут орлом вверх, равна \(\dfrac{1}{16}\).

    Пример \(\PageIndex{7}\): Независимые события для вытягивания шариков

    В мешке пять красных и четыре белых шарика. Из мешка достают шарик, записывают его цвет и возвращают в мешок. Затем вытягивается второй шарик. Какова вероятность того, что первый шарик красный, а второй белый?

    Так как первый шарик кладут обратно в мешок до того, как вытащите второй шарик, это независимые события.

    \[\begin{align*} P(\text{1-й красный и 2-й белый}) &= P(\text{1-й красный}) \cdot P(\text{2-й белый}) \\[4pt] & = \dfrac{5}{9} \cdot \dfrac{4}{9} = \dfrac{20}{81}\end{align*} \nonumber \]

    Вероятность того, что первый шарик красный, а второй второй шарик белый — это \(\dfrac{20}{81}\).

    Пример \(\PageIndex{8}\): Независимые события для неисправных будильников

    У Эбби утром важная встреча. На всякий случай она ставит три будильника на батарейках. Если вероятность неисправности каждого будильника равна 0,03, какова вероятность того, что все три будильника выйдут из строя одновременно? 9{-5} \end{align*} \nonumber \]

    Вероятность отказа всех трех часов составляет приблизительно 0,000027 или 0,0027%. Маловероятно, что все три будильника выйдут из строя.

    Правило по крайней мере один раз для независимых событий

    Много раз нам нужно вычислить вероятность того, что событие произойдет хотя бы один раз во многих испытаниях. Расчет может стать довольно сложным, если имеется более пары испытаний. Использование дополнения для вычисления вероятности может значительно упростить задачу. Следующий пример поможет вам понять формулу.

    Пример \(\PageIndex{9}\): Хотя бы один раз Правило

    Вероятность того, что ребенок забудет домашнее задание в данный день, равна 0,15. {n}\) 9{8}\)

    \( = 1 — (0,152) = 0,848\)

    Вероятность увидеть сокола хотя бы один раз из восьми заходов на озеро составляет примерно 0,848 или 84,8%.

    Пример \(\PageIndex{11}\): Правило хотя бы один раз для угадывания в тестах с множественным выбором

    Тест с множественным выбором состоит из шести вопросов. Каждый вопрос имеет четыре варианта ответа, только один из которых правильный. Студент угадывает все шесть вопросов. Какова вероятность того, что он даст хотя бы один правильный ответ? 9{6} \\[4pt] &= 1 — (0,178) = 0,822 \end{align*} \nonumber \]

    Вероятность того, что он даст хотя бы один правильный ответ, составляет 0,822 или 82,2%.

    Вероятности «И» из двусторонних таблиц

    Вероятности «И» обычно вычисляются одним из двух методов. Если вы знаете, что события независимы, вы можете использовать правило \(P(A \text{and} B) = P(A) \cdot P(B)\). Если события не являются независимыми, вы можете использовать условные вероятности в разделе 3. 3. Существует исключение, когда у нас есть данные, приведенные в двусторонней таблице. Мы можем вычислить вероятности «и», не зная, независимы ли события или нет.

    Пример \(\PageIndex{12}\): вероятность «И» из двусторонней таблицы

    Продолжение примера \(\PageIndex{5}\):

    Двести пятьдесят человек, недавно купивших автомобиль, опрошены, и результаты сведены в следующую таблицу.

    Таблица \(\PageIndex{2}\): Удовлетворенность покупателей автомобилей
    х 10 х 10 х 10 х 10
    х 10 х 10 х 10 х 10
    х 10 х 10 х 10 х 10
    х 10 х 10 х 10 х 10

    Человек выбирается случайным образом. Найдите вероятность того, что человек:

    1. купил новую машину и остался доволен.

    \[\begin{align*} P(\text{новая машина и довольные}) &= \dfrac{\text{номер новой машины и довольные}}{\text{количество людей}} \\[4pt ] &= \dfrac{92}{250} = 0,368 = 36,8 \% \end{align*} \nonumber \]

    1. купил подержанную машину и остался недоволен.

    \[\begin{align*} P(\text{подержанный и неудовлетворенный автомобиль}) &= \dfrac{\text{количество подержанных и неудовлетворенных}}{\text{количество человек}} \\[ 4pt] &= \dfrac{47}{250} = 0,188 = 18,8 \% \end{align*} \nonumber \]

      Эта страница под заголовком 3.2: Объединение вероятностей с «И» и «Или» распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Макси Иниго, Дженнифер Джеймсон, Кэтрин Козак, Майей Ланцетта, & Kim Sonier через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *