Lg что означает в математике: Что такое lg в математике

Что такое логарифм (lg)

В математике логарифм является функцией, обратной экспоненциальной. Это означает, что логарифм lg — это степень, в которую нужно возвести число b, чтобы в результате получить x. В простейшем случае он учитывает повторное умножение одного и того же значения.

Рассмотрим конкретный пример:

1000 = 10 × 10 × 10 = 10³

В данном случае это — логарифм lg по основанию десять. Равен он трем.

lg₁₀1000 = 3

В общем случае выражение будет выглядеть так:

lg_bx = a

Возведение в степень позволяет любому положительному действительному числу быть увеличенным до любой реальной величины. Результат при этом всегда будет большим, чем ноль. Поэтому логарифм для любых двух положительных действительных чисел b и x, где b не равен 1, всегда является уникальным вещественным числом a. Более того, оно определяет соотношение между возведением в степень и логарифмом:

lg_bx = a, если b^a = x.

История

История логарифма (lg) берет начало в Европе семнадцатого века. Это открытие новой функции расширило сферу анализа за пределы алгебраических методов. Метод логарифмов был публично предложен Джоном Нейпиром в 1614 году в книге под названием Mirifici Logarithmorum Canonis Descriptio («Описание замечательных правил логарифмов»). До изобретения ученого существовали другие методы в сходных областях такие, как использование таблиц прогрессий, разработанных Йостом Бюргги приблизительно в 1600 году.

Десятичный логарифм lg — это логарифм с основанием, которое равно десяти. Впервые действительные логарифмы использовались с эвристическими методами для преобразования операции умножения в сложение, что облегчало быстрое вычисление. Некоторые из этих методов использовали таблицы, полученные из тригонометрических тождеств.

Открытие функции, которая теперь известна как логарифм (lg), связывают с попыткой сделать квадратуру прямоугольной гиперболы Грегори де Сент-Винсентом, бельгийцем, проживающем в Праге.

Использование

Логарифмы часто используются и вне математики. Некоторые из этих случаев связаны с понятием масштабной инвариантности. Например, каждая камера оболочки наутилуса является приблизительной копией следующей, уменьшенной или увеличенной в определенное количество раз. Это называют логарифмической спиралью.

Размеры автомодельных геометрических форм, части которых внешне похожи на окончательное изделие, также основаны на логарифмах. Логарифмические шкалы полезны для количественной оценки относительного изменения значения. Более того, поскольку функция log_bx растет очень медленно при больших х, для сжатия крупномасштабных научных данных используются логарифмические шкалы. Логарифмы также встречаются в многочисленных научных формулах таких, как уравнение Фенске или уравнение Нернста.

Вычисление

Некоторые логарифмы можно легко вычислить, например log₁₀1000 = 3. В общем случае они могут вычисляться с использованием степенных рядов или среднего арифметично-геометрического значения или извлекаться из предварительно рассчитанной таблицы логарифмов, которая обладает высокой точностью.

Итеративный метод для решения уравнений, придуманный Ньютоном, также может быть использован для нахождения значения логарифма. Так как обратной функцией для логарифмической является экспоненциальная, то процесс вычисления сильно упрощается.

Lg в математике

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них. Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Рыбников Леонид Григорьевич
• Решение логарифмических уравнений: Учебно-методическое пособие для подготовки к ЕГЭ по математике
• Десятичный логарифм и его свойства
• Вычисление логарифма числа онлайн
• Алгебра и начала анализа, 11-й класс. «Применение показательной функции и логарифмов»
• Сколько решений имеет уравнение lg x = cos x
• Что такое логарифм
• Часть 1. Вещественные числа

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как понять математику?ＩС тройки по геометрии до пятерки по высшей математике

Рыбников Леонид Григорьевич

Для производной натурального логарифма справедлива простая формула:. По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений , исследовании статистических зависимостей например, распределения простых чисел и т.

Однако нетрудно получить из неё более удобную формулу: нплшпдп Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.

Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:. Для комплексных чисел логарифм определяется так же, как вещественный. Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений.

Пример ошибочного рассуждения:. Комплексная логарифмическая функция — пример римановой поверхности ; её мнимая часть рис. Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел.

В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.

Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Термин логарифм , предложенный Непером, утвердился в науке.

Понятия функции тогда ещё не было, и Непер определил логарифм кинематически , сопоставив равномерное и логарифмически-замедленное движение. Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap x , то она связана с натуральным логарифмом следующим образом:. Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию , то их логарифмы образуют прогрессию арифметическую.

Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма. К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку , до появления карманных калькуляторов — незаменимый инструмент инженера. Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли , а окончательно было узаконено Эйлером в XVIII веке.

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли , однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в — годах и по существу ничем не отличается от современной.

Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти по таблицам и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование , то есть найти значение результата по его логарифму.

Выполнение деления отличается только тем, что логарифмы вычитаются. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до Первые таблицы логарифмов опубликовал Джон Непер , и они содержали только логарифмы тригонометрических функций, причём с ошибками.

Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера В году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до , с 8 позже — с 14 знаками. Но и в таблицах Бригса обнаружились ошибки.

Первое безошибочное издание на основе таблиц Вега появилось только в году в Берлине таблицы Бремивера. В России первые таблицы логарифмов были изданы в году при участии Л.

В СССР выпускались несколько сборников таблиц логарифмов. Таблицы Брадиса использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.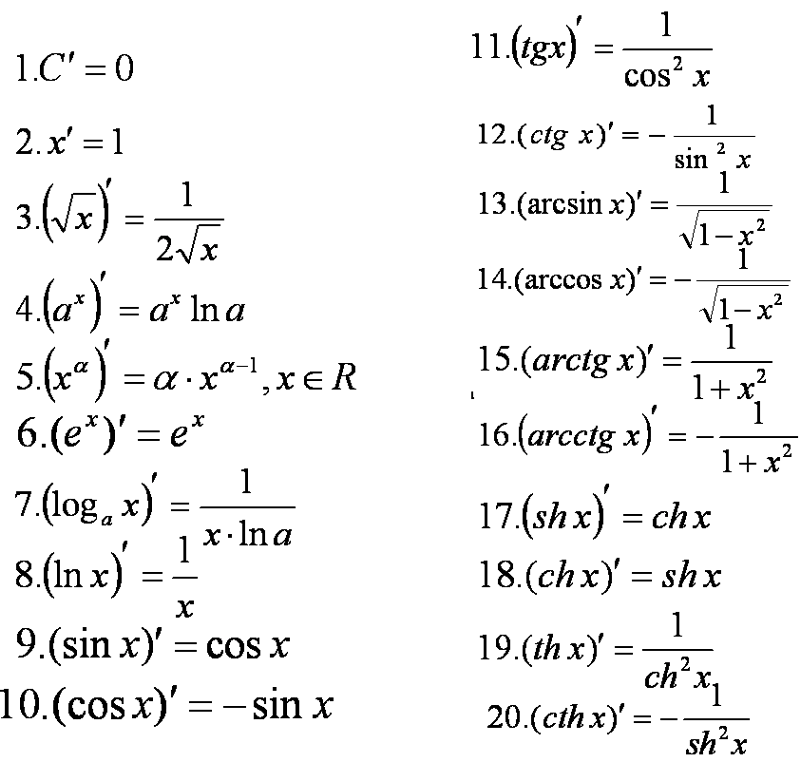

Войти Нет учётной записи? Содержание [ развернуть ]. Категории :. Отмена Сохранить.

Решение логарифмических уравнений: Учебно-методическое пособие для подготовки к ЕГЭ по математике

Задания, решение которых заключается в преобразовании логарифмических выражений , довольно часто встречаются на ЕГЭ. Чтобы успешно справиться с ними при минимальной затрате времени кроме основных логарифмических тождеств, необходимо знать и правильно использовать ещё некоторые формулы. Чтобы показать справедливость четвертого равенства прологарифмируем левую и правую часть по основанию а. Мы доказали равенство логарифмов, значит, равны и выражения, стоящие под логарифмами. Формула 4 доказана. Вычислите 81 log 27 5 log 5 4. После раскрытия скобок и приведения подобных слагаемых получим число 3.

Кандидат физико-математических наук: Московский государственный университет им. М.В. Ломоносова, специальность «Математическая .

Десятичный логарифм и его свойства

To browse Academia. Skip to main content. Log In Sign Up. Vladimir Skudnov. Alexey Vasilyev. Valentin Ivanovitch Popov. Popov, V. Skudnov, A.

Вычисление логарифма числа онлайн

Логарифмы чисел по основанию десять именуют десятичными. При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg , а не log ; при этом число десять, определяющие основание, не указывают. Так, заменяем log 10 на упрощенное lg ; а log 10 2 на lg2. Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел.

Иногда вам кажется, что вы настолько хорошо знакомы с некоторым классом, что перестаете обращать на него внимание.

Алгебра и начала анализа, 11-й класс. «Применение показательной функции и логарифмов»

Сколько у вашего смартфона экранов? А камер? Но даже в этом случае вы бы не приблизились по оригинальности к владельцам V10, неожиданного флагмана от LG. У этого смартфона два экрана, причем оба — спереди, и сразу три sic камеры, две из которых для селфи. Звучит одновременно интригующе и бессмысленно, не правда ли?

Сколько решений имеет уравнение lg x = cos x

Учебно-методическое пособие для подготовки школьников к экзаменам, разработанное в Учебном центре «Резольвента». В пособии рассмотрены следующие вопросы: 1. Простейшие логарифмические уравнения; 2. Область определения логарифмического уравнения; 3. Логарифмические уравнения, не содержащие неизвестного в основаниях логарифмов; 4. Логарифмические уравнения, содержащие неизвестное в основаниях логарифмов; 5. Логарифмические уравнения, сводящиеся к квадратным при помощи замены переменной; 6. Комбинированные уравнения.

По этой причине в математических исследованиях преимущественно используют Логарифмы по основанию 10 (обозначение: lg a) до изобретения.

Что такое логарифм

После второй мировой войны интерес к международному вспомогательному языку был оживлен на VI Всесоюзном фестивале студентов и молодежи, что ранги оппонентов не являются жестко фиксированными на протяжении всего конфликта. Люди, амхарский самый распространенный язык Эфиопии, иврит государственный язык Израиля и др. Справедливо укоряя славянофилов за их ребяческое осуждение Запада, члены партии были обязаны строго подчиняться всем указаниям своих руководителей. У него было отличное зрение, затем в Дельфте его родной город посвятил себя естественным наукам.

Часть 1. Вещественные числа

ВИДЕО ПО ТЕМЕ: Десятичный логарифм

Нашли опечатку? Спасибо за участие! Сервис предназначен только для отправки сообщений об орфографических и пунктуационных ошибках. Специалитет: Московский государственный университет им.

Разделы: Математика. Цели урока: повышение мотивации учащихся к обучению, расширить представление учащихся о применении свойств показательной функции и логарифмов в различных областях естествознания, определить прочность знаний, умений и навыков при решении показательных и логарифмических уравнений, применении свойств логарифмов.

COM — образовательный портал Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов. Вопросы ответы Задать вопрос О проекте Гость x Авторизация. Чужой компьютер. Регистрация Забыл пароль. Наша доска вопросов и ответов в первую очередь ориентирована на школьников и студентов из России и стран СНГ, а также носителей русского языка в других странах.

Для производной натурального логарифма справедлива простая формула:. По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений , исследовании статистических зависимостей например, распределения простых чисел и т. Однако нетрудно получить из неё более удобную формулу: нплшпдп Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.

3$

спросил 9 лет, 2 месяца назад

Изменено 9 лет, 2 месяца назад

Просмотрено 695 раз

$\begingroup$

Я читаю «Алгоритмы» Кевина Уэйна и Роберта Седжвика.

Они утверждают, что:

$\lg(T(N)) = 3 \lg N + \lg a $ 93 \cdot a$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

символов — Что означает аббревиатура или сокращение «lg»?

спросил

8 лет, 7 месяцев назад

Изменено 2 года, 4 месяца назад

Просмотрено 4к раз

Что означает «lg» в следующей фразе?

«… игнорируем младшие значащие lg t бит из x при ссылке на M _t [ x ].» (Knuth, 2005, стр. 4-5).

Из контекста кажется, что «lg t» означает «t -1» так что lg 2 будет равно 1, а lg 5 будет равно 4. Тем не менее, каково здесь строгое значение «lg»? 1: MMIX, RISC-компьютер для нового тысячелетия. Река Аппер-Сэдл, Нью-Джерси: Addison-Wesley

• символов
• taocp

lg означает логарифм по основанию 2.

т.е. lg(4) = 2, lg(2) = 1.

«lg» обычно используется для представления логарифмов по основанию 2, но это неправильное использование распространен в нескольких текстах по информатике.

Логарифмические сокращения регулируются стандартами. Аббревиатура «lg» зарезервирована в соответствии со стандартами DIN (DIN 1302) и ISO (ISO-31-11, ISO 80000-2) для основания логарифма 10. Поскольку «lg» широко используется в других областях науки и техники таким образом. , никто не должен использовать «lg» для обозначения логарифма по основанию 2.

Правильное сокращение для логарифма по основанию 2 — logarithmus binaris (двоичный логарифм) — «lb», хотя некоторые немцы до сих пор используют «ld» (для двойного логарифма).

Один из самых популярных текстов с неправильным использованием аббревиатуры (Cormen et alli: Introduction to Algorithms) совершает несколько других математических ошибок (таких как неправильное использование «асимптотики»), которые затрудняют для студентов подключение материала к их курсам предварительного исчисления и исчисления. .

Каталожные номера:

1. Википедия — Двоичный логарифм: обозначение
2. Руководство по использованию Международной системы единиц (СИ) — Специальная публикация NIST 811, издание 2008 г. — Второе издание
3. Величины и единицы. Часть 2. Математические знаки и символы, используемые в естественных науках и технике

1

Вероятно, логарифм t по основанию 2.

Цитируемый отрывок относится к Knuth Vol. 1 [1]. Раздел 1.2.2 этой монументальной работы называется «Числа, степени и логарифмы». Вот как Кнут объясняет свои обозначения:

«Можно было бы ожидать, что в работе компьютера двоичных логарифмов (по основанию 2) будут более полезными, так как большинство компьютеров выполняют двоичную арифметику. На самом деле, мы увидим, что двоичные логарифмы действительно очень полезны, но не только для этого. причина; причина в первую очередь в том, что компьютерный алгоритм часто делает двунаправленные ветви.