Что означает ln в математике? – Обзоры Вики
Когда вы видите ln, это означает натуральный логарифм (мы определим натуральные логарифмы ниже). В этом курсе будут использоваться только десятичные и натуральные логарифмы.
Аналогично, что такое значение ln? Ln называется натуральным логарифмом. Его также называют логарифмом по основанию e. Здесь константа e обозначает число, являющееся трансцендентным числом и иррациональным, которое приблизительно равно значению 2.71828182845. Натуральный логарифм (ln) может быть представлен как ln x или logex. .
Возможен ли журнал 0? журнал 0 не определен. Это ненастоящее число, потому что вы никогда не получите ноль, возведя что-либо в степень чего-либо другого. Вы никогда не сможете достичь нуля, вы можете приблизиться к нему только с помощью бесконечно большой и отрицательной силы. … Это потому, что любое число, увеличенное до 0, равно 1.
Может ли ln быть отрицательным? Функция натурального логарифма ln(x) определена только для x>0. Таким образом, натуральный логарифм отрицательное число не определено.
Таким образом, натуральный логарифм отрицательное число не определено.
Во-вторых, log10 такой же, как ln? Нет, log10(x) не совпадает с ln(x), хотя оба они являются специальными логарифмами, которые чаще встречаются при изучении математики, чем какие-либо…
Что такое ln и e в математике?
Натуральный бревно, или ln, является обратным e.
Буква «e» представляет собой математическую константу, также известную как натуральный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e равно примерно 2.71828. … Итак, ln(x) = loge(Икс). Например, ln (5) = loge(5) = 1.609.
Каково значение ln 10? Значение журнала от 1 до 10 для базы журнала e
| Натуральный логарифм числа (log e x) | LnValue |
|---|---|
| пер (7) | 1. 94591 94591 |
| пер (8) | 2.079442 |
| пер (9) | 2.197225 |
| пер (10) | 2.302585 |
Что такое бесконечность?
Это означает, что е увеличивается с очень высокой скоростью, когда е возводится в бесконечную степень, и, таким образом, приводит к очень большому числу, поэтому мы заключаем, что е возводится в бесконечную степень. это бесконечность. Теперь рассмотрим, когда e возводится в степень отрицательной бесконечности. ⇒ е–∞
Существует ли логарифмическая бесконечность? Ложа ∞ = ∞, или ln (∞) = ∞ Мы можем заключить, что как натуральный логарифм, так и значение десятичного логарифма для обратного бесконечности имеют одно и то же значение, т. е. бесконечность.
Что такое бесконечность?
Ответ на этот вопрос ∞ . Естественная логарифмическая функция строго возрастает, поэтому она всегда растет, хотя и медленно.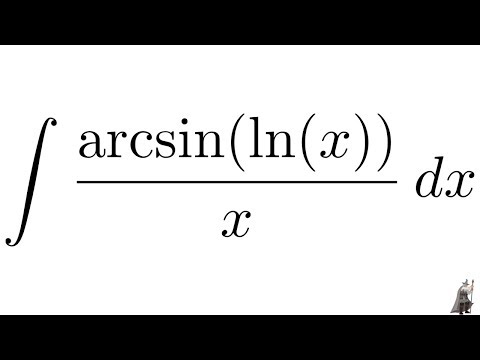 Производная y’=1x, поэтому она никогда не равна 0 и всегда положительна. Следовательно, n должно быть большим.
Производная y’=1x, поэтому она никогда не равна 0 и всегда положительна. Следовательно, n должно быть большим.
Как умножить ln? Правило продукта
- пер(х)(у) = пер(х) + пер(у)
- Натуральный логарифм произведения x и y представляет собой сумму ln x и ln of y.
- Пример: пер(8)(6) = пер(8) + пер(6)
Можете ли вы взять ln нуля?
Какой натуральный логарифм нуля? … Функция вещественного натурального логарифма ln (x) определена только для x> 0. Итак, натуральный логарифм нуля не определено.
К чему подходит ln of 0?
Таким образом, натуральный логарифм нуля равен не определено. ln(0) не определено.
Почему мы используем ln? Мы предпочитаем натуральные логарифмы (то есть логарифмы по основанию e), потому что, как описано выше, коэффициенты при натуральном логарифме шкалы непосредственно интерпретируются как приблизительные пропорциональные различия: с коэффициентом 0.06 разница в 1 в x соответствует примерно 6% разнице в y и так далее. х). Натуральный журнал — это функция «один к одному».
х). Натуральный журнал — это функция «один к одному».
Как отписаться от бывшего? Функции f(x) = ln x и g(x) = ex нейтрализуют друг друга, когда одна функция используется для результата другой. Это то же самое, что и с f(x) = log x и g(x) = 10.x или возведения числа в квадрат, а затем извлечения квадратного корня из результата.
Как упростить Lnx?
Как сокращаются ln и e?
Подставьте базовое число e в обе части уравнения. e и ln отменить друг друга оставив нам квадратное уравнение. x = 0 невозможно, так как нет возможности записать 0 как степень. Запишите левую часть как один логарифм.
Каково значение логарифма ln 52? Таблицы значений натуральных логарифмов
| журнал e (Х) | Отзывы | Значение |
|---|---|---|
| журнал e (51) | п (51) | 3.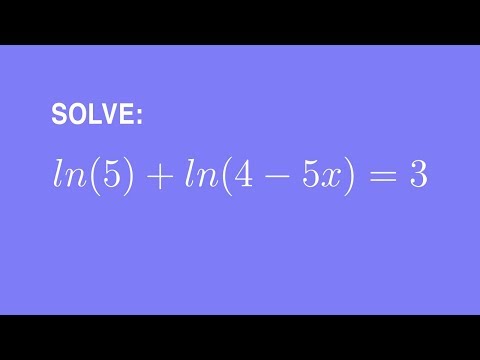 931826 931826 |
| журнал e (52) | п (52) | 3.951244 |
| журнал e (53) | п (53) | 3.970292 |
| журнал e (54) | п (54) | 3.988984 |
Что является основанием ln 3?
Кроме того, ln3 означает логарифм 3 с e в качестве основания и e = 2.71828, и, следовательно, ln3 =1.0986 (используя научный калькулятор) и, следовательно, ln3≠1 .
Что такое лн в математике
Натуральный логарифм
Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718 281 828 . Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается. [1]
Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x.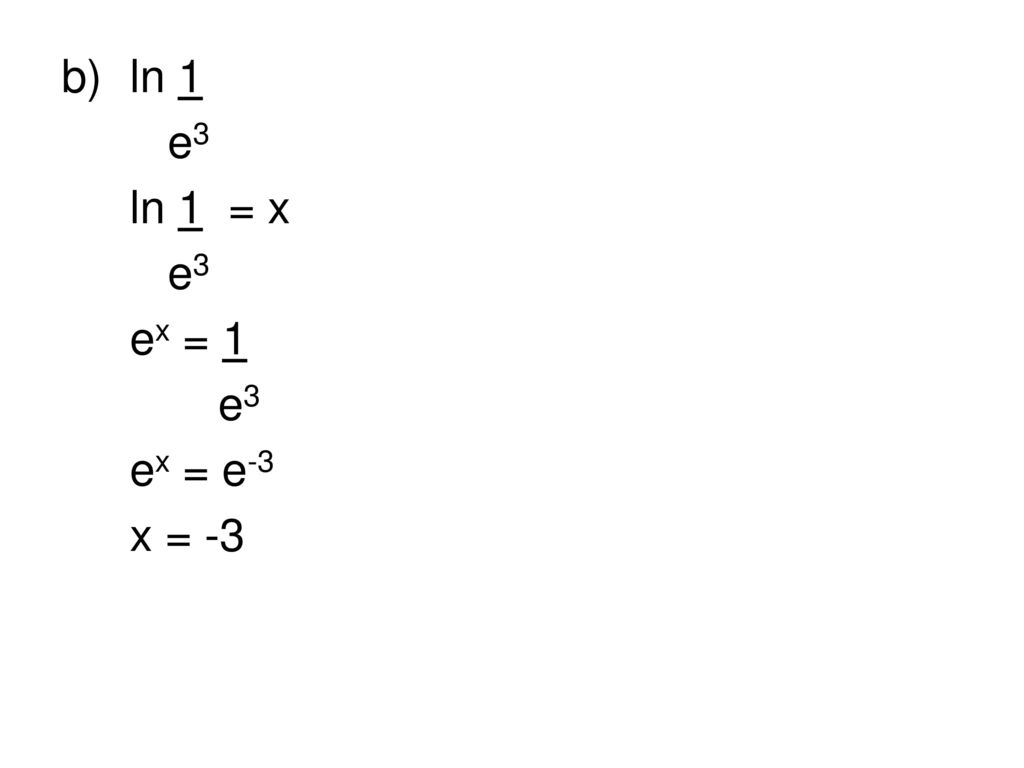 Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1.
Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:
Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:
е. как интеграл:
Это можно продемонстрировать, допуская следующим образом:
Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 < x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.
Производная натурального логарифма равна
На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:
Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.
Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:
Ниже дан пример для g(x) = tan(x):
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Перед нами — не что иное как определение логарифма.
 Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.Как считать логарифмы
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ).
 Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log2 0,5 = −1, т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Составим и решим уравнение:
log5 25 = b ⇒ (5 1 ) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - Получили ответ: 2.
Задача. Вычислите логарифм:
- Представим основание и аргумент как степень тройки: 3 = 3 1 ; 1/81 = 81 −1 = (3 4 ) −1 = 3 −4 ;
- Составим и решим уравнение:
- Получили ответ: −4.
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log4 64 = b ⇒ (2 2 ) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2 b = 6 ⇒ b = 3; - Получили ответ: 3.

- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log16 1 = b ⇒ (2 4 ) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4 b = 0 ⇒ b = 0; - Получили ответ: 0.
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1 < 14 < 7 2 ;
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log10 xВсе, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x .
 Обозначение: ln x .
Обозначение: ln x .Многие спросят: что еще за число e ? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459.Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log e xТаким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Что такое логарифм в математике и в жизни
Для многих логарифм — это самая странная часть в математике: непонятно, как их считать, где применять и как они могут пригодиться в жизни. Сегодня ответим на все эти вопросы.
Если интересно, как в математике работают остальные функции и символы, вот что у нас уже есть:
Что такое логарифм
Задача логарифма — ответить на такой вопрос:
В какую степень нужно возвести одно число, чтобы получилось другое?
На языке математики это будет выглядеть вот так:
Теперь сделаем то же самое, но уже с числами.
 Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.
Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.Десятичный, натуральный и другие логарифмы
Число A, которое возводят в какую-то степень, называется основанием логарифма. Самые популярные у математиков логарифмы — десятичный и натуральный.
Десятичный логарифм — это когда в основании логарифма стоит число 10. Наша задача в этом случае — найти, в какую степень нужно возвести 10, чтобы получить желаемое число. Обозначается так — lg:
Натуральный логарифм устроен похоже, только вместо десятки в основании логарифма стоит число e, которое примерно равно 2,71828 и называется числом Эйлера. В математике число e играет такую же важную роль, как в геометрии — число пи, поэтому логарифм по основанию e часто встречается во многих математических выкладках и доказательствах.

Обозначается натуральный логарифм так — ln:
Логарифмическая шкала
Если мы возьмём линию и отметим на ней точки через каждый сантиметр, то мы получим арифметическую шкалу. Арифметическую — потому что каждая новая отметка считается арифметическим действием — сложением шага и предыдущего значения:
Но если мы вместо сложения возьмём логарифм, например, по основанию 10, то каждая новая отметка будет зависеть от значения десятичного логарифма:
Это выглядит странно, но логарифмическая шкала постоянно применяется в экономике и маркетинге, когда нужно оценить рост или падение стоимости товара. Если взять обычную арифметическую шкалу, то разница между парами (1, 2) и (9, 10) будет одной и той же — 1 пункт.
Но при этом в первом случае цена выросла в 2 раза, с 1 до 2, а во втором случае — всего лишь на 10%. С логарифмической шкалой рост цены будет выглядеть логичнее:
Зачем нужны логарифмы в жизни
Вокруг нас и в быту мы встречаем гораздо больше логарифмов, чем кажется.
 Вот несколько примеров.
Вот несколько примеров.Децибелы, в которых измеряется относительная громкость любых звуков, считаются по десятичному логарифму. Относительная — потому что она считается от минимального порога громкости, которую только может расслышать человек. Например, если громкость звука равна 20 децибел, то это значит, что это громче самого тихого в 100 раз, а если 30 децибел — то в 1000 раз.
В химии активность водородных ионов тоже считается по логарифмической шкале.
Выдержки и диафрагмы в фотографии тоже меняются логарифмически — каждое новое значение больше или меньше предыдущего в определённое число раз.
В ракетостроении для вычисления скорости ракеты используется уравнение Циолковского. В основе этого уравнения — логарифмическая зависимость от массы ракеты с топливом и без него.
Логарифмы в природе
Больше всего логарифмов можно встретить в природе в виде логарифмической спирали. Математическая формула спирали выглядит так:
Если мы захотим построить график этого уравнения, то он будет выглядеть так:
Логарифмическая спираль в математике.

А вот логарифмическая спираль в природе — в ракушках, подсолнечнике и капусте. С капустой ещё связана другая интересная тема — фракталы, но про них поговорим в другой раз.
Даже рога у горных козлов закручиваются по логарифмической спирали:
Что дальше
Теперь мы знаем про логарифмы достаточно, чтобы понять, как они работают. В следующей статье напишем простую программу из двух циклов, которая посчитает нам практически любой логарифм по любому основанию.
Log ln в чем разница
Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718 281 828 . Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается. [1]
Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1.
Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:
Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:
е. как интеграл:
Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 < x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.
Производная натурального логарифма равна
На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:
Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.
Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:
Ниже дан пример для g(x) = tan(x):
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
вычислено, что е = 2,7182818284. .
.
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
Число е является иррациональным. Французский математик Эрмит (1822 — 1901) обосновал, что это число не может быть корнем никакого алгебраического уравнения с целыми коэффициентами. Такие иррациональные числа именуются трансцендентными.
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм, как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x. Он монотонно возрастает на своей области определения.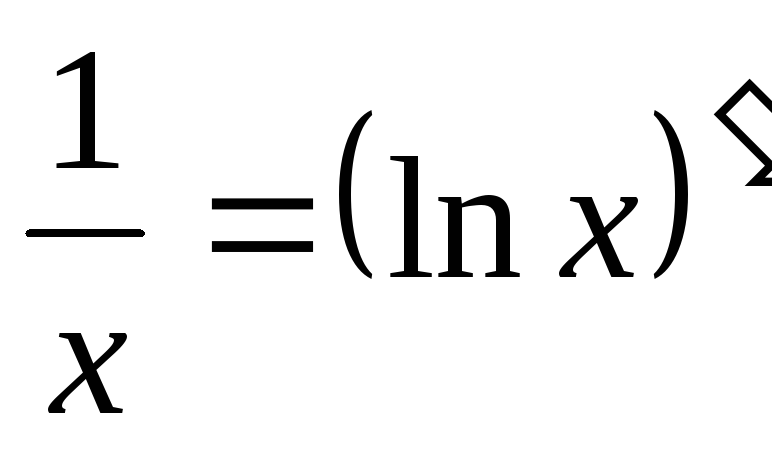
При x →0 пределом натурального логарифма выступает минус бесконечность ( –∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов.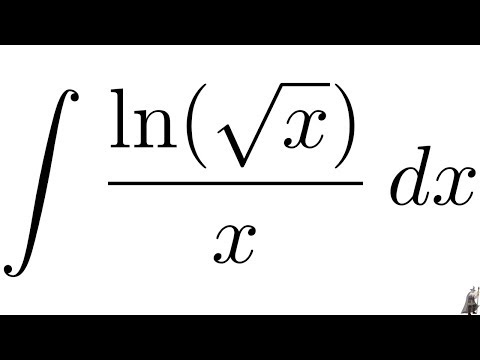 Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Что такое логарифм
Сейчас речь пойдет о трех страшных буквах: l o g.
Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?
На самом деле в этом и заключается основная формула (определение логарифма):
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c» . Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных.
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182. мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета. Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).
Два нужно четыре раза умножить само на себя, чтобы получить 16.
lg — это логарифм по основанию 10. 10 нужно 3 раза умножить само на себя, чтобы получить 1000.
А теперь посложнее, перейдем по определнию к показательному уравнению :
Следующий пример поможет нам узнать первую формулу логарифмов:
Преобразуем выражение по определению логарифма и получим показательное уравнение. Единица — это же любое значение в нулевой степени?
Тогда можно сделать вывод, что при любом основании и аргументе логарифма, равном 1, все эти логарифмы будут равны нулю.
Нетрудно тогда понять, что есть еще одно следствие:
В какую степень нужно возвести 2, чтобы получить 2? Напряжем все свои извилины и получим — один!
Дальше будут формулы, которые я позволю себе не выводить, чтобы не испугать неискушенных в математике читателей.
Хотя мой вам совет: отследить, откуда эта формула появилась. У логарифмов самое главное помнить, что логарифм — это действие, обратное возведению в степень.
Основное логарифмическое тождество:
В какую степень нужно возвести 3, чтобы получить 9? Значит, логарифм в показателе степени равен двум.
Это единственная формула, где логарифм в показатели степени. Видишь логарифм в степени? Тебе поможет только эта формула.
Еще примерчик, двойка перед логарифмом никак не влияет, формула все так же работает:
А вот квадрат в логарифме тоже быть может, только лучше сначала разложить:
Дальше с этим ничего сделать не сможем.
Дальнейшие формулы тоже уникальны, это тебе не косинус двойного угла.
Видим сложение логарифмов, выпускаем эту формулы:
А вот примерчик, чтобы порадовать тебя этой формулой, только наоборот:
Видим разность логарифмов, выпускаем эту формулы:
А теперь сразу сумма и разность. По отдельности логарифмы не найти, но вместе они и мы сила:
Теперь посмотрим на степени у аргмента логарифма:
А в основании тоже можно? Нужно!
Минус два — это степень у основания:
А все вместе можно? Конечно, логарифмы — это такая свобода:
А здесь нужно будет соединить две формулы: 1) вынесение степени из основания и 2) разность логарифмов
С основными формулами разобрались, теперь для решения более сложных уравнений/выражений.
Формула перехода к новому основанию:
Обрати внимание, чем она отличается от разности логарифмов (4). Тут мы делим один логарифм на другой, а там деление происходит под логарифмом.
Тут все просто, разве что стоит вспомнить, что квадратный корень — это степень одна вторая.
Тут первым действием воспользуемся изучаемой формулой, а дальше каждый логарифм в виде числа, потихонечку−полегонечку.
Последняя формула, меняем местами аргумент и основание логарифма:
Используется тоже нечасто, но если ее не знаешь, то никак не выкрутишься через другие формулы.
Закрепим обе формулы. Используем формулу (9), после (8), а так же не забудь порадовать десятичные дроби — переведи их в обыкновенные, а они порадуют тебя. Теперь посмотрим еще на пару примеров:
Логарифм в логарифме, что может быть прекраснее? Только решенный логарифм в логарифме.
Начинаем с внутреннего:
И постепенно раскрываем каждый последующий:
После того, как с формулами разобрались, (а их всего 9! Согласись, несложно выучить?), перейдем к уравнениям.
Все логарифмические уравнения решаем по одному из двух алгоритмов.
Первый появляется из определения логарифма:
Только не забываем про ОДЗ:
Второй вариант, когда логарифм с одним основанием равен логарифму с точно таким же основнанием:
Не забываем про ОДЗ, тогда получится:
Подставив в ОДЗ x = 15, видим, что все выполняется!
Обязательно только логарифм (без всяких множителей и т.п.) с одним основанием должен быть равен другому логарифму с таким же основанием:
Здесь перед логарифмами стоят разные множители, поэтому прежде всего нужно их внести в логарифм (6 формула), а после убрать логарифмы:
Если стоят одинаковые множители, их можно сократить сразу или сократить на общий множитель:
Бывает, что с одной стороны уравнения есть сумма логарифмов (4) или обычное число, сокращать их сразу нельзя! Только после того, как приведем и левую, и правую часть к одному логарифму:
Что же касается неравенств, убирать логарифмы можно так же, как и в уравнениях, только здесь нужно внимательно смотреть на значение оснований. Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный:
Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный:
Если же основание а > 1, то убираем логарифмы без смены знака и дорешиваем обычное неравенство:
Говорящий в этом видео имеет то, что мне кажется австралийским акцентом (приношу свои извинения всем киви, если он на самом деле новозеландец), поэтому мне интересно, отличается ли это от страны к стране — я из Соединенных Штатов. и никогда не слышал, чтобы это произносилось таким образом.
Итак, вопрос: как вы произносите $\ln$? Как это произносится другими в вашем регионе?
Пожалуйста, включите в свой ответ всю важную региональную информацию ( Редактировать: или профессиональный контекст), что может иметь значение.
ОТРЕДАКТИРОВАНО ДОБАВИТЬ: Я прекрасно понимаю, что многие математики предпочитают использовать обозначение «$\log x$» для $\log_e x$, и многие возражают против использования $\log$ для $\log_{ 10}$, также известный как «десятичный логарифм». Пожалуйста, не используйте этот вопрос как возможность спорить о том, что более «естественно» $\log_e$ или $\log_{10}$. Для целей этого вопроса предположим, что вы находитесь в контексте, в котором нотация $\log$ зарезервирована для $\log_{10}$, а $\log_e$ обозначается как $\ln$. Вопрос не в том, хороша ли эта система обозначений, а в том, что как произносится .
Пожалуйста, не используйте этот вопрос как возможность спорить о том, что более «естественно» $\log_e$ или $\log_{10}$. Для целей этого вопроса предположим, что вы находитесь в контексте, в котором нотация $\log$ зарезервирована для $\log_{10}$, а $\log_e$ обозначается как $\ln$. Вопрос не в том, хороша ли эта система обозначений, а в том, что как произносится .
ВТОРОЕ РЕДАКТИРОВАНИЕ : Я должен был включить это в свой первоначальный пост, но может случиться так, что произношение также зависит от профессионального контекста: то есть, возможно, математики в вашем университете произносят это как «бревно», химики произносят это «элл эн», а школьный учитель в соседнем квартале говорит «ланн». Поэтому, отвечая на вопрос, предоставьте любую соответствующую контекстную информацию, которая может помочь уточнить объем вашего ответа. 92$) Я бы сказал: «элл энн экс в квадрате».
$\endgroup$
$\begingroup$
Ванкувер, Канада. Я произношу его исключительно как /lɑn/.
Я произношу его исключительно как /lɑn/.
$\endgroup$
6
$\begingroup$
Поскольку английский язык не является родным, и мне приходится довольно часто читать математические выражения, я пользуюсь следующими справочниками:
- Справочник по разговорной математике, Научно-исследовательский институт, Inc.: Это, вероятно, самый полный справочник. Однако не из легких консультаций.
- Х. Валиахо, Произношение математических выражений (pdf): краткий список, разделенный по темам (например, логика, множества, функции и т. д.). Сообщает также варианты.
Что касается $\ln$, эти руководства рекомендуют:
натуральный бревно х
из [1] и [2];
л н х
из [1], и это совпадает с вашим примером; [2] рекомендует и другие варианты произношения, но я подозреваю, что они встречаются реже.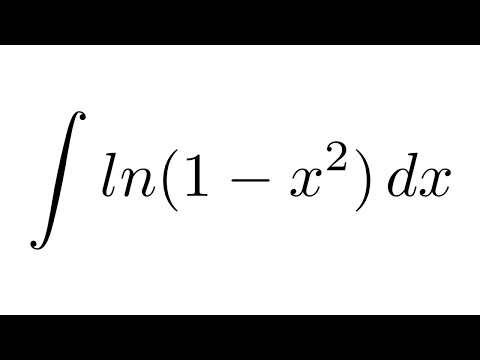
$\endgroup$
1
$\begingroup$
Я произношу $\ln x$ как «log ex» и обычно пишу его как $\log x,$ или иногда, когда разговариваю с первокурсниками или подобными неопытными людьми, как $\log_e x$ .
К сожалению, в учебниках по алгебре для средней школы учащихся учат, что «логарифм» без нижнего индекса всегда означает логарифм с основанием 10$. Поскольку натуральный логарифм действительно представляет собой натуральный логарифм для использования в вычислениях, он записывается как $\log$ без нижнего индекса. Некоторые математики пишут его как $\ln$, но все же понимают, что $\log$, написанное другими, означает логарифм по основанию $e$. Только среди нематематиков этот последний факт неизвестен.
Что в нем «естественного» можно увидеть здесь:
\начать{выравнивать}
& \frac d {dx} \log_{10} x = \frac{\text{некоторая постоянная}} x \\[10pt]
& \frac d {dx} \log_6 x = \frac{\text{некоторая другая константа}} x \\[10pt]
& \текст{и т. д. Но только когда основание $e$, а не 6 или 10 или что-то в этом роде} \\
& \ фантом {\ текст {и т. д. }} \text{другое число, кроме $e$, является «константой», равной 1, т.е.} \\[10pt]
& \frac d {dx} \log_e x = \frac 1 x.
\end{выравнивание}
д. Но только когда основание $e$, а не 6 или 10 или что-то в этом роде} \\
& \ фантом {\ текст {и т. д. }} \text{другое число, кроме $e$, является «константой», равной 1, т.е.} \\[10pt]
& \frac d {dx} \log_e x = \frac 1 x.
\end{выравнивание}
$\endgroup$
17
$\begingroup$
Обычно я говорю «журнал», несмотря ни на что, а если используется конкретная база, я говорю «логарифм базы-n». К особым случаям относится «двоичный журнал» для журнала с основанием 2, который я записываю как $\lg$.
Вместо $\ln$ я просто произношу буквы «ell-enn» или, вернее, всю эту чертовщину — «натуральное бревно». Иногда я слышал, как ставили ударение на букву «л» и говорили «лин» или «лен», но это случается редко.
Я говорю как американский студент — я живу в Техасе, но на самом деле я не уроженец какого-либо другого штата (хотя я жил в Сан-Диего, когда учился в старшей школе).
$\endgroup$
$\begingroup$
Когда я учился в школе (в Англии), мы произносили это слово «лонн», но я сижу рядом с учителем математики (английского языка), который говорит «ланн». Теперь я просто произношу это «журнал» FWIW.
(Чтобы уточнить, я произношу это «log ex» даже в контекстах, которые требуют от меня писать $\ln x$, с чем мне иногда приходится иметь дело!)
$\endgroup$
4
$\begingroup$
Я израильтянин, учусь в очень международном австралийском университете.
В Израиле мы говорим «lan» (произносится близко к английскому слову «gun»). Здесь я столкнулся со столькими вариациями:
- Произнесение двух букв l n
- Произнесение «логарифм»/»логарифм»
- Высказывание «натуральное бревно»
- Произнесение «log e»
Все вышеперечисленные были носителями английского языка из разных уголков мира. Никто не произносил это так, как мы, израильтяне, как «лан».
Никто не произносил это так, как мы, израильтяне, как «лан».
Что касается твоего «линна», я думаю, что это был новозеландец. Иногда их e звучит как i.
$\endgroup$
$\begingroup$
Когда я произносил это вслух, единственный способ, которым я когда-либо говорил или слышал, это как «натуральный логарифм $x$ в квадрате» или «логарифм $x$ в квадрате». У меня также иногда в голове было написано «ell-enn», что значительно экономит время, но может быть неправильным путем, если вы также имеете дело с другими переменными.
Я никогда раньше не слышал, чтобы кто-то использовал «linn» или «lunn», хотя это также кажется хорошим способом сэкономить время во время разговора, не путая его с именами переменных.
$\endgroup$
3
$\begingroup$
Отправляясь в среднюю школу в Техасе, я всегда говорил это как аббревиатуру: «el en of ex». Затем, когда я сдавал AP Stats, моя учительница статистики была из Канады, и она сказала «лужайка бывшего». Я на самом деле приобрел эту привычку различать два:
Затем, когда я сдавал AP Stats, моя учительница статистики была из Канады, и она сказала «лужайка бывшего». Я на самом деле приобрел эту привычку различать два:
«log of ex» = $log(x)$
«лужайка ex» = $ln(x)$
$\endgroup$
$\begingroup$
Однажды я произнес это «лин» перед кучей математических гиков, и все они надо мной смеялись. (Я в США.) На самом деле я никогда раньше не слышал, чтобы это произносилось, и у всех было много раз.
Я также слышал «log-en» для естественного журнала, но обычно просто «log», если вы не конкретны.
$\endgroup$
$\begingroup$
Я привык:
- Натуральный логарифм ( )
- лин ( )
- журнал ( )
Запомнить $$ \ln(x) =\log_{2,718…}(x) $$ поэтому вполне оправдано называть его журналом
. $\endgroup$
$\endgroup$
$\begingroup$
Мой преподаватель из Центральной/Восточной Европы, и она произносит $\ln x$ как «Logaritmus x».
$\endgroup$
4
$\begingroup$
Эта тема была причиной многих довольно горячих споров, когда я был 16-17-летним студентом. По крайней мере, в Великобритании «элл-энн» и «лунь» довольно распространены. В университете «бревно» было всем, что имело значение. Это похоже на то, как a/b равно «a на b», «a на b» и «a делится на b»: как только вы достигаете определенного уровня, все понимают, что вы имеете в виду, и вы не чувствуете необходимости спорить. об этом.
$\endgroup$
$\begingroup$
Я австралиец, и его акцент кажется мне британским, а не австралийским. Я могу только вспомнить, что слышал, как это произносится как el en или log в Австралии, из этого поста на Reddit, где я вижу два ответа, говорящих о произношении этого слова lun, оба из которых являются британскими (один говорит, что слышал это произношение, делая его A-levels , другой прямо говорит об этом).
Я могу только вспомнить, что слышал, как это произносится как el en или log в Австралии, из этого поста на Reddit, где я вижу два ответа, говорящих о произношении этого слова lun, оба из которых являются британскими (один говорит, что слышал это произношение, делая его A-levels , другой прямо говорит об этом).
$\endgroup$
1
$\begingroup$
Так как я ежедневно занимаюсь в основном логикой, двусмысленность — это грех. Я всегда говорю «натуральный логарифм» или «логарифмическая база e», чтобы предотвратить неправильное толкование из-за двусмысленности простого слова логарифм.
$\endgroup$
1
$\begingroup$
Исходя из американского опыта компьютерных наук (мы тоже используем журналы!), мы обычно называем его просто «журнал» независимо от того, натуральный это журнал или нет. В приложениях, где журнал, являющийся ln, действительно имеет значение, мы просто говорим «натуральный журнал». Я тоже слышал «l n» (el en), но это кажется менее распространенным. Я также слышал «лин», но это достаточно редкое слово, поэтому оно звучит странно, когда я его слышу.
В приложениях, где журнал, являющийся ln, действительно имеет значение, мы просто говорим «натуральный журнал». Я тоже слышал «l n» (el en), но это кажется менее распространенным. Я также слышал «лин», но это достаточно редкое слово, поэтому оно звучит странно, когда я его слышу.
$\endgroup$
$\begingroup$
По моему опыту, по крайней мере, в области математики, большинство людей называют это просто «бревно».
Можно с уверенностью сказать, что когда речь идет о математике, общепризнано, что число ln естественно. Таким образом, когда математики говорят log, они, скорее всего, имеют в виду ln, а не $\log_{10}$. Ваша ситуация, когда «журнал» означает исключительно $\log_{10}$ (о чем вы беспокоитесь), будет редкой. Если кто-то когда-нибудь использует $\log_{10}$, он или она, вероятно, добавит: «Я имею в виду общий журнал с основанием 10».
Неспециалисты (я полагаю) редко используют журнал (во всех смыслах), поэтому меня не беспокоит путаница.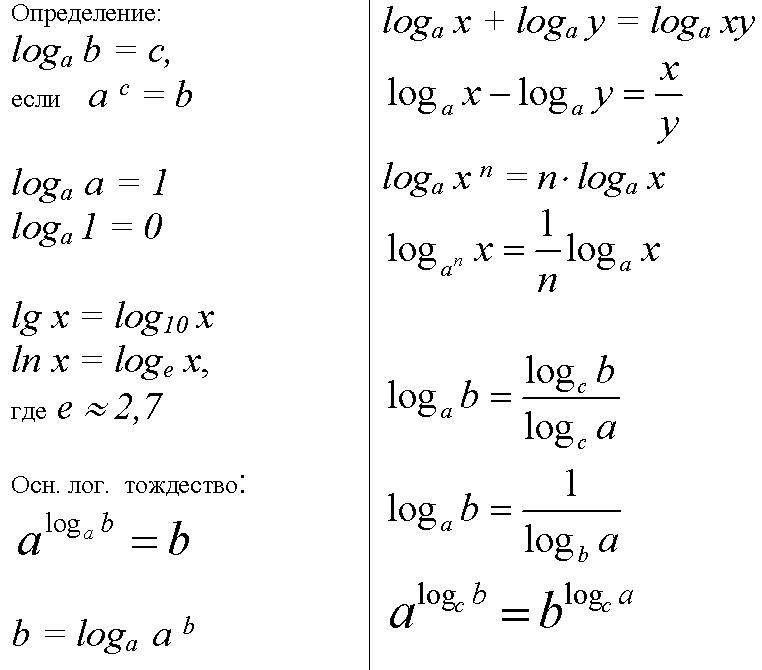
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Алгебра — Логарифмические функции
Онлайн-заметки Пола
Главная
/
Алгебра
/
Экспоненциальные и логарифмические функции
/ Логарифмические функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 6-2: Логарифмические функции
В этом разделе нам нужно перейти к функциям логарифмирования. Это может быть сложной функцией для построения графика сразу. Будут некоторые другие обозначения, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивными. Однако не отчаивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж плохи, и обычно требуется немного поработать с ними, чтобы понять их.
Вот определение функции логарифма. 9y} = x\) называется экспоненциальной формой .
Обратите внимание, что требование \(x > 0\) на самом деле является результатом того факта, что мы также требуем \(b > 0\). Если вы думаете об этом, это будет иметь смысл. Мы возводим положительное число в степень, поэтому результат не может быть ничем иным, как другим положительным числом. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Если вы думаете об этом, это будет иметь смысл. Мы возводим положительное число в степень, поэтому результат не может быть ничем иным, как другим положительным числом. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Теперь давайте обратимся к используемым здесь обозначениям, так как обычно это самое большое препятствие, которое ученики должны преодолеть, прежде чем начать понимать логарифмы. Во-первых, «логарифмическая» часть функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не являются переменными и не означают умножения. Они здесь только для того, чтобы сказать нам, что мы имеем дело с логарифмом. 9x}\) в такой форме, но это не так. Просто похоже, что это может быть то, что происходит.
Важно соблюдать прямолинейность записи логарифмов, иначе вам будет очень сложно их понять и работать с ними.
Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы.
Пример 1 Оцените каждый из следующих логарифмов.
- \({\log _4}16\)
- \({\log _2}16\)
- \({\log _6}216\)
- \(\displaystyle {\log _5}\frac{1}{{125}}\)
- \({\log _{\frac{1}{3}}}81\)
- \({\log _{\frac{3}{2}}}\displaystyle \frac{{27}}{8}\)
Показать все решения Скрыть все решения
Показать обсуждение
Реальность такова, что прямое вычисление логарифмов может быть очень трудным процессом даже для тех, кто действительно в них разбирается. Обычно гораздо проще сначала преобразовать логарифмическую форму в экспоненциальную. В такой форме мы обычно можем получить ответ довольно быстро. 94}\), и т. д. , пока не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно
. \[{\log _2}16 = 4\]
Перед тем, как перейти к следующей части, обратите внимание, что основа для них является очень важной частью обозначений. Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
c \({\log _6}216\) Показать решение 93}}} = \frac{{27}}{8}\]
Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете разбираться в обозначениях. Есть еще несколько оценок, которые мы хотим сделать, однако нам нужно ввести некоторые специальные логарифмы, которые встречаются на очень регулярной основе. Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов.
\[\ begin{align*}& {\mbox{десятичный логарифм:}}\hspace{0,25 дюйма}\log x = {\log _ {10}}x\\ & {\mbox{натуральный логарифм:}}\ hspace {0,25 дюйма} \ ln x = {\ log _ {\ bf {e}}} x \ end {align *} \]
Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы опустили часть обозначения «по основанию 10».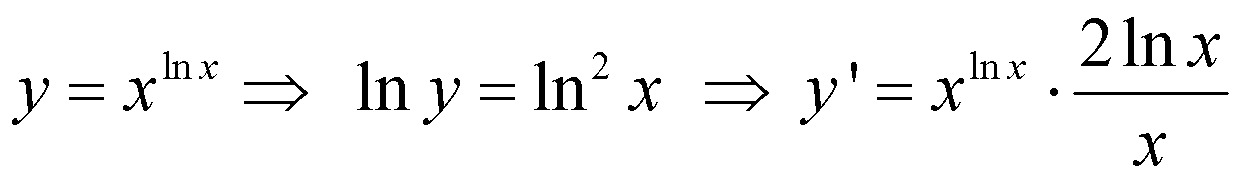 Точно так же натуральный логарифм — это просто логарифмическая база \(\bf{e}\) с другим обозначением, где \(\bf{e}\) — то же число, которое мы видели в предыдущем разделе и определяется как \({\bf{e}} = 2,718281828 \ldots\).
Точно так же натуральный логарифм — это просто логарифмическая база \(\bf{e}\) с другим обозначением, где \(\bf{e}\) — то же число, которое мы видели в предыдущем разделе и определяется как \({\bf{e}} = 2,718281828 \ldots\).
Давайте взглянем еще на пару оценок.
Пример 2 Оцените каждый из следующих логарифмов.
- \(\лог 1000\)
- \(\log \displaystyle \frac{1}{{100}}\)
- \(\ln \displaystyle \frac{1}{{\bf{e}}}\)
- \(\ln \sqrt {\bf{e}} \)
- \({\log _{34}}34\)
- \({\log _8}1\)
Показать все решения Скрыть все решения
Показать обсуждение
Чтобы выполнить первые четыре вычисления, нам просто нужно вспомнить, как они обозначаются и какое основание подразумевается этими обозначениями. Последние две оценки должны проиллюстрировать некоторые свойства всех логарифмов, которые мы в конечном итоге рассмотрим. 90} = 1\). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
90} = 1\). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
Таким образом, при вычислении логарифмов все, что мы действительно спрашиваем, это какой показатель степени мы положили в основание, чтобы получить число в логарифме.
Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала нарисуем пару быстрых графиков.
Пример 3 Нарисуйте график десятичного логарифма и натурального логарифма на одной системе координат.
Показать решение
Этот пример имеет две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам некоторую практику использования нашего калькулятора для оценки этих логарифмов, потому что реальность такова, что именно так нам нужно будет выполнять большинство этих оценок.
Вот таблица значений двух логарифмов.
| \(х\) | \(\лог х\) | \(\ln х\) |
|---|---|---|
| \(\frac{1}{2}\) | -0,3010 | -0,6931 |
| 1 | 0 | 0 |
| 2 | 0,3010 | 0,6931 |
| 3 | 0,4771 | 9r}} \right) = r{\log _b}x\)

 Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает. Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.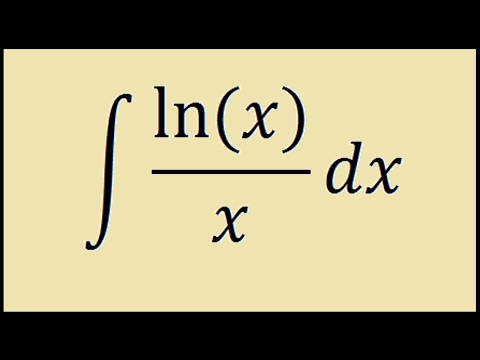
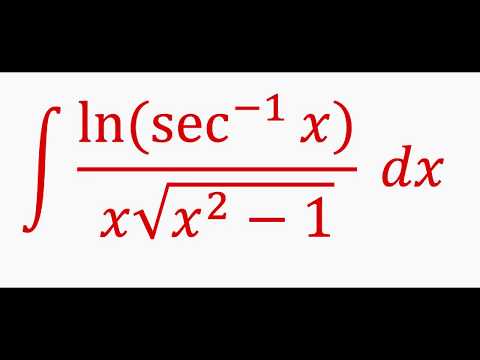

 Обозначение: ln x .
Обозначение: ln x . Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.
Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.
 Вот несколько примеров.
Вот несколько примеров.
 Нам просто нужно быть осторожными с этими свойствами и использовать их правильно.
Нам просто нужно быть осторожными с этими свойствами и использовать их правильно. 5}} \вправо)\]
9{\ гидроразрыва {1} {2}}} \]
5}} \вправо)\]
9{\ гидроразрыва {1} {2}}} \] Кроме того, мы можем иметь дело с показателями степени только в том случае, если член в целом возводится в степень. Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме.
Кроме того, мы можем иметь дело с показателями степени только в том случае, если член в целом возводится в степень. Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме. 8}} \right)\]
98}}}} \справа)\]
8}} \right)\]
98}}}} \справа)\] Если бы 7 было 5, или 25, или 125, и т. д. . мы могли бы сделать это, но это не так. Поэтому приходится использовать формулу замены основания.
Если бы 7 было 5, или 25, или 125, и т. д. . мы могли бы сделать это, но это не так. Поэтому приходится использовать формулу замены основания. x$ при одном конкретном значении x: 9x$ решение многих типов уравнений.
x$ при одном конкретном значении x: 9x$ решение многих типов уравнений.