Высшая математика. Методическое пособие для студентов-заочников
- формат pdf
- размер 454.1 КБ
- добавлен 24 ноября 2008 г.
В пособии приведены основные теоретические сведения и типовые задачи с решениями и рекомендациями по темам: элементы линейной алгебры, элементы векторной алгебра и аналитической геометрии, пределы функций, непрерывность функций, производная и дифференциал, исследование функций и построение графиков, наибольшее и наименьшее значение функции на отрезке.
Читать онлайн
Смотрите также
- формат djvu
- размер 6.66 МБ
- добавлен
14 ноября 2009 г.

Высшая школа. 1985 г. Для студентов заочников инженерно-технических высших учебных заведений. Методички Арутюнова 1981,1983,1985 годов идентичны.
- формат doc
- размер 875.46 КБ
- добавлен 15 мая 2010 г.
Данное издание предназначено для студентов заочной формы обучения при самостоятельном изучении курса «Высшая математика». Часть 1 содержит программу, методические указания, рекомендуемую учебную литературу и контрольные задания (1-4 контрольные работы) для студентов-заочников инженерных и инженерно-экономических специальностей приборостроительного факультета БНТУ. Составители: В. А. Ибрагимов, С. В. Стрельцов, А. Н. Мелешко, О. Г. Вишневская. Рец…
Практикум
- формат pdf
- размер 5.
 55 МБ
55 МБ - добавлен 22 ноября 2010 г.
Учебно-методическое пособие для студентов первого курса заочного факультета/ сост. Ж. Н. Горбатович, А. С. Семенкова, Е. А. Шинкевич — Мн.: БГТУ, 2005. — 88 с. Приведены основные теоретические сведения, примеры решения задач, задачи для самостоятельного решения. Учебно-методическое пособие предназначено для оказания помощи студентам заочной формы обучения при самостоятельном изучении следующих тем курса «Высшая математика», «Линейная и векторна…
Практикум
- формат pdf
- размер 10.35 МБ
Учебно-методическое пособие для студентов заочного факультета/ сост. Ж. Н. Горбатович, А. С. Семенкова, Е. А. Шинкевич — Мн.: БГТУ, 2006. — 78 с. Приведены основные теоретические сведения, примеры решения задач, задачи для самостоятельного решения. Учебно-методическое пособие предназначено для оказания помощи студентам заочной формы обучения при самостоятельном изучении следующих тем курса «Неопределенный интеграл», «Определенный интеграл», «Не…
Ж. Н. Горбатович, А. С. Семенкова, Е. А. Шинкевич — Мн.: БГТУ, 2006. — 78 с. Приведены основные теоретические сведения, примеры решения задач, задачи для самостоятельного решения. Учебно-методическое пособие предназначено для оказания помощи студентам заочной формы обучения при самостоятельном изучении следующих тем курса «Неопределенный интеграл», «Определенный интеграл», «Не…
- формат pdf
- размер 3.69 МБ
- добавлен 03 марта 2011 г.
Учебное пособие для студентов — заочников. – Баpнаул: АлтГТУ, 2009. – (139+151+152) с. Пособие ориентировано на организацию самостоятельной работы студентов-заочников по изучению учебной дисциплины «Математика» на первом курсе. Содержит кpаткое изложение основных теоpетических понятий и методов pешения типовых пpимеpов по двенадцати разделам высшей математики: линейная алгебра, элементы линейной алгебры и аналитической геометрии, введение в ма.
- формат doc
- размер 3.84 МБ
- добавлен 02 июля 2009 г.
А. Н. Мелешко, О. Г. Вишневская Рецензент И. В. Прусова Данное издание предназначено для студентов заочной формы обучения при самостоятельном изучении курса «Высшая математика». Часть 1 содержит программу, методические указания, рекомендуемую учебную литературу и контрольные задания (1-4 контрольные работы) для студентов-заочников инженерных и инженерно-экономических специально-стей приборостроительного факультета.
- формат doc
- размер 4.96 МБ
- добавлен 02 июля 2009 г.
А. Н. Мелешко, О. Г. Вишневская Рецензент И. В. Прусова Данное издание предназначено для студентов заочной формы обучения при самостоятельном изучении курса «Высшая математика». Часть 2 содержит контрольные задания (5-8 контрольные работы и образцы их решения) для студентов-заочников инженерных и инженерно-экономических специальностей приборостроительного факультета.rn
Часть 2 содержит контрольные задания (5-8 контрольные работы и образцы их решения) для студентов-заочников инженерных и инженерно-экономических специальностей приборостроительного факультета.rn
- формат doc
- размер 1.76 МБ
- добавлен 23 ноября 2011 г.
Составитель — разработчик: ст. преподаватель Кобяк Г.Ф. Учебно-методическое пособие по дисциплине Высшей математике для студентов-заочников 1 курса в МЭСИ. Основные формулы по дисциплине «Высшей математике», а также примеры решения задач на темы: прямая в пространстве, прямая и плоскость в пространстве, матрицы и определители, системы линейных алгебраических уравнений, линейное векторное пространство, базис и размерность линейного пространства, п…
- формат doc
- размер 282.77 КБ
- добавлен
25 июня 2011 г.

Высшая математика для менеджеров: Учебное пособие. — Калининградский университет — Калининград,2004 г. Рассматриваются основные понятия высшей математики, которые являются базой математического инструментария современного менеджмента. Приводятся краткие теоретические сведения по аналитической геометрии, линейной алгебре и математическому анализу и их применение при решении прикладных задач в экономике и управлении. Рассмотрены решения типовых за…
- формат doc
- размер 138.07 КБ
- добавлен 30 января 2005 г.
Высшая математика. Методические указания и контрольные задания (с программой) для студентов заочников инженерно-технических высших учебных заведений. Высшая школа. 1985 г. под редакцией Ю.С.Арутюнова.
Методички и книги по математике.
- Statistics.
 Basic principles (Natalia Shyriaieva)
Basic principles (Natalia Shyriaieva) - А. З. Рывкин и Е. С. Куницкая Задачник-практикум по математическому анализу
- А.С. Шапкин Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями.
- Алгебра и Геометрия (Толстиков А. В.)
- Алгебраические уравнения и неравенства. Функции. Логарифмы.
- Аналитическая геометрия. Линейная алгебра.
- Аналитическая геометрия. Методические указания.
- Введение в теорию и методы Принятия решений (Дмитриенко В.Д., Кравец В.А., Леонов С.Ю.)
- Вероятность и Комбинаторика Новоселов О.В., Скиба Л.П.
- Вступ до функціонального аналізу (на украинском языке)
- Высшая алгебра (Конспект лекций для студентов физико-технического факультета)
- Высшая математика (Учебное пособие)
 Ерохина А.П., Байбакова Л.Н.
Ерохина А.П., Байбакова Л.Н.- Высшая математика. Курс лекций. А. С. Гринберг, О. А.Кастрица, Е. А.Скуратович
- Высшая математика. Методические указания 1 часть. Карданов С. О.
- Высшая математика. Методические указания 2 часть. Карданов С. О
- Вычислительная математика
- Вычислительная математика (Е.Н. Платонов)
- Вычислительная математика. Практикум.
- Графы
- Дискретная математика (Учебное пособие)
- Дискретная математика. Курс лекций. В.Н.Семенчук
- Дифференциальное исчисление
- Дифференциальное исчисление функции действительной переменной. Практическое пособие.
- Дифференциальное исчисление функции многих переменных (Под ред.
 Н.Н. Ясницкой)
Н.Н. Ясницкой) - Дифференциальное исчисление функции нескольких переменных
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения. Системы дифференциальных уравнений
- Интегральное исчисление. Дифференциальные уравнения. (А.А. Ельцов)
- Интегрирование функций одной переменной (Е.В. Пастухова)
- Исследование операций в экономике-модели, задачи, решения. Афанасьев М.Ю., Суворов Б. П.
- Комбинаторика
- Конспект лекций по высшей математике. Комогорцев В. Ф.
- Конспект лекций по теории вероятностей и математической статистике Комогорцев В. Ф.
- Краткий курс лекций по аналитической геометрии
- Краткий курс лекций по дифференциальному исчислению
- Краткий курс математики и общей теории статистики.
 В. Г. Рау
В. Г. Рау - Краткий курс математического анализа для студентов МГТУ им. Н. Э. Баумана (второй семестр) Галкин С. В.
- Кривые второго порядка
- Курс высшей математики
- Курс высшей математики 2
- Курс высшей математики 3
- Курс высшей математики 4
- Курс лекций по линейной алгебре
- Курс лекций по линейной алгебре и аналитической геометрии
- Курс лекций по математической логике и теории алгоритмов (Алиев)
- Курс лекций по теории вероятностей
- Лекции по MahtCad
- Лекции по дискретной математике
- Лекции по дискретной математике (1 курс)
- Лекции по дифференциальной геометрии.
 Л. А. Масальцев
Л. А. Масальцев - Лекции по математическому анализу. Попов (2 сем)
- Лекции по математическому анализу. Попов (3 сем)
- Лекции по математическому программированию
- Лекции по теории вероятностей
- Лекции по теории вероятностей, Завьялова
- Линейная алгебра (3й семестр)
- Линейная алгебра — учебное пособие(З.И. Андреева)
- Линейная алгебра и аналитическая геометрия
- Линейная алгебра. Методические указания.
- Линейное программирование
- Линейные операторы. Квадратичные формы.
- Логика
- Логика и аргументация. Г.И. Рузавин
- Логика. Учебное пособие для студентов ВУЗов
- Логика.
 Учебное пособие. Ивин А. А.
Учебное пособие. Ивин А. А. - Математика (2 семестр). Сост. М. А. Башкин, А. И. Бурцев, Н. И. Гусарова
- Математика — учебное пособие (Лапузина Е.Н., Лобода А.И.)
- Математика и информатика (для специальности Юриспруденция) А.В.Костромин
- Математика-1 часть (институт мировой экономики и информатизации)
- Математика-2 часть (институт мировой экономики и информатизации)
- Математика-3 часть (институт мировой экономики и информатизации)
- Математика-4 часть (институт мировой экономики и информатизации)
- Математика. Учебный курс для юристов. Н.Б. Тихомиров, А.М. Шелехов
- Математическая логика и теория алгоритмов
- Математический анализ
- Математический анализ (ответы на билеты)
- Математический анализ — методические указания (Кирюков С.
 Р)
Р) - Математический анализ в вопросах и задачах. Бутузов В.Ф.
- Математическое программирование (Составитель Е. М. Колодная)
- Матричная теория
- Методические указания к изучению дисциплины теории вероятностей
- Методические указания по дисциплине «Математика» для студентов заочной формы обучения технических направлений
- Методичка по высшей математике с примерами решений (3й семестр)
- Методичка по дискретной математике с примерами решений
- Методы вычислений. О. Н. Гавришина, М. Р. Екимова, Л. Н. Фомина.
- Методы вычисления вероятностей случайных событий. Анисимова Л.Н. Федоткин М.А.
- Методы многомерной безусловной минимизации В. П. Северин
- Методы оптимальных решений (Астахова И.
 С.)
С.) - Методы оптимальных решений. М.А.Козлова
- Методы оптимизации. Некрасова М. Г.
- Методы оптимитизации
- Множества и операции над ними. Отношения и функции. Мощность множеств. Комбинаторика.
- Множества. Логика. Аксиоматические теории. Роберт Столл.
- Надёжность информационных систем
- Неопределенный интеграл. (Под редакцией Н.Н. Ясницкой)
- О методике изложения некоторых разделов теории алгоритмов проблема применимости для нормальных алгорифмов Маркова
- Обыкновенные дифференциальные уравнения
- Одномерные случайные величины. Т. С. Бородина
- Операційне числення. Н.К. Дорошенко, В.Ф. Мясникова (на украинском языке)
- Определенный интеграл и его приложения.
 Несобственные интегралы. (Под редакцией Н.Н. Ясницкой)
Несобственные интегралы. (Под редакцией Н.Н. Ясницкой) - Оптимизационные задачи
- Основы высшей математики
- Основы дискретной математики
- Основы математики и ее приложения в экономическом образовании. Красс М.С., Чупрынов Б.П.
- Основы математического моделирования: Учебное пособие. Пустовойтов П. Е.
- Основы теории вероятностей. Элементы математической статистики. С. И. Колесникова
- Основы теории систем и системного анализа (конспект лекций)
- Пособие по теории вероятности
- Практикум по дисциплине «статистика». Часть 1. Общая теория статистики
- Практикум по дисциплине «статистика». Часть II. Социально-экономическая статистика
- Предел последовательности и предел функции одной переменной
- Пределы функций.
 Производные.
Производные. - Решение задач в среде MathCad
- Решение систем линейных дифференциальных уравнений с постоянными коэффициентами. Устойчивость решений
- Ряды
- Ряды и интегралы Фуръе
- Справочник — А.А. Гусак, В.М. Гусак.
- Статистический анализ в маркетинговых исследованиях
- Сходимость несобственных интегралов
- Теория вероятностей (Лекции)
- Теория вероятностей (Практикум) Л.С. Барковская, Л.В. Станишевская, Ю.Н. Черторицкий
- Теория вероятностей, математическая статистика и случайные процессы
- Теория вероятности и математическая статистика. Курс лекций (Фадеева).
- Теория вероятности. Конспект лекций КПИ.
- Теория графов
- Теория графов и комбинаторика
- Теория игр
- Теория игр.
 Исследование операций.
Исследование операций. - Теория обыкновенных дифференциальных уравнений
- Теория функций комплексного переменного (конспект лекций)
- УМК — Теория вероятностей и элементы математической статистики
- Учебник логики. Г. И. Челпанов
- Учебник по нечёткой математике с примерами
- Учебно-методический комплекс – дискретная математика
- Учебно-методическое пособие для студентов и курсантов инженерных специальностей
- Функции комплексного переменного
- Функции комплексного переменного (теория, примеры, задачи)
- Функции комплексной переменной и ряды.
- Функциональный анализ
- Цепные дроби
- Численные методы
- Численные методы.
 Ю. Я. Кацман
Ю. Я. Кацман - Числовые последовательности и пределы
- Эконометрика (М.А. Кривцова)
- Эконометрика — учебное пособие (А.И.Афоничкин)
- Эконометрика для начинающих. Носко В.П.
- Эконометрика. Учебное пособие для экономических специальностей
- Элементарные функции и их графики. И. Э. Гриншпон, Я. С. Гриншпон
- Элементы аналитической геометрии на плоскости (уравнения прямой)
- Элементы дифференциальной геометрии
- Элементы мат анализа
- Элементы матричной алгебры и теории систем линейных уравнений
- Элементы теории вероятностей. Руководство к решению задач.
- Элементы теории вероятностей. Руководство к решению задач. Часть 2.

- Юнит 1. Аналитическая геометрия на плоскости.
- Юнит 2. Аналитическая геометрия в пространстве.
- Юнит 3. Векторная алгебра.
Подробное руководство по изучению высшей математики
Подробно изучите 10 метакогнитивных принципов, которые люди, занимающиеся высшей математикой, используют для быстрого усвоения математики, преодоления интеллектуального застоя и отличного времяпрепровождения.
Большинство руководств по математическому обучению либо слишком поверхностны , либо слишком узки , либо слишком K-12 , поэтому вместо этого мы решили создать лучшее.
Да! Это именно то, что я искал!
Итак, вот что произошло…
Как репетиторское агентство, работающее на стыке младших классов и высшей математики , мы часто обслуживаем широкий круг учащихся с разным уровнем знаний по математике.
Но из-за этого существует также тревожная тенденция , которую мы не можем не заметить…
А именно,
Мы заметили, что подавляющее большинство учащихся действительно плохо подготовлены к занятиям математикой выше уровня К-12 вообще!
. Испытывать трудности при выполнении логических выводов из одного конца в другой
Бороться с проблемами там, где их приходится решать методы или теория самостоятельно
Но потом, вот тогда у нас было дежа вю,
потому что было время, когда мы были такими же как они например,
8:
8 мы бы: Взглянуть на доказательство или математический отрывок и понятия не иметь, что мы только что прочитали займись этим
Попытаться насильно выучить тему высшей математики — только для того, чтобы забыть большую ее часть в ближайшие дни
Разозлиться на себя и спросить « зачем нам это? » — когда нет результата ожидается
Итак, что случилось, что мы и многие другие пропали без вести ?
«Высшие математические навыки обучения
» Но вы можете спросить: «Как же так!?» В конце концов, у большинства из нас есть как минимум 10 лет математики за плечами к тому времени, когда мы закончим среднюю школу.
Но вот в чем дело…
«Наша система — по крайней мере, здесь, в Северной Америке — в первую очередь предназначена для обучения самой миниатюрной форме математики, стремясь почти к наименьшему общему знаменателю.»
Математика без почему и строгости
Математика без особого абстрактного мышления более высокого уровня or deduction
Mathematics as tools and algorithms
Mathematics done for you in a box — with little room for struggle , exploration and invention
So неудивительно, почему наше общество стало таким математически хрупким — при том, что большинство из нас не имеет ни малейшего представления о том, как заниматься математикой, кроме самой простой.
Или, говоря более прямо, мы живем в » математическая матрица «, не понимая, что мы математически одомашниваем , пока мы говорим.
Мы также начали много вспоминать о нашем собственном опыте и почти сразу же проводить некоторые исследования по теме .
Однако.0008 ,
Мы также поняли, что на самом деле не так много ресурсов, когда речь идет о высшем математическом обучении!
Вместо этого мы нашли материалов , таких как:
1-страничные статьи о общих советах и рекомендациях для изучения математики K-12 решение задач
Исследования и диссертации по состоянию Математическое образование
Очерки преподавателей, отражающих различные T Каждую методологию
, по сути, мы не смогли найти Руководство . Основанный
Основанный
Практичный Проницательный Комплексный Практический 9 9 Итак, мы решили сделать,0007 очевидная вещь …
— это до пишем путеводитель сами .
, а затем, после 5 месяцев из:
- ИССЛЕДОВАНИЕ
- Мозговой штурм
-
- . скомпилируйте наши исследования и опыт в руководство, подобное описанному выше…
— где мы раскрываем 10 мощных , редко разрабатываемых принципов по высшему математическому обучению.
Введение…
— 10 принципов математической трансцендентности
A 10 глав , полная версия 85+ страниц электронной книги по фундаментальным принципам в каждой главе высший уровень.
A плотная , преимущественно нетехническая направляющая в высшем математическом обучении, где принципы структурированного обучения сочетаются с действенными советами, чтобы сэкономить годы потраченных впустую и ошибочных усилий.
Итак, о каких принципах и концепциях мы говорим?
Итак, вот оглавление для записи:
Например, для каждой главы :
Принцип обучения сначала вводится при изучении исследования и обоснование за ним.
Затем разрабатывается их применимость к изучению высшей математики — с помощью серии действенных советов , приемов и стратегий .
Время от времени вспомогательная информация предоставляется для заполнения пробелов в знаниях.
И когда все сделано, глава завершается резюме всех основных выводов.
И хотя руководство в основном построено так, чтобы быть нетехническим, оно также обеспечивает баланс, включив широкий спектр примеров из таких областей, как: Комплексный анализ
- Линейная алгебра
- Теория чисел
0007 первый год типичного математического бакалавриата).
К ним относятся:
Мощная педагогическая концепция S не стал явным в других местах
Не очень очевиден, противоречивые « когнитивные модные слова»
- 0008 s и методы придуманные по эту сторону угла
Во всяком случае, есть шанс, что вы можете найти там некоторые советы контринтуитивные или шокирующие .
Черт возьми, это может даже изменить ваше представление о роли изучающего математику / педагога в нашем обществе !
Попутно мы также представили серию модулей , чтобы сделать руководство более полным и информативным:
Definition modules
Pro-tip modules
Did-you-know modules
Famous mathematicians and quotes
And some other примечательные особенности , такие как:
И, конечно же. Обзор был бы неполным без запоминающихся строк из руководства, таких как:
Обзор был бы неполным без запоминающихся строк из руководства, таких как:
«Лучше взять на себя ответственность за выбор наших собственных математических материалов, чем получать удары от ресурсов, которые мы не находим особенно полезными».
Другими словами, если вы заинтересованы в:
Поглощение абстрактных концепций быстрее с лучшим удержанием
Решение Проблемы Более эффективно, пока развлекается
. и независимо друг от друга
Сделать высшую математику неотъемлемой частью вашего благополучия
тогда «Полное руководство по изучению высшей математики» будет хорошим началом для вашего пробуждение !
На самом деле, это то руководство, которое мы хотели бы иметь — еще до того, как начали наше путешествие по высшей математике !
Хорошо.
 Время для некоторых вопросов.
Время для некоторых вопросов. Каковы
предварительные условия для этого руководства — если таковые имеются? Как
самодостаточен / самодостаточен Полное руководство по изучению высшей математики? Почему этот проект занял 5
месяцев завершить? Чем это руководство отличается от других пособий по математике
, представленных на рынке? Научит ли это руководство меня лучше решать проблемы
? Сделает ли это руководство меня лучшим математическим мыслителем
? Научит ли это руководство меня новой
математике ? Это руководство поможет мне стать лучше
математик — любитель или профессионал? Получите максимум от математики с помощью Полного руководства по изучению высшей математики уже сегодня.

П.С. — Поздравляю! Похоже, вы только что дочитали до конца нашей презентации! Если у вас возникнут какие-либо вопросы, просто напишите нам по адресу [email protected], и мы будем рады вам помочь!
Высшая математика. Обзор курса и ресурсы
Математика
Национальный 4
Национальный 5
Выше
Ад выше
Обратите внимание: для сессии 2022-23 в этот курс внесены изменения. Поэтому материалы для понимания стандартов следует просматривать вместе с кратким изложением изменений национального курса, доступным по номеру в разделе «Информация о курсе 2022–23».
Примеры возможных свидетельств с комментариями
- Примеры возможных свидетельств с комментариями
Обзор оценки курса
- Обзор оценки курса — презентация со звуком (8 минут) (11,34 МБ)
Изменения в материалах стандартов понимания
- Изменения в опубликованных материалах стандартов понимания по всем предметам
Пожалуйста, обратите внимание: материалы стандартов понимания регулярно пересматриваются, чтобы обеспечить их актуальность.
Сеанс дополнительных ресурсов 2021-22
Новое – Новые материалы, не опубликованные ранее не опубликованы
Обновлены- , опубликованные в 2020/21 году, но внесены поправки на 2021/22
, перенесенные- , опубликованные в 2020/21 году. презентация — Вопросник (2018, 2019) с применением принципов выставления оценок
Перенесено – Таблицы анализа ответов на вопросы (опубликованы на защищенном сайте SQA. Вы можете получить к ним доступ через своего координатора SQA). Предоставляет информацию об успеваемости кандидатов, которая полезна учителям, лекторам и оценщикам при подготовке кандидатов к будущей оценке.
Отчеты по курсу
- Отчет по курсу высшей математики за 2017 г., октябрь 2017 г.
- Отчет по курсу высшей математики за 2018 г., август 2018 г.
- Отчет по курсу высшей математики за 2019 г., сентябрь 2019 г.

- Отчет по курсу высшей математики за 2022 г., сентябрь 2022 г.
- Математика: обеспечение качества — внешняя проверка
2021 Ключевые сообщения
Альтернативная модель сертификации включала национальную деятельность по обеспечению качества, проведенную в мае 2021 года.
- Высшая математика 2020-21 ключевые сообщения
июнь 2021
Отчеты о проверке
- Ключевые сообщения проверки математики Раунд 1
март 2017 - Отчет по курсу высшей математики за 2019 г., сентябрь 2019 г.
- Отчет по курсу высшей математики за 2018 г., август 2018 г.
- Математика: обеспечение качества — внешняя проверка
Дополнительная поддержка в области повышения квалификации
При выявлении каких-либо конкретных проблемных областей, которые не рассматриваются в наших мероприятиях по стандартам понимания или вспомогательных материалах, мы предлагаем бесплатное обучение непрерывному профессиональному развитию (CPD) по запросу.
Взглянуть на доказательство или математический отрывок и понятия не иметь, что мы только что прочитали займись этим
Попытаться насильно выучить тему высшей математики — только для того, чтобы забыть большую ее часть в ближайшие дни
Разозлиться на себя и спросить « зачем нам это? » — когда нет результата ожидается

Математика без почему и строгости
Математика без особого абстрактного мышления более высокого уровня or deduction
Mathematics as tools and algorithms
Mathematics done for you in a box — with little room for struggle , exploration and invention

1-страничные статьи о общих советах и рекомендациях для изучения математики K-12 решение задач
Исследования и диссертации по состоянию Математическое образование
Очерки преподавателей, отражающих различные T Каждую методологию
 Основанный
Основанный — где мы раскрываем 10 мощных , редко разрабатываемых принципов по высшему математическому обучению.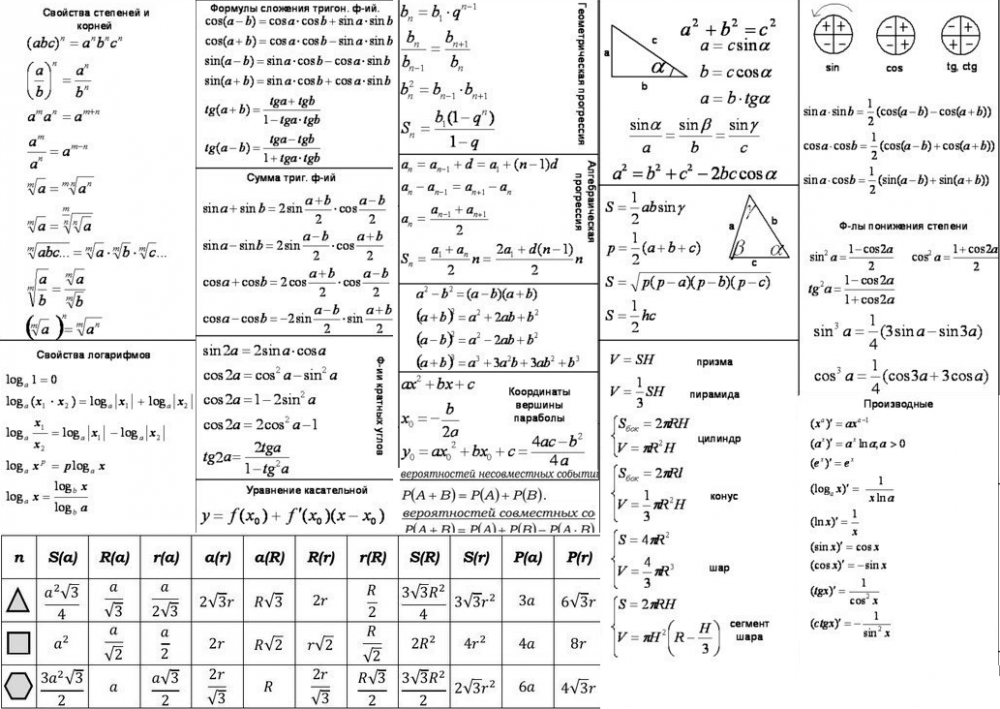
Введение…
— 10 принципов математической трансцендентности
A 10 глав , полная версия 85+ страниц электронной книги по фундаментальным принципам в каждой главе высший уровень.
A плотная , преимущественно нетехническая направляющая в высшем математическом обучении, где принципы структурированного обучения сочетаются с действенными советами, чтобы сэкономить годы потраченных впустую и ошибочных усилий.
Итак, о каких принципах и концепциях мы говорим?
Итак, вот оглавление для записи:
Например, для каждой главы :
Принцип обучения сначала вводится при изучении исследования и обоснование за ним.

Затем разрабатывается их применимость к изучению высшей математики — с помощью серии действенных советов , приемов и стратегий .
Время от времени вспомогательная информация предоставляется для заполнения пробелов в знаниях.
И когда все сделано, глава завершается резюме всех основных выводов.
И хотя руководство в основном построено так, чтобы быть нетехническим, оно также обеспечивает баланс, включив широкий спектр примеров из таких областей, как: Комплексный анализ

Мощная педагогическая концепция S не стал явным в других местах
Не очень очевиден, противоречивые « когнитивные модные слова»
Definition modules
Pro-tip modules
Did-you-know modules
Famous mathematicians and quotes
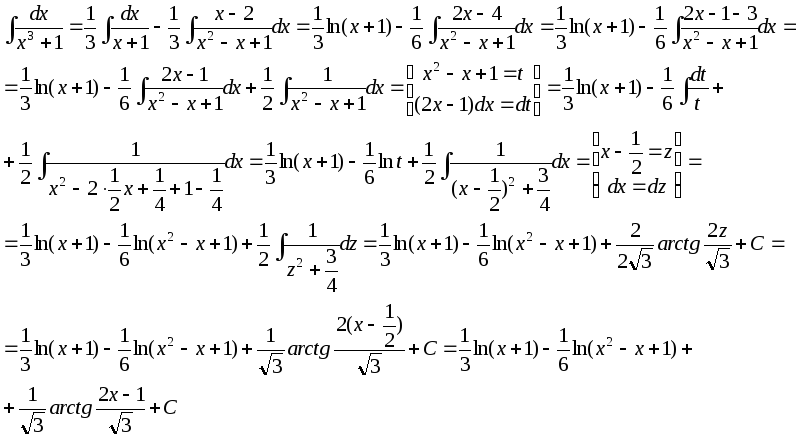 Обзор был бы неполным без запоминающихся строк из руководства, таких как:
Обзор был бы неполным без запоминающихся строк из руководства, таких как:Поглощение абстрактных концепций быстрее с лучшим удержанием
Решение Проблемы Более эффективно, пока развлекается
. и независимо друг от друга
Сделать высшую математику неотъемлемой частью вашего благополучия


июнь 2021
март 2017



 55 МБ
55 МБ
 Basic principles (Natalia Shyriaieva)
Basic principles (Natalia Shyriaieva) Ерохина А.П., Байбакова Л.Н.
Ерохина А.П., Байбакова Л.Н. Н.Н. Ясницкой)
Н.Н. Ясницкой) В. Г. Рау
В. Г. Рау Л. А. Масальцев
Л. А. Масальцев Учебное пособие. Ивин А. А.
Учебное пособие. Ивин А. А. Р)
Р) С.)
С.) Несобственные интегралы. (Под редакцией Н.Н. Ясницкой)
Несобственные интегралы. (Под редакцией Н.Н. Ясницкой) Производные.
Производные. Исследование операций.
Исследование операций. Ю. Я. Кацман
Ю. Я. Кацман

 Время для некоторых вопросов.
Время для некоторых вопросов.