Минорский — Высшая математика — PDF
PDF-файл из архива «Минорский — Высшая математика», который расположен в категории «». Всё это находится в предмете «математический анализ» из раздела «», которые можно найти в файловом архиве МГУ им. Ломоносова. Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .
ОГЛАВЛЕНИЕ ИЗ ПРЕДИСЛОВИЯ АВТОРА П ТРГТЬЕМУ ИЗДАНИЭО От редакпии Глава 11 12 !О 21 29 35 38 40 44 48 4!Э о1 51 Глава 53 58 60 3 1! зб 11 12 ~3 16 з 7. 3 8. 110 ЦЭ! 3 12 113 314 115 3 16 з17 118 Аналитичоская геометрия на пласкости !!оординаты го пли па прямой и на и;юскости. Расстояние между двумя точками Деление отрезка и данном отношении. Плоше,ль треугольн- икаа и многоугольника Уравнение линии как гсометричсского места точек…. Уравнение прямой: 1) с уг.ловьлм ковффипиентом, 2) об- щее, 3) в отрезках на осях Угол между прямыми. Уравнение пучка прямых, прохо- дяших через данную точку.
Уравнение прямой, прохо- дяшсй через гплс данные точки.
Параболы у = = ахд + бх + с и х = аул + бу + с. Гипербола ху = А .. Смешанные задачи на кривые второго порядка Общее уравнение липни второго порядка Полярные координаты Алгебраические кривые третьего и высших порядков ‘1’рансцен,юнтныс кривые 2. Векторная алгебра Сложение векторов.
Умлло’кение вектора па скадар Прямоугольные координаты точки и вектора в пространстве Скалярное произведение двух векторов Векторное произведение двух векторов Смешанное проллзведенис трех векторов……. Ол.лав.гение 3. Аналитическая геометрия в пространстве Уравпсние плоскости Основные зацачи па плоскость Уравнения прямой Прямая и плоскость Сферические и цилиндрические поверхности,.
Свойства пределов. Раскрытие неопределенностей 0 ж вида — и — . 0 ос 90 93 ма- ашы Предел отношения — — пря а -а 0 Неопределенности вида ос — ос и 0 ос …. Смешанныс примеры па вычислснне пределов Сравнение бесконечно малых Непрерывность функции Асимптоты Число с Глава 6. Прончводнап н дифференциал !08 Произво,лные алгебраических и тригонометрических функций .. Произво.шая сложной функции Касательная и нормаль к плоской кривой Случаи нелиффсренцируемости непрерывной функции .. Производныс логарифмических и показательных функций Проллзлзодные обратных тригосл(эалетрическллх функпий .
Произво„сные гиперболических функпий Смсшанныс прилсеры и задачи на дифферснпированис Производныс высших порядков. ………….. Производная неявной функции Глава з2. ~ 3. 54. 3 6. ‘3 7 ‘3 4. 3 5. з 6. з 7. з 8. 59 510 3 2. ‘3 3 ~4 3 6. з 7. 38 3 9. з10 4. Высшая алгебра Определители Сис гомы .шнейных Компдексные числа Уравнения кысших уравнений уравнений степеней и приближенное решение 62 62 68 70 72 74 99 100 Г01 !02 105 106 108 !10 111 !13 !14 116 !17 118 119 !2! Огла влепив 123 124 Глава 11 ‘2 2 ~3 21 55 ‘2 6 Глава 140 110 142 145 147 148 150 24 ~л 6 17 152 1оо ‘2 8 156 157 ‘210 160 ‘2 5 26 27 ‘2 9 178 1’ л а в а 178 !80 ‘2 11. Дифференциал функции л 12.
………….. Производная неявной функции Глава з2. ~ 3. 54. 3 6. ‘3 7 ‘3 4. 3 5. з 6. з 7. з 8. 59 510 3 2. ‘3 3 ~4 3 6. з 7. 38 3 9. з10 4. Высшая алгебра Определители Сис гомы .шнейных Компдексные числа Уравнения кысших уравнений уравнений степеней и приближенное решение 62 62 68 70 72 74 99 100 Г01 !02 105 106 108 !10 111 !13 !14 116 !17 118 119 !2! Огла влепив 123 124 Глава 11 ‘2 2 ~3 21 55 ‘2 6 Глава 140 110 142 145 147 148 150 24 ~л 6 17 152 1оо ‘2 8 156 157 ‘210 160 ‘2 5 26 27 ‘2 9 178 1’ л а в а 178 !80 ‘2 11. Дифференциал функции л 12.
Параметрические уравнения кривой 7. Приложения производной Скорость и усьорепие Теоревлы о среднем Раскрытие неопределенностей. Правило Лопиталя Возрастание и убывание функции. Максимум и минимум За,лачи о наибольших и наименьших значениях величин Направлеллие выпуклости н точки перегиба кривой.
Построение кривых 8. Неопределенный интеграл Неопределенный интеграл. Интегрирование разложением Интегрирование подстановкой и непосредственное г!в / л/л / л/в Интегралы вида „,, / / 22 ~ о2′ / /о2,2′ / /гав+ 5 и к ним приводнщисся Интегрирование по частям. .. Интегрирование тригонометрических функций Интегрирование рациональных алгебраических функций Интегрирование некоторых иррациональных алгебраических функций Интегрирование ллекоторых трансцендентных фушьций Интегрирование гиперболических функций.
.. Интегрирование тригонометрических функций Интегрирование рациональных алгебраических функций Интегрирование некоторых иррациональных алгебраических функций Интегрирование ллекоторых трансцендентных фушьций Интегрирование гиперболических функций.
Гиперболические подстановки Смешанные приьлерьл на интегрирование 1’лава 9. Определенный интеграл Вычисление определенного интеграла Вычисление площадей Объем тела вращелшя Длина дуги плоской кривой Площадь поверхности вращения Задачи из физики Несобственные интегралы Среднее значение функции . лйоралула трапеций и формула Симпсона 10. Кривизна плоской и пространственной кривой …. Кривизна п.щекой кривой. Центр и радиус кривизны.
‘!лзоллота Длина дуги кривой в пространстве………….. 127 127 128 !31 133 136 138 160 163 165 167 169 170 172 175 176 Оллладхление 180 183 Глава 185 185 187 189 191 192 194 198 199 200 20! 203 20о Г л а в а 12. Дифференциальные уравнения 207 207 208 21! 217 219 221 3 10 111 222 51. 3 2. 3 ‘1. 35. 3 6. 3 7. 38. 39. 310 311 ‘3 12 Производная вектор-функцин по скаляру и ее механическое и геометрическое значение. Естественный трехгранник крввой Кривизна и кручение пространственной кривой 11.
3 6. 3 7. 38. 39. 310 311 ‘3 12 Производная вектор-функцин по скаляру и ее механическое и геометрическое значение. Естественный трехгранник крввой Кривизна и кручение пространственной кривой 11.
Частныо производные, полные дифференциалы и их приложения гйун1лции двух переменных и их геол1стрическос изобра- жсшле . Частпыс производные первого порядка Полный дифференциал первого порядка……….. Производные сложных функций Производньлс неявных фуншплй……………. Частные производные и полпыс,шффсренциалы высших порядков Инте! рирование полных дифференциалов Особые точки плоской кривой…………….. Огиоающая семейства плоских кривых Касательная плоскость и нормаль к поверхности Гкалярное поле..1инии и поверхности уровней. Производная в данном направлении. Градиент Экстремум функции двух переменных………… Понятие о дифференциальном уравнении……….
Дифференциальное уравнение первого порядка с разделяющимися переменпымп. Ортогональпые траектории… Дифференциальные уравнения первого порядка 1) однородное, 2) линейное, 3) Бернулли ;1ифферснпиа. льныс уравнения, содсржа1пие дифференпиалы произведения и частного……………. Дифференциальные уравнения первого порядка в полных дифференциалах. 1111тсгрирующллй множитель Дифференпиальпые уравнения первого порядка, не разрешенные относительно производной.
льныс уравнения, содсржа1пие дифференпиалы произведения и частного……………. Дифференциальные уравнения первого порядка в полных дифференциалах. 1111тсгрирующллй множитель Дифференпиальпые уравнения первого порядка, не разрешенные относительно производной.
Уравнения Лагранжа и Клеро Дифференциальные уравнения высших порядков, допускающие понижение порядка Линейные однородные дифференциальные уравнения с постояппымя кооффициснтами Линейные неоднородные циффе1н.*нпиальныс уравнения с постоянными 1 озффнцнептами Примеры дифференциальных уравнений разных типов ;1инейное дифференциальное уравнение Эйлера ж» у1″1 + ч — 1 (ч — 11+ +в, 1+ л( Оглавление ‘! 12. Системы линейных дифференциальных уравнений с постоянпымя козффициентами …………….. 223 1 13.
Тинейные дифференциальные уравнения в частных проиаводных второго порядка (хгетод характеристик)….. 224 Глава 226 226 228 230 231 232 234 ‘3 3 ~4 !! 5 36 ‘а 7 14. Ряды Ответы 260 332 Приложение. Некоторые кривые (для справок) Глава 5! т2. т’ 3. т4. а 5. т 7. 13 Двойные, тройные и криволинейные интегралы Вычисление площади с помощью двойг|ого интеграла Пептр масс и момент инерции площади с равномерно раг- прелсленной массой (при плотности р = 1)……… Вычислснис объема с помощью двойного интеграла !!лощади кривых поверхностей «1’ройной интеграл и ого приложения Приволинейный ингеграгг.
т’ 3. т4. а 5. т 7. 13 Двойные, тройные и криволинейные интегралы Вычисление площади с помощью двойг|ого интеграла Пептр масс и момент инерции площади с равномерно раг- прелсленной массой (при плотности р = 1)……… Вычислснис объема с помощью двойного интеграла !!лощади кривых поверхностей «1’ройной интеграл и ого приложения Приволинейный ингеграгг.
Формула Грина……… Поверхностные интегралы. Формулы Остроградского Гаусса и Стокса Числовые ряды Равномерная сходимость функционального ряда .. Сгепенпые ряды 1’яды Тейлора и 5!аклорепа Приложения рядов к приближенным вычислениям Ряд Тейлора для функции двух переменных…. Ряд Фурье. Интеграл Фурье…………..
242 242 245 247 249 251 254 ИЗ ПРЕДИСЛОВИЯ АВТОРА К ТРЕТЬЕМУ ИЗДАНИЮ В настоящем «Сборнике » подобраны н методически распределены задачи и примеры по аналитической геометрии и математическому аналнсу. В начале каждого параграфа приведены формулы, определения и другие краткие пояснения теории, необходимые для решения последующих задач.
Кроме того, при таком распределении задач легко опреде.шть минимум, необходимый для усвоения курса, который мо«кпо рекомендовать заочникам илп для работы на вечерних факультетах. «Сборник » может быть использован как для работы под руководством преподавателя, так н для самостоятельного изучения курса высшей математики во втузах, так как почти все задачи имен » т ответы, а некоторые н решения н, кроме того, ко многим задачам в тексте нлн в ответах даны указания к вх решению. Этому же способствуют краткие пояснения теории.
ОТ РЕДАКЦИИ Издание настоящего «Сборника » осуществлено в связи с многочисленными заявками, поступившими в наш адрес от математических кафедр, библиотек, студентов и преподавателей различных втузав России.
Координаты точки на прямой и на плоскости. Расстояние между двумя точками 1′. Расстояние г1 между тгжками А)иг) и Л)аа) на оси: — *- ° 1- Т* — вг. 2′. Величина ЛВ )а.псбраип:сная) напргтнвннага атрвакгг на аса: )2) АВ = Ха — к1. 3′. Р асс та я н ис г1 мсгггду точками Л)иг, уг) и В)ха, уа) н а плоскости: 4′. Пров к ц и и на аси координат направлвннава отравна, иггн ввктаРа г)ут на плоскости с началом Л(ив, Уг) и концом В)игб Уа): ггрхА~ Л иа лм гйга’4у) 1 ‘гуа ум 1. Построить ца числовой оси гочки А( — 5), В(+4) н С( — 2) и найти величины ЛВ, ВС и ЛС» отрезков на оси, Проверитгч что АВ+ ВС= АС.
РЕШЕНИЕ ЗАДАЧ ПО МАТЕМАТИКЕ Задания по высшей математике. Большой сборник решений Контрольные работы по курсу «математика» для I ОЗО СП Ф. Клейн — Элементарная математика с точки зрения высшей Высшая математика на Mathcad 2009 Высшая математика в примерах и задачах. Компьютерный практик Линьков В.М., Яременко Н.Н. Сборник книг. Высшая математика: теория вероятностей Высшая математика: обыкновенные дифференциальные уравнения Высшая математика: математический анализ Высшая математика: динамические системы Высшая математика: вариационное исчисление и вариационные принципы Высшая математика: асимптотические методы Высшая математика в примерах и задачах В. Д. Черненко Практические занятия
по высшей математике И. Сборник индивидуальных задач по высшей математике А. П. Рябушко, В. В. Бархатов Высшая математика в упражнениях и задачах Данко, Попов, Кожевникова Курс высшей математики Ларин А.А Справочник по высшей математике И.Фихтенгольц Лекции по высшей математике Ларин А. А. Минеева О.М.,Неклюдов А.В.,Скуднева О.В. — Несобственные интегралы Минорский В. П. — Сборник задач по высшей математике Дмитрий Письменный — Конспект лекций по высшей математике Сборник справочников по высшей математике Зимина О.В., Кириллов А.И., Сальникова Т.А. — [Математика] Высшая математика (решебник) Ермаков В.И. — [Математика] Сборник задач по высшей математике для экономистов под ред. Ермакова В.И. А. В. Матросов — Maple 6. Решение задач высшей математики и механики Я.Б. Зельдович, И.М. Яглом — Высшая математика для начинающих физиков и техников Шипачев В.С. — Шипачев. Высшая Математика. djvu Кремер Н. Кузнецов Л.А. — Сборник заданий по высшей математике (типовые расчеты) Минорский В.П. — Сборник задач по высшей математике: Учеб. пособие для втузов Выгодский М.Я. — Справочник по высшей математике И.И.Ляшко, А.К.Боярчук,Я.Г.Гай,Г.П.Головач. — Справочное пособие по высшей математике (АнтиДемидович) — 5 томов Выгодский М.Я. — Справочник по высшей математике Я.С. Бугров, С.М. Никольский — Высшая математика Смирнов В.И. Курс высшей математики (в пяти томах) Книги по высшей и линейной алгебре [DjVu, PDF] {18 книг} Справочник по высшей математике [DJVU] 3000 конкурсных задач по математике. Куланин Е.Д., Норин В.П., Федин С.Н., Шевченко Ю.А. (2003, 624с.) Алгебра и теория чисел для математических школ. Алфутова Н.Б. Устинов А.В. (2002, 264с.) Алгебра,
тригонометрия и элементарные функции. Потапов
М.К., Александров В.В., Пасиченко П. Введение в высшую математику. Черкасов А.Н. (1964, 244с.) Высшая математика для начинающих и ее приложения к физике. Зельдович Я.Б. (1963, 560с.) Высшая математика для начинающих физиков и техников. Зельдович Я.Б., Яглом И.М. (1982, 512с.) Геометрические неравенства и задачи на максимум и минимум. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. (1970, 336с.) Геометрические оценки и задачи из комбинаторной геометрии. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. (1974, 384с.) Геометрия. Прасолов В.В., Тихомиров В.М. (2007, 328с.) Геометрия масс. Балк М.Б., Болтянский В.Г. (1987, 160с.) Задачи вступительных экзаменов по математике (МГУ). Нестеренко Ю.В., Олехник С.Н., Потапов М.К. (1996, 632с.) Задачи на составление уравнений. Лурье М.В., Александров Б.И. (1990, 96с.) Задачи по алгебре, арифметике и анализу. Прасолов В.В. (2005, 545с.) Задачи по
геометрии (планиметрия). Задачи по геометрии (стереометрия). Шарыгин И.Ф. (1984, 160с.) Задачи по математике. Алгебра и анализ. Башмаков М.И., Беккер Б.М., Гольховой В.М. (1982, 192с.) Задачи по планиметрии. Прасолов В.В. (2006, 640с.) Задачи по элементарной математике и началам математического анализа. Бачурин В.А. (2005, 712с.) Задачи с параметрами. Горнштейн П.И., Полонский В.Б., Якир М.С. (1992, 290с.) Задачи с параметром и другие сложные задачи. Козко А.И., Чирский В.Г. (2007, 296с.) Избранные задачи и теоремы элементарной математики. ч. 1 Арифметика и алгебра. Шклярский Д.О, Ченцов Н.Н. Яглом И.М. (1976, 384с.) Избранные задачи и теоремы элементарной математики. ч. 2 Геометрия (Планиметрия). Шклярский Д.О, Ченцов Н.Н. Яглом И.М. (1952, 380с.) Избранные задачи и теоремы элементарной математики. ч. 3 Геометрия (Стереометрия). Шклярский Д.О, Ченцов Н.Н. Яглом И.М. (1954, 267с.) Избранные задачи
повышенной сложности по математике. Как решать задачи по математике на вступительных экзаменах. Мельников И.И., Сергеев И.Н. (1990, 304с.) Как решают нестандартные задачи. Канель-Белов А.Я., Ковальджи А.К. (2008, 4-е изд., 96с.) Конкурсные задачи по математике. Потапов М.К., Олехник С.Н., Нестеренко Ю.В. (2003, 3-е изд., 416с.) Лекции и задачи по элементарной математике. Болтянский В.Г., Сидоров Ю.В., Шабунин М.И. (1974, 592с.) Математика — абитуриенту. Ткачук В.В. (2007, 14-е изд., 976с.) Математика: Пособие для поступающих в вузы. Моденов В.П. (2002, 800с.) Математика: Справочные материалы. Гусев В.А., Мордкович А.Г. (1990, 416с.) Сборник задач по математике для поступающих в вузы. под ред. М.И. Сканави (с решениями, несколько книг) (1992-2003) Сборник задач по математике с решениями. Кравчук Д.Н. и др. (1997, 192с.) Сборник задач по
математике Стэнфордского университета: с подсказками и решениями. Сборник задач по элементарной математике повышенной трудности. Шахно К.У. (1965, 523с.) Свойства геометрических фигур — ключ к решению любых задач по планиметрии. Юзбашев А.В. (2005, 216с.) Современная элементарная алгебра в задачах и решениях. Гашков С.Б. (2006, 328с.) Справочник по математике для поступающих в вузы. Решение задач с параметрами. Родионов Е.М. (1992, 144с.) Справочник по элементарной математике. Выгодский М.Я. (2006, 509с.) Стереометрические задачи и методы их решения. Готман Э.Г. (2006, 160с.) Стереометрия. Геометрия в пространстве. Александров А.Д., Вернер А.Л., Рыжик В.И. (1998, 576с.) Теоремы и задачи по алгебре и элементарным функциям. Сивашинский И.Х. (1971, 368с.) Тригонометрия. Гельфанд И.М., Львовский С.М., Тоом А.Л. (2003, 200с.) Уравнения в школьном курсе математики. Бекаревич А.Н. (1968, 192с.) Уравнения и
неравенства. Уравнения и неравенства, содержащие параметры. Ястребинецкий Г.А. (1972, 128с.) Учебное пособие по математике. Сахабиева Г.А., Сахабиев В.А. (2005, 160с.) Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. Шарыгин И.Ф. (1989, 352с.) Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред. шк. Шарыгин И.Ф. (1991, 384с.) Что такое математика? Р. Курант, Г. Роббинс (2001, 568с.) Школьный курс математики: Краткий справочник. Мордкович А.Г. (1995, 48с.) Элементарная геометрия. В 2-х томах. Планиметрия. Стереометрия. Понарин Я.П. (2004, 312с.; 2006, 256с.) Элементарная геометрия. В двух частях. Планиметрия. Стереометрия. Ж. Адамар (1948 -608с; 1951 -760с.) Элементарная математика в современном изложении. Люсьенн Феликс (1967, 488с.) Элементы
математического анализа. Адамар Ж. Исследование психологии процесса
изобретения в области математики
РЕШЕНИЕ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ Магазинников Л.И. Высшая математика IV. Теория вероятностей: Учебное пособие.- Томск: — Томский гос. университет систем управления и радиоэлектроники, 200. — 150с. Секей Г. — Парадоксы в теории вероятностей и математической статистике Сборник книг. В.А.Колемаев,В.Н. Калинина-Теория вероятностей в примерах и задачах:учебное пособие Борель — Теория вероятности. Вероятность и достоверность Е. С. ВЕНТЦЕЛЬ, Л. А. ОВЧАРОВ — ЗАДАЧИ И УПРАЖНЕНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ В. Феллер (под ред. А. Н. Колмогорова) — Введение в теорию вероятностей и ее приложения.(т. 1, т. 2) Математическая статистика и теория вероятностей [2009, Обычный текст] Н. Ш. Кремер / N. Sh. Kremer — Теория вероятностей и математическая статистика [2004, DjVu] В. Е. Гмурман — Теория Вероятностей И Математическая Статистика(Учебник и Задачник). Книги по теории вероятностей и математической статистике Боровков А.А. — Теория вероятностей Колмогоров, Феллер — Теория вероятностей (Колмогоров и Феллер — 2 книги) Лоэв М. — Теория вероятностей М.В. Козлов — Элементы теории вероятностей в примерах и задачах Гнеденко Б.В. — Курс теории вероятностей Колемаев В.
РЕШЕНИЕ ЗАДАЧ ПО СТАТИСТИКЕ Б.И. Башкатов — Социально-экономическая статистика Никитина Н.Ш. — Математическая статистика для экономистов Секей Г. — Парадоксы в теории вероятностей и математической статистике Шибалкин А. Е. — Математическая статистика — тесты, для промежуточного итогового контроля Математическая статистика и теория вероятностей Математическая статистика для психологов Теория вероятностей и математическая статистика Айвазян С.А., Бухштабер В.М., Енюков Е.С. — Прикладная статистика С.А.Айвазян В.С.Мхитарян — Прикладная статистика и основы эконометрки Минашкин В.Г. — Теория статистики Ван дер Варден — Математическая статистика Колемаев В.А., Письменный Д., Кибзун А.И. — Теория вероятностей и математическая статистика»
РЕШЕНИЕ ЗАДАЧ ПО ЭКОНОМИКЕ Черника Д. Схиртладзе А.Г. Ревенко Н.Ф. Гайворонская К.Д. — Экономика предприятия: Сборник задач: Учебное пособие для вузов (под ред. Ревенко Н.Ф.) Экономика организаций (предприятий) под ред. проф. В.Я. Горфинкеля, проф. В. А. Швандера [2003, PDF] Афанасьев М.Ю., Суворов Б.П. — Исследование операций в экономике: модели, задачи, решения [2003, DOC] Розен В.В. — Математические модели принятия решений в экономике [2002, DjVu] Мулен Э. (пер. с
франц.) — Теория игр с примерами из математической экономики [1985,
DjVu] |
Высшая математика (книги 2010-2012 гг.)
Агальцов В. П. Математические методы в программировании : учеб. / В. П. Агальцов. — Изд. 2-е, перераб. и доп. — Москва : ФОРУМ, 2010. — 239 с.
/ В. П. Агальцов. — Изд. 2-е, перераб. и доп. — Москва : ФОРУМ, 2010. — 239 с.
Аладьев В. З. Системы компьютерной алгебры: Maple: искусство программирования : произв.-практ. изд. / В. З. Аладьев. — Москва : Лаборатория Базовых Знаний, 2010. — 791 с.
Алгоритмы. Построение и анализ : [учеб.] / Т. Кормен [и др.]. — 2-е изд. — Москва ; Санкт-Петербург ; Киев : Вильямс, 2011. — 1290 с.
Александров А. Д. Геометрия : учеб. / А. Д. Александров, Н. Ю. Нецветаев. — 2-е изд., испр. — Санкт-Петербург : БХВ-Петербург, 2010. — 612 с.
Балдин К. В. Высшая математика : учеб. / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. — Москва : Флинта: МПСИ, 2010. — 359 с.
Балдин К. В. Математическое программирование : учеб. / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев. — 2-е изд. — Москва : Дашков и К°, 2012. — 218 с.
Барашков А. С. Математика : [учеб.] / А. С. Барашков. — Москва : АСТ: СЛОВО ; Владимир : ВКТ, 2011. — 479 с.
С. Математика : [учеб.] / А. С. Барашков. — Москва : АСТ: СЛОВО ; Владимир : ВКТ, 2011. — 479 с.
Белякова Е. И. Начертательная геометрия : учеб. пособие / Е. И. Белякова, П. В. Зелёный. — 3-е изд., испр. — Минск ; Москва : Новое знание: ИНФРА-М, 2012. — 264 с.
Битнер Г. Г. Теория вероятностей : учеб. пособие / Г. Г. Битнер. — Ростов-на-Дону : Феникс, 2012. — 330 с.
Блау С. Л. Финансовая математика : учеб. / С. Л. Блау, С. Г. Григорьев. — М. : Академия, 2011. — 189 с.
Бобоева Р. М. Математико-статистические модели анализа и прогнозирования рынка труда (на примере Республики Таджикистан) : автореф… канд. экон. наук: 08.00.13 / Р. М. Бобоева ; Ин-т предпринимательства и сервиса М-ва энергетики и пром-ти Респ. Таджикистан. — Душанбе : [б. и.], 2012. — 24 с.
Бубнов В. А. Линейная алгебра. Компьютерный практикум : [учеб. пособие] / В. Бубнов, Г. Толстова, О. Клемешова. — 2-е изд., испр. и доп. — Москва : Лаборатория Базовых Знаний, 2010. — 168 с.
Бубнов, Г. Толстова, О. Клемешова. — 2-е изд., испр. и доп. — Москва : Лаборатория Базовых Знаний, 2010. — 168 с.
Валитов Ш. М. Математика в экономике : учеб. пособие / Ш. М. Валитов, Р. Ш. Марданов. — [Москва] : Экономика, 2011. — 182 с.
Вентцель Е. С. Теория вероятностей : учеб. / Е. С. Вентцель. — 11-е изд., стер. — Москва : КноРус, 2010. — 658 с.
Виленкин И. В. Высшая математика. Интегралы по мере. Дифференциальные уравнения. Ряды : [учеб. пособие] / И. В. Виленкин, В. М. Гробер, О. В. Гробер. — Ростов-на-Дону : Феникс, 2011. — 300 с.
Виленкин И. В. Высшая математика. Линейная алгебра. Аналитическая геометрия. Дифференциальное и интегральное исчисление : [учеб. пособие] / И. В. Виленкин, В. М. Гробер. — Изд. 6-е. — Ростов-на-Дону : Феникс, 2011. — 415 с.
Высшая математика в упражнениях и задачах : в 2 ч.: [учеб. пособие для вузов] / П. Е. Данко [и др.]. — 7-е изд., испр. — Москва : Мир и Образование [и др.]. — Ч. 1. — 2012. — 368 с.
Е. Данко [и др.]. — 7-е изд., испр. — Москва : Мир и Образование [и др.]. — Ч. 1. — 2012. — 368 с.
Высшая математика для экономистов : курс лекций / П. С. Геворкян [и др.]. — Москва : Экономика, 2010. — 351 с.
Высшая математика для экономистов : учеб. / Н. Ш. Кремер [и др.]. — 3-е изд. — Москва : ЮНИТИ, 2010. — 479 с.
Высшая математика для экономистов. Практикум : учеб. пособие / Н. Ш. Кремер [и др.]. — 2-е изд., перераб. и доп. — Москва : ЮНИТИ, 2010. — 478 с.
Высшая математика для экономических специальностей : учеб. и практикум / Н. Ш. Кремер [и др.]. — 3-е изд., перераб. и доп. — Москва : Юрайт, 2011. — 909 с.
Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике : учеб. пособие / В. Е. Гмурман. — 11-е изд., перераб. и доп. — Москва : Юрайт, 2011. — 404 с.
Гмурман В. Е. Теория вероятностей и математическая статистика : учеб. пособие / В. Е. Гмурман. — 12-е изд. — Москва : Юрайт, 2012. — 479 с.
Е. Теория вероятностей и математическая статистика : учеб. пособие / В. Е. Гмурман. — 12-е изд. — Москва : Юрайт, 2012. — 479 с.
Григорьев В. П. Сборник задач по высшей математике : учеб. пособие / В. П. Григорьев, Т. Н. Сабурова. — Москва : Академия, 2010. — 155 с.
Гринченков Д. В. Математическая логика и теория алгоритмов для программистов : учеб. пособие / Д. В. Гринченков, С. И. Потоцкий. — Москва : КноРус, 2010. — 206 с.
Гулиян Б. Ш. Математика. Базовый курс : учебник / Б. Ш. Гулиян, Р. Я. Хамидуллин. — 2-е изд., перераб. и доп. — Москва : Московская финансово-промышленная академия, 2011. — 709 с.
Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах : учеб. пособие / А. Б. Васильева [и др.]. — Изд. 3-е, испр. — Санкт-Петербург [и др.] : Лань, 2010. — 429 с.
Есипов Б. А. Методы исследования операций : учеб. пособие / Б. А. Есипов. — Санкт-Петербург [и др.] : Лань, 2010. — 253 с.
пособие / Б. А. Есипов. — Санкт-Петербург [и др.] : Лань, 2010. — 253 с.
Жуков В. М. Практические занятия по математике: теория, задания, ответы : [учеб. пособие] / В. М. Жуков. — Ростов-на-Дону : Феникс, 2012. — 344 с.
Захаров Е. В. Уравнения математической физики : учеб. / Е. В. Захаров, И. В. Дмитриева, С. И. Орлик. — Москва : Академия, 2010. — 315 с.
Ильин В. А. Высшая математика : учеб. / В. А. Ильин, А. В. Куркина. — 3-е изд., перераб. и доп. — [Москва] : Проспект: Изд-во Московского университета, 2011. — 592 с.
Карлов А. М. Теория вероятностей и математическая статистика для экономистов : учеб. пособие / А. М. Карлов. — Москва : КноРус, 2011. — 260 с.
Конышева Л. К. Основы теории нечетких множеств : для бакалавров и специалистов: учеб. пособие / Л. К. Конышева, Д. М. Назаров. — Санкт-Петербург [и др.] : Питер, 2011. — 190 с.
Красс М. С. Математика для экономистов : учеб. пособие / М. С. Красс, Б. П. Чупрынов. — Санкт-Петербург [и др.] : Питер, 2010. — 464 с.
Красс М. С. Математика для экономического бакалавриата : учеб. / М. С. Красс, Б. П. Чупрынов. — Москва : ИНФРА-М, 2011. — 471 с.
Красс М. С. Математические методы и модели для магистрантов экономики : учеб. пособие / М. С. Красс, Б. П. Чупрынов. — 2-е изд., доп. — Санкт-Петербург [и др.] : Питер, 2010. — 496 с.
Кузнецов А. В. Высшая математика. Математическое программирование : учеб. / А. В. Кузнецов, В. А. Сакович, Н. И. Холод. — Изд. 3-е, стер. — Санкт-Петербург; Москва Краснодар : Лань, 2010. — 351 с.
Кузнецова О. С. Краткий курс по теории вероятностей и математической статистике : [учеб. пособие] / О. С. Кузнецова. — Москва : Окей-книга, 2010. — 191 с.
Куликов В. В. Дискретная математика : учеб. пособие / В. В. Куликов. — Москва : РИОР, 2010. — 173 с.
В. Дискретная математика : учеб. пособие / В. В. Куликов. — Москва : РИОР, 2010. — 173 с.
Мазалов В. В. Математическая теория игр и приложения : учеб. пособие / В. В. Мазалов. — Санкт-Петербург [и др.] : Лань, 2010. — 446 с.
Макаров С. И. Математика для экономистов : учеб. пособие / С. И. Макаров. — 2-е изд., стер. — Москва : КноРус, 2011. — 263 с.
Малыхин В. И. Высшая математика : учеб. пособие / В. И. Малыхин. — 2-е изд., перераб. и доп. — Москва : ИНФРА-М, 2010. — 364 с.
Математика для экономистов. Задачник : учеб.-практ. пособие / Р. И. Горбунова [и др.]. — Москва : КноРус, 2011. — 358 с.
Мельников Ю. Б. Алгебра и теория чисел [Электронный ресурс] : электрон. учеб. для сопровождения лекций и практ. занятий / Ю. Б. Мельников. — Изд. 3-е, испр. и доп. — Электрон. текстовые дан. — Екатеринбург : [б. и.], 2010. — 1 эл. опт. диск (CD-ROM).
диск (CD-ROM).
Мельников Ю. Б. Алгебра и теория чисел: практикум по линейной и матричной алгебре, тензорам и полям Галуа : учеб. пособие / Ю. Б. Мельников. — Екатеринбург : [Изд-во УрГЭУ], 2010. — 281 с.
Минорский В. П. Сборник задач по высшей математике : [учеб. пособие] / В. П. Минорский. — Изд. 15-е. — Москва : Изд-во Физико-математической литературы, 2010. — 336 с.
Общий курс высшей математики для экономистов : учеб. / Б. М. Рудык [и др.]. — Москва : ИНФРА-М, 2010. — 655 с.
Павлов С. В. Теория вероятностей и математическая статистика : учеб. пособие / С. В. Павлов. — Москва : РИОР: ИНФРА-М, 2010. — 186 с.
Панкратьев Е. В. Элементы компьютерной алгебры : учеб. пособие / Е. В. Панкратьев. — Москва : Интернет-Университет Информационных Технологий: БИНОМ. Лаборатория знаний, 2010. — 247 с.
Пантина И. В. Вычислительная математика : учеб. / И. В. Пантина, А. В. Синчуков. — 2-е изд., перераб. и доп. — [Москва] : Московский финансово-промышленный университет «Синергия», 2012. — 175 с.
В. Вычислительная математика : учеб. / И. В. Пантина, А. В. Синчуков. — 2-е изд., перераб. и доп. — [Москва] : Московский финансово-промышленный университет «Синергия», 2012. — 175 с.
Петрова С. Н. Элементы теории устойчивости : учеб. пособие / С. Н. Петрова, О. В. Дружинина. — Екатеринбург : [Изд-во УрГЭУ], 2012. — 51 с.
Письменный Д. Т. Конспект лекций по высшей математике : [в 2 ч.] / Д. Письменный. — 10-е изд. — Москва : Айрис-пресс. — Ч. 1. — 2010. — 280 с.
Письменный Д. Т. Конспект лекций по высшей математике : [в 2 ч.] / Д. Письменный. — 7-е изд. — Москва : Айрис-пресс. — Ч. 2. — 2011. — 252 с.
Письменный Д. Т. Конспект лекций по высшей математике : [полн. курс] / Д. Т. Письменный. — 10-е изд., испр. — Москва : Айрис-пресс, 2011. — 603 с.
Письменный Д. Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам : [курс лекций] / Д. Т. Письменный. — 5-е изд. — Москва : Айрис-пресс, 2010. — 287 с.
Т. Письменный. — 5-е изд. — Москва : Айрис-пресс, 2010. — 287 с.
Попов А. М. Высшая математика для экономистов : учеб. / А. М. Попов, В. Н. Сотников. — Москва : Юрайт, 2012. — 564 с.
Прасолов А. В. Динамические модели с запаздыванием и их приложения в экономике и инженерии : учеб. пособие / А. В. Прасолов. — Санкт-Петербург [и др.] : Лань, 2010. — 192 с.
Примаков Д. А. Геометрия и топология : учеб. пособие / Д. А. Примаков, Р. Я. Хамидуллин. — [2-е изд., перераб. и доп.]. — Москва : Московская финансово-промышленная академия, 2011. — 267 с.
Рыбников К. К. Введение в дискретную математику и теорию решения экстремальных задач на конечных множествах : учеб. пособие / К. К. Рыбников. — Москва : Гелиос АРВ, 2010. — 317 с.
Самаров Е. К. Страховая математика. Практический курс : учеб. пособие / Е. К. Самаров. — Москва : Альфа-М : ИНФРА-М, 2011. — 79 с.
— 79 с.
Сборник задач по высшей математике для экономистов : учеб. пособие / П. С. Геворкян [и др.]. — [Москва] : Экономика, 2011. — 383 с.
Сборник задач по высшей математике. С контрольными работами : 1 курс / К. Н. Лунгу [и др.]. — 8-е изд. — Москва : Айрис-пресс, 2010. — 575 с.
Сборник задач по высшей математике. С контрольными работами : 2 курс / К. Н. Лунгу [и др.]. — 7-е изд. — Москва : Айрис-пресс, 2011. — 590 с.
Седелев Б. В. Методы конечных рядов Фурье и целевого синтеза как альтернативные инструменты исследования амплитудно-частотных структур временных рядов : науч. изд. / Б. В. Седелев. — Москва : [НИЯУ МИФИ], 2010. — 20 с.
Сидняев Н. И. Теория вероятностей и математическая статистика : учеб. / Н. И. Сидняев. — Москва : Юрайт, 2011. — 219 с.
Талалай П. Г. Начертательная геометрия на примерах : науч. изд. / П. Талалай. — Санкт-Петербург : БХВ-Петербург, 2011. — 271 с.
изд. / П. Талалай. — Санкт-Петербург : БХВ-Петербург, 2011. — 271 с.
Талалай П. Г. Начертательная геометрия. Инженерная графика : интернет-тестирование базовых знаний : учеб. пособие / П. Г. Талалай. — Санкт-Петербург ; Москва ; Краснодар : Лань, 2010. — 254 с.
Теория вероятностей и математическая статистика : учеб. пособие / В. С. Мхитарян [и др.]. — 2-е изд., перераб. и доп. — Москва : Московская финансово-промышленная академия, 2011. — 327 с.
Теория вероятностей и математическая статистика : учеб. пособие / Л. Г. Бирюкова [и др.]. — Москва : ИНФРА-М, 2010. — 286 с.
Турецкий В. Я. Математика и информатика : учеб. пособие / В. Я. Турецкий. — 3-е изд., перераб. и доп. — Москва : ИНФРА-М, 2010. — 558 с.
Фадеева Л. Н. Теория вероятностей и математическая статистика : учеб. пособие / Л. Н. Фадеева, А. В. Лебедев. — 2-е изд., перераб. и доп. — Москва : Эксмо, 2010. — 493 с.
и доп. — Москва : Эксмо, 2010. — 493 с.
Фролов С. А. Начертательная геометрия : учеб. / С. А. Фролов, А. А. Чекмарев. — 3-е изд., перераб. и доп. — Москва : ИНФРА-М, 2010. — 285 с.
Хомяков П. М. Системный анализ : экспресс-курс лекций: [в 10 лекциях]: [учеб. пособие] / П. М. Хомяков. — Изд. 4-е. — Москва : URSS: [Изд-во ЛКИ], 2010. — 212 с.
Чекмарев А. А. Начертательная геометрия и черчение : учеб. / А. А. Чекмарев. — 3-е изд., перераб. и доп. — Москва : Юрайт, 2011. — 471 с.
Шипачев В. С. Высшая математика. Базовый курс : учеб. пособие / В. С. Шипачев. — 8-е изд., перераб. и доп. — Москва : Юрайт, 2011. — 447 с.
Шипачев В. С. Высшая математика. Полный курс : учеб. / В. С. Шипачев. — 4-е изд., испр. и доп. — Москва : Юрайт, 2012. — 608 с.
Юдин Д. Б. Линейное программирование. Теория, методы и приложения : [моногр. ] / Д. Б. Юдин, Е. Г. Гольштейн. — Изд. 2-е. — Москва : URSS: [КРАСАНД], 2012. — 424 с.
] / Д. Б. Юдин, Е. Г. Гольштейн. — Изд. 2-е. — Москва : URSS: [КРАСАНД], 2012. — 424 с.
Консультационные материалы для несовершеннолетних | SUNY Geneseo
Цель этой страницы — предоставить вам, студенту, дополнительную информацию о различных курсах, которые мы предлагаем на факультете математики. В настоящее время он находится в стадии разработки, и его не следует рассматривать как полное и всестороннее описание всех доступных курсов. Его также не следует рассматривать как замену вашему научному руководителю. Мы просто предоставляем вам эту информацию в качестве дополнительной помощи при планировании вашей карьеры в бакалавриате.
Ниже вы найдете полезную информацию о математических курсах, которые особенно хороши для разных профессий, а также немного больше информации о конкретных курсах. Для получения дополнительной информации о конкретном курсе см. Каталог курсов и Страницы ротации курсов.
Информацию о конкретных требованиях к получению степени см. в описании программ.
в описании программ.
- Какие курсы я должен выбрать, если я:
- Math Major?
- Незначительная математика?
- Основная специальность начального образования с математической концентрацией?
- Чему мы учимся на этих курсах?
Какие курсы я должен пройти в качестве второстепенного по математике?
Если вы не получили зачет по предварительному исчислению в средней школе или нуждаетесь в переподготовке, пройдите Предварительное исчисление (Математика 112). Обратите внимание, что это , а не засчитывается в математику Minor.
Если вы не получили зачет по математике в колледже, сдайте математику 1 (математика 221).
Если вы завершили Исчисление 1, переходите к Исчислению 2 (Математика 222).
Помимо этих двух обязательных курсов вам потребуются 4 дополнительных курса, выбранных из следующих: «Дискретная математика» (математика 237) или «Введение в доказательство» (математика 239), «Исчисление 3» (математика 223), «Линейная алгебра I» (математика 233) или 3- кредит 300-уровневая математика по выбору.

Если вы закончили сдавать Calc 2, возьмите один или два из Calculus 3 (Math 223), Linear Algebra I (Math 233) или Mathematical Proof (Math 239).). Каждая из этих трех прекрасно дополняет другие. Некоторые преподаватели считают, что студенты должны сдавать Calc 3 сразу после Calc 2. Линейную алгебру можно сдавать в любое время после Calc 2.
НЕ изучайте дискретную математику (математика 237), если вы думаете, что захотите пройти курсы 300-уровневой математики с введением в доказательство (математика 239) в качестве предварительного условия, или если вы думаете, что когда-нибудь захотите получить двойную специализацию по математике, поскольку Math 237 не засчитывается в основной курс Math.
Вы можете сдать Элементы вероятности и статистики (математика 242), прикладную статистику (математика 262), вероятность и статистику (математика 341) или статистику (математика 361), чтобы выполнить требования к статистике. Обратите внимание, что Math 361 предлагается только в Spring, а Math 242 предлагается по мере необходимости.
 Кроме того, обратите внимание, что математика 223 является обязательным условием для математики 341, а математика 223 и математика 360 являются предварительными условиями для математики 361. Также обратите внимание, что математика 242 и математика 262 не засчитываются в основной курс математики.
Кроме того, обратите внимание, что математика 223 является обязательным условием для математики 341, а математика 223 и математика 360 являются предварительными условиями для математики 361. Также обратите внимание, что математика 242 и математика 262 не засчитываются в основной курс математики.
Если вы изучаете физику…
…тогда вы должны пройти математику 223 и дифференциальные уравнения (математика 326) в дополнение к математике 221 и математике 222. Настоятельно рекомендуется пройти линейную алгебру 1 (математика 233) в качестве предварительного или дополнительного необходим для изучения математики 326. Неплохой идеей будет какая-нибудь статистика. Кроме того, если вы получаете Intro to Proof (Math 239), другие хорошие математические опции включают векторный анализ (Math 350), комплексный анализ (Math 371) и вейвлеты и их приложения (Math 382).
Если вы специалист по экономике…
…не берите прикладное исчисление (математика 213), берите исчисление (математика 221). Math 233 — очень хороший вариант, как и некоторые статистические данные, а также Linear Programming and Operations Research (Math 332).
Math 233 — очень хороший вариант, как и некоторые статистические данные, а также Linear Programming and Operations Research (Math 332).
Если вы изучаете биологию…
…вам следует выбрать Математика 222 вместо Математики для биологов (Математика 228). Моделирование биологических систем (Math 340) является обязательным. Неплохой идеей было бы ведение какой-либо статистики, и если вам нравится моделирование, дифференциальные уравнения (математика 326) — хорошая идея, при условии, что вы получите Calc 3 (математика 223) в качестве предварительного условия и математику 233 в качестве предварительного условия. или сопутствующий реквизит.
Примечание. Математика 237, Математика 242 и Математика 262 не будут засчитываться в основной курс математики.
Примечание. Все курсы должны быть завершены с оценкой C- или выше, чтобы засчитываться в Minor.
Чему мы учимся на этих курсах?
Базовые курсы
Продвинутые курсы
Базовые курсы
- 221 Исчисление I.
 Это курс, который рассказывает замечательную историю и дает вам практические навыки вдобавок. История посвящена трем вопросам: Что такое мгновенная скорость изменения? Чему равна площадь под кривой? Как они связаны? Хотя эта история была впервые рассказана более 300 лет назад Ньютоном (или Лейбницем?), ответы на поставленные вопросы продолжают лежать в основе большей части того, что мы делаем в практической и теоретической математике сегодня.
Это курс, который рассказывает замечательную историю и дает вам практические навыки вдобавок. История посвящена трем вопросам: Что такое мгновенная скорость изменения? Чему равна площадь под кривой? Как они связаны? Хотя эта история была впервые рассказана более 300 лет назад Ньютоном (или Лейбницем?), ответы на поставленные вопросы продолжают лежать в основе большей части того, что мы делаем в практической и теоретической математике сегодня.Для кого 221? Всем! Майоры, несовершеннолетние, концентраторы, дилетанты и специалисты по естественным наукам.
- 222 Исчисление II. Есть еще накипь? Да! Вы узнаете больше об интеграции и узнаете о логарифмах и экспоненциальных функциях. Вы узнаете о последовательностях, сериях и многом другом. Лучше всего взять это сразу после Исчисления 1. Вы не хотите ничего забыть — это вторая глава саги.
Для кого 222? Еще бы всем! Майоры, несовершеннолетние, концентраторы, дилетанты и специалисты по естественным наукам.

- 233 Линейная алгебра I. Этот курс изучает системы линейных уравнений, возникающие во многих областях математики, и практические приложения. Этот курс также служит мостом к высшей математике. Вы узнаете о векторных пространствах, линейной независимости и охвате. Вы должны взять это в начале второго года обучения, самое позднее.
Для кого 233? Это для майоров, концентраторов и несовершеннолетних. Это также очень полезно для бизнеса, экономики, статистики, физиков и других ученых, потому что у него так много приложений.
Курсы повышения квалификации
- 301 Математическая логика. Что такое математический объект? Что такое математическое доказательство? Что значит что-то доказать? Этот курс заставит вас исследовать свои предположения о том, как делается математика и каковы пределы математики.
Кто должен принимать 301 и когда? Определенно после того, как вы прошли 239 и освоились с абстрактными аргументами.
 Курс, который хорош для тех, кто собирается получить диплом по математике, философии или информатике. Также хорошо для тех, кто просто любит думать об основах нашего предмета.
Курс, который хорош для тех, кто собирается получить диплом по математике, философии или информатике. Также хорошо для тех, кто просто любит думать об основах нашего предмета.
- 302 Теория множеств. Множества — основа всего в математике! Узнайте, что мы предполагаем о множествах и что мы можем доказать о них. Потратьте время на знакомство с бесконечными ординалами и бесконечными кардиналами!
Кто должен принимать 302 и когда? Это абстрактный курс, поэтому вам должно быть удобно писать доказательства и усердно думать о необычных вещах. Так что берите его после 239 и, возможно, не в качестве первого курса математики с 300 уровнями. Отличный курс для студентов, планирующих поступление в аспирантуру, и для тех, кто действительно хочет исследовать множества и некоторые безумно большие числа.
- 303 Теория вычислительной сложности. Когда расчет, который занимает всю ночь, считается «быстрым»? Когда альтернативе нужно больше, чем оставшееся время жизни Вселенной, чтобы закончить.
 Пройдите этот курс, чтобы узнать, почему мы считаем, что такие расчеты существуют, а также исследовать границы математики и компьютерных наук, которые все еще полны важных, но оставшихся без ответа вопросов.
Пройдите этот курс, чтобы узнать, почему мы считаем, что такие расчеты существуют, а также исследовать границы математики и компьютерных наук, которые все еще полны важных, но оставшихся без ответа вопросов.Кто должен принимать 303 и когда? Пройдите этот курс, если вас интересуют связи между математикой и информатикой. Этот курс посвящен логическому анализу алгоритмов, а не их программированию, поэтому пройдите его после 239. Помимо этого предварительного условия, возьмите его как можно скорее, если хотите, поскольку он не так часто предлагается.
- 304 Теория вычислимости. Что значит вычислить? Казалось бы, простой вопрос, на который не было ответа до 1930-х годов, а затем с непосредственным следствием того, что, несмотря на очень реальные успехи вычислений, большинство вещей на самом деле вообще не поддаются вычислению. Выясните, откуда все это взялось и что это значит, и по ходу дела сделайте несколько аккуратных связей с математической логикой.

Кто должен принимать 304 и когда? Это еще один хороший курс для студентов, интересующихся общими основами математики и информатики. Это также интересно для студентов, которым нравятся доказательства и логика — такие студенты могут рассматривать это как часть пакета вместе с Math 301 и / или 302, чтобы распространять его на третий и четвертый курсы. Будьте готовы к большому количеству доказательств, особенно с использованием построений, противоречий и случайной индукции; это определенно то, что нужно взять после Math 239.
- 315 Комбинаторика. Комбинаторика считает. Считать не так просто, как кажется, но это универсально полезно, как кажется. Мы изучаем широкий спектр вопросов «сколько способов». Мы начинаем со знакомых и строим дальше, но всегда сохраняем связь с легко понятными вопросами.
Кто должен принимать 315 и когда? Это отличное первое блюдо после корректуры (или даже 237). Это относится ко всей математике — везде появляется счет.
 Он проявляется во многих прикладных контекстах и во многих теоретических ситуациях. Кроме того, простые вопросы со сложными ответами являются отличными примерами для учащихся средней школы.
Он проявляется во многих прикладных контекстах и во многих теоретических ситуациях. Кроме того, простые вопросы со сложными ответами являются отличными примерами для учащихся средней школы.
- 319 Теория чисел. Прайм-тайм для простых чисел! Теория чисел заключается в правильном понимании того, как работают числа, с упором на простые числа. Это может показаться простым, но факты о простых числах найти нелегко. Узнайте, почему простые числа улучшают работу модульной арифметики. По пути мы увидим, как мы можем использовать их сложную структуру для создания хороших схем шифрования.
Кто должен принимать 319 и когда? Этот курс можно пройти в любое время после 239, хотя 233 тоже рекомендуется. Это дает ценную информацию о природе натуральных чисел, которая будет полезна будущим учителям. Это может познакомить потенциальных исследователей с богатой и активной областью. Это также может открыть возможности для карьерного роста.

- 324 Реальный анализ I. Это берет курс Доказательства (239) и применяет его к аспектам исчисления 1. Теория, лежащая в основе исчисления, строго доказана. Это абсолютно необходимо для всех математических специальностей, особенно для учителей, которые могут преподавать расчет AP, и для всех, кто планирует заниматься какой-либо продвинутой математикой или вероятностью.
Кто должен принимать 324 и когда? Этот курс должен пройти каждый, кто занимается математикой. Любой, кто пытается расширить минор или концентрацию, чтобы оставить открытой возможность будущего изучения математики, должен взять его. Когда принимать? After Math 239. Если вы планируете заниматься математикой на более высоком уровне (возможно, в аспирантуре), вам следует пройти этот курс как можно раньше. Первый семестр младшего года лучше всего. Однако, если вам не совсем комфортно с Math 239, вы должны немного подождать и пройти один или два других 300-уровневых факультатива, прежде чем приступать к математике 324.

- 326 Дифференциальные уравнения. Этот курс является естественным продолжением Исчисления. Если вам нужна веская причина для изучения исчисления, этот курс для вас. Дифференциальные уравнения — это уравнения, в которые входят функции и их производные. Есть отличные приложения к финансам, экономике, биологии, физике и, действительно, к повседневной жизни.
Кто должен принимать 326 и когда? Всем, кто интересуется математическим моделированием или инженерией. Этот курс необходим для получения степени бакалавра прикладной математики. Это требуется от специалистов по физике и очень полезно для любых ученых. Если вам действительно понравилось исчисление, этот курс для вас. Если вы хотите заниматься финансовой инженерией или экономикой, этот курс для вас. Когда? Как можно скорее после Calc 3. Рекомендуется пройти Math 233 перед этим.
- 328 Теория обыкновенных дифференциальных уравнений. Этот курс является продолжением курса Math 326, охватывающего теорию существования в метрике для скалярного дифференциального уравнения с помощью итераций Пикара и теорем о неподвижной точке.
 Анализ фазовой плоскости двумерных линейных и нелинейных систем, включая теорию бифуркаций, устойчивость и предельные циклы, теорию индексов и теорему Пуанкараре-Бендиксона. Будут рассмотрены различные приложения к населению, экологические модели и физические системы.
Анализ фазовой плоскости двумерных линейных и нелинейных систем, включая теорию бифуркаций, устойчивость и предельные циклы, теорию индексов и теорему Пуанкараре-Бендиксона. Будут рассмотрены различные приложения к населению, экологические модели и физические системы.Кто должен принимать 328 и когда? Студенты, которые увлекались дифференциальными уравнениями, которые хотят увидеть теоретическую сторону ДУ, системы ДУ, приложения. Берите его всякий раз, когда его предлагают после Math 326. Его предлагают каждую вторую осень нечетных лет!
- 330 Абстрактная алгебра. Основная предпосылка абстрактной алгебры состоит в том, чтобы извлечь основные свойства алгебры, которые вы знаете из школьной алгебры и линейной алгебры, и абстрагировать их для использования в более общих целях. На предыдущих уроках алгебры мы, как правило, изучали определенный набор объектов, таких как числа, функции или матрицы, и узнавали об их алгебраических свойствах.
 В абстрактной алгебре мы начинаем с основных свойств и структуры, не уделяя особого внимания объектам, к которым они применяются. Это означает, что мы будем изучать алгебраические свойства отдельно от конкретных реальностей, конкретных объектов или реальных случаев. Многие из тем, которые мы изучим в этом курсе абстрактной алгебры, могут применяться в других областях математики и других научных областях, включая физику, химию, теорию кодирования, нейробиологию и многие другие.
В абстрактной алгебре мы начинаем с основных свойств и структуры, не уделяя особого внимания объектам, к которым они применяются. Это означает, что мы будем изучать алгебраические свойства отдельно от конкретных реальностей, конкретных объектов или реальных случаев. Многие из тем, которые мы изучим в этом курсе абстрактной алгебры, могут применяться в других областях математики и других научных областях, включая физику, химию, теорию кодирования, нейробиологию и многие другие.Кто должен принимать 330 и когда? Почти все! Это требуется для всех, кто участвует в программе вторичной сертификации. абсолютно необходим для всех, кто подумывает об аспирантуре. Это хороший факультатив для специалистов по концентрации и компьютерных наук. Студенты, направляющиеся в аспирантуру, могут захотеть сдать ее до окончания младшего года обучения. Однако, если вам не совсем комфортно с Math 239, вам следует немного подождать и пройти один или два других 300-уровневых факультатива, прежде чем приступать к Math 330.
 Нет необходимости сначала изучать Math 333, но может быть полезно сделать так.
Нет необходимости сначала изучать Math 333, но может быть полезно сделать так.
- 332 Линейное программирование и исследование операций. Это курс, который начинается с того места, где Элементарная линейная алгебра заканчивается линейными системами, расширяется до систем линейных неравенств и предлагает несколько действительно крутых реальных приложений, в основном связанных с оптимизацией. Если вы ищете курс с большим количеством математических приложений, это то, что вам нужно! Студенты узнают, что такое задачи исследования операций, как их формулировать, а также освоят различные методы их решения. Темы, которые будут затронуты, могут включать симплексный метод, двойственность, модели оптимизации сети (включая максимальный поток и минимальные остовные деревья), динамическое программирование, целочисленное программирование и теорию игр. Студенты работают над групповым проектом не менее двух недель в конце семестра с реальным приложением. Студенты напишут и представят свои модели или результаты до представления проекта классу и приглашенным преподавателям.
 Среди недавних проектов: планирование эвакуации, лечение рака, оптимальный дизайн дома, сбор мусора, решение судоку и многое другое!
Среди недавних проектов: планирование эвакуации, лечение рака, оптимальный дизайн дома, сбор мусора, решение судоку и многое другое!Кто должен принимать 332 и когда? Любой, кто прошел линейную алгебру (математика 233), введение в доказательства (математика 239) и курс программирования (математика 230), не , потому что это курс «кодирования», а потому что вам нужно будет следовать и реализовать алгоритмы. Любой, кто интересуется финансовой математикой, бизнесом, наукой о данных, экономикой или «реальными приложениями», должен пройти этот курс.
- 333 Линейная алгебра II. Это более теоретическая версия Math 233. В зависимости от преподавателя в этом курсе могут преподаваться приложения. В любом случае, это хорошая основа для поступления в аспирантуру. Этот курс необходим для получения степени бакалавра прикладной математики. Вы погрузитесь намного глубже в векторные пространства, но в более абстрактной обстановке.
 Подробнее о линейных преобразованиях, матрицах, собственных значениях и собственных векторах как с алгебраической, так и с геометрической точки зрения. Линейная алгебра особенно полезна во многих областях прикладной математики, например. в решении линейных систем ОДУ, в нахождении численных решений УЧП, в постановке и решении задач линейного программирования, в прикладной матричной теории, в статистике высокого уровня и в квантовой механике.
Подробнее о линейных преобразованиях, матрицах, собственных значениях и собственных векторах как с алгебраической, так и с геометрической точки зрения. Линейная алгебра особенно полезна во многих областях прикладной математики, например. в решении линейных систем ОДУ, в нахождении численных решений УЧП, в постановке и решении задач линейного программирования, в прикладной матричной теории, в статистике высокого уровня и в квантовой механике.Кто должен принимать 333 и когда? Большинству математических специальностей, вероятно, следует сдавать этот экзамен, но особенно тем, кто планирует поступать в аспирантуру, его следует сдавать. Это требуется для получения степени бакалавра прикладной математики. Это хороший курс для актуарных студентов. Это хорошо для тех, кто рассматривает ученую степень в области статистики или науки о данных. Поскольку это продолжение курса «Математика 233», рекомендуется пройти его как можно скорее после уроков «Математика 233» и «Математика 239».

- 338 Топология. Как выглядит математика без расстояний, без углов, без измерений? Это топология. Речь идет об открытых множествах, поверхностях и узлах. Топология — это изучение пространств и множеств, и ее можно рассматривать как расширение геометрии. Это совершенно другой способ познания окружающего мира и математики за его пределами.
Кто должен брать 338? Этот курс требует определенного уровня математической подготовки и большого воображения. Если вы планируете поступать в аспирантуру, вам, вероятно, следует пройти этот курс. Это также будет хорошим курсом для тех, кто любит абстрактные мысли, которые могут вас удивить или даже поразить (в хорошем смысле)!
- 345 Численный анализ I. Курс представляет собой сочетание теории, приложений и вычислений, связанных с численным приближением решений. Курс вращается вокруг получения алгоритмов (или рецептов) из теорем, в основном из исчисления или линейной алгебры, для поиска приближенных решений проблем, где точные или аналитические решения найти слишком сложно или невозможно.
 Еще одним важным аспектом курса является изучение того, как анализировать точность решений, повышать точность и улучшать скорость сходимости.
Еще одним важным аспектом курса является изучение того, как анализировать точность решений, повышать точность и улучшать скорость сходимости.Кто должен принимать 345 и когда? Этот курс необходим для получения степени бакалавра прикладной математики. Это особенно важно для специальностей по математике и естественным наукам, и оно составляет основу для многих областей прикладной математики и актуарной науки. Курс требует кодирования. Вам следует подумать о том, чтобы взять его вскоре после завершения математики 230, математики 233 и математики 239.
- 348 Устная презентация и исследовательский семинар. Требуется один кредит. Студенты изучат методы презентации и методы работы с библиотекой. Каждый в нем прочитает соответствующую журнальную статью и сделает презентацию.
Кто должен брать 348? Официально любой, кто должен выполнить требование устного исследования по математике, но не участвует в программе сертификации.
 Это требование может быть отменено с помощью других утвержденных математических курсов или утвержденных презентаций. Требование удовлетворено INTD 302 для студентов, желающих получить аттестат о среднем образовании.
Это требование может быть отменено с помощью других утвержденных математических курсов или утвержденных презентаций. Требование удовлетворено INTD 302 для студентов, желающих получить аттестат о среднем образовании.
- 360 Вероятность. Вероятностный курс, основанный на исчислении.
Кому брать 360? Целью этого курса является введение студентов в течение одного семестра в область теории вероятностей, которая включает в себя основные методы подсчета, случайные величины и их распределения вероятностей, многомерные распределения, а также теоретические средние значения и дисперсии этих переменных. Это критический курс для тех, кто интересуется актуарной наукой, карьерой в области финансов или бизнеса или некоторыми карьерами в области прикладной математики. Это вариант для специальностей, желающих получить вторичную сертификацию (при условии, что вы также принимаете Math 361). Он может заменить 262 для второстепенной математики или математики 242 или 262 для математического концентратора, если взять его с 361.
 Необходим для всех, кто хочет специализироваться в статистике.
Необходим для всех, кто хочет специализироваться в статистике.
- 361 Статистика. Курс вероятностной статистики.
Кто должен брать 361? Целью этого курса является предоставление студентам односеместрового курса статистики, основанного на вероятностях. Как и 360 (вероятность), это критический курс для тех, кто интересуется актуарной наукой, статистикой, анализом данных, карьерой в области финансов или бизнеса или некоторыми карьерами в области прикладной математики. С 360 это считается требованием вероятности и статистики для учащихся средних школ. Этот курс необходим для всех, кто хочет специализироваться в статистике.
- 371 Комплексный анализ. Комплексный анализ начинается как примерно эквивалентный исчислению II, но с комплексными числами, и приводит к некоторым удивительным приложениям. Тем не менее, это занимает некоторое время, чтобы добраться туда, и есть намного больше.
 По пути он проходит через сложную арифметику, алгебру, тригонометрию и геометрию. Кульминация исследует свойства пределов, производных, рядов и интегралов с комплексными числами. В целом это позволяет получить унифицированный взгляд на многие свойства исчисления с действительными значениями, которые можно увидеть более четко, если признать, что они находятся в более широкой структуре комплексных чисел.
По пути он проходит через сложную арифметику, алгебру, тригонометрию и геометрию. Кульминация исследует свойства пределов, производных, рядов и интегралов с комплексными числами. В целом это позволяет получить унифицированный взгляд на многие свойства исчисления с действительными значениями, которые можно увидеть более четко, если признать, что они находятся в более широкой структуре комплексных чисел.Кто должен брать 371? Комплексный анализ связан с большинством других разделов математики. Он особенно полезен для многих прикладных областей математики, включая обыкновенные дифференциальные уравнения и уравнения в частных производных, динамические системы и вейвлеты, а также для приложений в физике и электротехнике благодаря способности представлять полные решения, как периодические, так и переходные. Вот только пример: задачи на вибрирующие струны и мембраны, уравнение Лапласа, уравнение теплопроводности, волновое уравнение и обработку сигналов. Это также дает хороший опыт, чтобы связать воедино огромное количество математики средней школы с концепциями исчисления.

- 380 Темы по математике. Это курс «специальные темы», и детали варьируются от предложения к предложению, в зависимости от инструктора. Если есть конкретная тема, которую вы хотели бы изучить и которая не рассматривается подробно в другом курсе, посмотрите, сможете ли вы найти профессора, который будет преподавать ее в рамках курса «Темы математики».
Нажмите здесь, чтобы просмотреть список некоторых прошлых курсов по темам.
Кому брать 380? Этот факультативный курс идеально подходит для студентов, которые ищут трехчасовой курс и интересуются конкретной темой, предлагаемой в этом семестре. Конечно, было бы неплохо проконсультироваться с преподавателем, отвечающим за курс.
- 381 Темы по алгебре. Исследование продвинутой алгебраической темы, которая расширяет широту и/или глубину дискретной области математики, не доступной в наших обычных предложениях.
Нажмите здесь, чтобы просмотреть список некоторых прошлых курсов по темам, включая Math 380 и Math 381.

Кто должен брать 381? Студенты, желающие большего углубления, или в качестве возможной последовательности для одной из программ бакалавриата.
- 382 Введение в вейвлеты и их приложения. Это междисциплинарный курс, который устраняет разрыв между теоретической, прикладной и вычислительной математикой, используя практический подход. Курс начинается с управления цифровым звуком и изображениями с помощью линейной алгебры для развития теории и быстро переходит к областям комплексного анализа и рядов Фурье для разработки вейвлет-преобразований Хаара и Добеши. В качестве языка вычислений используется Matlab. Студенты работают над групповым проектом не менее двух недель в конце семестра, используя вейвлеты в реальном мире. Учащиеся записывают и отправляют результаты и код до представления проекта классу и приглашенным преподавателям. Недавние проекты включают в себя: Взлом Captchas, Прогнозирование фьючерсов на нефть, Сжатие звуковых файлов и файлов изображений, Обнаружение подделок рукописного текста и произведений искусства, Идентификация изображений, Сжатие отпечатков пальцев ФБР и многое другое!
Кто должен брать 382? Этот факультативный курс идеально подходит для студентов, которые хотят увидеть, как теория и применение работают в тандеме для получения реальных результатов.
 Курс требует кодирования. Студенты должны пройти 233, 239 и 230 до прохождения этого курса.
Курс требует кодирования. Студенты должны пройти 233, 239 и 230 до прохождения этого курса.
- 384 Вычислительная графика. Компьютерная графика, благодаря которой работают современные видеоигры и фильмы. И почти все это сводится к высокооптимизированной интеграции определенных функций в пространстве, а иногда и в нескольких других измерениях. Откройте капот технологии, которая нравится большинству людей каждый день, и увидьте внутри множество математических вычислений и линейной алгебры.
Кто должен принимать 384 и когда? Пройдите этот курс, если вас интересуют вычислительные аспекты прикладной математики или вы просто хотите узнать, как работает компьютерная графика. В этом курсе вы немного попрограммируете, так что пройдите его после 230 и, возможно, после другого курса или опыта, который улучшит ваши навыки программирования. Вы также должны хорошо разбираться в материалах из Math 223 и частей 233.
Вернуться к началу
Математика (бакалавр, минор)
Математика сложная, полезная и веселая. Это и логично, и креативно. Влияние математики повсюду вокруг нас. Компьютеры, автомобили, сотовые телефоны, лекарства, робототехника, здания, космические корабли, фондовый рынок и даже маршрут, по которому ваш местный грузовик доставляет вашу посылку, — все это продукты математики. Если вы так же заинтригованы вопросами, как и поиском ответов, математическая степень может быть для вас.
Это и логично, и креативно. Влияние математики повсюду вокруг нас. Компьютеры, автомобили, сотовые телефоны, лекарства, робототехника, здания, космические корабли, фондовый рынок и даже маршрут, по которому ваш местный грузовик доставляет вашу посылку, — все это продукты математики. Если вы так же заинтригованы вопросами, как и поиском ответов, математическая степень может быть для вас.
В 21 веке математика и статистика являются не только инструментами для математиков, ученых-физиков и инженеров, но также имеют решающее значение для бизнеса, экономики, социальных наук, медицины и многих других областей. Применение математики является важнейшим элементом современной цивилизации.
Зачем изучать математику в AU?
В Университете Аврора аналитическое мышление, решение проблем и рассуждения высокого уровня лежат в основе основных направлений математики. Программа использует ваше природное любопытство для исследования и развивает вашу способность критически мыслить и ставить цели. В AU наш опытный математический факультет готовит студентов к формированию будущего науки, технологий и образования.
В AU наш опытный математический факультет готовит студентов к формированию будущего науки, технологий и образования.
Мы гордимся тем, что работаем со студентами индивидуально для достижения их целей, в том числе участвуя в исследовательских проектах бакалавриата. Заботливые преподаватели помогают учащимся приобретать навыки, которые способствуют пониманию математических концепций и методов, выявлению проблем, использованию конструктивных рассуждений для выдвижения убедительных аргументов и применению математики в реальной жизни.
Наша интенсивная учебная программа и завершающий опыт позволяют учащимся успешно пройти один из двух следующих направлений:
Основная математика. Этот курс предназначен для студентов, заинтересованных в карьере в бизнесе и промышленности, требующих сильных аналитических навыков и навыков решения проблем. Он также предназначен для студентов, которые хотят получить ученую степень по математике или другим дисциплинам. Для студентов, которые хотят сосредоточиться на определенной области математики, доступны следующие три области акцента:
Для студентов, которые хотят сосредоточиться на определенной области математики, доступны следующие три области акцента:
- Статистика
- Чистая математика
- Прикладная математика
Специальность по математике с лицензией на получение среднего образования. Этот курс предназначен для учащихся, желающих получить сертификат учителя математики на уровне подготовки к колледжу. Учащиеся, которые планируют преподавать, должны получить дополнительное среднее образование по специальности . Эта степень дает студентам сильный опыт аналитических навыков и навыков решения проблем, что позволит им быть успешными учителями в классе.
Учебная программа по математике разработана таким образом, чтобы дать учащимся возможность интегрировать свои математические занятия с другими программами. Вы можете расширить свою карьеру и возможности для получения высшего образования, выбрав двойную специализацию в области биологии, компьютерных наук, уголовного правосудия или образования. Даже имея вторую специальность, вы все равно сможете получить высшее образование за четыре года. Вы также можете получить дополнительную специальность по математике, чтобы дополнить другую специальность.
Даже имея вторую специальность, вы все равно сможете получить высшее образование за четыре года. Вы также можете получить дополнительную специальность по математике, чтобы дополнить другую специальность.
Математика — самое прекрасное и самое сильное творение человеческого духа. 904:00 Стефан Банах, польский математик
Изучение математики в AU принесет вам много пользы.
- Ты познаешь мир.
Математика влияет на проблемы реального мира, а также на решения этих проблем. Степень математики поможет вам внести свой вклад в будущее развитие многих отраслей. - Вы станете решать проблемы.
Математика — это решение задач. Вы не только научитесь решать сложные математические уравнения, но и разовьете навыки решения проблем, которые пригодятся во многих профессиях и ситуациях. - Вы разовьете передаваемые навыки.
Приобретенные навыки пригодятся вам на протяжении всей жизни. Некоторые из передаваемых навыков, которые может дать вам математическая степень, включают анализ данных, организацию, критическое мышление, управление временем, общение и принятие решений. Вы также разовьете способность манипулировать точными и сложными идеями, строить логические аргументы и разоблачать нелогичные аргументы.
Некоторые из передаваемых навыков, которые может дать вам математическая степень, включают анализ данных, организацию, критическое мышление, управление временем, общение и принятие решений. Вы также разовьете способность манипулировать точными и сложными идеями, строить логические аргументы и разоблачать нелогичные аргументы. - Вас подготовят к поступлению в аспирантуру или профессиональную школу.
- Степень по математике необходима для студентов, которые намереваются получить степень магистра в области математики, прикладной математики, статистики или компьютерных наук.
- Приемные комиссии для аспирантов по астрономии, физике, технике, экономике или финансам часто отдают предпочтение студентам со степенью бакалавра математики.
- Выпускники факультета математики могут использовать свою степень в качестве первого шага к получению профессиональных степеней в области права и медицины, особенно в сочетании с курсовой работой или двойной специализацией в интересующей области.

$ 98 680
2021 Годовой средний зарплата для математических занятий
29%
2021-2031 Прогнозируемые темпы роста рабочих мест
Источник: Бюро статистики труда США
КОРИЦИЯ КОРИЦИИ
Возможности кампуса
- Финансовая ассоциация Университета Аврора (AUFA)
- Воспитание воспитателей
- Каппа Му Эпсилон (Общество чести математиков)
- Репетиторство
Возможности карьерного роста с ученой или профессиональной степенью
- Астроном
- Биометрист
- Ученый-компьютерщик
- Специалист по данным
- Инженер
- Профессор математики
- Метеоролог
- Физик
- Аналитик рисков
- Статистик
- Исследователь-опросник
JSU Математические, вычислительные и информационные науки
| Бакалавриат | Выпускник | |||
Бакалавриат
100. Алгебра среднего уровня (3). Предварительное условие: LS 098 или удовлетворительный балл по ACT/SAT или тесту на размещение в отделении. Операции/свойства действительных чисел, показателей степени и комплексных чисел; факторинг, решение/применение линейных и квадратных уравнений; операции над полиномами и рациональными выражениями. (Недоступно для студентов с кредитом в MS 125 или выше.) Оценки: A, B, C, NC.
Алгебра среднего уровня (3). Предварительное условие: LS 098 или удовлетворительный балл по ACT/SAT или тесту на размещение в отделении. Операции/свойства действительных чисел, показателей степени и комплексных чисел; факторинг, решение/применение линейных и квадратных уравнений; операции над полиномами и рациональными выражениями. (Недоступно для студентов с кредитом в MS 125 или выше.) Оценки: A, B, C, NC.
108. Изучение математики (3). Условие: MS 100 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Введение в математику с темами, полезными и актуальными для любого человека. Темы включают элементарную логику, методы решения проблем, использование количественных методов, статистические рассуждения и моделирование. (Недоступно для студентов с кредитом в MS 133. Кредит факультета не предоставляется для основных или несовершеннолетних математики.)
110. Конечная математика (3). Условие: MS 100 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Системы уравнений и матриц, линейное программирование, финансовая математика, множества и счет, вероятность, распределение вероятностей и статистика. Компьютерные приложения с использованием Microsoft Excel. (Зачет факультета не дается за основные или дополнительные предметы математики.)
Условие: MS 100 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Системы уравнений и матриц, линейное программирование, финансовая математика, множества и счет, вероятность, распределение вероятностей и статистика. Компьютерные приложения с использованием Microsoft Excel. (Зачет факультета не дается за основные или дополнительные предметы математики.)
111. Конечная математика с отличием (3). Предварительное условие: Удовлетворительный балл по ACT/SAT или тесту на размещение в отделении или по рекомендации. Углубленное изучение матриц, линейного программирования, математики финансов, вероятности, распределения вероятностей и статистики с упором на письмо, проекты и технологии. Компьютерное приложение с использованием Microsoft Excel. (Зачет факультета не дается для основных или несовершеннолетних по математике.)
112. Алгебра предварительного исчисления (3). Условие: MS 100 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Уравнения и неравенства первой и второй степени; линейные и квадратичные функции и графики; полиномиальные и рациональные функции; экспоненциальные и логарифмические функции; и системы уравнений. (Недоступно для студентов с кредитом в MS 125 или выше.)
Уравнения и неравенства первой и второй степени; линейные и квадратичные функции и графики; полиномиальные и рациональные функции; экспоненциальные и логарифмические функции; и системы уравнений. (Недоступно для студентов с кредитом в MS 125 или выше.)
113. Тригонометрия предварительного исчисления (3). Условие: MS 112 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Тригонометрические функции и обратные, приложения, графики, тождества и уравнения, законы синусов и косинусов, векторы и комплексные числа.
115. Алгебра предварительного исчисления и тригонометрия (4). Предварительные требования: MS 112 с оценкой «B» или выше или MS 113 с оценкой «C» или выше или удовлетворительно по ACT/SAT или вступительному тесту отдела. Курс представляет собой смесь алгебры и тригонометрии, предоставляя студенту математическую основу, необходимую для исчисления или других курсов, требующих аналогичной математической подготовки.
117. Высшая техническая математика I (2). Условие: MS 112 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Избранные темы из: преобразование единиц измерения, геометрия, тригонометрия, дифференциальное и интегральное исчисление. Приложения подчеркивают решение проблем в технологии. Открыто только для учащихся программы «Технологии», кроме как с разрешения преподавателя. Студент не может получить зачет одновременно по этому курсу и по TEC 302. (Зачет по кафедре не выдается за основные или дополнительные предметы по математике.)
119. Высшая техническая математика II (2) Требование: MS 117 с «C» или выше. Избранные темы: перевод единиц измерения, геометрия, тригонометрия, дифференциальное и интегральное исчисление. Приложения подчеркивают решение проблем в технологии. Открыто только для учащихся программы «Технологии», кроме как с разрешения преподавателя. Студент не может получить зачет как по этому курсу, так и по TEC 302. (Зачет по кафедре не выдается за основные или дополнительные предметы по математике.)
(Зачет по кафедре не выдается за основные или дополнительные предметы по математике.)
120. Исчисление и его приложения (3). Предварительное условие: MS 112 с оценкой «C» или лучше или удовлетворительно по ACT/SAT или вступительному тесту отдела. Темы дифференциального и интегрального исчисления с бизнес-приложениями, функций нескольких переменных, частных производных с бизнес-приложениями, множителей Лагранжа и множественной интеграции. (Зачет кафедры не дается для основных или несовершеннолетних по математике.)
125. Исчисление I (4). Условие: MS 113 с оценкой «B» или выше или MS 115 с оценкой «C» или выше или удовлетворительным баллом по ACT/SAT или вступительному тесту отдела. Введение в аналитическую геометрию, функции и пределы, дифференцирование с приложениями, первообразные, определенные интегралы, численное интегрирование, исчисление трансцендентных функций.
126. Исчисление II (4). Требование: MS 125 с «C» или выше. Приложения интегрирования, методы интегрирования, несобственные интегралы, неопределенные формы, бесконечные ряды, векторы на плоскости и в трехмерном пространстве.
Требование: MS 125 с «C» или выше. Приложения интегрирования, методы интегрирования, несобственные интегралы, неопределенные формы, бесконечные ряды, векторы на плоскости и в трехмерном пространстве.
133. Математические понятия I (3). Необходимое условие: MS 112. Подготовка к внедрению стандартов, установленных NCTM. Решение задач, теория множеств, теория чисел, операции с действительными числами, историческое развитие и структура систем счисления. (Недоступно для студентов с кредитом в MS 108.) (Зачисление только по рекомендации.) Два часа лекций и два часа лабораторных работ.
134. Математические понятия II (3). Предпосылки: MS 112 и 133. Тщательное изучение геометрии, измерений и статистики в соответствии с рекомендациями NCTM. Особое внимание уделяется решению проблем и применению. (Запись только по рекомендации.) Два часа лекций и два часа лабораторных работ.
135. Математические понятия III (3). Предварительные требования: MS 112 и 133. Дальнейшее изучение в NCTM рекомендовало математическое содержание, чтобы включить логику, вероятность, принципы подсчета, алгебраические рассуждения и представление. (Запись только по рекомендации.) Два часа лекций и два часа лабораторных работ.
Математические понятия III (3). Предварительные требования: MS 112 и 133. Дальнейшее изучение в NCTM рекомендовало математическое содержание, чтобы включить логику, вероятность, принципы подсчета, алгебраические рассуждения и представление. (Запись только по рекомендации.) Два часа лекций и два часа лабораторных работ.
204. Базовая статистика (3). Предварительное условие: MS 108, или 110, или 112, или удовлетворительный балл по ACT/SAT или вступительный тест. Численные описательные методы, аксиомы вероятности, случайные величины, статистический вывод, точечная и интервальная оценка среднего и проверка гипотез. (Зачет факультета не дается для основных или несовершеннолетних по математике.)
227. Исчисление III (4). Требование: MS 126 с «C» или выше. Полярные координаты, параметрические уравнения, вектор-функции, многомерные функции, кратные интегралы, векторный анализ.
250. Введение в линейную алгебру (3). Предпосылки: MS 113 или 115. Основы теории линейных уравнений, матриц, вещественных векторных пространств, базисов, размерностей, линейных преобразований, определителей, собственных значений, собственных векторов, пространств скалярных произведений и диагонализации симметричных матриц.
Введение в линейную алгебру (3). Предпосылки: MS 113 или 115. Основы теории линейных уравнений, матриц, вещественных векторных пространств, базисов, размерностей, линейных преобразований, определителей, собственных значений, собственных векторов, пространств скалярных произведений и диагонализации симметричных матриц.
300. Введение в высшую математику (3). Требования: MS 126 с «C» или лучше. Математическое письмо, включая методы доказательства и основы множеств и функций. Может также включать избранные темы по алгебре, анализу, теории чисел или дискретной математике.
302. Прикладная вероятность и статистика (3). Условие: MS 120 с «C» или выше или MS 125 с «C» или выше. Содержит сводную информацию о вероятности и статистике, основанную на примерах анализа данных и компьютерном моделировании. Включает дискретные и непрерывные распределения вероятностей, оценку и проверку гипотез.
304. Математическая статистика I (3). Требование: MS 126 с «C» или выше. Вероятность, дискретные случайные величины и их распределения вероятностей, непрерывные случайные величины и их распределения вероятностей, оценка и доверительные интервалы, проверка гипотез и анализ численных данных.
Математическая статистика I (3). Требование: MS 126 с «C» или выше. Вероятность, дискретные случайные величины и их распределения вероятностей, непрерывные случайные величины и их распределения вероятностей, оценка и доверительные интервалы, проверка гипотез и анализ численных данных.
305. Теория чисел (3). Требование: MS 126 с «C» или выше. Введение в основные темы элементарной теории чисел, включая делимость, линейные диофантовы уравнения, распределение простых чисел, сравнения, теорему Ферма и теоретико-числовые функции.
309. Комбинаторика (3). Требование: MS 126 с «C» или выше. Введение в методы подсчета, такие как перестановки и комбинации, принцип включения-исключения, рекуррентные соотношения и производящие функции. Может также включать темы из теории графов, комбинаторного проектирования и дискретной вероятности.
322. Избранный обзор математики средней школы (3). Необходимые условия: MS 112 и 113 или эквивалентные. Для студентов, желающих получить сертификат по математике. Обзор математики средней школы для будущих и работающих учителей математики. (Зачет факультета не выдается за основные или дополнительные предметы математики.)
Необходимые условия: MS 112 и 113 или эквивалентные. Для студентов, желающих получить сертификат по математике. Обзор математики средней школы для будущих и работающих учителей математики. (Зачет факультета не выдается за основные или дополнительные предметы математики.)
323. Геометрия колледжа (3). Пререквизиты: MS 300. Евклидова геометрия, включая синтетические и аналитические доказательства, геометрические построения, свойства треугольника и окружности; введение в неевклидову геометрию.
331. Равный наставник (1). Академический кредит предоставляется студентам старших курсов бакалавриата, которые оказывают помощь в обучении на факультете математики. Студенты будут работать под руководством опытного преподавателя математики. Требуется разрешение начальника отдела. (Зачет факультета не выдается за основные или дополнительные предметы математики. Курс оценивается как зачет/незачет.)
332. Равный преподаватель (2). Академический кредит предоставляется студентам старших курсов бакалавриата, которые оказывают помощь в обучении на факультете математики. Студенты будут работать под руководством опытного преподавателя математики. Требуется разрешение начальника отдела. (Зачет факультета не выдается за основные или дополнительные предметы математики. Курс оценивается как зачет/незачет.)
Равный преподаватель (2). Академический кредит предоставляется студентам старших курсов бакалавриата, которые оказывают помощь в обучении на факультете математики. Студенты будут работать под руководством опытного преподавателя математики. Требуется разрешение начальника отдела. (Зачет факультета не выдается за основные или дополнительные предметы математики. Курс оценивается как зачет/незачет.)
344. Дифференциальные уравнения (3 ). Требование: MS 126 с «C» или выше. Методы решения дифференциальных уравнений первого или второго порядка и высших линейных уравнений, в том числе решения рядов и избранные приложения.
352. Линейная алгебра (3). Требование: MS 126 с «C» или выше. Матрицы, линейные системы, векторные пространства с упором на алгебраические структуры.
390. Численный анализ (3). Требования: MS 352 и CS 231 с «C» или лучше в обоих. Численный анализ и вычисления с упором на методы, адаптируемые к электронным вычислительным машинам.
399. Ознакомительная поездка (3). Темы, экскурсии и требования определяются кафедрой. Может быть продублирован для кредита; тем не менее, только три (3) кредита могут быть применены к любому основному или второстепенному. Нечасто запланировано и зависит от минимального и максимального количества. Требуется предварительный депозит.
403. Векторный анализ (3). Пререквизиты: MS 227. Алгебра и векторное исчисление; приложения к геометрии, электричеству, гармоническим функциям и потенциалам.
404. Математическая статистика II (3). Предварительные требования: MS 227 и 304. Продолжение MS 304. Избранные темы из многомерных распределений вероятностей, функций случайных величин, приближений к распределениям вероятностей, методов оценки, линейных моделей и оценок методом наименьших квадратов, дисперсионного анализа и непараметрических статистика.
415. Расширенный расчет I (3). Пререквизиты: MS 227 и 300. Действительная система счисления, элементарная теория множеств точек, пределы, теория непрерывных функций, дифференцируемые функции.
Расширенный расчет I (3). Пререквизиты: MS 227 и 300. Действительная система счисления, элементарная теория множеств точек, пределы, теория непрерывных функций, дифференцируемые функции.
416. Усовершенствованное исчисление II (3). Требование: MS 415. Отдельные темы из расширенного исчисления. Элементы частичного дифференцирования, включая общие теоремы, якобианы. Темы по теории интеграции.
423. Обзор геометрий (3). Предварительное требование: MS 323. Избранные темы из углубленной евклидовой геометрии, конечных геометрий, неевклидовой геометрии и других связанных тем.
441. Абстрактная алгебра I (3). Пререквизиты: MS 300 и 352. Алгебраические структуры, кольца и поля. Аксиоматический подход.
442. Абстрактная алгебра II (3). Пререквизиты: MS 441. Введение в теорию групп и смежные темы.
451. Функции комплексного переменного (3). Пререквизиты: MS 227 и 300 и 415. Основные операции с комплексными числами, теоремы дифференцирования и интегрирования, отображения, ряды и вычеты.
Функции комплексного переменного (3). Пререквизиты: MS 227 и 300 и 415. Основные операции с комплексными числами, теоремы дифференцирования и интегрирования, отображения, ряды и вычеты.
475. Старший семинар по математике (3). Предпосылки или дополнительные условия: MS 415, или 441, или 451, а также старший статус. Завершающий курс высшей математики. Цели включают глубокое изучение фундаментальных идей математики и связей между различными разделами математики, изучение исторического развития основных концепций и дальнейшее развитие склада ума, определяющего математические подходы к проблемам.
480. Введение в топологию (3). Требование: MS 415. Основные топологические понятия, включая топологические пространства, отображение, компактность, связность и аксиомы разделения.
484. Уравнения в частных производных (3). Необходимые условия: MS 227 и 344. Стандартные методы решения: разделение переменных, ряды Фурье, преобразования Лапласа. Выбранные приложения.
Выбранные приложения.
499. Бакалавриат по математике (3). Требования: MS 302 или 304 или 415 или 441, старший статус и разрешение инструктора. Направляемое независимое исследование темы, выходящей за рамки обычных курсов кафедры, завершающееся написанием письменной работы и устной презентацией для преподавателей.
Вернуться к началу
Выпускник
ПРИМЕЧАНИЕ. Необходимое условие для всех курсов математики для выпускников:
Курсы для выпускников по математике открыты только для студентов, которые
(1) допущены к программе последипломного обучения по математике, или
(2) приняты в аспирантуру среднего образования с преподаванием в области математики и с устранением всех недостатков бакалавриата по математике, или
(3) завершили 32 семестровых часа по математике с не менее чем 19часы высшего дивизиона. Некоторые отдельные курсы имеют дополнительные требования; см. описания курсов ниже. Исключения из предварительных условий курса требуют разрешения заведующего кафедрой.
описания курсов ниже. Исключения из предварительных условий курса требуют разрешения заведующего кафедрой.
403G. Векторный анализ (3). Требования: MS 227 и см. «Необходимые условия для всех математических курсов». Алгебра и исчисление векторов, теорема Стокса и теорема о расходимости; приложения к геометрии, массовым потенциальным функциям, электричеству и течению жидкости.
404G. Математическая статистика II (3). Предварительные требования: MS 227 и MS 304, а также см. «Необходимые условия для всех математических курсов». Продолжение MS 304; избранные темы из многомерных распределений вероятностей, функций случайных величин, приближений к распределениям вероятностей, методов оценки, линейных моделей и оценок методом наименьших квадратов, дисперсионного анализа и непараметрической статистики.
416Г. Расширенное исчисление II (3 ). Требования: MS 415 и см. «Необходимые условия для всех математических курсов». Избранные темы из расширенного исчисления; элементы частичного дифференцирования, включая общие теоремы, якобианы; темы по теории интеграции.
Избранные темы из расширенного исчисления; элементы частичного дифференцирования, включая общие теоремы, якобианы; темы по теории интеграции.
423G. Обзор геометрий (3). Требования: MS 323 и см. «Необходимые условия для всех математических курсов». Избранные темы из расширенной евклидовой геометрии, конечных геометрий, неевклидовой геометрии и других геометрий.
451Г. Функции комплексной переменной (3). Предварительные требования: MS 227, MS 300 и MS 415, а также см. «Необходимые условия для всех математических курсов». Основные операции с комплексными числами, теоремы дифференцирования и интегрирования, отображения, ряды и вычеты.
480G. Вводная топология (3). Требования: MS 415 и см. «Необходимые условия для всех математических курсов». Основные топологические понятия, включающие топологические пространства, отображение, компактность, связность и аксиомы разделения.
484G. Уравнения в частных производных (3). Требования: MS 227 и MS 344, а также см. «Необходимые условия для всех математических курсов». Стандартные методы решения; разделение переменных, ряды Фурье, преобразования Лапласа; выбранные приложения.
504. Прикладные статистические методы (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Основные понятия описательной и логической статистики, распределения вероятностей, оценивания и проверки гипотез; Пакеты статистического программного обеспечения используются для облегчения достоверного анализа и интерпретации результатов; упор делается на метод и выбор надлежащих статистических методов для анализа реальных ситуаций.
505. Базовая логика и теория множеств (3). Требования: MS 415 или MS 441 и см. «Необходимые условия для всех математических курсов». Основные темы символической логики и наивной теории множеств, включая множества и операции над множествами, символическую логику, язык теории множеств и приложения теории множеств.
515. Вещественные переменные I (3). Необходимое условие: MS 416 или разрешение инструктора, а также см. «Необходимое условие для всех математических курсов». Избранные темы из реального анализа с упором на функции одной и нескольких переменных, меру и интеграл Римана и/или Дарбу.
516. Вещественные переменные II (3). Требования: MS 515 и см. «Необходимые условия для всех математических курсов». Избранные темы из реального анализа с акцентом на интеграцию Лебега, последовательности и ряды функций.
517. Введение в функциональный анализ (3). Требования: MS 352 и MS 415 и см. «Необходимые условия для всех математических курсов». Введение в фундаментальные темы функционального анализа. Темы включают метрические пространства, полноту, линейные операторы, нормированные пространства и банаховы пространства, пространства внутреннего произведения и гильбертовы пространства. Задачи включают теорему Рисса о представлении, теорему Хана-Банаха и теорему об отображении сжатия.
523. Темы по геометрии для учителей (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Классические теоремы, идеи и конструкции евклидовой и неевклидовой геометрии в теоремах Чевы, Меналая, Паппа и Фейербаха; гомотетические преобразования, инверсия, гармонические множества точек и чевианы.
526. Темы по аналитической геометрии для учителей (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Применение евклидовых и однородных координат, геометрических преобразований, тригонометрических и векторных методов к геометрическим задачам.
528. Теория уравнений и функций для учителей (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Вопросы теории полиномиальных и других уравнений, а также свойств трансцендентных функций. (Целью является развитие более глубокого понимания уравнений и функций, обычно встречающихся в математике предварительного исчисления. ) Может потребоваться использование компьютерного программного обеспечения.
) Может потребоваться использование компьютерного программного обеспечения.
530. Основы исчисления для учителей (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Теория, методы решения задач и приложения дифференциального и интегрального исчисления, включая использование графических калькуляторов и компьютерного программного обеспечения. (Рекомендуется для учащихся, которые преподают или планируют преподавать Advanced Placement Calculus.)
533. Темы современного анализа для учителей (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Логика и теория множеств, функции и последовательности, структура и развитие системы действительных чисел, включая полноту.
535. Темы конечной математики для учителей (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Элементарный комбинаторный анализ, вероятность, векторы и матрицы, теория игр, линейное программирование и построение моделей в социальных и физических науках.
537. Основы алгебры для учителя средней школы (3 ). Требования: MS 441 и см. «Необходимые условия для всех математических курсов». Понятия школьной алгебры с точки зрения теории колец.
541. Абстрактная алгебра I (3). Требования: MS 441 и см. «Необходимые условия для всех математических курсов». Общая теория групп, включая циклические группы и группы перестановок, теоремы о гомоморфизме и изоморфизме.
542. Абстрактная алгебра II (3). Предпосылки: MS 441 и см. «Необходимые условия для всех математических курсов». Теория колец, идеалов, полей и областей целостности.
549. Избранные темы по математике для учителя средней школы (3). Предварительное условие: см. «Необходимое условие для всех математических курсов». Выбранные темы, подходящие для среднего учителя; решение проблем; математика средней школы с углубленной точки зрения.
552. Линейная алгебра (3). Требования: MS 352 и MS 441 и см. «Необходимые условия для всех математических курсов». Абстрактная трактовка конечномерных векторных пространств. Линейные преобразования, определители, собственные значения и собственные векторы, инвариантные подпространства, рациональные и жордановые канонические формы, пространства скалярных произведений, унитарные и нормальные операторы, билинейные формы.
Линейная алгебра (3). Требования: MS 352 и MS 441 и см. «Необходимые условия для всех математических курсов». Абстрактная трактовка конечномерных векторных пространств. Линейные преобразования, определители, собственные значения и собственные векторы, инвариантные подпространства, рациональные и жордановые канонические формы, пространства скалярных произведений, унитарные и нормальные операторы, билинейные формы.
591. Семинар по алгебре (3) (3). Требования: MS 541 и MS 542 или разрешение инструктора и см. «Необходимые условия для всех математических курсов». Избранные темы современной алгебры, выходящие за рамки последовательности алгебры для выпускников. Темы могут быть выбраны из теории групп, колец, полей или модулей; линейная алгебра; гомологическая алгебра; или другие темы, в зависимости от интересов студента и преподавателя.
595. Семинар по анализу (3) (3). Требования: MS 515 и MS 516 или разрешение инструктора и см. «Необходимые условия для всех математических курсов». Избранные темы современного анализа, выходящие за рамки последовательности анализа для выпускников. Темы могут быть выбраны из области реального анализа (теория меры и интегрирование, специальные функции, конечные разности, функциональные уравнения, последовательности и ряды), комплексные переменные, анализ Фурье и гармонический анализ, интегральные преобразования, теория операторов или другие темы, в зависимости от интересы ученика и преподавателя.
«Необходимые условия для всех математических курсов». Избранные темы современного анализа, выходящие за рамки последовательности анализа для выпускников. Темы могут быть выбраны из области реального анализа (теория меры и интегрирование, специальные функции, конечные разности, функциональные уравнения, последовательности и ряды), комплексные переменные, анализ Фурье и гармонический анализ, интегральные преобразования, теория операторов или другие темы, в зависимости от интересы ученика и преподавателя.
598. Направленные чтения (3) (3). Предварительные требования: учащиеся должны пройти два курса в выбранной тематической области и получить одобрение консультанта факультета по математике и преподавателя, а также см. «Необходимые условия для всех математических курсов». Алгебра, анализ, геометрия и топология.
599. Диссертация (3) (3). (только оценка «зачет» или «незачет»). Предварительное условие: одобрение заявки на диссертацию.

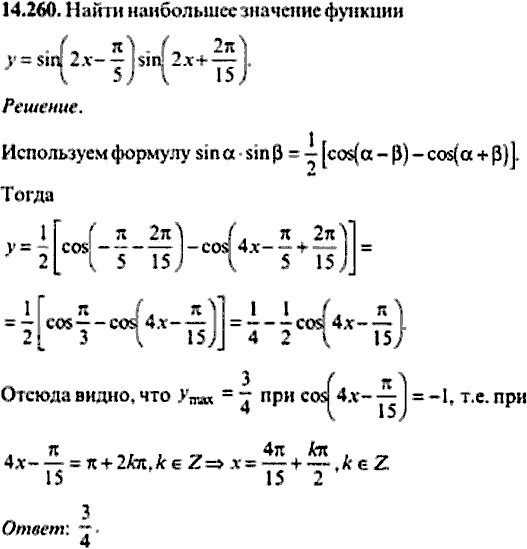 А.Каплан
А.Каплан Ш. — Высшая
математика для экономистов
Ш. — Высшая
математика для экономистов И. (2001, 736с.)
И. (2001, 736с.) Шарыгин
И.Ф. (1982, 160с.)
Шарыгин
И.Ф. (1982, 160с.) Супрун
В.П. (1998, 108с.)
Супрун
В.П. (1998, 108с.)  Дж.Пойа, Д.Килпатрик (2002, 96с.)
Дж.Пойа, Д.Килпатрик (2002, 96с.)  Нестандартные методы решения: Справочник. Олехник С.Н., Потапов М.К., Пасиченко
П.И. (1997, 219с.)
Нестандартные методы решения: Справочник. Олехник С.Н., Потапов М.К., Пасиченко
П.И. (1997, 219с.) Никольский
С.М. (1989, 224с.)
Никольский
С.М. (1989, 224с.)  djvu
djvu Высшая
математика: теория вероятностей
Высшая
математика: теория вероятностей А.,
Письменный Д., Кибзун А.И. — Набор из трёх учебников Теория вероятностей
и математическая статистика»
А.,
Письменный Д., Кибзун А.И. — Набор из трёх учебников Теория вероятностей
и математическая статистика» Г.-
Введение в экономико-математиские модели налогообложения(djvu)
Г.-
Введение в экономико-математиские модели налогообложения(djvu) — Математические
Методы Оптимизации И Экономическая Теория (djvu)
— Математические
Методы Оптимизации И Экономическая Теория (djvu)
 Кроме того, обратите внимание, что математика 223 является обязательным условием для математики 341, а математика 223 и математика 360 являются предварительными условиями для математики 361. Также обратите внимание, что математика 242 и математика 262 не засчитываются в основной курс математики.
Кроме того, обратите внимание, что математика 223 является обязательным условием для математики 341, а математика 223 и математика 360 являются предварительными условиями для математики 361. Также обратите внимание, что математика 242 и математика 262 не засчитываются в основной курс математики. Это курс, который рассказывает замечательную историю и дает вам практические навыки вдобавок. История посвящена трем вопросам: Что такое мгновенная скорость изменения? Чему равна площадь под кривой? Как они связаны? Хотя эта история была впервые рассказана более 300 лет назад Ньютоном (или Лейбницем?), ответы на поставленные вопросы продолжают лежать в основе большей части того, что мы делаем в практической и теоретической математике сегодня.
Это курс, который рассказывает замечательную историю и дает вам практические навыки вдобавок. История посвящена трем вопросам: Что такое мгновенная скорость изменения? Чему равна площадь под кривой? Как они связаны? Хотя эта история была впервые рассказана более 300 лет назад Ньютоном (или Лейбницем?), ответы на поставленные вопросы продолжают лежать в основе большей части того, что мы делаем в практической и теоретической математике сегодня.
 Курс, который хорош для тех, кто собирается получить диплом по математике, философии или информатике. Также хорошо для тех, кто просто любит думать об основах нашего предмета.
Курс, который хорош для тех, кто собирается получить диплом по математике, философии или информатике. Также хорошо для тех, кто просто любит думать об основах нашего предмета. Пройдите этот курс, чтобы узнать, почему мы считаем, что такие расчеты существуют, а также исследовать границы математики и компьютерных наук, которые все еще полны важных, но оставшихся без ответа вопросов.
Пройдите этот курс, чтобы узнать, почему мы считаем, что такие расчеты существуют, а также исследовать границы математики и компьютерных наук, которые все еще полны важных, но оставшихся без ответа вопросов.
 Он проявляется во многих прикладных контекстах и во многих теоретических ситуациях. Кроме того, простые вопросы со сложными ответами являются отличными примерами для учащихся средней школы.
Он проявляется во многих прикладных контекстах и во многих теоретических ситуациях. Кроме того, простые вопросы со сложными ответами являются отличными примерами для учащихся средней школы.

 Анализ фазовой плоскости двумерных линейных и нелинейных систем, включая теорию бифуркаций, устойчивость и предельные циклы, теорию индексов и теорему Пуанкараре-Бендиксона. Будут рассмотрены различные приложения к населению, экологические модели и физические системы.
Анализ фазовой плоскости двумерных линейных и нелинейных систем, включая теорию бифуркаций, устойчивость и предельные циклы, теорию индексов и теорему Пуанкараре-Бендиксона. Будут рассмотрены различные приложения к населению, экологические модели и физические системы. В абстрактной алгебре мы начинаем с основных свойств и структуры, не уделяя особого внимания объектам, к которым они применяются. Это означает, что мы будем изучать алгебраические свойства отдельно от конкретных реальностей, конкретных объектов или реальных случаев. Многие из тем, которые мы изучим в этом курсе абстрактной алгебры, могут применяться в других областях математики и других научных областях, включая физику, химию, теорию кодирования, нейробиологию и многие другие.
В абстрактной алгебре мы начинаем с основных свойств и структуры, не уделяя особого внимания объектам, к которым они применяются. Это означает, что мы будем изучать алгебраические свойства отдельно от конкретных реальностей, конкретных объектов или реальных случаев. Многие из тем, которые мы изучим в этом курсе абстрактной алгебры, могут применяться в других областях математики и других научных областях, включая физику, химию, теорию кодирования, нейробиологию и многие другие. Нет необходимости сначала изучать Math 333, но может быть полезно сделать так.
Нет необходимости сначала изучать Math 333, но может быть полезно сделать так. Среди недавних проектов: планирование эвакуации, лечение рака, оптимальный дизайн дома, сбор мусора, решение судоку и многое другое!
Среди недавних проектов: планирование эвакуации, лечение рака, оптимальный дизайн дома, сбор мусора, решение судоку и многое другое! Подробнее о линейных преобразованиях, матрицах, собственных значениях и собственных векторах как с алгебраической, так и с геометрической точки зрения. Линейная алгебра особенно полезна во многих областях прикладной математики, например. в решении линейных систем ОДУ, в нахождении численных решений УЧП, в постановке и решении задач линейного программирования, в прикладной матричной теории, в статистике высокого уровня и в квантовой механике.
Подробнее о линейных преобразованиях, матрицах, собственных значениях и собственных векторах как с алгебраической, так и с геометрической точки зрения. Линейная алгебра особенно полезна во многих областях прикладной математики, например. в решении линейных систем ОДУ, в нахождении численных решений УЧП, в постановке и решении задач линейного программирования, в прикладной матричной теории, в статистике высокого уровня и в квантовой механике.
 Еще одним важным аспектом курса является изучение того, как анализировать точность решений, повышать точность и улучшать скорость сходимости.
Еще одним важным аспектом курса является изучение того, как анализировать точность решений, повышать точность и улучшать скорость сходимости. Это требование может быть отменено с помощью других утвержденных математических курсов или утвержденных презентаций. Требование удовлетворено INTD 302 для студентов, желающих получить аттестат о среднем образовании.
Это требование может быть отменено с помощью других утвержденных математических курсов или утвержденных презентаций. Требование удовлетворено INTD 302 для студентов, желающих получить аттестат о среднем образовании. Необходим для всех, кто хочет специализироваться в статистике.
Необходим для всех, кто хочет специализироваться в статистике. По пути он проходит через сложную арифметику, алгебру, тригонометрию и геометрию. Кульминация исследует свойства пределов, производных, рядов и интегралов с комплексными числами. В целом это позволяет получить унифицированный взгляд на многие свойства исчисления с действительными значениями, которые можно увидеть более четко, если признать, что они находятся в более широкой структуре комплексных чисел.
По пути он проходит через сложную арифметику, алгебру, тригонометрию и геометрию. Кульминация исследует свойства пределов, производных, рядов и интегралов с комплексными числами. В целом это позволяет получить унифицированный взгляд на многие свойства исчисления с действительными значениями, которые можно увидеть более четко, если признать, что они находятся в более широкой структуре комплексных чисел.

 Курс требует кодирования. Студенты должны пройти 233, 239 и 230 до прохождения этого курса.
Курс требует кодирования. Студенты должны пройти 233, 239 и 230 до прохождения этого курса. Некоторые из передаваемых навыков, которые может дать вам математическая степень, включают анализ данных, организацию, критическое мышление, управление временем, общение и принятие решений. Вы также разовьете способность манипулировать точными и сложными идеями, строить логические аргументы и разоблачать нелогичные аргументы.
Некоторые из передаваемых навыков, которые может дать вам математическая степень, включают анализ данных, организацию, критическое мышление, управление временем, общение и принятие решений. Вы также разовьете способность манипулировать точными и сложными идеями, строить логические аргументы и разоблачать нелогичные аргументы.