Обучающие карточки на тему «Оформление задач в начальной школе»
Материал опубликовала
3
#1 класс #2 класс #3 класс #4 класс #Математика #ФГОС #Учебно-дидактические материалы #Учитель начальных классов #Школьное образование #УМК любой #Обучающие карточки
Основные виды краткой записи в начальной школе
Аннотация: Ученикам часто тяжело представить наглядно задачу. Облегчить процесс решения поможет краткая запись условия задачи. В краткой записи фиксируются величины, числа – данные и искомые, а также некоторые слова, показывающие, о чём говорится в задаче: «было», «положили», «стало» и т. п. и знаки, означающие отношения: «больше», «меньше», «одинаково» и т. п.
Краткую запись задачи ученик выполнять в виде: опорной схемы, таблицы, чертежа, с помощью геометрических фигур.
Для того чтобы краткая запись в максимальной степени способствовала решению задачи, нужно:
1)Краткую запись составлять на основе анализа текста задачи;
2)В краткой записи должно быть минимальное количество условных обозначений;
3)Количество вопросительных знаков в краткой записи должно соответствовать количеству действий в задаче;
4)Форму краткой записи выбирать такую, чтобы она более наглядно представляла условие задачи.
Варианты краткой записи
Задача: В двух бочонках у медведя было 17 кг меда. Из первого бочонка он съел 5 кг и в обоих стало поровну. Сколько кг мёда было в первом бочонке у медведя?
Нагляднее представит задачу запись в виде схемы
Пояснения к решению задачи
Над составной задачей форма работы предусматривает проверку умения учащихся по данным действиям решения задачи пояснить, на какой вопрос и с какой целью отвечает действие.
В конце каждого действия пишем пояснение, доказательство того, что мы нашли этим действием. Эта форма помогает учащимся увидеть другие отношения, вести необходимую цепочку логических рассуждений, анализировать и делать выводы.
Ответ задачи
Если использовались пояснения, ответ можно записать кратко. Если же не использовались, пишем полный ответ.
Задача на нахождение остатка
Задача: В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось?
Было — 20 л и 20 л
Выпили — 12 л
Осталось — ? л
В I коробке Количество коробок Всего камней
? к. 3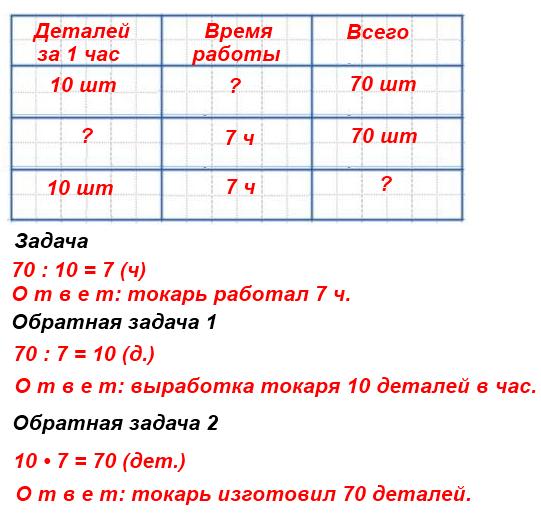 к.
18 к.
Задача. Когда Маша полила 6 грядок, а Ира — 2 грядки, им осталось полить 3 грядки. Сколько всего грядок должны полить дети?
Было — ? гр.
Полили — 6 гр. и 2 гр.
Осталось — 3 гр.
Задача: Серёжа высадил 9 луковиц, по 3 луковицы в ряд. Сколько получилось рядов?
Это простая задача на деление по содержанию. Такую задачу нагляднее оформить картинкой.
Составная задача на разностное сравнение, лучше оформить в виде таблицы.
Задача: Одну деталь мастер должен делать за 45 мин, а делает за 38 мин. Сколько времени сэкономит мастер, когда он сделает 8 деталей?
В помощь родителям!
Можно купить памятку в магазине книг!
Опубликовано
Чтобы написать комментарий необходимо авторизоваться.
Огромное спасибо за ответы! Ontt в сообщении #688243 писал(а): Denis Russkih в сообщении #688201 писал(а): 1. Зачем вообще это упомянуто, если нигде впоследствии не используется? Но ведь значения параметров уже заданы в условии. Если бы я решал уравнение, там ОДЗ могло бы пригодиться. А здесь мне дают готовые числа, которые нужно подставить в выражение после того, как я его упрощу. Разве в этом случае имеет смысл находить ОДЗ?.. Не могу понять, для чего это нужно делать? В надежде, что авторы привели некорректные условия задачи, и если это выявить заранее, то выражение можно будет не упрощать?. mihailm в сообщении #688252 писал(а): Это понты от решателей. Ага… То есть, если я правильно понял, эта фраза в решении была добавлена как бы для красоты? 🙂 А на самом деле в данном случае можно было вообще ничего не писать про допустимые значения параметров?.. И выражение можно упрощать цепочкой, просто через знаки «равно», как в моём решении? mihailm в сообщении #688252 писал(а): Литературы как оформлять решение нет. Очень жаль! В принципе, я так и думал, потому что в сети не удалось найти ничего толкового по данной теме. (И всё же оставалась слабая надежда. :)) mihailm в сообщении #688252 писал(а): В первую очередь надо смотреть оформление решений задач в учебниках математики. Это ясно, но тут возникает ещё один вопрос. В учебниках очень часто встречаются сокращённые рассуждения, к примеру: Цитата: Мы получили квадратное уравнение . Как я понимаю, в реальности нужно вместо этой фразы написать подробное решение с нахождением дискриминанта и подставлением его в формулы корней, если он не отрицательный? 🙂 То есть, встретив такую фразу, идём и смотрим, как в учебнике оформляется решение квадратного уравнения?.. Или в некоторых случаях можно спрямить дорогу? Корни ведь иногда можно просто найти в уме. Писать дольше, чем считать. Можно же уснуть, выводя: Тем более что печатаю я «вслепую» и очень быстро, а вот на бумаге авторучкой пишу медленно как черепаха… Я-то для себя, конечно, могу делать сколь угодно краткие записи, занимаясь самостоятельно. mihailm в сообщении #688252 писал(а): решение должно быть правильным с точки зрения математики, в большинстве методических указаний как ставить оценки, прямым текстом написано, что способ оформление решения не играет роли Большое спасибо, Вы меня сильно успокоили. 🙂 Я думал, требования к оформлению гораздо строже. Но остаётся вопрос, какие существуют требования к подробности рассуждений. Xaositect в сообщении #688278 писал(а): Очевидно, оформлять решение надо так, чтобы его можно было прочитать, понять и проверить. В принципе, больше ничего не требуется. Согласен, вот только у всех разные представления о читабельности и понятности. 🙂 Хотелось узнать, каковы сейчас общепринятые требования. |
. 🙂 Бред какой-то… (Хотя, может, я чего-то не понимаю?)
Решив его, получаем корни и .
Что такое решение проблем? | NZ Maths
На этой странице мы обсуждаем «Что такое решение задач?» под тремя заголовками: введение, четыре этапа решения проблемы и научный подход.
Введение
Вполне естественно, что решение проблем связано с решением проблем. И мы ограничимся здесь размышлениями о математических задачах, хотя решение задач в школе преследует более широкую цель. Если подумать, вся цель образования состоит в том, чтобы подготовить учащихся к решению проблем.
Но решение задач также способствует развитию самой математики. Математика состоит из навыков и процессов. Навыки — это то, с чем мы все знакомы. К ним относятся основные арифметические процессы и сопутствующие им алгоритмы. Они включают алгебру на всех ее уровнях, а также сложные области, такие как исчисление. Это та сторона предмета, которая широко представлена в разделах «Числа и алгебра», «Геометрия и измерения» и «Статистика».
С другой стороны, математические процессы — это способы творческого использования навыков в новых ситуациях. Математические процессы включают решение проблем, логику и рассуждение, а также передачу идей. Это части математики, которые позволяют нам использовать навыки в самых разных ситуациях.
Начать стоит с различения трех слов «метод», «ответ» и «решение». Под «методом» мы подразумеваем средства, используемые для получения ответа. Обычно это включает одну или несколько стратегий решения проблем. С другой стороны, мы используем «ответ» для обозначения числа, количества или какой-либо другой сущности, которую запрашивает проблема. Наконец, «решение» — это весь процесс решения задачи, включая способ получения ответа и сам ответ.
метод + ответ = решение
Но как решать проблемы? Есть четыре основных шага. Полиа провозгласил их в 1945 году, но все они были известны и использовались задолго до этого. Ниже перечислены четыре этапа решения проблем Полиа.
1. Понять и изучить проблему
2. Найти стратегию
3. Использовать стратегию для решения проблемы
4. Оглянуться назад и подумать над решением.
Хотя мы перечислили четыре этапа по порядку, для сложных задач может оказаться невозможным просто пройти через них последовательно, чтобы получить ответ. Часто ученики двигаются вперед и назад между ступенями и поперек.
Вы не сможете решить проблему, если сначала не поймете ее. Это требует не только знания того, что вам нужно найти, но и ключевых фрагментов информации, которые необходимо собрать воедино, чтобы получить ответ.
Часто учащиеся не могут усвоить всю важную информацию о задаче за один раз. Почти всегда нужно будет прочитать задачу несколько раз, как в начале, так и в процессе работы над ней. С младшими школьниками стоит повторить задачу, а затем попросить их сформулировать вопрос своими словами.
Старшие ученики могут использовать маркер, чтобы отметить важные части проблемы.
Поиск стратегии обычно предполагает, что придумать подходящую стратегию несложно. Однако для многих задач учащиеся могут счесть необходимым поиграться с информацией, прежде чем они смогут придумать стратегию, которая может привести к решению. Эта исследовательская фаза также поможет им лучше понять проблему и может помочь им осознать часть информации, которой они пренебрегли после первого прочтения.
Изучив проблему и выбрав стратегию, можно попытаться сделать третий шаг, решить проблему . Надеюсь теперь проблема будет решена и ответ получен. На этом этапе важно, чтобы учащиеся следили за тем, что они делают. Это полезно, чтобы показать другим, что они сделали, а также помогает найти ошибки, если правильный ответ не будет найден.
На этом многие ученики, особенно математически способные, останавливаются. Но стоит ввести их в привычку оглядываясь назад над тем, что они сделали.
Для этого есть несколько веских причин. Прежде всего, это хорошая практика для них, чтобы проверить свою работу и убедиться, что они не сделали никаких ошибок. Во-вторых, очень важно убедиться, что полученный ответ действительно является решением проблемы. В-третьих, оглянувшись назад и немного подумав о проблеме, учащиеся часто видят другой способ решения проблемы. Это новое решение может быть лучше, чем исходное, и может дать больше понимания того, что на самом деле происходит. Наконец, учащиеся могут обобщить или расширить проблему.
Обобщение проблемы означает создание проблемы, в которой исходная проблема является частным случаем. Таким образом, задачу о трех поросятах можно превратить в задачу с любым количеством поросят.
В Задаче 4 раздела Что такое проблема? есть проблема с башнями. Последняя часть этой задачи спрашивает, сколько башен можно построить для любой определенной высоты . Ответ на эту задачу будет содержать ответ на предыдущие три вопроса.
Там у нас спросили количество башен высотой один, два и три. Если у нас есть какая-то формула или выражение для любой высоты, то мы можем подставить ее в эту формулу, чтобы получить ответ, например, для высоты три. Таким образом, формула «любой» высоты является обобщением случая высоты три. В качестве специального примера он содержит случай высоты три.
Расширение проблемы — родственная идея. Однако здесь мы рассматриваем новую проблему, которая каким-то образом связана с первой. Например, можно рассмотреть задачу, связанную с сложением, чтобы понять, имеет ли она какой-либо смысл с умножением. Довольно интересная задача — взять любое целое число и разделить его на два, если оно четное, умножить на три и прибавить единицу, если оно нечетное. Продолжайте повторять эту манипуляцию. Ответ, который вы получите в конечном итоге 1? Сделаем пример. Начнем с 34. Тогда получится
34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
Тогда мы точно добрались до 1.
Теперь оказывается, что никто в мире не знает, всегда ли вы доберетесь до 1 таким образом, независимо от того, с чего вы начнете. Вам есть о чем беспокоиться. Но при чем здесь расширение? Что ж, мы можем расширить эту задачу, просто изменив 3 на 5. Итак, на этот раз вместо деления на 2, если число четное, и умножения его на три, и добавления единицы, если оно нечетное, попробуйте разделить на 2, если число четное, и умножение на 5 и добавление единицы, если оно нечетное. Эта новая задача не содержит первую как частный случай, так что это не обобщение. Это 9Однако 0019 — это расширение — это проблема, тесно связанная с оригиналом.
Именно благодаря этому методу обобщения и расширения математика делает большие успехи. Вплоть до времени Пифагора было известно много прямоугольных треугольников. Например, было известно, что треугольник со сторонами 3, 4 и 5 является прямоугольным. Точно так же люди знали, что треугольники со сторонами 5, 12 и 13, а также 7, 24 и 25 являются прямоугольными.
Обобщение Пифагора состояло в том, чтобы показать, что КАЖДЫЙ треугольник со сторонами a, b, c был прямоугольным треугольником тогда и только тогда, когда a 2 + б 2 = в 2 .
Это подводит нас к аспекту решения проблем, который мы до сих пор не упоминали. Это оправдание (или доказательство). Ваши ученики часто могут угадать, каков ответ на задачу, но их решение не будет полным, пока они не смогут обосновать свой ответ.
Сейчас в некоторых задачах трудно найти обоснование. На самом деле вы можете полагать, что это не то, что может сделать любой из класса. Так что вы можете быть счастливы, что студенты могут найти ответ. Однако имейте в виду, что именно это обоснование отличает математику от любой другой дисциплины. Следовательно, шаг обоснования является важным, и его нельзя слишком часто пропускать.
Научный подход Другой взгляд на процесс решения проблем можно назвать научным подходом.
Мы показываем это на диаграмме ниже.
Здесь дается проблема, и первоначально идея состоит в том, чтобы поэкспериментировать с ней или изучить ее, чтобы понять, как действовать дальше. Через некоторое время есть надежда, что решатель сможет сделать предположение или угадать, каким может быть ответ. Если гипотеза верна, ее можно доказать или оправдать. В этом случае начинается процесс оглядывания назад, и делается попытка обобщить или расширить проблему. В этом случае вы, по сути, выбрали новую проблему, и весь процесс начинается сначала.
Иногда, однако, догадка неверна, и поэтому находится контрпример. Это пример, который противоречит гипотезе. В этом случае ищется другая гипотеза, и вы должны искать доказательство или другой контрпример.
Некоторые задачи слишком сложны, поэтому необходимо сдаться. Теперь вы можете сдаться, чтобы отдохнуть, и в этом случае это сдача «на данный момент». На самом деле это хорошая стратегия решения проблем. Часто, когда вы сдаетесь на некоторое время, ваше подсознание берет верх и предлагает хорошую идею, которой вы можете следовать.
С другой стороны, некоторые проблемы настолько сложны, что в конце концов вам придется сдаться «навсегда». На протяжении всей истории было много сложных задач, от которых математикам приходилось отказываться.
Решение проблем
Эта функция несколько больше, чем наши обычные функции, но это потому, что она содержит ресурсы, которые помогут вам разработать подход к решению проблем в преподавании и изучении математики. Прочтите статью Линн, в которой обсуждается место решения задач в новой учебной программе и устанавливается сцена. Во второй статье Дженни предлагает вам практические способы исследования аспектов вашего
культура в классе, а в третьей статье она предлагает три способа, которыми мы можем помочь детям стать компетентными в решении проблем. Четвертая статья дополняет третью, обсуждая, что мы подразумеваем под навыками решения проблем и как NRICH может помочь детям развить эти навыки. Прокрутите вниз, чтобы увидеть группы заданий с сайта, которые дадут учащимся опыт конкретных навыков.
Решение проблем и новая учебная программа
Возраст от 5 до 11 лет
Решение проблем лежит в основе вашей учебной программы? В этой статье для учителей Линн объясняет, почему так должно быть.
Развитие культуры в классе, поддерживающей подход к решению задач по математике
Возраст от 5 до 11 лет
В этой статье предлагаются практические способы изучения аспектов культуры вашего класса.
Развитие навыков решения проблем с учащимися младшего возраста
Возраст от 5 до 11 лет
Стать уверенным и компетентным в решении проблем — сложный процесс, требующий целого ряда навыков и опыта. В этой статье Дженни предполагает, что мы можем поддержать этот процесс тремя основными способами.
Использование заданий NRICH для развития ключевых навыков решения проблем
Возраст от 5 до 11 лет
конкретные навыки.
Испытания и улучшения в KS1
Возраст от 5 до 7 лет
Все эти второстепенные основные задачи можно решать с помощью подхода проб и улучшений.
Испытания и усовершенствования в KS2
Возраст от 7 до 11 лет
Все эти высшие основные задачи можно решить с помощью подхода проб и улучшений.
Систематическая работа в KS1
Возраст от 5 до 7 лет
Задания для детей KS1, направленные на систематическую работу.
Систематическая работа в KS2
Возраст от 7 до 11 лет
Задания для детей KS2, ориентированные на систематическую работу.
Образцы чисел
Возраст от 5 до 11 лет
Задания в этом сборнике побуждают детей создавать, распознавать, расширять и объяснять узоры чисел.
Работа в обратном направлении в KS1
Возраст от 5 до 7 лет
Каждая из низших основных задач в этой коллекции может быть решена путем работы в обратном порядке.
Работа в обратном направлении в KS2
Возраст от 7 до 11 лет
Каждую из верхних основных задач в этой коллекции можно решить, работая в обратном порядке.