Правила действий в математике: Порядок действий в Математике

Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий

Главная » Мамины лайфхаки » Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий

Содержание

1. Основные операции в математике
2. Что такое действия первой и второй ступени
3. Сложение и вычитание
4. Умножение
5. Что сначала — умножение или сложение?
6. Деление
7. Порядок действий без скобок
8. Порядок действий со скобками
9. Примеры на порядок действий 3-4 класс для тренировки

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).

2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком −­­­­­­ это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала — умножение или сложение?

Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:

• 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
• 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

• 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
• 50 + 50 – это кучки малолетних работников;
• 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Порядок действий без скобок

Установленный порядок арифметических действий без скобок:

1. Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
2. Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
3. Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):

Порядок действий со скобками

Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.

В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.

Примеры на порядок действий 3-4 класс для тренировки

Рассмотрим выражения, установим порядок действий и выполним вычисления.

Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

Узнаем, правильно ли определен порядок действий в следующих выражениях.

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание.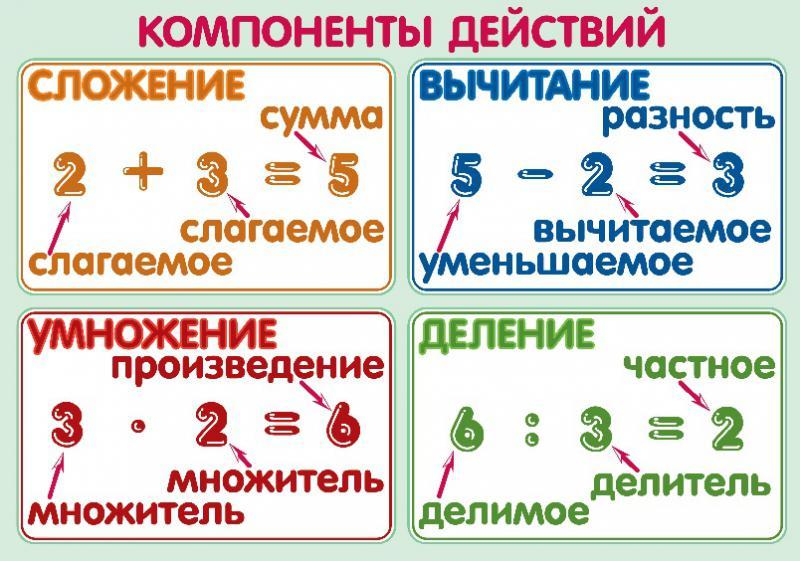 Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М. : «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Определи порядок действий в данных выражениях. Найди значение выражений.

***

Определи, в каком выражении такой порядок выполнения действий:

• умножение;
• деление;.
• сложение;
• вычитание;
• сложение.

Найди значение данного выражения.

***

Составь три выражения, в которых такой порядок выполнения действий:

• умножение; 2. сложение; 3. вычитание
• сложение; 2. вычитание; 3. сложение
• умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

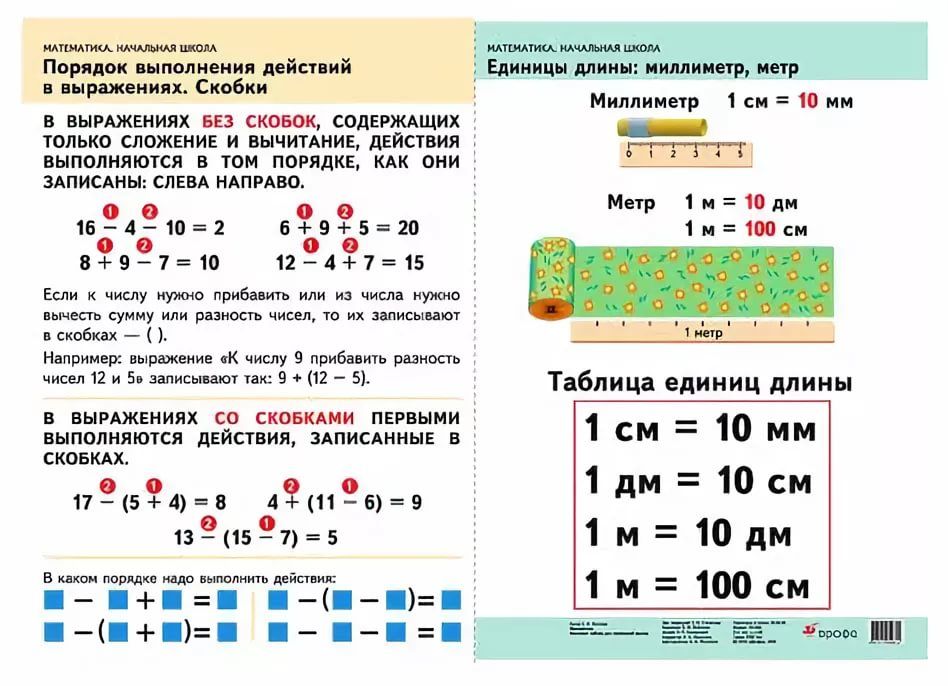
• в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
• в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

• сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
• затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1

Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7

Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.

Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4

действия в квадратных скобках дают:
14 – 3 · 2 = 8

выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29

Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150

Расставь порядок действий. Найди значение выражения:

1. (12 – 0 : 4) : 3 – (7 — 7)*45 + (36 : 6) : (15 : 15)
2. 36 : (12 – 6 : 20 – (0 *5 + 3) – (7 * 8) : 14 : 4
3. (3 + 27 : 3) * 5 – 60 * 3 : 90 + 8 * (7 – 7) : 4
4. (630 : 7 + 4 * 9) : (5 + 5 : 5) + (8 – 8) : (35 * 7 + 49)
5. 5 * (48 : 6 + 2 : 2) – 280 : 20 * 3 + (50 – 32) : 9
6. 8040 : 6 + (109004 – 76048) : 7
7. (64000 : 80 * 3 + 600) : 15 – (3200 * 100) : 2000
8. 240400 – (5796 + 1803200 : 400) * 8
9. 345 * (250 * 125) * (8 * 400)
10. 56432 : 8 * 50 – (223956 + 882630 : 9)
11. (62456715 + 548185) : 700 – 300 * 80450 : 5000
12. 80 – (17 * 4) : (20 – 380 : 20) + 90 * 40 : 120
13. (1000 – 999) * 40 – 0 : 24 + 360 : (16 * 5 + 280 : 7)
14. (600000 – 538704) * 500 : 300
15. 280 : (60 : 15) – (25 + 3 * 8) : 7 + 3 * (720 : 80)
16. (250 * 840 – 145 * 1008) : 60
17. (1000 – 832) * 715 : 30 + (104402 – 58842 : 7)

Источники

• https://skysmart. ru/articles/mathematic/poryadok-dejstvij-v-matematike
• https://Zaochnik.com/spravochnik/matematika/vyrazhenija/porjadok-vypolnenija-dejstvij/
• https://1Ku.ru/obrazovanie/62562-chto-snachala-slozhenie-ili-umnozhenie-pravila-porjadok-vypolnenija-dejstvija-i-rekomendacii/
• https://izamorfix.ru/matematika/arifmetika/poryadok_deystviy.html
• https://koncpekt.ru/nachalnye-klassy/rabochie-programmy/matematika-4-klass/5032-primery-na-poryadok-deystviy-so-skobkami-po-matematike-dlya-3-4-klassa.html

Что такое порядок действий и почему люди без него все время путаются | Бери и Делай

С порядком действий в математике каждый из нас знакомится в школе. Постепенно мы забываем эти правила, из-за чего легко допускаем ошибки в расчетах, которые совершаем в повседневной жизни.

«Бери и Делай» объясняет, чему учит порядок действий в математике, из-за которого даже взрослые часто допускают ошибки в «детских» задачках, и почему его важно знать в любом возрасте.

Зачем соблюдать правильный порядок действий

Основные арифметические операции в математике — это:

• сложение (+)
• вычитание (-)
• умножение (×)
• деление (÷)

Если в числовом выражении используется одна операция, то решить такой пример не составит труда. Например, 3 + 2 = 5 или 6 ÷ 3 = 2. Когда операций 2 или более, то, чтобы получить верный ответ, необходимо выполнять действия в определенном порядке.

Выше изображены 3 примера, каждый из которых легко решить неправильно, если забыть о правильном порядке действий в математике. Попробуйте решить эти примеры самостоятельно, а затем сверьте полученные результаты с правильными ответами в конце статьи. Если хотя бы в одном из них вы ошиблись, возможно, вам стоит повторить вместе с нами правила, касающиеся порядка действий.

Правило № 1. Действия выполняются слева направо по очереди

✅ Выполняя основные арифметические операции над числами, принято двигаться слева направо. Обратите внимание на картинку выше. Чтобы вычислить результат выражения 6 ÷ 3 × 2, необходимо выполнить действия поочередно слева направо, сначала разделив число 6 на 3, а затем умножив результат на 2. Выполнив операции в ином порядке (сначала умножение, а потом деление), мы получим неверный ответ. ❗ Если выражение состоит только из операций умножения или операций сложения, то, согласно переместительному закону, результат выражения не зависит от того, в какой последовательности выполнены операции.

Правило № 2. Сначала выполняются умножение и деление, затем сложение и вычитание

Одно выражение может содержать несколько разных арифметических операций, как на картинке выше. Запишем это выражение как 2 + 2 × 2. Если выполнить все действия по очереди слева направо, то получим 2 + 2 × 2 = 4 × 2 = 8. Этот ответ неверный (в этом можно удостовериться, пересчитав единичные квадратики на фотографии). Почему так получилось? ✅ Выше мы говорили о 4 основных арифметических операциях. Они неравнозначны по приоритету, что влияет на порядок, в котором нужно решать пример. Умножение и деление имеют больший приоритет, чем сложение и вычитание. Если действие имеет больший приоритет, то оно выполняется в первую очередь. Применим это на практике и решим пример еще раз: 2 + 2 × 2 = 2 + 4 = 6. Ответ верный.

❗ Если в выражении есть 2 и более равнозначные операции, то их выполняют по порядку слева направо. Таким образом, умножение и деление — это равнозначные операции и порядок их выполнения зависит только от порядка появления в выражении. То же самое касается сложения и вычитания. Выше показан пример решения выражения 12 ÷ 3 × 6 — 12 ÷ 6 × 3. По правилам, сначала необходимо выполнить деление и умножение, двигаясь слева направо, затем снова деление и умножение в правой части выражения, а только в конце перейти к вычитанию. Если порядок нарушить, ответ будет неверным.

Правило № 3. Возвести число в степень или извлечь корень нужно до перехода к другим операциям

✅ Если в выражении есть число, которое нужно возвести в степень, или произвести обратную операцию (извлечь корень), то это необходимо сделать перед тем, как выполнять основные арифметические операции. К примеру, попробуем решить, чему равно 4 + 2 +22 + 32. Для этого нужно сначала поочередно возвести в степень тройку и двойку, получив 4 + 2 + 4 + 9, а затем сложить все числа и получить в ответе 19. ❌ Здесь легко допустить ошибку, сложив между собой числа с одинаковыми показателями степени (то есть 22 и 32), а затем возведя полученную сумму в степень.

Правило № 4. Действия в скобках всегда выполняются в первую очередь

✅ Если часть выражения заключена в скобки, ее нужно решить в первую очередь. Затем вычислить степень или корень числа, после выполнить остальные операции, соблюдая приоритет и двигаясь слева направо. На картинке выше изображен простой пример. Слева ход решения, где соблюдаются правильный порядок действий: сначала получаем результат в скобках, затем выполняем умножение по очереди слева направо, в конце — операцию сложения. Справа неверный ход решения, где все операции выполняются поочередно слева направо, а в результате получается неправильный ответ.

✅ Между операциями в скобках действуют правила приоритета и очередности решений слева направо. В длинных выражениях можно проставлять над операциями числа, соответствующие очередности выполнения действий, как в примере выше. Это облегчает процесс решения.

Как запомнить порядок действий

1. Если в выражении есть скобки, сначала выполните действия внутри них. 2. Если в выражении число нужно возвести в степень или извлечь из него корень, сделайте это перед тем, как выполнять другие операции. 3 и 4. Среди 4 элементарных арифметических действий умножение и деление имеют больший приоритет, чем сложение и вычитание, поэтому выполняются в первую очередь. Равнозначные по приоритету операции выполняются по очереди, в порядке слева направо.

Ответы на примеры в начале статьи

• 8 ÷ 4 × 2 = 2 × 2 = 4

Это достаточно простой пример. Вы вряд ли допустили ошибку, так как решали его, инстинктивно выполняя действия по очереди, двигаясь слева направо.

• 6 ÷ 2(1 + 3) = ?

Этот пример выглядит простым, но способен поставить в тупик даже профессоров математики. Это связано с тем, что вы можете получить разные ответы в зависимости от того, как именно решаете его. Например, можно решить так: 6 ÷ 2(1 + 3) = 6 ÷ 2(4) = 3 * 4 = 12. Но если опереться на свойство дистрибутивности (где a(b+c) равняется a × b + a × c), то получается 6 ÷ 2(1 + 3) = 6 ÷ ((2 × 1) + (2 × 3)) = 6 ÷ (2 + 6) = 6 ÷ 8 = 3/4. Это возникает из-за того, что выражение можно интерпретировать по-разному, в результате чего ответы тоже получаются разными. В каком-то смысле это похоже на ситуации, когда из-за некорректной формулировки и порядка слов в предложении оно приобретает разные смыслы, например, «Как удивили его слова брата!» может означать, как его удивили слова брата, или как его слова удивили брата.

• 3(4 + 1) + 62 ÷ 3 — 7 = 3 × 5 + 62 ÷ 3 — 7 = 3 × 5 + 36 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20

В этом выражении легко допустить разные ошибки, но правильный алгоритм следующий: сначала выполняется операция в скобках, затем число 6 возводится во 2-ю степень, после нужно выполнить умножение, затем деление, после чего остаются сложение и вычитание. Аналогичный результат получится, если вспомнить свойство дистрибутивности (где a(b+c) равняется a × b + a × c) и решать пример следующим образом: 3(4 + 1) + 62 ÷ 3 — 7 = ((3 × 4) + (3 × 1)) + 62 ÷ 3 — 7 = (12 + 3) + 62 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20.

учебных занятий по математике | Департамент образования Айовы

Официальный веб-сайт штата Айова Вот откуда вы знаете

Агентства A-Z Programs & Services

Frameworks

Принципы действий — обеспечение математического успеха для всех: известная публикация NCTM, известная как «Библия преподавания математики», связывает исследования с практикой. Практика преподавания, основанная на исследованиях, для качественного математического образования всех учащихся. Изучите Обзор, который представляет собой сводку в формате PowerPoint и резюме, который предлагает руководство для учителей, тренеров по математике, администраторов, родителей и политиков.

Институт образовательных услуг (IES) — Комплект учебных материалов: практические руководства WWC, ориентированные на математику, расчет преимуществ: использование отчетов о вмешательстве для понимания эффективности программ и акцент на навыках раннего счета у детей раннего возраста

Проект оценки математики — TRU (Teaching Robust Understanding ) представляет собой основу для описания мощной учебной среды четкими и действенными способами. Он обеспечивает простой и доступный язык для обсуждения того, что происходит (и должно происходить) в классе, и согласуется с тем, что мы считаем хорошей практикой; и это фокусирует внимание класса на том, что имеет значение в обучении.

The Mathematical Education of Teachers II — также известный как MET II: в этом отчете представлены рекомендации по математической подготовке учителей на всех уровнях обучения: начальной, средней и старшей школе, профессиональному развитию и математическим знаниям для учителей. Написано Конференционным советом математических наук (CBMS), который состоит из семнадцати профессиональных обществ.

Principles to Actions

Набор инструментов Principles to Actions. Ресурсы, ориентированные на эффективные методы преподавания и руководящие принципы от NCTM для необходимых действий для всех учащихся, которые должны мыслить математически и быть готовыми к любой карьере или профессии.

Руководящие принципы — Преподавание и обучение имеют первенство среди Руководящих принципов принципов действия, а другие служат в качестве основных элементов, поддерживающих его.

Эффективная практика преподавания математики — восемь методик преподавания для учителей от принципов до действий.

Стратегии реализации Принципы действий

Принципы действий для учителей, руководителей, администраторов

Принципы действий — Презентация, описывающая убеждения в преподавании и изучении математики и действия учителей и учащихся.

План реализации PtA — это краткий план реализации Принципов действий согласно ведущему автору Стиву Лейнванду.

Десять стратегий перехода от принципов к действиям — Презентация с описанием десяти стратегий перехода от принципов к действиям.

Ресурсы

Иллюстративная математика — учебные ресурсы, приведенные в соответствие со стандартами, от Уильяма МакКаллума, ведущего автора Государственных стандартов по математике, главы математического факультета Университета Аризоны и партнера-основателя иллюстративной математики. Изучите планы и прогрессии курса.

Achieve the Core — Учебные практические ресурсы для коучинга, планирования уроков, преподавания и выравнивания рубрик. Изучите инструмент планирования уроков, разговаривайте с родителями, обучайте основным видео и многое другое.

Округ Ховард. Учебные практические ресурсы, соответствующие математическому содержанию и стандартам процесса. Выберите уровень обучения в разделе курса содержания и изучите ресурсы для процедур, годового обзора, ресурсов планирования и дополнительных ресурсов.

Teaching the Core — видеозапись уроков, которые включают описательные аннотации, определяющие элементы урока, а также действия и поведение учителя и ученика, поддерживающие обучение Common Core. Были тщательно проверены и аннотированы опытными преподавателями и экспертами по содержанию с использованием Практического руководства.

Язык закона

В некоторых предметах есть специальный словарный запас, который мы используем, чтобы мы могли говорить о сложных темах простыми словами. В математике некоторые слова сложение, дроби и десятичные дроби . Мы можем говорить о математике, не используя эти слова, но это может быстро запутать. Точно так же законы используют собственный специальный словарь. Если мы хотим понять, как создаются законы, мы должны начать с изучения словарного запаса.

Вот некоторые из основных слов и фраз, с которыми мы столкнемся, говоря о том, как принимаются законы, особенно федеральные законы:

Закон : Законодательство, принятое обеими палатами Конгресса и либо одобренное Президентом, либо прошедшее через его вето Конгресса, таким образом, становится законом.

Законопроект : Официально введенный закон. Большинство идей для новых законов, называемых законодательными предложениями , представлены в форме законопроектов и помечены как HR (Палата представителей) или S. (Сенат), в зависимости от того, где они внесены. Они также нумеруются в том порядке, в котором они представляются на каждом Конгрессе. Например, счет может называться H.R. 10 , если это десятый законопроект, внесенный в Палату представителей, или S. 42 , если это сорок второй законопроект, внесенный в Сенат.

Публичные законопроекты касаются вопросов, затрагивающих общественность, и становятся публичными законами или законами, если они одобрены Конгрессом и подписаны Президентом. Частные счета касаются вопросов, которые касаются конкретных лиц или частных организаций, таких как иски против федерального правительства, дела об иммиграции и натурализации, права собственности на землю и другие темы. Они становятся частными законами, если они одобрены и подписаны. 9Зарегистрированный законопроект 0049 был принят обеими палатами Конгресса (Сенат и Палата представителей), подписан их председательствующими должностными лицами и отправлен Президенту для подписания.

Календарь : список законопроектов, резолюций и других вопросов, которые планируется рассмотреть в комитетах или в зале любой из палат Конгресса. Календарь Конгресса — это повестка дня или список дел, ожидающих возможных действий со стороны Палаты представителей или Сената.

Комитет(ы) : Комитеты – это группы членов Конгресса, назначенные для расследования, обсуждения и составления отчетов по законодательству. Постоянные комитеты являются наиболее распространенным типом комитетов; они рассматривают законопроекты и другие законодательные акты, находящиеся на рассмотрении Палаты представителей или Сената. Подкомитеты являются подразделениями постоянного комитета, созданными с целью распределения рабочей нагрузки комитета. Рекомендации подкомитета должны быть одобрены всем комитетом, прежде чем они будут переданы в Сенат или Палату представителей.

Конгресс : Две палаты законодательной власти Федерального правительства: Сенат США и Палата представителей. В настоящее время насчитывается 100 сенаторов США, 435 представителей США, 5 делегатов и 1 постоянный комиссар. Конгресс также называют двухпалатным законодательным органом

из-за его двух законодательных палат или палат.

Federal : О центральном национальном правительстве Соединенных Штатов или в связи с ним.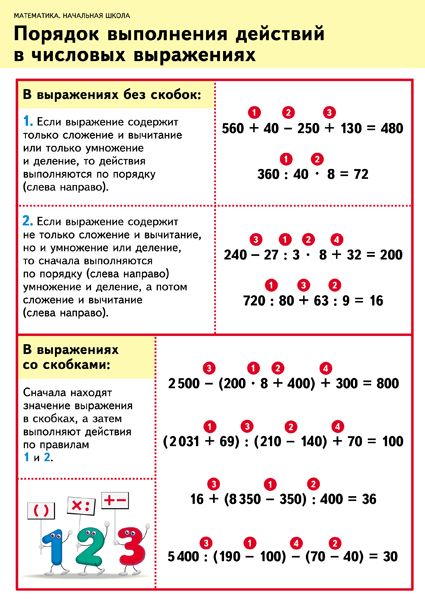

Хоппер : В Доме деревянный ящик, в который кладут купюры для официального представления. В Сенате законопроект передается клерку на трибуне.

Законодательство : Закон или свод (свод) законов.

Ходатайство : Официальное предложение или предложение о принятии мер, связанных с процессом принятия закона.

Отчет : распечатанный отчет о действиях комитета, включая его голоса, рекомендации и мнения по законопроекту, вопросу государственной политики или его выводы и заключения, основанные на надзорном расследовании, расследовании или другом исследовании.

Резолюция

: Предложение, одобренное одной или обеими палатами Конгресса, которое, за исключением совместных резолюций, подписанных Президентом, не имеет силы закона. Резолюции обычно относятся к одной из трех категорий. Простые разрешения , обозначаемые как H.Res. или S. Res., заниматься вопросами, полностью относящимися к прерогативам соответствующей палаты. Параллельные резолюции , обозначенные H. Con. Рез. или С. Кон. Рез., должны быть приняты обеими палатами, но не представляются на подпись Президенту. Параллельные резолюции обычно используются для создания или изменения правил, применимых к обеим палатам, или для выражения мнения двух палат. Совместные резолюции , обозначенные как HJ Res. или С.Дж. Рез., требуют одобрения обеих палат и, за одним исключением, подписи Президента и имеют силу закона в случае одобрения. Нет реальной разницы между законопроектом и совместным постановлением. Последнее обычно используется при решении ограниченных вопросов, таких как однократное присвоение для определенной цели или для объявления войны. Совместные резолюции также используются для предложения поправок к Конституции, но они не требуют подписи президента.

Предложение о вынесении на обсуждение : Предложение прекратить рассмотрение находящегося на рассмотрении предложения и отложить его на неопределенный срок. Когда Сенат или Палата представителей соглашаются с предложением о вынесении на обсуждение, внесенная мера фактически отклоняется.

Единодушное согласие : Соглашение между членами Конгресса об отмене определенного правила процедуры для ускорения разбирательства. В Сенате, например, при отсутствии возражений допускается единогласное согласие. Но если хотя бы один сенатор возражает, единогласный запрос на согласие отклоняется. Единодушные запросы на согласие с краткосрочными последствиями обычно удовлетворяются. Однако те, которые касаются расписания зала заседаний, условий рассмотрения законопроекта или других вопросов или прав других сенаторов, обычно не предлагаются, или лидер зала будет возражать против этого, пока все заинтересованные сенаторы не получат возможность его принять. .

Вето : Конституционная процедура, которая происходит, когда Президент не подписывает законопроект или совместную резолюцию в качестве закона. Обычное вето происходит, когда президент возвращает законопроект в исходную палату Конгресса без одобрения.