Площадь | это… Что такое Площадь?
У этого термина существуют и другие значения, см. Площадь (значения).
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.
Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.
Содержание
|
1 Площадь плоской фигурыСвойства
- Площадь единичного квадрата равна 1.
- Площадь аддитивна.
- Площадь неотрицательна.
- Площади конгруэнтных фигур равны.
Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими [2].
Общий метод определения площади
Площадь плоской фигуры
Декартовы координаты
Определённый интеграл как площадь фигуры
Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования
Площадь, заключённая между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:
Площадь, заключённая между графиками двух непрерывных функций на интервале находится как разность определённых интегралов от этих функций:
Полярные координаты
В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:
- .
Площадь поверхности
Основная статья: Площадь поверхности
Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:
То же в координатах:
Здесь .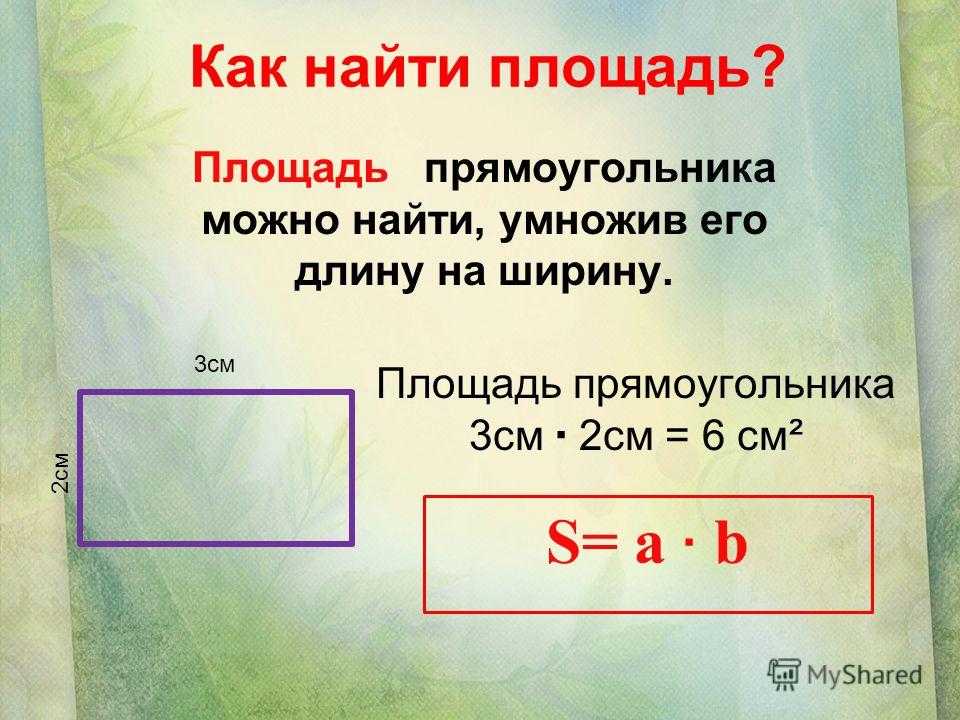
Единицы измерения площади
Метрические единицы
- Квадратный километр, 1 км² = 1 000 000 м²
- Гектар, 1 га = 10 000 м²
- Ар (сотка), 1 а = 100 м²
- Квадратный метр, производная единица системы СИ 1 м² = 1 са (сантиар)
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м².
Русские устаревшие
- Квадратная верста = 1,13806 км²
- Десятина = 10925,4 м²
- Копна = 0,1 десятины — сенные покосы меряли копнами
- Квадратная сажень = 4,55224 м²
Мерами земли при налоговых расчетах были выть, соха, обжа
, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.Античные
- Арура
Формулы вычисления площадей простейших фигур
Планиметрические фигуры
| Фигура | Формула | Переменные |
|---|---|---|
| Квадрат | — длина стороны квадрата. | |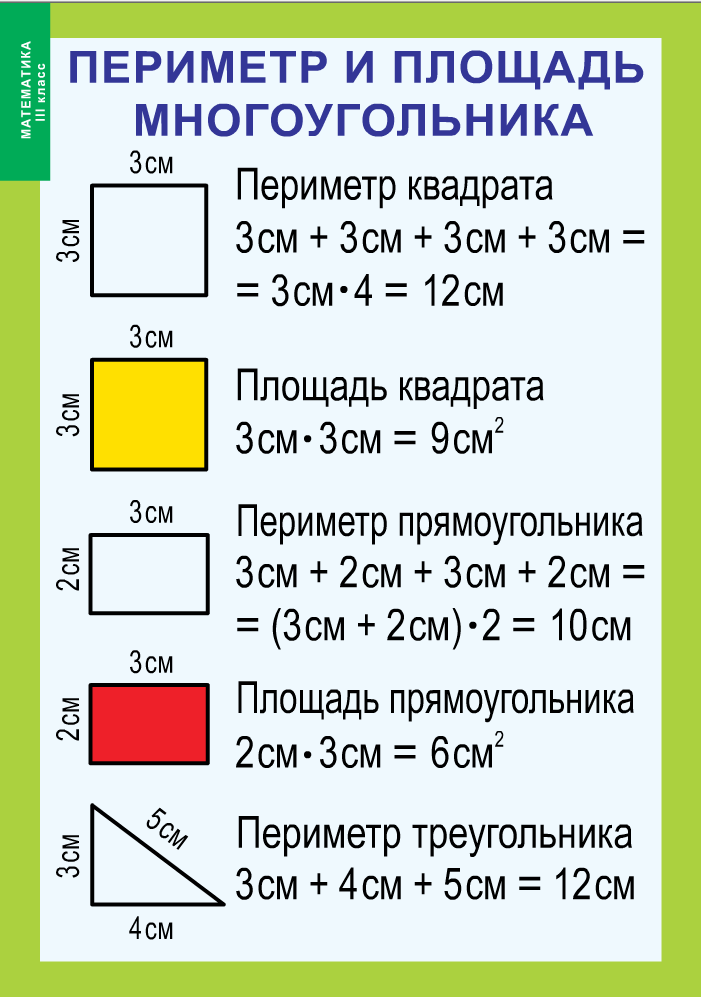
| Правильный треугольник | — длина стороны треугольника. | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — периметр, а — количество сторон. | |
| Прямоугольный треугольник | и — катеты треугольника. | |
| Произвольный треугольник | ||
| , — любые две стороны, — угол между ними. | ||
| (формула Герона) | , , — стороны треугольника, — полупериметр . | |
| в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный. | ||
| Прямоугольник | и — длины сторон прямоугольника (его длина и ширина). | |
| Параллелограмм | и — длина стороны и опущенной на неё высоты соответственно. | |
| и — соседние стороны параллелограмма, — угол между ними. | ||
| Ромб | и — длины диагоналей ромба. | |
| Эллипс | и — длины малой и большой полуосей. | |
| Трапеция | та — параллельные стороны, и — расстояние между ними (высота трапеции). |
Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур
| Фигура | Формула | Переменные |
|---|---|---|
| Круг | или | — радиус, а — диаметр круга. |
| Сектор круга | — радиус круга, — центральный угол сектора (в радианах). | |
| Сегмент | — радиус круга, — центральный угол сегмента (в радианах). | |
| Треугольник, вписанный в окружность | , , — стороны треугольника, — радиус описанной окружности. | |
| Произвольный многоугольник, описанный вокруг окружности | — радиус окружности, вписанной в многоугольник, и — периметр многоугольника. |
Формулы для вычисления площади поверхности тел в пространстве
| Тело | Формула | Переменные |
|---|---|---|
| Полная площадь поверхности цилиндра | и — радиус и высота соответственно. | |
| Площадь боковой поверхности цилиндра | и — радиус и высота соответственно. | |
| Полная площадь конуса | и — радиус и высота боковой поверхности соответственно. | |
| Площадь боковой поверхности конуса | и — радиус и образующая боковой поверхности соответственно. | |
| Площадь поверхности сферы (шара) | или | и радиус и диаметр, соответственно. |
См. также
- Площадь фигуры — математические аспекты понятия.
- Длина кривой
- Квадратура (математика)
- Объём
- Поверхность
Литература
- Рашевский П.
К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967. - Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.Ссылки
- Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977.
- Рохлин В. А. Площадь и объём. Энциклопедия элементарной математики, Книга 5, Геометрия.
Примечания
- ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186-224. — 800 с.
Площадь прямоугольника / Площадь фигуры / Основы геометрии / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
- Площадь прямоугольника
А теперь научимся вычислять площадь прямоугольника.
Например, прямоугольника со сторонами 2 см и 6 см.
Ты знаешь, что можно разделить прямоугольник на маленькие мерки — по 1 см².
Но можно сделать и по-другому: посмотрим, сколько квадратов по 1 см² уложится по длине прямоугольника:
Мы видим, по длине уложилось 6 квадратов площадью по 1 см². Площадь такой полоски 6 см². По ширине прямоугольника 2 см такая полоска уложится только 2 раза.
Тогда во всём прямоугольнике мы можем уложить 6 • 2 = 12 квадратов площадью 1 см².
Ответ: площадь прямоугольника 12 см ²
Рассуждаю дальше: Число 6 обозначает длину прямоугольника, а число 2 – ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Вывод:
Но чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Правило: площадь прямоугольника равна произведению его длины и ширины.
Советуем посмотреть:
Круг.
Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 60. Урок 24, Петерсон, Учебник, часть 2
Страница 65. Урок 26, Петерсон, Учебник, часть 2
Страница 79. Урок 32, Петерсон, Учебник, часть 2
Страница 27. Урок 9, Петерсон, Учебник, часть 3
Страница 33. Урок 11, Петерсон, Учебник, часть 3
Страница 38. Урок 13, Петерсон, Учебник, часть 3
Страница 47.
Урок 16,
Петерсон, Учебник, часть 3
Страница 90. Урок 35, Петерсон, Учебник, часть 3
Страница 108. Повторение, Петерсон, Учебник, часть 3
Страница 112. Повторение, Петерсон, Учебник, часть 3
3 класс
Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 31. ПР 1. Вариант 2, Моро, Волкова, Проверочные работы
Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98.
Урок 37,
Петерсон, Учебник, часть 1
Страница 99. Урок 38, Петерсон, Учебник, часть 1
Страница 78. Урок 33, Петерсон, Учебник, часть 2
Страница 88. Урок 38, Петерсон, Учебник, часть 2
Страница 5. Урок 2, Петерсон, Учебник, часть 3
4 класс
Страница 44, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 9.
Урок 3,
Петерсон, Учебник, часть 1
Что такое площадь в математике?
Автор:
Малкольм МакКинси
Проверено
015В геометрии площадь — это пространство плоской формы, например, многоугольника. , круг или эллипс, занимает плоскость. Площадь фигуры всегда измеряется в квадратных единицах.
Как только вы узнаете, как квадратные единицы соотносятся с площадью, вы сможете найти площадь практически любой двумерной фигуры.
Как найти площадь фигуры
Плоские фигуры имеют два измерения:
Ширина
Длина
Квадрат, например, имеет ширину равна его длине, так как длины всех сторон одинаковый. Эллипс также имеет ширину и длину.
Мы можем легко увидеть, как квадрат можно разделить на маленькие квадратные единицы, как на координатной плоскости.
Вы не можете легко увидеть, как эллипс может быть составлен из маленьких квадратов, но это возможно.
Поскольку он имеет ширину и длину, он покрывает пространство, и это пространство, даже с изогнутыми сторонами эллипса, может быть разделено на квадратные единицы:
Подсчет площади квадрата и прямоугольникаПодсчет квадратных единиц в квадрат легко: один, два, три и т. д. .
Но как посчитать все квадраты эллипса? Как определить, какая часть квадрата находится под верхней кривой? Как насчет кривых на левом и правом концах?
К счастью, у математиков есть быстрый способ сложить все квадратные единицы, не считая их. 9{2}mi2
Находите ли вы площадь четырехугольника, такого как трапеция и ромб, или любой другой замкнутой фигуры, площадь всегда будет возведена в квадрат.
Формула площади
Формула площади, которую вы используете, зависит от того, для какой фигуры вы пытаетесь найти площадь.
Площадь квадратов и прямоугольников
Чтобы найти площадь простых фигур, таких как квадрат или площадь прямоугольника, вам нужна только ширина w и длина l (или база, b ).
Площадь равна длине, умноженной на ширину:
Площадь всегда возводится в квадрат. Вы всегда будете выражать площадь в квадратных единицах, полученных из линейных единиц.
Вот прямоугольник 90 метров в ширину и 120 метров в длину (самый большой размер футбольного поля ФИФА). Чему равна площадь этого прямоугольника?
Пример площади прямоугольникаПоскольку футбольное поле измеряется в погонных метрах, его площадь равна квадратным метрам. Площадь прямоугольника 10 800 метров в квадрате .
Формула площади квадрата на самом деле даже проще, чем запись длина × ширина , потому что все стороны равны:
Вот квадрат со сторонами 15 дюймов в длину, такой же размер, как основания на бейсбольном мяче MLB поле. Вычисление площади для этого квадрата выглядит следующим образом:
Пример площади квадратаПлощадь других фигур
Все остальные многоугольники нелегко разделить на квадратные единицы.
Взгляните на параллелограмм.
Две стороны пересекают многие квадратные единицы. Конечно, параллелограмм — это просто опрокинутый прямоугольник.
Итак, математически, если бы мы могли отрезать один конец и присоединить его к другому, мы бы получили площадь в квадратных единицах. Мы можем сделать именно это, поскольку площадь параллелограмма с основанием b и шириной или высотой h находится по следующей формуле:
Это та же формула, что и для квадрата. или прямоугольник!
Если разделить параллелограмм по диагонали, что получится? Два треугольника. Это означает, что площадь любого треугольника равна половине площади параллелограмма с такой же длиной основания и высотой. Помните, что параллелограмм использует ту же формулу, что и прямоугольник.
Нахождение площади параллелограммаПлощадь треугольника равна половине основания, b , умноженной на высоту, h :
Вот прямоугольный треугольник, парус из 45-футовый парусник Morgan с базой 201420\frac{1}{4}2041 футов и высотой 441244\frac{1}{2}4421 футов.
Какова его площадь?
Для удобства умножения можно изменить дроби на десятичные:
Площадь треугольного паруса приблизительно равна 450,6 квадратных футов .
Как насчет домашней пластины бейсбольного поля Главной лиги бейсбола? Мы можем вычислить площадь домашней пластины пятиугольника , рассматривая его как две формы:
Прямоугольник 17 дюймов × 8,5 дюймов 90 003
9{2}216,5 дюймов2 Пример площади пятиугольника — домашняя плита
Найдите площадь круга
Некоторые двумерные фигуры даже не являются многоугольниками, например наш эллипс или окружность. Площадь круга с радиусом ( r ) находится по следующей формуле:
Если у вас есть круг с радиусом 4 см , вы можете легко вычислить площадь круга по формуле вверху:
Площадь круга составляет приблизительно 50,24 квадратных сантиметра.
Найти площадь эллипса
Площадь эллипса находится с использованием двух его осей: большая ось (длина от центра), обычно обозначаемая как аа, и малая ось (ширина от центра), обычно обозначаемая как bb, с помощью этой формулы:
Площадь круга и эллипсаНезависимо от того, имеете ли вы дело с правильным многоугольником или неправильной плоской фигурой, вы можете найти площадь!
Как рассчитать площадь | Что?, Вычисления, Единицы, Примеры
Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются.
Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Площадь сообщает нам размер формы или фигуры. Он сообщает нам размер квадратов, прямоугольников, кругов, треугольников, других многоугольников или любой замкнутой фигуры.
В реальном мире он сообщает нам размер листков бумаги, экранов компьютеров, комнат в домах, бейсбольных полей, городов, городов, стран и так далее. Знание местности может быть очень важным. Подумайте о том, чтобы постелить новый ковер в комнате вашего дома. Зная площадь комнаты, вы сможете убедиться, что ковер, который вы покупаете, достаточно большой, и в нем не останется лишнего.
Вычисление площадиПлощадь измеряется в квадратах (или квадратных единицах).
Сколько квадратов в этом прямоугольнике?
Мы можем посчитать квадраты или взять длину и ширину и использовать умножение.
Прямоугольник выше имеет площадь 15 квадратных единиц.
Площадь прямоугольника = длина x ширина
Примеры вычисления площади прямоугольника
Единицы измерения площадиМы измеряем площадь квадратами. Мы используем разные размеры квадратов в зависимости от того, насколько велика или мала площадь.
| Пример | Длина стороны квадрата | Блок |
| Размер ногтя на большом пальце | Миллиметр | мм 2 |
| Размер листа бумаги | Сантиметр | см 2 |
| Размер комнаты | Счетчик | м 2 |
| Размер города | км | км 2 |
| Не забудь пи 2 |
Мы пишем квадратные размеры, используя маленькую 2 рядом с единицей измерения. Пишем мм 2 , см 2 , м 2 , км 2 , см 2 Мы можем сказать «63 миллиметра в квадрате» или «63 миллиметра в квадрате» |
Мы могли бы использовать маленькие квадраты для измерения больших площадей. Единственная проблема заключается в том, что в конечном итоге нам придется использовать очень большие числа. Например, поле может быть измерено в 5 000 000 000 квадратных миллиметров, тогда как 5000 квадратных метров было бы гораздо легче произносить, писать и визуализировать.
Возможно, вы услышите больше единиц измерения площади; квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, акры, гектары — все это единицы измерения площади.
Дополнительные примеры вычисления площади
Площадь квадратаДлина и ширина квадрата одинаковы, поэтому нам просто нужно умножить длину на длину.
Площадь круга Площадь круга = πr 2
, где r — радиус круга, а π — отношение длины окружности к ее диаметру.
π (произносится как «пирог» и часто пишется как «пи») — бесконечное десятичное число с общим приближением 3,14159. Вы можете узнать больше о числе Пи здесь . Обратите внимание, как по мере того, как сектора становятся меньше, форма становится больше похожей на прямоугольник. Примечание. Нет предела тому, насколько маленькими могут быть эти сектора и насколько близко они могут напоминать прямоугольник при расположении.
Предполагая, что мы знаем, что длина окружности равна 2πr, мы можем добавить размеры к «прямоугольнику», как показано ниже. Используя формулу площади прямоугольника, площадь = ширина x высота, мы можем увидеть, как можно показать, что наш круг, преобразованный в прямоугольник, имеет площадь, которая приблизительно равна πr x r или πr . 2
Секторы круга переставлены Секторы круга переставлены – начинают выглядеть как прямоугольник Площадь составных фигур Во многих случаях для расчета общей площади необходимо вычислить более одной площади с последующим сложением, вычитанием или какой-либо другой комбинацией операций для нахождения требуемой площади.
Примечание: В приведенных ниже примерах единицы измерения не показаны, а ответы и значение π (Пи) округлены до сотых.
Пример: простые составные формыПриведенный ниже пример расчета площади относительно прост. Форму можно рассматривать как треугольник в сочетании с прямоугольником.
Приведенный выше пример иллюстрирует распространенное требование при работе с составными формами — поиск размеров, которые не показаны. Обучая своих детей, при необходимости помогите найти эти «недостающие» измерения. Ниже приведен еще один пример.
Нахождение размеров Пример: вычитание одной площади из другойВ приведенном ниже примере фигура выглядит как прямоугольник с вырезанным треугольником.
Пример: Частичные площади Пример ниже аналогичен приведенному выше, но поскольку у нас есть полукруг, нам нужно вычислить часть (половину) площади круга.