Предел функции в математике это: Предел функции | это… Что такое Предел функции?

alexxlab / / Математике

Урок по теме «Предел функции»

Разделы: Математика

Цели урока:

  • Образовательные:
    • ввести понятие предела числа, предела функции;
    • дать понятия о видах неопределенности;
    • научиться вычислять пределы функции;
    • систематизировать полученные знания, активизировать самоконтроль, взаимоконтроль.
  • Развивающие:
    • уметь применять полученные знания для вычисления пределов.
    • развивать  математическое мышление.
  • Воспитательная:
    воспитать интерес к математике и к дисциплинам умственного труда.

Тип урока: первый  урок

Формы работы учащихся:  фронтальная, индивидуальная

Необходимое оборудование:  интерактивная доска, мультимедиа проектор, карточки с устными и подготовительными упражнениями.

План урока

1. Организационный момент (3 мин.)
2. Ознакомление с теорией предела функции. Подготовительные упражнения. (12 мин.)
3. Вычисление пределов функции (10 мин.)
4. Самостоятельные упражнения (15 мин.)
5. Подведение итогов урока (2 мин.)
6. Домашнее задание (3 мин.)

ХОД УРОКА

1. Организационный момент

Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.

2. Ознакомление с теорией предела функции. Подготовительные упражнения.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом  .

Вычислим предел:
Подставляем вместо х – 3.
Заметим, что предел числа равен самому числу.

Примеры: вычислите пределы

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.

Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.

Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

Основные виды неопределенностей: 

Раскрытие неопределенностей

Для раскрытия неопределенностей используют следующее:

  • упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
  • если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

Пример: вычислим предел.
Разложим числитель на множители

3. Вычисление пределов функции

 Пример 1. Вычислите предел функции:

При прямой подстановке, получается неопределенность:

Разложим на множители числитель и знаменатель и вычислим предел.

Пример 2. Вычислите предел функции:

При прямой подстановке, получается неопределенность.

Помножим и числитель,  и знаменатель на .

Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел Аналогично

Пример 3. Вычислите предел функции:

При прямой подстановке, получается неопределенность.

Помножим и числитель,  и знаменатель на .

Мы учли, что 

4. Самостоятельные упражнения

Вычислите пределы:

5. Подведение итогов урока

Данный урок первый  по теме: «Предел функции». На уроке рассмотрены способы нахождения пределов. Разобрано что такое неопределенность, как раскрывать неопределенности. Надо заметить, что есть пределы, для которых невозможно найти числовое значение.

6. Домашнее задание

Домашнее задание раздается на карточках каждому ученику.

30.04.2014

ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ — Лекции по высшей математике

Лекции по высшей математике

Скачать все файлы (2163.9 kb.)

Доступные файлы (30):

n1.doc327kb.21.12.2005 16:14скачать
n2.doc266kb.21.12.2005 16:14скачать
n3.doc249kb.21.12.2005 16:14скачать
n4.doc448kb.21.12.2005 16:15скачать
n5.doc224kb.21.12.2005 16:13скачать
n6.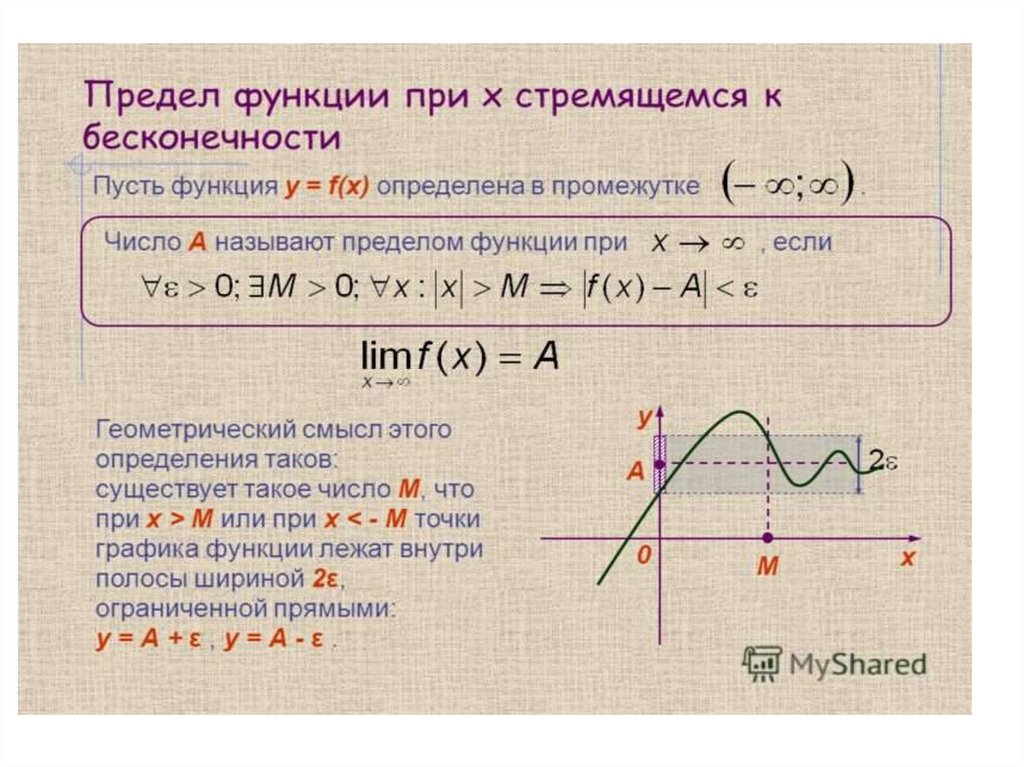 doc164kb.21.12.2005 16:17скачать
n7.doc259kb.21.12.2005 16:19скачать
n8.doc274kb.21.12.2005 16:20скачать
n9.doc336kb.21.12.2005 16:24скачать
n10.doc322kb.21.12.2005 16:31скачать
n11.doc311kb.21.12.2005 16:38скачать
n12.doc504kb.21.12.2005 16:54скачать
n13.doc118kb.21.12.2005 16:58скачать
n14.doc86kb.21.12.2005 17:01скачать
n15.doc225kb.21.12.2005 17:05скачать
n16.doc126kb.21.12.2005 17:15скачать
n17.doc156kb.21.12.2005 17:22скачать
n18.doc150kb.21.12. 2005 17:33скачать
n19.doc174kb.21.12.2005 17:45скачать
n20.doc227kb.21.12.2005 17:53скачать
n21.doc86kb.21.12.2005 17:58скачать
n22.doc105kb.21.12.2005 18:02скачать
n23.doc125kb.21.12.2005 18:07скачать
n24.doc260kb.21.12.2005 18:14скачать
n25.doc289kb.21.12.2005 18:29скачать
n26.doc108kb.12.07.2007 11:36скачать
n27.doc221kb.22.12.2005 19:03скачать
n28.doc402kb.22.12.2005 19:06скачать
n29.doc199kb.22.12.2005 19:11скачать
n30.doc295kb.22.12.2005 19:22скачать

n1.

doc

ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ
Аналитическая геометрия изучает геометрические образы (точки, прямые, плоскости, поверхности и т.д.) при помощи аналитического метода. В основе этого метода лежит метод координат Рене Декарта (французский математик 1596-1650), позволяющий ввести соответствия между основными понятиями геометрии (точки, прямые, плоскости) и упорядоченными тройками вещественных чисел. Изучение свойств и взаимного расположения геометрических образов в аналитической геометрии сводится к изучению описывающих эти образы уравнений с привлечением методов алгебры и математического анализа.

I. Вектор, геометрическое определение вектора. Равные векторы.

Пусть на некоторой прямой заданы две точки A и B . Тем самым выделен отрезок AB этой прямой с концами в точках A и B.

Можно считать, что точка A — начало отрезка, B — конец. Тогда мы зададим так называемый направленный отрезок, определяемый упорядоченной парой точек.

Определение . Направленный отрезок (упорядоченную пару точек) называют  вектором. Вектор обозначается или . Если точки A и B совпадают, то говорят, что вектор нулевой или нуль-вектор .

Расстояние между началом и концом вектора называется его  длиной или модулем и обозначается .

В
екторы называются  коллинеарными, если они имеют общую параллельную прямую. При совмещении начал коллинеарных векторов они оказываются лежащими на одной прямой.

В


екторы называются  компланарными, если они параллельны одной и той же плоскости. При совмещении начал компланарных векторов они оказываются лежащими в одной плоскости.

Теперь можно ввести следующее 

определение

: два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.


, если

, хотя но

Из определения равенства векторов следует, что каждый вектор можно перенести в любое место параллельно самому себе и не изменить его.

Тем самым мы ввели так называемый свободный вектор, задать который — значит задать его модуль и направление. Многие физические величины характеризуются не только числовым значением, но и направлением, и, следовательно, являются векторными (сила, скорость, перемещение, магнитная индукция…).

II. Линейные операции над векторами, их свойства.

Понятие о линейном пространстве.

К линейным операциям над векторами относятся сложение векторов и умножение вектора на скаляр.

Сложение двух векторов выполняется по правилу параллелограмма:  сумма  двух векторов представляет собой диагональ параллелограмма, построенного на равных им векторах.

Сумма нескольких векторов определяется как вектор, замыкающий ломаную линию, звеньями которой служат векторы-слагаемые, и направленный из начала первого вектора в конец последнего.
Определение: произведением вектора на вещественное число называется

такой вектор , что 1)

2) вектор коллинеарен ,

3) векторы и направлены одинаково,

если ,

и противоположно, если :

,если , ,если .

Вектор называется противоположным вектору . Сумма двух противоположных векторов равна нулевому вектору: .

Вычитание векторов — операция, обратная сложению:

Перечислим свойства введенных нами линейных операций:

1
) коммутативность сложения: ;

2) ассоциативность сложения: ;

3) существование нуль-вектора: ;

4) существование противоположного вектора: ;

5) дистрибутивность сложения по отношению к умножению на число:


6) дистрибутивность сложения:

A B C D E

7) ассоциативность умножения:  т.к.

8) существование единицы:  это следует из определения

операции умножения.

Пространство, для элементов которого вводятся операции сложения и умножения на число, обладающие свойствами (1)-(8), называют линейным (векторным) пространством. Элементы линейного пространства обычно называют векторами.
III. Разложение вектора по базису. Координаты вектора.

Пусть заданы векторы и числа  Составим комбинацию из этих векторов, используя только введенные линейные комбинации сложения и умножения вектора на число. В самом общем случае она имеет вид: . Такие комбинации называются линейными комбинациями векторов , а числа — коэффициентами линейной комбинации.

Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.

Пусть дан ненулевой вектор . Покажем, что любой коллинеарный ему вектор может быть представлен в виде единственным образом.

По определению операции умножения вектора на число векторы и коллинеарны, следовательно, коллинеарны и векторы и . Одинаковое направление векторов и обеспечивается выбором знака числа . Наконец, из равенства модулей равных векторов следует, что . Единственность представления следует из того, что при умножении вектора на другое число получается новый вектор: при .

Теорема 1. Любой вектор на плоскости может быть разложен по двум неколлинеарным векторам и единственным образом.

Доказательство: В общем случае отложим все три вектора из общей точки О. Из конца вектора (точки А) проведем прямые АР и AQ, параллельные векторам и . Тогда по правилу параллелограмма

.

Вектор коллениарен вектору и, следовательно, единственным образом может быть представлен в виде . Вектор коллинеарен вектору , поэтому . Тогда — единственное разложение вектора по векторам и .

Неколлинеарные векторы и , взятые в определенном порядке, называются базисом на плоскости, а коэффициенты линейной комбинации 1 и 2 — координатами вектора в базисе и .

Т
.
еорема2: любой вектор единственным образом раскладывается по трем фиксированным некомпланарным векторам:
Некомпланарные векторы образуют базис пространства. Коэффициенты разложения называют координатами вектора в базисе .

Таким образом, в пространстве с выбранным базисом нам удалось каждому вектору поставить в соответствие тройку чисел — его координат. Теперь при выполнении введенных линейных операций над векторами можно заменить геометрические построения аналитическими выражениями.

Пусть

тогда

и

Таким образом, при умножении вектора на число все его координаты умножаются на это число, а при сложении векторов складываются их соответствующие координаты, если они определены относительно одного и того же базиса.
IV. Линейная зависимость векторов. Размерность линейного пространства.

Запишем линейную комбинацию векторов Она называется тривиальной, если все ее коэффициенты одновременно равны нулю, то есть , и нетривиальной, если хотя бы один из коэффициентов отличен от нуля.

Определение: векторы называют линейно зависимыми, если можно найти их нетривиальную комбинацию, равную нулю:

при .

Определение: если для векторов обращается в нуль только их тривиальная комбинация, то такие векторы называют линейно независимыми:

при .

Векторы линейно зависимы, если хотя бы один из них можно представить как линейную комбинацию остальных. Пусть , тогда

Тогда на основании доказанных выше теорем оказывается, что линейно зависимыми являются любые два коллинеарных вектора (), любые три компланарных вектора () и любые четыре вектора в пространстве (). В свою очередь линейно независимыми всегда являются базисные векторы, т.е. два неколлинеарных вектора на плоскости и три некомпланарных вектора в пространстве.

Определение: количество векторов, образующих базис линейного пространства, называют размерностью этого пространства.

Размерность определяется наибольшим числом линейно независимых векторов пространства. Линейное пространство, имеющее размерность n, принято обозначать .
V. Системы координат.

Определение: декартовой системой координат называются совокупность точки и базиса.

Точка О называется началом координат,

Ox,Oy,Oz — координатными осями,

Oxy,Oyz,Oxz — координатными плоскостями.

Декартова система координат, базисные векторы которой взаимно перпендикулярны и имеют единичные длины, называется декартовой прямоугольной системой, а ее базис – ортонормированным.

Координатами точки А в выбранной cистеме координат называются координаты радиус-вектора этой точки в этой системе координат.

Если заданы координаты точек и , то можно найти выражение для координат вектора .

Из рисунка 6 следует, что , тогда . Если , то — координаты вектора .

На практике пользуются и другими системами координат, например, косоугольной декартовой, полярной, цилиндрической, сферической и др.

Исчисление

— Установление пределов внутри функций, когда пределы уходят в бесконечность

Я хорошо помню, как более 15 лет назад я читал старый учебник с более общей структурой, в которой эта теорема может быть доказана в очень общем виде. Нижеследующее основано на фрагментах того, что мне удалось вспомнить. Я не гарантирую, что моя номенклатура стандартна (и не гарантирую, что она уникальна!).

Предположим, $D \subseteq T \setminus \{\emptyset\}$ обладает следующими свойствами:

  • Для любых $U_1, U_2 \in D$ существует некоторое $U_3 \in D$ такое, что $U_3 \subseteq U_1 \cap U_2$ ($D$ — множество, направленное вниз относительно включения множества), и
  • Для любого $U \in D$ существует некоторый $U’ \in D$ такой, что $\operatorname{cl} U’ \subseteq U$.

Мы будем называть такой набор $D$ направлением . Мы можем использовать эту концепцию, чтобы в самом общем виде сформулировать и доказать свойство, о котором вы говорите.

Некоторые примеры направлений в $\Bbb{R}$: 9-, \infty, -\infty$ и т. д. Но это более гибко: одним определением мы определяем односторонние пределы и бесконечные пределы как в терминах зависимой переменной $x$, так и независимой переменной $f( х)$.

Предположим, что у нас есть топологические пространства $(X_1, T_1)$ и $(X_2, T_2)$ (опять же, не стесняйтесь подставлять их в $\Bbb{R}$ к обоим), и $D_i$ — направление в $ (X_i, T_i)$ для $i = 1, 2$. Далее, предположим, что $f : X_1 \to X_2$. Тогда мы говорим $$\lim_{x \to D_1} f(x) = D_2$$ если для всех $\mathcal{V} \in D_2$ существует некоторый $\mathcal{U} \in D_1$ такой, что $$x \in \mathcal{U} \подразумевает f(x) \in \operatorname{cl} \mathcal{V}.$$ Надеюсь, понятно, что в случае $\Bbb{R}$, делая $D_1 = a$ и $D_2 = L$, мы получаем обычное определение $\lim_{x \to a} f(x) = л$. Немного поработав, вы сможете убедиться, что все возможные определения точно инкапсулированы в эту структуру.

Имея это в виду, мы можем доказать следующую общую теорему:

Теорема. Предположим, что $(X_i, T_i)$ — топологическое пространство, а $D_i$ — направление в этом пространстве для $i = 1, 2, 3$. Далее, предположим, что $g : X_1 \to X_2$ и $f : X_2 \to X_3$. Затем, $$\lim_{x \to D_1} g(x) = D_2 \text{ и } \lim_{x \to D_2} f(x) = D_3 \подразумевает \lim_{x \to D_1} f(g(x )) = D_3.$$

Доказательство. Предположим, $\mathcal{W} \in D_3$. Поскольку $\lim_{x \to D_2} f(x) = D_3$, существует некоторый $\mathcal{V} \in D_2$ такой, что $$y \in \mathcal{V} \подразумевает f(y) \in \operatorname{cl} \mathcal{W}. $$ По второму свойству направлений должен существовать некоторый $\mathcal{V}’ \in D_2$, замыкание которого содержится в $\mathcal{V}$. Используя тот факт, что $\lim_{x \to D_1} g(x) = D_2$, существует некоторый $\mathcal{U} \in D_1$ такой, что $$x \in \mathcal{U} \подразумевается g(x) \in \operatorname{cl}\mathcal{V}’ \subseteq \mathcal{V} \подразумевается f(g(x)) \in \operatorname{ cl}\mathcal{W}.$$ Таким образом, по определению $\lim_{x \to D_1} f(g(x)) = D_3$. $\квадрат$ 9- \le a$ или $\infty, -\infty \le \pm \infty$. Более того, мы получаем хорошие результаты, например, если $\lim_{x \to D_1} f(x) = D_2$ и $D’ \le D_1$, то $\lim_{x \to D’} f(x) = Д_2$. Или, если $D’ \ge D_2$, то $\lim_{x \to D_1} f(x) = D’$.

  • Это раскрывает кое-что важное об ограничениях с направлениями: они (в основном) не уникальны! Действительно, использование обозначения $\lim_{x \to D_1} f(x) = D_2$ уже проблематично, так как левая часть не относится ни к одному направлению. Вместо этого, вероятно, было бы лучше сказать $f(x) \to D_2$ как $x \to D_1$.

  • Отношение $\le$ является предпорядковым, т. е. рефлексивным и транзитивным, но не обязательно антисимметричным. Симметричное отношение, $$D_1 \sim D_2 \iff D_1 \le D_2 \text{ и } D_2 \le D_1$$ является отношением эквивалентности, и действительно, было бы справедливо считать такие направления «эквивалентными». Это означало бы, что можно было бы поменять одно направление на эквивалентное в пределе по желанию. Мы могли бы, например, эквивалентно определить направление $a$ (где $a \in \Bbb{R}$) как $\{(a — 1/n, a + 1/n) : n \in \Bbb{ N}\}$, и мы получим эквивалентное направление.

  • Имейте в виду, что приведенное выше определение предела предполагает «полную» область определения, т. е. $g$ определено везде на $X_1$, а $f$ определено везде на $X_2$. Сначала это может показаться ограничивающим, но помните, что мы можем определить наше топологическое пространство как подмножество $\Bbb{R}$ и снабдить его топологией подпространства. Если у нас есть $Y \subseteq X$, а $D$ — направление в $X$, то $D_Y = \{U \cap Y : U \in D\}$ — направление, если $\emptyset \notin D_Y $.

    Это относится к действительным функциям, область определения которых не полностью $\Bbb{R}$.

    • Что такое предел? Объяснение математических понятий

    Давайте поговорим о понятии, которое может сбить с толку, когда вы впервые изучаете исчисление: ограничивает . Когда вы впервые знакомитесь с ограничениями, вы часто слышите, как ваш профессор говорит что-то вроде:
    » Каков предел f(x) =  при приближении x к 5? »

    В такой формулировке ограничения кажутся не очень естественными или интуитивными, но в сегодняшней статье я собираюсь убедить вас, что ограничения — это очень естественный способ смотреть на мир. Я также приведу несколько примеров пределов, которые мы можем решить, вообще не занимаясь «математикой»!

    Начнем с примера. Представьте, что вы наблюдаете, как ваша подруга едет на своем велосипеде по гладкой поверхности , и рисуете график зависимости положения ее велосипеда от времени.

    График может выглядеть примерно так:

    Теперь предположим, что, продолжая рисовать график, вы на мгновение отводите взгляд от своей подруги, так что вы пропустите, где она находится через 4 секунды. Итак, на вашем графике теперь есть «дыра» в тот момент, когда вы отвели взгляд.

    Даже если вы не знаете наверняка, где была ваша подруга в 4 секунды, можете ли вы угадать, где она была? Конечно, можете — она была, вероятно, на высоте 10 футов . Откуда вы знаете? Потому что прямо на до 4  секунд она была всего на меньше футов, а прямо на через секунд она была всего на после 10 футов. Если только она не была волшебным образом перенесена в тот самый момент, когда вы отвели взгляд, она должна была пройти 10 футов, чтобы график имел смысл.

    Ограничения — это просто очень очевидная идея — вы можете «угадать», какие значения функция принимает в точке, основываясь на том, какое значение она принимает в соседних точках.

    Когда вы видите выражение вроде:

    , вы должны подумать про себя: хм, какое значение я бы предположил, что функция f(x) должна принимать, когда x примерно равно h, основываясь ТОЛЬКО на значениях, которые функция принимает БЛИЗКО к час? (стрелка в выражении просто означает «приближается»).

    Если f(x)  это позиция вашего друга в момент времени x, то

    Я хочу отметить, что функция не обязательно должна быть линейной, чтобы вы могли принимать ограничения. Давайте рассмотрим другой пример, когда ваша подруга снова едет на своем велосипеде, но теперь замедляет скорость, когда доезжает до знака «стоп».

    График ее положения может выглядеть примерно так (это определенно не линейная функция!):

    На этом графике ваш друг начинает движение очень быстро, но резко замедляется, начиная примерно с полминуты. второй. Опять же, хотя мы «отвели взгляд» на x=4 , поэтому функция f(x)  не определена в этой точке, мы все еще можем оценить предел. В данном случае

    Итак, мы уже видели, что пределы позволяют нам «угадывать» поведение функций в тех точках, где мы по какой-либо причине не знаем точного значения функции.

    Часто нам интересно знать, какое значение примет функция при бесконечности . Мы не можем изобразить функцию до бесконечности, и мы не можем «вставить» бесконечность в формулу, чтобы напрямую оценить ответ.

    Оказывается, это еще один случай, когда нас могут выручить ограничения. Помните, что пределы — это наша лучшая «догадка» о том, как будет вести себя функция, основываясь на известных нам точках. Так, например, если мы снова посмотрим на этот последний график (воспроизведенный ниже) — когда ваш друг приближается к знаку остановки — мы можем спросить: «Если он продолжит свою текущую траекторию, где он окажется через бесконечное количество времени? ”

    В этом случае было бы разумно сказать, что есть асимптота на высоте 10 футов . Идея здесь в том, что ваш друг замедляется, замедляется и, в конце концов, остановится прямо у знака остановки, расположенного примерно в 10 футах. Если функция не изменится (другими словами, она снова не начнет ездить на велосипеде), то ее положение через бесконечное количество времени будет 10 футов.

    На математическом языке мы запишем это как:

    Пределы бесконечности немного отличаются от пределов в конечной точке — вместо того, чтобы смотреть на соседние значения, мы вместо этого смотрим на общий тренд функции, f(x) , и попытайтесь угадать, где закончится функция по мере того, как она становится все больше и больше.

    Иногда предел функции на бесконечности может быть положительной или отрицательной бесконечностью! Можете ли вы выяснить, каков предел первого (самого верхнего) графа, как ?

    Также бывают случаи, когда лимит не существует (или вы можете услышать, что лимит равен undefined ). Вот пример такого случая:

    Что бы вы назвали пределом, когда ? Это смотря куда смотреть! Если вы посмотрите на время меньше 4 секунд, может показаться, что она будет на высоте 8 футов, но если вы посмотрите на время больше 4 секунд, покажется, что она будет на высоте 11 футов! Когда у вас есть противоречивые предположения, вы можете сказать, что предела просто не существует.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *