Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами
Курс математики в выпускном классе посвящен изучению степеней и корней, знакомству с показательной и логарифмической функцией, интегралами и элементами математической статистикой. Отдельное внимание в 11 классе посвящено повторению изученного за весь курс математики и подготовке к грядущему экзамену.
В связи с этим, для учеников 11 класса особенно важно участие в олимпиадах по математике и дополнительные занятия, посвященные решению заданий различной сложности.
На этой странице собраны задания для подготовки к олимпиаде по математике для 11 класса. Представлены уравнения, задачи и математические загадки с ответами и решениями. Этот материал может быть использован учителями или репетиторами для повышения уровня знания учеников.
Уравнения
1. Решите уравнение: = 3
2. Решите уравнение: ( − 8)² = ( + 9)²
3. Решите уравнение: log2 (5 + ) = log2 (1 − ) + 1
4.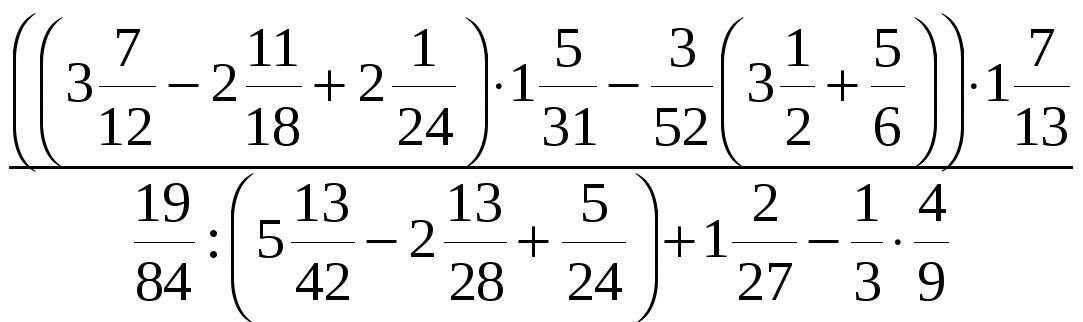
5. Решите уравнение: log2 (4 − ) = 7
6. Решите уравнение: − + 72 = 0
7. Решите уравнение: ( + 7)² = ( − 1)²
8. Решите уравнение: ( − 8)² = ( − 2)²
9. Решите уравнение: ( − 6)² = −
10. Решите уравнение: + 9 = ( + 9)²
Задачи
Задача №1
Докажите, что уравнение xy = 2006 (x + y) имеет решения в целых числах.
Задача №2
Докажите, что если α, β, γ — углы произвольного треугольника, то справедливо тождество cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1.
Задача №3
Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных шаров. Определите высоту «горки» из четырех шаров.
Задача №4
Докажите неравенство −< 1/6 на луче [1/4; + ∞).

Задача №5
В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.
Математические загадки
Загадка №1
Сколько лет человеку, если в 2012 году его возраст оказался равным сумме цифр года его рождения.
Загадка №2
Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе. Каждый участник решил не более шести задач. Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими. Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.
Загадка №3
Существует ли многогранник с нечетным числом граней, каждая из которых есть многоугольник с нечетным числом сторон?
Загадка №4
В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.
Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.
Загадка №5
Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800.
Чему равна сумма цифр числа 3n?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | 6 | 8,5 ∈ [8;9) | − 0,25 | 1,8 | -124 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | 9; 8 | -1,5 | 1 | -6 | -4 |
Ответы к задачам
Задача 1
Преобразуем уравнение к следующему виду: (x – 2006)(y − 2006) = 20062.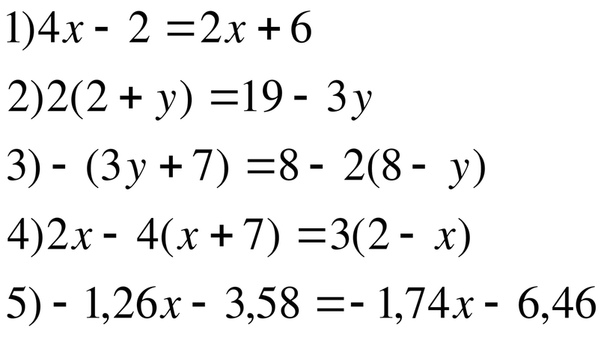 Уравнение имеет решения, например, x = y = 4012.
Уравнение имеет решения, например, x = y = 4012.
Задача 2
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π, и применяя формулы: cos² x = (1 + cos 2x)/2, cos x = − cos (π − x), cos x + cos y = (2cos((x + y)/2)) cos((x − y)/2), получим справедливое тождество.
Задача 3
Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 . Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R. Вершина D этой пирамиды проектируется в центр основания О.
Высота «горки» из четырех шаров равна сумме OD + 2R = 2R + 1
Задача 4
Пусть = −. Тогда = − и с помощью метода интервалов получаем, что < 0 при всех >2/9. Но 1/4>2/9, следовательно, функция убывает на луче [1/4; +∞]. Это значит, что − < 1/16 − 3/64 = 1/64 < 1/64.
Но 1/4>2/9, следовательно, функция убывает на луче [1/4; +∞]. Это значит, что − < 1/16 − 3/64 = 1/64 < 1/64.
Задача 5
Окружим каждый квадрат полоской шириной 1/2. Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4. Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов
Ответ: 175 центов
Ответы на загадки
Загадка 1
1 вар. Человек родился в 19mn году, тогда
2012 − 19mn= 1 + 9 + m + n
2012 − 1900 − m − n = 10 + m + n
102 = 11m + 2n
m = 8, n = 7, значит 1987 год, ему 25 лет.
2 вар. Человек родился в 200n году, тогда
2012 − 200n = 2 + n
2012 − 2000 − n = 2 + n
12 − 2 = 2n
n = 5, значит 2005 год, ему 7 лет.
Загадка 2
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков.
Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков).
Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику.
Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец.
По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 × 10 + 21 × 10 < 21²).
Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток.
Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками.
Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой.
Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.
Загадка 3
Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует
Загадка 4
Найдем произведение всех 25 чисел, записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек. Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1. А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50).
Загадка 5
Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n.
Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда.
Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.
Поэтому сумма цифр числа 3n равна 300.
Другие классы
Обновлено: , автор: Валерия ТокареваАлгебра, 11 класс: уроки, тесты, задания
Степени с рациональным показателем. Корни. Степенные функции
-
Понятие корня n-й степени из действительного числа
-
Функция корня n-й степени
-
Свойства корня n-й степени.
 Преобразование иррациональных выражений
Преобразование иррациональных выражений
-
Способы упрощения выражений, содержащих радикалы
-
Понятие степени с рациональным показателем, свойства степеней
-
Свойства степенных функций и их графики
Логарифмы.
 Показательная и логарифмическая функции
Показательная и логарифмическая функции
-
Свойства показательной функции и её график
-
Методы решения показательных уравнений
-
Методы решения показательных неравенств
-
Понятие логарифма.
 Основное логарифмическое тождество
Основное логарифмическое тождество
-
Свойства логарифмической функции и её график
-
Базовые свойства логарифмов
-
Методы решения логарифмических уравнений
-
Методы решения логарифмических неравенств
-
Переход к новому основанию логарифма
-
Системы показательных и логарифмических уравнений
-
Системы логарифмических и показательных неравенств
-
Производная показательной и логарифмической функции
Первообразная.
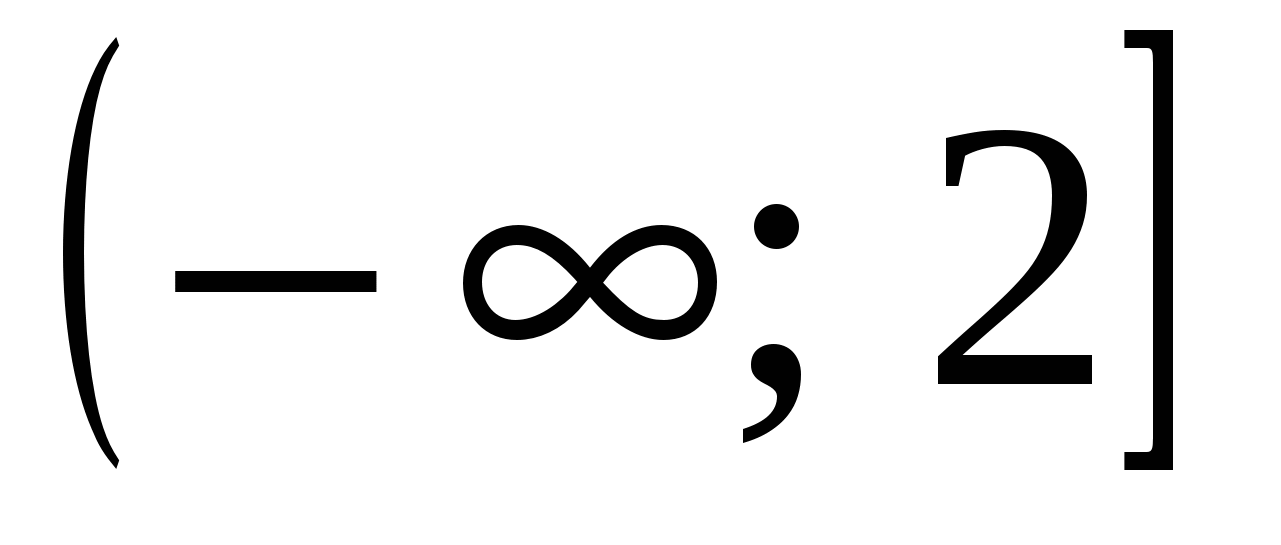 Неопределённые и определённые интегралы
Неопределённые и определённые интегралы
-
Понятие первообразной
-
Неопределённые и определённые интегралы. Методы интегрирования
-
Вычисление площадей с помощью интегралов
Начальные сведения комбинаторики
-
Правило суммы
-
Правило произведения
-
Перестановки.
 Перестановки без повторений
Перестановки без повторений
-
Размещения. Размещения с повторениями
-
Сочетания и их свойства
-
Треугольник Паскаля. Бином Ньютона
Начальные сведения теории вероятностей
-
Какие бывают случайные события
-
Комбинации событий.
 Противоположные события
Противоположные события
-
Вероятность события
-
Сложение вероятностей
-
Независимые события. Умножение вероятностей
-
Статистическая вероятность
Начальные сведения математической статистики
-
Случайные величины
-
Центральные тенденции
-
Меры разброса
-
Закон распределения вероятностей.
 Закон больших чисел
Закон больших чисел
Уравнения и неравенства
-
Равносильность уравнений. Теоремы о равносильности уравнений
-
Общие методы решения уравнений
-
Равносильность неравенств.
 Системы и совокупности неравенств
Системы и совокупности неравенств
-
Уравнения и неравенства с двумя переменными
-
Общие методы решения систем уравнений
-
Уравнения и неравенства с параметром
| 1. |
Значение функции
Сложность: лёгкое |
3 |
| 2. |
Определение показательной функции
Сложность: лёгкое |
1 |
3.
|
Свойства показательной функции (возрастание функции)
Сложность: лёгкое |
1 |
| 4. |
Умножение степеней с одинаковым основанием
Сложность: лёгкое |
1 |
5.
|
Деление степеней с одинаковыми основаниями
Сложность: лёгкое |
2 |
| 6. |
Возведение степени в степень
Сложность: лёгкое |
2 |
7.
|
Значение аргумента
Сложность: среднее |
1 |
| 8. |
Преобразования графика показательной функции
Сложность: среднее |
2 |
|
9. |
Область определения функции (показатель степени — дробь)
Сложность: среднее |
2 |
| 10. |
Свойства показательной функции (возрастание и убывание функции)
Сложность: среднее |
2 |
11.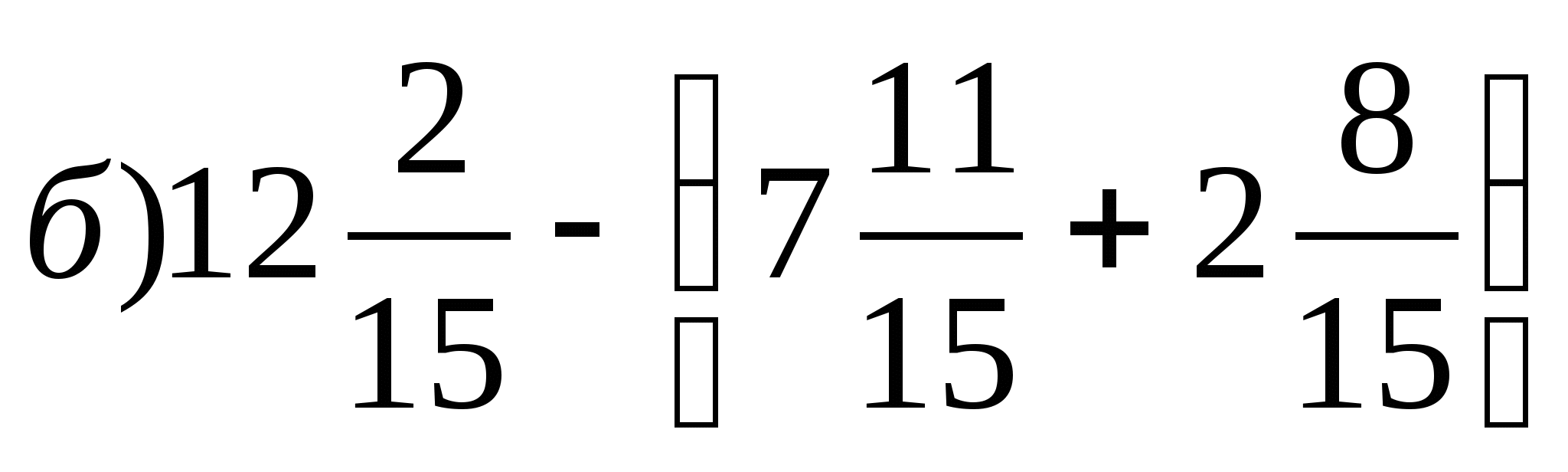
|
Свойства степени с рациональным показателем (деление)
Сложность: среднее |
3 |
| 12. |
Свойства степени с рациональным показателем (умножение)
Сложность: среднее |
5 |
13.
|
График показательной функции, область определения и область значений функции
Сложность: среднее |
3 |
| 14. |
Решение уравнения графически
Сложность: сложное |
4 |
15.
|
Свойства показательной функции (произведение степеней)
Сложность: сложное |
3 |
| 1. |
Табличные интегралы
Сложность: лёгкое |
1 |
2.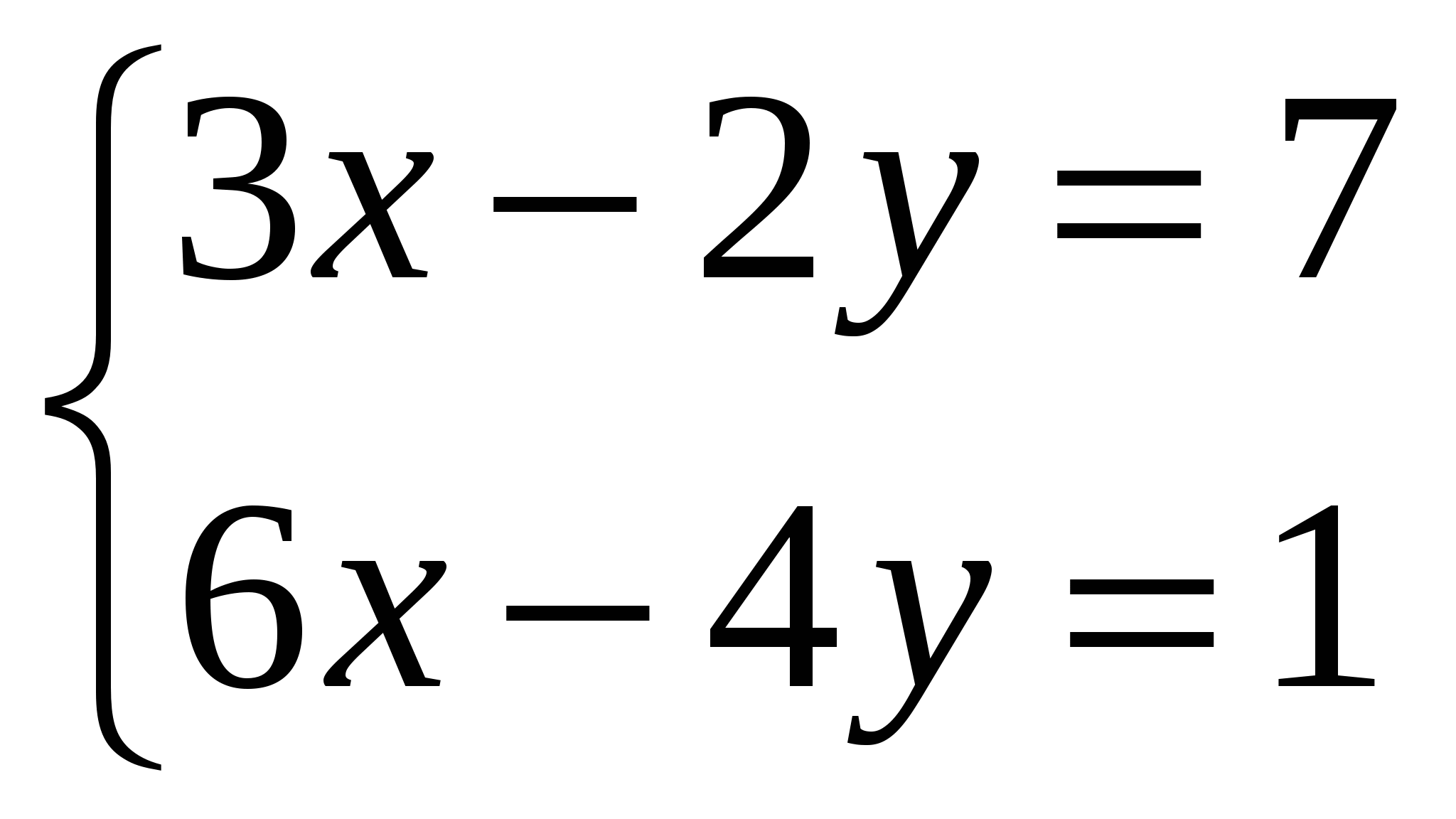
|
Определённый интеграл степенной функции
Сложность: лёгкое |
2 |
| 3. |
Основной интеграл тригонометрической функции
Сложность: лёгкое |
3 |
4.
|
Неопределённый интеграл от дробной функции
Сложность: среднее |
4 |
| 5. |
Неопределённый интеграл от дробной тригонометрической функции
Сложность: среднее |
3 |
6.
|
Неопределённый интеграл от показательной функции
Сложность: среднее |
4 |
| 7. |
Неопределённый интеграл, метод замены переменной, натуральный логарифм
Сложность: среднее |
4 |
8.
|
Неопределённый интеграл, метод замены переменной, тригонометрические функции
Сложность: среднее |
4 |
| 9. |
Определённый интеграл, функция, содержащая квадратный корень
Сложность: среднее |
4 |
10.
|
Определённый интеграл, тригонометрическая функция
Сложность: среднее |
4 |
| 11. |
Определённый интеграл, геометрический смысл
Сложность: сложное |
4 |
12.
|
Вычисление силы сжатия пружины
Сложность: сложное |
4 |
| 13. |
Физический смысл определённого интеграла
Сложность: сложное |
5 |
Демонстрационные варианты (демоверсии) ЕГЭ по математике
Демонстрационные варианты ЕГЭ по математике для 11 класса за 2002-2009 годы включали в себя три раздела: А (задачи с выбором ответа из нескольких предложенных), В (задачи с кратким ответом) и С (задания, для выполнения которых требовалось привести полное решение задачи).
В 2010 году из демонстрационного варианта ЕГЭ по математике были исключены задачи с выбором ответа, ранее составлявшие раздел А. Таким образом, демонстрационный вариант ЕГЭ стал состоять уже только из двух разделов В и С.
Демонстрационный вариант ЕГЭ 2011 года почти полностью совпадал с демонстрационным вариантом ЕГЭ 2010 года: были изменены лишь задания C1 и C5.
В 2014 году в демонстрационном варианте ЕГЭ по математике тематических изменений по сравнению с предыдущим годом не было: задачи В3, В9, В14, С2 и С4 были заменены на другие задачи той же тематики. Кроме того, было добавлено задание базового уровня сложности с кратким ответом, проверяющее практические навыки применения математики в повседневной жизни и изменен порядок заданий.
В 2015 году в порядке проведения ЕГЭ по математике произошли серьезные изменения: было решено проводить два отдельных экзамена – базового уровня и профильного уровня.
В связи с этим в 2015 году было представлено 2 демонстрационных варианта: новая модель демонстрационного варианта для ЕГЭ базового уровня и модернизированная модель демонстрационного варианта 2014 года для проведения ЕГЭ профильного уровня.
Демонстрационный вариант для ЕГЭ базового уровня содержал только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте было представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию было предложено только одно задание.
Демонстрационный вариант профильного экзамена 2015 года разработан на основе демонстрационного варианта ЕГЭ по математике 2014 года со следующими изменениями:
- Вариант стал состоять из двух частей (часть 1 — задания с кратким ответом, часть 2 — задания с кратким ответом и задания с развернутым ответом).

- Нумерация заданий стала сквозной по всему варианту без буквенных обозначений В, С.
- Во второй части добавлено 1 задание высокого уровня сложности с развёрнутым ответом, проверяющее практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
- Из первой части исключено 1 задание базового уровня сложности.
- Произведены несущественные изменения формы и тематики заданий 16 и 17
В демонстрационном варианте ЕГЭ по математике базового уровня 2016 года изменений не было .
В демонстрационном варианте ЕГЭ по математике профильного уровня 2016 года произошли следующие изменения:
- Из первой части варианта были исключены два задания: задание практического содержания базового уровня сложности и задание по стереометрии повышенного уровня сложности.

- Максимальный первичный балл за выполнение всей работы был уменьшен с 34 до 32 баллов.
В демонстрационных вариантах ЕГЭ по математике 2017 — 2021 годов как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2016 года изменений не было.
Олимпиадные задания (математика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»
В старых версиях браузеров сайт может отображаться некорректно. Для оптимальной работы с сайтом рекомендуем воспользоваться современным браузером.
Мы используем файлы cookies для улучшения работы сайта НИУ ВШЭ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь, наши правила обработки персональных данных – здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом НИУ ВШЭ и согласны с нашими правилами обработки персональных данных. Вы можете отключить файлы cookies в настройках Вашего браузера.
Вы можете отключить файлы cookies в настройках Вашего браузера.
Обычная версия сайта
2020/2021 учебный год
Для младших классов: максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100.
Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.
2019/2020 учебный год
Для младших классов: максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100.
Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.
2018/2019 учебный год
| Задания | Решения и критерии |
2017/2018 учебный год
2016/2017 учебный год
2015/2016 учебный год
2014/2015 учебный год
2013/2014 учебный год
2012/2013 учебный год
Задания 8 класс (задачи 1 и 2 имеют вес 16 баллов, остальные — 17 баллов)
Задания 9 класс (все задачи имеют равный вес (кроме 4): 17 баллов, задача 4 — 15 баллов)
Задания 10 класс (все задачи имеют равный вес (кроме 2): 17 баллов, задача 2 — 15 баллов)
Задания 11 класс (все задачи имеют равный вес (кроме 3): 17 баллов, задача 3 — 15 баллов)
2011/2012 учебный год
Сложные функции.
 {g(x)}$, где $a>0$, $a≠1$ равносильны уравнению $f(x)=g(x)$.
{g(x)}$, где $a>0$, $a≠1$ равносильны уравнению $f(x)=g(x)$.На применение данного метода накладывается серьезное ограничение: функция $h(x)$ должна быть строго монотонной, т.е. только возрастать или только убывать (другими словами — одно и тоже значение функция может принимать только один раз). Ребята, вспомните графики показательных, логарифмических и иррациональных функций. Они все строго монотонные.
Если функция h(x) – не монотонная, то данный метод применять нельзя, т.к. возможна потеря корней.
Давайте приведем простой пример. Тригонометрические функции – периодические (на определенных промежутках то возрастают, то убывают).
Уравнение $sin(15x)=sin(6x)$ – имеет бесконечно много корней. Можно представить схематично два графика и заметить, что пересекаться они будут бесконечно много раз.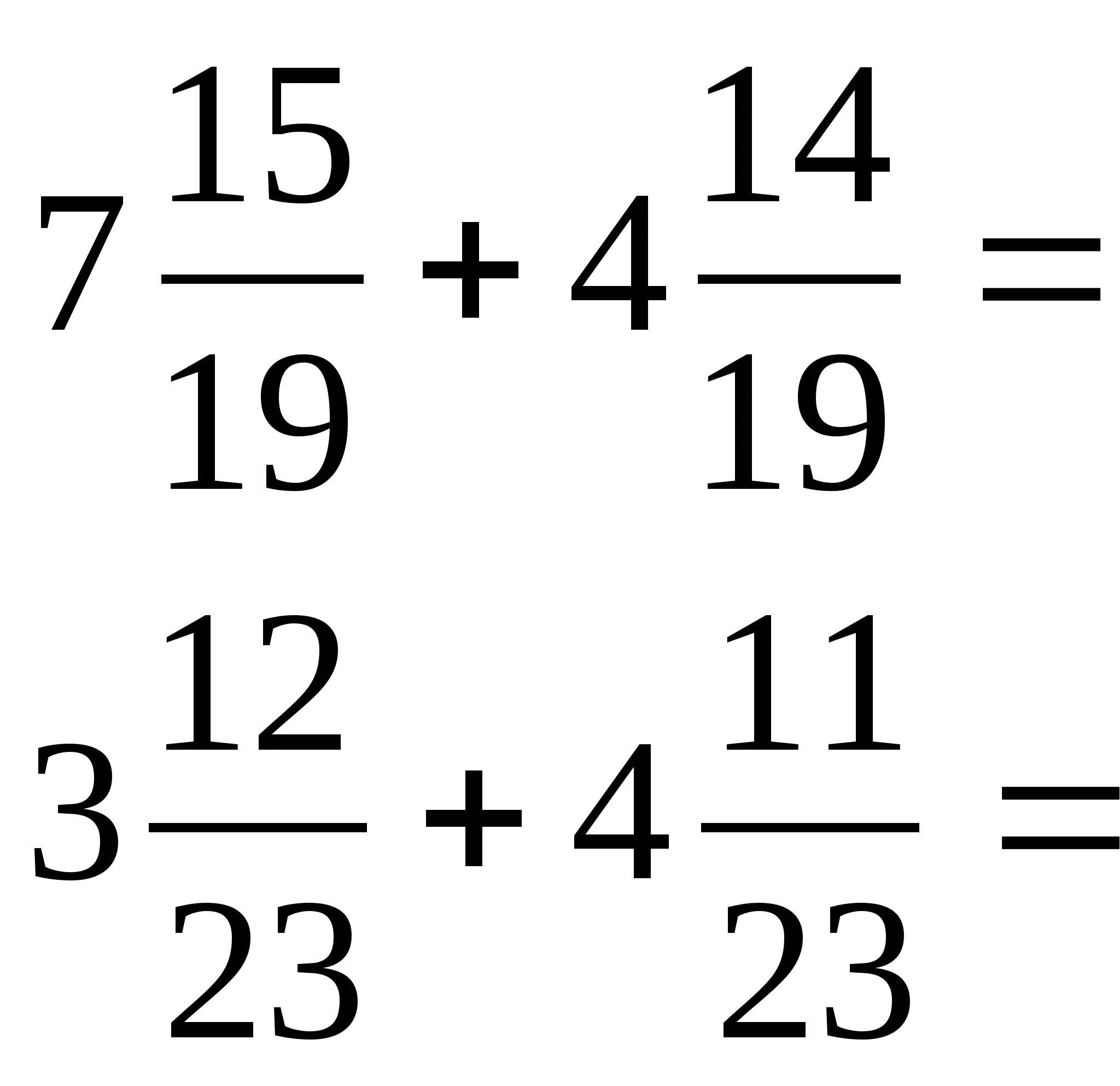 {2}(π+\frac{x}{2})-\frac{1}{2}sin(x)=0$.
{2}(π+\frac{x}{2})-\frac{1}{2}sin(x)=0$.
Вопросы и решения по математике для 11 класса
Консорциум Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя различные вопросы, усовершенствованные с помощью новых технологий.
Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Таблицы соответствия, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнение / числовое значение, Расширенный составной ответ, Краткий ответ и многие другие.
Эта страница содержит несколько примеров вопросов и ссылок на практические тесты по математике для 11 класса, которые дадут вам представление о вопросах, которые ваши ученики, вероятно, увидят на тесте.После каждого типового вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, придется учитывать в отношении навыков, процессов и информации, которые должны знать ваши ученики.
Домен: 11 класс >> Число и количество — Система вещественных чисел
Пример вопроса: Умножьте 36/49 и 21/63. К какому типу числа относится результат
- Числа нельзя умножать
- 57/112, рациональный
- 12/49, рациональный
- 12/49, иррациональный
Объяснение ответа: Напомним, что рациональное число — это любое число, которое может быть выражено как отношение или частное двух целых чисел (дробей).Иррациональные числа — это числа, которые нельзя выразить дробью. Оба числа являются дробными. Следовательно, они оба являются рациональными числами. Умножьте их вместе и упростите ответ:
36 / 49,21 / 63 = (4 / 7,9 / 7) .3 / 9,7 / 7 = 12/49. Ответ — дробь. Таким образом, это рациональное число.
Стандарты: HSN.RN.B.3
Нажмите здесь, чтобы попрактиковаться: Число и количество — Вопросы по системе вещественных чисел по математике в 11 классе
Домен: Уровень 11 >> Количество и количество — Количество
Пример вопроса: На графике ниже показаны колебания одной из струн скрипки во время игры. Что верно в отношении масштаба оси Y графика?
Что верно в отношении масштаба оси Y графика?
- Каждая отметка на оси Y, вероятно, может составлять один фут.
- Каждая отметка на оси Y, вероятно, может составлять один сантиметр.
- Каждая отметка на оси Y, вероятно, может составлять один миллиметр.
- Каждая отметка на оси Y, вероятно, может составлять один дюйм.
Ответ Пояснение: На графике представлена амплитуда вибрирующей струны скрипки. Когда струна скрипки следует этому графику, струна растягивается в одном направлении, а затем в другом.Каждый раз, когда строка пересекает ось x, она оказывается в исходном положении. Это движение настолько мало, что человеческий глаз почти не видит. Поэтому блок должен быть очень маленьким. Самый маленький выбор — миллиметр.
Стандарты: HSN.RN.A.1
Нажмите здесь, чтобы попрактиковаться: Число и количество классов 11 — Количество вопросов
Домен: 11 класс >> Число и количество — комплексная система счисления
Пример вопроса: Что такое спряжение комплексного числа 7 + 3i?
- -7 + 3i
- -7-3i
- 3i
- 7-3i
Объяснение ответа:
Стандарты: HSN. RN.A.1
RN.A.1
Нажмите здесь, чтобы попрактиковаться: Математические числа и количество в 11 классе — вопросы по комплексной системе счисления
Домен: 11 класс >> Число и количество — векторные и матричные количества
Пример вопроса: Вычтите эти два вектора − 12, −23⟩ − ⟨− 8, −14⟩.
- − 4, −9⟩
- (4,9)
- ⟨− 9, −4⟩
- ⟨− 20, −37⟩
Объяснение ответа:
Вопрос просит нас вычесть эти два вектора ⟨− 12, −23⟩ − ⟨− 8, −14⟩.Если у нас есть два вектора, v → = (x 1 , y 1 ) и w → = (x 2 , y 2 ), то разность двух векторов равна v → −w → = ⟨X 1 −x 2 , y 1 −y 2 ⟩. В этом вопросе мы вычитаем ⟨− 12, −23⟩ − ⟨− 8, −14⟩. Разница составляет ⟨− 12 — (- 8), — 23 — (- 14)⟩ = ⟨− 4, −9⟩
Стандарты: HSN.VM.B.4
Щелкните здесь, чтобы попрактиковаться: Число и количество — Вопросы о векторных и матричных величинах для 11 класса по математике
Область: 11 класс >> Алгебра — арифметика с многочленами и рациональными выражениями
Пример вопроса: Вычесть (x 3 + 2x 2 -x + 7) из (4x 3 + 6×2 + 2x-7)
- -3x 3 + 4x 2 + 3x-14
- -3x 3 -4x 2 -3x + 14
- 3x 3 + 4x 2 + 3x
- 3x 3 + 4x 2 + 3x-14
Объяснение ответа: При объединении многочленов объединяйте одинаковые члены путем объединения коэффициентов.
Вычесть (x 3 + 2x 2 -x + 7) из (4x 3 + 6x 2 + 2x-7)
(4x 3 } + 6x 2 + 2x-7) — (x 3 + 2x 2 -x + 7)
(4x 3 -x 3 ) + (6x 2 -2x 2 ) + (2x — (- x)) + (-7-7)
3x 3 + 4x 2 + 3x-14
Стандарты: HSA.APR.A.1
Щелкните здесь, чтобы попрактиковаться: Алгебра — Арифметика с многочленами и рациональными выражениями Вопросы для 11 класса по математике
Область: 11 класс >> Алгебра — видение структуры в выражениях
Пример вопроса: Каков коэффициент третьего члена выражения
5x 3 y 4 + 7x 2 y 3 −6xy 2 −8xy?
- 6
- 7
- -8
- -6
Ответ Объяснение: Выражение 5x 3 y 4 + 7x 2 y 3 −6xy 2 −8xy — это полиномиальное выражение с четырьмя членами. Коэффициент термина — это число перед термином. Если термин начинается с отрицательного числа, то коэффициент является отрицательным числом, независимо от того, содержит ли термин переменные или нет. Третий член — -6xy 2 , а число перед членом — -6.
Коэффициент термина — это число перед термином. Если термин начинается с отрицательного числа, то коэффициент является отрицательным числом, независимо от того, содержит ли термин переменные или нет. Третий член — -6xy 2 , а число перед членом — -6.
Стандарты: HSA.SSE.A.1
Щелкните здесь, чтобы попрактиковаться: Алгебра — определение структуры выражений Вопросы для 11 класса по математике
Область: 11 класс >> Алгебра — создание уравнений
Пример вопроса: Мэдисон является торговым представителем дилера транспортных средств.Каждый месяц она продает две машины на каждые 10 велосипедов и четыре мотоцикла на каждую машину. Если она делает 40 продаж в месяц, а переменная x представляет количество автомобилей, которые она продает, какое уравнение вы могли бы использовать, чтобы определить, сколько автомобилей она продает?
- х + 5х + 4х = 40
- х + 5х + 4х = 20
- 2x + 10x + 8x = 40
- 2x + 10x + 8x = 20
Ответ Объяснение: Если мы используем переменную x для количества автомобилей, которые продает Мэдисон, и она продает две машины на каждые 10 велосипедов, то она продает в пять раз больше велосипедов, чем автомобилей. Таким образом, она продает 5 велосипедов. Тогда, если она продаст четыре мотоцикла на каждую машину, количество проданных мотоциклов будет в 4 раза больше. Задача гласит, что она делает 40 продаж в месяц, поэтому сложите автомобили, велосипеды и мотоциклы и сделайте эту сумму равной 40. Уравнение: x + 5x + 4x = 40.
Таким образом, она продает 5 велосипедов. Тогда, если она продаст четыре мотоцикла на каждую машину, количество проданных мотоциклов будет в 4 раза больше. Задача гласит, что она делает 40 продаж в месяц, поэтому сложите автомобили, велосипеды и мотоциклы и сделайте эту сумму равной 40. Уравнение: x + 5x + 4x = 40.
Стандарты: HSA.CED.A.1
Щелкните здесь, чтобы попрактиковаться: Алгебра — Создание уравнений Вопросы для 11 класса по математике
Область: 11 класс >> Алгебра — Рассуждение с помощью уравнений и неравенств
Пример вопроса: Каково решение 6x + 5 = 101?
- 19
- 13
- 17
- 16
Объяснение ответа: Вопрос просит вас найти решение 6x + 5 = 101.Начните с вычитания 5 из обеих частей уравнения. Это дает вам 6x = 96. Затем разделите обе стороны на 6 и x = 16.
Стандарты: HSA.CED.A.4
Щелкните здесь, чтобы попрактиковаться: Алгебра — Рассуждение с помощью уравнений и неравенств Вопросы для 11 класса по математике
Домен: 11 класс >> Функции — функции устного перевода
Пример вопроса: Функция f (x) = — 1/8 (x − 7/2) 2 + 3/2 — это путь футбольного мяча во время тренировочной игры. Его график показан ниже. Какая часть домена этой функции фактически моделирует эту ситуацию?
Его график показан ниже. Какая часть домена этой функции фактически моделирует эту ситуацию?
- [7,0]
- [-1,7]
- (-∞, ∞)
- [0,7]
Ответ Объяснение: Функция является полиномиальной функцией. Область определения всех полиномиальных функций в математическом контексте равна (−∞, ∞). Однако в контексте реального мира домен должен позволять функции подчиняться правилам реального мира. Удар по мячу происходит за время, равное 0 секундам, и мяч приземляется, согласно графику, за время, равное 7 секундам.Следовательно, домен равен [0,7].
Стандарты: HSF.IF.B.5
Щелкните здесь, чтобы попрактиковаться: Функции — вопросы по интерпретации функций для 11 класса по математике
Домен: Уровень 11 >> Функции — Функции построения
Пример вопроса: Чем график f (x) = x + 7 отличается от g (x) = x + 12?
- При смещении f (x) на 5 единиц будет получено g (x)
- g (x) получается смещением f (x) вниз на 5 единиц
- Когда g (x) сдвигается вверх на 5 единиц, будет получено f (x)
- f (x) получается сдвигом g (x) вверх на 5 единиц
Ответ Объяснение: Значение, добавленное к функции, вызывает вертикальный сдвиг на графике. Поскольку 12 на 5 единиц больше, чем 7, график g (x) получается сдвигом f (x) на 5 единиц вверх.
Поскольку 12 на 5 единиц больше, чем 7, график g (x) получается сдвигом f (x) на 5 единиц вверх.
Стандарты: HSF.BF.B.3
Щелкните здесь, чтобы попрактиковаться: Functions — Building Functions Questions for 11 Grade 11 Math
Домен: 11 класс >> Функции — линейные, квадратичные и экспоненциальные модели
Пример вопроса: Какая функция изображена ниже на графике?
- f (x) = 5 (0,5) x
- f (x) = 5 (0.4) х
- f (x) = 4 (0,5) x
- f (x) = 5 (1,5) x
Ответ Пояснение: График показывает, что функция является функцией экспоненциального роста. Формула для экспоненциальной функции: f (x) = ab x , где a — точка пересечения по оси y, а b — коэффициент роста. Если экспоненциальная функция является функцией роста, то b> 1. Если экспоненциальная функция является функцией убывания, то 0 x.
Стандарты: HSF.LE.A.2
Щелкните здесь, чтобы попрактиковаться: Функции — вопросы по линейным, квадратичным и экспоненциальным моделям для 11 класса по математике
Домен: 11 класс >> Функции — тригонометрические функции
Пример вопроса: Если cosσ = −1, каково значение sinσ?
- undefined
- 1
- 0
- -1
Объяснение ответа: Правило:
В таблице ниже приведены точные значения триггерных функций для особых углов.
Угол, косинус которого равен -1, равен 180 градусам. Синус 180 градусов равен 0.
Стандарты: HSF.TF.C.8
Щелкните здесь, чтобы попрактиковаться: Функции — Вопросы по тригонометрическим функциям для 11 класса по математике
Домен: 11 класс >> Геометрия — соответствие
Пример вопроса: Предположим, что PQRS переведен, как показано на рисунке ниже. Как переводится параллелограмм?
Объяснение ответа: На рисунке видно, что перевод идет вправо и вниз. Судя по рисунку, расстояние, на которое параллелограмм смещается вправо, равно длине стороны PQ. Кроме того, судя по рисунку, расстояние, на которое параллелограмм перемещен вниз, составляет примерно половину длины бокового QR.
Судя по рисунку, расстояние, на которое параллелограмм смещается вправо, равно длине стороны PQ. Кроме того, судя по рисунку, расстояние, на которое параллелограмм перемещен вниз, составляет примерно половину длины бокового QR.
Стандарты: HSG.CO.A.4
Щелкните здесь, чтобы попрактиковаться: Геометрия — вопросы на соответствие для 11 класса по математике
Область: 11 класс >> Геометрия — подобие, прямоугольные треугольники и тригонометрия
Пример вопроса: Выполните растяжение точки C с центром в начале координат с масштабным коэффициентом, равным 1/2.Какова координата точки C ’полученного изображения?
- (2, -3/2)
- (-3/2, 2)
- (8, -6)
- (-6, 8)
Ответ Объяснение: Когда расширение выполняется относительно начала координат, координаты точки изображения являются произведением масштабного коэффициента и координат исходной точки. ½ * 4 = 2. ½ * -3 = -3/2.
Стандарты: HSG.SRT.A.1
Щелкните здесь, чтобы попрактиковаться: вопросы по геометрии — подобию, прямоугольным треугольникам и тригонометрии для 11 класса по математике
Домен: 11 класс >> Геометрия — круги
Пример вопроса: Касательная линия проводится к окружности из точки вне окружности.Радиус проводится от центра окружности до точки касания прямой. Какой угол образует радиус с касательной?
- 0 или
- 90 или
- 180 или
- 270 или
Ответ Объяснение: Радиус окружности, проведенной до точки касания касательной, перпендикулярен касательной.
Стандарты: HSG.C.A.2
Щелкните здесь, чтобы попрактиковаться: Геометрия — Круги Вопросы для 11 класса по математике
Домен: 11 класс >> Геометрия — выражение геометрических свойств с помощью уравнений
Пример вопроса: При написании уравнения y = x 2 + 6x + 7 Анжелика использовала следующие шаги. Если она допустила какие-либо ошибки, объясните их и напишите правильное уравнение.
Если она допустила какие-либо ошибки, объясните их и напишите правильное уравнение.
y = x 2 + 6x + 7
y − 7 = x 2 + 6x
y − 7−9 = x 2 + 6x + 9
y − 16 = (x + 3) 2
y = (x + 3) 2 +16
Объяснение ответа: Чтобы преобразовать уравнение в стандартную форму, мы должны заполнить квадрат, чтобы получить квадрат бинома, который необходим для стандартной формы. Чтобы завершить квадрат, мы берем половину коэффициента линейного члена, равного 3, затем возводим его в квадрат и прибавляем к обеим сторонам.Затем разложите на множители полный квадрат трехчлена, чтобы получить квадрат бинома. Затем решите относительно y.
Стандарты: HSG.GPE.A.2
Щелкните здесь, чтобы попрактиковаться: Геометрия — Выражение геометрических свойств с помощью уравнений Вопросы для 11 класса по математике
Домен: 11 класс >> Геометрия — Моделирование с помощью геометрии
Пример вопроса: Какова плотность кирпича, занимающего 310 см 3 при массе 853 г?
- .
 36см 3 / г
36см 3 / г - 2,75 г / см 3
- 2,64 г / см 3
- 0,36 г / см 3
Объяснение ответа: V = Bh = lwh Объем прямоугольной призмы
Формула плотности d = m / V. Объем составляет 310 см 3 , а масса — 853 г. Подставьте эти значения в формулу, чтобы найти плотность.
Стандарты: HSG.MG.A.2
Щелкните здесь, чтобы попрактиковаться: Геометрия — моделирование с помощью вопросов по геометрии для 11 класса по математике
Домен: 11 класс >> Геометрия — геометрические измерения и размеры
Пример вопроса: Полусфера радиусом 3 см находится на конусе такого же диаметра и высоты 10 см, как показано на схеме ниже.Найдите общий объем составного объекта.
- 24πсм 3
- 36πсм 3
- 48πсм 3
- 60πсм 3
Ответ Пояснение: Общий объем объекта — это сумма объемов полусферы и конуса.
V = ½ (4/3) πr 3 + (1/3) πr 2 h
V = ½ (4/3) π (3m) 3 + (1/3) π (3m) 2 (10 см) V = 48πсм 3
Стандарты: HSG.GMD.A.3
Нажмите здесь, чтобы попрактиковаться: Геометрия — геометрические измерения и вопросы о размерах для 11 класса по математике
Домен: 11 класс >> Статистика и вероятность — интерпретация категориальных и количественных данных
Пример вопроса: Какое влияние оказывает группа очень больших значений на среднее и медианное значение набора данных?
- Среднее и медианное значение увеличиваются
- Среднее значение не изменилось, но медиана увеличилась
- Среднее значение и медиана не изменены
- Среднее значение увеличилось, но медиана уменьшилась
Объяснение ответа: На рисунке ниже показано влияние на среднее и медианное значение в результате добавления некоторых очень больших элементов в набор данных.Поскольку новые элементы очень большие, они оказывают значительное влияние на среднее значение, поскольку их очень большие значения усредняются с другими значениями в наборе. Медиана также подвержена влиянию и движется в том же направлении, что и среднее.
Стандарты: HSS.ID.A.3
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятности — Интерпретация категориальных и количественных данных Вопросы для 11 класса по математике
Область: 11 класс >> Статистика и вероятность — выводы и обоснование выводов
Пример вопроса: Есть десять игральных карт, четыре из них красные и шесть черных.Джулиан выбирает карту наугад. Какова вероятность того, что он получит красную карточку?
Объяснение ответа: Вероятность рассчитывается как отношение количества успехов к количеству возможных вариантов выбора.
Вопрос спрашивает вероятность выбора красной карточки. Из десяти карт четыре красные.
Таким образом, вероятность выбрать красную карточку составляет четыре из десяти, что сокращается до двух из пяти.Это соотношение составляет 2/5
.Стандарты: HSS.IC.A.1
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — делать выводы и обосновывать выводы Вопросы для 11 класса по математике
Область: 11 класс >> Статистика и вероятность — условная вероятность и правила вероятности
Пример вопроса: На диаграмме Венна ниже показаны результаты опроса о том, какие виды спорта люди любят смотреть по телевизору. Участники опроса могли выбрать один вид спорта, два вида спорта или все три вида спорта.В каком регионе (ах) содержатся ответы, в которых участник опроса указал, что он / она любит смотреть только один вид спорта?
- B, C, D
- E, F, G
- B, A, D
- A, B, C
Объяснение ответа: Каждый кружок содержит ответы, которым нравится этот определенный цвет. Следовательно, в регионах A, B, C, E содержатся ответы о том, что нравится смотреть бейсбол. Области D, A, D, G содержат ответы о том, что нравится смотреть баскетбол.Области A, B, D, F содержат ответы о том, что любят смотреть футбол. Если буква находится в двух кружках, регион содержит ответы о том, что любил смотреть спортивные состязания, представленные обоими кружками. Если регион находится во всех трех кругах, этот регион содержит ответы, которые хотели бы посмотреть все три вида спорта. Если регион находится только в одном круге, этот регион содержит ответы, в которых говорится, что им нравится смотреть только спорт, представленный этим кругом. Области, которые находятся только в одном круге, — это E, F, G.
Стандарты: HSS.CP.A.1
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — условная вероятность и правила вероятностных вопросов для 11 класса по математике
Область: 11 класс >> Статистика и вероятность — использование вероятности для принятия решений
Пример вопроса: Бюро переписи населения предоставило отчет, в котором говорилось, что средний уровень дохода жителей Флориды составляет 47 463 человека. Основываясь на этой информации, если вы провели опрос 100 случайных работников во Флориде, какова вероятность, что доход респондентов превышает 47 463 человека?
- 65%
- 35%
- 80%
- 50%
Объяснение ответа: Медиана — это среднее число, когда все числа в наборе расположены от наименьшего значения к наибольшему значению.В вопросе говорится, что средний уровень дохода во Флориде составляет 47 463 человека, то есть половина рабочих во Флориде составляет менее 47 463 человек, а половина рабочих во Флориде — более 47 463 человек. Это означает, что, согласно отчету Бюро переписи населения, вероятность того, что доход случайно выбранного человека превышает 47 463 человека, составляет 50%.
Стандарты: HSS.MD.A.4
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы для 11 класса по математике
ВопросыРешения вышеуказанных вопросов
|
Spectrum математика 8 класс ответы
5 Проверьте, что вы знаете НАЗВАНИЕ Spectrum Math Проверьте, что вы знаете 2 класс Глава 1 Понимание и использование чисел Напишите нечетное или четное.Напишите уравнение, соответствующее массиву.
15 ноября 2018 г. · Учебное пособие по математике Spectrum, 8 класс [PDF] 1. Учебное пособие по математике Spectrum, 8 класс [PDF] 2. Сведения о книге Автор: Страниц: 160 страниц Издатель: Spectrum 2014-08-15 Язык: английский ISBN- 10: 1483808769 ISBN-13: 9781483808765 3. Сводная книга Укрепите свои математические навыки восьмиклассника с помощью Spectrum Math.
Предоставляется ключ для ответа на викторину. Викторина по солнечной системе; Планы уроков Держите своих учеников в курсе наших планов уроков.Учащиеся используют математические навыки для вычисления силы тяжести, массы и веса, а также для создания солнечного затмения в практических занятиях и завершения эксперимента по закону движения. Гравитация и вес на других планетах
Spectrum Math, 6-й класс Описание книги Spectrum Math, 6-й класс Читать электронную книгу Онлайн PDF EPUB KINDLE, Spectrum Math, 6-й класс pdf, Spectrum Math, 6-й класс читать онлайн …
Простая математика язык, а также головоломки, игры, викторины, рабочие листы и форум. Для школьников, учителей и родителей.
процент правильных ответов = 60% (20-8) / 20 * 100% = 12/20 * 100% = 60% В большинстве школьных систем это переводится как F — для НЕУДАЧИ Какого возраста вы учитесь в 8 классе? Большинство детей учатся в возрасте от 13 до 14 лет …
Подготовка к тесту Spectrum 8 класс включает стратегические задания по языковым искусствам и математике, советы по тестам, которые помогут ответить на вопросы, а также критическое мышление и рассуждения. Серия Spectrum Test Prep для 1-8 классов была разработана экспертами в области образования и была создана, чтобы помочь учащимся улучшить и укрепить свои навыки сдачи тестов.
Деньги Оценка 6 Рубрика Основными элементами производительности, требуемыми этой задачей, являются: • интерпретация гистограмм. На их основе баллы за определенные аспекты производительности должны быть присвоены следующим образом: баллы, раздел баллы 1. Дает правильные ответы: Дэнни Крис Бен Али Все четыре правильных ответа Частичный балл Три правильных ответа
Выпущенные тесты и наборы предметов
Ваш браузер не поддерживает джаваскрипт! Этот сайт использует JavaScript, но полностью работает без него.Стандарты обучения (SOL) и тестированияВыпущенные тесты являются репрезентативными для содержания и навыков, включенных в тесты SOL в Вирджинии, и предназначены для помощи в понимании формата тестов и вопросов. Для некоторых курсов SOL предоставляются наборы тестовых заданий, а не полные выпущенные тесты, поскольку банк тестовых заданий для этих курсов не может поддерживать полную версию. Для наборов тестовых заданий невозможно предоставить исходные баллы для таблиц масштабированных баллов, поскольку они не представляют собой полные формы тестов.Точно так же таблица необработанных баллов по шкале оценок не может быть предоставлена для компонента MC / TEI письменного теста в конце курса, поскольку он не представляет собой полную форму теста.
Онлайн-версия тестов или наборов тестовых заданий больше не доступна, так как программное обеспечение доставки тестов было изменено. Версия PDF будет содержать ключ ответа для всех элементов теста или набора тестовых элементов.
В PDF-документах для тестов и наборов тестовых заданий, выпущенных весной 2015 г. и весной 2014 г., показаны изображения тестовых заданий в том виде, в каком они появились в формате онлайн-теста.Из-за различий в компьютерных мониторах цвет объекта на одном мониторе может отличаться от цвета другого.
Чтение
| Класс 3 | выпущен весной 2015 г .: PDF | Лист ответов |
|---|---|---|
| 4 класс | выпущен весной 2015 г .: PDF | |
| Класс 5 | выпущен весной 2015 г .: PDF | |
| 6 класс | выпущен весной 2015 г .: PDF | |
| Класс 7 | выпущен весной 2015 г .: PDF | |
| 8 класс | выпущен весной 2015 г .: PDF | |
| Окончание курса | выпущен весной 2015 г .: PDF |
Запись
Наука
| 5 класс | выпущен весной 2015 г .: PDF | Лист ответов |
| 8 класс | выпущен весной 2015 г .: PDF | |
| Науки о Земле | Модельвыпущена весной 2015 г. PDF | |
| Биология | выпущен весной 2015 г .: PDF | |
| Химия | выпущен весной 2015 г .: PDF |
Математика
| Оценка 3 | выпущен весной 2014 г .: PDF | Лист ответов |
| 4 класс | выпущен весной 2014 г .: PDF | |
| 5 класс | выпущен весной 2014 г .: PDF | |
| 6 класс | выпущен весной 2014 г .: PDF | |
| 7 класс | выпущен весной 2014 г .: PDF | |
| 8 класс | выпущен весной 2014 г .: PDF | |
| Алгебра I | выпущен весной 2015 г .: PDF выпущен весной 2014 г .: PDF | |
| Геометрия | выпущен весной 2015 г .: PDF выпущен весной 2014 г .: PDF | |
| Алгебра II | выпущен весной 2015 г .: PDF выпущен весной 2014 г .: PDF |
История и общественные науки
Банкноты
- Если у вас возникли проблемы с печатью или просмотром, посетите страницу Adobe «Устранение проблем с печатью».
- Последние версии выпущенных тестов SOL со шрифтом Брайля и крупным шрифтом доступны в печатном виде. Пожалуйста, свяжитесь с директором отдела тестирования в вашем местном школьном отделении для получения дополнительной информации.
© 2014 Содружество Вирджиния, Департамент образования, P.O. Box 2120, Ричмонд, Вирджиния, 23218-2120. Все права защищены. За исключением случаев, предусмотренных законом, этот материал не может быть воспроизведен или использован в любой форме или любыми средствами, электронными или механическими, включая фотокопирование или запись, или любой системой хранения или поиска информации, без письменного разрешения владельца авторских прав.Преподаватели государственных школ Содружества Вирджиния могут воспроизводить любую часть этих опубликованных тестов в некоммерческих образовательных целях без запроса разрешения. Все остальные должны направлять свои письменные запросы в Департамент образования штата Вирджиния, Отдел оценки учащихся и улучшения школ, по указанному выше адресу или по электронной почте на адрес [email protected].
Начало страницы
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Слово неравенство означает математическое выражение, в котором стороны не равны друг другу.По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
Как правило, для представления уравнений неравенства используются пять символов неравенства.
Символы неравенства
Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) .Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Операции с неравенствами
Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже.
Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥.
- Символ неравенства не меняется при добавлении одного и того же числа к обеим сторонам неравенства.Например, если a
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
- Умножение обеих частей неравенства на положительное число не меняет знака неравенства. Например, если a
- Разделение обеих сторон неравенства на положительное число не меняет знака неравенства. Если a
- Умножение обеих сторон уравнения неравенства на отрицательное число изменяет направление символа неравенства.Например, если a b *
- Аналогичным образом, разделение обеих сторон уравнения неравенства на отрицательное число изменяет символ неравенства. Если a b / c
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
Как устранить неравенства?
Подобно линейным уравнениям, неравенства можно решить, применяя аналогичные правила и шаги за некоторыми исключениями. Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Линейные неравенства могут быть решены с помощью следующих операций:
- Сложение
- Вычитание
- Умножение
- Деление
- Распределение собственности
Решение линейных неравенств с добавлением
Давайте посмотрим на несколько примеров ниже, чтобы понять это понятие.
Пример 1
Решите 3x — 5 ≤ 3 — x.
Решение
Начнем с добавления обеих сторон неравенства на 5
3x — 5 + 5 ≤ 3 + 5 — x
3x ≤ 8 — x
Затем сложим обе стороны на x.
3x + x ≤ 8 — x + x
4x ≤ 8
Наконец, разделите обе части неравенства на 4, чтобы получить;
x ≤ 2
Пример 2
Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5.
Решение
Сложите обе части неравенства на 4.
y — 4 + 4 <2y + 5 + 4
y <2y + 9
Вычтите обе части на 2y.
y — 2y <2y - 2y + 9
Y <9 Умножьте обе части неравенства на -1 и измените направление символа неравенства. y> — 9
Решение линейных неравенств с вычитанием
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 3
Решите x + 8> 5.
Решение
Изолируйте переменную x, вычтя 8 из обеих сторон неравенства.
x + 8-8> 5-8 => x> −3
Следовательно, x> −3.
Пример 4
Решите 5x + 10> 3x + 24.
Решение
Вычтите 10 из обеих сторон неравенства.
5x + 10-10> 3x + 24-10
5x> 3x + 14.
Теперь вычтем обе части неравенства на 3x.
5x — 3x> 3x — 3x + 14
2x> 14
x> 7
Решение линейных неравенств с умножением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 5
Решить x / 4> 5
Решение:
Умножить обе стороны неравенства на знаменатель дроби
4 (x / 4)> 5 x 4
x> 20
Пример 6
Решите -x / 4 ≥ 10
Решение:
Умножьте обе стороны неравенства на 4.
4 (-x / 4) ≥ 10 x 4
-x ≥ 40
Умножьте обе стороны неравенства на -1 и измените направление символа неравенства на противоположное.
x ≤ — 40
Решение линейных неравенств с делением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 7
Решите неравенство: 8x — 2> 0.
Решение
Прежде всего, сложите обе части неравенства на 2
+ 2> 0 + 2
8x> 2
Теперь решите, разделив обе части неравенства на 8, чтобы получить;
x> 2/8
x> 1/4
Пример 8
Решите следующее неравенство:
−5x> 100
91 9324 Оба решения сторон неравенства на -5 и измените направление символа неравенства
= −5x / -5 <100 / -5
= x <- 20
Решение линейных неравенств с использованием свойства распределения
Давайте посмотрим на несколько примеров ниже, чтобы понять эту концепцию.
Пример 9
Решить: 2 (x — 4) ≥ 3x — 5
Решение
2 (x — 4) ≥ 3x — 5
Примените свойство распределения, чтобы удалить скобки.
⟹ 2x — 8 ≥ 3x — 5
Сложить обе стороны на 8.
⟹ 2x — 8 + 8 ≥ 3x — 5 + 8
⟹ 2x ≥ 3x + 3
Вычесть обе стороны на 3.
⟹ 2x — 3x ≥ 3x + 3 — 3x
⟹ -x ≥ 3
⟹ x ≤ — 3
Пример 10
Студент набрал 60 баллов за первый тест и 45 баллов во втором тесте заключительного экзамена.Сколько минимальных баллов должен набрать ученик в третьем тесте, получив в среднем не менее 62 баллов?
Решение
Пусть в третьем тесте выставлены оценки x.
(60 + 45 + x) / 3 ≥ 62
105 + x ≥ 196
x ≥ 93
Таким образом, ученик должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов.
Пример 11
Джастину требуется не менее 500 долларов для празднования своего дня рождения.Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Решение
Пусть минимальная ежемесячная экономия = x
150 + 7x ≥ 500
Решить для x
150-150 + 7x ≥ 500-150
x ≥ 50
Следовательно, Джастин должен экономить 50 долларов США или больше
Пример 12
Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40.
Решение
Пусть меньшее нечетное число = x
Следовательно, следующее число будет x + 2
x> 10 ………. больше 10
x + (x + 2) <40 …… сумма меньше 40
Решите уравнения.
2x + 2 <40
x + 1 <20
x <19
Объедините два выражения.
10 Следовательно, последовательные нечетные числа — 11 и 13, 13 и 15, 15 и 17, 17 и 19. Лучшим инструментом для представления и визуализации чисел является числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа. Линейные уравнения также могут быть решены графическим методом с использованием числовой прямой.Например, чтобы построить x> 1 на числовой прямой, вы обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и заполните или заштрихуйте круг.Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства. Пример 14 x ≥ 1 Та же процедура используется для решения уравнений, включающих интервалы. Пример 15 –2 < x <2 Пример 16 –1122000 –1 Пример 17 –1 < x ≤ 2 Решите следующие неравенства и представьте свой ответ на числовой прямой. Ответы Оценка учащихся, домашняя страница | Справочник по оценке успеваемости учащихся | Связаться с программой оценки успеваемости учащихся Агентство по образованию штата Техас (TEA) выпускает два типа тестовых вопросов для программы оценки академической готовности штата Техас (STAAR ® ) — образцы вопросов и формы тестов.Примеры тестовых вопросов — это небольшие подгруппы тестовых вопросов, выпущенные из банков тестов STAAR. Эти тестовые вопросы могли быть заданы ранее. Тестовая форма — это набор выпущенных тестовых вопросов, которые ранее совместно задавались студентам из Техаса, которые отражают тестовые планы STAAR. Чтобы увидеть все доступные ресурсы STAAR, посетите веб-страницу ресурсов STAAR. STAAR содержат разное количество аутентичных опубликованных текстов. Разрешение на авторские права на эти тексты получено от издателей подрядчиком по тестированию от имени TEA.Эти соглашения об авторских правах могут включать, а могут и не включать разрешение на выпуск более широкого небезопасного выпуска после тестирования. Если материал, который использовался во время тестирования, не мог быть включен в выпущенную тестовую форму из-за определенных разрешений авторского права, предоставляется текст в форме, указывающий, откуда был взят исходный материал. STAAR выпустил тестовую информацию об авторских правах Выпущенные тестовые формы, которые вводились на бумаге, выпускаются в виде PDF-файлов.Эти документы доступны по ссылкам ниже. Руководства по выставлению оценок доступны на веб-странице ресурсов STAAR Writing и English I, II, III. Выпущенные формы тестов, которые вводились в режиме онлайн, выпускаются как практические тесты. Эти выпущенные практические тесты доступны на платформе онлайн-тестирования STAAR. Практические онлайн-тесты недоступны для печати или оценки. Если вы хотите получить балл за прохождение практического онлайн-теста своего ученика, вам следует попросить ученика записать свои ответы на отдельном листе бумаги. Затем вы можете использовать ключ ответа ниже, чтобы набрать балл в практическом тесте STAAR. Руководства по выставлению оценок доступны на веб-странице ресурсов STAAR Writing и English I, II, III. Выпущенные тестовые формы, которые вводились на бумаге, выпускаются в виде PDF-файлов. Эти документы доступны по ссылкам ниже. Руководства по выставлению оценок доступны на веб-странице ресурсов STAAR Writing и English I, II, III. Выпущенные формы тестов, которые вводились в режиме онлайн, выпускаются как практические тесты.Эти выпущенные практические тесты доступны на платформе онлайн-тестирования STAAR. Практические онлайн-тесты недоступны для печати или оценки. Если вы хотите получить балл за прохождение практического онлайн-теста своего ученика, вам следует попросить ученика записать свои ответы на отдельном листе бумаги. Затем вы можете использовать приведенный ниже ключ ответа, чтобы получить балл за практический тест, выпущенный STAAR SOA. Печатные копии опубликованных тестов Брайля можно заказать, позвонив в службу заказа ETS по телефону 800-537-3160. Руководства по выставлению оценок доступны на веб-странице ресурсов STAAR Writing и English I, II, III. По ссылкам ниже открытые PDF-версии STAAR опубликовали образцы вопросов. По ссылкам ниже открытые PDF-версии STAAR опубликовали образцы вопросов. Марка Примеры вопросов 3 4 5 Предыдущие тестовые вопросы, выпущенные STAAR Неравенства и числовая линия
00 00
Предыдущий урок | Главная страница | Следующий урок Тестовые вопросы, выпущенные STAAR | Агентство образования штата Техас
STAAR Выпущены тестовые бланки и ключи для ответов (бумажные администрации)
Выпущенные формы тестов и ключи ответов (онлайн-администрирование)
Выпущены тестовые бланки и ключи для ответов (бумажные администрации)
Стандартизованное пероральное администрирование STAAR (SOA) Выпущенные тестовые формы и ключи ответов (онлайн-администрирование)
STAAR Брайля Выпущены тестовые бланки и ключи для ответов (бумажные администрации)
STAAR Испанский Выпущены примеры вопросов
Математика: 2015 | 2011 Математика: 2015 | 2011 Математика: 2015 | 2011 Наука: 2011
Архив 11 класс (9780544569546) :: Домашнее задание Помощь и ответы :: Slader
Анализ текста с.435 Стратегия словарного запаса: точное использование п.436 Анализ текста п.444 Анализ текста п.454 Анализ текста с.486 Анализ текста п.504 Анализ текста п. 526 Анализ текста п.541 Язык и стиль: диалог с.542 Анализ текста и мультимедиа с. 544 Анализ текста и мультимедиа п.547 Анализ текста и мультимедиа п.548 Анализ текста с.566 Критический словарь стр. 567 Словарный запас: юридическая терминология стр. 567 Анализ текста с.579 Словарная стратегия: этимология с.580 Критический словарь с. 580 Анализ текста с.585 Критический словарь п.586 Анализ текста с.594 Стратегия словарного запаса: шаблоны изменения слов стр.595 Критический словарь стр.

 Преобразование иррациональных выражений
Преобразование иррациональных выражений
 Основное логарифмическое тождество
Основное логарифмическое тождество
 Перестановки без повторений
Перестановки без повторений
 Противоположные события
Противоположные события
 Закон больших чисел
Закон больших чисел
 Системы и совокупности неравенств
Системы и совокупности неравенств
 Алгебра, 11 класс: уроки, тесты, задания.
Алгебра, 11 класс: уроки, тесты, задания.

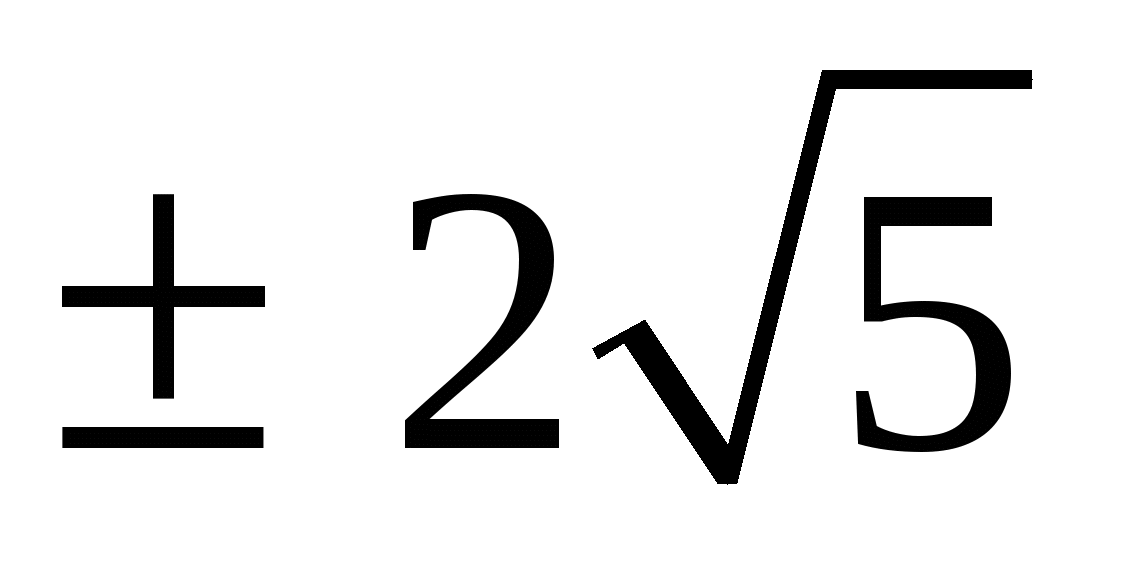 36см 3 / г
36см 3 / г