3 класс — сложение и вычитание трехзначных чисел и вычитание столбиком. Примеры
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Задачи на вычитание трехзначных чисел столбиком. Примеры (PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Л.Г. Петерсон
М.И. Моро
Т.Е. Демидовой
Вычитание двузначных чисел (повторение)
1. Запиши заданные предложения в виде числовых выражений и реши их.
1.1. Из числа 78 вычти число 49.1.2. Из числа 92 вычти число 63.
1.3. Из числа 49 вычти число 38.
2. Реши примеры.
| 633 — 159 = | 272 — 174 = | 395 — 182 = | 799 — 527 = |
| 782 — 618 = | 509 — 456 = | 308 — 241 = | 579 — 258 = |
| 367 — 250 = | 885 — 663 = | 285 — 172 = | 789 — 252 = |
3. Вместо … поставь числа, чтобы выражение стало верным.
Вместо … поставь числа, чтобы выражение стало верным.
| 856 — … = 589 | 695 — … = 384 | 672 — … = 298 | 314 — … = 273 |
| … — 256 = 488 | … — 423 = 573 | … — 347 = 478 | … — 243 = 45 |
| 357 — … = 298 | … — 312 = 237 | 405 — … = 69 | … — 232 = 388 |
Вычитание трехзначных чисел
1. Запиши заданные предложения в виде числовых выражений и реши их.
1.1. Из числа 798 вычти число 647.1.2. Из числа 458 вычти число 412.
1.3. Из числа 599 вычти число 241.
2. Реши примеры.
| 936 — 287 = | 745 — 293 = | 366 — 182 = | 959 — 235 = |
| 862 — 192 = | 779 — 503 = | 848 — 472 = | 729 — 531 = |
| 374 — 233 = | 852 — 634 = | 773 — 117 = | 892 — 442 = |
Решение текстовых задач на вычитание
1. В школе учится 670 учеников, из них 370 – мальчики. Сколько девочек учится в школе?
Сколько девочек учится в школе?
2. На склад завезли 690 мешков с сахаром. В первый день увезли 130 мешков, а во второй день увезли ещё 357 мешков. Сколько всего мешков с сахаром осталось на складе после второго дня?
3. В библиотеку привезли 702 книги, из них 268 книг раздали 3 классу и 211 книг – 1 классу. Сколько книг осталось в библиотеке для 2 класса?
4. В цистерну было налито 869 литров бензина, 347 литров бензина было израсходовано. Сколько литров бензина осталось в цистерне?
Табличное вычитание и проверка вычитания сложением
1. Выполни вычитание и проверь результат.
| 385 — 247 = | 164 — 95 = | 548 — 118 = | 338 — 144 = |
| 436 — 147 = | 235 — 215 = | 696 — 23 = | 985 — 566 = |
| 757 — 664 = | 347 — 164 = | 654 — 147 = | 179 — 155 = |
2. Запиши заданные предложения в виде числовых выражений, реши их и проверь результат.
2.2. Из числа 851 вычти число 676.
2.3. Из числа 352 вычти число 213.
2.4. Из числа четыреста шестнадцать вычти число триста тридцать пять.
III. Устный счет | Посмотрите, перед вами карта нашего путешествия. Такие же карты у вас у каждого на парте. В процессе путешествия вы сможете оценить свою работу на каждом острове и сделать вывод, все ли у вас получилось. Вы готовы? Тогда отдать швартовые! Первый остров на пути Бамбуковый — Мы будем считать и при этом узнавать, что такое бамбук. Задание — Посмотрите на слайд, как вы думаете, что такое бамбук? На слайде: К какой группе растений принадлежит бамбук? — дерево – 95 — трава – 0 — куст – 50 — Наши мнения разделились, чтобы ответить на этот вопрос, выполним задание: цепочка примеров на слайде. Спрашиваю ответ. — Проверим (ответы на доске с комментированием) — Значит, что такое бамбук? — У нас Максим М. подготовил небольшое сообщение о бамбуке, пожалуйста, поделись своей информацией с нами. — Молодцы, вы справились с заданием, на картах отметьте смайликом как вы справились с этим заданием. | Знакомятся с картами путешествия. Настраиваются на работу. Пре6дположения детей Мнения детей Устные вычисления. Самоконтроль трава Максим:Некоторые виды бамбука (в основном тропические и субтропические) имеют гигантские размеры, достигая высоты 40 м. Есть бамбуки с травянистыми стеблями высотой менее 1 м. Характерная особенность бамбука — необыкновенно быстрый рост, до 70-80 см в сутки. Большинство бамбуков зацветает и плодоносит очень редко, иногда через 60 и свыше 100 лет. Самооценка | восприятие сообщений действия контроля и оценки сбор и подготовка материалов по предлагаемой учителем теме | Регулятивные УУД: определение последовательности промежуточных целей с учётом конечного результата; составление плана и последовательности действий Коммуникативные УУД : принятие решения и его реализация Познавательные УУД: поиск и выделение информации Личностные УУД: оценивание усваиваемого содержания, исходя из социальных и личностных ценностей | IV. Гимнастика для глаз Работа с учебником Физкультминутка | И мы можем отправляться на следующий остров. Как он называется? — Как вы думаете, кто живет на этом острове? — А кто это? Максим С. тоже подготовился и хотел бы с вами поделиться. — Спасибо, Максим. Действительно, разнообразие варанов очень велико. -Самым крупным точно измеренным экземпляром был варан, выставленный в 1937 г. в зоопарке США. Его длина была равна 310 см, а масса — 166 кг. Кабарогойя Тонкотелый варан Сальвадора, или кабарогойя из Папуа-Новой Гвинеи, по данным точных измерений, достигает длины 475 см, но примерно 70% его общей длины приходится на хвост. — Какие числа вам запомнились из моего рассказа? Придумайте задание с этими числами: 310, 166, 475 Хорошие идеи. Молодцы! На картах отметьте смайликом как вы справились с этим заданием. Немного отдохнем, сделаем гимнастику для глаз Путешествуем дальше. Нас ждёт следующий остров. Как вы думаете, какое задание нам предстоит выполнить на острове Горилл? — Обезьяны очень ловкие животные и очень хорошо прыгают по лианам. Какое задание нам предстоит выполнить на этом острове, нам расскажет Юля З. — Для того, чтобы узнать, на какое расстояние можно приблизиться к горилле, выполним задание из учебника с. 66 № 2 под а. Вычисли, вырази в метрах: 2м 8 см – 49 см + 24 дм 1 см — Сможем сразу решать? — Что нужно сделать? 2м 8 см = 208 см 24 дм 1 см = 241 см — Подставляем в выражение 208 см – 49 см + 241 см — Решаем как обычное выражение — Вычисления проще делать столбиком, решаем по действиям в столбик. — Ответ 400 см. Переводим в указанную единицу 4 м. Проверяем. Решение на слайде. Молодцы. На картах отметьте смайликом как вы справились с этим заданием. Корабль продолжает путь. На горизонте новый остров. Почему его назвали остров пиратов? . — Считалось, что среди кладов было очень много старинных и медных монет. Предлагаю придумать задачу, используя схему на с. 67 №:б — РАЗБОР – вопросы по схеме. — Составим задачу. — Можно ли сразу ответить на вопрос задачи? — Что нам нужно для этого знать? — Сможем ли мы узнать, сколько медных и старинных монет оказалось на корабле? Как? — Узнав, сколько было всех монет в обоих множествах всего, сможем ответить на главный вопрос? — Как узнаем? (вычесть монеты, которые являются и медными, и старинными) — Сколько действий будет в задаче? — Какое первое действие? Второе? — Решаем. — Как легче выполнять вычисления? Работали все хорошо. Продолжаем путь. Нас ждёт следующий остров. Какое испытание приготовил нам остров водопадов? — Чтобы узнать высоту этого водопада, вам нужно будет выполнить небольшую проверочную работу. Ответ в последнем примере и будет ответом на наш вопрос: какова высота самого высокого водопада? Но примеры не простые, ответ первого примера, будет первым числом во втором выражении, соответственно ответ второго выражения, будет первым числом третьего и так до конца. Проверочнаяработа. Перед вами проверочная работа. Работаем по вариантам . Кто справится со своей работой, может решать другой вариант . Запиши выражения столбиком и реши. Его высота – 978 метров. На картах отметьте смайликом как вы справились с этим заданием | Остров варанов. вараны Максим С.: Вараны являются крупными ящерицами. Большинство варанов ведут наземный образ жизни, но существуют и такие, которые хорошо плавают и ныряют, и могут оставаться под водой около часа. Вараны яйцекладущие животные. Прослушивают информацию Называют числа, записывают на доске — Можно придумать задачу, можно составить примеры и вычислить в столбик, можно составить уравнения и решить. Работа у доски и в тетрадях Самооценка Следят за бегающей точкой на слайде Решать задачи про гарилл и др. Юля: Гориллы спят в гнездах, которые делают из мягких листьев и соответствующим образом переплетенных веток. В таких гнездах в основном спят самки — самцы предпочитают спать на земле. Эти крупные обезьяны очень вполне миролюбивы и не конфликтны. При правильном поведении к ним можно приблизиться Задание: На сколько метров можно приблизится к горилле? Дети выполняют задание в тетради с последующей проверкой на слайде. Нет Выразить все в одну единицу измерения Самоконтроль Люба: О пиратах существует много мифов, один из них — что Пираты закапывали клады. Дети: Пираты собрали на своем корабле 245 старинных монет и 356 медных. Сколько среди этих монет оказалось старинных медных монет, если всего они собрали 365 монет? Решение задачи в столбик Самоконтроль Игра «4 стихии» Ваня: Самым высоким водопадом в мире является Водопад Анхель. Водопад берет начало от вершины плоской горы АуянТепуй и находится в труднодоступных джунглях Венесуэлы. Туристических троп к этому месту не существует. Самостоятельная работа детей по вариантам с последующей взаимопроверкой Взаимопроверка. Самоконтроль | действия контроля и оценки Построение системы частных задач предметно-практические действия предметно-практические действия выполнение системы собственно учебных действий письменное изложение усвоенного материала преобразование условий учебной задачи с целью обнаружения некоторого общего отношения изучаемого предмета | Личностные УУД: уметь находить ответ на вопрос, участвовать в диалоге; Коммуникативные УУД : слушать и понимать других, высказывать свою точку зрения на события, поступки Регулятивные УУД: волевая саморегуляция Коммуникативные УУД: поиск и оценка альтернативных способов решения, инициативное сотрудничество в поиске и сборе информации Познавательные УУД: самостоятельное создание способов решения проблем творческого и поискового характера Коммуникативные УУД: инициативное сотрудничество в поиске и сборе информации Регулятивные УУД: внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта Познавательные УУД: анализ с целью выделения признаков, построение логической цепи рассуждений, выдвижение гипотез и их обоснование Регулятивные УУД: определение последовательности промежуточных целей с учётом конечного результата; составление плана и последовательности действий Познавательные УУД: синтез как составление целого из частей, восполняя недостающие компоненты, построение логической цепи рассуждений | V. Домашнее задание | Наш корабль вернулся в порт. Путешествие подошло к концу. Задание какого острова вам особенно понравилось? На каком острове было трудно? Еще раз вернемся к картам нашего путешествия. Внизу вы увидите 2 строчки с названиями: 1- что мне понравилось и 2- что было трудным. Заполните эти строчки, напишите свои впечатления. Спрашиваю несколько детей о трудностях, делаем выводы, над чем еще поработать. И несколько детей о том, что понравилось. Мы возвращаемся в класс. И мне бы особенно хотелось выделить работу на уроке….. Более активным надо быть….Внимательным…. Обсуждаем, подтвердились ли ожидания. С. 66 № 1,5, 8(доп.) | Самооценка детей, заполнение карт путешествия с последующим проговариванием. Написание своих впечатлений от урока. Проговаривание трудностей и выводов. Выставление оценок за урок Запись д/з в дневник | оценка качества действия, события, поведения | Личностные УУД: оценивание усваиваемого содержания, исходя из социальных и личностных ценностей, обеспечивающее личностный моральный выбор Регулятивные УУД: выделение и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения |
Что такое метод столбца? Определение, сложение, вычитание, деление
Что такое столбцовый метод?
Когда мы располагаем числа, фигуры или объекты друг над другом, мы называем это методом столбца. Другими словами, метод столбцов — это математический способ выполнения вычислений, при котором числа, которые нужно сложить, вычесть или умножить, располагаются друг над другом в столбцах.
Другими словами, метод столбцов — это математический способ выполнения вычислений, при котором числа, которые нужно сложить, вычесть или умножить, располагаются друг над другом в столбцах.
Например:
Мы используем метод столбцов для трех основных операций: сложения, вычитания и умножения.
Столбчатый метод сложения и вычитания
Столбчатый метод сложения и вычитания — это метод, в котором числа «переносятся» и «заимствуются». Она изложена так: вычисления при сложении и вычитании производятся путем «переноса» и «заимствования» чисел из столбца в столбец.
Колоночный метод сложения
Колоночный метод сложения также известен как колоночный метод сложения. Добавление столбца — это формальный метод добавления двух или более чисел.
Например:
Что такое вычитание столбцов?
Вычитание по столбцу — это способ найти разницу между двумя или более числами, расположив их одно над другим.
Столбчатый метод Вычитание:
Почему разрядное значение важно в столбцовом методе?
Метод столбца — самый быстрый способ сложения и вычитания, но разрядное значение играет важную роль в методе столбца.
Давайте посмотрим на пример ниже и используем добавление столбцов.
- Сначала числа выстраиваются одно над другим.
- Во-вторых, добавляем единицы и пишем ответ.
Например: Сложение $9$ и $5$ дает ответ $14$, но мы пишем только те, которые находятся под чертой – в данном случае это цифра $4$.
- Третий шаг — перегруппировать десятки в столбце десятков. В $14$ цифра $1$ является значением десятков.
- Сложите цифры в разряде десятков. В нашем примере $8 + 1 = 9$, но мы добавляем 1 из-под черты. Таким образом, ответ для десятков составляет 9 долларов.$.
- Когда два числа с разными цифрами складываются, мы можем правильно разместить их, используя разрядность. Например: десятичное число $0,1$ и число $28$.
Метод расширенного столбца
Расширенный метод заключается в разбиении каждого числа в вашей сумме на меньшие, более управляемые числа, из которых они состоят. Мы в основном разбиваем числа в развернутом виде.
Например, число $782$ можно разбить на: $700 + 80 + 2$
Расширенный метод сложения суммы осуществляется следующим образом:
Допустим, мы должны сложить 47$ + 134$
Во-первых, мы расширим 47$ и 134$.
47$ = 40 и 7 и 134 = 100, 30 и 4$
Теперь рассортируем числа по сотням, десяткам и единицам и сложим их по группам.
- Мы будем складывать цифры на единицу.
В этом примере мы складываем 7 долларов + 4 = 11 долларов. Оставляем 1 на разряде единиц и берем еще $1$ на разряде десятков.
- Мы добавим цифры в разряде десятков.
В этом примере мы сложим 30$ + 40 + 10 = 80$
- Мы добавим цифры в разряде сотен.
В этом примере мы складываем 100 долларов США + 0 = 200 долларов США
Теперь мы складываем все наши цифры вместе, мы получаем 100 долларов США + 80 + 1 = 181 доллар США
Другой пример приведен ниже:
Возьмем пример метода расширенного столбца вычитания.
Метод столбца для вычитания без заимствования
Иногда нам не нужно заимствовать цифры из столбца при вычитании.
Например: $76 – 42$
Первый шаг – рассортировать числа по десяткам и единицам:
Десятки $→ 7 и 6$
Единицы $→ 4 и 2$
Мы всегда должны ставить самые большие числа в верхней строке столбцов.
Теперь вы можете вычесть числа в каждом столбце:
Ответ на сумму $76 – 42$ равно $34$.
Колонковый метод сложения без заимствования
Мы используем метод столбца для сложения без заимствования или переноса значений между столбцами.
Например: 282$ + 615$
При расширении получаем
Сотни $→ 200$ и 600$
Десятки $→ 80$ и 10$
Единицы$→ 2$ и 5$
5, поместите значения в их столбцы:
Затем мы сложим все ваши значения в их группах.
Следовательно, ответом на сумму $262 + 615$ будет $897$.
Столбчатый метод умножения
Мы также используем метод столбца для умножения двух чисел, который включает запись одного числа под другим аналогично сложению и вычитанию столбца.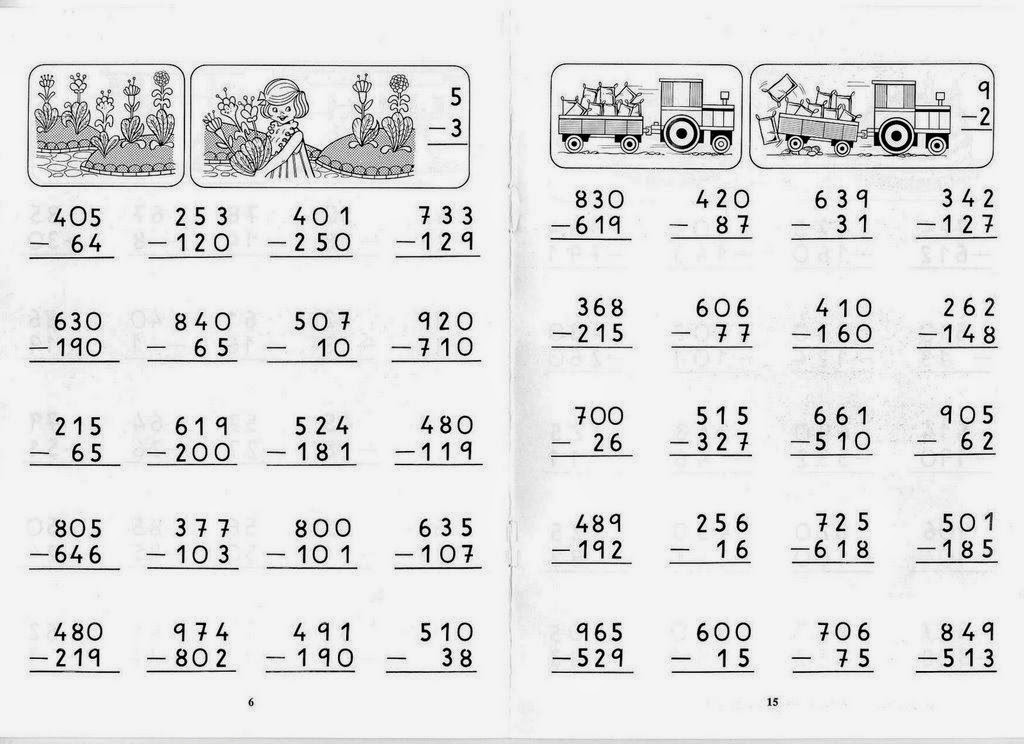
Когда мы умножаем два числа, используя метод умножения столбцов, мы используем следующие шаги:
Предположим, мы умножаем 96$ и 36$.
Шаг I: Умножаем множимое $(96)$ на единицу множителя $(6)$, т. е.
Шаг II: Следующим шагом является умножение множимого $(96)$ на разряд десятков множителя $(3)$, т. е.
Шаг III: Следующим шагом является сложение частичных произведений, т. е.
Частичное произведение $1 (576 единиц) +$ Частичное произведение $2 (288 десятков) $
$ 576 × 1 + 288 × 10 $
$ 576 + 2880 = 3456 $
На самом деле это означает:
Теперь мы применим тот же метод для умножения трехзначного числа на двузначное число.
Пример:
Возьмем другой пример. Найдите произведение 145$, умноженное на 12$, используя метод столбца.
Шаг I:
Шаг II:-
Шаг III:
Шаг IV:
Шаг V:
. 1. Найдите ошибку в следующем.
1. Найдите ошибку в следующем.
Ответ: Ошибка в том, что столбцы десятков и сотен добавлены неправильно. Переходящие цифры не добавлялись. Правильная сумма будет:
2. Найдите значение «А» в следующем.
Решение: $300 – $A$ = 200$
$Итак, $A$ = 100$
3. Стоимость 1 ожерелья составляет рупий 342 $ . Какова будет стоимость ожерелий по 23$ по долларов? Если у Шэрон есть рупий, 8000 долларов, долларов, сколько денег останется после оплаты ожерелий?
Ответ: Стоимость 1 ожерелья $=$ Rs $342$
Стоимость ожерелья $23$ $= 342 ✕ 23 =$ Rs $7866$
Стоимость ожерелья $23$ $= 6000 + 900 + 800 + 120 + 40 + 6 = $ рупий $ 7866 $
Сумма, оставленная $ = 8000 — 7866 $
Сумма, оставленная $ = $ 134 $
Практические задачи
7
8
6
Ни один из этих
Правильный ответ: 8
$ 6 \ Time3 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 3 = = = = = = 18$, так что в одном месте мы получим 8$.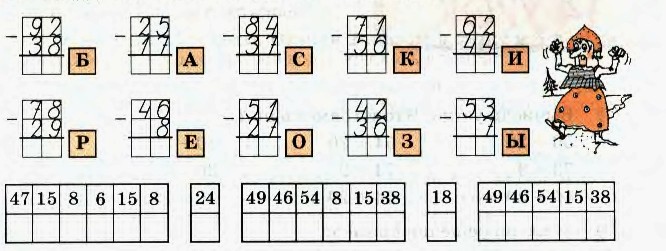
4
5
3
2
Correct answer is: 4
$4500 − 1352 = 3148$
So, at tens place, we get 4.
4533
4674
4733
4534
Правильный ответ: 4733
2785 $ + 1948 = 4733 $
Часто задаваемые вопросы
В чем разница между методом столбцов и горизонтальным методом?
Метод столбцов — это метод расположения чисел друг над другом и сложения, вычитания или умножения в столбцах. С другой стороны, горизонтальный метод — это способ расположения чисел в горизонтальной строке, а затем термины располагаются так, чтобы собрать все группы одинаковых терминов.
Как еще называется метод сложения столбцов?
Другим названием столбцового метода сложения является столбцовое сложение или вертикальное сложение.
Что такое разделение методом столбца?
Деление по методу столбцов — это простой способ традиционного метода деления по столбцам. Линии рисуются для того, чтобы разделить цифры делителя. Каждый столбец разрядных значений решается слева направо.
Линии рисуются для того, чтобы разделить цифры делителя. Каждый столбец разрядных значений решается слева направо.
Сложение и вычитание — сложение и вычитание с перегруппировкой
Сложение и вычитание — это арифметические операции в математике, которые используются для вычисления суммы и разности между различными операндами, такими как целые числа, целые числа, дроби, алгебраические выражения и т. д. Давайте узнаем о различных методах сложения и вычитания в этой статье.
| 1. | Что такое сложение и вычитание? |
| 2. | Сложение и вычитание с перегруппировкой |
| 3. | Сложение и вычитание в числовой строке |
| 4. | Часто задаваемые вопросы о сложении и вычитании |
Что такое сложение и вычитание?
Сложение осуществляется путем суммирования или соединения вещей.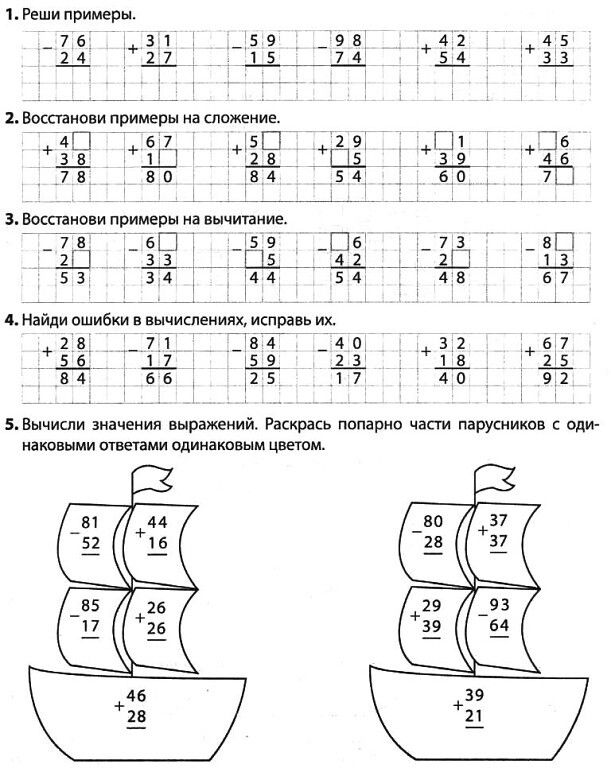 Это способ объединения чисел, операндов или объектов. С другой стороны, вычитание осуществляется путем удаления или удаления вещей. Это способ сокращения чисел, операндов или объектов.
Это способ объединения чисел, операндов или объектов. С другой стороны, вычитание осуществляется путем удаления или удаления вещей. Это способ сокращения чисел, операндов или объектов.
Формула сложения выглядит следующим образом: сложение + сложение = сумма. Здесь слагаемые — это добавляемые числа, символ (+) указывает на операцию сложения, а сумма указывает на результат.
Формула вычитания записывается как Уменьшаемое — Вычитаемое = Разность. Здесь уменьшаемое — это число, из которого вычитается другое число, а вычитаемое — это число, которое вычитается из уменьшаемого. Символ (-) указывает на операцию вычитания, а разность указывает на результат. В приведенном ниже примере показана формула вычитания.
Теперь давайте посмотрим на сложение и вычитание двузначных чисел.
Сложение и вычитание двухзначных чисел
Сложение и вычитание двухзначных чисел можно выполнять с перегруппировкой и без нее. Перегруппировка происходит, когда сумма значений столбца превышает 9. В этом случае одна цифра записывается под этим конкретным столбцом, а лишняя цифра переносится в следующий столбец и добавляется вместе с слагаемыми этого конкретного столбца. Давайте рассмотрим пример сложения без перегруппировки.
В этом случае одна цифра записывается под этим конкретным столбцом, а лишняя цифра переносится в следующий столбец и добавляется вместе с слагаемыми этого конкретного столбца. Давайте рассмотрим пример сложения без перегруппировки.
Пример: Складываем числа 15 + 24
Решение: Складываем числа следующим образом.
Здесь следует позаботиться о разрядности чисел. Двузначные числа имеют разрядное значение как единицы и десятки, начиная с правой стороны. Складывая 2 цифры вместе, мы располагаем числа по столбцам, как показано выше, под соответствующими разрядами. В столбце единиц 5 + 4 = 9, а в столбце десятков 1 + 2 = 3. Следовательно, 15 + 24 = 39..
Аналогично сложению, давайте выполним вычитание 2-значного числа без перегруппировки. Вычтем из 76 34 следующим образом.
Расположение разрядов остается таким же, как описано в операции сложения. Таким образом, в столбце единиц у нас 6 — 4 = 2, а в столбце десятков 7 — 3 = 4. Следовательно, 76 — 34 = 42.
Следовательно, 76 — 34 = 42.
Сложение и вычитание с перегруппировкой
Кроме того, перегруппировка происходит всякий раз, когда сумма столбца превышает 9. Здесь лишняя цифра переносится в предыдущий столбец и добавляется туда вместе с слагаемыми. При вычитании перегруппировка выполняется, если какая-либо цифра уменьшаемого меньше соответствующей цифры вычитаемого. Давайте сначала узнаем о сложении с перегруппировкой, а затем перейдем к вычитанию с перегруппировкой.
Сложение с перегруппировкой
Кроме с перегруппировкой, когда мы получаем сумму, превышающую 9 в любом из столбцов, мы переносим лишнюю цифру в предыдущий столбец и добавляем ее вместе с слагаемыми там. Давайте разберемся в этом с помощью примера.
Пример: Сложите числа 355 + 466
Решение:
- Шаг 1: Начните с десятков в столбце единиц → 6 + 5 = 11. Здесь сумма цифр 11. суммы (т. е. 1) будет перенесено в разряд десятков.

- Шаг 2: Затем мы добавим цифры десятков вместе с переносом 1 → 1(перенос) + 5 + 6 = 12. Здесь сумма равна 12. Десятки разряда суммы ( т. е. 1) будет перенесено в столбец сотен.
- Шаг 3: Теперь мы добавим цифры разряда сотен вместе с цифрой переноса 1 → 1(перенос) + 3 + 4 = 8. Здесь сумма равна 8.
- Шаг 4: Таким образом, 355 + 466 = 821
Ниже показана операция перегруппировки для 355 + 466.
Теперь давайте изучим вычитание с перегруппировкой.
Вычитание с перегруппировкой
Вычитание с перегруппировкой имеет место, когда любая цифра в вычитаемом меньше, чем соответствующая цифра в вычитаемом. Здесь мы заимствуем 1 из предыдущего столбца и комбинируем его с этим уменьшаемым, так что оно становится больше вычитаемого. Давайте разберемся в этом с помощью примера.
Пример: Вычтем числа 432 — 256
Решение: Давайте выполним следующие действия, чтобы вычесть эти числа.
- Шаг 1: Начните с разряда единиц. Мы видим, что 2 меньше 6. Итак, мы возьмем 1 из столбца десятков, что даст 12. Теперь 12 — 6 = 6.
- Шаг 2: После присвоения 1 столбцу единиц на шаге 1 число 3 в столбце десятков становится равным 2. Теперь давайте вычтем цифры в разряде десятков (2 — 5). Здесь 2 меньше 5, поэтому мы возьмем 1 из столбца сотен. Получится 12. Итак, 12 — 5 = 7,9.0036
- Шаг 3: На шаге 2 мы поставили 1 в столбце десятков, поэтому у нас осталось 3 в разряде сотен. Теперь мы вычтем цифры в разряде сотен, то есть (3 — 2). Итак, 3 — 2 = 1.
- Шаг 4: Таким образом, разница между двумя заданными числами составляет: 432 — 256 = 176.
Сложение и вычитание в числовой строке
Сложение и вычитание в числовой строке можно выполнять, используя следующие правила.
- Сложение в числовой строке выполняется, начиная с первого слагаемого.
 Затем мы двигаемся вправо в зависимости от количества единиц второго числа, чтобы получить сумму.
Затем мы двигаемся вправо в зависимости от количества единиц второго числа, чтобы получить сумму. - Вычитание по числовой строке выполняется перемещением к левой стороне числовой строки в зависимости от количества единиц второго числа.
Давайте разберемся в этом подробно в следующем разделе.
Сложение в числовой строке
Сложение в числовой строке так же просто, как подсчет положительных чисел путем перемещения к правой стороне числовой строки. Это помогает нам визуально понять операцию сложения, используя маленькие числа. Давайте выполним операцию 1 + 2, используя числовую прямую, как показано ниже.
Мы отмечаем первое число (1) и двигаемся вправо на 2 единицы, используя второе число, которое здесь равно 2. Таким образом, мы перемещаемся на 2 единицы вправо, начиная с 1, и приземляемся на 3, что дает нам результат 1 + 2 = 3.
Вычитание по числовой прямой
Вычитание по числовой прямой помогает очень легко вычитать меньшие числа..jpg) При вычитании чисел из числовой строки нам нужно прыгать (перемещаться) к левой стороне числовой строки. Давайте вычтем 5 — 3, используя числовую строку, как показано ниже.
При вычитании чисел из числовой строки нам нужно прыгать (перемещаться) к левой стороне числовой строки. Давайте вычтем 5 — 3, используя числовую строку, как показано ниже.
Отмечаем первую цифру (5) и движемся влево на 3 единицы, которая здесь является второй цифрой. Таким образом, мы перемещаемся на 3 единицы влево, начиная с 5, и приземляемся на 2, что дает нам результат 5 — 3 = 2.
Часто задаваемые вопросы о сложении и вычитании
Что такое сложение и вычитание?
Сложение — это арифметическая операция, используемая для нахождения суммы целых чисел, целых чисел, дробей и т. д. Он представлен с помощью символа (+). Например, 4 + 7 = 11, что означает, что если прибавить 4 к 7, то в сумме получится 11. Вычитание — это арифметическая операция, которая используется для нахождения разности целых чисел, целых чисел, дробей и т.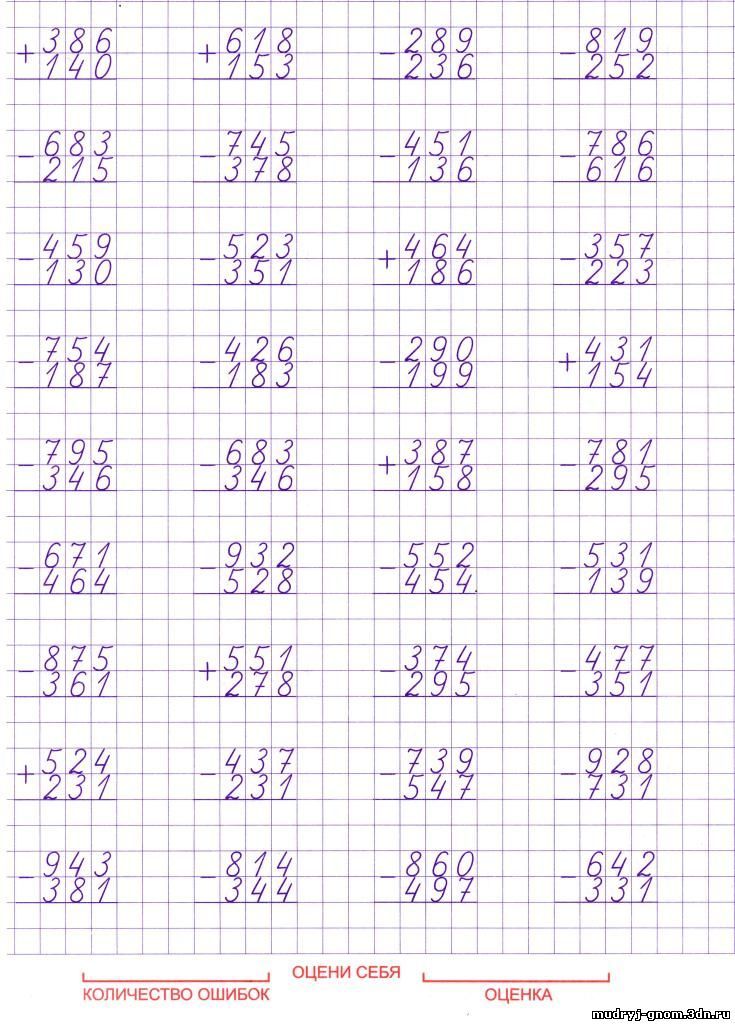 д. Он представлен с помощью символа (-). Например, 9- 7 = 2, это означает, что если из 9 вычесть 7, то получится 2 как разность.
д. Он представлен с помощью символа (-). Например, 9- 7 = 2, это означает, что если из 9 вычесть 7, то получится 2 как разность.
Почему важны сложение и вычитание?
Сложение и вычитание играют очень важную роль в нашей повседневной жизни, которая включает в себя счет, например, выставление счета в магазине, покупка продуктов, путешествие, скорость автомобиля, проверка веса и т.д. Это помогает нам понять ситуационные проблемы. Следовательно, сложение и вычитание важны в нашей жизни.
Как называется умножение, деление, сложение и вычитание?
Умножение, деление, сложение и вычитание называются арифметическими операциями в математике. Умножение представлено символом (×), деление представлено символом (÷), сложение представлено символом (+), а вычитание представлено символом (-)
Какая связь между сложением и вычитанием ?
Сложение и вычитание являются обратными операциями. Это означает, что мы можем проверить правильность нашего ответа, выполнив обратную операцию. Например, 9- 6 = 3. Теперь мы можем проверить правильность нашего вычитания, прибавив 3 к 6, 3 + 6 = 9. Это показывает, что наши вычисления верны.
Например, 9- 6 = 3. Теперь мы можем проверить правильность нашего вычитания, прибавив 3 к 6, 3 + 6 = 9. Это показывает, что наши вычисления верны.
Что такое сложение и вычитание дробей?
Сложение и вычитание дробей означает сложение или вычитание дробей в зависимости от вида дробей. В случае одинаковых дробей мы работаем только с числителями, потому что знаменатели одинаковы. В случае разных дробей у нас разные знаменатели, и нам нужно сделать их одинаковыми, найдя их НОК (наименьшее общее кратное) и преобразовав их в эквивалентные дроби таким образом, чтобы знаменатели остались одинаковыми. После этого шага мы добавляем или вычитаем числители в соответствии с требованием.
Что такое факты сложения и вычитания?
Некоторые из известных фактов сложения и вычитания перечислены ниже:
- Добавление или вычитание 0 к любому числу приводит к самому числу. Например, 6 + 0 = 6 .
- Добавление 1 к любому числу дает его последующее число, а вычитание 1 из любого числа дает его предшественник.



 Дети считают цепочку примеров устно, поднимают руку при завершении счета
Дети считают цепочку примеров устно, поднимают руку при завершении счета  Закрепление материала
Закрепление материала Предлагаю составить уравнения. Составляем 3 уравнения. Решаем у доски 3 человека и в тетрадях.
Предлагаю составить уравнения. Составляем 3 уравнения. Решаем у доски 3 человека и в тетрадях.
 На картах отметьте смайликом как вы справились с этим заданием. На этом острове мы отдохнём.
На картах отметьте смайликом как вы справились с этим заданием. На этом острове мы отдохнём. Самым крупным считается комодский варан, достигающий 3 метров в длину. Наиболее мелкий вид — варан короткохвостый, длиной всего 28 см.
Самым крупным считается комодский варан, достигающий 3 метров в длину. Наиболее мелкий вид — варан короткохвостый, длиной всего 28 см.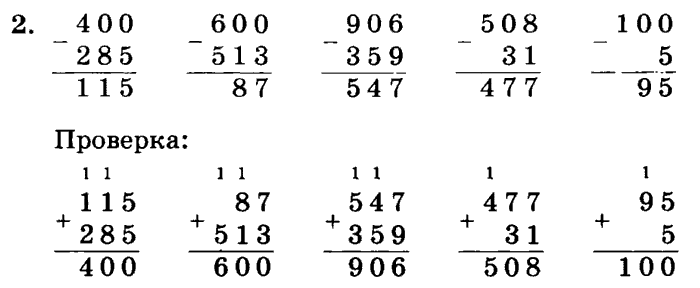 2 детей выполняют задание на доске.
2 детей выполняют задание на доске. Меняемся тетрадями, проверяем
Меняемся тетрадями, проверяем Рефлексия
Рефлексия
 Затем мы двигаемся вправо в зависимости от количества единиц второго числа, чтобы получить сумму.
Затем мы двигаемся вправо в зависимости от количества единиц второго числа, чтобы получить сумму.