Самые красивые физические и математические формулы.: moris_levran — LiveJournal
Математик Анри Пуанкаре в книге «Наука и метод» писал: «Если бы природа не была прекрасна, она не стоила бы того, чтобы ее знать, жизнь не стоила бы того, чтобы ее переживать. Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».
П.А.М. Дирак писал: «У теоретической физики есть еще один верный путь развития. Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой. Чтобы понять эту теорию, нужно обладать необычайно высокой математической квалификацией.
Вы можете спросить: почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе».
Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы.
В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было.
В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер.
Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».
2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице.
Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.
3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе» темную энергию»). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.
4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц.
Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.
5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.
6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.
7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света.
Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.
8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.
9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.
10. Уравнение минимальной поверхности.
Это равенство объясняет формирование мыльных пузырей.
11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.
12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера – которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён – Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией – до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон – антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.
13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»
14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.
Прекрасные чудовища математики / Хабр
UPD: добавлен график функции.
Подобно своему создателю Карлу Вейерштрассу, это чудовище возникло из ниоткуда. Потратив четыре года учёбы в университете на кутежи и фехтование, Вейерштрасс выпустился из него с пустыми руками. В конце концов он взялся за преподавание и бо́льшую часть 1850-х был школьным учителем в Браунсберге. Ему была отвратительна жизнь в маленьком прусском городишке, он находил своё существование там одиноким.
Единственной отдушиной для него стали математические задачи, над которыми он работал между уроками. Но ему не с кем было поговорить о математике, и у него не было технической библиотеки для обучения. Даже результатам его работ не удавалось покинуть пределов Браунберга. Вместо публикации в академических журналах, как это сделал бы университетский исследователь, Вейерштрасс добавлял их к школьным проспектам, пугая потенциальных учеников заумными уравнениями.
В конце концов Вейерштрасс отправил одну из своих статей в уважаемый «Журнал Крелле». Несмотря на то, что предыдущие статьи остались едва замеченными, эта вызвала огромный всплеск интереса. Вейерштрасс обнаружил способ работы с ужасным классом уравнений, известным как «абелевы функции». В статье было приведено краткое изложение его методов, но этого было достаточно, чтобы убедить математиков в наличии у автора уникального таланта. Не прошло и года, как Кёнигсбергский университет дал Вейерштрассу почётную докторскую степень, а вскоре после этого Берлинский университет предложил ему должность профессора.
Несмотря на то, что Вейерштрасс проделал интеллектуальный аналог пути «из грязи в князи», многие из его старых привычек сохранились. Он редко публиковал статьи, предпочитая делиться своими работами со студентами. Но он был малопочтителен не только к процессу публикации: не пугали его и «священные коровы» математики.
Вскоре Вейерштрасс взялся за изучение работ Огюстена Луи Коши, одного из наиболее выдающихся математиков века. Во многих работах Коши исследовались математический анализ и скорости изменения (или «производные»). Он создал основы словаря математического анализа, определив важнейшие концепции этой тематики. Но когда Вейерштрасс увидел его определения, то нашёл их многословными и расплывчатыми. В них было слишком много «жестов руками» и мало подробностей.
Он решил пересмотреть словарь Коши, заменив прозу логическими условиями. Основной целью в этой его ранней работе стало переопределение производной. Для вычисления градиента кривой в точке, а значит и скорости её изменения, Исаак Ньютон изначально рассматривал прямую, проходящую через эту точку и соседнюю точку кривой.
Затем он сдвигал эту соседнюю точку всё ближе и ближе, пока наклон кривой не становился равным градиенту кривой. Но эту концепцию сложно было определить математически. Что указывает на «близость» двух точек друг к другу?
По многословному определению Коши, градиент «неограниченно приближается к фиксированному значению, таким образом, что в результате отличается от него настолько, насколько это требуется». Вейерштрасс не считал, что такое описание достаточно чётко. Он хотел создать более практичное определение, поэтому решил превратить концепцию в формулу. Вместо манипуляций с абстрактными идеями математики должны иметь возможность изменить уравнения. Работая над этим, он заложил основы своего чудовища.
В ту эпоху математики во многом вдохновлялись природой. Когда Ньютон разрабатывал математический анализ, он в первую очередь вдохновлялся физическим миром: траекториями планет, колебаниями маятника, движением падающего фрукта. Такое мышление привело к возникновению геометрической интуиции относительно математических структур.
По общепринятому тогда мнению, у любой непрерывной кривой можно было найти градиент для любого конечного числа точек. Казалось, это соответствовало интуитивному понимаю: у линии может быть несколько неровных кусков, но всегда есть несколько частей, которые являются «гладкими». Французский физик и математик Андре-Мари Ампер даже опубликовал доказательство этого утверждения. Его аргументация была построена на том «интуитивно очевидном» факте, что непрерывная кривая имеет части, на которых она увеличивается, уменьшается или остаётся плоской.
Но в 1860-х появились слухи о странном существе — математической функции, противоречившей теореме Ампера. В Германии великий Бернхард Риман рассказывал своим студентам, что знает непрерывную функцию, не имеющую гладких частей, и для которой невозможно вычислить производную функции в любой точке. Риман не опубликовал доказательств, как и Шарль Селлерье из Женевского университета, который писал, что обнаружил что-то «очень важное и, как мне кажется, новое», однако спрятал свои работы в папку, ставшую достоянием общественности только после его смерти несколько десятков лет спустя.
Чудовище окончательно родилось в 1872 году, когда Карл Вейерштрасс объявил, что нашёл функцию, являющуюся непрерывной, но не гладкой во всех точках. Он создал её, сложив вместе бесконечно длинный ряд функций косинуса:
Как функция она была уродливой и отвратительной. Было даже непонятно, как она будет выглядеть на графике. Но Вейерштрасса это не волновало. Его доказательство состояло не из форм, а из уравнений, и именно это делало его заявление таким мощным. Он не только создал чудовище, но и построил его на железной логике. Он взял собственное новое строгое определение производной и доказал, что для этой новой функции её вычислить невозможно.
Результат привёл математическое сообщество в состояние шока. Французский математик Эмиль Пикар сказал, что если бы Ньютон знал о таких функциях, то не создал бы математический анализ. Вместо вынашивания идей о физике природы он завяз бы в попытках пробраться через жёсткие математические преграды. Чудовище начало расшатывать и предыдущие исследования. Результаты, казавшиеся «доказанными», трещали по швам. Ампер использовал выбранные Коши пространные определения для доказательства своей теоремы о гладкости. Теперь его доказательства начинали рушиться. Неопределённые понятия прошлого были бессильны против чудовища. Ещё хуже было то, что теперь стало неочевидным, из чего же состоит математическое доказательство. Интуитивные геометрические аргументы двух прошедших веков стали бесполезными. Когда математики пытались прогнать чудовище, оно оставалось непреклонным. Одним странным уравнением Вейерштрасс показал, что физическая интуиция не была надёжным основанием для построения математических теорий.
Авторитетные математики попытались отмахнуться от результата, утверждая, что он некрасив и ненужен. Они опасались, что буквоеды и возмутители спокойствия внесут хаос в их любимую область знания. В Сорбонне Шарль Эрмит писал: «Я в отвращении и ужасе отворачиваюсь от прискорбной скверны функций, не имеющих производных». Анри Пуанкаре, впервые назвавший такие функции чудовищами, назвал работу Вейерштрасса «оскорблением здравого смысла». Он утверждал, что такие функции — нахальное отвлечение от сути предмета.
«Их изобрели с целью показать ошибочность рассуждений наших предшественников», — говорил он. «И кроме этого, мы не сможем ничего из них взять».
Многие из «старой гвардии» хотели оставить чудовище Вейерштрасса на задворках математики. Мешало и то, что никто не мог представить облик животного, с которым они встретились — только после изобретения компьютеров появилась возможность создать его график. Его непостижимая форма мешала осознанию математическим сообществом того, как такая функция вообще может существовать.
Кроме того, стиль доказательства Вейерштрасса был неизвестен многим математикам. Его доказательство содержало десятки логических шагов и простиралось на несколько страниц. Цепочка рассуждений была едва уловимой и требовала серьёзных технических знаний, а в реальном мире аналогов, которые бы помогли в понимании, не было. Инстинкт призывал избегать этого доказательства.
Но чудовища имеют обычай прокладывать дорогу самостоятельно. На самом деле многие концепции, кажущиеся сегодня очевидными, даже необходимыми, когда-то были чудовищами. Веками математики отвергали отрицательные числа. Древние греки, в основном работавшие с геометрией, не видели в них нужды. То же самое справедливо и для средневековых академиков, перенявших идеи греков. Тень этого монстра иногда мелькает и сегодня, например, в вопросах ребёнка, спрашивающего, почему при умножении двух отрицательных чисел получается положительное. Но в целом мы приручили этого зверя: никто не мечтает снова его изгнать.
То же самое случилось с чудовищем Вейерштрасса — оно начало получать призвание.
Когда стало очевидно, что так называемые «функции Вейерштрасса» на самом деле достаточно полезны, учёные начали разрабатывать способы элегантной работы с негладкими функциями. Вместо того, чтобы анализировать путь отдельной частицы в жидкости, они стали рассматривать среднее поведение множества частиц.
Насколько далеко они могут переместиться? Когда они могут достичь заданной точки? За пределами области изучения броуновского движения математики также начали переосмысливать основные инструменты матанализа. Скорость изменений всегда определялась относительно расстояний, а площадь под кривой измерялась геометрически. Но когда функции были негладкими, то такие идеи не имели смысла.
Киёси Ито из Токийского университета обнаружил способ обойти проблему, подойдя к ней с точки зрения вероятностей. Это была неортодокасальная, если не сказать рискованная, тактика: в 1940-х едва ли кто-то считал теорию вероятности серьёзной областью. Однако Ито настаивал на своём. Он подошёл к функциям как к случайным процессам и перевёл определения Вейерштрасса на новый язык, основанный на вероятностях. Он заявил, что два случайных процесса «близки» друг к другу, если их ожидаемые результаты одинаковы. Он ввёл метод работы с математической функцией, зависящий от величины негладкости, как в броуновском движении, вместо более традиционной переменной, например, расстояния.
С помощью своих новых методов он вывел «лемму Ито» для вычисления изменения такой функции со временем.
К 1970-х его работа развернулась в совершенно новую область математики, называемую стохастическим исчислением (математики любят называть всё связанное со случайностью «стохастическим»). Как и в самом матанализе, в ней появился совершенно новый набор инструментов и теорем. Сегодня стохастическое исчисление используется для изучения всевозможных явлений, от работающих в мозге нейронов до распространения заболеваний в популяции. Также оно стало основой финансовой математики, в которой помогает банкам оценивать стоимость опционов. Оно может учитывать неровное поведение биржевого курса, а значит, показывает, насколько меняется со временем ценность опциона. Получившееся уравнение, которое известно как формула Блэка-Шоулза, теперь используется на всех торговых площадках мира. Однако Ито всегда вводили в замешательство похвалы банкиров. Он был математиком-теоретиком, и не ожидал, что его работа станет известной благодаря практическому применению.
Чудовище Вейерштрасса перетряхнуло и принципы геометрии. В конце 19-го века шведский математик Хельге фон Кох заинтересовался идеей негладких функций, но хотел изучить их форму. Он приступил к созданию формы (а не функции), которая нигде не будет гладкой, таким образом показав, что те же монстры скрываются и в алгебре с геометрией. Хоть он и не смог нарисовать функцию Вейерштрасса, но ему удалось запечатлеть её близкого родственника. Работая над этой задачей в процессе постоянного поиска временных работ на должности преподавателя-стажёра, фон Кох в 1904 году обнаружил своё существо. Он взял равносторонний треугольник, затем добавил с каждой стороны три меньших треугольника, и так до бесконечности. Получившаяся геометрическая форма была непрерывной, но не имела производных. Благодаря своему выдающемуся внешнему виду фигура быстро стала известна как «снежинка Коха».
Коху удалось расширить власть чудовища Вейерштрасса за пределы мира уравнений и функций. Но в результате его работы было ещё кое-что, заслуживавшее внимания.
При более близком изучении оказалось, что у его снежинки было любопытное самоподобие: увеличьте одну часть снежинки, и она будет выглядеть так же, как бо́льшая фигура. Спустя много лет стало очевидно, что функция Вейерштрасса обладает тем же свойством.
По прошествии времени такое самоподобие стало проявляться во всевозможных явлениях. Для популяризации идеи «фрактальных» объектов в 1980-х потребовалась основополагающая работа Бенуа Мандельброта. Такие объекты имеют формы, повторяющиеся во всё меньших и меньших масштабах. Береговые линии, облака, растения, кровяные сосуды — математики обнаружили, что фракталы вездесущи в природе. Как и снежинка Коха, ни один из них не был гладким. Да и как бы они были гладкими? Если фигура имеет гладкие части, то паттерн при достаточном увеличении исчезнет. Как обнаружил Кох, простейшим способом получения негладкой фигуры является создание фрактального объекта. Возможно, работа Вейерштрасса должна была неизбежно направить математиков в сторону изучения самоподобных паттернов, познакомив исследователей с миром изысканных, прекрасных структур.
Чудовище Вейерштрасса продолжает свою работу и по сей день. Уравнения Навье-Стокса описывают движение жидкости и лежат в основе современной динамики жидкостей и аэродинамики, управляющих всем — от конструкции самолётов до прогнозирования погоды. Однако несмотря на то, что они впервые были созданы в 1840-х, математики до сих пор не знаю, всегда ли их можно решить. В 2000 году Математический институт Клэя предложил премию в 1 миллион долларов любому, кто докажет, что эти уравнения всегда имеют гладкие решения — или найдёт пример обратного. Эта задача считается одной из шести самых важных выдающихся задач математики, потому что несмотря на широкое использование уравнений Навье-Стокса, математики не знают, всегда ли эти уравнения дают физически достоверные результаты. Премия в 1 миллион долларов до сих пор никем не востребована. Во многих смыслах это плата за голову, провоцирующая математиков на охоту за опасными чудовищами.
В различных областях: от динамики жидкостей до финансового сектора существа, подобные функции Вейерштрасса, ставили под сомнение наши взгляды на связь между математикой и естественным миром.
Математики, жившие во времена Вейерштрасса, полагали, что самая полезная математика вдохновляется природой, и что работа Вейерштрасса не вписывается в это определение. Но стохастическое исчисление и фракталы Мандельброта доказали их неправоту. Оказалось, что в реальном мире — в хаотичном, сложном реальном мире — чудовища прячутся повсюду. Как сказал Мандельброт, «природа сыграла с математиками шутку». Даже сам Вейерштрасс стал жертвой этого трюка. Он создал свою функцию, чтобы возразить, что математика должна основываться только на физических наблюдениях. Его последователи полагали, что Ньютон был ограничен интуитивным восприятием реального мира, и теперь они, свободные от этих ограничений, смогут открыть более универсальные и элегантные новые теории. Они думали, что математике больше не нужна будет природа. Но чудовище Вейерштрасса доказало, что всё обстоит совершенно наоборот. Связь математики и природы намного более глубока, чем кто-либо мог представить.
Об авторе: Адам Кучарски — научный сотрудник Лондонской школы гигиены и тропической медицины, занимающийся математической эпидемиологией.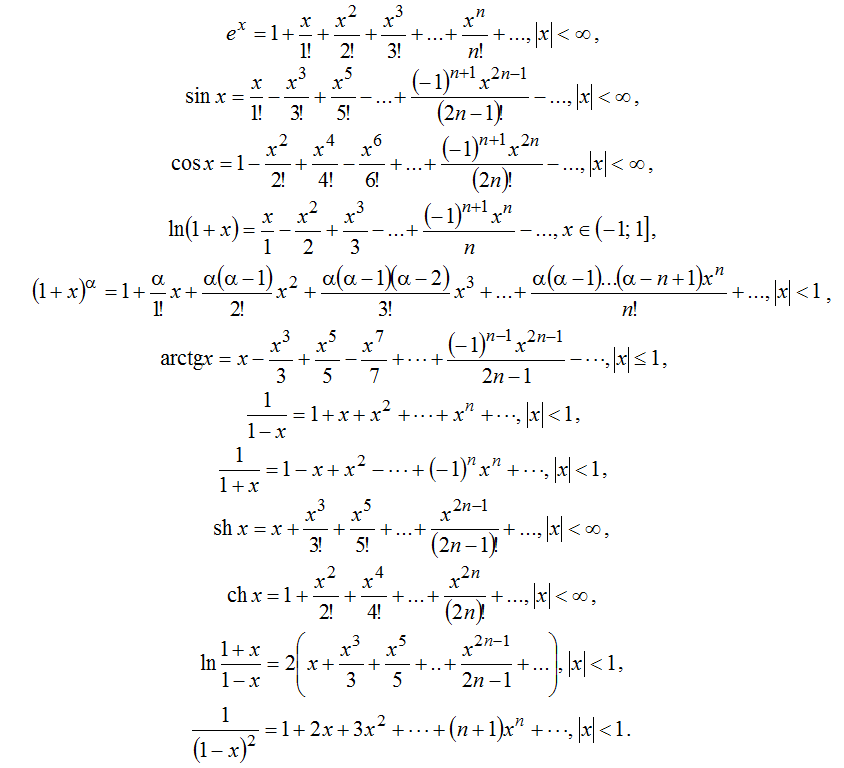
Математические формулы для 10-го класса
Нельзя отрицать, что 10-й класс имеет решающее значение для определения вашего карьерного пути и закладки его основы. Многие учащиеся считают математику самым сложным предметом в 10-м классе. Этот блог станет универсальным хранилищем всех основных математических формул для 10-го класса, которые помогут вам быстро решать задачи.
Оглавление
- Математические формулы для 10 класса | Сдайте экзамены с этими формулами
- Математические формулы для линейных уравнений для 10 класса
- Математические формулы для алгебры и квадратных уравнений для 10 класса
- Математические формулы для окружностей для 10 класса
- Тригонометрические формулы для математики для 10 класса
- Формулы цилиндра
- Формулы конуса
- Формулы куба
Математические формулы для 10 класса важны и служат основой для изучения математических предметов более высокого уровня.
Математические формулы также полезны в различных секторах высшего образования, таких как машиностроение, медицина, бизнес, финансы, информатика, аппаратное обеспечение и т. д.
Наиболее распространенные формулы, описанные в классе 10, используются практически в каждом бизнесе. Вещественные числа, многочлены, квадратные уравнения, треугольники, окружности, статистика, вероятность и другие темы рассматриваются в математических формулах класса 10. Эти математические формулы будут очень полезны учащимся для более точного и быстрого решения задач.
Математические формулы класса 10 для линейных уравнений| Линейные уравнения с одной, двумя и тремя переменными имеют следующие формы: Линейное уравнение с одной переменной ax + b=0 Где a ≠ 0 и a & b являются действительными числами Линейное уравнение с двумя переменными ax + by + c = 0 Где a ≠ 0 & b ≠ 0 и a, b и c являются действительными числами Линейное уравнение с тремя переменными ax + by + cz + d = 0 Где a ≠ 0, b ≠ 0, c ≠ 0 и a, b, c, d — действительные числа Пара линейных уравнений с двумя переменными задается как: a1x+b1+c1=0 и a2x+b2+c2=0 Где a1, b1, c1, & a2, b2, c2 — действительные числа & a12+b12 ≠ 0 и a22 + b22 ≠ 0 Примечание.  Линейные уравнения также могут быть представлены в графической форме. |
| Чтобы знать алгебраические формулы для 10 класса, сначала необходимо ознакомиться с ними. Квадратная формула: Для квадратного уравнения px2 + qx + r = 0 значения x, которые являются решениями уравнения, определяются как: Теперь вы знаете основное квадратное уравнение. Теперь пройдемся по списку алгебраических формул для 10 класса – (a+b) = a+ b22 + 2ab (a–b)2 = a2 + b2– 2ab (a+b) (ab) = a2 – b2 (x + a)(x + b) = x2 + (a + b)x + ab (x + a)(x – b) = x2 + (a – b)x – ab ( a +b)3 = a3+ b3 + 3ab(a + b) ( а -b)3 = а3 – Ь3 – 3аб(а – Ь) (х – а)(х + Ь) = х2 + (б – а)х – аб (х – а)(х – Ь ) = x2 – (a + b)x + ab (x + y +z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz (x + y – z)2 = x2 + y2 + z2 + 2xy – 2yz – 2xz (x – y + z)2 = x2 + y2 + z2 – 2xy – 2yz + 2xz (x – y – z)2 = x2 + y2 + z2– 2xy + 2yz – 2xz x2 + y2 + z2 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz -xz) y2 + z2 =½ [(x +y)2 + (x – y)2] (x + а) (x + b) (x + c) = x3 + (a + b + c)x2 + (ab + bc + ca)x + abc (x3 + y3= (x + y) (x2 – xy + y2) x3 – y3 = (x – y) (x2 + xy + y2) x2 + y2 + z2 -xy – yz – zx = ½ [ (x-y)2 + (y-z)2 + (z-x)2] Краткое примечание: эти формулы будут важны в старших классах и на различных конкурсных экзаменах, поэтому запомните их и хорошо поймите |
Формулы для кругов служат основой для измерения. Математические формулы для круга класса 10 для круга радиуса r приведены ниже: 1. Длина окружности = 2 π r2. Площадь круга = π r23. Площадь сектора угла θ = (θ/360) × π r24. Длина дуги сектора угла θ = (θ/360) × 2 π r |
| Тригонометрические формулы для класса 10 охватывают основные тригонометрические функции для прямоугольного треугольника, т. е. синус (sin), косинус (cos) и тангенс (tan), которые можно использовать для получения косеканса (cos), секанса ( сек) и котангенс (кот). Пусть прямоугольный треугольник ABC прямоугольный в точке B и имеет один из двух других углов. |
Подробнее: Отец математики | 6 вещей, которые вам нужно знать о нем
| Тригонометрическая таблица, содержащая значения этих тригонометрических функций для стандартных углов, выглядит следующим образом: Angle0°30°45°60°90°sinθ01/21/√ 2√3/21cosθ1√3/21/√2½0tanθ01/√31√3UndefinedcotθUndefined√311/√30secθ12/√3√22UndefinedcosecθUndefined2√22/√31 |
| Некоторые другие тригонометрические формулы приведены ниже ° – θ) = tan θсек (90° – θ) = cosecθcosec (90° – θ) = secθsin2θ + cos2 θ = 1сек2 θ = 1 + tan2θ для 0° ≤ θ < 90°Cosec2 θ = 1 + cot2 θ для 0 ° ≤ θ ≤ 90° |
| Diameter of sphere | 2r |
| Surface area of sphere | 4 π r2 |
| Volume of Sphere | 4/3 π r3 |
| Площадь изогнутой поверхности цилиндра | 2 πrh |
| Площадь двух круговых оснований | 2 π R2 |
| Общая площадь поверхности цилиндра | Окружность цилиндра + изогнутая поверхность поверхности полосы. |
| Объем цилиндра | π r2 H |
| Высота Slat of Cone | 1. 40049 |
| Высота Slat of Cone | 1. 40049 |
| . | πrl |
| Общая площадь поверхности конуса | πr (L + R) |
| Объем конуса | ⅓ π R2 H |
- Из-за огромного количества математических формул большинство учащихся боятся математики.
- Однако математика включает в себя больше, чем просто запоминание фактов из учебников; это также о решении и понимании проблем.
- Изучение математических формул или их понимание — самый эффективный способ сделать эту тему интересной.
- Таким образом, освоение математических формул поможет детям стать увереннее в себе и улучшить свои способности решать задачи.
- Очень важно понимать метод, лежащий в основе определенной формулы, так как он помогает запоминать формулы.
- Мы все знаем, что практика делает совершенным. В результате постоянное решение задач путем повторения математических формул на повторение приводит к запоминанию.
- Поскольку наш мозг запоминает то, что мы регулярно пишем, повторное написание математических формул может помочь вам запоминать их в течение более длительного периода времени. Поэтому заведите привычку записывать сложные формулы.
Мы надеемся, что вам понравилось читать этот блог. В случае каких-либо сомнений, свяжитесь с нами или оставьте комментарий ниже и поделитесь своими мыслями.
Понравился этот блог? Читать далее: Отец математики | 6 вещей, которые вам нужно знать о нем
Часто задаваемые вопросыQ1. Какое самое длинное уравнение в мире?
Ответ – Проблема булевых пифагорейских троек была первоначально введена в 1980-х годах калифорнийским математиком Рональдом Грэмом. Согласно Sciencealert, это самое длинное арифметическое уравнение, которое включает примерно 200 гигабайт текста.
Q2. Сколько формул в 10 классе по математике?
Ответ – Действительные числа, многочлены, квадратные уравнения, треугольники, окружности, статистика, вероятность и другие темы рассматриваются в математических формулах 10 класса.
Q3. Как вы запоминаете формулы?
Ответ – С практикой вы добьетесь безупречности. Когда вы практикуетесь в использовании формул, ваш мозг понимает и запоминает применение формулы.
Вы заметите результаты, если будете решать и практиковать задачи, запоминая и применяя формулы.
Насколько полезен был этот пост?
Нажмите на звездочку, чтобы оценить!
Средняя оценка 5 / 5. Всего голосов: 1
Голосов пока нет! Будьте первым, кто оценит этот пост.
WRITTEN BY
Dhriti Chadha
Study Abroad Expert
`
Самая большая в мире математическая задача решена, и она занимает 200 ТБ : ScienceAlert
придумали три математика, чье решение одной математической задачи занимает 200 терабайт базового текста — даже с помощью суперкомпьютера.
Если учесть, что всего в 1 терабайте может храниться 337 920 экземпляров «Войны и мира » — одного из самых длинных когда-либо написанных романов, — вы можете начать понимать, насколько это безумие. Сообщается, что предыдущим рекордсменом было 13-гигабайтное доказательство, опубликованное в 2014 году.
Так что же это за нелепая математическая задача? Она была названа проблемой булевых пифагорейских троек и впервые была поставлена калифорнийским математиком Рональдом Грэмом еще в 1980-х годах.
Проблема сосредоточена вокруг формулы Пифагора a 2 + b 2 = c 2 , где a и b — меньшие стороны треугольника, а c — гипотенуза или самая длинная сторона.
Некоторые наборы из трех положительных целых чисел, известные как тройки Пифагора, могут быть вставлены в формулу, например, 3 2 + 4 2 = 5 2 , 5 2 + 12 2 3 = 13 , и 8 2 + 15 2 = 17 2 .
Имея это в виду, представьте, что каждое целое число окрашено в красный или синий цвет.
Грэм спросил, можно ли покрасить все целые числа в красный или синий цвет так, чтобы ни один набор пифагорейских троек — a, b и c — не был одного цвета. Он поставил на кон 100 долларов тому, кто решит проблему. (Это должно покрыть диск объемом 1 терабайт.)
Эндрю Мозман из Popular Mechanics объясняет, почему эти 100 долларов выглядят очень скудными, учитывая предстоящую задачу:
«Сложным является то, что одно целое число может быть частью нескольких пифагорейских троек.
Перенеси эту логику на гораздо большие числа, и ты увидишь, где это может стать запутанным. Если 12 должно быть красным в этой тройке 5-12-13, это может вызвать изменения в строке, которые приведут где-то к монохромной тройке.»
Возьмем 5. Итак, 3, 4 и 5 являются пифагорейскими тройками. Но то же самое делают и 5, 12 и 13. первый пример, то во втором он должен быть синим, то есть либо 12, либо 13 должны быть красными. Математики Марин Хеул из Техасского университета, Виктор Марек из Университета Кентукки и Оливер Кульманн из Университета Суонси в Великобритании объединились, чтобы выяснить это, загрузив ряд различных методов в суперкомпьютер Stampede Техасского университета и позволив ему сократить число возможных комбинаций цветов со 102 300 триллионов (это 10 2,300 ) всего до 1 трлн.
800-процессорному суперкомпьютеру потребовалось два дня, чтобы обдумать оставшийся триллион и найти решение: 7824. Как только вы попробуете 7825 или более целых чисел, вы не сможете создать шаблон, который искал Грэм.
Угадай, кто теперь на 100 долларов богаче… Делим на троих! Хороший парень Грэм пришел с чеком в начале этого месяца.
Доказательство, которое в математике означает письменный дедуктивный аргумент, показывающий, как вы пришли к своему ответу, занимает на суперкомпьютере 200-терабайтный файл, что примерно эквивалентно всему оцифрованному тексту, хранящемуся в Библиотеке Конгресса США.
По словам Эвелин Лэмб из Nature , трио создало 68-гигабайтную сжатую версию своего решения, на загрузку, реконструкцию и проверку которой уйдет около 30 000 часов. Эта проблема? Ни один человек не мог надеяться прочитать такое.
Вместо этого команде пришлось использовать другую компьютерную программу, чтобы проверить результаты и показать, что их решение соответствует критериям исходного вопроса, и Грэм был удовлетворен подтверждением.
Но критики спрашивают, достаточно ли этого. Если ни один человек не может прочитать решение, это не значит, что оно неправильное, но оно не касается одного очень важного компонента решения математических задач — оно не может объяснить, почему раскраска невозможна, начиная с 7825, оно просто знает Это.