Таблица корней по математике: Таблица корней по алгебре

Справочные таблицы по математике

В наш век информационных технологий справочные таблицы уже давно стали неотъемлемой частью повседневной жизни многих наших сограждан. Эти структуры представляют собой определенным образом отсортированные и систематизированные данные, которые были получены в ходе длившихся на протяжении многих лет исследований. Правильное и своевременное использование такого рода информации позволяет форсировать новые разработки и упростить анализ многих процессов. Помимо этого справочные таблицы используются для установления зависимости между немалым количеством разнородных параметров, значениями которых оперируют при анализе физических свойств различных объектов и осуществлении математических операций.

• Римская нумерация
• Греческий алфавит
• Латинский алфавит
• Таблица постоянных величин
• Метрическая система измерения
• Таблица простых чисел
• Математические обозначения
• Значение синусов и косинусов
• Таблица значений синусов и косинусов
• Таблица значений тангенса и котангенса
• Свойства тангенса и котангенса
• Определение тангенса и котангенса
• Табличные значения тангенса и котангенса
• Таблица возведения в степень
• Таблица свойства степеней
• Таблица значения степеней
• Таблица основных степеней
• Свойства n-ой степени
• Таблица степеней по алгебре
• Таблица n-ой степени
• Числа в степени таблица
• Таблица квадратных корней
• Таблица извлечения корней
• Таблица извлечения квадратного корня
• Таблица извлечения кубического корня

Математические справочные таблицы являются источником ценной информации, которую с успехом используют специалисты для разработки множества проектов, имеющих большое научное и сугубо практическое значение.

Что касается достоинств, справочной таблицы, то, пожалуй, самой главной из них является быстрота доступа к содержащейся в ней информации, причем в том виде, который прост и удобен для восприятия даже неспециалистам.

 

Эксперты придерживаются того мнения, что справочные таблицы на сегодняшний день являются наиболее удобной формой, в которой представляются необходимые для работы данные, причем она предполагает очень удобный функционал для работы, включающий в себя возможность сортировки по определенному признаку.

Среди всех точных наук математика стоит несколько особняком и многими считается основной. Для этого есть все основания, и наиболее существенное из них заключается в том, что в ней нет места необоснованным количественным показателям или толкованиям и закономерностям, которые не доказаны опытным путем. Строжайшая упорядоченность, жесткая логика и безукоризненная взаимосвязь явлений и событий, которые имеют место в окружающей действительности, признаются в математике источниками и методами исследования.

Именно математика является тем средством, которое ученые всего мира чаще всего используют для своих исследований. Такой подход позволяет им не только с успехом подтверждать уже давно известные (пусть даже и в узких кругах) законы мироздания, но и вплотную приближаться к открытию новых. Ученые отлично знают, что практически все процессы, происходящие в окружающей нас действительности, можно описать в виде математических моделей, а для их исследования использовать соответствующие методы, причем с большим успехом. Вопрос только в том, насколько корректно будет составлена та или иная математическая модель и будут ли в ней учтены все значимые факторы.

Таким образом, можно с полной уверенностью утверждать, что справочные таблицы существенно расширяют возможности научного познания окружающей нас действительности. Более того, сейчас уже нет такой области знаний, в которой они не использовались бы исследователями.

Конечно, математика является прикладной наукой, однако ее богатый инструментарий великолепно используется практически во всех областях человеческой деятельности. При помощи четких, строгих и выверенных математических моделей можно исследовать многие аспекты окружающей нас действительности, причем таким образом, чтобы результаты были действительно обоснованными. Дальнейший прогресс абсолютно невозможен без использования математических методов исследований.

Знание математических методов исследований и наличие практического опыта их применения является основной многих профессий. Само собой разумеется, что это в первую очередь касается «технарей», однако и «гуманитариям» нелишне овладеть основами математического исследовательского аппарата, поскольку это существенно расширяет границы познания в их специфической профессиональной области.

Исследовательская работа «Квадратные корни и сложные радикалы»

XVI Районная научно-практическая конференция «Эврика»

 

 

 

 

 

 

 

 

 

 

       Направление: Математика

 

 

 

      Исследовательская работа на тему:

«Квадратные корни и сложные радикалы»

 

 

           

                   Автор:

                                                Дугулубгов Ислам, ученик 10 класса

                                       МОУ СОШ№1 с. п.В.Куркужин

                              Руководитель:

                               Дугулубгова Фатимат Султановна,

                                          учитель математики  высшей категории           

                                           МОУ СОШ№1 с.п.В.Куркужин

 

 

2020год

 

 

Содержание

 

Введение …………………………………………………………………………3

1. Различные способы извлечения квадратного корня…….………………….5

1.1. Способ извлечения корня, оканчивающегося на 25………………………5

1.2. Способ разложения на множители………………………………………….5

1.3.Способ оценки и отбора ………………………………..……………………6

1.4.Способ отбрасывания полного квадрата…..…………………………………6

2. Вавилонский способ………………………………………………………. ….7

3.Сложные радикалы………………………………………………………….…8

Заключение……………………………………………………………………….10Список литературы………………………………………………………………11

Приложение 1 ……………………………………………………………………12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение.

В средних классах  я и мои одноклассники  изучали тему квадратные корни.

Все было замечательно, пока под рукой была таблица квадратов.  А рассмотрев один вариант профильной математики и столкнувшись в нескольких местах с извлечением квадратного  корня и узнав, что на профильной математике в справочном материале нет таблицы квадратов, я понял, что извлечение квадратного корня, который без проблем делает любой школьник, может стать проблемой на ЕГЭ.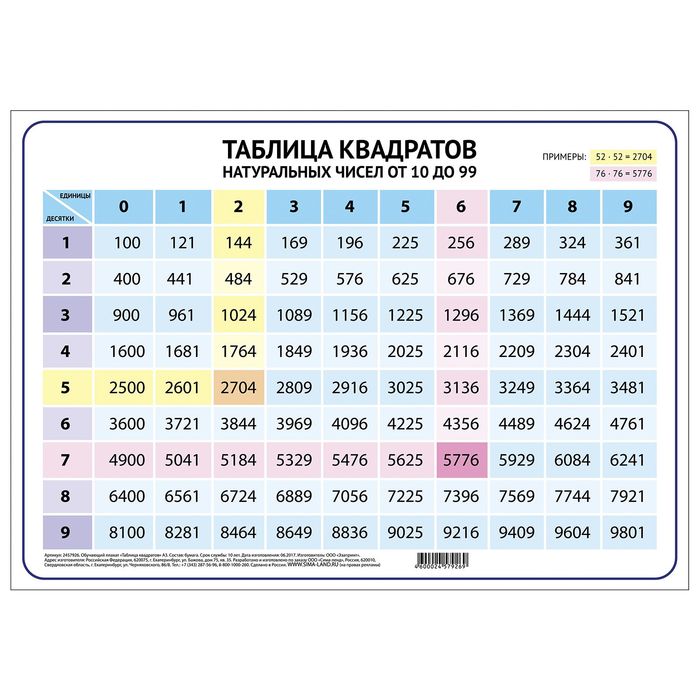

Все знают, что извлечь квадратный корень без калькулятора — это непосильная задача. В лучшем случае, в ситуации, когда решение задач требует извлечения корня, а калькулятор вне зоны досягаемости, прибегают к методу подбора и стараются вспомнить данные из таблицы квадратов целых чисел, но это не всегда спасает. Сколько раз мы попадали в подобные ситуации? Почти все, к кому я обращался с этим вопросом, не знали ни одного способа решения этой проблемы.

С этим вопросом я обратился  к своей учительнице математики, она ответила, что такие способы есть, и посоветовала мне самому исследовать этот вопрос.

Я узнал, что извлекать корни люди научились задолго до изобретения «умной» техники. Мои вопросы и легли в основу исследования, которое для меня стало маленьким открытием. Исследуя эту тему, я нашел не один, а несколько способов решения данной проблемы, и более того я вместе с моим учителем нашли свой способ извлечения корня (правда для некоторых чисел). И еще я научился решать примеры на радикалы, что в переводе с латинского radix означает – корень.

 Актуальность исследования обусловлена стремлением углублять математические знания через применение простейших способов извлечения квадратных корней без калькулятора, распространение алгоритмов извлечения корней среди учащихся, что особенно актуально при сдаче экзаменов, где запрещено использование калькулятора, а также использовать эти знания при работе с вычислениями корней на уроках математического цикла в ситуациях недоступности калькулятора.

 Цель работы: Исследовать различные способы вычисления арифметических корней. Изучить все известные способы извлечения квадратных корней без калькулятора и отобрать самые рациональные для практического применения.

 Задачи:   Изучить всю найденную литературу по данному вопросу, научные статьи, исторические справки и работы современных учёных и исследователей; рассмотреть особенности каждого найденного способа и описать его алгоритм; показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов и их использование при работе с радикалами.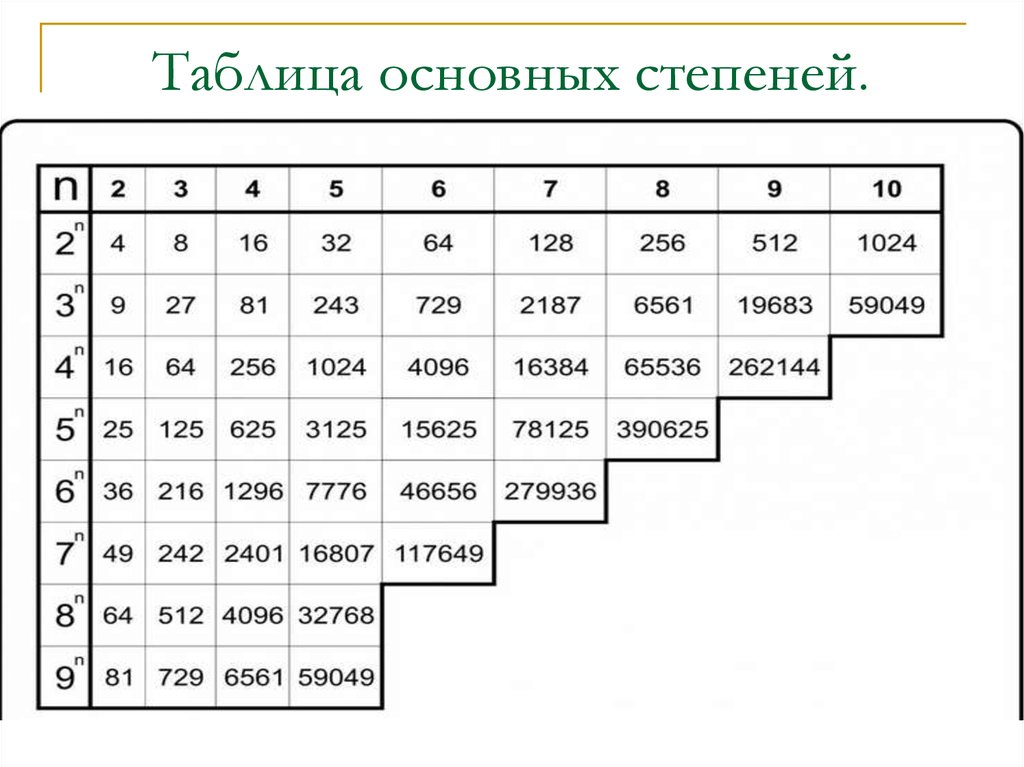

Гипотеза: Существует несколько способов извлечения квадратных корней без калькулятора.

Объект исследования:  квадратные корни, сложные радикалы.

Предмет исследования: особенности способов извлечения квадратных корней без калькулятора, сложные радикалы.

Методы исследования: поиск способов и алгоритмов; сравнение найденных способов и выявление их преимущества и недостатков.

         Научная новизна работы заключается в подборе материала по теме, не изучаемой в школьной математике.

Практическая значимость: материал используется на итоговой аттестации

                          

 

 

1.Различные способы извлечения квадратного корня

1.1.Способ извлечения корня, оканчивающегося на 25

 1)Число, образованное цифрами слева от  25 представляем в виде произведения двух  последовательных множителей

2) в ответ надо записать меньшее из этих множителей и приписать число 5.

=115

 

Вывод: Этот замечательный способ можно использовать только в том случае, когда число оканчивается на 25 и если цифры левее 25 являются произведением двух последовательных чисел. Недостаток в том, что если перед 25 трехзначное (и более) не очень просто разложить на два множителя, которые являются последовательными.

1.2. Способ разложения на множители.

  Для применения этого способа достаточно  используя признаки делимости чисел, разложить подкоренное выражение на множители

Пример: Вычислить= ==3*19=57

Вывод: Этот способ уникальный,  подходит для всех чисел, если оно рациональное.           Недостаток: Его не смогут использовать те, кто не знает признаки делимости чисел.

1.3. Способ оценки и отбора

 Здесь необходимо оценить наш корень справа и слева.  Число  находится между числами 50 и 60  и оканчивается цифрой 9. Это может быть 53 или 57. Число 3249 ближе к 3600, чем к 2500, значит 3249=57². Итак, =57

Вывод: Один из самых легких и оптимальных способов. Нужно знать лишь квадраты чисел до 9.

1.4. Способ отбрасывания полного квадрата

  Над этим способом мне пришлось изрядно  потрудиться, т.к. этого способа нет  ни в сети Интернет, ни в каких либо источниках. Это способ, который составлен нами, мною и моим учителем.

После произведения большого количества вычислений, нам удалось составить алгоритм, в основу которого легло правило возведения в квадрат чисел близких к 50.   

2.Вавилонский способ

Потребность в действиях возведения в степень и извлечения корня была вызвана, как и другие четыре арифметические действия, практической жизнью. Так, наряду с задачей вычисления площади квадрата сторона которого а известна, с давних времен встречалась обратная задача: какую длину должна иметь сторона квадрата, при нужной площади?

Ещё 4000 лет назад вавилонские ученые составляли  таблицы квадратов чисел и квадратных корней из чисел. При этом они умели находить приблизительное значение квадратного корня  из  любого  целого числа. Вавилонский метод извлечения квадратного корня можно иллюстрировать на следующем примере, изложенном в одном из найденных при раскопках клинописных табличек.

Правило, применявшееся вавилонянами, может быть выражено так: чтобы извлечь корень из числа с, представляют его как сумму а²+в (в должно быть достаточно малым в сравнении с а² ) и вычисляют по приближенной формуле:

 =  = а + ^в/_2а

 

Пример: Найти квадратный корень из 8464.

Для решения задачи данное число разлагается на сумму двух слагаемых:

8464 = 8100 + 364 = 90² + 364,

первое из которых является полным квадратом. Затем указывается, что

 

 90 + ³⁶⁴/_2∙90 =90+2,1..=92

Применим этот способ, с учетом рассмотренных правил, для шестизначного числа:

 = =750+ ⁴⁵⁰⁹/_2∙750 =750+3,…=753 

 

 

3. Сложные радикалы

  Работая над данной темой я столкнулся со сложными радикалами, т.е. изучил двойные радикалы вида , где а,в,с – целые числа, причем корень из числа с не извлекается.

Здесь самое главное, нужно подкоренное выражение представить в виде квадрата суммы или квадрата разности.

Рассмотрим пример: 1.Вычислить:  

 = = = =                = , т.к.

 

Пример 2.      

       

 

 

                 

 

 

 

 

 

 

 

 

 = = =

 

 

    Вывод: изучив тему и рассмотрев различные способы извлечения корня и после проведения опроса одноклассников (Приложение 1)  можно сказать:

1.Самым легким способом является способ оценки и отброса

2. Способ разложения на множители трудоемкий и длинный, но его можно отнести к самому нужному, так можно с помощью этого способа извлечь корни  третьей, четвертой и более степеней.  Здесь нужно знать признаки делимости.

3. Вавилонский способ требует знания формулы, но самый оптимальный, так как его можно использовать для больших чисел.

    А вывод такой:  В математике нет царских путей, все достигается упорным трудом.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заключение

Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные   алгоритмы позволят всем, кто заинтересуется данной темой,  быстрее овладеть навыками вычисления квадратного корней, их можно использовать  при проверке своего решения  и не зависеть от наличия в кармане калькулятора. Тем более что на экзамене в 9 и 11 классах применение калькулятора не допускается.

Я  думаю, что моя работа пригодится мне на профильной математике при решении заданий, где встречается извлечение корня,  а таких задании несколько.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список литературы

 

1. Г.И. Глейзер «История математики в школе» С. 18-20

2. Б.А. Кордамский, А. А. Ахадов «Удивительный мир чисел» М.: Просвящение,1986

3.В.А. Гусев, А.Т. Мордкович «Математика: справочные материалы»; Книга для учащихся – 2-е издание. –М: Просвещение,1990

4. Интернет ресурсы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1

 

Результаты опроса одноклассников (в процентах)

 

Кто какой предпочитает способ?

Опрос провели после знакомства класса с темой на уроке по внеурочной деятельности.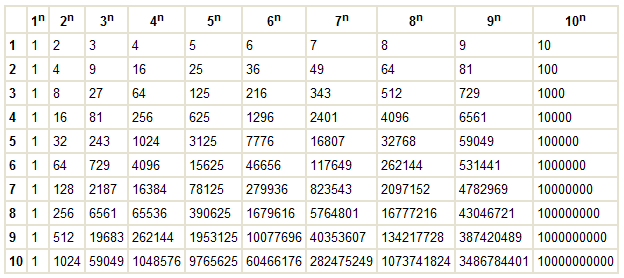

 

 

 

 

 

 

 

 

 

Используя таблицу квадратных корней, найдите квадратные корни следующих 540…

Перейти к

• Квадраты и квадратные корни. Упражнение 3.1.
• Квадраты и квадратные корни. Упражнение 3.2.
• Квадраты и квадратные корни. Упражнение 3.3.
• Квадраты и квадратные корни. Упражнение 3.4.
• Квадраты и квадратные корни. Упражнение 3. 5.
• Квадраты и квадратные корни. Упражнение 3.6.
• Квадраты и квадратные корни. Упражнение 3.7.
• Квадраты и квадратные корни. Упражнение 3.8.
• Квадраты и квадратные корни. Упражнение 3.9.

• Рациональное число
• Полномочия
• Квадраты и квадратные корни
• Куб и кубические корни
• Игра с числами
• Алгебраические выражения и тождества
• Факторизация
• Отдел алгебраических выражений
• Линейное уравнение с одной переменной
• Прямые и обратные варианты
• Время и работа
• Процент
• Скидка на убыток и налог на добавленную стоимость
• Сложные проценты
• Понимание многоугольников фигур
• Понимание фигур Четырехугольники
• Понимание фигур Специальные типы четырехугольников
• Практическая геометрия
• Визуализация фигур
• Площадь трапеции и многоугольника
• Объем Площадь Прямоугольный Куб
• Площадь поверхности и объем правого кругового цилиндра
• Классификация и табулирование данных
• Классификация и табулирование данных Графическое представление данных в виде гистограмм
• Графическое представление данных в виде круговых диаграмм или круговых диаграмм
• Вероятность обработки данных
• Введение в графики

Главная > РД Шарма Решения Класс 8 Математика > Глава 3.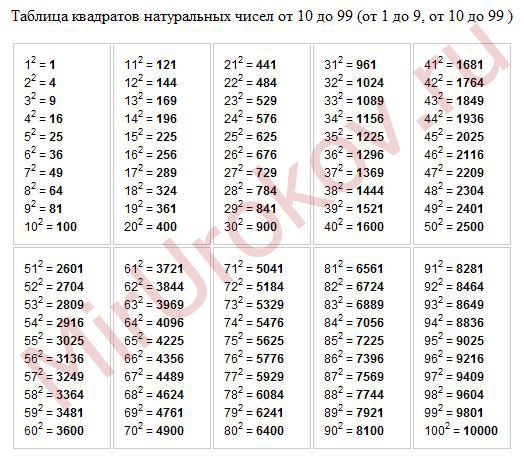 Квадраты и квадратные корни > Квадраты и квадратные корни. Упражнение 3.9. > Вопрос 6

Вопрос 6 Квадраты и квадратные корни Упражнение 3.9

Используя таблицу квадратных корней, найдите квадратные корни из следующего:

540

Ответ:

Из таблицы Square Croot. Используя таблицу квадратных корней, найдите квадратные корни из следующего: 7

Используя таблицу квадратных корней, найдите квадратные корни из следующих чисел: 15

Используя таблицу квадратных корней, найдите квадратные корни следующего:74

Используя таблицу квадратных корней, найдите квадратные корни следующего:82

Используя таблицу квадратных корней, найдите квадратные корни следующего:198

Используя таблицу квадратных корней, найдите квадратные корни следующего числа: 8700

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Квадраты и квадратные корни Упражнение 3. 1

Квадраты и квадратные корни Упражнение 3.2

Квадраты и квадратные корни Упражнение 3.3

квадраты и квадратные корни упражнения 3.4

Квадраты и квадратные корни упражнения 3,5

Квадраты и квадратные корни упражнения 3.6

Упражнения и квадратные корни и квадратные корни и квадратные упражнения 3.9

.

Рациональные числа

Степени

Квадраты и квадратные корни

Куб и кубические корни

Игра с числами

Алгебраические выражения и тождества

Факторизация

Отдел алгебраических выражений

Линейное уравнение в одной переменной

Прямые и обратные вариации

Время и работа

Процент

Скидки на прибыль и добавленная стоимость

Проценты

Понимание соревнования. Понимание фигур Четырехугольники

Понимание фигур Специальные типы четырехугольников

Практическая геометрия

Визуализация фигур

Площадь трапеции и многоугольника

Объем Площадь поверхности прямоугольного куба

Площадь поверхности и объем правого кругового цилиндра

Классификация и табулирование данных

Классификация и табулирование данных Графическое представление данных в виде гистограмм

Графическое представление данных В виде круговых диаграмм или круговых диаграмм

Вероятность обработки данных

Знакомство с диаграммами

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Используя таблицу квадратных корней, найдите квадратные корни из следующих 74.

.. Квадраты и квадратные корни. Упражнение 3.1.

Квадраты и квадратные корни. Упражнение 3.2.

Квадраты и квадратные корни. Упражнение 3.3.

Квадраты и квадратные корни. Упражнение 3.4.

Квадраты и квадратные корни. Упражнение 3.5.

Квадраты и квадратные корни. Упражнение 3.6.

Квадраты и квадратные корни. Упражнение 3.7.

Квадраты и квадратные корни. Упражнение 3.8.

Квадраты и квадратные корни. Упражнение 3.9.

• Рациональное число
• Полномочия
• Квадраты и квадратные корни
• Куб и кубические корни
• Игра с числами
• Алгебраические выражения и тождества
• Факторизация
• Отдел алгебраических выражений
• Линейное уравнение с одной переменной
• Прямые и обратные варианты
• Время и работа
• Процент
• Скидка на убыток и налог на добавленную стоимость
• Сложные проценты
• Понимание многоугольников фигур
• Понимание фигур Четырехугольники
• Понимание фигур Специальные типы четырехугольников
• Практическая геометрия
• Визуализация фигур
• Площадь трапеции и многоугольника
• Объем Площадь Прямоугольный Куб
• Площадь поверхности и объем правого кругового цилиндра
• Классификация и табулирование данных
• Классификация и табулирование данных Графическое представление данных в виде гистограмм
• Графическое представление данных в виде круговых диаграмм или круговых диаграмм
• Вероятность обработки данных
• Введение в графики

Главная > РД Шарма Решения Класс 8 Математика > Глава 3. Квадраты и квадратные корни > Квадраты и квадратные корни. Упражнение 3.9. > Вопрос 3

Вопрос 3 Квадраты и квадратные корни Упражнение 3.9

Используя таблицу квадратного корня, найдите квадратные корни из следующего:

74

Ответ:

Из таблицы квадратного корня мы знаем, что

Квадратный корень из 74:

√74 = 8,6023

3

3 корень из 74: 8,602

Стенограмма видео

«привет, дорогие студенты, я сунита наир и я здесь, чтобы помочь тебе сделать эту задачу, которая читается как это с помощью таблицы квадратного корня найдите квадратный корень из следующего число, которое 74 справа поэтому 74 — это число, квадратный корень которого мы должен узнать поэтому, когда у нас есть такая сумма, когда мы нужно использовать таблицу квадратного корня мы сначала начнем с факторизации данного количество с точки зрения его основных факторов, поэтому я имею 74 здесь и я разложу его на множители, так что мой первый главный фактор 2 2 3 — это 6, 2 7 — это 14. так что теперь у меня есть 37, что вы знаете, простое число так что нет другого фактора, так что я буду поставить 37 и сбить 1 здесь все в порядке ок так что теперь 74 равно 74 равно 2 на 37 вправо мы пишем, что здесь 74 равно 2 из 37 поэтому, если мне нужно найти квадратный корень из 74 мне нужно найти квадратный корень из правая сторона тоже сейчас это сделаю разделить как корень 2 на корень 37 все прямо сейчас у меня из таблицы квадратного корня закинул сюда эти цифры квадратный корень из 2 и квадратный корень из 37 так позвольте мне использовать их, чтобы найти товар так что у меня здесь 1.414 умножить на шесть целых ноль восемь три так что позвольте мне сделать умножение с этой стороны шесть целых ноль восемь три умножить на один балл четыре один четыре так четыре тройки 12 фури 32 и 133 шесть четверок равно 24. так вот у меня тот самый номер 6083 потому что это умножается на 1 и здесь у меня тот же номер, что и первый ряд, потому что он снова умножается на 4 так что будет 2 3 3 4 2 2 4 3 3 2 и последняя строка будет 1 нет 6 0 8 3 теперь я складываю их и получаю два шесть восемнадцать три и три шесть и один семь и четыре одиннадцать ну это будет десять и десять двадцать ноль нести два это шесть и 8 хорошо, это мой произведение так и сколько знаков после запятой я шесть знаков после запятой, так что это мой отвечать восемь целых шесть ноль два я округлю до третьего десятичный разряд так что я надеюсь, что вы поняли решение пожалуйста, напишите комментарий в комментарии раздел и регулярно посещайте наш канал для большего количества домашних заданий подписывайтесь на наш канал, если найдете это полезно спасибо»

Связанные вопросы

Используя таблицу квадратных корней, найдите квадратные корни из следующего: 7

Используя таблицу квадратных корней, найдите квадратные корни из следующих чисел: 15

Используя таблицу квадратных корней, найдите квадратные корни следующего:82

Используя таблицу квадратных корней, найдите квадратные корни следующего:198

Используя таблицу квадратных корней, найдите квадратные корни следующего: 540

Используя таблицу квадратных корней, найдите квадратные корни следующего числа: 8700

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнения квадратов и квадратных корней 3.

No related posts.