Мерзляк 6 класс — § 8. Сокращение дробей
- Ответы к учебнику для 6 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Что называют сокращением дроби?
Сокращением дроби называют деление числителя и знаменателя на их общий делитель, отличный от 1.
2. Какую дробь называют несократимой?
Несократимая дробь — это дробь, у которой числитель и знаменатель являются взаимно простыми числами.
3. На какое число надо сократить дробь, чтобы получилась несократимая дробь?
Чтобы получилась несократимая дробь, надо разделить числитель и знаменатель дроби на их наибольший общий делитель (НОД).
Решаем устно
1. Объясните, почему верно равенство:
1)
Равенство верно потому, что если умножить числитель и знаменатель первой дроби на число 3, то получиться вторая дробь:
2)
Равенство верно потому, что если разделить числитель и знаменатель первой дроби на число 6, то получиться вторая дробь:
2. Сколько двенадцатых частей:
Сколько двенадцатых частей:
1) в — три двенадцатых части, так как ;
2) в — четыре двенадцатых части, так как ;
3) в — девять двенадцатых частей, так как ;
4) в — десять двенадцатых частей, так как ;
5) в — восемнадцать двенадцатых частей, так как .
3. Сколько сотых частей:
1) в — десять сотых части, так как ;
2) в — пятнадцать сотых части, так как ;
3) в — двадцать восемь сотых частей, так как ;
4) в — двадцать шесть сотых частей, так как ;
5) в — шестьдесят две сотых частей, так как .
4. Какую часть года составляет:
Мы знаем, что всего в году 12 месяцев. Значит:
Значит:
1) 1 месяц — это часть года.
2) 2 месяца — это часть года.
3) 6 месяцев — это часть года.
5. Сколько граммов составляет:
Мы знаем, что 1 кг = 1 000 грамм.
1) кг = 1 000 : 2 = 500 г;
2) кг = 1 000 : 4 = 250 г;
3) кг = 1 000 : 8 = 125 г;
4) кг = 1 000 : 5 • 2 = 200 •2 = 400 г
6. Сократимой или несократимой дробью является значение выражения ?
1) Сумма цифр числителя дроби 4 563 равна 4 + 5 + 6 + 3 = 18. Это число делится нацело на 9. Значит числитель нацело делится на 9.
2) Знаменатель дроби 10³ — 1 = 1 000 — 1 = 999. Сумма цифр этого числа 9 + 9 + 9 = 27. Значит и знаменатель нацело делится на 9.
3) Если и числитель, и знаменатель можно нацело поделить на одно и то же число, то дробь является сократимой.
Ответ: да, выражение сократимо.
Упражнения
210. Сократите дробь:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
211. Сократите дробь:
Сократите дробь:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
212. Какие из дробей несократимы?
— несократимая дробь, так как у числителя и знаменателя нет общих делителей, кроме единицы.
— сократимая дробь, так как и числитель, и знаменатель можно разделить на 7.
— сократимая дробь, так как и числитель, и знаменатель можно разделить на 3.
— несократимая дробь, так как у числителя и знаменателя нет общих делителей, кроме единицы.
— сократимая дробь, так как и числитель, и знаменатель можно разделить на 4.
— несократимая дробь, так как у числителя и знаменателя нет общих делителей, кроме единицы.
Ответ: несократимыми являются дроби: .
213. Найдите среди дробей несократимые.
— сократимая дробь, так как и числитель, и знаменатель можно разделить на 5.
— сократимая дробь, так как и числитель, и знаменатель можно разделить на 3.
— несократимая дробь, так как у числителя и знаменателя нет общих делителей, кроме единицы.
— несократимая дробь, так как у числителя и знаменателя нет общих делителей, кроме единицы.
— сократимая дробь, так как и числитель, и знаменатель можно разделить на 2.
— несократимая дробь, так как у числителя и знаменателя нет общих делителей, кроме единицы.
Ответ: несократимыми являются дроби: .
214. Запишите десятичную дробь к виде обыкновенной дроби и результат, если возможно, сократите:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
215. Найдите среди данных дробей равные между собой. Запишите соответствующие равенства.
1)
, так как
, так как и
2)
, так как и
, так как
216. Найдите среди дробей равные между собой и запишите соответствующие равенства.
, так как и
, так как
217. Какую часть часа составляют:
Какую часть часа составляют:
1 час = 60 минут. Значит:
1) 4 мин = часа, так как
2) 10 мин = часа, так как
3) 36 мин = часа, так как
4) 54 мин = часа, так как
5) 72 мин = часа, так как
218. Какую часть суток составляют:
1 сутки = 24 часа. Значит:
1) 3 ч = суток, так как
2) 8 ч = суток, так как
3) 12 ч = суток, так как
4) 16 ч = суток, так как
5) 21 ч = суток, так как
219. Какую часть развёрнутого угла составляет угол, градусная мера которого равна:
Развёрнутый угол составляет 180°. Значит:
1) 4° = части развёрнутого угла, так как
2) 12° = части развёрнутого угла, так как
3) 27° = части развёрнутого угла, так как
4) 126° = части развёрнутого угла, так как
5) 153° = части развёрнутого угла, так как
220. Какую часть прямого угла составляет угол, градусная мера которого равна:
Прямой угол составляет 90°. Значит:
Значит:
1) 2° = части прямого угла, так как
2) 15° = части прямого угла, так как
3) 36° = части прямого угла, так как
4) 75° = части прямого угла, так как
5) 54° = части прямого угла, так как
221. Выполните действие и сократите результат:
1)
2)
3)
4)
222. Выполните действие и сократите результат:
1)
2)
3)
4)
223. Запишите все правильные несократимые дроби со знаменателем 18.
Для того, чтобы дробь со знаменателем 18 была несократимой, надо подобрать такой числитель, который будет взаимно простым числом с 18. При этом числитель должен быть меньше числа 18, чтобы дробь была правильной.
224. Запишите все неправильные несократимые дроби с числителем 20.
Для того, чтобы дробь с числителем 20 была несократимой, надо подобрать такой знаменатель, который будет взаимно простым числом с 20. При этом знаменатель должен быть меньше или равен числу 20, чтобы дробь была неправильной.
При этом знаменатель должен быть меньше или равен числу 20, чтобы дробь была неправильной.
225. Сократите:
226. Сократите:
227. Сократите (буквами обозначены натуральные числа):
228. Дробь сократили на 2 и получили дробь . Найдите значения x и y.
Условие задачи можно записать так:
У равных дробей числители и знаменатели равны между собой. Можно составить уравнения:
х : 2 = 2
х = 2 • 2
х = 4
6 : 2 = y
y = 6 : 2
y = 3
Ответ: х = 4, y = 3.
229. После сокращении дроби на 3 получили дробь . Найдите значения а и b.
Условие задачи можно записать так:
У равных дробей числители и знаменатели равны между собой. Можно составить уравнения:
21 : 3 = b
b = 21 : 3
b = 7
a : 3 = 4
a = 4 • 3
a = 12
Ответ: a = 12, b = 7.
Упражнения для повторения
230. Запишите, используя каждую цифру от 0 до 9 только один раз:
Запишите, используя каждую цифру от 0 до 9 только один раз:
1) наименьшее число, кратное 2:
1 023 456 798 — Это число чётное, а значит оно кратно 2.
2) наибольшее число, кратное 18.
9 876 543 210 — Это число чётное, а значит оно кратно 2. Кроме того, сумма чисел данного числа делится на 9, то есть число кратно 9. Значит число кратно и числу 18, так как 2 • 9 = 18.
231. К какому числу надо прибавить 5,7, чтобы произведение полученной суммы и числа 3,6 было равно 120,6?
Пусть х — неизвестное число. Составим и решим уравнение:
Ответ: Неизвестное число равно 27,8.
232. Из какого числа надо вычесть 3,8, чтобы произведение полученной разности и числа 5,5 было равно 34,1?
Пусть х — неизвестное число. Составим и решим уравнение:
Ответ: Неизвестное число равно 10.
Готовимся к изучению новой темы
233. Расположите в порядке возрастания дроби:
234. Сравните:
Сравните:
1) , так как знаменатели дробей одинаковы, а числитель первой дроби больше, чем числитель второй дроби.
2) , так как числители дробей одинаковы, а знаменатель первой дроби больше, чем знаменатель второй дроби.
3) , так как — это правильная дробь, а правильная дробь всегда меньше единицы.
4) , так как — это неправильная дробь, а неправильная дробь может быть только больше либо равна единицы, но наша дробь не равна единице, то есть она больше 1.
5) , так как — это правильная дробь, а правильная дробь всегда меньше единицы.
6) , так первая дроби правильная, а вторая — неправильная, а правильная дробь всегда меньше неправильной.
7) , так как , а единица с правильной дробью всегда меньше, чем 2 целых.
8) , так как , а две целых с правильной дробью всегда больше, чем 2 целых.
Задача от мудрой совы
235. Из старинной книги выпала часть страниц, идущих подряд. Первая выпавшая страница имеет номер 251, а номер последней записан теми же цифрами в другом порядке. Какой номер последней выпавшей страницы?
Какой номер последней выпавшей страницы?
- Теми же цифрами можно записать только 2 трёхзначных числа, больших, чем 251. Это числа: 512 и 521.
- Номер страницы 251 — это нечётный номер, значит на обратной стороне листа будет располагаться чётный номер.
- На последнем выпавшем листе также будет располагаться две страницы — первая с нечётным номером, а вторая (она же и последняя выпавшая страница) — с чётным.
- Значит последняя выпавшая страница будет обозначена чётным номером. Это число 512.
Ответ: номер последней выпавшей страницы — 512.
- Ответы к учебнику для 6 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Сокращение дробей — презентация по математике 6 класс
Слайды и текст этой презентации
| Слайд №1 | |
| Сложение и вычитание дробей с разными знаменателями. 6 классматематика Урок №23-25 Сокращение дробей 10. | |
| Слайд №2 | |
| Цели: 10.05.2012 ввести понятие сокращения дробей и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби 2 www.konspekturoka.ru | |
| Слайд №3 | |
| На основании чего мы можем умножать числитель и знаменатель дроби? На основании основного свойства дроби мы можем умножать числитель и знаменатель дроби Вспомним! 10.05.2012 3 www.konspekturoka.ru | |
| Слайд №4 | |
| На какие числа можно разделить числитель и знаменатель дроби? На 2, 3, 4, 6, 12. Если разделить числитель и знаменатель дроби на наибольший общий делитель, на 12. Какая дробь получится? = = = — такое преобразование называется сокращением дроби. Определение. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.  При сокращении дроби ее числовое значение не меняетеизменилась только ее запись. Изучение нового материала 10.05.2012 4 www.konspekturoka.ru | |
| Слайд №5 | |
Если дробь больше сократить нельзя, то ее называют несократимой Они взаимно простые. Определение. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой. 10.05.2012 5 www.konspekturoka.ru | |
| Слайд №6 | |
| Способы сокращения дробей: 1. Сократить числитель и знаменатель на их НОД. = = 2. Последовательно сокращать на общие делители. = = = = 3. Разложить числитель и знаменатель на множители, а потом сократить. = = 1 1 1 1 1 1 10.05.2012 6 www.konspekturoka.ru | |
| Слайд №7 | |
Назвать несократимую дробь. Почему эти дроби являются несократимыми? 10.05.2012 7 www.konspekturoka.ru | |
| Слайд №8 | |
| 10.05.2012 www.konspekturoka.ru 8 Назовите наибольший делитель числителя и знаменателя. Разделите числитель и знаменатель данной дроби на их общий делитель. Как называется получившаяся дробь? = = = = наибольший делитель числителя и знаменателя — 2 наибольший делитель числителя и знаменателя — 3 наибольший делитель числителя и знаменателя -70а наибольший делитель числителя и знаменателя – 7п | |
| Слайд №9 | |
| Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин? 10.05.2012 9 www.konspekturoka.ru | |
| Слайд №10 | |
| Сократите дробь: Общий делитель 3с. = = = Числитель и знаменатель дроби представим в виде множителей: = Назовите общий делитель числителя и знаменателя: = Общий делитель 25b.  = Общий делитель 3bc. 10.05.2012 10 www.konspekturoka.ru | |
| Слайд №11 | |
| 10.05.2012 www.konspekturoka.ru 11 Сократите дроби: | |
| Слайд №12 | |
| Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел. 1 и 3; 1 и 10; 1 и 12; 1 и 13; 1 и 15; 1 и 16; 1 и 39; 3 и 10; 3 и 13; 3 и 16; 10 и 13; 10 и 39; 12 и 13; 13 и 15; 13 и 16; 15 и 16; 16 и 39. 10.05.2012 12 www.konspekturoka.ru | |
| Слайд №13 | |
| Представить в виде обыкновенной несократимой дроби: 0,2 = 0,8 = 0,5 = 0,15 = 0,24 = 0,35 = 0,75 = 0,05 = 0,125 = 0,025 = 0,008 = 0,375 = 10.05.2012 13 www.konspekturoka.ru | |
| Слайд №14 | |
| 10.05.2012 www.  konspekturoka.ru konspekturoka.ru14 Сократите дроби: = = = = = 6 = = 1 | |
| Слайд №15 | |
| 10.05.2012 www.konspekturoka.ru 15 Сократите дроби: 2 = = = = = = = = = 2 | |
| Слайд №16 | |
| Сократите дроби: 3 = = = = = = 10.05.2012 16 www.konspekturoka.ru | |
| Слайд №17 | |
| Сократите дроби: = 4 = = = = = = = 10.05.2012 17 www.konspekturoka.ru | |
| Слайд №18 | |
| Какую часть килограмма составляют 125 г, 250 г, 750 г? 125 г = 250 г = 750 г = 10.05.2012 18 www.konspekturoka.ru | |
| Слайд №19 | |
| Ответить на вопросы: 10.05.2012 19 www.  konspekturoka.ru konspekturoka.ruЧто значит сократить дробь? Что меняется при сокращении дробей? В каком случае дробь будет несократимой? Приведите примеры несократимой дроби. На каком свойстве основано сокращение дробей? | |
- Автор: Виктория
- Распечатать
Оцените статью:
(2 голоса, среднее: 4.5 из 5)
Поделитесь с друзьями!Большой сборник презентаций в помощь школьнику.
закрыть
Скопируйте этот код и вставьте его на своем сайте:
<div><strong><a href=»https://volna.org/matematika/sokrashchieniie_drobiei.html»
title=»Сокращение дробей — презентация по математике 6 класс» target=»_blank»
>Сокращение дробей — презентация по математике 6 класс</a></strong><iframe
src=»https://volna. org/iframe/673/» frameborder=»0″ marginwidth=»0″ marginheight=»0″
scrolling=»no»
allowfullscreen></iframe></div>
org/iframe/673/» frameborder=»0″ marginwidth=»0″ marginheight=»0″
scrolling=»no»
allowfullscreen></iframe></div>
Сокращение дробей 6 класс презентация, доклад, проект
6 класс
Сокращение дробей
Повторение
Найдите наибольший общий делитель
НОД(24; 40)=
НОД(14, 25)=
Д(24)={1, 2, 3, 4, 6, 8, 12, 24}
8
Д(14)={1, 2, 7, 14}
1
14 и 25 взаимно простые числа
Повторение
Найдите наибольший общий делитель методом перебора
НОД(4; 6)=
2
НОД(12;15 )=
3
НОД(12;25 )=
1
НОД(17;51 )=
17
НОД(26; 39 )=
13
НОД(70; 140 )=
70
НОД(27; 36 )=
9
НОД(25; 31 )=
1
НОД(125; 1000 )=
125
НОД(15; 16 )=
1
12 и 25, 15 и 16, 25 и 31 взаимно простые числа
Если числитель и знаменатель дроби
умножить
на одно и то же натуральное число, то получится равная ей дробь.
или разделить
Сокращение дроби
Приведение дроби к новому знаменателю
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
Сокращение дроби
2
9
1
10
2
9
Несократимая дробь
Эту дробь сократить нельзя, так как её числитель и знаменатель
взаимно простые числа.
НОД(2;9) = 1
Сокращение дроби на
наибольший общий делитель.
2
3
НОД(210; 315)
210
315
= 10*21
= 2*5*3*7
= 2*3*5*7
= 5*63
= 5*7*9
= 3*3*5*7
= 5*3*7 = 105
Последовательное сокращение дроби
70
105
14
21
2
3
Верно ли, что дробь при таком сокращении становится все меньше и меньше???
Найди несократимые дроби. Сделай клик мышью
Сделай клик мышью
по букве рядом с несократимыми дробями.
Р
А
А
Д
У
Г
Ш
Я
0,7
0,23
0,8
0,1
М
0,25
Запиши множество значений переменной х, при
которых дробь является правильной
несократимой дробью.
1
2
3
4
5
6
7
8
9
10
11
12
13
Запиши множество значений переменной у, при
которых дробь является неправильной
несократимой дробью.
1
2
3
4
5
6
7
8
9
10
11
12
13
17
14
15
16
Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой 24 такие же детали за 15 ч.
Какой из них тратил на изготовление 1 детали больше времени?
Найдите скорость работы каждого рабочего.
Из 20 м ткани сшили 8 одинаковых платьев для взрослых , а из 12 м ткани сшили 8 детских платьев. Сколько метров ткани пошло на одно детское платье и сколько на одно платье для взрослых?
Из 42 м полотна сшили 10 пододеяльников,
а из 33 м – 15 простыней. Сколько полотна идет на комплект, в который входит 1 простыня и 1 пододеяльник.
12,8км/ч
Собственная скорость катера 12,8 км/ч, а скорость течения 1,7км/ч. Найдите скорость катера по течению и против течения.
12,8км/ч
Против течения
По течению
1,7км/ч
vпо теч=22,7км/ч
1,9км/ч
По течению
Скорость теплохода по течению равна 22,7км/ч.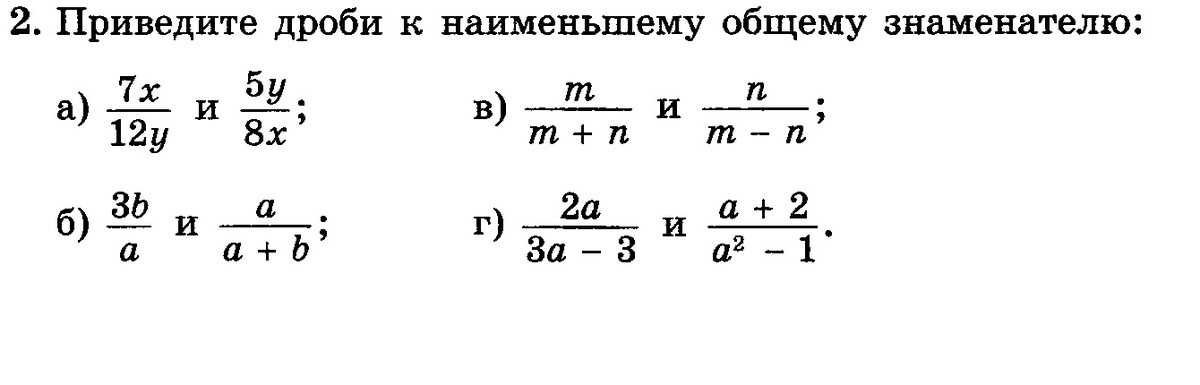
Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 1,9км/ч.
Путешественник проплыл против течения реки на моторной лодке 3ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч?
24 км/ч
Против течения
По течению
3 км/ч
3ч
?ч
Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?
28 км/ч
75км
Против течения
По течению
?ч
25ч
Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч.
Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч.
Найдите длину всего пути туриста на теплоходе.
Показать
? км
1,2ч
3,6ч
Скачать презентацию
эквивалентных дробей — определение, как найти эквивалентные дроби?
Эквивалентные дроби могут быть определены как дроби, которые могут иметь разные числители и знаменатели, но представляют одно и то же значение. Например, 9/12 и 6/8 являются эквивалентными дробями, потому что в упрощенном виде обе равны 3/4.
Все эквивалентные дроби сводятся к одной и той же дроби в их простейшей форме, как показано в приведенном выше примере. Изучите данный урок, чтобы лучше понять, как найти эквивалентные дроби и как проверить, эквивалентны ли данные дроби.
| 1. | Что такое эквивалентные дроби? |
| 2. | Как найти равные дроби? |
3. | Как узнать, эквивалентны ли две дроби? |
| 4. | Таблица эквивалентных дробей |
| 5. | Часто задаваемые вопросы об эквивалентных дробях |
Что такое эквивалентные дроби?
Две или более дроби называются эквивалентными, если они равны одной и той же дроби в упрощенном виде. Например, эквивалентными дробями 1/5 являются 5/25, 6/30 и 4/20, которые при упрощении дают одну и ту же дробь, то есть 1/5.
Равнозначные дроби Определение
Равнозначные дроби определяются как те дроби, которые равны одному и тому же значению независимо от их числителей и знаменателей. Например, и 6/12, и 4/8 равны 1/2 в упрощенном виде, что означает, что они эквивалентны по своей природе.
Эквивалентные дроби Примеры
Вот несколько примеров эквивалентных дробей.
Пример: 1/2, 2/4, 3/6 и 4/8 — эквивалентные дроби. Посмотрим, насколько их значения равны. Мы будем представлять каждую из этих дробей в виде кругов с заштрихованными частями. Можно видеть, что заштрихованные части на всех рисунках представляют одну и ту же часть, если рассматривать ее как единое целое.
Мы будем представлять каждую из этих дробей в виде кругов с заштрихованными частями. Можно видеть, что заштрихованные части на всех рисунках представляют одну и ту же часть, если рассматривать ее как единое целое.
Здесь мы видим, что количество заштрихованных частей одинаково во всех кругах. Следовательно, 1/2, 2/4, 3/6 и 4/8 — эквивалентные дроби.
Как найти равные дроби?
Равные дроби можно записать путем умножения или деления числителя и знаменателя на одно и то же число. Вот почему эти дроби при упрощении сокращаются до одного и того же числа. Давайте поймем два способа, которыми мы можем сделать эквивалентные дроби:
- Умножить числитель и знаменатель на одно и то же число.
- Разделите числитель и знаменатель на одно и то же число.
Умножение числителя и знаменателя на одно и то же число
Чтобы найти эквивалентные дроби для любой заданной дроби, умножьте числитель и знаменатель на одно и то же число. Например, чтобы найти эквивалентную дробь 3/4, умножьте числитель 3 и знаменатель 4 на одно и то же число, скажем, на 2. Таким образом, 6/8 — это эквивалентная дробь 3/4. Мы можем найти некоторые другие эквивалентные дроби, умножив числитель и знаменатель данной дроби на одно и то же число.
Например, чтобы найти эквивалентную дробь 3/4, умножьте числитель 3 и знаменатель 4 на одно и то же число, скажем, на 2. Таким образом, 6/8 — это эквивалентная дробь 3/4. Мы можем найти некоторые другие эквивалентные дроби, умножив числитель и знаменатель данной дроби на одно и то же число.
- 3/4 = \(\dfrac{3 \times 3}{4 \times 3}\) = 9/12
- 3/4=\(\dfrac{3 \times 4}{4 \times 4}\) = 12/16
- 3/4=\(\dfrac{3 \times 5}{4 \times 5}\) =15/20
Таким образом, эквивалентными дробями числа 3/4 являются 6/8, 9/12, 12/16 и 15/20.
Разделить числитель и знаменатель на одно и то же число
Чтобы найти эквивалентные дроби для любой заданной дроби, разделите числитель и знаменатель на одно и то же число. Например, чтобы найти эквивалентную дробь 72/108, мы сначала найдем их общие делители. Мы знаем, что 2 является общим делителем как 72, так и 108. Следовательно, эквивалентную дробь 72/108 можно найти, разделив ее числитель и знаменатель на 2. Таким образом, 36/54 является эквивалентной дробью 72/108. Давайте посмотрим, как дробь еще больше упрощается:
Таким образом, 36/54 является эквивалентной дробью 72/108. Давайте посмотрим, как дробь еще больше упрощается:
- 2 является общим делителем 36 и 54. Таким образом, 36/54= \(\dfrac{36 \div 2}{54 \div 2}\)= 18/27
- Опять же, 3 является общим делителем 18 и 27. Таким образом, 18/27= \(\dfrac{18 \div 3}{27 \div 3}\)= 6/9
- Опять же, 3 является общим делителем 6 и 9. Таким образом, 6/9=\(\dfrac{6 \div 3}{9 \div 3}\)= 2/3
Следовательно, несколько эквивалентных дробей числа 72/108 равны 36/54, 18/27, 6/9 и 2/3. Здесь 2/3 — это упрощенная форма 72/108, поскольку у 2 и 3 нет общего делителя (кроме 1).0005
Как узнать, эквивалентны ли две дроби?
Нам нужно упростить данные дроби, чтобы узнать, эквивалентны они или нет. Упрощение для получения эквивалентных чисел может быть выполнено до такой степени, что и числитель, и знаменатель должны быть целыми числами. Существуют различные методы определения эквивалентности данных дробей. Вот некоторые из них:
Вот некоторые из них:
- Приравняв знаменатели.
- Нахождение десятичной формы обеих дробей.
- Метод перекрестного умножения.
- Визуальный метод.
Определим, являются ли 2/6 и 3/9 эквивалентными дробями, каждым из этих методов.
Приведение знаменателей к одному
Знаменатели дробей 2/6 и 3/9 равны 6 и 9. Наименьшее общее кратное (НОК) знаменателей 6 и 9 равно 18. Приведем знаменатели обеих дроби 18, умножив их на подходящие числа.
- 2/6=\(\dfrac{2 \times 3}{6 \times 3}\)= 6/18
- 3/9=\(\dfrac{3 \times 2}{9 \times 2}\)= 6/18
Мы можем заметить, что обе дроби эквивалентны одной и той же дроби 6/18. Таким образом, данные дроби равнозначны.
Примечание: Если дроби НЕ эквивалентны, мы можем проверить большую или меньшую дробь, взглянув на числитель обеих дробей. Следовательно, этот метод также может быть использован для сравнения дробей.
Нахождение десятичной формы обеих дробей
Давайте найдем десятичную форму обеих дробей 2/6 и 3/9, чтобы увидеть, дают ли они одно и то же значение.
- 2/6= 0,3333333…
- 3/9= 0,3333333…
Десятичные значения обеих дробей одинаковы и , следовательно, они эквивалентны.
Метод перекрестного умножения
Чтобы определить, эквивалентны ли 2/6 и 3/9, мы перемножаем их. Если оба произведения одинаковы, дроби равны.
Поскольку оба произведения здесь равны 18, данные дроби называются эквивалентными дробями.
Визуальный метод
Давайте изобразим каждую из дробей 2/6 и 3/9 на одинаковых фигурах и проверим, равны ли заштрихованные части обеих.
Мы видим, что заштрихованные части обоих кругов отображают одно и то же значение. Другими словами, можно видеть, что заштрихованные части на обеих фигурах представляют собой одну и ту же часть, если рассматривать ее как единое целое. Следовательно, данные дроби равнозначны.
Таблица эквивалентных дробей
Диаграммы и таблицы часто используются для лучшего представления концепций, поскольку они служат удобным справочником для расчетов и их легче понять. Опорные диаграммы и таблицы, подобные приведенной ниже, облегчают учащимся понимание эквивалентных дробей. Давайте используем следующую таблицу, чтобы найти эквивалентные дроби 1/4.
Опорные диаграммы и таблицы, подобные приведенной ниже, облегчают учащимся понимание эквивалентных дробей. Давайте используем следующую таблицу, чтобы найти эквивалентные дроби 1/4.
Из этой таблицы видно, что эквивалентные дроби 1/4: 2/8, 3/12, 4/16,…
Советы по эквивалентным дробям
- Две дроби называются эквивалентными, если их значения (десятичное число/графическое значение) совпадают.
- Обычно мы умножаем числитель и знаменатель дроби на одно и то же число, чтобы получить эквивалент дроби.
- ‘Метод перекрестного умножения’ используется для определения того, эквивалентны ли какие-либо две дроби.
- «Приведение знаменателей в соответствие» — еще один метод, используемый для определения эквивалентности двух или более дробей.
☛ Статьи по теме
- Сокращение дробей
- Умножение дробей
- Сложение дробей
- Деление дробей
- Упрощение дробей
- Правильные дроби
Часто задаваемые вопросы об эквивалентных дробях
Что такое эквивалентные дроби в математике?
Две или более фракций считаются эквивалентными фракциями , если они равны одному и тому же значению независимо от их числителей и знаменателей. Например, 2/4 и 8/16 являются эквивалентными дробями, потому что при упрощении они уменьшаются до 1/2.
Например, 2/4 и 8/16 являются эквивалентными дробями, потому что при упрощении они уменьшаются до 1/2.
Каковы примеры эквивалентных дробей?
Может быть много примеров эквивалентных дробей, например, 8/12 и 6/9 являются эквивалентными дробями, потому что при упрощении они сводятся к одной и той же дроби (2/3). Точно так же 4/7 и 28/49 также являются эквивалентными дробями.
Как найти равные дроби?
Если данные дроби упростить и привести к обыкновенной дроби, то их можно назвать эквивалентными дробями. Помимо этого, существуют различные другие методы определения того, являются ли данные дроби эквивалентными или нет. Вот некоторые из них:
- Приравняв знаменатели.
- Нахождением десятичной формы обеих дробей.
- Метод перекрестного умножения.
- Визуальный метод.
Что означает равенство двух дробей?
Когда две дроби эквивалентны, это означает, что они равны одному и тому же значению независимо от их различных числителей и знаменателей. Другими словами, когда они упрощаются, они сводятся к одной и той же дроби.
Другими словами, когда они упрощаются, они сводятся к одной и той же дроби.
Почему равные дроби важны?
Эквивалентные дроби помогают нам складывать, вычитать, умножать, делить дроби и сравнивать дроби, что помогает нам решать многие задачи в реальном времени.
Что такое эквивалентная неправильная дробь?
Эквивалентная неправильная дробь означает эквивалентную дробь в неправильной форме. Дробь называется неправильной, если ее числитель больше знаменателя. Например, 3/2 — неправильная дробь, равная 9/6.
Как вычислить эквивалентные дроби?
Любые две дроби могут считаться эквивалентными, если они равны одному и тому же значению. Существуют различные способы узнать, равны ли дроби. Основной метод заключается в их уменьшении. Если они сведены к одной и той же дроби, они считаются эквивалентными.
Как написать эквивалентные дроби?
Равные дроби можно записать путем умножения или деления числителя и знаменателя на одно и то же число. Вот почему эти дроби при упрощении сокращаются до одного и того же числа. Например, давайте запишем эквивалентную дробь для 2/3. Умножим числитель и знаменатель на 4 и получим (2 × 4)/(3 × 4) = 8/12. Следовательно, 8/12 и 2/3 равнозначные дроби.
Вот почему эти дроби при упрощении сокращаются до одного и того же числа. Например, давайте запишем эквивалентную дробь для 2/3. Умножим числитель и знаменатель на 4 и получим (2 × 4)/(3 × 4) = 8/12. Следовательно, 8/12 и 2/3 равнозначные дроби.
Дайте 2 эквивалентные дроби для 6/8.
Чтобы записать эквивалентную дробь для 6/8, умножим числитель и знаменатель на 2, и мы получим (6 × 2)/(8 × 2) = 12/16. Следовательно, 6/8 и 12/16 — равнозначные дроби. Теперь получим другую эквивалентную дробь для 6/8, разделив ее на обычное число, скажем, на 2. После деления числителя и знаменателя на 2 получим (6 ÷ 2)/(8 ÷ 2) = 3 /4. Следовательно, 6/8 и 3/4 — равнозначные дроби.
Какие дроби равны 1/4?
Чтобы найти эквивалентные дроби 1/4, умножим числитель и знаменатель на одно и то же число. Итак, мы умножим его на 2, что будет (1 × 2)/(4 × 2) = 2/8. Теперь, чтобы найти другую эквивалентную дробь для 1/4, давайте умножим ее на 3. Это будет (1 × 3)/(4 × 3) = 3/12. Итак, мы получаем две равнозначные дроби для 1/4, а это 2/8 и 3/12.
Дайте две эквивалентные дроби для 2/3.
Чтобы найти эквивалентные дроби 2/3, умножим числитель и знаменатель на одно и то же число. Итак, мы умножим его на 5, что будет (2 × 5) / (3 × 5) = 10/15. Теперь, чтобы найти другую эквивалентную дробь для 2/3, давайте умножим ее на 6. Это будет (2 × 6)/(3 × 6) = 12/18. Итак, мы получаем две равнозначные дроби для 2/3, а это 10/15 и 12/18.
Mr. Nussbaum Math Дроби Действия
Этот раздел содержит действия и ресурсы, связанные с фракциями.
Фракция Pal — Онлайн
Описание: Эти инновационные программы позволяют учащимся интерактивно работать с программой для решения математических задач. Программа шаг за шагом знакомит учащихся с математическими задачами, разбивая операции деления, уравнений и дробей на ряд последовательных, более простых математических задач в стиле интервью. Они работают на всех компьютерах и планшетах.
Они работают на всех компьютерах и планшетах.
Тип: Математическая мастерская
Формат: онлайн-активность
Уровни оценок: 4, 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
EZ Fractions — сложение, вычитание, умножение и деление дробей
Описание: EZ Fractions — это популярный семинар по дробям, который позволяет учащимся выполнять операции с дробями в упрощенной среде, которая помогает им переименовывать, уменьшать, перекрестно умножать или находить LCM и GCF. Настраиваемый! Это похоже на наш Fraction Workshop, но некоторым пользователям такой формат нравится больше.
Тип: Математическая мастерская
Формат: онлайн-активность
Уровни оценок: 4, 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Мастерская фракций — онлайн
Описание: Fraction Workshop — это удивительное приложение с функцией перетаскивания, которое позволяет учащимся выполнять любые операции с дробями на онлайн-сцене с помощью вспомогательных инструментов. Мастерская дробей позволяет пользователям практиковаться в упорядочивании, уменьшении, сложении, вычитании, умножении и делении дробей и смешанных чисел. Наша система перетаскивания упрощает заказ и организацию номеров. Выберите количество задач для отработки, конкретный навык для отработки и нажмите «Начать». Решите задачу на сцене и перетащите правильные числа в поле для ответа. Система сразу укажет, правильный ли ваш ответ. Когда закончите, распечатайте сводку результатов. Студенты могут использовать инструмент калькулятора или инструмент визуализации, чтобы помочь им работать над проблемами. Инструмент визуализации превращает конкретную математическую задачу в изображение. Это помогает учащимся лучше «видеть» проблему.
Выберите количество задач для отработки, конкретный навык для отработки и нажмите «Начать». Решите задачу на сцене и перетащите правильные числа в поле для ответа. Система сразу укажет, правильный ли ваш ответ. Когда закончите, распечатайте сводку результатов. Студенты могут использовать инструмент калькулятора или инструмент визуализации, чтобы помочь им работать над проблемами. Инструмент визуализации превращает конкретную математическую задачу в изображение. Это помогает учащимся лучше «видеть» проблему.
Тип: Математическая мастерская
Формат: онлайн-активность
Уровни оценок: 3, 4, 5, 6
Стандарты СС: 3. NF.A.3, 4.NF.A.1, 4.NF.A.2, 4.NF.A.3, 4.NF.B.4, 4.NF.C.5, 5. NF.A.1, 5.NF.B.3, 5.NF.B.4, 5.NF.B.7
NF.A.3, 4.NF.A.1, 4.NF.A.2, 4.NF.A.3, 4.NF.B.4, 4.NF.C.5, 5. NF.A.1, 5.NF.B.3, 5.NF.B.4, 5.NF.B.7
Ланг. Стандарты искусства:
Пиццерия Тони Фракции — Онлайн-игра
Описание: Tony Fraction — забавная игра, которая усиливает идентификацию, сокращение и эквивалентные дроби. Студенты играют роль Тони, владельца пиццерии, который должен выполнять просьбы своих требовательных клиентов. Клиенты Тони заказывают пиццу с нечетными фракциями начинки, а не только с традиционными «1/2 пепперони и 1/2 обычной». Клиенты Тони обычно заказывают пиццу с дробями, такими как четвертые, шестые, восьмые, двенадцатые и даже шестнадцатые, в зависимости от размера заказанной пиццы. У студентов есть пять минут, чтобы выполнить как можно больше заказов на пиццу и заработать как можно больше денег. ТЕПЕРЬ ИГРАТЬ С ИЛИ БЕЗ ОТСЧЕТА.
Студенты играют роль Тони, владельца пиццерии, который должен выполнять просьбы своих требовательных клиентов. Клиенты Тони заказывают пиццу с нечетными фракциями начинки, а не только с традиционными «1/2 пепперони и 1/2 обычной». Клиенты Тони обычно заказывают пиццу с дробями, такими как четвертые, шестые, восьмые, двенадцатые и даже шестнадцатые, в зависимости от размера заказанной пиццы. У студентов есть пять минут, чтобы выполнить как можно больше заказов на пиццу и заработать как можно больше денег. ТЕПЕРЬ ИГРАТЬ С ИЛИ БЕЗ ОТСЧЕТА.
Тип: Математическая игра
Формат: игра
Уровни оценок: 4, 5, 6
Стандарты СС: 3. НФ.А.3, 4.НФ.А.1
НФ.А.3, 4.НФ.А.1
Ланг. Стандарты искусства:
Обмен песочных долларов — Онлайн-игра
Описание: В игре «Обмен песчаных долларов» вы играете роль храброго маленького морского краба, который должен собирать плоские плоские ежи и их части и бросать их на правильные раковины моллюсков. Время имеет существенное значение! Если вы закончите игру, Обмен песочных долларов наградит вас сертификатом. Если вы закончите игру в течение 200 секунд, вы можете получить сертификат ската, в течение 300 секунд — сертификат мечехвоста, а в течение 600 секунд — сертификат краба-отшельника.
Время имеет существенное значение! Если вы закончите игру, Обмен песочных долларов наградит вас сертификатом. Если вы закончите игру в течение 200 секунд, вы можете получить сертификат ската, в течение 300 секунд — сертификат мечехвоста, а в течение 600 секунд — сертификат краба-отшельника.
Тип: Математическая игра
Формат: Игра
Уровни оценок: 3, 4, 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Фракция Америка — Онлайн игра
Описание: Зажгите Соединенные Штаты цветом, а затем определите, какая часть штатов имеет каждый цвет. Выберите одну из 2, 3, 4, 5, 6, 7 или 8 фракций. Думайте о Соединенных Штатах как об одном большом целом, а о каждом из его штатов (независимо от размера) — как о равной части. Когда закончите, распечатайте красивую карту со всеми правильными дробями. Fraction America — это отличная возможность для учащихся объединить свои навыки дробей с картой Соединенных Штатов. Программа также требует, чтобы учащиеся сокращали дроби до наименьших членов, и будет подсказывать им, когда дроби не сокращаются.
Когда закончите, распечатайте красивую карту со всеми правильными дробями. Fraction America — это отличная возможность для учащихся объединить свои навыки дробей с картой Соединенных Штатов. Программа также требует, чтобы учащиеся сокращали дроби до наименьших членов, и будет подсказывать им, когда дроби не сокращаются.
Тип: Математическая игра
Формат: игра
Уровни оценок: 4, 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Очередь за обедом — Онлайн игра
Описание: Очередь за обедом — это забавная (и забавная) игра, в которой учащиеся тренируются в упорядочивании дробей, десятичных знаков и процентов. Студенты должны расположить знаменитостей и исторических деятелей в очереди за обедом, основываясь на значениях, плавающих в их головах, от наименьшего к наибольшему. Если учащиеся расставят все десять правильно, очередь за обедом плавно переместится в столовую по прямой линии, и они смогут распечатать справку с указанием лидера очереди. При неправильном расположении фигур обеденная очередь будет криво и неэффективно шататься к столовой, тем самым разозлив учителя.
Если учащиеся расставят все десять правильно, очередь за обедом плавно переместится в столовую по прямой линии, и они смогут распечатать справку с указанием лидера очереди. При неправильном расположении фигур обеденная очередь будет криво и неэффективно шататься к столовой, тем самым разозлив учителя.
Тип: Математическая игра — Фокус на десятичных дробях
Формат: игра
Уровни оценок: 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Больше, равно или меньше 1/2? — Классификация фракций
Описание: Это задание требует, чтобы учащиеся классифицировали дроби как <, = или > 1/2. Обеспечивается мгновенная обратная связь.
Обеспечивается мгновенная обратная связь.
Тип: Категоризация
Формат: онлайн-активность
Уровни оценок: 3, 4, 5
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Используйте в качестве оценки в Google Classroom.
Дроби — Сравнение дробей по признакам неравенства и = — Онлайн
Описание. В этом упражнении учащиеся должны использовать знаки <, > и = для сравнения дробей.
В этом упражнении учащиеся должны использовать знаки <, > и = для сравнения дробей.
Тип: Математическая тренировка
Формат: онлайн-активность
Уровни оценок: 3, 4, 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Используйте в качестве оценки в Google Classroom.
ОБНОВЛЕНИЕ ДО MRN365.
 COM
COMЭто задание можно скопировать непосредственно в ваш Google Classroom, где вы можете использовать его для практики, в качестве оценки или для сбора данных.
Узнать больше
ОБНОВИТЬ ДО MRN365.COM
Узнать больше
Не хотите обновляться?
Вы по-прежнему можете купить этот ресурс по отдельности на Учителя платят учителям за .
Щелкните здесь, чтобы купить.
Шестой класс (6 класс) Дроби и отношения Вопросы для тестов и рабочих листов
Из них можно создавать печатные тесты и рабочие листы. Дроби и отношения 6 класс вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Предыдущий Страница 1 из 20 Далее
Выбрать все вопросы Напишите стоимость единицы.200 долларов за 8 часов
25 долларов в час
В классе мисс Джеймс 30 учеников, из них 17 девочек. Напишите соотношение девочек и мальчиков.17:13
Уменьшить дробь.
[математика]27/36[/математика]
- [математика]27/36[/математика]
- [математика]9/12[/математика]
- [математика]7/9[/математика]
- [математика]3/4[/математика]
Какие коэффициенты равны?
- [математика]5/10 и 15/20[/математика]
- [математика] 2/3 и 4/9[/математика]
- [математика]3/4 и 9/12[/математика]
- [математика]13.
 10 и 17.13[/математика]
10 и 17.13[/математика]
[математика]1/2 -: 21/7 =[/математика]
- 3 1/2
- 1/6
- 1/7
- 1/14
[математика]-:[/математика] [математика]=[/математика]
- [математика]5/4[/математика]
- [математика]4/5[/математика]
- [математика]5/9[/математика]
- [математика]9/5[/математика]
 Голосуют 250 студентов.
Голосуют 250 студентов. Кандидат 1 получает 10/50 от общего числа голосов. 904:45 Кандидат 2 получает 9/25 от общего числа голосов.
Кандидат 3 получает 4/10 от общего числа голосов
Кандидат 4 получает 5/125 от общего числа голосов.
Каков правильный порядок расположения кандидатов от наименьшего количества голосов к наибольшему?
- Кандидат 2, Кандидат 3, Кандидат 4, Кандидат 1
- Кандидат 4, Кандидат 1, Кандидат 2, Кандидат 3
- Кандидат 3, Кандидат 1, Кандидат 2, Кандидат 4
- Кандидат 3, Кандидат 2, Кандидат 1. Кандидат 4
Выберите заштрихованную фигуру, которая показывает решение приведенной ниже задачи о дробях.
[математика]1/4 -: 3/8 = [/математика]
Сколько [math]1/3[/math] разделить на [math]8/11[/math]?
- 24.11
- 16/11
- 11/36
- 8/33
Дмитрий может прочитать 45 страниц за 30 минут. Какова его скорость чтения в страницах в минуту?
Какова его скорость чтения в страницах в минуту?
- 135
- 15
- 1,5
- 2
В классе математики 15 девочек и 5 мальчиков. Какое утверждение сравнения не является точным утверждением?
- В классе девочек на 10 больше, чем мальчиков.
- Соотношение девочек и мальчиков 3 к 1.

- Соотношение мальчиков и девочек 15 к 5.
200 миль за 5 часов.
40 миль в час
Упростите эту дробь:[математика]5/15[/математика]
- [математика]3/4[/математика]
- [математика]1/2[/математика]
- [математика]1/3[/математика]
Соотношение снеговика и санок [математика]1:4[/математика].
- Истинный
- ЛОЖЬ
[математика]6/9[/математика]
- [математика]1/3[/математика]
- [математика]2/3[/математика]
- [математика]3/3[/математика]
Разделить. [математика]1/3 -: 2/5[/математика]
- [математика]3/15[/математика]
- [математика]2/15[/математика]
- [математика]5/6[/математика]
- [математика]5/8[/математика]

Пример: 2 красных мелка на 6 синих мелков
- оценивать
- соотношение
- эквивалентное отношение
У Эшли есть 4 пары низких кроссовок, 7 пар высоких кроссовок, 3 пары сандалий и 1 пара ботинок. Каково соотношение пар низких кроссовок к общему количеству пар обуви?
- от 4 до 15
- от 7 до 15
- с 4 по 3
- 1 к 2
Соотношение варежек к общему количеству предметов 3:5.
- Истинный
- ЛОЖЬ
В классе Нади 10 мальчиков и 14 девочек. Какое соотношение эквивалентно [math]10//14[/math]?
- [математика]10//21[/математика]
- [математика]5//7[/математика]
- [математика]5//6[/математика]
- [математика]17//14[/математика]
Предыдущий Страница 1 из 20 Далее
У вас должно быть не менее 5 репутации, чтобы голосовать против вопроса. Узнайте, как заработать значки.
Узнайте, как заработать значки.
Ключ к ответу для 6 класса Go Math Глава 2 Дроби и десятичные дроби – ключ к ответу на урок математики
Хотите, чтобы ваши ученики получали лучший учебный материал? Тогда вы находитесь в правильном месте. Go Math Class 6 Ключ к ответу Глава 2 Дроби и десятичные дроби PDF включен сюда бесплатно. Все решения и объяснения позволят вам понять простой способ обучения и практиковать математику простым способом. Получите поддержку, обратившись к Go Math Grade 6 Chapter 2 Fractions and Decimals Solution Key. Первое, что каждый человек предпочитает для достижения своей цели, — это ответ HMH Go Math 6 класса.
Улучшите навыки решения математических задач вашего ученика с помощью 6-го стандартного ключа ответов Go Math. Неограниченный доступ к практике со всеми математическими вопросами и ответами, а также практическими вопросами. Используйте удобные решения Go Math Grade 6 Answer Key, чтобы изучать глубокую математику онлайн. Вы также можете бесплатно скачать Go Math Class 6 Answer Key Chapter 2 Fractions and Decimals.
Go Math Class 6 Глава 2 Дроби и десятичные дроби Ключ решения поможет вам оценить уровень вашей подготовки. Вы можете легко узнать, какие понятия сложны для подготовки, и найти простой способ решить проблемы, используя ключ для ответов на вопросы по математике для 6 класса. Легко изучите концепции и применяйте их в реальной жизни, чтобы жизнь была гладкой.
Урок 1: Дроби и десятичные дроби
- Дроби и десятичные дроби – Страница № 71
- Дроби и десятичные дроби — Страница № 72
- Проверка урока дробей и десятичных знаков — страница № 73
- Дроби и десятичные дроби Проверка урока 1 — Страница № 74
Урок 2: Сравнение и упорядочивание дробей и десятичных знаков
- Сравнение и упорядочивание дробей и десятичных знаков — страница № 77
- Сравнение и упорядочивание дробей и десятичных знаков — стр. № 78
- Сравнение и упорядочивание дробей и десятичных дробей Проверка урока — страница № 79
- Сравнение и упорядочивание дробей и десятичных знаков Проверка урока 1 — Страница № 80
Урок 3: Умножение дробей
- Умножение дробей – Страница № 83
- Умножение дробей — страница № 84
- Проверка урока «Умножение дробей» — страница № 85
- Проверка урока «Умножение дробей 1» — страница № 86
Урок 4. Упрощение факторов
Упрощение факторов
- Упрощение факторов — страница № 89
- Упрощение факторов — страница № 90
- Проверка урока Simplify Factors — Страница № 91
- Simplify Factors Проверка урока 1 — Страница № 92
Контрольный пункт в середине главы
- Контрольный пункт в середине главы — стр. № 93
- Проверка урока в середине главы — страница № 94
Урок 5: Исследование • Модель дробного деления
- Образцовое дробное деление – Страница № 97
- Модель Дробное деление – стр. № 98
- Модель Дробное деление Проверка урока – Страница № 99
- Модель Дробное деление Урок Проверка 1 – Страница № 100
Урок 6: Расчетные коэффициенты
- Оценочные коэффициенты – Страница № 103
- Расчетные коэффициенты — страница № 104
- Оценка коэффициентов Проверка урока — страница № 105
- Оценочные коэффициенты Проверка урока 1 — страница № 106
Урок 7: Разделение дробей
- Разделение дробей – Страница № 109
- Разделение дробей – Страница № 110
- Проверка урока деления дробей — страница № 111
- Проверка урока деления дробей 1 — страница № 112
Урок 8: Исследование • Модельный смешанный номерной отдел
- Модельный смешанный номерной отдел — № страницы 115
- Модель Смешанная нумерация — № страницы 116
- Model Mixed Number Division Lesson Check – стр.
 № 117
№ 117 - Модель Смешанная нумерация Проверка урока 1 — стр. № 118
Урок 9: Разделение смешанных чисел
- Разделение смешанных чисел – Страница № 121
- Разделение смешанных чисел — № страницы 122
- Проверка урока «Разделение смешанных чисел» — страница № 123
- Разделение смешанных чисел Проверка урока 1– Страница № 124
Урок 10: Решение задач • Дробные операции
- Дробные операции – Страница № 127
- Операции с дробями — страница № 128
- Проверка урока операций с дробями — страница № 129
- Проверка урока операций с дробями 1– стр. № 130
Обзор/тест главы 2
- Обзор/тест – стр. № 131
- Обзор/Тест — Страница № 132
- Обзор/Тест — Страница № 133
- Обзор/Тест — Страница № 134
- Обзор/Тест — Страница № 135
- Обзор/Тест — Страница № 136
Поделись и покажи — Страница № 71
Запишите в виде дроби или смешанного числа в простейшей форме.
Вопрос 1.
95,5
_____ \(\frac{□}{□}\)
Ответ:
\(\frac{1}{2}\)
Объяснение:
95,5
95 единиц. и 5 десятых.
5 десятых = \(\frac{5}{10}\)
Упростите с помощью GCF.
GCF 5 и 10 равен 10.
Разделить числитель и знаменатель на 10
\(\frac{5 ÷ 10}{10 ÷ 10}\) = \(\frac{1}{2}\)
Вопрос 2.
0,6
\(\frac{□}{□}\)
Ответ:
\(\frac{3}{5}\)
Объяснение:
0,6
6 десятых = \(\frac{6}{10} \)
Упрощение с помощью GCF.
GCF 6 и 10 равен 2.
Разделить числитель и знаменатель на 10
\(\frac{6 ÷ 2}{10 ÷ 2}\) = \(\frac{3}{5}\)
Вопрос 3.
5.75
_____ \(\frac{□}{□}\)
Ответ:
5\(\frac{3}{4}\)
Объяснение:
5.75 равно 5 единицам и 75 сотым .
75 сотых = \(\frac{75}{100}\)
Упрощение с использованием GCF.
GCF 75 и 100 равен 25.
Разделить числитель и знаменатель на 25
5\(\frac{75 ÷ 25}{100 ÷ 25}\) = 5\(\frac{3}{4}\ )
Пишите в виде десятичного числа.
Вопрос 4.
\(\frac{7}{8}\)
_____
Ответ:
0,875
Объяснение:
Используйте деление, чтобы переименовать дробную часть в десятичную.
7/8 = 0,875
В частном 3 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,875 = 0,875.
Итак, \(\frac{7}{8}\) = 0,875
Вопрос 5.
\(\frac{13}{20}\)
_____
Ответ:
0,65
Объяснение:
Используйте деление чтобы переименовать дробную часть как десятичную.
\(\frac{13}{20}\) = 0,65
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,65 = 0,65.
Итак, \(\frac{13}{20}\) = 0,65
Вопрос 6.
\(\frac{3}{25}\)
_____
Ответ:
0,12
Объяснение:
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{3}{25}\) = 0,12
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,12 = 0,12.
Итак, \(\frac{3}{25}\)= 0,12
Самостоятельно
Запишите в виде дроби или смешанного числа в простейшей форме.
Вопрос 7.
0,27
\(\frac{□}{□}\)
Ответ:
\(\frac{27}{100}\)
Объяснение:
0,27 составляет 0 единиц и 27 сотых.
27 сотых = \(\frac{27}{100}\)
Упростите с помощью GCF.
GCF 27 и 100 равен 1.
Разделить числитель и знаменатель на 1
\(\frac{27 ÷ 1}{100 ÷ 1}\) = \(\frac{27}{100}\)
Вопрос 8.
0,055
\(\frac{□}{□}\)
Ответ:
\(\frac{11}{200}\)
Объяснение:
0,055 равно 0 единицам и 55 тысячным.
55 тысячных = \(\frac{55}{1000}\)
Упростите с помощью GCF.
GCF 55 и 1000 равен 5,
Разделить числитель и знаменатель на 5. \frac{□}{□}\)
Ответ:
\(\frac{9}{20}\)
Объяснение:
2,45 равно 2 единицам и 45 сотым.
45 сотых = \(\frac{45}{100}\)
Упростите с помощью GCF.
GCF 45 и 100 равен 5.
Разделить числитель и знаменатель на 1
\(\frac{45 ÷ 5}{100 ÷ 5}\) = \(\frac{9}{20}\)
Запись в виде десятичного числа.
Вопрос 10.
\(\frac{3}{8}\)
_____
Ответ:
0,375
Объяснение:
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{3}{8}\) = 0,375
В частном 3 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,375 = 0,375.
Итак, \(\frac{3}{8}\) = 0,375
Вопрос 11.
3 \(\frac{1}{5}\)
_____
Ответ:
3,2
Объяснение:
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{1}{5}\) = 0,2
В частном 1 десятичный знак.
Добавьте целое число к десятичной дроби.
3 + 0,2 = 3,2. Вопрос 12 Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{11}{20}\) = 0,55
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
2 + 0,55 = 2,55.
Итак, 2 \(\frac{11}{20}\) = 2,55
Определите десятичную и дробную части в простейшей форме для точки.
Question 13.
Point A
Type below:
__________
Answer:
0.2
Question 14.
Point B
Type below:
__________
Answer:
0.9
Explanation:
Point B is между 0,8 и 1,0. Каждая точка разделена на 0,1. Итак, точка B находится на 0,9
Вопрос 15.
Point C
Введите ниже:
__________
Ответ:
0,5
Объяснение:
Point C находится между 0,4 и 0,6. Каждая точка разделена на 0,1. Итак, точка C находится на 0,5
Вопрос 16.
Точка D
Введите ниже:
__________
Ответ:
0,1
Объяснение:
Точка D находится между 0 и 0,2. Каждая точка разделена на 0,1. Итак, точка D находится на 0,1
Используйте таблицу для 17 и 18.
Вопрос 17.
Члены туристического клуба Ozark Trail Hiking Club прошли крутой участок тропы в июне и июле. В таблице указаны расстояния, пройденные членами клуба, в милях. Запишите июльское расстояние Марии в виде десятичной дроби.
_____ миль
Ответ:
2,625 миль
Объяснение:
Июльское расстояние Марии = 2 \(\frac{5}{8}\)
Используйте деление, чтобы преобразовать дробную часть в десятичную.
\(\frac{5}{8}\) = 0,625
В частном 3 знака после запятой.
Добавьте целое число к десятичной дроби.
2 + 0,625 = 2,625.
2 \(\frac{5}{8}\) = 2,625
Вопрос 18.
Насколько дальше прошла пешком Зои в июне и июле, чем Мария в июне и июле? Объясните, как вы нашли ответ.
_____ миль
Ответ:
0,7 мили
Объяснение:
Мария: июнь = 2,95, июль = 2 \(\frac{5}{8}\) = 2,58
Зои: июнь = 2,85, июль = 3 \( \frac{3}{8}\) = 3,38
[2,85 + 3,38] – [2,95 + 2,58] = 0,7 мили
Вопрос 19.
В чем ошибка? Расстояние, пройденное Табитой в июле, составило 2 \(\frac{1}{5}\) миль. Она написала расстояние как 2,02 мили. Какую ошибку она сделала?
Введите ниже:
__________
Ответ:
Расстояние, пройденное Табитой в июле, составило 2 \(\frac{1}{5}\) миль.
2 \(\frac{1}{5}\)
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{1}{5}\) = 0,2
В частном 1 десятичный знак.
Добавьте целое число к десятичной дроби.
2 + 0,2 = 2,2.
2 \(\frac{1}{5}\) = 2,2
Она по ошибке написала расстояние 2,02 мили.
Вопрос 20.
Использование шаблонов Записывайте \(\frac{3}{8}, \frac{4}{8}, \text { и } \frac{5}{8}\) в виде десятичных дробей. Какой узор вы видите? Используйте шаблон, чтобы предсказать десятичную форму \(\frac{6}{8}\) и \(\frac{7}{8}\).
Введите ниже:
__________
Ответ:
\(\frac{3}{8}, \frac{4}{8}, \text { и } \frac{5}{8}\) в виде десятичных знаков.
0,375, 0,5, 0,625
Каждое десятичное число разделено на 0,125.
Итак, 6/8 = 0,625 + 0,125 = 0,75
7/8 = 0,75 + 0,125 = 0,875
Вопрос 21.
Определите десятичную и дробную части в простейшей форме для точки.
Введите ниже:
__________
Ответ:
Точка A: 0,5
Точка B: 0,7
Точка C: 0,3
Точка D: 0,8
Объяснение:
Каждая точка отличается на 0,1 расстояния.
A находится в диапазоне от 0,4 до 0,6, что составляет 0,5
B находится в диапазоне от 0,6 до 0,8, что составляет 0,7
C находится в диапазоне от 0,1 до 0,6, что составляет 0,53
Дроби и десятичные дроби – № страницы 73
Напишите в виде дроби или смешанного числа в простейшей форме.
Вопрос 1.
0,52
\(\frac{□}{□}\)
Ответ:
\(\frac{13}{25}\)
Объяснение:
0,52
5 2 сотых есть.
52 сотых = \(\frac{52}{100}\)
Упростите с помощью GCF.
GCF 52 и 100 равен 4.
Разделить числитель и знаменатель на 4
\(\frac{52 ÷ 4}{100 ÷ 4}\) = \(\frac{13}{25}\)
Вопрос 2.
0,02
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{50}\)
Объяснение:
0,02
0,02 равно 2 сотым.
2 сотых = \(\frac{2}{100}\)
Упростите с помощью GCF.
GCF 2 и 100 равен 2.
Разделить числитель и знаменатель на 2
\(\frac{2 ÷ 2}{100 ÷ 2}\) = \(\frac{1}{50}\)
Вопрос 3.
4.8
______ \(\frac{□}{□}\)
Ответ:
\(\frac{4}{5}\)
Объяснение:
4.8
4.8 это 4 единицы и 8 десятых.
8 десятых = \(\frac{8}{10}\)
Упростите с помощью GCF.
GCF 8 и 10 равен 2.
Разделить числитель и знаменатель на 2
\(\frac{8 ÷ 2}{10 ÷ 2}\) = \(\frac{4}{5}\)
Вопрос 4.
6.025
______ \(\frac{□}{□}\)
Ответ:
\(\frac{1}{40}\)
Объяснение:
6.025 равно 6 единицам и 25 тысячным.
25 тысячных = \(\frac{25}{1000}\)
Упростите с помощью GCF.
GCF 25 и 1000 равен 25.
Разделите числитель и знаменатель на 25
\(\frac{25 ÷ 25}{1000 ÷ 25}\) = \(\frac{1}{40}\)
Запишите в виде десятичной дроби.
Вопрос 5.
\(\frac{17}{25}\)
______
Ответ:
0,68
Объяснение:
Используйте деление, чтобы преобразовать дробную часть в десятичную.
17/25 = 0,68
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,68 = 0,68.
Итак, \(\frac{17}{25}\) = 0,68
Вопрос 6.
\(\frac{11}{20}\)
______
Ответ:
0,55
Объяснение:
Используйте деление, чтобы преобразовать дробную часть в десятичную.
11/20 = 0,55
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,55 = 0,55.
Итак, \(\frac{11}{20}\) = 0,55
Вопрос 7.
4 \(\frac{13}{20}\)
______
Ответ:
4,65
Объяснение:
Использование деление, чтобы переименовать дробную часть в десятичную.
\(\frac{13}{20}\) = 0,65
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
4 + 0,65 = 4,65.
Итак, 4 \(\frac{13}{20}\) = 4,65
Вопрос 8.
7 \(\frac{3}{8}\)
______
Ответ:
7,375
Объяснение:
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{3}{8}\) = 0,375
В частном 3 знака после запятой.
Добавьте целое число к десятичной дроби.
7 + 0,375 = 7,375.
Итак, 7 \(\frac{3}{8}\) = 7,375
Определите десятичное и дробное или смешанное число в простейшей форме для каждой точки.
Вопрос 9.
Точка A
Введите ниже:
__________
Ответ:
0,4
Объяснение:
Точка A находится в диапазоне от 0 до 0,5. Каждая точка разделена на 0,1. Итак, точка A находится на 0,4
Вопрос 10.
Точка D
Введите ниже:
__________
Ответ:
1,9
Объяснение:
Точка D находится между 1,5 и 2. Каждая точка разделена на 0,1. Итак, точка D находится на уровне 1,9.
Вопрос 11.
Точка C
Введите ниже:
__________
Ответ:
1. 2
2
Объяснение:
Точка C между 1 и 1,5. Каждая точка разделена на 0,1. Итак, точка C находится на 1,2
Вопрос 12.
Точка B
Введите ниже:
__________
Ответ:
0,6
Объяснение:
Точка C находится между 0,5 и 1. Каждая точка разделена 0,1. Итак, точка C находится на 0,6
Решение проблем
Вопрос 13. 904:45 Грейс продала \(\frac{5}{8}\) свою коллекцию марок. Какова эта сумма в виде десятичной дроби?
______
Ответ:
0,625
Объяснение:
Грейс продала \(\frac{5}{8}\) свою коллекцию марок.
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{5}{8}\) = 0,625
В частном 3 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,625 = 0,625.
Итак, \(\frac{5}{8}\) = 0,625
Вопрос 14.
Что, если вы набрали 0,80 на тесте? На какую часть теста в простейшей форме вы ответили правильно?
\(\frac{□}{□}\)
Ответ:
\(\frac{4}{5}\)
Объяснение:
0,80 равно 0 единиц и 8 десятых.
8 десятых = \(\frac{8}{10}\)
Упростите с помощью GCF.
GCF 8 и 10 равен 2.
Разделить числитель и знаменатель на 2
\(\frac{8 ÷ 2}{10 ÷ 2}\) = \(\frac{4}{5}\)
Вопрос 15.
Какая дробь в простейшем виде эквивалентна 0,45? Какое десятичное число эквивалентно \(\frac{17}{20}\)? Объясните, как вы нашли ответы.
Введите ниже:
__________
Ответ:
0,45 равно 0 единиц и 45 сотых.
45 сотых = \(\frac{45}{100}\)
Упростите с помощью GCF.
GCF 45 и 100 равен 5.
Разделить числитель и знаменатель на 5
\(\frac{45 ÷ 5}{100 ÷ 5}\) = \(\frac{9}{20}\)
\(\frac{17}{20}\)
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{17}{20}\) = 0,85
В частном 2 знака после запятой.
Добавьте целое число к десятичной дроби.
0 + 0,85 = 0,85.
Итак, \(\frac{17}{20}\) = 0,85
Проверка урока – страница № 74
Вопрос 1.
После шторма Майкл измерил 6 \(\frac{7}{8}\ ) дюймов снега. Какова эта сумма в виде десятичной дроби?
Какова эта сумма в виде десятичной дроби?
______ дюймов
Ответ:
6,875 дюймов
Объяснение:
Майкл намерил 6 \(\frac{7}{8}\) дюймов снега.
Используйте деление, чтобы переименовать дробную часть в десятичную.
\(\frac{7}{8}\) = 0,875
В частном 3 знака после запятой.
Добавьте целое число к десятичной дроби.
6 + 0,875 = 6,875.
Итак, 6 \(\frac{7}{8}\) = 6,875.
Вопрос 2.
Рецепт требует 3,75 стакана муки. Чему равна эта сумма в виде смешанного числа в простейшей форме?
______ \(\frac{□}{□}\) чашек
Ответ:
3 \(\frac{3}{4}\) чашек
Объяснение:
Рецепт требует 3,75 чашек муки.
3 + 0,75
0,75 равно 0 единиц и 75 сотых.
75 сотых = \(\frac{75}{100}\)
Упростите с помощью GCF.
GCF 75 и 100 равен 25.
Разделить числитель и знаменатель на 25
\(\frac{75 ÷ 25}{100 ÷ 25}\) = \(\frac{3}{4}\)
3 \(\frac{3}{4 }\)
Спиральный обзор
Вопрос 3.
Джина купила 2,3 фунта красных яблок и 2,42 фунта зеленых яблок. Они продавались по цене 0,75 доллара за фунт. Сколько стоили все яблоки?
$ ______
Ответ:
$3,54
Пояснение:
Джина купила 2,3 фунта красных яблок и 2,42 фунта зеленых яблок. Они продавались по цене 0,75 доллара за фунт.
0,75 x 2,3 = 1,725
0,75 x 2,42 = 1,815
1,725 + 1,815 = 3,54
Таким образом, стоимость яблок составляет 3,54 долл. Он смешивает их вместе и делит поровну по 18 мешкам. Сколько фунтов орехов в каждом мешке?
______ фунтов
Ответ:
0,82 фунта
Пояснение:
У Кена 4,66 фунта грецких орехов, 2,1 фунта кешью и 8 фунтов арахиса.
4,66 + 2,1 + 8 = 14,76
Он смешивает их вместе и делит поровну на 18 мешков.
14,76/18 = 0,82
Вопрос 5.
Мии нужно разложить по пачкам 270 синих и 180 красных ручек. В каждом наборе будет одинаковое количество синих ручек и одинаковое количество красных ручек. Какое наибольшее количество упаковок она может сделать? Сколько красных ручек и сколько синих ручек будет в каждой пачке?
Введите ниже:
__________
Ответ:
В каждой упаковке 2 красных и 3 синих ручки.
Пояснение:
Мии нужно разложить по упаковкам 270 синих и 180 красных ручек.
GCF 270 и 180 равен 90
Максимальное количество упаковок, которое она может сделать, равно 90.
Разделите общее количество красных ручек на общее количество упаковок.
180/90 = 2
Разделите общее количество синих ручек на общее количество упаковок.
270/90 = 3
В каждой упаковке 2 красных и 3 синих ручки.
Вопрос 6.
Эван покупает 19 тюбиков акварельной краски за 50,35 доллара. Какова стоимость каждого тюбика краски?
$ ______
Ответ:
$2,65
Пояснение:
Эван покупает 19 тюбиков акварельной краски за $50,35.
50,35 долл. США/19 = 2,65 долл. США
Поделись и покажи – № страницы 77
Порядок от наименьшего к наибольшему.
Вопрос 1.
\(3 \frac{3}{6}, 3 \frac{5}{8}, 2 \frac{9}{10}\)
Введите ниже:
__________
Ответ:
2 \(\frac{9}{10}\) < 3 \(\frac{3}{6}\) < 3 \(\frac{5}{8}\)
Объяснение:
\(3 \frac{3}{6}, 3 \frac{5}{8}, 2 \frac{9}{10}\)
Сначала сравните целые числа.
2 < 3
Если целые числа совпадают, сравните дроби.
3 \(\frac{3}{6}\), 3 \(\frac{5}{8}\)
6 и 8 кратны 48.
Итак, 48 является общим знаменателем.
3 \(\frac{3 x 8}{6 x 8}\) = 3 \(\frac{24}{48}\), 3 \(\frac{5 x 6}{8 x 6}\) = 3 \(\frac{30}{48}\)
3 \(\frac{24}{48}\) < 3 \(\frac{30}{48}\)
Итак, 3 \(\frac {3}{6}\) < 3 \(\frac{5}{8}\)
Расположите дроби от наименьшего к наибольшему.
2 \(\ гидроразрыва{9}{10}\) < 3 \(\frac{3}{6}\) < 3 \(\frac{5}{8}\)
Напишите <, > или =.
Вопрос 2.
0,8 _____ \(\frac{4}{12}\)
Ответ:
0,8 < латекс]\frac{4}{12}[/latex]
Объяснение:
Напишите десятичную дробь форма \(\frac{4}{12}\) = 0,3333
0,8 > 0,333
Итак, 0,8 < латекс]\frac{4}{12}[/latex]
Вопрос 3.
0,22 _____ \(\ frac{1}{4}\)
Ответ:
0,22 < \(\frac{1}{4}\)
Объяснение:
Запишите десятичную форму \(\frac{1}{4}\) = 0,25
0,22 < 0,25
Итак, 0,22 < \(\frac{1}{4}\)
Вопрос 4.
\(\ frac{1}{20}\) _____ 0,06
Ответ:
\(\frac{1}{20}\) < 0,06
Объяснение:
Напишите десятичную форму \(\frac{1}{20} \) = 0,05
0,05 < 0,06
Итак, \(\frac{1}{20}\) < 0,06
Используйте числовую линейку для упорядочивания от меньшего к большему.
Вопрос 5.
\(1 \frac{4}{5}, 1.25, 1 \frac{1}{10}\)
Введите ниже:
__________
Ответ:
1\(\frac{1}{10}\), 1.25, 1\(\frac{4}{5}\)
Объяснение:
Напишите десятичную форму 1\(\frac{4}{5}\) = 1,8
Напишите десятичную форму 1\(\frac{1}{10}\) = 1,1
1,8, 1,25, 1,1
Найдите каждую десятичную дробь в числовой строке .
Итак, от наименьшего к наибольшему, порядок 1.1, 1.25, 1.8
1\(\frac{1}{10}\), 1.25, 1\(\frac{4}{5}\)
On Ваш собственный
Порядок от меньшего к большему.
Вопрос 6.
0,6, \(\frac{4}{5}\), 0,75
Введите ниже:
__________
Ответ:
0,6, 0,75, \(\frac{4}{5}\)
Объяснение:
Напишите десятичную форму \(\frac{4}{5}\) = 0,8
0,6, 0,8, 0,75
Сравните десятичные дроби.
Все равны.
Сравните десятые: 6 < 7 < 8
Итак, от меньшего к большему, порядок 0,6, 0,75, 0,8
Итак, 0,6, 0,75, \(\frac{4}{5}\)
Вопрос 7.
\(\frac{1}{2}\), \(\frac{2}{5}\), \(\frac{7}{15}\)
Введите ниже:
__________
Ответ:
\(\frac{2}{5}\), \(\frac{7}{15}\), \(\frac{1}{2}\)
Объяснение:
Запишите десятичную форму \(\frac{1}{2}\) = 0,5
Запишите десятичную форму \(\frac{2}{5}\) = 0,4
Запишите десятичную форму \(\frac{2}{5}\) = 0,4 (\frac{7}{15}\) = 0,466
0,5, 0,4, 0,466
Сравните десятичные дроби.
Все равны.
Сравните десятые доли: 4 < 5
Сравните сотые доли 0,4 и 0,466; 0 < 6
Итак, от наименьшего к наибольшему порядок 0,4 < 0,466 < 0,5
Итак, \(\frac{2}{5}\), \(\frac{7}{15}\), \(\frac{1}{2}\)
Вопрос 8.
5 \( \frac{1}{2}\), 5.05, 5 \(\frac{5}{9}\)
Введите ниже:
__________
Ответ:
5.05, 5 \(\frac{1}{2} \), 5 \(\frac{5}{9}\)
Объяснение:
Запишите десятичную форму числа 5 \(\frac{1}{2}\) = 5,5
Запишите десятичную форму числа 5 \( \frac{5}{9}\) = 5,555
5,5, 5,05, 5,5555
Сравните десятичные дроби.
Все равны.
Сравните десятые доли: 0 < 5
Сравните сотые доли 5,5 и 5,55; 0 < 5
Итак, от меньшего к большему, порядок 5,05 < 5,5 < 5,55
Итак, 5,05, 5 \(\frac{1}{2}\), 5 \(\frac{5}{9}\)
Вопрос 9.
\(\frac{5}{7}\), \(\frac{5}{6}\), \(\frac{5}{12}\)
Введите ниже:
__________
Ответ:
\(\frac{5}{12}\), \(\frac{5}{7}\), \(\frac{5}{6}\)
Объяснение:
\(\frac {5}{7}\), \(\frac{5}{6}\), \(\frac{5}{12}\)
Чтобы сравнить дроби с одинаковыми числителями, сравните знаменатели.
Таким образом, от меньшего к большему, порядок \(\frac{5}{12}\), \(\frac{5}{7}\), \(\frac{5}{6}\)
Вопрос 10.
\(\frac{7}{15}\) _____ \(\frac{7}{10}\)
Ответ:
\(\frac{7}{15}\) < \ (\frac{7}{10}\)
Объяснение:
\(\frac{7}{15}\) и \(\frac{7}{10}\)
Чтобы сравнить дроби с одинаковыми числителями, сравните знаменатели.
Итак, \(\frac{7}{15}\) < \(\frac{7}{10}\)
Вопрос 11.
\(\frac{1}{8}\) _____ 0,125
Ответ:
\(\frac{1}{8}\) = 0,125
Объяснение:
Запишите десятичную форму \(\frac{1}{8}\) = 0,125
0,125 = 0,125
Вопрос 12.
7 \(\frac{1}{3}\) _____ 6 \(\frac{2}{3}\)
Ответ:
7 \(\frac{1} {3}\) > 6 \(\frac{2}{3}\)
Объяснение:
Сначала сравните целые числа.
7 > 6.
Итак, 7 \(\frac{1}{3}\) > 6 \(\frac{2}{3}\)
Вопрос 13.
1 \(\frac{2}{ 5}\) _____ 1 \(\frac{7}{15}\)
Ответ:
1 \(\frac{2}{5}\) < 1 \(\frac{7}{15}\)
Объяснение:
1 \(\frac{2}{5}\) _____ 1 \(\frac{7}{15}\)
Если целые числа совпадают, сравните дроби.
Сравните \(\frac{2}{5}\) и \(\frac{7}{15}\)
5 и 15 кратны 15.
Итак, \(\frac{2 x 3}{5 x 3}\) = \(\frac{6}{15}\)
\(\frac{6}{15}\) < \(\frac{7}{15}\)
Используйте общие знаменатели для записи эквивалентные дроби.
1 \(\frac{2}{5}\) < 1 \(\frac{7}{15}\)
Вопрос 14.
Даррелл провел 3 \(\frac{2}{5}\) часа над проектом для школы. Ян потратил на проект 3 \(\frac{1}{4}\) часа, а Мейв — 3,7 часа. Кто потратил меньше всего времени? Покажите, как вы нашли ответ. Тогда опишите другой возможный метод.
Введите ниже:
__________
Ответ:
Ян провел меньше всего времени.
Пояснение:
Даррелл потратил 3 \(\frac{2}{5}\) часа на школьный проект. Ян потратил на проект 3 \(\frac{1}{4}\) часа, а Мейв — 3,7 часа.
Запишите десятичную форму числа 3 \(\frac{2}{5}\) = 3,4
Запишите десятичную форму числа 3 \(\frac{1}{4}\) = 3,25
3,4, 3,25, 3,7
3,25 является наименьшим.
Итак, Ян провел меньше всего времени.
Решение проблем + Приложения – Страница № 78
Используйте таблицу для 15–18.
Вопрос 15.
В течение одной недели в Алтуне, штат Пенсильвания, и Вифлееме, штат Пенсильвания, каждый день с понедельника по пятницу выпадал снег. В какие дни в Алтуне выпадало на 0,1 дюйма больше снега, чем в Вифлееме?
Введите ниже:
__________
Ответ:
Алтуна получила на 1 дюйм больше снега, чем Вифлеем в пятницу
Объяснение:
Алтуна (преобразовать в десятичную форму): 2. 25, 3.25, 2.625, 4.6, 4.75 Вифлеем
25, 3.25, 2.625, 4.6, 4.75 Вифлеем
, 2,5, 4,8, 2,7
В Алтуну выпало на 1 дюйм больше снега, чем в Вифлееме в пятницу
Вопрос 16.
Что, если в Алтуну в четверг выпало дополнительно 0,3 дюйма снега? Каково будет общее количество снега в Алтуне по сравнению с количеством снега, выпавшим в тот день в Вифлееме?
Введите ниже:
__________
Ответ:
В четверг в Алтуну выпало на 0,1 дюйма больше снега, чем в Вифлеем
Объяснение:
В четверг в Алтуну выпало дополнительно 0,3 дюйма снега = 4,6 + 0,3 = 4,9
Вифлеем выпало в четверг = 4,8
В Алтуне выпало на 0,1 дюйма больше снега, чем в Вифлееме в четверг
Вопрос 17.
Объясните два способа сравнения количества снегопадов в Алтуне и Вифлееме в понедельник.
Введите ниже:
__________
Ответ:
Объяснение:
Алтуна получила в понедельник = 2,25
Вифлеем получил в понедельник = 2,6
Вифлеем получил на 0,35 дюйма больше снега, чем Алтуна в понедельник.
Поскольку целые числа равны, сравните 1/4 и 0,6.
0.25 < 0.6
Итак, в Алтуну выпало меньше снега по сравнению с Вифлеемом в понедельник.
Вопрос 18.
Объясните, как можно сравнить количество снегопадов в Алтуне в четверг и пятницу.
Введите ниже:
__________
Ответ:
Алтуна получила в четверг = 4,6
Алтуна получила в пятницу = 4,75
4,6 < 4,75
В Алтуну выпало меньше снега в четверг по сравнению с пятницей.
Вопрос 19.
Запишите значения в порядке от наименьшего к наибольшему.
Тип ниже:
__________
Ответ:
1/3, 0,39, 2/5, 0,45
Объяснение:
1/3 = 0,333
0,45
0,39
2/5 = 0,4
.
Сравните сотые доли:
0,33 < 0,39
0,4 < 0,45
Итак, 1/3, 0,39, 2/5, 0,45
Вопрос 1.
0,64 _____ \(\frac{7}{10}\)
Ответ:
0,64 < \(\frac{7}{10}\)
Объяснение:
Напишите десятичную форму \(\frac{7}{10}\) = 0,7
Сравните десятые доли: 6 < 7
Итак, 0,64 < 0,7
0,64 < \(\frac{7}{10} \)
Вопрос 2.
0,48 _____ \(\frac{6}{15}\)
Ответ:
0,48 > \(\frac{6}{15}\)
Объяснение:
Запишите десятичную форму of \(\frac{6}{15}\) = 0,4
Сравните сотые доли:
0,48 > 0,4
0,48 > \(\frac{6}{15}\)
Вопрос 3.
0,75 _____ \(\frac {7}{8}\)
Ответ:
0,75 < \(\frac{7}{8}\)
Объяснение:
Запишите десятичную форму \(\frac{7}{8}\) = 0,875
Сравните десятые доли:
7 < 8
0,75 < \(\frac{7}{8}\)
Вопрос 4.
7 \(\frac{1}{8}\) _____ 7,025
Ответ:
7 \(\frac{1}{ 8}\) > 7,025
Объяснение:
Запишите десятичную форму числа 7 \(\frac{1}{8}\) = 7,125
Сравните десятые доли:
1 > 0
7 \(\frac{1}{8 }\) > 7.025
Порядок от меньшего к большему.
Вопрос 5.
\(\frac{7}{15}\), 0,75, \(\frac{5}{6}\)
Введите ниже:
__________
Ответ:
\(\frac{ 7}{15}\), 0,75, \(\frac{5}{6}\)
Объяснение:
Запишите десятичную форму \(\frac{7}{15}\) = 0,466
0,75
Запишите десятичная форма \(\frac{5}{6}\) = 0,833
Порядок от меньшего к большему: \(\frac{7}{15}\), 0,75, \(\frac{5}{6} \)
Вопрос 6.
0,5, 0,41, \(\frac{3}{5}\)
Введите ниже:
__________
Ответ:
0,41, 0,5, \(\frac{3}{5}\)
Объяснение:
Запишите десятичную форму \(\frac{3}{5}\) = 0,6
Сравните десятые доли:
0,41 , 0,5, 0,6
Порядок от наименьшего к наибольшему: 0,41, 0,5, \(\frac{3}{5}\)
Вопрос 7.
3,25, 3 \(\frac{2}{5}\), 3 \(\frac{3}{8}\)
Введите ниже:
__________
Ответ:
3.25, 3 \(\frac{2}{5}\), 3 \(\frac{3}{8} \)
Объяснение:
Запишите десятичную форму числа 3 \(\frac{2}{5}\) = 3,4
Запишите десятичную форму числа 3 \(\frac{3}{8}\) = 3,375
Сравните десятые:
В порядке убывания: 3,25, 3 \(\frac{2}{5}\), 3 \(\frac{3}{8}\)
Вопрос 8.
0,9, \( \frac{8}{9}\), 0,86
Введите ниже:
__________
Ответ:
0,86, \(\frac{8}{9}\), 0,9
Объяснение:
Запишите десятичную форму \ (\frac{8}{9}\) = 0,88
Сравните десятые доли:
0,86, 0,88, 0,9
Порядок от меньшего к большему: 0,86, \(\frac{8}{9}\), 0,9
Порядок от большего к меньшему.
Вопрос 9.
0,7, \(\frac{7}{9}\), \(\frac{7}{8}\)
Введите ниже:
__________
Ответ:
\(\frac{7}{8}\ ), \(\frac{7}{9}\), 0,7
Объяснение:
0,7 = 7/10
Чтобы сравнить дроби с одинаковыми числителями, сравните знаменатели.
7/10, 7/9, 7/8
Порядок от наибольшего к наименьшему: 7/8, 7/9, 7/10
Вопрос 10.
0,2, 0,19, \(\frac{3}{5} \)
Введите ниже:
__________
Ответ:
\(\frac{3}{5}\), 0.2, 0.19
Объяснение:
Напишите десятичную форму \(\frac{3}{5}\) = 0,6
Сравните десятые доли:
0,6, 0,2, 0,19
Упорядочьте от наибольшего к наименьшему: \(\frac{3}{5}\), 0.2, 0.19
Вопрос 11.
6\(\frac{1}{20}\), 6.1, 6.07
Введите ниже:
__________
Ответ:
Объяснение:
Запишите десятичную форму числа 6\(\ frac{1}{20}\) = 121/20 = 6,05
Сравните десятые доли:
6,1, 6,07, 6,05
Порядок от наибольшего к наименьшему: 6,1, 6,07, 6\(\frac{1}{20}\)
Вопрос 12.
2 \(\frac{1}{2}\), 2.4, 2.35, 2 \(\frac{1}{8}\)
Введите ниже:
__________
Ответ:
2 \(\frac{1 {2}\), 2.4, 2.35, 2 \(\frac{1}{8}\)
Объяснение:
Напишите десятичную форму числа 2 \(\frac{1}{2}\) = 2,5
Запишите десятичную форму числа 2 \(\frac{1}{8}\) = 2,125
Сравните десятые доли: 2,5, 2,4, 2,35, 2,125
Упорядочьте от наибольшего к наименьшему: 2 \(\frac{1}{2}\ ), 2.4, 2.35, 2 \(\frac{1}{8}\)
Вопрос 13.
Однажды выпало снега 3 \(\frac{3}{8}\) дюйма в Алтуне и 3,45 дюйма в Вифлееме . В каком городе в этот день выпало меньше снега?
__________
Ответ:
Алтуна
Объяснение:
Однажды в Алтуне выпало 3 \(\frac{3}{8}\) снега, а в Вифлееме — 3,45 дюйма.
Напишите десятичную форму 3 \(\frac{3}{8}\) = 27/8 = 3,375
3,375 < 3,45.
В этот день в Алтуне выпало меньше снега
Вопрос 14.
Малия и Джон купили по 2 фунта семечек подсолнуха. Каждый съел несколько семян. У Малии остался 1 \(\frac{1}{3}\) фунтов, а у Джона остался 1 \(\frac{2}{5}\) фунтов. Кто съел больше семечек?
Кто съел больше семечек?
__________
Ответ:
Малия
Пояснение:
Малия и Джон купили по 2 фунта семечек подсолнуха. Каждый съел несколько семян. У Малии остался 1 \(\frac{1}{3}\) фунтов, а у Джона остался 1 \(\frac{2}{5}\) фунтов.
2 – 1 \(\frac{1}{3}\) = 0,667
2 – 1 \(\frac{2}{5}\) = 0,6
0,667 > 0,6
Итак, Малия съела больше семечек подсолнуха
Вопрос 15.
Объясните, как бы вы сравнили числа 0,4 и \(\frac{3}{8}\).
Введите ниже:
__________
Ответ:
Напишите десятичную форму \(\frac{3}{8}\) = 0,375
Сравните десятые доли:
0,4 > 0,375
Проверка урока – Страница № 80
Вопрос 1.
У Андреа 3 \(\frac{7}{8}\) ярдов фиолетовой ленты, 3,7 ярда розовой ленты и 3 \(\frac{4}{5}\) ярда голубой ленты. Перечислите числа в порядке от наименьшего к наибольшему.
Введите ниже:
__________
Ответ:
У Андреа есть 3 \(\frac{7}{8}\) ярдов фиолетовой ленты, 3,7 ярда розовой ленты и 3 \(\frac{4}{5}\ ) ярдов голубой ленты.
Запишите десятичную форму 3 \(\frac{7}{8}\) = 3,875
3,7
Запишите десятичную форму 3 \(\frac{4}{5}\) = 3,8
От наименьшего к наибольшему: 3,7 , 3 \(\frac{4}{5}\), 3 \(\frac{7}{8}\)
Вопрос 2.
Нассим завершил \(\frac{18}{25}\) домашнее задание по математике. Кара завершила 0,7 из них. Дебби завершила \(\frac{5}{8}\) его. Перечислите числа в порядке от большего к меньшему.
Введите ниже:
__________
Ответ:
$1,39, $0,70, $0,63
Объяснение: 904:45 Нассим выполнил \(\frac{18}{25}\) домашнее задание по математике. Кара завершила 0,7 из них. Дебби завершила \(\frac{5}{8}\) его.
Запишите десятичную форму 18/25 = 1,39
0,7
Запишите десятичную форму 5/8 = 0,63
Теперь они расположены в порядке от большего к меньшему.
Думайте о суммах как о деньгах:
1,39 доллара, 0,70 доллара, 0,63 доллара
Обзор спирали
Вопрос 3.
Тайлер купил 3 \(\frac{2}{5}\) фунтов апельсинов. Нарисуйте 3 \(\frac{2}{5}\) на числовой прямой и запишите это количество, используя десятичную дробь.
Нарисуйте 3 \(\frac{2}{5}\) на числовой прямой и запишите это количество, используя десятичную дробь.
Введите ниже:
__________
Ответ:
Тайлер купил 3 \(\frac{2}{5}\) фунтов апельсинов.
Десятичная форма: 17/5 = 3,4
Вопрос 4.
На фабрике бейсбольная карточка кладется в каждую 9-ю упаковку хлопьев. В каждую 25-ю упаковку каши вложена футбольная карточка. Какой первый пакет, который получает и бейсбольную карточку, и футбольную карточку?
Введите ниже:
__________
Ответ:
225-й пакет
Объяснение:
Найдите первое число, где и 25, и 9являются фактором.
25 x 1 = 25, что не является множителем 9, поэтому оно не будет 25.
25 x 2 = 50, что не является множителем 9.
75 не является множителем 9. (вы
100 не является делителем 9, как и 125, 150, 175 или 200.
Однако 225 является делителем как 25, так и 9. Это имеет смысл, потому что 25 x 9 равно 225.
Это означает, что первый пакет с обоими будет 225-м пакетом.
Вопрос 5.
15 долларов 30 центов делятся между 15 студентами. Сколько получает каждый ученик?
$ _____
Ответ:
$1,02
Объяснение:
$15,30 делится между 15 студентами.
$15,30/15 = $1,02
каждый ученик получает $1,02
Вопрос 6.
Кэрри покупает 4,16 фунта яблок за $5,20. Сколько стоит 1 фунт?
$ _____
Ответ:
1,25 доллара
Объяснение:
Кэрри покупает 4,16 фунта яблок за 5,20 доллара.
5,20/4,16 долл. США = 1,25 долл. США
Стоимость 1 фунта стерлингов = 1,25 долл. США
Поделись и покажи – № страницы 83
Найти продукт. Напишите в простейшей форме.
Вопрос 1.
6 × \(\frac{3}{8}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{9}{4}\ )
Объяснение:
\(\frac{6 × 3}{1 × 8}\)
\(\frac{18}{8}\)
Упрощение с использованием GCF.
GCF 18 и 8 равен 2.
Разделите числитель и знаменатель на 2.
\(\frac{18 ÷ 2}{8 ÷ 2}\) = \(\frac{9}{4}\)
Вопрос 2.
\(\frac{3}{8}\) × \(\frac{8}{9}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{3}\)
Объяснение:
Умножьте числители и умножьте знаменатели.
\(\frac{3 × 8}{8 × 9}\) = \(\frac{24}{72}\)
Упростите с помощью GCF.
GCF 24 и 72 равен 24.
Разделите числитель и знаменатель на 24.
\(\frac{24 ÷ 24}{72 ÷ 24}\) = \(\frac{1}{3}\)
Вопрос 3.
Сэм и его друзья съели 3 \(\frac{3}{4}\) пакета фруктовых закусок. Если в каждом пакете было 2 \(\frac{1}{2}\) унций, сколько унций фруктовых закусок съели Сэм и его друзья?
\(\frac{□}{□}\)
Ответ:
\(\frac{75}{8}\) унций
Объяснение:
Сэм и его друзья съели 3 \(\frac{3}{ 4}\) пакеты с фруктами. Если каждый пакет содержит 2 \(\frac{1}{2}\) унций
3 \(\frac{3}{4}\) x 2 \(\frac{1}{2}\)
\(\ frac{15}{4}\) x \(\frac{5}{2}\)
\(\frac{15 x 5}{4 x 2}\) = \(\frac{75}{8} \)
Принять участие в точной алгебре Оценить, используя порядок операций.
Запишите ответ в простейшей форме.
Вопрос 4.
\(\left(\frac{3}{4}-\frac{1}{2}\right) \times \frac{3}{5}\)
\(\frac{ □}{□}\)
Ответ:
\(\frac{3}{20}\)
Объяснение:
\(\left(\frac{3}{4}-\frac{1}{2) }\right) \times \frac{3}{5}\)
Выполнить операции в скобках.
\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{1}{4}\)
\(\frac{1}{4} \) x \(\frac{3}{5}\) = \(\frac{1 x 3}{4 x 5}\) = \(\frac{3}{20}\)
Вопрос 5.
\(\frac{1}{3}+\frac{4}{9} \times 12\)
\(\frac{□}{□}\)
Ответ:
\(\frac{28}{3}\)
Объяснение:
\(\frac{1}{3}\) + \( \frac{4}{9}\) = \(\frac{7}{9}\)
\(\frac{7 x 12}{9 x 1}\) = \(\frac{84}{9 }\)
Упрощение с помощью GCF.
GCF 84 и 9 равен 3.
Разделите числитель и знаменатель на 3.
\(\frac{84 ÷ 3}{9 ÷ 3}\) = \(\frac{28}{3}\)
Вопрос 6.
\(\frac{5}{8} \times \frac{7}{10}-\frac{1}{4}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{11}{16}\)
Объяснение:
\(\frac{5 x 7}{8 x 10}\) = \(\frac{35}{80}\)
\(\frac{35}{80}\) – \( \frac{1}{4}\) = \(\frac{11}{16}\)
Вопрос 7.
3 × (\(\frac{5}{18}\) + \(\frac{ 1}{6}\)) + \(\frac{2}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{38}{15}\ )
Объяснение:
3 x \(\frac{4}{9}\) + \(\frac{2}{5}\)
3 x \(\frac{38}{45}\) = \ (\frac{38}{15}\)
Самостоятельно
Практика: Скопируйте и решите Найдите продукт. Напишите в простейшей форме.
Вопрос 8.
\(1 \frac{2}{3} \times 2 \frac{5}{8}\)
\(\frac{□}{□}\)
Ответ:
\ (\frac{35}{8}\)
Объяснение:
1 \(\frac{2}{3}\) = \(\frac{5}{3}\)
2 \(\frac{5 {8}\) = \(\frac{21}{8}\)
\(\frac{5 × 21}{3 × 8}\) = \(\frac{105}{24}\)
Упростите с помощью GCF
GCF 105 и 24 равен 3.
Разделите числитель и знаменатель на 3.
\(\frac{105 ÷ 3}{24 ÷ 3}\) = \(\frac{35}{ 8}\)
Вопрос 9.
\(\frac{4}{9} \times \frac{4}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{16}{45}\)
Объяснение:
\( \frac{4 × 4}{9 × 5}\) = \(\frac{16}{45}\)
Вопрос 10.
\(\frac{1}{6} \times \frac{2} {3}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{9}\)
Объяснение:
\(\frac{1 × 2}{ 6 × 3}\) = \(\frac{2}{18}\)
Упростите с помощью GCF
GCF 2 и 18 равен 2.
Разделите числитель и знаменатель на 2.
\(\frac{ 2 ÷ 2}{18 ÷ 2}\) = \(\frac{1}{9}\)
Вопрос 11.
\(4 \frac{1}{7} \times 3 \frac{1}{9}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{116}{7}\)
Объяснение:
4\(\frac{1}{7}\) = \(\frac{29}{7}\)
3\(\frac {1}{9}\) = \(\frac{28}{9}\)
\(\frac{29 × 28}{7 × 9}\) = \(\frac{812}{63}\ )
Упростите с помощью GCF
GCF 812 и 63 равен 7.
Разделите числитель и знаменатель на 7.
\(\frac{812 ÷ 7}{63 ÷ 7}\) = \(\frac{116 {7}\)
Вопрос 12.
\(\frac{5}{6}\) из 90 питомцев на выставке домашних животных — кошки. \(\frac{4}{5}\) кошек — трехцветные кошки. Какую часть домашних животных составляют трехцветные кошки? Сколько домашних животных — трехцветные кошки?
Введите ниже:
__________
Ответ:
60 ситцевых кошек
Пояснение:
5/6 x 90 = 450/6 = 150/2
150/2 x 4/5 = 60
0 45. Вопрос 13. каждый съел \(\frac{1}{4}\) чашки кошачьего корма. Еще четыре кошки съели по \(\frac{1}{3}\) чашки кошачьего корма. Сколько еды съели девять кошек?
Вопрос 13. каждый съел \(\frac{1}{4}\) чашки кошачьего корма. Еще четыре кошки съели по \(\frac{1}{3}\) чашки кошачьего корма. Сколько еды съели девять кошек?
Введите ниже:
__________
Ответ:
\(\frac{31}{12}\)
Объяснение:
5 x 1/4 = 5/4
4 x 1/3 = 4/3
5/ 4 + 4/3 = 31/12
Принять участие в точной алгебре Оценить, используя порядок операций.
Запишите ответ в простейшей форме.
Вопрос 14.
\(\frac{1}{4} \times\left(\frac{3}{9}+5\right)\)
\(\frac{□}{□}\)
Ответ:
\(\frac{4}{3}\)
Объяснение:
3/9+ 5 = 16/3
1/4 x 16/3
1 x 16 = 16
4 x 3 = 12
16/12
Упростите, используя GCF
GCF 16 и 12 равен 4.
Разделите числитель на знаменатель на 4.
\(\frac{16 ÷ 4}{12÷ 4}\) = \(\frac{4}{3}\)
Вопрос 15.
\(\frac{9}{10 }-\frac{3}{5} \times \frac{1}{2}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{3}{5} \)
Объяснение:
3/5 x 1/2 = 3/10
9/10 – 3/10 = 6/10
Упростите с помощью НОД
НОД 6 и 10 равен 2,
Разделить числитель и знаменатель на 2.
\(\frac{6 ÷ 2}{10 ÷ 2}\) = \(\frac{3}{5}\)
Вопрос 16.
\(\frac {4}{5}+\left(\frac{1}{2}-\frac{3}{7}\right) \times 2\)
\(\frac{□}{□}\)
Ответ:
\(\frac{33}{35}\)
Объяснение:
1/2 – 3/7 = 1/14
1/14 x 2 = 1/7
4/5 + 1/7 = 33/35
Вопрос 17.
\(15 \times \frac{3}{10}+\frac{7}{8}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{141}{8}\)
Объяснение:
3/10 + 7/8 = 47/40
15 x 47/40 = 141/8
\(\frac{141}{8}\)
Номер страницы 84
Вопрос 18.
Напишите и решите текстовую задачу для выражения \(\frac{1}{4} \times \frac{2}{3}\). Показать свою работу.
Введите ниже:
__________
Ответ:
\(\frac{1}{6}\)
Объяснение:
\(\frac{1}{4} \times \frac{2}{3}\) = \(\frac{1 X 2}{4 X 3}\) = \(\frac{2}{12}\)
Упростить с помощью GCF
GCF 2 и 12 равен 2,
Разделите числитель и знаменатель на 2.
\(\frac{2 ÷ 2}{12 ÷ 2}\) = \(\frac{1}{6}\)
Вопрос 19.
У Мишель есть рецепт который просит 2 \(\frac{1}{2}\) чашки растительного масла. Она хочет использовать \(\frac{2}{3}\) это количество масла и заменить остальное яблочным пюре. Сколько яблочного пюре она будет использовать?
Введите ниже:
__________
Ответ:
\(\frac{10}{6}\)
Объяснение:
2 1/2 * 2/3 = 5/2 * 2/3 = 10/6 Она будет используйте 10/6 или 1 2/3 стакана растительного масла
Вопрос 20.
Рецепт маффинов Кары требует 1 \(\frac{1}{2}\) стакана муки для маффинов и \(\frac{1}{4}\) стакана муки для посыпки. Если она приготовит \(\frac{1}{2}\) по оригинальному рецепту, сколько муки она использует для кексов и начинки?
Введите ниже:
__________
Ответ:
Кара использует 1\(\frac{1}{8}\) стакана муки.
Пояснение:
Для начала найдем, сколько чашек муки нужно для приготовления оригинального рецепта. Кара использует 1 1/2 стакана муки для маффинов и 1/4 стакана муки для посыпки.
Итак, 1 1/2 + 1/4 стакана муки для приготовления оригинального рецепта.
1 1/2 = 3/2
3/2 + 1/4 = 7/4
Для приготовления оригинального рецепта Каре нужно 7/4 стакана муки.
Если она сделает \(\frac{1}{2}\) по оригинальному рецепту, то
7/4 x 1/2 = 7/8 = 1 1/8
Кара будет использовать 1 1/8 стакана муки .
Умножение дробей – № страницы 85
Найдите продукт. Напишите в простейшей форме.
Вопрос 1.
\(\frac{4}{5} \times \frac{7}{8}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{7}{10}\)
Объяснение:
Умножьте числители и умножьте знаменатели.
\(\frac{4 × 7}{5 × 8}\) = \(\frac{28}{40}\)
Упростите с помощью GCF.
GCF 28 и 40 равен 4.
Разделите числитель и знаменатель на 4.
\(\frac{28 ÷ 4}{40 ÷ 4}\) = \(\frac{7}{10}\)
Вопрос 2.
\(\frac{1}{8} \times 20\)
\(\frac{□}{□}\)
Ответ:
\(\frac{5}{2}\ )
Объяснение:
\(\frac{1 × 20}{1 × 8}\)
\(\frac{20}{8}\)
Упрощение с использованием GCF.
GCF 20 и 8 равен 4.
Разделите числитель и знаменатель на 4.
\(\frac{20 ÷ 4}{8 ÷ 4}\) = \(\frac{5}{2}\)
Вопрос 3.
\(\frac{4}{5} \times \frac{3}{8}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {3}{10}\)
Объяснение:
Умножьте числители и умножьте знаменатели.
\(\frac{4 × 3}{5 × 8}\) = \(\frac{12}{40}\)
Упростите с помощью GCF.
GCF 12 и 40 равен 4,
Разделить числитель и знаменатель на 4.
\(\frac{12 ÷ 4}{40 ÷ 4}\) = \(\frac{3}{10}\)
Вопрос 4.
\(1 \ frac{1}{8} \times \frac{1}{9}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{8}\)
Объяснение:
1\(\frac{1}{8}\) = \(\frac{9}{8}\)
Умножьте числители и умножьте знаменатели.
\(\frac{9 × 1}{8 × 9}\) = \(\frac{9}{72}\)
Упростите с помощью GCF.
GCF 9 и 72 равен 9.
Разделить числитель и знаменатель на 9.
\(\frac{9 ÷ 9}{72 ÷ 9}\) = \(\frac{1}{8}\)
Вопрос 5.
\(\frac{3}{4} \times \frac {1}{3} \times \frac{2}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{10}\)
Объяснение:
Умножьте числители и умножьте знаменатели.
\(\frac{3 × 1 × 2}{4 × 3 × 5}\) = \(\frac{6}{60}\)
Упростите с помощью GCF.
GCF 6 и 60 равен 6.
Разделите числитель и знаменатель на 6.
\(\frac{6 ÷ 6}{60 ÷ 6}\) = \(\frac{1}{10}\)
Вопрос 6.
Карен выгребла \(\frac{3}{5}\) двор. Минни загребла \(\frac{1}{3}\) от суммы, заработанной Карен. Какую часть двора сгребла Минни?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{3}\)
Объяснение:
Минни сгребла 1/5 двора.
Итак, минни сгребла 3/5 от 1/3, значит 3/5 x 1/3
Умножьте числители и умножьте знаменатели.
\(\frac{3 × 1}{5 × 3}\) = \(\frac{3}{15}\)
Упрощение с использованием GCF.
GCF 3 и 15 равен 3,
Разделить числитель и знаменатель на 3.
\(\frac{3 ÷ 3}{15 ÷ 3}\) = \(\frac{1}{3}\)
Вопрос 7.
\(\frac {3}{8}\) домашних животных на выставке домашних животных — собаки. \(\frac{2}{3}\) собак имеют длинную шерсть. Какую часть домашних животных составляют собаки с длинной шерстью?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{4}\) собаки с длинной шерстью
Объяснение:
\(\frac{3}{8} \) из питомцев на выставке домашних животных — собаки. \(\frac{2}{3}\) собак имеют длинную шерсть.
\(\frac{2}{3}\) собак имеют длинную шерсть.
\(\frac{3}{8}\) of \(\frac{2}{3}\) = \(\frac{3 × 2}{8 × 3}\) = \(\frac{6 }{24}\)
GCF 6 и 24 равен 6.
Разделите числитель и знаменатель на 6.
\(\frac{6 ÷ 6}{24 ÷ 6}\) = \(\frac{1 }{4}\)
\(\frac{1}{4}\) — собаки с длинной шерстью
Оцените, используя порядок операций.
Вопрос 8.
\(\left(\frac{1}{2}+\frac{3}{8}\right) \times 8\)
______
Ответ:
7
Объяснение:
1/2 + 3/8 = 7/8
7/8 × 8 = 7
Вопрос 9.
\(\frac{3}{4} \times\left(1-\frac{1}{9}\right)\)
\(\frac{ □}{□}\)
Ответ:
\(\frac{2}{3}\)
Объяснение:
1 – 1/9 = 8/9
3/4 × 8/9 = 24/36
GCF 24 и 36 равен 12.
Разделите числитель и знаменатель на 12.
\(\frac{24 ÷ 12}{36 ÷ 12}\) = \(\frac{2}{3}\)
Вопрос 10.
\(4 \times \frac{1}{8} \times \frac{3}{10}\)
\(\frac{□}{□}\)
Ответ:
\ (\фракция{3}{20}\)
Объяснение:
Умножьте числители и умножьте знаменатели.
\(\frac{4 × 1 × 3}{1 × 8 × 10}\) = \(\frac{12}{80}\)
Упростите с помощью GCF.
GCF 12 и 80 равен 4.
Разделите числитель и знаменатель на 4.
\(\frac{12 ÷ 4}{80 ÷ 4}\) = \(\frac{3}{20}\)
Вопрос 11.
\(6 \times\left(\frac{4}{5}+\frac{2}{10}\right) \times \frac{2}{3}\)
______
Ответ:
4
Объяснение:
4/5 + 2/10 = 1
6 × 1 × 2/3 = 12/3
GCF 12 и 3 равен 4.
Разделите числитель и знаменатель на 3.
\(\frac{12 ÷ 3}{3 ÷ 3}\) = \(\frac{4}{1}\) = 4
Решение задач
Вопрос 12.
Джейсон пробежал \(\frac{5}{7}\) расстояния по школьной дорожке. Сара пробежала \(\frac{4}{5}\) расстояния Джейсона. Какую часть общего расстояния по дорожке пробежала Сара?
\(\frac{□}{□}\)
Ответ:
\(\frac{4}{7}\)
Объяснение: 904:45 Джейсон пробежал \(\frac{5}{7}\) дистанции вокруг школьной дорожки. Сара пробежала \(\frac{4}{5}\) расстояния Джейсона.
\(\frac{5}{7}\) × \(\frac{4}{5}\) = 20/35
GCF 20 и 35 равен 5.
Разделите числитель и знаменатель на 5.
\(\frac{20 ÷ 5}{35 ÷ 5}\) = \(\frac{4}{7}\)
Вопрос 13.
Группа учащихся посещает математический кружок. Половина учеников — мальчики, и у \(\frac{4}{9}\) мальчиков карие глаза. Какую часть группы составляют мальчики с карими глазами?
\(\frac{□}{□}\)
Ответ:
\(\frac{2}{9}\) группа мальчиков с карими глазами
Пояснение:
Группа школьников посещает математический кружок. Половина учеников — мальчики, и у \(\frac{4}{9}\) мальчиков карие глаза.
\(\frac{4}{9}\) × \(\frac{1}{2}\) = 4/18 = 2/9
2/9 группа — мальчики с карими глазами
Вопрос 14.
Напишите и решите задачу на умножение на дробь.
Введите ниже:
__________
Ответ: 904:45 Группа студентов посещает математический кружок. Половина учеников — мальчики, и у \(\frac{6}{9}\) мальчиков карие глаза. Какую часть группы составляют мальчики с карими глазами?
\(\frac{□}{□}\)
Ответ:
Группа студентов посещает математический кружок. Половина учеников — мальчики, и у \(\frac{6}{9}\) мальчиков карие глаза.
Половина учеников — мальчики, и у \(\frac{6}{9}\) мальчиков карие глаза.
\(\frac{6}{9}\) × \(\frac{1}{2}\) = 6/18 = 1/3
1/3 группы составляют мальчики с карими глазами.
Проверка урока – № страницы 86
Вопрос 1. 904:45 Мама Вероники оставила \(\frac{3}{4}\) торта на столе. Ее братья съели его \(\frac{1}{2}\). Какую часть торта они съели?
\(\frac{□}{□}\)
Ответ:
\(\frac{2}{4}\)
Объяснение:
Мама Вероники ушла \(\frac{3}{4}\) торт на столе. Ее братья съели его \(\frac{1}{2}\).
Поскольку дробь съеденного пирога равна 1/2, вы можете умножить числитель и знаменатель на и получить эквивалентную дробь, которая равна 2/4.
Вопрос 2.
Один круг по школьной дорожке составляет \(\frac{5}{8}\) мили. Карин пробежала 3 \(\frac{1}{2}\) круга. Как далеко она пробежала?
_____ \(\frac{□}{□}\)
Ответ:
2\(\frac{3}{16}\)
Объяснение:
Один круг по школьной дорожке равен \(\frac{5 }{8 миля. Карин пробежала 3 \(\frac{1}{2}\) круга.
3 \(\frac{1}{2}\) = \(\frac{7}{2}\)
Следовательно, общее пройденное расстояние = 7/2 × 5/8 = 35/16 = 2 3/ 16
Spiral Review
Вопрос 3.
Том купил 2 \(\frac{5}{16}\) фунтов арахиса и 2,45 фунта кешью. Чего он купил больше? Объяснять.
Введите ниже:
__________
Ответ:
Объяснение:
Том купил 2 \(\frac{5}{16}\) фунтов арахиса и 2,45 фунта кешью.
2 \(\frac{5}{16}\) = 2,3125
2,3125 < 2,45
Он покупает больше орехов кешью.
Вопрос 4.
У Евы есть 24 марки по 24,75 доллара каждая. Какова общая стоимость ее марок?
$ _____
Ответ:
$594
Пояснение:
У Евы есть 24 марки по 24,75 доллара каждая.
24 х 24,75 долл. США = 59 долл. США4
Вопрос 5.
Наоми отправилась в поход на 10,5 миль. Утром она прошла 1,75 мили, отдохнула, а затем прошла еще 2,4 мили. Она завершила поход во второй половине дня. Насколько дальше она прошла утром, чем днем?
_____ миль
Ответ:
Наоми отправилась в поход на 6,5 миль. Утром она прошла 1,75 мили, отдохнула, а затем прошла еще 2,4 мили. Она завершила поход во второй половине дня.
Утром она прошла 1,75 мили, отдохнула, а затем прошла еще 2,4 мили. Она завершила поход во второй половине дня.
Чтобы узнать, сколько миль она прошла днем, просто вычтите утренние мили 4,15 из общего количества миль 6,5.
6,5 – 4,15 = 2,35
Чтобы узнать, сколько еще миль она прошла утром, нужно просто вычесть утро из полудня: 4,15 – 2,35 = 1,8 мили.
Утром она прошла еще 1,8 мили.
Вопрос 6.
У владельца книжного магазина есть 48 книг по научной фантастике и 30 детективов, которые он хочет быстро продать. Он сделает дисконтные пакеты с одним типом книг в каждом. Он хочет, чтобы в каждом пакете было как можно больше книг, но все пакеты должны содержать одинаковое количество книг. Сколько пакетов он может сделать? Сколько у него упаковок каждого типа книг?
Введите ниже:
__________
Ответ:
18 упаковок
Объяснение:
Владелец книжного магазина может сделать 18 возможных упаковок
48 – 30 = 18 упаковок
Найти продукт. Упрощайте перед умножением.
Упрощайте перед умножением.
Вопрос 1.
\(\frac{5}{6} \times \frac{3}{10}\)
\(\frac{□}{□}\)
Ответ:
\(\ frac{1}{4}\)
Объяснение:
\(\frac{5}{6} \times \frac{3}{10}\)
Умножьте числители и умножьте знаменатели.
\(\frac{5 × 3}{6 × 10}\) = \(\frac{15}{60}\)
Упрощение с использованием GCF.
GCF 15 и 60 равен 15.
Разделите числитель и знаменатель на 15.
\(\frac{15 ÷ 15}{60 ÷ 15}\) = \(\frac{1}{4}\)
Вопрос 2.
\(\frac{3}{4} \times \frac{5}{9}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {5}{12}\)
Объяснение:
\(\frac{3}{4} \times \frac{5}{9}\)
Умножьте числители и умножьте знаменатели.
\(\ гидроразрыва {3 × 5} {4 × 9}\) = \(\frac{15}{36}\)
Упрощение с помощью GCF.
GCF чисел 15 и 36 равен 3.
Разделите числитель и знаменатель на 3.
\(\frac{15 ÷ 3}{36 ÷ 3}\) = \(\frac{5}{12}\)
Вопрос 3.
\(\frac{2}{3} \times \frac{9}{10}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {3}{5}\)
Объяснение:
\(\frac{2}{3} \times \frac{9}{10}\)
Умножьте числители и умножьте знаменатели.
\(\frac{2 × 9}{3 × 10}\) = \(\frac{18}{30}\)
Упрощение с использованием GCF.
GCF 18 и 30 равен 6.
Разделите числитель и знаменатель на 6.
\(\frac{18 ÷ 6}{30 ÷ 6}\) = \(\frac{3}{5}\)
Вопрос 4.
После пикника осталось \(\frac{5}{12}\) кукурузного хлеба. Вал ест \(\frac{3}{5}\) оставшегося кукурузного хлеба. Какую часть кукурузного хлеба съедает Вэл?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{4}\)
Объяснение:
После пикника, \(\frac{5}{12}\ ) кукурузного хлеба осталось. Вал ест \(\frac{3}{5}\) оставшегося кукурузного хлеба.
\(\frac{5}{12} \times \frac{3}{5}\)
Умножить числители и Умножить знаменатели.
\(\frac{5 × 3}{12 × 5}\) = \(\frac{15}{60}\)
Упростите с помощью GCF.
GCF 15 и 60 равен 15.
Разделите числитель и знаменатель на 15.
\(\frac{15 ÷ 15}{60 ÷ 15}\) = \(\frac{1}{4}\)
Вопрос 5.
В домике для рептилий в зоопарке живет игуана длиной \(\frac{5}{6}\) ярдов. У него есть монстр Хила, длина которого составляет \(\frac{4}{5}\) длины игуаны. Какова длина монстра Гила?
Какова длина монстра Гила?
\(\frac{□}{□}\)
Ответ:
\(\frac{2}{3}\)
Объяснение:
В доме рептилий в зоопарке есть игуана, которая \(\frac {5}{6}\) ярдов в длину. У него есть монстр Хила, длина которого составляет \(\frac{4}{5}\) длины игуаны.
\(\frac{5}{6} \times \frac{4}{5}\)
Умножьте числители и умножьте знаменатели.
\(\frac{5 × 4}{6× 5}\) = \(\frac{20}{30}\)
Упрощение с использованием GCF.
GCF 20 и 30 равен 10.
Разделить числитель и знаменатель на 10.
\(\frac{20 ÷ 10}{30 ÷ 10}\) = \(\frac{2}{3}\)
Самостоятельно
Найдите продукт. Упрощайте перед умножением.
Вопрос 6.
\(\frac{3}{4} \times \frac{1}{6}\)
\(\frac{□}{□}\)
Ответ:
Объяснение:
\(\frac{3}{4} \times \frac{1}{6}\)
Умножьте числители и умножьте знаменатели.
\(\frac{3 × 1}{4 × 6}\) = \(\frac{3}{24}\)
Упростите с помощью GCF.
GCF 3 и 24 равен 3,
Разделить числитель и знаменатель на 3.
\(\frac{3 ÷ 3}{24 ÷ 3}\) = \(\frac{1}{8}\)
Вопрос 7.
\(\frac {7}{10} \times \frac{2}{3}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{7}{15}\)
Объяснение:
\(\frac{7}{10} \times \frac{2}{3}\)
Умножьте числители и умножьте знаменатели.
\(\frac{7 × 2}{10 × 3}\) = \(\frac{14}{30}\)
Упростите с помощью GCF.
GCF 14 и 30 равен 2.
Разделить числитель и знаменатель на 2.
\(\frac{14 ÷ 2}{30 ÷ 2}\) = \(\frac{7}{15}\)
Вопрос 8.
\(\frac{5}{8} \times \frac {2}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{4}\)
Объяснение:
\(\frac{5} {8} \times \frac{2}{5}\)
Умножить числители и Умножить знаменатели.
\(\frac{5 × 2}{8 × 5}\) = \(\frac{10}{40}\)
Упростите с помощью GCF.
GCF 10 и 40 равен 10.
Разделите числитель и знаменатель на 10.
\(\frac{10 ÷ 10}{40 ÷ 10}\) = \(\frac{1}{4}\)
Вопрос 9.
\(\frac{9}{10} \times \frac{5}{6}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {3}{4}\)
Объяснение:
\(\frac{9}{10} \times \frac{5}{6}\)
Умножьте числители и умножьте знаменатели.
\(\frac{9 × 5}{10 × 6}\) = \(\frac{45}{60}\)
Упростите с помощью GCF.
GCF 45 и 60 равен 15.
Разделите числитель и знаменатель на 15.
\(\frac{45 ÷ 15}{60 ÷ 15}\) = \(\frac{3}{4}\)
Вопрос 10.
\(\frac{11}{12} \times \frac{3}{7}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{11}{28 }\)
Объяснение:
\(\frac{11}{12} \times \frac{3}{7}\)
Умножьте числители и умножьте знаменатели.
\(\frac{11 × 3}{12 × 7}\) = \(\frac{33}{84}\)
Упростите с помощью GCF.
GCF чисел 33 и 84 равен 3.
Разделите числитель и знаменатель на 3.
\(\frac{33 ÷ 3}{84 ÷ 3}\) = \(\frac{11}{28}\)
Вопрос 11.
Баскетбольная команда Шелли выиграла \(\frac{3}{4}\) своих игр в прошлом сезоне. В \(\frac{1}{6}\) выигранных ими играх они опередили своих противников более чем на 10 очков. Какую часть своих игр команда Шелли выиграла с разницей более 10 очков?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{8}\)
Объяснение:
Пусть общее количество игр равно x.
Количество игр, выигранных командой Шелли = 3/4x
Количество игр, в которых команда Шелли опередила своих соперников более чем на 10 очков = 1/6 X 3/4x = 1/8x
Следовательно, 1/8 от общего числа игр команда Шелли выиграла на 10 баллов.
Вопрос 12.
У мистера Ортиса есть \(\frac{3}{4}\) фунта овсянки. Он использует \(\frac{2}{3}\) овсянки, чтобы испечь кексы. Сколько овсянки осталось у мистера Ортиса?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{2}\)
Объяснение:
У мистера Ортиса есть \(\frac{3}{4}\ ) фунт овсянки. Он использует \(\frac{2}{3}\) овсянки, чтобы испечь кексы.
\(\frac{3}{4} \times \frac{2}{3}\)
Умножить числители и Умножить знаменатели.
\(\frac{3 × 2}{4 × 3}\) = \(\frac{6}{12}\)
Упрощение с использованием GCF.
GCF 6 и 12 равен 6.
Разделите числитель и знаменатель на 6.
\(\frac{6 ÷ 6}{12 ÷ 6}\) = \(\frac{1}{2}\)
Вопрос 13.
Стратегии сравнения Чтобы найти \(\frac{16}{27}\) × \(\frac{3}{4}\), можно умножить дроби и затем упростить произведение или можно упростить дроби, а затем умножить. Какой метод вы предпочитаете? Объяснять.
Какой метод вы предпочитаете? Объяснять.
Введите ниже:
__________
Ответ:
\(\frac{16}{27}\) × \(\frac{3}{4}\)
\(\frac{16 × 3}{27 × 4 }\) = \(\frac{16 × 3}{4 × 27}\)
\(\frac{48}{96}\)
Упрощение с использованием GCF.
GCF чисел 48 и 96 равен 48.
Разделить числитель и знаменатель на 48.
\(\frac{48 ÷ 48}{96 ÷ 48}\) = \(\frac{1}{2}\)
Решение проблем + Приложения – № страницы 90
Вопрос 14.
Три каждый учащийся лопнул \(\frac{3}{4}\) стакана зерен попкорна. В таблице показана доля нелопнувших ядер каждого ученика. У какого учащегося было \(\frac{1}{16}\) чашек нелопнувших зёрен?
__________
Ответ:
Мирза
Объяснение:
Каждый из трех студентов лопнул по \(\frac{3}{4}\) чашке зерен попкорна. В таблице показана доля нелопнувших ядер каждого ученика.
Кэти = 3/4 x 1/10 = 3/40
Мирза = 3/4 x 1/12 = 1/16
Вопрос 15.
Беговая дорожка в школе Франсин: \(\frac{3}{4 }\) длиной в милю. Вчера Франсин проехала два круга по трассе. Если она пробежала \(\frac{1}{3}\) дистанции, а оставшуюся часть пути прошла пешком, то какое расстояние она прошла?
Вчера Франсин проехала два круга по трассе. Если она пробежала \(\frac{1}{3}\) дистанции, а оставшуюся часть пути прошла пешком, то какое расстояние она прошла?
____ мили
Ответ:
1 миля
Объяснение:
Длина беговой дорожки в школе Франсин = 3/4 мили
Пусть расстояние, пройденное бегом, равно = x
Пусть расстояние, пройденное пешком, равно = y
Общее количество кругов, пройденных Франсин = 2
Общее расстояние, пройденное Франсин = количество кругов X расстояние, пройденное за один круг
2 x 3/4 = 3/25 мили
Теперь,
расстояние, пройденное бегом = 1/3 общего расстояния
x = 1/3 x 3/2
расстояние, пройденное ходьбой y = общее расстояние – расстояние, пройденное бегом
3/2 – x = 3/2 – 1/ 2 = 1 миля
Следовательно, Франсин прошла 1 милю.
Вопрос 16.
В магазине закусок \(\frac{7}{12}\) покупателей купили крендели с солью и \(\frac{3}{10}\) из них купили крендели с низким содержанием соли. Билл утверждает, что \(\frac{7}{30}\) клиентов купили крендельки с низким содержанием соли. Имеет ли смысл заявление Билла? Объяснять.
Имеет ли смысл заявление Билла? Объяснять.
Введите ниже:
__________
Ответ:
Утверждение Билла не имеет смысла, потому что оно неверно:
7/12 клиентов купили крендельки.
3/10 Из этих клиентов купили крендельки с низким содержанием соли (x)
3/10 от 7/12 = x
21/120 = x
Упрощенно: 7/40
Чтобы быть точным, Билл должен был бы сказать, что 7/40 клиентов купили крендели с низким содержанием соли, но вместо этого он сказал 7/30.
Вопрос 17.
В таблице показано домашнее задание Тони. Учитель Тони поручил классу упростить каждое выражение, разделив числитель и знаменатель на НОК. Заполните таблицу, упростив каждое выражение и найдя значение.
Введите ниже:
__________
Ответ:
Упрощение факторов — страница № 91
Найдите продукт. Упрощайте перед умножением.
Вопрос 1.
\(\frac{8}{9} \times \frac{5}{12}\)
\(\frac{□}{□}\)
Ответ:
\(\ frac{10}{27}\)
Объяснение:
\(\frac{8}{9} \times \frac{5}{12}\)
Умножьте числители и умножьте знаменатели.
\(\frac{8 × 5}{9 × 12}\) = \(\frac{40}{108}\)
Упрощение с использованием GCF.
GCF 40 и 108 равен 4.
Разделите числитель и знаменатель на 4.
\(\frac{40 ÷ 4}{108 ÷ 4}\) = \(\frac{10}{27}\)
Вопрос 2.
\(\frac{3}{4} \times \frac{16}{21}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {4}{7}\)
Объяснение:
\(\frac{3}{4} \times \frac{16}{21}\)
Умножьте числители и умножьте знаменатели.
\(\frac{3 × 16}{4 × 21}\) = \(\frac{48}{84}\)
Упростите с помощью GCF.
GCF 48 и 84 равен 12.
Разделите числитель и знаменатель на 12.
\(\frac{48 ÷ 12}{84 ÷ 12}\) = \(\frac{4}{7}\)
Вопрос 3.
\(\frac{15}{20} \times \frac{2}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {3}{10}\)
Объяснение:
\(\frac{15}{20} \times \frac{2}{5}\)
Умножьте числители и умножьте знаменатели.
\(\frac{15 × 2}{20 × 5}\) = \(\frac{30}{100}\)
Упростите с помощью GCF.
GCF 30 и 100 равен 10,
Разделить числитель и знаменатель на 10.
\(\frac{30 ÷ 10}{100 ÷ 10}\) = \(\frac{3}{10}\)
Вопрос 4.
\(\frac {9}{18} \times \frac{2}{3}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{3}\)
Объяснение:
\(\frac{9}{18} \times \frac{2}{3}\)
Умножьте числители и умножьте знаменатели.
\(\frac{9 × 2}{18 × 3}\) = \(\frac{18}{54}\)
Упростите с помощью GCF.
GCF 18 и 54 равен 18.
Разделить числитель и знаменатель на 18.
\(\frac{18 ÷ 18}{54 ÷ 18}\) = \(\frac{1}{3}\)
Вопрос 5.
\(\frac{3}{4} \times \frac {7}{30}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{7}{40}\)
Объяснение:
\(\frac{3} {4} \times \frac{7}{30}\)
Умножить числители и Умножить знаменатели.
\(\frac{3 × 7}{4 × 30}\) = \(\frac{21}{120}\)
Упростите с помощью GCF.
GCF 21 и 120 равен 3.
Разделите числитель и знаменатель на 3.
\(\frac{21 ÷ 3}{120 ÷ 3}\) = \(\frac{7}{40}\)
Вопрос 6.
\(\frac{8}{15} \times \frac{15}{32}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {1}{4}\)
Объяснение:
\(\frac{8}{15} \times \frac{15}{32}\)
Умножьте числители и умножьте знаменатели.
\(\frac{8 × 15}{15 × 32}\) = \(\frac{120}{480}\)
Упростите с помощью GCF.
GCF 120 и 480 равен 120.
Разделите числитель и знаменатель на 120.
\(\frac{120 ÷ 120}{480 ÷ 120}\) = \(\frac{1}{4}\)
Вопрос 7.
\(\frac{12}{21} \times \frac{7}{9}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{ 4}{9}\)
Объяснение:
\(\frac{12}{21} \times \frac{7}{9}\)
Умножьте числители и умножьте знаменатели.
\(\frac{12 × 7}{21 × 9}\) = \(\frac{84}{189}\)
Упростите с помощью GCF.
GCF чисел 84 и 189 равен 21.
Разделите числитель и знаменатель на 21.
\(\frac{84 ÷ 21}{189 ÷ 21}\) = \(\frac{4}{9}\)
Вопрос 8.
\(\frac{18}{22} \times \frac{8}{9}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{8}{11 }\)
Объяснение:
\(\frac{18}{22} \times \frac{8}{9}\)
Умножьте числители и умножьте знаменатели.
\(\frac{18 × 8}{22 × 9}\) = \(\frac{144}{198}\)
Упростите с помощью GCF.
GCF чисел 144 и 198 равен 18.
Разделите числитель и знаменатель на 18.
\(\frac{144 ÷ 18}{198 ÷ 18}\) = \(\frac{8}{11}\)
Решение проблем
Вопрос 9.
У Эмбер есть мешок цветного песка весом в 1,5 кг. Она использует \(\frac{1}{2}\) сумки для художественного проекта. Сколько песка она использует для проекта?
\(\frac{□}{□}\) фунтов
Ответ:
\(\frac{2}{5}\) фунтов
Объяснение:
Эмбер имеет \(\frac{4}{5} \)-килограммовый мешок цветного песка. Она использует \(\frac{1}{2}\) сумки для художественного проекта.
4/5 X 1/2 = 2/5
Вопрос 10.
У Тайлера есть \(\frac{3}{4}\) месяц, чтобы написать отчет о книге. В тот раз он закончил отчет за \(\frac{2}{3}\). Сколько времени потребовалось Тайлеру, чтобы написать отчет?
\(\frac{□}{□}\) месяц
Ответ:
\(\frac{1}{2}\) месяц
Объяснение:
Тайлер имеет \(\frac{3}{4}\ ) месяц, чтобы написать отчет о книге. В тот раз он закончил отчет за \(\frac{2}{3}\).
3/4 X 2/3 = 1/2
Вопрос 11.
Укажите два способа умножения \(\frac{2}{15} \times \frac{3}{20}\). Затем скажите, какой путь проще, и обоснуйте свой выбор.
Введите ниже:
__________
Ответ:
\(\frac{2}{15} \times \frac{3}{20}\)
2/15 X 3/20 = 2/20 X 3/15 = 1/10 х 1/5 = 1/50
Проверка урока – № страницы 92
Найдите каждый продукт. Упрощайте перед умножением.
Вопрос 1.
В школе Сьюзи \(\frac{5}{8}\) всех учеников занимаются спортом. Из студентов, которые занимаются спортом, \(\frac{2}{5}\) играют в футбол. Какая часть учеников школы Сьюзи играет в футбол?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{4}\)
Объяснение:
В школе Сьюзи, \(\frac{5}{8}\ ) всех учащихся занимаются спортом. Из студентов, которые занимаются спортом, \(\frac{2}{5}\) играют в футбол.
Умножьте 5/8 X 2/5, и ответ будет 0,25, что преобразуется в 25/100 или 1/4
Вопрос 2.
Коробка попкорна весит \(\frac{15}{16}\) фунтов . В коробке находится \(\frac{1}{3}\) попкорн с маслом и \(\frac{2}{3}\) сырный попкорн. Сколько весит сырный попкорн?
Сколько весит сырный попкорн?
\(\frac{□}{□}\)
Ответ:
\(\frac{5}{8}\)
Объяснение:
Общий вес коробки попкорна = 15/16 фунтов.
Нам дают два вида попкорна: попкорн с маслом и попкорн с сыром.
Сливочное масло для попкорна составляет одну треть от общего веса = 1/3 от общего веса
Подставляя значение общего веса, получаем
= 1/3 * 15/16 = 5/16 фунтов.
Сырный попкорн = 2/3 от общего веса
Подставив значение общего веса, получим
= 2/3 * 15/16 = 10/16 или 5/8 фунтов.
Следовательно, сырный попкорн весит 5/8 фунта.
Spiral Review
Вопрос 3.
Рамон купил дюжину кукурузных початков за 1,80 доллара. Сколько стоил каждый початок кукурузы?
$ ______
Ответ:
$0,15
Пояснение:
Рамон купил дюжину кукурузных початков за 1,80 доллара.
Итак, при стоимости каждого початка кукурузы 1,80/12 = 0,15 доллара
Вопрос 4.
Банка корицы весом 1,8 унции стоит 4,05 доллара. Какова стоимость за унцию?
Какова стоимость за унцию?
$ ______
Ответ:
2,25 доллара за унцию
Объяснение:
Если банка на 1,8 унции стоит 4,05 доллара, разделите 4,05 доллара на 1,8.
4,05 доллара / 1,8 = 2,25 доллара за унцию.
Вопрос 5.
Роуз купила \(\frac{7}{20}\) килограмм имбирных конфет и 0,4 килограмма конфет с корицей. Чего она купила больше? Объясните откуда вы знаете.
Введите ниже:
__________
Ответ:
Роза купила имбирных конфет = 7/20 кг = 0,35 кг
Она купила коричных конфет = 0,4 кг
0,4 > 0,35
Следовательно, Она купила коричных конфет больше.
Вопрос 6.
Дон прошел 3 \(\frac{3}{5}\) мили в пятницу, 3,7 мили в субботу и 3 \(\frac{5}{8}\) мили в воскресенье. Перечислите расстояния от наименьшего к наибольшему.
Введите ниже:
__________
Ответ:
3 \(\frac{3}{5}\), 3 \(\frac{5}{8}\), 3,7
Объяснение:
3 \(\frac{3}{5}\) = 18/5 = 3,6
3 \(\frac{5}{8}\) = 29/8 = 3,625
3,6 < 3,625 < 3,7
3 \(\frac{3}{5}\), 3 \(\frac{5}{8}\), 3. 7
7
Контрольная точка в середине главы – Словарь – Страница № 93
Выберите лучший термин из коробки, чтобы закончить предложение.
Вопрос 1.
Дроби \(\frac{1}{2}\) и \(\frac{5}{10}\) равны _____.
Введите ниже:
__________
Ответ:
Равные дроби
Вопрос 2.
_____ — это знаменатель, который совпадает в двух или более дробях.
Введите ниже:
__________
Ответ:
Общий знаменатель
Понятия и навыки
Запишите в виде десятичной дроби. Скажите, использовали ли вы деление, числовую прямую или какой-либо другой метод.
Вопрос 3.
\(\frac{7}{20}\)
_____
Ответ:
0,35
Объяснение:
Используя деление,
\(\frac{7}{20}\) = 0,35
Вопрос 4.
8 \(\frac{39}{40}\)
_____
Ответ:
8.975
Объяснение:
Используя деление,
8 \(\frac{39}{40}\) = 359/40 = 8,975
Вопрос 5.
1 \(\frac{5}{8}\)
_____
Ответ:
1,625
Объяснение:
Используя деление,
1 \(\frac{5 {8}\) = 13/8 = 1,625
Вопрос 6.
\(\frac{19}{25}\)
_____
Ответ:
0,76
Объяснение:
Используя деление,
\(\frac{19}{25}\) = 0,76
Порядок от меньшего к большему.
Вопрос 7.
\(\frac{4}{5}, \frac{3}{4}, 0,88\)
Введите ниже:
__________
Ответ:
\(\frac{3}{4 }\), \(\frac{4}{5}\),0,88
Объяснение:
Запишите десятичную форму 4/5 = 0,8
Запишите десятичную форму 3/4 = 0,75
0,88
0,75 < 0,8 < 0,88
Вопрос 8.
0,65, 0,59, \(\frac{3}{5}\)
Введите ниже:
__________
Ответ:
0,59, \(\frac{3}{5}\), 0,65
Объяснение:
Запишите десятичную форму числа 3/5 = 0,6
0,59 < 0,6 < 0,65
Вопрос 9.
\(1 \frac{1}{4}, 1 \frac{2}{3}, \frac{11}{12}\)
Введите ниже:
__________
Ответ:
\(\frac{11}{12} \), 1\(\frac{1}{4}\), 1\(\frac{2}{3}\)
Объяснение:
Напишите десятичную форму 1 1/4 = 5/4 = 1,25
Запишите десятичную форму 1 2/3 = 5/3 = 1,66
Запишите десятичную форму 11/12 = 0,916
0,916 < 1,25 < 1,66
Вопрос 10.
0,9, \(\frac{7}{8}\), 0,86
Введите ниже:
__________
Ответ:
0,86, \(\frac{7}{ 8}\), 0,9
Объяснение:
Запишите десятичную форму \(\frac{7}{8}\) = 0,875
0,86 < 0,875 < 0,9
Найдите произведение. Напишите в простейшей форме.
Вопрос 11.
\(\frac{2}{3} \times \frac{1}{8}\)
\(\frac{□}{□}\)
Ответ:
\(\ гидроразрыв{1}{12}\)
Объяснение:
\(\frac{2}{3} \times \frac{1}{8}\)
Умножьте числители и умножьте знаменатели.
\(\frac{2 × 1}{3 × 8}\) = \(\frac{2}{24}\)
Упрощение с использованием GCF.
GCF 2 и 24 равен 2.
Разделите числитель и знаменатель на 2.
\(\frac{2 ÷ 2}{24 ÷ 2}\) = \(\frac{1}{12}\)
Вопрос 12.
\(\frac{4}{5} \times \frac{2}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac {8}{25}\)
Объяснение:
\(\frac{4}{5} \times \frac{2}{5}\)
Умножить числители и Умножить знаменатели.
\(\frac{4 × 2}{5 × 5}\) = \(\frac{8}{25}\)
Вопрос 13.
12 × \(\frac{3}{4}\)
_____
Ответ:
9
Объяснение:
12 × \(\frac{3}{4}\)
Умножьте числители и умножьте знаменатели.
\(\frac{12 × 3}{1 × 4}\) = \(\frac{36}{4}\) = 9
Вопрос 14.
Mia поднимается \(\frac{5}{8} \) от высоты скальной стены. Ли поднимается на \(\frac{4}{5}\) расстояния Мии. Какую часть стены преодолевает Ли?
\(\frac{□}{□}\)
Ответ:
\(\frac{7}{40}\)
Объяснение:
найти НОК (наименьший общий знаменатель) для 5/8 и 4/ 5.
5/8= 25/40 и 4/5= 32/40.
Вычтите, и вы получите 7/40.
Страница № 94
Вопрос 15.
В классе Зои у \(\frac{4}{5}\) учеников есть домашние животные. Из студентов, у которых есть домашние животные, \(\frac{1}{8}\) есть грызуны. У какой части учеников в классе Зои есть домашние грызуны? У какой части учеников в классе Зои есть домашние животные, не являющиеся грызунами?
Введите ниже:
__________
Ответ:
\(\frac{1}{10}\) учеников в классе Зои имеют домашних животных — грызунов
\(\frac{7}{10}\) учеников в классе Зои есть домашние животные, не являющиеся грызунами
Пояснение:
В классе Зои у \(\frac{4}{5}\) учеников есть домашние животные. Из студентов, у которых есть домашние животные, \(\frac{1}{8}\) есть грызуны.
Из студентов, у которых есть домашние животные, \(\frac{1}{8}\) есть грызуны.
4/5 X 1/8 = 1/10
4/5 – 1/10 = 7/10
Вопрос 16.
Рецепт требует 2 \(\frac{2}{3}\) стаканов муки . Терелл хочет сделать \(\frac{3}{4}\) по рецепту. Сколько муки он должен использовать?
_____ чашек
Ответ:
2 чашки
Объяснение:
2 \(\frac{2}{3}\) = 8/3
8/3 * 3/4 = 2
Вопрос 17.
После Во время Baltimore Running Festival в 2009 году волонтеры собрали и переработали 3,75 тонны мусора. Начертите 3,75 на числовой прямой и запишите вес в виде смешанного числа.
Введите ниже:
__________
Ответ:
Волонтеры собрали и переработали 3,75 тонны мусора.
Нам нужно преобразовать 3,75 в смешанное число.
Смешанное число состоит из целого числа и правильной дроби.
В заданном числе 3,75 возьми 3 за целое число и преобразуй 0,75 в дробь.
3,75 = 3 + 0,75 = 3 + 75/100
Мы можем уменьшить дробь 75/100 = 3+ 3/4 = 3 3/4
Вопрос 18.
Четыре студента сдавали экзамен. Дана доля от общего количества возможных баллов, полученных каждым игроком. У кого из учеников был самый высокий балл? Если учащиеся получают целое число баллов по каждому элементу экзамена, может ли экзамен в сумме дать 80 баллов? Объяснять.
Введите ниже:
__________
Ответ:
22/25 = 0,88
17/20 = 0,85
4/5 = 0,8
3/4 = 0,75 17/20 + 4/5 + 3/4)x = 80
x = 24,39
Это не целое число точек.
Поделись и покажи — № страницы 97
Используйте модель, чтобы найти частное.
Вопрос 1.
\(\frac{1}{2}\) ÷ 3
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{6} \)
Объяснение:
1/2 группы по 3
\(\frac{1}{2}\) ÷ 3
1/2 × 1/3 = 1/6
Вопрос 2.
\(\frac{3} {4} \div \frac{3}{8}\)
______
Ответ:
2
Объяснение:
3/4 группы по 3/8
3/4 × 8/3 = 2
Используйте полоски дробей, чтобы найти частное. Затем нарисуйте модель.
Затем нарисуйте модель.
Вопрос 3.
\(\frac{1}{3}\) ÷ 4
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{12}\ )
Объяснение:
\(\frac{1}{3}\) ÷ 4
\(\frac{1}{3}\) × \(\frac{1}{4}\)
\(\frac{1}{ 12}\)
Вопрос 4.
\(\frac{3}{5} \div \frac{3}{10}\)
______
Ответ:
2
Объяснение:
\(\frac{ 3}{5} \div \frac{3}{10}\)
\(\frac{3}{5}\) × \(\frac{10}{3}\)
2
Нарисуйте модель для решения. Затем напишите уравнение модели. Интерпретируйте результат.
Вопрос 5.
Сколько \(\frac{1}{4}\) порций изюма в \(\frac{3}{8}\) стакане изюма?
Введите ниже:
__________
Ответ:
1,5
Объяснение:
3/8 × 1/4 = 1,5
Вопрос 6.
Сколько \(\frac{1}{3}\) фунтов мешков с тропой смесь, которую Джош может сделать из \(\frac{5}{6}\) фунтов смеси?
Введите ниже:
__________
Ответ:
2
Объяснение:
Умножьте 1/3 на 2
1/3 × 2 = 2/6. 2/6 может дважды перейти в 5/6, поэтому ответ — две сумки.
2/6 может дважды перейти в 5/6, поэтому ответ — две сумки.
Вопрос 7.
Постановка задачи Напишите и решите задачу на \(\frac{3}{4}\) ÷ 3, которая показывает, сколько в каждой из 3 групп.
Введите ниже:
__________
Ответ:
\(\frac{1}{4}\)
Объяснение:
\(\frac{3}{4}\) ÷ 3
\(\frac{3} {4}\) × \(\frac{1}{3}\) = 1/4
Решение задач + Приложения – № страницы 98
В таблице показано количество каждого материала, которое учащиеся на уроке шитья нужен один кошелек.
Используйте таблицу для 8–10. Используйте модели для решения.
Вопрос 8.
У миссис Браун есть \(\frac{1}{3}\) ярдов синей джинсовой ткани и \(\frac{1}{2}\) ярдов черной джинсовой ткани. Сколько кошельков можно сшить, используя джинсовую ткань в качестве основной ткани?
_____ кошельки
Ответ:
5 кошельков
Объяснение:
Миссис Браун имеет \(\frac{1}{3}\) ярдов синей джинсовой ткани и \(\frac{1}{2}\) ярдов джинсовой ткани. черный деним.
черный деним.
3 + 2 = 5
Вопрос 9.
Один ученик приносит \(\frac{1}{2}\) ярдов ленты. Если 3 ученика получат ленточки одинаковой длины, сколько ленточек получит каждый ученик? Хватит ли у каждой из них ленты на кошелек? Объяснять.
Введите ниже:
__________
Ответ:
Один ученик приносит \(\frac{1}{2}\) ярдов ленты. Если 3 ученика получат ленту одинаковой длины,
\(\frac{1}{2}\) ÷ 3
1/2 × 1/3 = 1/6
У них не хватает ленты для кошелька
Вопрос 10.
Приводить аргументы Было \( \frac{1}{2}\) ярдов ткани в фиолетовую и розовую полоску. Джесси сказала, что может сделать только \(\frac{1}{24}\) сумочку, используя эту ткань в качестве отделки. Она правильная? Используйте то, что вы знаете о значениях умножения и деления, чтобы защитить свой ответ.
Введите ниже:
__________
Ответ:
Было \(\frac{1}{2}\) ярдов ткани в фиолетовую и розовую полоску. Джесси сказала, что может сделать только \(\frac{1}{24}\) сумочку, используя эту ткань в качестве отделки.
1/2 × 12 = 1/24
Итак, ответ 12
Вопрос 11.
Нарисуйте модель, чтобы найти частное.
\(\frac{1}{2}\) ÷ 4 =
Введите ниже:
__________
Ответ:
Объяснение:
1/2 × 1/4 = 1/8
Модель Дробь Деление – Стр. № 99
Используйте модель, чтобы найти частное
Вопрос 1.
\(\frac{1}{4}\) ÷ 3 =
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{12}\)
Объяснение:
\(\frac{1}{4}\) ÷ 3
\(\frac{1}{4}\) × \(\frac{1}{3}\) = \(\frac{ 1}{12}\)
Вопрос 2.
\(\frac{1}{2} \div \frac{2}{12}=\)
______
Ответ:
3
Объяснение:
\(\frac{1}{2} \div \frac{2}{12}=\)
\(\frac{1}{2}\) × \(\frac{12}{2}\) = \(\frac{12}{4}\) = 3
Используйте полосы дробей, чтобы найти частное.
Вопрос 3.
\(\frac{5}{6} \div \frac{1}{2}=\)
______ \(\frac{□}{□}\)
Ответ:
\(\frac{5}{3}\)
Объяснение:
\(\frac{5}{6} \div \frac{1}{2}=\)
\(\frac {5}{6}\) × \(\frac{2}{1}\) = \(\frac{5}{3}\)
Вопрос 4.
\(\frac{2}{3} \) ÷ 4 =
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{6}\)
Объяснение:
\(\frac{2}{3} \) ÷ 4
\(\frac{2}{3}\) × \(\frac{1}{4}\) = \(\frac{2}{12}\) = 1/6
Вопрос 5.
\(\frac{1}{2}\) ÷ 6 =
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{12}\)
Объяснение:
\(\frac{1}{2}\) ÷ 6
\(\frac{1}{2}\) × \(\frac{1}{6}\) = \(\frac {1}{12}\)
Вопрос 6.
\(\frac{1}{3} \div \frac{1}{12}\)
______
Ответ:
4
Объяснение:
\ (\frac{1}{3} \div \frac{1}{12}\)
\(\frac{1}{3}\) × \(\frac{12}{1}\) = \( \frac{12}{3}\) = 4
Нарисуйте модель для решения. Затем напишите уравнение модели. Интерпретируйте результат.
Вопрос 7.
Если Джерри пробегает \(\frac{1}{10}\) мили каждый день, сколько дней ему потребуется, чтобы пробежать \(\frac{4}{5}\) мили?
______ дней
Ответ:
8 дней
Объяснение:
Если Джерри пробегает \(\frac{1}{10}\) мили каждый день,
\(\frac{4}{5}\) ÷ \( \frac{1}{10}\)
\(\frac{4}{5}\) × \(\frac{10}{1}\) = \(\frac{40}{5}\) = 8
Решение проблем
Вопрос 8.
У миссис Дженнингс есть \(\frac{3}{4}\) галлонов краски для художественного проекта. Она планирует разделить краску поровну по баночкам. Если она нальет \(\frac{1}{8}\) галлонов краски в каждую банку, сколько банок она израсходует?
______ банок
Ответ:
6 банок
Пояснение:
У миссис Дженнингс есть 3/4 галлона краски для художественного проекта.
В 1 банку она кладет 1/8 галлона краски.
Количество банок, в которых она планирует разделить краску поровну, определяется выражением
n= 3/4 ÷ 1/8
n = \(\frac{3}{4}\) × \(\frac{ 8}{1}\) = \(\frac{24}{4}\) = 6
Вопрос 9.
Если одна банка клея весит \(\frac{1}{12}\) фунтов, сколько банок, которые Рикки может получить из \(\frac{2}{3}\) фунта клея?
______ банок
Ответ:
8 банок
Объяснение:
Вес клея в одной банке = 1/12 фунта
Чтобы получить 2/3 фунта клея, Рикки может получить количество банок
2/3 ÷ 1/ 12
2/3 × 12/1 = 24/3 = 8
Вопрос 10.
Объясните, как использовать модель для отображения \(\frac{2}{6} \div \frac{1}{12}\ ) и \(\frac{2}{6}\) ÷ 4.
Введите ниже:
__________
Ответ:
Объяснение:
\(\frac{2}{6} \div \frac{1 {12}\)
2/6 = 1/3
1/3 x 12/1 = 4
\(\frac{2}{6}\) ÷ 4
1/3 x 1/4 = 1/12
Проверка урока – страница № 100
Вопрос 1
Дарси нужно \(\frac{1}{4}\) ярдов ткани, чтобы сделать баннер. У нее 2 метра ткани. Сколько баннеров она может сделать?
______ баннеры
Ответ:
8 баннеров
Пояснение:
Дарси нужно \(\frac{1}{4}\) ярдов ткани, чтобы сделать баннер. У нее 2 метра ткани.
2 ÷ \(\frac{1}{4}\) = 2 x 4 = 8
Вопрос 2. 904:45 Лоренцо купил \(\frac{15}{16}\) фунтов говяжьего фарша. Он хочет делать гамбургеры весом \(\frac{3}{16}\) фунтов каждый. Сколько гамбургеров он может приготовить?
______ гамбургеров
Ответ:
5 гамбургеров
Пояснение:
Лоренцо купил \(\frac{15}{16}\) фунтов говяжьего фарша. Он хочет делать гамбургеры весом \(\frac{3}{16}\) фунтов каждый.
Он хочет делать гамбургеры весом \(\frac{3}{16}\) фунтов каждый.
\(\frac{15}{16}\) ÷ \(\frac{3}{16}\)
15/3 = 5
Спиральный обзор
Вопрос 3.
Летиша хочет читать по 22 страницы за ночь. При такой скорости за сколько времени она прочитает книгу из 300 страниц?
______ ночей
Ответ:
14 ночей
Объяснение:
Летиша хочет читать по 22 страницы за ночь. Ей нужно прочитать книгу из 300 страниц
300/22 = 13,6
13,6 близко к 14
Итак, это за 2 недели.
Вопрос 4.
Директор хочет заказать тетради для 624 учеников. Блокноты поставляются в коробках по 28 штук. Сколько коробок он должен заказать?
______ ящиков
Ответ:
22 ящика
Объяснение:
Директор хочет заказать тетради для 624 учеников. Блокноты поставляются в коробках по 28 штук.
624/28 = 22,2857
22,2857 ближе к 22
22 коробки.
Вопрос 5.
Каждый квартал в районе Тона имеет длину \(\frac{2}{3}\) мили. Если он пройдет 4 \(\frac{1}{2}\) квартала, сколько он пройдет?
Если он пройдет 4 \(\frac{1}{2}\) квартала, сколько он пройдет?
______ миль
Ответ:
3 мили
Объяснение:
Если каждый блок имеет длину 2/3 мили и он проходит 4 1/2 квартала, мы можем просто умножить на два. Выглядит так:
(2/3)(4 1/2)
умножить, преобразовать 4 1/2 в неправильную дробь и нормально умножить
(2/3)(9/4)
Тонн проходит 3 мили всего.
Вопрос 6.
В саду Кэти \(\frac{5}{6}\) участка засажены цветами. Из цветов \(\frac{3}{10}\) красные. Какая часть сада Кэти засажена красными цветами?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{4}\)
Объяснение:
В саду Кэти, \(\frac{5}{6}\ ) участка засажены цветами. Из цветов \(\frac{3}{10}\) красные.
5/6 x 3/10 = 1/4
Поделись и покажи – № страницы 103
Оцените, используя совместимые числа.
Вопрос 1.
\(22 \frac{4}{5} \div 6 \frac{1}{4}\)
_______
Ответ:
4
Объяснение:
22 \(\frac{ 4}{5}\) = 114/5 = 22,8
6 \(\frac{1}{4}\) = 25/4 = 6,25
22,8 ближе к 24
6,25 ближе к 6
24/6 = 4
Вопрос 2.
\(12 \div 3 \frac{3}{4}\)
_______
Ответ:
3
Объяснение:
3 \(\frac{3}{4}\) = 15/4 = 3,75
3,75 ближе к 4
12/4 = 3
Вопрос 3.
\(33 \frac{ 7}{8} \div 5 \frac{1}{3}\)
_______
Ответ:
7
Объяснение:
33 \(\frac{7}{8}\) = 271/8 = 33,875
5 \(\frac{1}{3}\) = 16/3 = 5,333
33,875 ближе к 35
5,333 ближе к 5
35/5 = 7
Вопрос 4.
\(3 \frac{ 7}{8} \div \frac{5}{9}\)
_______
Ответ:
4
Объяснение:
3 \(\frac{7}{8}\) = 31/8 = 3,875
\(\frac{5}{9}\) = 0,555
3,875 ближе к 4
0,555 равно ближе к 1
4/1 = 4
Вопрос 5.
\(34 \frac{7}{12} \div 7 \frac{3}{8}\)
_______
Ответ:
5
Объяснение :
34 \(\frac{7}{12}\) = 415/12 = 34,583
7 \(\frac{3}{8}\) = 59/8 = 7,375
34,583 ближе к 35
7,375 равно ближе к 7
35/7 = 5
Вопрос 6.
\(1 \frac{2}{9} \div \frac{1}{6}\)
_______
Ответ:
5
Объяснение:
1 \(\frac{2}{9}\) = 11/9 = 1,222
\(\frac {1}{6}\) = 0,1666
1,222 ближе к 1
0,1666 ближе к 0,2
1/0,2 = 5
Самостоятельно
Оцените, используя совместимые числа.
Вопрос 7.
\(44 \frac{1}{4} \div 11 \frac{7}{9}\)
_______
Ответ:
4
Объяснение:
44 \(\frac{ 1}{4}\) = 177/4 = 44,25
11 \(\frac{7}{9}\) = 106/9 = 11,77
44,25 ближе к 44
11,77 ближе к 11
44/11 = 4
Вопрос 8.
\(71 \frac{ 11}{12} \div 8 \frac{3}{4}\)
_______
Ответ:
8
Объяснение:
71 \(\frac{11}{12}\) = 863/12 = 71,916
8 \(\frac{3}{4}\) = 35/4 = 8,75
71,916 ближе к 72
8,75 ближе к 9
72/9 = 8
Вопрос 9.
\(1 \frac{ 1}{6} \div \frac{1}{8}\)
_______
Ответ:
12
Объяснение:
1 \(\frac{1}{6}\) = 7/6 = 1,166
\(\frac{1}{8}\) = 0,125
1,166 ближе к 1,2
0,125 равно ближе к 0,1
1,2/0,1 = 12
Оценка для сравнения. Напишите <, > или =.
Вопрос 10.
\(21 \frac{3}{10} \div 2 \frac{5}{6}\) _______ \(35 \frac{7}{9} \div 3 \frac{2 }{3}\)
Ответ:
\(21 \frac{3}{10} \div 2 \frac{5}{6}\) < \(35 \frac{7}{9} \div 3 \frac{2}{3}\)
Объяснение:
21 \(\frac{3}{10}\) = 213/10 = 21,3
2 \(\frac{5}{6}\) = 17/6 = 2,833
21,3 ближе к 21
2,833 ближе до 3
21/3 = 7
35 \(\frac{7}{9}\) = 322/9 = 35,777
3 \(\frac{2}{3}\) = 11/3 = 3,666
35,777 ближе к 36
3,666 ближе к 4
36/4 = 9
7 < 9
Итак, \(21 \frac{3}{10} \div 2 \frac{5}{6}\) < \( 35 \frac{7}{9} \div 3 \frac{2}{3}\)
Вопрос 11.
\(29 \frac{4}{5} \div 5 \frac{1}{6} \) _______ \(27 \фрак{8}{9} \div 6 \frac{5}{8}\)
Ответ:
\(29 \frac{4}{5} \div 5 \frac{1}{6}\) > \(27 \frac{ 8}{9} \div 6 \frac{5}{8}\)
Объяснение:
29 \(\frac{4}{5}\) = 149/5 = 29,8
5 \(\frac{1 {6}\) = 31/6 = 5,1666
29,8 ближе к 30
5,1666 ближе к 5
30/5 = 6
27 \(\frac{8}{9}\) = 251/9 = 27,888
6 \(\frac{5}{8}\) = 53/8 = 6,625
27,888 ближе к 30
6,625 ближе 7
30/7 = 5
6 > 5
\(29 \frac{4} {5} \div 5 \frac{1}{6}\) > \(27 \frac{8}{9}} \div 6 \frac{5}{8}\)
Вопрос 12.
\(55 \frac{5}{6} \div 6 \frac{7}{10}\) _______ \(11 \frac {5}{7} \div \frac{5}{8}\)
Ответ:
\(55 \frac{5}{6} \div 6 \frac{7}{10}\) < \( 11 \frac{5}{7} \div \frac{5}{8}\)
Объяснение:
55 \(\frac{5}{6}\) = 335/6 = 55,833
6 \(\ frac{7}{10}\) = 67/10 = 6,7
55,833 ближе к 56
6,7 ближе к 7
56/7 = 8
11 \(\frac{5}{7}\) = 82/ 7 = 11,714
\(\frac{5}{8}\) = 0,625
11,714 ближе к 12
0,625 ближе к 1
12/1 = 12
8 < 12
Вопрос 13.
Марион делает школьные флаги. На каждый флаг уходит 2 \(\frac{3}{4}\) ярда войлока. У Марион есть 24 \(\frac{1}{8}\) ярдов войлока. Примерно сколько флагов он может сделать?
О _______ флагах
Ответ:
О 8 флагах
Пояснение:
Марион делает школьные флаги. На каждый флаг уходит 2 \(\frac{3}{4}\) ярда войлока. У Марион есть 24 \(\frac{1}{8}\) ярдов войлока.
2 \(\frac{3}{4}\) = 11/4
24 \(\frac{1}{8}\) = 193/8
193/8 ÷ 11/4
193/8 x 4/11 = 8,77
Около 8 флажков
Вопрос 14.
Садовая улитка путешествует около 2 \(\frac{3}{5}\) футов за 1 минуту. При такой скорости сколько часов потребуется улитке, чтобы пройти 350 футов?
Около _______ часов
Ответ:
Около 2 часов
Объяснение:
2 \(\frac{3}{5}\) = 2,6
Столько времени он проходит за одну минуту. В часе 60 минут, так что умножьте это на 60 и посмотрите, приблизится ли это к 350.
60 x 2,6 = 156
Теперь добавим еще один час.
156 + 156 = 312
14 x 2,6 = 36,4
312 + 36,4 = 348,4
348,4 + 2,6 = 351
Так два часа и четырнадцать минут
Решение проблем + приложения — Страница № 104
Что была ошибка?
Вопрос 15.
Меган делает вымпелы из куска плотной бумаги длиной 10 \(\frac{3}{8}\) ярдов. Для каждого вымпела требуется \(\frac{3}{8}\) ярдов бумаги. Чтобы оценить количество вымпелов, которые она могла бы сделать, Меган оценила частное 10 \(\frac{3}{8}\) ÷ \(\frac{3}{8}\).
Посмотрите, как Меган решила проблему. Найдите ее ошибку
Оценка:
10 \(\frac{3}{8}\) ÷ \(\frac{3}{8}\)
10 ÷ \(\frac{1}{2}\) = 5
Исправьте ошибку. Оцените частное.
Итак, Меган может сделать около _____ вымпелов.
Опишите ошибку, которую допустила Меган
Объясните Укажите, какие совместимые числа вы использовали для оценки 10 \(\frac{3}{8}\) ÷ \(\frac{3}{8}\). Объясните, почему вы выбрали именно эти числа.
Введите ниже:
__________
Ответ:
10 \(\frac{3}{8}\) ÷ \(\frac{3}{8}\)
10 \(\frac{3}{8}\) = 83/8 = 10,375
\(\frac{3}{8}\) = 0,375
Она написала 10 ÷ \(\frac{1}{2 }\) = 5
10,375 ближе к 10
0,375 ближе к 0,5
10/0,5 = 20
Но она написала 5 вместо 20.
Меган может сделать около 20 вымпелов.
Для чисел 16a–16c оцените для сравнения. Выберите <, > или =.
Вопрос 16.
16а. 18 \(\frac{3}{10} \div 2 \frac{5}{6}\) ? \(30 \frac{7}{9} \div 3 \frac{1}{3}\)
_____
Ответ:
16а. 18 \(\frac{3}{10} \div 2 \frac{5}{6}\) < \(30 \frac{7}{9} \div 3 \frac{1}{3}\)
Объяснение:
18 \(\frac{3}{10}\) = 183/10 = 18,3
2 \(\frac{5}{6}\) = 17/6 = 2,833
18,3 ближе к 18
2,833 ближе к 3
18/3 = 6
30 \(\frac{7}{9}\) = 277/9 = 30,777
3 \(\frac{1}{3}\) = 10/3 = 3,333
30,777 ближе к 30
3,333 ближе к 3
30/3 = 10
6 < 10
Вопрос 16.
16b. 17 \(\frac{4}{5} \div 6 \frac{1}{6}\) ? \(19\frac{8}{9} \div 4 \frac{5}{8}\)
_____
Ответ:
17 \(\frac{4}{5} \div 6 \frac{1}{6} \) < \(19 \frac{8}{9} \div 4 \frac{5}{8}\)
Объяснение:
17 \(\frac{4}{5}\) = 89/5 = 17,8
6 \(\frac{1}{6}\) = 37/6 = 6,1666
17,8 ближе к 18
6,1666 ближе к 6
18/6 = 3
19 \(\frac{8}{9 }\) = 179/9 = 19,888
4 \(\frac{5}{8}\) = 37/8 = 4,625
19,888 ближе к 20
4,625 ближе к 5
20/5 = 4
3 < 4
17 \(\frac{4}{5} \div 6 \frac{1}{6}\) < \(19\frac{8}{9} \div 4 \frac{5}{8}\)
Вопрос 16.
16c. 17 \(\frac{5}{6} \div 6 \frac{1}{4}\) ? \(11 \frac{5}{7} \div 2 \frac{3}{4}\)
_____
Ответ:
17 \(\frac{5}{6} \div 6 \frac{1} {4}\) < \(11 \frac{5}{7} \div 2 \frac{3}{4}\)
Объяснение:
17 \(\frac{5}{6}\) = 107 /6 = 17,833
6 \(\frac{1}{4}\) = 25/4 = 6,25
17,833 ближе к 18
6,25 ближе к 6
18/6 = 3
11 \(\frac{5 {7}\) = 82/7 = 11,714
2 \(\frac{3}{4}\) = 11/4 = 2,75
11,714 ближе к 12
2,75 ближе к 3
12/3 = 4
3 < 4
17 \(\frac{5}{6} \div 6 \frac{1}{4}\) < \( 11 \frac{5}{7} \div 2 \frac{3}{4}\)
Расчетные коэффициенты – № страницы 105
Оценка с использованием совместимых чисел.
Вопрос 1.
\(12 \frac{3}{16} \div 3 \frac{9}{10}\)
______
Ответ:
3
Объяснение:
12 \(\frac{ 3}{16}\) = 195/16 = 12,1875
3 \(\frac{9}{10}\) = 39/10 = 3,9
12.1875 ближе к 12
3.9 ближе к 4
12/4 = 3
Вопрос 2.
\(15 \frac{3}{8} \div \frac{1}{2}\)
______
Ответ:
30
Объяснение:
15 \(\frac{3}{8}\) = 123/8 = 15,375
\(\frac{1}{2}\) = 0,5
15,375 ближе к 15
0,5 ближе к 0,5
15/0,5 = 30
Вопрос 3.
\(22 \frac{1}{5} \div 1 \frac{5}{6}\)
______
Ответ:
11
Объяснение:
22 \(\frac{1}{5}\) = 111/5 = 22,2
1 \(\frac{5}{6}\) = 11/6 = 1,8333
22,2 ближе к 22
1,8333 ближе к 2
22/2 = 11
Вопрос 4.
\(7 \frac{ 7}{9} \div \frac{4}{7}\)
______
Ответ:
16
Объяснение:
7 \(\frac{7}{9}\) = 70/9 = 7,777
\(\frac{4}{7}\) = 0,571
7,777 ближе к 8
0,571 ближе к 0,5
8/0,5 = 16
Вопрос 5.
\(18 \frac{1}{4} \ div 2 \frac{4}{5}\)
______
Ответ:
6
Объяснение:
18 \(\frac{1}{4}\) = 73/4 = 18,25
2 \(\frac{4}{5}\) = 14/5 = 2,8
18,25 ближе к 18
2.8 ближе к 3
18/3 = 6
Вопрос 6.
\(\frac{15}{16} \div \frac{1}{7}\)
______
Ответ:
10
Объяснение :
\(\frac{15}{16}\) = 0,9375
\(\frac{1}{7}\) = 0,1428
0,9375 ближе к 1
0,1428 ближе к 0,1
1/0,1 = 10
Вопрос 7.
\(14 \frac{7}{8} \div \frac{5}{11}\)
______
Ответ:
30
Объяснение:
14 \(\frac{7}{8}\) = 119/8 = 14,875
\(\frac{5}{11}\) = 0,4545
14,875 is ближе к 15
0,4545 ближе к 0,5
15/0,5 = 30
Вопрос 8.
\(53 \frac{7}{12} \div 8 \frac{11}{12}\)
______
Ответ :
6
Объяснение:
53 \(\frac{7}{12}\) = 643/12 = 53,58
8 \(\frac{11}{12}\) = 107/12 = 8,916
53,58 равно ближе к 54
8,916 ближе к 9
54/9 = 6
Вопрос 9.
\(1 \frac{1}{6} \div \frac{1}{9}\)
______
Ответ:
10
Объяснение:
1 \ (\frac{1}{6}\) = 7/6 = 1,166
\(\frac{1}{9}\) = 0,111
1,166 ближе к 1
0,111 ближе к 0,1
1/0,1 = 10
Решение задач
Вопрос 10.
Оцените, сколько кусков будет у Шэрон, если она разделит 15 \(\frac{1}{3}\) ярдов ткани на 4 \(\frac{4}{5) }\) длины ярдов.
Около ______ шт.
Ответ:
Около 3 штук
Объяснение:
Шэрон будет, если она разделит 15 \(\frac{1}{3}\) ярдов ткани на 4 \(\frac{4}{5}\) ярдов длины.
3 7/36 — это ответ.
Итак, около 3 штук
Вопрос 11.
Оцените, сколько \(\frac{1}{2}\) литровых контейнеров Итан может заполнить из контейнера с 8 \(\frac{7}{8}\) кварт воды.
Около ______ контейнеров
Ответ:
Около 18 контейнеров
Вопрос 12.
Чем оценка частных отличается от оценки продуктов?
Введите ниже:
__________
Ответ:
Чтобы вычислить произведение и частное, нужно сначала округлить числа. Чтобы округлить до ближайшего целого числа, посмотрите на цифру в десятом разряде. Если меньше 5, округлить в меньшую сторону. Если 5 или больше, округляем в большую сторону. Помните, что оценка — это не точный, но приблизительный и обоснованный ответ.
Давайте рассмотрим пример оценки продукта.
Оцените произведение: 11,256×6,81
Сначала округлим первое число. Поскольку на десятом месте стоит двойка, 11,256 округляется до 11,9.0445 Далее округляем второе число. Поскольку на десятом месте стоит 8, 6,81 округляется до 7.
Затем умножьте округленные числа. 11×7=77
Ответ равен 77.
Давайте рассмотрим пример вычисления частного.
Оцените частное: 91,93÷4,39
Сначала округлим первое число. Поскольку на десятом месте стоит 9, 91,93 округляется до 92.
Затем округляем второе число. Поскольку на десятом месте стоит 3, 4,39 округляется до 4.
Затем разделите округленные числа.
92÷4=23
Ответ: 23.
Проверка урока – Страница № 106
Вопрос 1.
На каждую буханку тыквенного хлеба требуется 1 \(\frac{3}{4}\) чашки изюма . Примерно сколько буханок можно приготовить из 10 чашек изюма?
Про ______ буханок
Ответ:
Про 5 буханок
Пояснение:
Разделите 10 на 1 3/4.
Ответ: 5,714285
Таким образом, вы можете испечь около 5 буханок хлеба с 10 чашками изюма, если на каждую буханку нужно 1 3/4 чашки изюма.
Вопрос 2.
Цель Перри — пробегать 2 \(\frac{1}{4}\) мили каждый день. Один круг по школьной трассе составляет \(\frac{1}{3}\) мили. Примерно сколько кругов он должен пробежать, чтобы достичь своей цели?
Около ______ кругов
Ответ:
Около 9 кругов
Объяснение:
Цель Перри — пробегать 2 \(\frac{1}{4}\) мили каждый день. Один круг по школьной трассе составляет \(\frac{1}{3}\) мили.
2 \(\frac{1}{4}\) = 9/4 = 2,25
\(\frac{1}{3}\) = 0,333
Перри придется пробежать 9кругов, чтобы достичь своей цели.
Spiral Review
Вопрос 3.
Рецепт требует \(\frac{3}{4}\) чайной ложки красного перца. Ури хочет использовать \(\frac{1}{3}\) от этой суммы. Сколько красного перца он должен использовать?
\(\frac{□}{□}\) чайная ложка
Ответ:
\(\frac{1}{4}\) чайная ложка
Объяснение:
Рецепт требует \(\frac{3}{4 }\) чайная ложка красного перца. Ури хочет использовать \(\frac{1}{3}\) от этой суммы.
Ури хочет использовать \(\frac{1}{3}\) от этой суммы.
\(\frac{1}{3}\) из \(\frac{3}{4}\) = \(\frac{1}{4}\)
Вопрос 4.
Рецепт требует 2 \(\frac{2}{3}\) чашек нарезанных яблок. Зои хочет использовать 1 \(\frac{1}{2}\) раз больше этой суммы. Сколько чашек яблок должна съесть Зоя?
______ чашек
Ответ:
4 чашки
Объяснение:
Рецепт требует 2 2/3 чашки нарезанных яблок.
Зоя хочет использовать в полтора раза больше этой суммы.
Мы умножим количество ломтиков яблока на 1 1/2
2 2/3 X 1 1/2
8/3 X 3/2 = 24/6 = 4 чашки
Зоя использует 4 чашки ломтиков яблок.
Вопрос 5.
У Эдгара 2,8 метра веревки. Если он разрежет его на 7 равных частей, какой длины будет каждая часть?
______ метров
Ответ:
0,4 метра
Объяснение:
2,8/7 = 0,4 метра
Вопрос 6.
У Ками есть 7 литров воды, чтобы наполнить бутылки по 2,8 литра каждая. Сколько бутылок она может заполнить?
______ бутылок
Ответ:
2 бутылки
Объяснение:
7/2,8 = 2,5
она может наполнить только 2, потому что все, что больше, составило бы 8,4 литра воды
Поделись и покажи – № страницы 109
Оценка. Затем найдите частное.
Затем найдите частное.
Вопрос 1.
\(\frac{5}{6}\) ÷ 3
\(\frac{□}{□}\)
Ответ:
\(\frac{3}{10}\ )
Объяснение:
5/6 = 0,8333 ближе к 0,9
0,9/3 = 0,3 = 3/10
Используйте числовую прямую, чтобы найти частное.
Вопрос 2.
\(\frac{3}{4} \div \frac{1}{8}\)
_______
Ответ:
Объяснение:
3/4 x 8 = 3 x 2 = 6
Вопрос 3.
\(\frac{3}{5} \div \frac{3}{10}\)
_______
Ответ:
Объяснение:
3/5 x 10/3 = 2
Оценка. Затем запишите частное в простейшей форме.
Вопрос 4.
\(\frac{3}{4} \div \frac{5}{6}\)
\(\frac{□}{□}\)
Ответ:
\(\ frac{1}{1}\)
Объяснение:
3/4 = 0,75 ближе к 0,8
5/6 = 0,8333 ближе к 0,8
0,8/0,8 = 1
Вопрос 5.
\(3 \div \frac{3}{4}\)
_______
Ответ:
4
Объяснение:
3/4 = 0,75
3/0,75 = 4
4 Вопрос 4 5. \(\frac{1}{2} \div \frac{3}{4}\)
\(\frac{1}{2} \div \frac{3}{4}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{625}{1000} \)
Объяснение:
1/2 = 0,5
3/4 = 0,75 ближе к 0,8
0,5/0,8 = 0,625 = 625/1000
Вопрос 7.
\(\frac{5}{12} \div 3\)
\(\frac{□}{□}\)
Ответ:
\(\frac{2}{10}\)
Объяснение:
5/12 = 0,4166 ближе к 0,6
0,6/3 = 0,2 = 2/10
Самостоятельно
Практика: Скопируйте и решите оценку. Затем запишите частное в простейшей форме
Вопрос 8.
\(2 \div \frac{1}{8}\)
_______
Ответ:
20
Объяснение:
1/8 = 0,125 ближе к 0,1
2/0,1 = 20
Вопрос 9.
\(\frac{3}{4} \div \frac{3}{5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{1}\)
Объяснение:
3/4 = 0,75 ближе к 0,8
3/5 = 0,6 ближе к 0,8
0,8/0,8 = 1
Вопрос 10.
\ (\frac{2}{5} \div 5\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{10}\)
Объяснение:
2 /5 = 0,4 ближе к 0,5
0,5/5 = 0,1 = 1/10
Вопрос 11.
\(4 \div \frac{1}{7}\)
_______
Ответ:
40
Объяснение :
1/7 = 0,1428 ближе к 0,1
4/0,1 = 40
Практика: копирование и решение Оцените, используя порядок операций.
Запишите ответ в простейшей форме.
Вопрос 12.
\(\left(\frac{3}{5}+\frac{1}{10}\right) \div 2\)
\(\frac{□}{□}\)
Ответ:
\(\frac{7}{20}\)
Объяснение:
3/5 + 1/10 = 7/10 = 0,7
0,7/2 = 7/20
Вопрос 13.
\ (\frac{3}{5}+\frac{1}{10} \div 2\)
\(\frac{□}{□}\)
Ответ:
\(\frac{13}{20 }\)
Объяснение:
\(\frac{3}{5}+\frac{1}{10} \div 2\)
(1/10)/2 = 1/20
3/5 + 1/20 = 0,65 = 13/20
Вопрос 14.
\(\frac{3}{5}+2 \div \frac{1}{10}\)
_______ \(\frac{□}{□}\)
Ответ:
Объяснение:
2/(1/10) = 1/5
3/5 + 1/5 = 4/5
Вопрос 15.
Обобщение Предположим, что делитель и делимое в задаче на деление равны дроби от 0 до 1, а делитель больше делимого. Является ли частное меньше, равно или больше 1?
Является ли частное меньше, равно или больше 1?
Введите ниже:
__________
Ответ:
Делитель и делимое — это дроби от 0 до 1
Кроме того, Делитель > Делимое
Меньшее число делится на большее число
Всякий раз, когда меньшее число делится на большее число, частное меньше 1
Пример:
0,5/0,6 Здесь оба числа от 0 до 1, и делитель больше делимого.
Результат 0,8333, МЕНЬШЕ 1
Следовательно, ответ таков, что частное будет меньше 1
Решение проблем + Приложения – № страницы 110
Используйте таблицу для 16–19.
Вопрос 16.
Кристен хочет вырезать ступеньки лестницы из 6-футовой доски. Сколько ступеней лестницы она может перерезать?
_______ перекладины лестницы
Ответ:
8 перекладин лестницы
Пояснение:
Кристен хочет вырезать перекладины лестницы из 6-футовой доски.
перекладин лестницы = 3/4 фута
6/(3/4) = 8 перекладин
Вопрос 17.
Постановка задачи Вернитесь к задаче 16. Напишите и решите новую задачу, изменив длину доски, которую разрезает Кристен. для ступеней лестницы.
Введите ниже:
__________
Ответ:
Кристен хочет вырезать ступеньки лестницы из 9-футовой доски. Сколько ступеней лестницы она может перерезать?
Кристен хочет вырезать ступеньки лестницы из 9-футовой доски.
перекладины лестницы = 3/4 фута
9/(3/4) = 12 перекладин
Вопрос 18.
Дэн рисует рисунок, состоящий из 8 равных частей по всей длине подоконника. Какова длина каждой части дизайна?
\(\frac{□}{□}\) ярдов
Ответ:
\(\frac{1}{16}\) ярдов
Пояснение:
Дэн рисует рисунок, состоящий из 8 равных частей по всей длине подоконника.
(1/2)/8 = 1/2 x 1/8 = 1/16 ярда
Вопрос 19.
У Дэна есть доска размером \(\frac{15}{16}\) ярдов. Сколько знаков «Не входить» он сможет сделать, если длина знака будет уменьшена вдвое?
_______ знаков
Ответ:
3 знака
Объяснение:
У Дэна есть доска размером \(\frac{15}{16}\) ярдов.
Если длина знака изменена на половину исходной длины, (5/8)/2 = 5/16
(15/16) ÷ 5/16 = 15/16 x 16/5 = 3
Вопрос 20.
У Лорен есть \(\frac{3}{4}\) чашка сухофруктов. Она раскладывает сухофрукты по мешочкам, в каждый из которых входит \(\frac{1}{8}\) чашка. Сколько сумок будет использовать Лорен? Объясните свой ответ, используя слова и числа.
Введите ниже:
__________
Ответ:
6
Пояснение:
У Лорен есть \(\frac{3}{4}\) чашка сухофруктов. Она раскладывает сухофрукты по мешочкам, в каждый из которых входит \(\frac{1}{8}\) чашка.
3/4 ÷ 1/8 = 3/4 х 8 = 6
Лорен имеет 3/4, а в 1/4 есть 2 1/8. Что 3 четверти умножить на два = 6, значит, 6 один восьмой
Разделить дроби – Страница № 111
Оценка. Затем запишите частное в простейшей форме.
Вопрос 1.
\(5 \div \frac{1}{6}\)
_____
Ответ:
25
Объяснение:
1/6 = 0,166 ближе к 0,2
2/0,5
Вопрос 2.
\(\frac{1}{2} \div \frac{1}{4}\)
_____
Ответ:
5
Объяснение:
1/2 = 0,5 ближе к 1
1/4 = 0,25 ближе к 0,2
1/0,2 = 5
Вопрос 3.
\(\frac{4}{5} \div \frac{ 2}{3}\)
_____ \(\frac{□}{□}\)
Ответ:
1 \(\frac{1}{5}\)
Объяснение:
4/5 = 0,8 равно ближе к 0,8
2/3 = 0,66 ближе к 0,6
0,8/0,6 = 1 1/5
Вопрос 4.
\(\frac{14}{15} \div 7\)
\(\frac{□ }{□}\)
Ответ:
\(\frac{2}{15}\)
Объяснение:
14/15 = 0,9333
0,9/7 = 2/15
Вопрос 5.
\(8 \div \frac{1}{3}\)
_____
Ответ:
20
Объяснение:
1/3 = 0,33 ближе до 0,4
8/0,4 = 20
Вопрос 6.
\(\frac{12}{21} \div \frac{2}{3}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{1}\)
Объяснение:
12/21 = 0,571 ближе к 0,6
2/3 = 0,666 ближе к 0,6
0,6/0,6 = 1
Вопрос 7 ,
\(\frac{5}{6} \div \frac{5}{12}\)
_____
Ответ:
2
Объяснение:
5/6 = 0,833 ближе к 0,8
5/12 = 0,416 ближе к 0,4
0,8/0,4 = 2
_____ \(\frac{□}{□}\)
Ответ:
1 \(\frac{2}{10}\)
Объяснение:
5/8 = 0,625 ближе к 0,6
1/2 = 0,5 ближе к 0,5
0,6/0,5 = 1,2 = 1 2/10
Вопрос 9.
Радость съела \(\frac{1}{4 }\) пиццы. Если она разделит оставшуюся часть пиццы на куски, равные \(\frac{1}{8}\) пиццы для ее семьи, сколько кусков получит ее семья?
_____ штук
Ответ:
6 штук
Объяснение:
Пицца разделена на 4 части, Радость съела 1/4.
Итак, оставшиеся части 1 – 1/4 = 3/4
теперь 3/4 пиццы и Джой разделит эту оставшуюся часть пиццы на части равные 1/8, поэтому нам нужно сделать деление
(3/4) ÷ (1/8) = 24/4 = 6 штук.
Вопрос 10.
У Хидэко есть \(\frac{3}{5}\) ярд ленты, чтобы повязать воздушные шары для фестиваля. Для каждого воздушного шара потребуется \(\frac{3}{10}\) ярдов ленты. Сколько воздушных шаров Хидеко может связать лентой?
_____ воздушные шары
Ответ:
2 воздушных шара
Объяснение:
3/10 ярда ленты, необходимой для завязывания = 1 воздушный шар баллоны
С помощью 3/5 ярда Хидеко может связать 2 воздушных шара
Решение задач
Вопрос 11.
Рик знает, что 1 стакан клея весит \(\frac{1}{18}\) фунта. У него \(\frac{2}{3}\) фунт клея. Сколько у него стаканов клея?
_____ чашек
Ответ:
12 чашек
Объяснение:
Для 1/18 фунта, 1 чашка
Для 2/3 фунта, x чашек.
1/8x = 1 x 2/3
1/8x = 2/3
x = 2/3 x 18
x = 2 x 6 = 12 чашек
Вопрос 12.
У миссис Дженнингс было \(\frac{ 5}{7}\) галлонов краски. Она дала по \(\frac{1}{7}\) галлона некоторым студентам. Сколько учеников получили краску, если миссис Дженнингс отдала всю краску?
_____ студентов
Ответ:
4 студента
Объяснение:
У миссис Дженнингс было \(\frac{5}{7}\) галлонов краски. Она дала по \(\frac{1}{7}\) галлона некоторым студентам.
\(\frac{5}{7}\) ÷ \(\frac{1}{7}\) = 25/7 = 3,571 ближе к 4
Вопрос 13.
Напишите задачу на две дроби . Включите решение.
Введите ниже:
__________
Ответ:
У миссис Дженнингс было \(\frac{5}{7}\) галлонов краски. Она дала по \(\frac{1}{7}\) галлона некоторым студентам. Сколько учеников получили краску, если миссис Дженнингс отдала всю краску?
Она дала по \(\frac{1}{7}\) галлона некоторым студентам. Сколько учеников получили краску, если миссис Дженнингс отдала всю краску?
Ответ:
У миссис Дженнингс было \(\frac{5}{7}\) галлонов краски. Она дала по \(\frac{1}{7}\) галлона некоторым студентам.
\(\frac{5}{7}\) ÷ \(\frac{1}{7}\) = 25/7 = 3,571 ближе к 4
Проверка урока – страница № 112
Вопрос 1.
Было \(\frac{2}{3}\) пиццы на 6 друзей, которых поровну поделили. Какую часть пиццы получил каждый?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{9}\)
Объяснение:
Было \(\frac{2}{3}\) из пицца для 6 друзей, чтобы разделить поровну.
\(\frac{2}{3}\) ÷ 6 = 2/3 x 1/6 = 2/18 = 1/9
Вопрос 2.
Рашаду нужно \(\frac{2}{3}\) фунта воска, чтобы сделать свечу. Сколько свечей он может сделать из 6 фунтов воска?
_____ свечи
Ответ:
9 свечей
Пояснение:
Рашаду нужно 2/3 фунта воска, чтобы сделать свечи.
1 свеча = 2/3 фунта.
Итак, для 2 фунтов
3 x 2/3 = 3 свечи
2 фунта = 3 свечи
1 фунт = 3/2 свечи
Итак, для 6 фунтов
6 x 3/2 = 9 свечей
Спираль Обзор
Вопрос 3. 904:45 Джереми съел \(\frac{3}{4}\) сэндвича с подводной лодкой и дал его своему другу \(\frac{1}{3}\) его. Какую часть бутерброда получил друг?
904:45 Джереми съел \(\frac{3}{4}\) сэндвича с подводной лодкой и дал его своему другу \(\frac{1}{3}\) его. Какую часть бутерброда получил друг?
\(\frac{□}{□}\)
Ответ:
\(\frac{1}{4}\)
Объяснение:
У Джереми было \(\frac{3}{4}\) из бутерброд с подводной лодкой и дал его своему другу \(\frac{1}{3}\) его.
1/3 x 3/4 = 1/4
Вопрос 4.
Черное дерево шло со скоростью 3 \(\frac{1}{2}\) миль в час за 1 \(\frac{1}{ 3 часа. Сколько она прошла?
_____ \(\frac{□}{□}\)
Ответ:
4 \(\frac{2}{3}\)
Объяснение:
Черное дерево шло со скоростью 3 \(\frac{1 {2}\) миль в час за 1 \(\frac{1}{3}\) часа.
3 1/2 мили = 7/2 мили … 1 час
х миль = ? … 1 1/3 часа = 4/3 часа
7/2 x 4/3 = 1 x x
x = 7/2 x 4/3
x = 14/3 = 4 2/3 мили
Правильным результатом будет 4 2/3 мили.
Вопрос 5.
Пенни использует \(\frac{3}{4}\) ярда ткани для изготовления каждой подушки. Сколько подушек она может сшить из 6 м ткани?
_____ подушек
Ответ:
8 подушек
Объяснение:
Пенни использует \(\frac{3}{4}\) ярдов ткани на каждую подушку, которую она делает.
Используя 6 ярдов ткани 6/(3/4) = 24/3 = 8
Вопрос 6.
Во время тренировки на беговой дорожке Крис пробежал 2,5 круга за 81 секунду. Каково его среднее время на круге?
_____ секунд
Ответ:
32,4 секунды
Объяснение:
Во время тренировки Крис пробежал 2,5 круга за 81 секунду.
81/2,5 = 32,4 секунды
Поделись и покажи — № страницы 115
Используйте модель, чтобы найти частное.
Вопрос 1.
\(3 \frac{1}{3} \div \frac{1}{3}\)
_____
Ответ:
21
Объяснение:
Модель 3 с 3 шестигранными блоками .
Модель 1/2 с 1 трапециевидным блоком.
Для 1/6,
6 треугольных блоков равны 1 шестиугольнику.
Итак, треугольный блок показывает 1/6.
Сосчитай треугольники.
Есть 21 треугольный блок.
Итак, 3 1/2 ÷ 1/6 = 21,
Вопрос 2.
\(2 \frac{1}{2} \div \frac{1}{6}\)
_____
Ответ:
15
Пояснение:
Модель 2 с 2 шестиугольными блоками.
Модель 1/2 с 1 трапециевидным блоком.
Для 1/6,
6 треугольных блоков равны 1 шестиугольнику.
Итак, треугольный блок показывает 1/6.
Сосчитай треугольники.
Есть 15 треугольных блоков.
Итак, \(2 \frac{1}{2} \div \frac{1}{6}\) = 15.
Используйте блоки шаблонов, чтобы найти частное. Затем нарисуйте модель.
Вопрос 3.
\(2 \frac{2}{3} \div \frac{1}{6}\)
_____
Ответ:
Объяснение:
2 2/3 = 8/3
8/3 ÷ 1/6 = 16
Вопрос 4.
\(3 \frac{1}{2} \div \frac{1}{2}\)
_____
Ответ:
Объяснение:
3 1/2 = 7/2
7/2 ÷ 1/2 = 7
Нарисуйте модель, чтобы найти частное.
Вопрос 5.
\(3 \frac{1}{2} \div 3\)
_____ \(\frac{□}{□}\)
Ответ:
Объяснение:
3 1/2 = 7/2
7/2 ÷ 3 = 21/2
Вопрос 6.
\(1 \frac{1}{4} \div 2\)
\(\frac{□}{□}\)
Ответ:
Объяснение:
1/4 ÷ 2 = 1/2
Вопрос 7.
Используйте соответствующие инструменты Объясните, как можно использовать модели для деления смешанных чисел дробями или целыми числами
Введите ниже:
__________
Ответ:
Умножьте целую часть числа на знаменатель дроби. Добавьте это к числителю. Затем запишите результат над знаменателем.
Решение проблем + Приложения – № страницы 116
Используйте модель для решения. Затем напишите уравнение модели.
Вопрос 8.
Использование моделей Элиза открывает коробку с наборами бисера. Коробка весит 2 \(\frac{2}{3}\) фунтов. Каждый комплект бусин весит \(\frac{1}{6}\) фунтов. Сколько комплектов в коробке? Что означает ответ?
Введите ниже:
__________
Ответ:
В коробке 16 наборов
Пояснение:
Элиза открывает коробку с наборами бус. Коробка весит 2 \(\frac{2}{3}\) фунтов. Каждый комплект шариков весит \(\frac{1}{6}\) фунтов, 2 \(\frac{2}{3}\) ÷ \(\frac{1}{6}\) = 8/3 ÷ 1/6 = 16,
В коробке 16 комплектов.
Вопрос 9.
У Хасана две коробки трейловой смеси. Каждая коробка вмещает 1 \(\frac{2}{3}\) фунт смеси. Он съедает \(\frac{1}{3}\) фунтов смеси каждый день. Сколько дней Хасан может есть трейловую смесь, прежде чем она закончится?
_____ дней
Ответ:
10 дней
Пояснение:
У Хасана есть две коробки со смесью. Каждая коробка вмещает 1 \(\frac{2}{3}\) фунт смеси.
1 \(\frac{2}{3}\) = 5/3
2 x (5/3) = 10/3
Он съедает \(\frac{1}{3}\) фунтов смеси каждый день.
10/3 ÷ 1/3 = 10
Хассан 10 дней ел смесь, пока не закончился.
Вопрос 10.
Разум или вздор? Стив сделал эту модель, чтобы показать \(2 \frac{1}{3} \div \frac{1}{6}\). Он говорит, что частное равно 7. Его ответ разумен или бессмыслица? Объясните свои рассуждения
Введите ниже:
__________
Ответ:
\(2 \frac{1}{3} \div \frac{1}{6}\) = 7/3 ÷ 1/6 = 14.
Он сказал, что частное равно 7.
Его ответ — Бред.
Вопрос 11.
Ева готовит кексы для продажи на благотворительном мероприятии. У нее есть 2 \(\frac{1}{4}\) стакана муки, и по рецепту требуется \(\frac{3}{4}\) стакана муки на каждую партию кексов. Объясните, как использовать модель для определения количества партий кексов, которое может приготовить Ева.
Введите ниже:
__________
Ответ:
3
Пояснение:
Ева готовит кексы для продажи на благотворительном мероприятии. У нее есть 2 \(\frac{1}{4}\) стакана муки, и по рецепту требуется \(\frac{3}{4}\) стакана муки на каждую партию кексов.
2 \(\frac{1}{4}\) ÷ \(\frac{3}{4}\) = 9/4 ÷ 3/4 = 3
Модель Смешанный номерной раздел – № страницы 117
Используйте модель, чтобы найти частное.
Вопрос 1.
\(4 \frac{1}{2} \div \frac{1}{2}\)
_____
Ответ:
9
Пояснение:
Подсчитайте количество трапеций, чтобы найти ответ.
Вопрос 2.
\(3 \frac{1}{3} \div \frac{1}{6}\)
_____
Ответ:
20
Используйте шаблоны или другую модель, чтобы найти частное. Затем нарисуйте модель.
Затем нарисуйте модель.
Вопрос 3.
\(2 \frac{1}{2} \div \frac{1}{6}\)
_____
Ответ:
Пояснение:
Модель 2 с 2 шестиугольными блоками.
Модель 1/2 с 1 трапециевидным блоком.
Для 1/6,
6 треугольных блоков равны 1 шестиугольнику.
Итак, треугольный блок показывает 1/6.
Сосчитай треугольники.
Есть 15 треугольных блоков.
Итак, 212÷16 = 15.
Вопрос 4.
\(2 \frac{3}{4} \div 2\)
_____
Ответ:
Объяснение:
2 3/4 ÷ 2 = 11/2
Решение проблем
Вопрос 5.
У Марти 2 \(\frac{4}{5}\) литров сока. Он наливает одинаковое количество сока в 2 бутылки. Сколько он наливает в каждую бутылку?
_____ \(\frac{□}{□}\) кварты
Ответ:
1\(\frac{2}{5}\) кварты
Объяснение:
У Марти 2 \(\frac{4}{ 5}\) литров сока. Он наливает одинаковое количество сока в 2 бутылки.
2 \(\frac{4}{5}\) = 14/5 = 2,8
2,8/2 = 1,4 = 1 2/5
Вопрос 6.
Сколько \(\frac{1}{3}\ ) порции в фунтах составляют 4 \(\frac{2}{3}\) фунтов сыра?
_____ фунтов
Ответ:
14 фунтов
Объяснение:
4 2/3 = 14/3
(14/3)/(1/3) = 14
Вопрос 7.
Напишите текстовую задачу на деление смешанного числа на целое число. Решите задачу и опишите, как вы нашли ответ.
Введите ниже:
__________
Ответ:
Сколько \(\frac{1}{3}\) фунтовых порций содержится в 4 \(\frac{2}{3}\) фунтах сыра?
Объяснение:
4 2/3 = 14/3
(14/3)/(1/3) = 14
Проверка урока – страница № 118
Нарисуйте модель, чтобы найти частное.
Вопрос 1. 904:45 У Эммы есть 4 фунта птичьего корма. Она хочет разделить его поровну между 3 кормушками для птиц. Сколько птичьего корма она должна положить в каждую?
_____ \(\frac{□}{□}\) фунтов
Ответ:
1\(\frac{1}{2}\) фунтов
Пояснение:
У Эммы есть 4 1/2 фунта птичьего корма.
Преобразуйте это в неправильную дробь.
4 1/2 = 9/2
Эмма хочет разделить его поровну между 3 кормушками для птиц.
Итак, она должна поставить (9/2)/3 = 3/2 = 1 1/2
Вопрос 2.
Коробка крекеров весит 11 \(\frac{1}{4}\) унций. По оценке Кадена, одна порция составляет \(\frac{3}{4}\) унции. Сколько порций в коробке?
_____ порций
Ответ:
15 порций
Объяснение:
11 1/4 на 3/4
11 1/4 = 45/4
45/4 / 3/4 = 45/4 × 4/3 = 180 /12 = 15
есть 15 порций
Обзор спирали
Вопрос 3.
Экологический клуб вызвался очистить 4,8 километра шоссе. Участники организованы в 16 команд. Каждая команда очистит одинаковое количество шоссе. Сколько шоссе очистит каждая команда?
_____ километров
Ответ:
0,3 км
Пояснение:
Экологический клуб вызвался очистить 4,8 км шоссе. Участники организованы в 16 команд.
Общая длина шоссе дается на чистку = 4,8 километра
Если участники организованы в 16 команд.
4,8/16 = 0,3
Следовательно, каждая команда очистит 0,3 км шоссе.
Вопрос 4.
У Тайрона $8,06. Сколько рогаликов он может купить, если каждый рогалик стоит 0,65 доллара?
_____ рогалики
Ответ:
12 рогаликов
Объяснение:
8,06 долл. США/0,65 долл. США = 12,4
12 рогаликов
Вопрос 5.
Гвоздь имеет толщину 0,1875 дюйма. Какова его толщина в дроби? 0,1875 дюйма ближе к \(\frac{1}{8}\) дюймам или \(\frac{1}{4}\) дюймам на числовой прямой?
Введите ниже:
__________
Ответ:
0,1875 = 3/16, что находится на одинаковом расстоянии от 1/4 и 1/8
Это одинаковое расстояние друг от друга.
Вопрос 6.
Мария хочет найти произведение 5 \(\frac{3}{20}\) × 3 \(\frac{4}{25}\), используя десятичные дроби вместо дробей. Как она может переписать задачу, используя десятичные дроби?
Тип ниже:
__________
Ответ:
16.274
Объяснение:
Десятичный для 5 3/20 составляет 5,15
. Десятина для 3 4/25 — 3,16
Десятина для 3 4/25 — 3,16
5.15 × 3.16 = 16.274
8888888 годы — No. 121
Оценка. Затем запишите частное в простейшей форме.
Вопрос 1.
\(4 \frac{1}{3} \div \frac{3}{4}\)
______ \(\frac{□}{□}\)
Ответ:
5 \(\frac{375}{1000}\)
Объяснение:
4 1/3 = 13/3 = 4,333 ближе к 4,3
3/4 = 0,75 ближе к 0,8. Сколько трековой смеси получил каждый турист?
\(\frac{□}{□}\)
Ответ:
\(\frac{75}{100}\)
Объяснение:
6 туристов = 4,5 фунта смеси для тропы
4,5/6= 0,75 фунтов на каждого туриста.
Вопрос 3.
\(5 \frac{2}{3} \div 3\)
______ \(\frac{□}{□}\)
Ответ:
2\(\frac{947}{ 1000}\)
Объяснение:
5 2/3 = 17/3 = 5,666 ближе к 5,6
5,6/3 = 1,866 ближе к 1,9
5,6/1,9 = 2,947 = 2 947/1000
Вопрос 4.
\(7 \frac {1}{2} \div 2 \frac{1}{2}\)
______
Ответ:
3
Объяснение:
7 1/2 = 15/2 = 7,5
2 1/2 = 5/ 2 = 2,5
7,5/2,5 = 3
Самостоятельно
Оценка. Затем запишите частное в простейшей форме.
Затем запишите частное в простейшей форме.
Вопрос 5.
\(5 \frac{3}{4} \div 4 \frac{1}{2}\)
______ \(\frac{□}{□}\)
Ответ:
1\(\frac{27}{100}\)
Объяснение:
5 3/4 = 23/4 = 5,75
4 1 /2 = 9/2 = 4,5
5,75/4,5 = 1,27 = 1 27/100
Вопрос 6.
\(5 \div 1 \frac{1}{3}\)
______ \(\frac{□} {□}\)
Ответ:
3\(\frac{84}{100}\)
Объяснение:
1 1/3 = 4/3 = 1,33 ближе к 1,3
5/1,3 = 3,84 = 3 84/100
Вопрос 7.
\(6 \frac{3}{4} \div 2\)
______ \(\frac{□}{□}\)
Ответ:
3\(\frac{2}{5}\)
Объяснение:
6 3/4 = 27/4 = 6,75 ближе к 6,8
6,8/2 = 3,4 = 3 2/5
Вопрос 8.
\(2 \frac{2}{9} \div 1 \frac{3}{7}\)
______ \(\frac{□}{□}\)
Ответ:
1\(\ frac{571}{1000}\)
Объяснение:
2 2/9 = 20/9 = 2,22 ближе к 2,2
1 3/7 = 10/7 = 1,428 ближе к 1,4
2,2/1,4 = 1,571 = 1 571/1000
Вопрос 9.
Сколько 3 \(\frac{1}{3}\) ярдов может получить Аманда из 3 \(\frac{1}{3}\) ярдов ленты?
______
Ответ:
1
Объяснение:
(3 1/3) ÷ (3 1/3) = 1
Вопрос 10.
Саманта разрезала 6 \(\frac{3}{4}\) ярдов пряжи на 3 равные части. Объясните, как она могла вычислить в уме длину каждой части
Введите ниже:
__________
Ответ:
27/12
Объяснение:
Саманта отрезала 6 \(\frac{3}{4}\) ярдов пряжу на 3 равные части.
6 3/4 = 27/4
(27/4)/3
(27/4)(1/3) = 27/12
Вычислить Алгебра Вычислить, используя порядок операций. Запишите ответ в простейшей форме.
Вопрос 11.
\(1 \frac{1}{2} \times 2 \div 1 \frac{1}{3}\)
_____ \(\frac{□}{□}\)
Ответ:
2\(\frac{1}{4}\)
Объяснение:
(1 1/2) × 2 = 3/2 × 2 = 3
1 1/3 = 4/3
3/( 4/3) = 9/4 = 2,25 = 2 1/4
Вопрос 12.
\(1 \frac{2}{5} \div 1 \frac{13}{15}+\frac{5}{ 8}\)
_____ \(\frac{□}{□}\)
Ответ:
1\(\frac{3}{8}\)
Объяснение:
(1 2/5)/(1 13/15) = (7/5)/(28/15) = 3/4 = 0,75
0,75 + 0,625 = 1,375 = 1 3/8
Вопрос 13.
\(3 \frac{1}{2}-1 \frac{5}{6} \div 1 \frac{2}{9}\ )
_____
Ответ:
2
Объяснение:
(1 5/6)/(1 2/9) = (11/6)/11/9 = 3/2 = 1 1/2 = 1,5
3 1/2 = 7/2 = 3,5
3,5 – 1,5 = 2
Вопрос 14.
Найдите закономерность Найдите следующие частные: \(20 \div 4 \frac{4}{5}\), \(10 \ div 4 \frac{4}{5}\), \(5 \div 4 \frac{4}{5}\). Опишите закономерность, которую вы видите.
Введите ниже:
__________
Ответ:
20 ÷ 4 4/5 = 20 ÷ 24/5 = 20/4,8 = 4,1666
10 ÷ 4 4/5 = 10 ÷ 24/5 = 10/4,8 = 2,08333
5 ÷ 4 4/5 = 5 ÷ 24/5 = 5/4,8 = 1,04166
Шаблон каждый раз умножается на 2.
Страница № 122
Вопрос 15.
Дина идет пешком \(\frac{1}{2}\) по легкой тропе и останавливается на перерыв каждые 3 \(\frac{1}{4}\) мили . Сколько перерывов она сделает?
а. Какую проблему вам предлагается решить?
Введите ниже:
__________
Ответ:
Сколько остановок сделает Дина при переходе \(\frac{1}{2}\) по легкому маршруту с остановками для отдыха через каждые 3 \(\frac{1}{4}\) мили.
Вопрос 15.
б. Как вы будете использовать информацию в таблице для решения задачи?
Введите ниже:
__________
Ответ:
Дина длина легкой тропы, время перерыва
Вопрос 15.
c. Как узнать расстояние, которое проходит Дина? Как далеко она ходит?
______ \(\frac{□}{□}\) миль
Ответ:
9\(\frac{3}{4}\) миль
Объяснение:
19 1/2 × 1/2 = 39/2 × 1/2 = 39/4 = 9 3/4
Вопрос 15.
d. Какую операцию вы будете использовать, чтобы найти, сколько перерывов делает Дина?
Введите ниже:
__________
Ответ:
Отдел
Вопрос 15.
e. Сколько перерывов сделает Дина?
______ перерывы
Ответ:
3 перерыва
Объяснение:
39/4 ÷ 13/4 = 3
Вопрос 16.
Карло упаковывает 15 \(\frac{3}{4}\) фунтов книг в 2 коробки. Каждая книга весит 1 \(\frac{1}{8}\) фунта. В коробке A на 4 книги больше, чем в коробке B. Сколько книг в коробке A? Объясни свою работу.
______ книг
Ответ:
Карло упаковывает 15 \(\frac{3}{4}\) фунтов книг в 2 коробки. Каждая книга весит 1 \(\frac{1}{8}\) фунтов
15 \(\frac{3}{4}\) ÷ 1 \(\frac{1}{8}\) = 63/4 ÷ 9/8 = 14
14 книг в 2 коробках.
В коробке A на 4 книги больше, чем в коробке B.
В коробке A 5 + 4 = 9 книг.
В коробке B 5 книг. 4}\) миль за 5 дней. Он хочет пробегать одно и то же расстояние каждый день. Джордан сказал, что Рексу придется пробегать по 3 \(\frac{3}{4}\) мили каждый день, чтобы достичь своей цели. Вы согласны с Джорданом? Объясните свой ответ, используя слова и числа.
Введите ниже:
__________
Ответ:
Цель Рекса — пробежать 13 \(\frac{3}{4}\) миль за 5 дней. Он хочет пробегать одно и то же расстояние каждый день.
13 \(\frac{3}{4}\) ÷ 5 = 55/4 ÷ 5 = 11/4 или 2 3/4.
Джордан ответ неверен
Разделить смешанные числа – № страницы 123
Оценка. Затем запишите частное в простейшей форме.
Вопрос 1.
\(2 \frac{1}{2} \div 2 \frac{1}{3}\)
______ \(\frac{□}{□}\)
Ответ:
1\(\frac{1}{2}\)
Объяснение:
2 1/2 = 5/2 = 2,5 ближе к 3
2 1/3 = 7/3 = 2,333 ближе к 2
3/2 = 1,5 = 1 1/2
Вопрос 2.
\(2 \frac{2}{3} \div 1 \frac{1}{3}\)
______
Ответ:
2
Объяснение:
2 2/3 = 8/3 = 2,666 ближе к 2,6
1 1/3 = 4/3 = 1,333 ближе к 1,3
2,6/1,3 = 2
Вопрос 3.
\(2 \div 3 \frac{5}{8}\)
\(\frac {□}{□}\)
Ответ:
\(\frac{1}{2}\)
Объяснение:
3 5/8 = 29/8 = 3,625 ближе к 3,6
2/3,6 = 0,5 = 1/2
Вопрос 4.
\(1 \frac{13}{15} \div 1 \frac{2} {5}\)
\(\frac{□}{□}\)
Ответ:
\(\frac{126}{100}\)
Объяснение:
1 13/15 = 28/15 = 1,8666 ближе к 1,9
1 2/5 = 7/5 = 1,4 ближе к 1,5
1,9/1,5 = 1,266
126/100
Вопрос 5.
\(10 \div 6 \frac{2}{3}\ )
______ \(\frac{□}{□}\)
Ответ:
1\(\frac{1}{2}\)
Объяснение:
6 2/3 = 20/3 = 6,666 ближе к 6,7
10/6,7 = 3/2 = 1 1/2
Вопрос 6.
\(2 \frac{3}{5} \div 1 \frac {1}{25}\)
______ \(\frac{□}{□}\)
Ответ:
2\(\frac{3}{5}\)
Объяснение:
2 3/5 = 13/5 = 2,6
1 1/25 = 26/25 = 1,04 ближе к 1
2,6/1 = 13/5 или 2 3/5
Вопрос 7.
\(2 \frac{1}{5} \div 2\)
______ \(\frac{□}{□}\)
Ответ:
1\(\frac{1}{10}\)
Объяснение:
2 1/5 = 11/5 = 2,2 ближе к 2,2
2,2/2 = 1,1 = 11/10 = 1 1/10
Вопрос 8.
Сид и Джилл прошли 4 \(\frac{1}{8}\) мили утром и 1 \(\frac{7 {8}\) миль во второй половине дня. Во сколько раз они прошли утром больше, чем днем?
______ \(\frac{□}{□}\) раз
Ответ:
2\(\frac{1}{5}\) раз
Объяснение:
Сид и Джилл прошли пешком 4 \(\frac{1 {8}\) миль утром и 1 \(\frac{7}{8}\) миль днем.
4 \(\frac{1}{8}\) = 33/8
1 \(\frac{7}{8}\) = 15/8
(33/8) ÷ (15/8) = 33/15 = 11/5 или 2 1/5
Решение проблем
Вопрос 9.
Требуется 2 ним \(\frac{2}{3 }\) часов, чтобы сплести корзину. Работал с понедельника по пятницу по 8 часов в день. Сколько корзин он сделал?
______ корзин
Ответ:
15 корзин
Объяснение:
он работал (пн-пт) 5 дней по 8 часов в день = 5 × 8= 40 часов
40/(2 2/3) = 40/(8 /3) = 40 × 3/8 = 120/8 = 15 корзин
Вопрос 10.
Дерево растет на 1 \(\frac{3}{4}\) фута в год. Сколько времени понадобится дереву, чтобы вырасти с высоты 21 \(\frac{1}{4}\) фута до высоты 37 футов?
______ лет
Ответ:
9 лет
Пояснение:
Дерево растет на 1 3/4 = 7/4 фута в год.
Если вы хотите знать, сколько времени потребуется дереву, чтобы вырасти с высоты 21 1/4 = 85/4 фута до высоты 37 футов,
37 – 21 1/4 = 37 – 85/4 = 148/4 – 85/4 = 63/4 = 15 3/4
15 3/4 / 1 3/4 = 63/4 / 7/4 = 63/4 × 4/7 = 9 лет
Вопрос 11.
Объясните, как найти количество порций по 1 \(\frac{1}{2}\) чашек в кастрюле с 22 \(\frac{1}{2}\) чашками супа.
Введите ниже:
__________
Ответ:
Учитывая, что общее количество чашек = 22 1/2
Количество чашек, необходимое для каждой порции = 1 1/2
Количество порций = 22 1/2 ÷ 1 1 /2
= 45/2 ÷ 3/2 = 45/3 = 15. }\) квадратные метры. Каждая доска на заборе имеет площадь \(\frac{3}{16}\) квадратных метров. Сколько досок он может покрасить?
______ доски
Ответ:
200 досок
Пояснение:
У Тома есть банка краски, которой покрывается 37 \(\frac{1}{2}\) квадратных метров. Каждая доска на заборе имеет площадь \(\frac{3}{16}\) квадратных метров.
Каждая доска на заборе имеет площадь \(\frac{3}{16}\) квадратных метров.
37 \(\frac{1}{2}\) ÷ \(\frac{3}{16}\) = 200 квадратных метров
Вопрос 2.
Пекарь хочет положить 3 \(\frac{3} {4}\) фунтов яблок в каждом пироге, который она делает. Она купила 52 \(\frac{1}{2}\) фунтов яблок. Сколько пирогов она может испечь?
______ пирогов
Ответ:
14 пирогов
Пояснение:
Пекарь хочет положить 3 \(\frac{3}{4}\) фунтов яблок в каждый пирог, который она испечет. Она купила 52 \(\frac{1}{2}\) фунтов яблок.
52 \(\frac{1}{2}\) ÷ 3 \(\frac{3}{4}\) = 14 кругов
Обзор спирали
Вопрос 3.
Мера трех сторон треугольника 9,97 метра, 10,1 метра и 0,53 метра. Каково расстояние вокруг треугольника?
______ метров
Ответ:
20,6 метра
Объяснение:
Расстояние вокруг треугольника называется периметром, чтобы получить его, мы должны сложить 3 стороны.
Итак, 9,97 + 10,1 + 0,53 = 20,6 метра
Вопрос 4.
Селена купила 3,75 фунта мяса по цене 4,64 доллара за фунт. Какова общая стоимость мяса?
$ ______
Ответ:
$17,40
Пояснение:
Селена купила 3,75 фунта мяса.
Стоимость одного фунта мяса = 4,64 доллара
Общая стоимость мяса = 4,64 × 3,75 = 17,40 доллара
Общая стоимость 3,75 фунта мяса составила 17,40 доллара.
Вопрос 5.
Мелани приготовила 7 \(\frac{1}{2}\) столовых ложек смеси специй. Она использует \(\frac{1}{4}\) столовую ложку, чтобы приготовить порцию соуса для барбекю. Оцените, сколько порций соуса для барбекю она может приготовить, используя смесь специй.
Введите ниже:
__________
Ответ:
30 порций соуса
Объяснение:
Мелани приготовила 7 \(\frac{1}{2}\) столовых ложек смеси специй. Она использует \(\frac{1}{4}\) столовую ложку, чтобы приготовить порцию соуса для барбекю.
4 х 1/4 ст.л. = 1 ст.л.
4 X 7 1/2 = 30.
она может приготовить 30 порций соуса
Вопрос 6.
Артуро смешал 1,24 фунта кренделей, 0,78 фунта орехов, 0,3 фунта конфет и 2 фунта попкорна. Затем он упаковал его в пакеты по 0,27 фунта каждый. Сколько мешков он мог заполнить?
______ пакетов
Ответ:
16 пакетов
Объяснение:
Артуро смешал 1,24 фунта кренделей, 0,78 фунта орехов, 0,3 фунта конфет и 2 фунта попкорна.
1,24 + 0,78 + 0,3 + 2 = 4,32
4,32/0,27 = 16
Номер страницы 127
Вопрос 1.
В классе научных принадлежностей есть \(\frac{4}{5}\) фунтов песка . Если одна ложка песка весит \(\frac{1}{20}\) фунтов, сколько ложек песка Мария может получить из классных принадлежностей и оставить \(\frac{1}{2}\) фунтов в запасы?
Введите ниже:
__________
Ответ:
16 мерных ложек
Объяснение:
В классе научных принадлежностей есть \(\frac{4}{5}\) фунтов песка. Если одна ложка песка весит \(\frac{1}{20}\) фунтов,
\(\frac{4}{5}\) ÷ \(\frac{1}{20}\) = 4/5 × 1/20 = 16 мерных ложек
Вопрос 2.
Что, если Мария уйдет \(\ frac{2}{5}\) фунтов песка в запасах? Сколько ложек песка она может получить?
______ мерных ложек
Ответ:
8 мерных ложек
Объяснение:
В школьных принадлежностях есть \(\frac{2}{5}\) фунтов песка. Если один совок песка весит \(\frac{1}{20}\) фунтов,
\(\frac{2}{5}\) ÷ \(\frac{1}{20}\) = 2/5 × 20 = 8
Вопрос 3.
В научных запасах есть 6 галлонов дистиллированной воды. Если 10 студентов используют равное количество дистиллированной воды и в запасах остается 1 галлон, сколько получит каждый студент?
\(\frac{□}{□}\) галлон
Ответ:
\(\frac{1}{2}\) галлон
Объяснение:
В научных запасах есть 6 галлонов дистиллированной воды.
В расходных материалах остался 1 галлон, 6 – 1 = 5
10 учащихся используют равное количество дистиллированной воды = 5/10 = 1/2
0,5 галлона на каждого ученика
Самостоятельно – Номер страницы 128
Вопрос 4.
Общий вес рыбы в аквариуме с тропическими рыбами в Fish ‘n’ Fur составлял \(\frac{7}{8}\) фунтов. Каждая рыба весила \(\frac{1 }{64}\) фунтов. После того, как Эрик купил немного рыбы, общий вес рыбы, оставшейся в аквариуме, составил \(\frac{1}{2}\) фунтов. Сколько рыбы купил Эрик?
Каждая рыба весила \(\frac{1 }{64}\) фунтов. После того, как Эрик купил немного рыбы, общий вес рыбы, оставшейся в аквариуме, составил \(\frac{1}{2}\) фунтов. Сколько рыбы купил Эрик?
______ рыба
Ответ:
386 рыба
Объяснение:
Общий вес рыбы в аквариуме с тропическими рыбами в Fish ‘n’ Fur составлял \(\frac{7}{8}\) фунтов. Каждая рыба весила \(\frac{1}{64}\) фунтов. После того, как Эрик купил немного рыбы, общий вес рыбы, оставшейся в аквариуме, составлял \(\frac{1}{2}\) фунтов.
386 ответ
Вопрос 5. У
Fish ‘n’ Fur была корзина, содержащая 2 \(\frac{1}{2}\) фунтов корма для песчанок. После продажи мешков с кормом для песчанок, каждый из которых содержал \(\frac{3}{4}\) фунтов, в мусорном ведре осталось \(\frac{1}{4}\) фунтов корма. Если каждый мешок корма для песчанок будет продаваться по 3,25 доллара, сколько заработает магазин?
$ ______
Ответ:
$9,75
Объяснение:
Магазин заработает 9,75$, потому что продано 3 мешка корма для песчанок. Тогда вы должны умножить 3 на 3,25.
Тогда вы должны умножить 3 на 3,25.
Вопрос 6.
Описать Нико купил 2 фунта собачьих лакомств. Он давал своей собаке \(\frac{3}{5}\) фунтов лакомств одну неделю и \(\frac{7}{10}\) фунтов лакомств на следующей неделе. Опишите, как Нико может узнать, сколько осталось.
Введите ниже:
__________
Ответ:
Нико купил 2 фунта собачьих лакомств. Он давал своей собаке \(\frac{3}{5}\) фунтов лакомств одну неделю и \(\frac{7}{10}\) фунтов лакомств на следующей неделе.
Найдем количество собачьего корма, съеденного собаками за два месяца.
3/5 + 7/10 = 13/10
Теперь мы вычтем количество еды, съеденной собакой, из первоначального количества еды, чтобы найти оставшееся количество собачьей еды.
2 – 13/10 = 7/10
Таким образом, к концу двух месяцев в мешке оставалось 7/10 фунтов еды.
Вопрос 7.
В контейнере было 14 \(\frac{1}{4}\) чашек яблочного сока. Каждый день Элиза выпивала 1 \(\frac{1}{2}\) чашки яблочного сока. Сегодня осталось \(\frac{3}{4}\) стакана яблочного сока. Дерек сказал, что Элиза пила яблочный сок девять дней. Вы согласны с Дереком? Используйте слова и числа, чтобы объяснить свой ответ.
Дерек сказал, что Элиза пила яблочный сок девять дней. Вы согласны с Дереком? Используйте слова и числа, чтобы объяснить свой ответ.
Введите ниже:
__________
Ответ:
Дерек прав.
Объяснение:
Яблочного сока в контейнере было 14 1/2 = 14,25
Она выпила за день 1 1/2 = 1,5
Оставшаяся часть в контейнере 3/4 = 0,75
14,25 чашки – 0,75 чашки = 13,5 чашек
13,5 чашек ÷ 1,5 чашек в день= 9 дней
Решение задач Дробные операции – Страница № 129
Прочитайте каждую задачу и решите.
Вопрос 1. Осталось
\(\frac{2}{3}\) пиццы. Группа друзей разделила оставшуюся пиццу на части, каждая из которых равна \(\frac{1}{18}\) исходной пиццы. После того, как каждый друг взял по одному кусочку, осталось \(\frac{1}{6}\) исходной пиццы. Сколько друзей было в группе?
______ друзей
Ответ:
9 друзей
Объяснение:
Допустим, есть x друзей.
Каждый получает 1/18 часть исходной пиццы, но в свою очередь остается 1/6 из оставшихся 2/3.
1x/18 = 2/3 – 1/6
x = 12 – 3 = 9
Вопрос 2.
В поделке Сары используются отрезки пряжи длиной \(\frac{1}{8}\) ярдов. У нее есть отрезок пряжи длиной 3 метра. Сколько \(\frac{1}{8}\) -ярдовых кусков она может отрезать, и при этом остается 1 \(\frac{1}{4}\) ярдов?
______ шт.
Ответ:
14 шт.
Пояснение:
В поделке Сары используются отрезки пряжи длиной \(\frac{1}{8}\) ярдов. У нее есть отрезок пряжи длиной 3 метра.
Если она оставила 1 \(\frac{1}{4}\) ярда, 3 – 1 \(\frac{1}{4}\) = 7/4
7/4 ÷ \(\frac{1 }{8}\) = 14
Вопрос 3.
Алекс открывает литровую банку апельсинового масла. Он намазывает \(\frac{1}{16}\) масла на свой хлеб. Затем он делит оставшееся масло на \(\frac{3}{4}\) литровые емкости. Сколько \(\frac{3}{4}\) литровых контейнеров он может заполнить?
______ \(\frac{□}{□}\) контейнеров
Ответ:
1\(\frac{1}{4}\) контейнеров
Объяснение:
Алекс открывает 1-пинтовый контейнер апельсинового масла. Он намазывает \(\frac{1}{16}\) масла на свой хлеб.
Он намазывает \(\frac{1}{16}\) масла на свой хлеб.
1 – 1/16 = 15/16
Затем он делит оставшееся масло на \(\frac{3}{4}\) литровые емкости.
(15/16) ÷ (3/4) = 5/4 = 1 1/4
Вопрос 4.
Кейтлин покупает \(\frac{9}{10}\) фунт апельсиновых долек. Она съедает \(\frac{1}{3}\) из них, а остальные делит поровну на 3 мешка. Сколько в каждом мешке?
______ lb
Ответ:
17/90 lb
Объяснение:
Кейтлин покупает \(\frac{9}{10}\) фунт апельсиновых долек. Она съедает \(\frac{1}{3}\) из них, а остальные делит поровну на 3 мешка.
Если она начинает с 9/10 фунтов и съела 1/3 из них, 9/10 – 1/3 = 17/30
Это количество, которое у нее осталось. Давайте разделим это значение на 3, чтобы узнать, сколько фунтов в одном мешке.
(17/30)/3 = 17/90
В одном мешке 17/90 фунтов.
Вопрос 5.
Объясните, как нарисовать модель, представляющую \(\left(1 \frac{1}{4}-\frac{1}{2}\right) \div \frac{1}{8} \).
Введите ниже:
__________
Ответ:
Разделите 2 такта на 8 четвертей.
Ниже этого рисунка на 1 1/4 или 5 четвертей.
Удалить 1/2 или 2 четверти
Разделить каждую из 3 оставшихся четвертей на 2 восьмых
Объяснение:
\(\left(1 \frac{1}{4}-\frac{1}{2}\right) \div \frac{1}{8}\)
1 1/4 -1/2 = 5/4 – 1/2 = 3/4
3/4 ÷ 1/8 = 6
Проверка урока – номер страницы 130
Вопрос 1.
Ева хотела наполнить мешки \(\frac{3}{4}\) фунтами смеси. Она начала с 11 \(\frac{3}{8}\) фунтов, но съела \(\frac{1}{8}\) фунтов, прежде чем начала набивать мешки. Сколько мешков она могла заполнить?
______ пакетов
Ответ:
15 пакетов
Объяснение:
11 и 3/8-1/8=11 и 2/8=11 и 1/4
3/4 x пакетов=11 и 1/4
преобразовать 11 и 1/4 в неправильную дробь
11 и 1/4 = 11 + 1/4 = 44/4 + 1/4 = 45/4
3/4 x мешков = 45/4
x мешков = 45/ 4 × 4/3 = 15 мешков
она могла бы заполнить 15 мешков
Вопрос 2.
У Джона есть рулон, содержащий 24 \(\frac{2}{3}\) фута оберточной бумаги. Он хочет разделить его на 11 частей. Однако сначала он должен отрезать \(\frac{5}{6}\) ногу, потому что она была разорвана. Какой длины будет каждая часть?
Он хочет разделить его на 11 частей. Однако сначала он должен отрезать \(\frac{5}{6}\) ногу, потому что она была разорвана. Какой длины будет каждая часть?
______ \(\frac{□}{□}\) футов
Ответ:
2\(\frac{4}{25}\) футов
Объяснение:
У Джона был рулон оберточной бумаги = 24 2/ 3 = 74/3
Во-первых, он должен отрезать 5/6 фута, потому что он был разорван.
Он хочет разделить его на 11 частей.
74/3 – 5/6
Принимая НОК 3 и 6 равно 6
(148-5)/6 = 143/6 = 23,83 фута
Он хочет разделить его на 11 частей. длина каждой детали = 23,83/11 = 2,16 фута
Spiral Review
Вопрос 3.
У Алексис есть 32 \(\frac{2}{5}\) унций бус. Сколько ожерелий она может сделать, если каждое из них использует 2 \(\frac{7}{10}\) унций бус?
______ ожерелья
Ответ:
12 ожерелий
Пояснение:
У Алексис 32 \(\frac{2}{5}\) унций бус.
Если каждый использует 2 \(\frac{7}{10}\) унций бус, 32 \(\frac{2}{5}\) × 2 \(\frac{7}{10}\)
32 \(\frac{2}{5}\) = 162/5
2 \(\frac{7}{10}\) = 27/10
162/5 × 27/10 = 12 ожерелий
Вопрос 4.
У Джозефа есть 32,40 доллара. Он хочет купить несколько комиксов по 2,70 доллара каждый. Сколько комиксов он может купить?
______ комиксы
Ответ:
12 комиксов
Пояснение:
У Джозефа есть 32,40 доллара. Он хочет купить несколько комиксов по 2,70 доллара каждый.
$32,40/$2,70 = 12 комиксов
Вопрос 5.
Прямоугольник имеет ширину 2 \(\frac{4}{5}\) метра и длину 3 \(\frac{1}{2}\) метра. Какова его площадь?
______ \(\frac{□}{□}\) м 2
Ответ:
9\(\frac{4}{5}\) м2
Объяснение:
2 \(\frac{4}{5}\) = 14/5
3 \(\frac {1}{2}\) = 7/2
14/5 × 7/2 = 9 4/5
Вопрос 6.
Прямоугольник имеет ширину 2,8 метра и длину 3,5 метра. Какова его площадь?
______ м 2
Ответ:
9,8 м 2
Пояснение:
Прямоугольник имеет ширину 2,8 м и длину 3,5 м.
2,8 × 3,5 = 9,8
Обзор/тестирование главы 2 – страница № 131
Вопрос 1.
Запишите значения в порядке от наименьшего к наибольшему.
Тип ниже:
__________
Ответ:
0,45, 0,5, 5/8, 3/4
Объяснение:
3/4 = 0,75
5/8 = 0,625
0,45, 0,5
0,45 <0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.00.00.0.00.0.00.0.00.0.00.0.00.0.00.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.625. 0,75
Вопрос 2.
Для чисел 2a–2d сравните. Выберите <, > или =.
2а. 0,75 _____ \(\frac{3}{4}\)
2б. \(\frac{4}{5}\) _____ 0,325
2c. 1 \(\frac{3}{5}\) _____ 1,9
2d. 7.4 _____ 7 \(\frac{2}{5}\)
Ответ:
2а. 0,75 = \(\frac{3}{4}\)
2б. \(\frac{4}{5}\) > 0,325
2c. 1 \(\frac{3}{5}\) < 1,9
2d. 7,4 = 7 \(\frac{2}{5}\)
Объяснение:
2а. 3/4 = 0,75
0,75 = 0,75
2б. \(\frac{4}{5}\) = 0,8
0,8 > 0,325
2c. 1 \(\frac{3}{5}\) = 8/5 = 1,6
1,6 < 1,9
2d. 7 \(\frac{2}{5}\) = 37/5 = 7,4
7,4 = 7,4
Вопрос 3.
В таблице указаны высоты 4 деревьев.
Для номеров 3a–3d выберите True или False для каждого утверждения.
3а. Дуб самый низкий. Верно Неверно
3b. Береза самая высокая. Верно Неверно
3c. Два дерева одинаковой высоты. Верно Неверно
3d. Платан выше клена. Верно Неверно
Введите ниже:
__________
Ответ:
3a. Дуб самый низкий. Правда
3б. Береза самая высокая. Ложный
3c. Два дерева одинаковой высоты. Ложь
3d. Платан выше клена. Ложь
Пояснение:
Явор = 15 2/3 = 47/3 = 15,666
Дуб = 14 3/4 = 59/4 = 14,75
Клен = 15 3/4 = 63/4 = 15,75
Береза = 15,72
Номер страницы 132
Вопрос 4.
Для номеров 4a–4d выберите Да или Нет, чтобы указать, верно ли утверждение.
4а. Точка А представляет 1,0. Да Нет
4б. Точка B представляет \(\frac{3}{10}\). Да Нет
4c. Точка С представляет 6,5. Да Нет
4д. Точка D представляет \(\frac{4}{5}\). Да Нет
Введите ниже:
__________
Ответ:
4а. Точка А представляет 1,0. Да
Точка А представляет 1,0. Да
4б. Точка B представляет \(\frac{3}{10}\). Да
4с. Точка С представляет 6,5. №
4д. Точка D представляет \(\frac{4}{5}\). Да
Вопрос 5.
Выберите значения, эквивалентные одной двадцать пятой. Отметьте все подходящие варианты.
Опции:
а. 125
б. 25
г. 0,04
г. 0,025
Ответ:
c. 0,04
Объяснение:
одна двадцать пятая = 1/25 = 0,04
Вопрос 6.
В таблице показано домашнее задание Лили. Учитель Лили велел классу упростить каждое выражение, разделив числитель и знаменатель на НОК. Заполните таблицу, упростив каждое выражение и найдя произведение.
Введите ниже:
___________
Ответ:
a. Упрощенное выражение: 1/10
Продукт: 0,1
b. Упрощенное выражение: 1/2
Продукт: 0,5
c. Упрощенное выражение: 15/56
Произведение: 0,267
d. Упрощенное выражение: 1/12
Продукт: 0,083
Объяснение:
а. 2/5 × 1/4 = 2/20
Упростите, используя GCF.
GCF 2 и 20 равен 2.
Разделите числитель и знаменатель на 2.
Таким образом, ответ равен 1/10.
Продукт: 0,1
б. 4/5 × 5/8 = 1/2
Произведение: 0,5
c. 3/7 × 5/8 = 15/56
Произведение: 0,267
d. 4/9 × 3/16 = 1/12
Продукт: 0,083
Номер страницы 133
Вопрос 7.
Две пятых рыб в аквариуме Гэри — гуппи. Четвертая часть гуппи рыжая. Какую часть рыб в аквариуме Гэри составляют красные гуппи? Какая часть рыб в аквариуме Гэри не является красными гуппи? Показать свою работу.
Введите ниже:
___________
Ответ:
1/10 часть рыбок — красные гуппи.
и 9/10 рыбок не красные гуппи.
Пояснение:
две пятых рыбы в аквариуме Гэри — гуппи.
Четверть гуппи рыжие.
Пусть общее количество рыб в аквариуме Гэри равно x.
Известно, что две пятых рыб в аквариуме Гэри составляют гуппи.
Итак, количество гуппи в аквариуме Гэри равно 2/5 × x
Учитывая, что четверть гуппи красные.
количество красных гуппи = 1/4 × 2x/5 = x/10
Итак, 1/10 рыбок составляют красные гуппи.
1 – 1/10 = 9/10 рыбок не красные гуппи.
Вопрос 8.
Треть учащихся средней школы Финли занимаются спортом. Две пятых учащихся, занимающихся спортом, составляют девочки. Какую часть всех учащихся составляют девушки, занимающиеся спортом? Используйте числа и слова, чтобы объяснить свой ответ.
Введите ниже:
___________
Ответ:
Треть учащихся средней школы Финли занимаются спортом. Две пятых учащихся, занимающихся спортом, составляют девочки.
1/3 × 2/5 = 2/15 девочек в школе занимаются спортом.
Вопрос 9.
Нарисуйте модель, чтобы найти частное.
\(\frac{3}{4}\) ÷ 2 =
\(\frac{3}{4}\) ÷ \(\frac{3}{8}\) =
Чем похожи ваши модели? Насколько они разные?
Введите ниже:
___________
Ответ:
Объяснение:
\(\frac{3}{4}\) ÷ 2 = 3/4 × 1/2 = 3/8
\(\frac{3} {4}\) ÷ \(\frac{3}{8}\) = 3/4 × 8/3 = 2
Обе модели умножают на 3/4.
Модель с числовыми линиями показывает, сколько групп чисел 3/8 содержится в числе 3/4.
Вопрос 10.
Объясните, как использовать модель для нахождения частного.
2 \(\frac{1}{2}\) ÷ 2 =
Введите ниже:
___________
Ответ:
5/4
Объяснение:
2 1/2 = 5/2
5/2 групп 2
5/2 ÷ 2 = 5/2 × 1/2 = 5/4
Номер страницы 134
Разделить. Показать свою работу.
Вопрос 11.
\(\frac{7}{8}\) ÷ \(\frac{3}{5}\) =
_______ \(\frac{□}{□}\)
Ответ :
1 \(\frac{11}{24}\)
Объяснение:
\(\frac{7}{8}\) ÷ \(\frac{3}{5}\)
\(\frac{7}{8}\) × \(\frac{5} {3}\) = 35/24 = 1 \(\frac{11}{24}\)
Вопрос 12.
\(2 \frac{1}{10} \div 1 \frac{1}{5 }=\) =
_______ \(\frac{□}{□}\)
Ответ:
1 \(\frac{3}{4}\)
Объяснение:
2 \(\frac{1} {10}\) = 21/10
1 \(\frac{1}{5}\) = 6/5
(21/10) ÷ (6/5) = 7/4 или 1 3/4
Вопрос 13.
У Софи есть \(\frac{3}{4}\) литр лимонада. Если она разделит лимонад на стаканы вместимостью \(\frac{1}{16}\) кварты, сколько стаканов сможет наполнить Софи? Покажи свою работу
_______ стаканов
Ответ:
12 стаканов
Объяснение:
Пусть x будет количеством стаканов
1/16x = 3/4
x = 3/4 × 16 = 3 × 4 = 12 стаканов
Вопрос 14.
Чернильные картриджи весят \(\frac{1}{8}\) фунтов. Общий вес патронов в коробке составляет 4 \(\frac{1}{2}\) фунта. Сколько патронов в коробке? Покажите свою работу и объясните, почему вы выбрали ту операцию, которую сделали.
_______ патронов
Ответ:
36 патронов
Объяснение:
Вес чернильных картриджей = 1/8 фунта
Общий вес картриджей в коробке = 4 1/2 = 9/2 фунта
Таким образом, количество картриджей в коробке определяется как
9/2 ÷ 1/8 = 36
Следовательно, в коробке 36 патронов.
Вопрос 15.
У Бет был 1 ярд ленты. Она использовала двор \(\frac{1}{3}\) для проекта. Она хочет разделить оставшуюся часть ленты на куски длиной \(\frac{1}{6}\) ярдов. Сколько \(\frac{1}{6}\) ярдов лент она может сделать? Объясните свое решение.
Она хочет разделить оставшуюся часть ленты на куски длиной \(\frac{1}{6}\) ярдов. Сколько \(\frac{1}{6}\) ярдов лент она может сделать? Объясните свое решение.
_______ штук
Ответ:
4 штуки
Пояснение:
У Бет был 1 ярд ленты. Она использовала двор \(\frac{1}{3}\) для проекта.
1 – \(\frac{1}{3}\) = осталось 2/3 ярда
Она хочет разделить оставшуюся часть ленты на части длиной \(\frac{1}{6}\) ярда.
2/3 ÷ 1/6 = 4
Номер страницы 135
Вопрос 16.
Заполните таблицу, найдя продукты. Затем ответьте на вопросы в частях A и B.
Часть A
Объясните, в чем сходство каждой пары задач на деление и умножение и чем они отличаются.
Введите ниже:
___________
Ответ:
1/5 ÷ 3/4 = 4/15; 1/5 × 4/3 = 4/15
2/13 ÷ 1/5 = 10/13; 2/13 × 5/1 = 10/13
4/5 ÷ 3/5 = 4/3; 4/5 × 5/3 = 4/3
произведение каждой пары задач на деление и умножение одинаковы.
Они отличаются от выполняемой операции.
Вопрос 16.
Часть B
Объясните, как использовать образец в таблице, чтобы переписать задачу на деление, включающую дроби, как задачу на умножение.
Введите ниже:
___________
Ответ:
Во-первых, поскольку это деление, вы должны изменить вторую дробь, которая называется обратной. Это означает, что вторую дробь нужно перевернуть, прежде чем вы сможете умножать дроби.
Страница № 136
Вопрос 17.
Марджи прошла 17 \(\frac{7}{8}\) миль. Она останавливалась каждые 3 \(\frac{2}{5}\) миль, чтобы сделать снимок. Мартин и Тина подсчитали, сколько раз Марджи останавливалась.
Кто лучше оценил? Используйте числа и слова, чтобы объяснить свой ответ.
Введите ниже:
___________
Ответ:
Марджи прошла тропу длиной 17 7/8 миль.
Расстояние, пройденное Марджи = 17 7/8 = 143/8 мили.
Она останавливалась каждые 3 2/5 мили, чтобы сделать снимок = 17/5 мили
Количество снимков = (143/8) ÷ (17/5) = 715/136 = 5,28
Таким образом, она может сделать максимум 6 снимков и не менее 5 фотографий.
Б — правильный ответ.
Вопрос 18.
Брэд и Уэс строят дом на дереве. Они разрезали кусок дерева длиной 12 \(\frac{1}{2}\) на 5 кусков одинаковой длины. Какой длины каждый кусок дерева? Показать свою работу.
_______ \(\frac{□}{□}\) фут
Ответ:
2 \(\frac{1}{2}\) фут
Объяснение:
Брэд и Уэс отрезали 12 1/2-футовый кусок дерева на 5 одинаковых по длине.
Пусть длина 1 детали будет x
Итак, длина 5 деталей = 5x
Общая длина древесины = 25/2
5x = 25/2
x = 5/2 = 2 1/2
Свободный класс 6 HMH Ключ к ответу на вопросы по математике в формате PDF Скачать
Вы можете бесплатно скачать ключ для ответов на вопросы по математике для 6-го класса в формате PDF с нашей страницы. Получите бесплатный доступ ко всем вопросам и объяснениям на нашем веб-сайте. Получите все вопросы, ответы вместе с пояснениями. Скачать бесплатно pdf-файл Go Math Class 6 Answer Key.
Обучение отношениям и единицам измерения в математике
Сердцем математики в средней школе и ключевой частью подготовки к алгебре является понимание отношений и значений. Приведенный ниже обзор и уроки представляют собой инструменты для подготовки учащихся, обычно 6-х классов и старше, к изучению этих концепций. Уроки ниже, как правило, охватывают два дня обучения.
Приведенный ниже обзор и уроки представляют собой инструменты для подготовки учащихся, обычно 6-х классов и старше, к изучению этих концепций. Уроки ниже, как правило, охватывают два дня обучения.
Отношения и коэффициенты
Отношение представляет собой сравнение двух чисел или измерений. Сравниваемые числа или измерения иногда называют 9.0003 условия отношения. Например, если в магазине продается 6 красных и 8 зеленых рубашек, соотношение красных и зеленых рубашек составляет 6 к 8. Вы можете записать это соотношение как 6 красных/8 зеленых, 6 красных:8 зеленых — или при быстром или быстром письме. пытаясь донести суть — просто 6/8 или 6:8. Оба выражения означают, что «на каждые» 8 зеленых рубашек приходится 6 красных. Обратите внимание, как вы можете переписать 6/8 как 3/4, что ничем не отличается от любого другого случая, когда математическое понятие может отображаться как дробь.
Курс — это особый коэффициент, в котором два члена выражены в разных единицах. Например, если банка кукурузы на 12 унций стоит 69¢, курс составляет 69 центов за 12 унций. Это не соотношение двух одинаковых единиц, таких как рубашки. Это соотношение двух разных единиц: центов и унций. Первый член отношения (69 центов) измеряется в центов , а второй член (12) в унций . Вы можете записать этот курс как 69 центов/12 унций или 69 центов:12 унций. Оба выражения означают, что вы платите 69 центов «за каждые» 12 унций кукурузы, и, как и в случае с коэффициентом рубашки, вы можете вводить расчеты как дробь 69/12. Но обратите внимание, что на этот раз создается новый юнит: центов в час .
Например, если банка кукурузы на 12 унций стоит 69¢, курс составляет 69 центов за 12 унций. Это не соотношение двух одинаковых единиц, таких как рубашки. Это соотношение двух разных единиц: центов и унций. Первый член отношения (69 центов) измеряется в центов , а второй член (12) в унций . Вы можете записать этот курс как 69 центов/12 унций или 69 центов:12 унций. Оба выражения означают, что вы платите 69 центов «за каждые» 12 унций кукурузы, и, как и в случае с коэффициентом рубашки, вы можете вводить расчеты как дробь 69/12. Но обратите внимание, что на этот раз создается новый юнит: центов в час .
Ставки используются людьми каждый день, например, когда они работают 40 часов в неделю или получают процентов каждый год в банке. Когда скорости выражаются как количество 1, например, 2 фута в секунду (то есть за 1 секунду) или 5 миль в час (то есть за 1 час), они могут быть определены как единиц скорости . Вы можете записать любую ставку как единицу, уменьшив дробь так, чтобы она имела 1 в качестве знаменателя или второго члена. В качестве примера удельной стоимости вы можете показать, что удельная стоимость 120 студентов на каждые 3 автобуса составляет 40 студентов на автобус.
В качестве примера удельной стоимости вы можете показать, что удельная стоимость 120 студентов на каждые 3 автобуса составляет 40 студентов на автобус.
120/3 = 40/1
Вы также можете найти удельную ставку, разделив первый член отношения на второй член.
120 ÷ 3 = 40
Когда цена выражается как количество 1, например, 25 долларов за билет или 0,89 доллара за банку, это называется ценой за единицу . Если у вас есть неединичная цена, например 5,50 доллара за 5 фунтов картофеля, и вы хотите найти цену за единицу, разделите члены отношения.
5,50 долл. США ÷ 5 фунтов = 1,10 долл. США за фунт
Цена за единицу картофеля стоимостью 5,50 долларов США за 5 фунтов составляет 1,10 долларов США за фунт.
Ставки в реальном мире
Ставки и удельные ставки используются для решения многих реальных задач. Посмотрите на следующую проблему. «Тоня работает по 60 часов каждые 3 недели. При таком уровне, сколько часов она будет работать за 12 недель?» Задача говорит вам, что Тоня работает из расчета 60 часов каждые 3 недели. Чтобы найти количество часов, которое она проработает за 12 недель, напишите отношение, равное 60/3, которое имеет второй член, равный 12.
При таком уровне, сколько часов она будет работать за 12 недель?» Задача говорит вам, что Тоня работает из расчета 60 часов каждые 3 недели. Чтобы найти количество часов, которое она проработает за 12 недель, напишите отношение, равное 60/3, которое имеет второй член, равный 12.
60/3 = ?/12 60/3 = 240/12
Удаление единиц облегчает просмотр расчета. Однако важно помнить о единицах измерения при интерпретации нового соотношения.
Тоня будет работать 240 часов за 12 недель.
Вы также можете решить эту задачу, сначала найдя удельный расход и умножив его на 12.
60/3 = 20/120 × 12 = 240
Когда вы найдете равные отношения, важно помнить, что если вы умножаете или делите один член отношения на число, то вам нужно умножить или разделить другой член отношения на то же число.
Давайте рассмотрим задачу, связанную с ценой за единицу товара. «Вывеска в магазине гласит: 3 ручки за 2,70 доллара . Сколько будут стоить 10 ручек?» Чтобы решить эту задачу, найдите цену за единицу ручек, затем умножьте на 10.
Сколько будут стоить 10 ручек?» Чтобы решить эту задачу, найдите цену за единицу ручек, затем умножьте на 10.
2,70 долл. США ÷ 3 ручки = 0,90 долл. США за ручку 0,90 долл. США × 10 ручек = 9,00 долл. США
Нахождение стоимости одной единицы позволяет вам найти стоимость любого количества единиц.
Что такое единица измерения в математике?
Ваши учащиеся, несомненно, сталкивались с нормами и соотношениями раньше (видели ли они знак ограничения скорости?), но это может помочь им просмотреть эти понятия перед решением задач, в которых они используются.
Стандарт: Понимать концепцию удельной ставки a / b , связанную с отношением a : b с b ≠ 0. (6.RP.A.2)
3 Необходимые навыки и понятия:
Учащиеся должны иметь общее представление о пропорциях, о том, как их записывать, и уметь упрощать пропорции. Студенты также должны иметь возможность работать с дробями и находить эквивалентные дроби.
- Произнесите: Сегодня мы рассмотрим особый тип коэффициента, называемый ставкой. Кто-нибудь знает, что я имею в виду под тарифом? Учащиеся могут сказать, что скорость – это соотношение, в котором сравниваемые количества используют разные единицы измерения, такие как доллары и унции или мили и часы. Студенты могут использовать распространенные английские синонимы для rate , такие как speed . Если это так, укажите, что скорость означает вычисление скорости движения путем сравнения расстояния со временем, например миль с часами. Если необходимо, объясните, что такое ставка.
- Скажите: Тарифы часто встречаются в повседневной жизни. Цены в продуктовых магазинах и универмагах часто являются тарифами. Тарифы также используются при ценообразовании бензина или билетов, измерении скорости или оплате почасовой оплаты труда и ежемесячных сборов. Предложите учащимся подумать о других примерах ставок.
 В дополнение к обычным примерам из реальной жизни поощряйте глупые или необычные расценки, такие как артисты хип-хопа за почтовый индекс или бриллиантовые ошейники за чихуахуа.
В дополнение к обычным примерам из реальной жизни поощряйте глупые или необычные расценки, такие как артисты хип-хопа за почтовый индекс или бриллиантовые ошейники за чихуахуа. - Скажем: Две важные идеи — это тарифы за единицу и цены за единицу. В чем разница между тарифом и тарифом за единицу? Или цена и цена за единицу? У кого-нибудь есть идеи? Учащиеся, вероятно, не знают, что такое ставка за единицу, поэтому дайте им следующее объяснение, чтобы объяснить соотношение между ставкой и ставкой за единицу.
- Скажем: Единица означает один чего-то. Ставка за единицу означает ставку за что-то одно. Запишем это как отношение со знаменателем, равным единице. Например, если вы пробежали 70 ярдов за 10 секунд, вы пробежали в среднем 7 ярдов за 1 секунду. Оба соотношения, 70 ярдов за 10 секунд и 7 ярдов за 1 секунду, являются нормами, но 7 ярдов за 1 секунду — это 9.0003 единица скорость.
- Спросите: Теперь, когда вы знаете, что такое цена за единицу, как вы думаете, что такое цена за единицу? Студенты скажут, что это цена одного предмета.
 Если нет, скажите им, что это такое.
Если нет, скажите им, что это такое. - Спросите: Какова цена за единицу 10 фунтов картофеля, который стоит 2,80 доллара? Помогите учащимся подсчитать, что цена за единицу составляет 0,28 доллара за фунт, разделив цену на 10.
- Поделитесь следующей задачей: «В одном магазине морковь продается по 1,14 доллара за 3 фунта, а в другом магазине морковь продается по 0,78 доллара за два фунта. фунты. В каком магазине выгоднее?»
- Спросите: Что мы пытаемся найти в этой задаче? Студенты должны сказать, что мы пытаемся выяснить, какая морковь выгоднее, когда думаем о стоимости каждой моркови.
- Спросите: Что поможет нам найти лучшее предложение? Учащиеся должны сказать, что если мы найдем цену за единицу моркови в каждом магазине, то узнаем, что выгоднее.
- Скажите: Найдите цены за единицу моркови в обоих магазинах, и тогда мы обсудим, что вы сделали.
 Предложите учащимся самостоятельно рассчитать цену за единицу товара и ответить, в каком магазине выгоднее. Сравните, как разные учащиеся выполняли расчеты, и предложите учащимся обсудить сходства и различия между моделями, которые они использовали, и найденными решениями. Допускайте разные варианты ответов, например: «Во втором магазине было лучшее предложение для меня, потому что я все равно хотел бы только две морковки». Если позволяет время, предложите учащимся также решить следующую задачу. «Одно животное может пробежать 60 футов за 4 секунды, а другое животное может пробежать 100 футов за 8 секунд. Какое животное бегает быстрее?» (Первое животное бегает быстрее со скоростью 15 футов в секунду.)
Предложите учащимся самостоятельно рассчитать цену за единицу товара и ответить, в каком магазине выгоднее. Сравните, как разные учащиеся выполняли расчеты, и предложите учащимся обсудить сходства и различия между моделями, которые они использовали, и найденными решениями. Допускайте разные варианты ответов, например: «Во втором магазине было лучшее предложение для меня, потому что я все равно хотел бы только две морковки». Если позволяет время, предложите учащимся также решить следующую задачу. «Одно животное может пробежать 60 футов за 4 секунды, а другое животное может пробежать 100 футов за 8 секунд. Какое животное бегает быстрее?» (Первое животное бегает быстрее со скоростью 15 футов в секунду.)
Развитие концепции: коэффициенты
Теперь, когда учащиеся знают, как найти удельный вес, они узнают, как найти эквивалентный коэффициент, используя удельные коэффициенты. Для поиска эквивалентных отношений используется тот же мыслительный процесс, что и для поиска эквивалентных дробей.
Стандарт: Используйте рассуждения об отношении и скорости, чтобы найти эквивалентные отношения и решить реальные задачи (6.RP.A.3)
- Произнесите: До того, как мы научились находить норму единицы. Теперь мы узнаем, как использовать эту единичную скорость для решения задач. Посмотрите на эту проблему.
- Поделитесь следующей проблемой: «Вчера Эбони пробежал 18 кругов по трассе за 12 минут. Если она пробежит с такой скоростью 30 кругов, сколько времени это займет?» (Совет: вы можете заменить контекст любым, что может заинтересовать ваших учеников.)
- Спросите: Что мы пытаемся найти в этой задаче? Мы пытаемся выяснить, сколько времени потребуется Эбони, чтобы пробежать 30 кругов.
- Спросите: Какая известная нам информация поможет нам решить эту проблему? Мы знаем, что Эбони может пробежать 18 кругов за 12 минут. Мы также знаем, что она будет бежать с той же скоростью 30 кругов.

- Спросите: Какое расстояние пробежит Эбони за одну минуту? Предложите учащимся самостоятельно решить это. Сравните решения учащихся и обсудите, почему Эбони пробегает 1,5 круга за одну минуту.
- Скажем: Давайте составим таблицу, чтобы перечислить известную нам информацию. Создайте следующую таблицу, но оставьте поле «Протоколы» пустым. Заполните его, запрашивая входные данные класса.
Laps Minutes 1.5 1 3 2 6 4 12 8 18 12 24 16 30 20 - Спросите: . В любом случае, когда мы могли найти время в 20 минут без написания. В целом? Сравните различные идеи, предложенные учащимися.
 Некоторые студенты могут понять, что если они разделят 30 на 1,5, то получат 20 минут. Обсудите эту стратегию с классом.
Некоторые студенты могут понять, что если они разделят 30 на 1,5, то получат 20 минут. Обсудите эту стратегию с классом. - Напишите на доске следующую задачу: «Мария хочет купить карандаш для всех в своем классе. 3 карандаша стоят 0,78 доллара. Сколько пришлось бы потратить Марии, если бы она купила по карандашу каждому из своих 24 одноклассников?»
- Скажите: Я бы хотел, чтобы вы сами решили эту задачу, а потом мы обсудим, что вы сделали. Предложите учащимся индивидуально поделиться своими решениями. Некоторые учащиеся могли решить ее, найдя цену за единицу или заполнив таблицу. Другие, возможно, решили ее, заметив, что 3 карандаша стоят 0,78 доллара, а 24 = 3 × 8. Поэтому они умножили 0,78 доллара на 8, чтобы получить 6,24 доллара.
***
Ищете другие бесплатные уроки математики и занятия для учащихся начальной школы? Обязательно изучите наш центр бесплатных учебных ресурсов.
Если вы ищете учебную программу по математике, которая откроет доступ к обучению для учащихся, испытывающих трудности с математикой, ознакомьтесь с Math 180 , наше решение по математике для учащихся 5–12 классов.
Поток задач по водяному знаку
Главная > Учебный контент > Планы на неделю
Дроби: 6 класс
Ср, 2 ноября
Урок 1: предварительное тестирование
Цель SWBAT определить мои ожидания от занятий по математике
Разминка Чтение Дроби = Проблемы (чтение вслух)
Действие 1 Пройти предварительное тестирование
Упражнение 2 Пройтись по ожиданиям: «Ни за что Бовэ, когда поднимать руки/выкликать/все говорят вместе, думать/пары/делиться, домашние задания
Домашнее задание Дополнительный рабочий лист для дополнительных кредитов.
Чт, 3 ноября
Урок 2: Книги о буррито
Цель SWBAT создать графический органайзер, определяющий стратегии, которые помогут им решать арифметические задачи с использованием дробей (создать, СР)
Разминка Часть=Часть=Часть (прочитано вслух)
Действие 1 Создать Книга буррито (BB)
-Обложка: определить дроби, имя
-Словарь (1 страница)
— Рецепт смешанных чисел и неправильных дробей (1 страница)
-GCF и LCD (2 страницы)
-Сложение и вычитание (2 страницы)
-Умножение (1 страница)
-Разделить (1 страница)
-Вопросы, которые у меня остались (1 страница)
-Ага Моменты (1 страница)
-Задняя обложка: дроби в реальной жизни
Домашнее задание нет
Пт, 4 ноября
Урок 3. Словарь дробей
Словарь дробей
Цель SWBAT определить следующее: числитель, знаменатель, дробь,
Разминка Рабочий лист Twality Pizza
Действие 1 A Дробь является частью целого (напишите на обложке BB)
Как «говорить» о дробях
Числитель — это часть, это число сверху (напишите в словарном разделе BB)
Знаменатель — это целое число внизу (запишите в словарный запас ББ)
Занятие 2 учащихся составляют невербальное определение дроби/числителя/знаменателя
Домашнее задание Детектив дробей Рабочий лист
Пн, 7 ноября
Урок 4. Сравнение дробей, неправильных дробей и смешанных чисел
Цель(и) SWBAT превращает смешанные числа в неправильные дроби и наоборот (применить, CP)
SWBAT находит актуальность в дробях, определяя 2+ способа, которыми они используют дроби в своей повседневной жизни. (оценить, А)
(оценить, А)
Разминка: Поделиться Детектив дробей Рабочий лист. (Написать/нарисовать ответы на задней обложке ББ)
Упражнение 1: Сравнение и упорядочивание дробей
Занятие 2: Неправильные дроби и смешанные числа
Рецепт перехода туда и обратно (напишите в разделе смешанный #/неправильный рецепт ББ)
Домашнее задание: Сравнение и упорядочивание дробей Рабочий лист (узнать шансы)
Смешанные числа и неправильные дроби Рабочий лист (узнать шансы)
Вт, 8 ноября
Урок 5. Сложение и вычитание дробей 1
Цель SWBAT сложение и вычитание дробей с одинаковыми знаменателями (применить, CP)
SWBAT приводит дроби к их простейшей форме (применяется, CP)
SWBAT превращает смешанные числа в неправильные дроби и наоборот (применить, CP)
Упражнение 1 Сложение и вычитание чисел с одинаковыми знаменателями (запишите шаги в BB)
Действие 2 Сокращение дробей
Наибольший общий делитель (GCF)
Упражнение 3 M&Ms Сложение и вычитание ( Сбор домашнего задания)
Домашнее задание Сложение/вычитание дробей Рабочий лист 1 (выберите и выполните любые 5 на обеих страницах)
Ср, 9 ноября
Урок 6. Сложение и вычитание дробей 2
Сложение и вычитание дробей 2
Цель SWBAT сложение и вычитание дробей с разными знаменателями (применить, CP)
SWBAT приводит дроби к их простейшей форме (применяется, CP)
SWBAT превращает смешанные числа в неправильные дроби и наоборот (применить, CP)
Разминка Обзор Сравнение/порядок дробей
Задание 1 Наименьший общий знаменатель (LCD)
Упражнение 2 Сложение и вычитание дробей с разными знаменателями
Домашнее задание Сложение/вычитание дробей Рабочий лист 2 (выберите и выполните любые 5 на обеих страницах)
Повторите таблицу сравнения/упорядочивания фракций (узнайте шансы)
Пн, 14 ноября
Урок 7: Умножение
Объектив SWBAT умножить дроби (применить, CP)
SWBAT приводит дроби к их простейшей форме (применяется, CP)
SWBAT превращает смешанные числа в неправильные дроби и наоборот (применить, CP)
Разминка Дроби на числовом ряду
Упражнение 1 Умножение дробей
Занятие 2 Практика умножения дробей в партнерах
Домашнее задание: Рабочий лист «Умножение дробей» (умножьте шансы на обе стороны)
Вт, 15 ноября
Урок 8: Деление
Объектив SWBAT разделить дроби
SWBAT приводит дроби к их простейшей форме (применяется, CP)
SWBAT превращает смешанные числа в неправильные дроби и наоборот (применить, CP)
Разминка Незавершенные дела: Повторить недельный график, вернуть исправленную работу
Занятие 1 Деление дробей
Занятие 2 Музыкальные стулья (практика умножения и деления)
Домашнее задание Рабочий лист «Деление дробей» (Деление коэффициентов)
Ср, 16 ноября
Урок 9. Как вычислять дроби
Как вычислять дроби
Цель Создать графический органайзер, определяющий стратегии, которые помогут им решать арифметические задачи с использованием дробей (создать, СР)
Упражнение 1/Разминка Эстафета фракций (обзор)
Действие 2 Назначение страниц (тем) группам:
-словарь
-сокращающие дроби (наибольший общий делитель)
-нахождение наименьшего общего знаменателя (LCD)
-сложение и вычитание дробей с одинаковыми и разными знаменателями
-умножение дробей
-деление дробей
-фракции в реальной жизни
Деятельность 3 Рабочее время
Домашнее задание: Подготовка к экзамену
Чт, 17 ноября
Урок 10: Настоящие страницы книги
Цель SWBAT создать графический органайзер, определяющий стратегии, которые помогут им решать арифметические задачи с использованием дробей (создать, СР)
Разминка Изучение техник/техник групповой работы
Деятельность 1 Завершение проектов
Занятие 2 Мини-конференции с каждым учащимся
Занятие 3 Настоящие страницы книг
Домашнее задание Исследование для теста
Пт, 18 ноября
Урок 11: Последующее тестирование
Разминка Показать продукт проекта («книгу») Разместить книгу со словарями в классе.

 05.2012
05.2012