Треугольник и его виды / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Треугольник и его виды
Треугольник — это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки — сторонами.
Данная фигура является треугольником (произносят: треугольник АВС, пишут: ∆ АВС). Точки А, В, С — вершины треугольника, а отрезки АВ, ВС, АС ‒ стороны.
Периметр треугольника — это сумма длин всех его сторон.
Виды треугольников
По виду углов:
- Остроугольный треугольник — это треугольник, у которого все три угла острые.
- Тупоугольный треугольник — это треугольник, у которого один из углов тупой.
- Прямоугольный треугольник — это треугольник, у которого один из углов прямой.
Сумма углов любого треугольника равна 1800.
По количеству равных сторон:
- Равнобедренный треугольник — это треугольник, у которого две стороны равны.
∆OXP — равнобедренный: XO = XP. Равные стороны на рисунке отмечают равным количеством чёрточек (в нашем случае одной чёрточкой). В равнобедренном треугольники равные стороны называют боковыми сторонами, а третью сторону — основанием, т.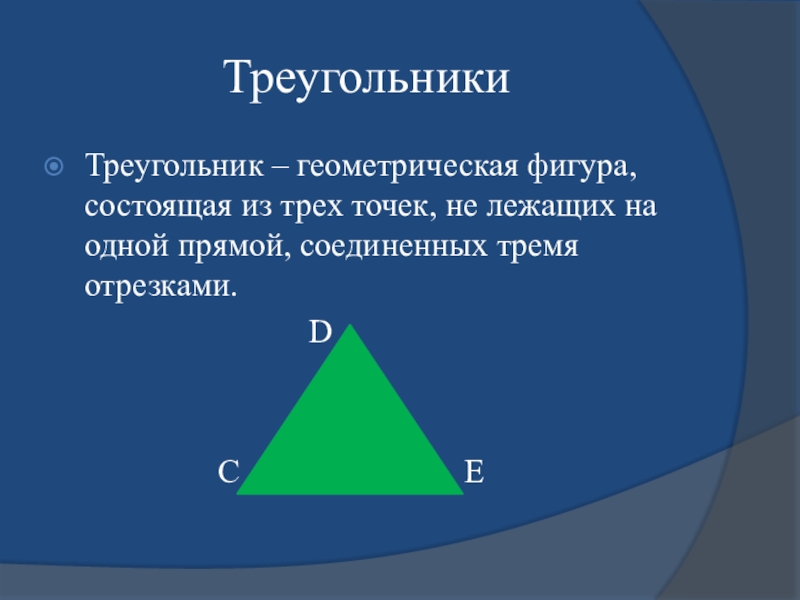
е. в ∆OXP: XO и XP — боковые стороны, а OP — основание.
- Равносторонний треугольник — это треугольник, у которого все стороны равны.
∆WYZ — равносторонний: WY = YZ = ZW. Равносторонний треугольник также называют правильным. Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле:
| P = 3 |
- Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники.
Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 367, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 508, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 935, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1027, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1668, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1704, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 338, Мерзляк, Полонский, Якир, Учебник
Номер 344, Мерзляк, Полонский, Якир, Учебник
Номер 352, Мерзляк, Полонский, Якир, Учебник
Номер 370, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 39, Мерзляк, Полонский, Якир, Учебник
Номер 298, Мерзляк, Полонский, Якир, Учебник
Номер 684, Мерзляк, Полонский, Якир, Учебник
Номер 685, Мерзляк, Полонский, Якир, Учебник
Номер 1184, Мерзляк, Полонский, Якир, Учебник
Номер 1225, Мерзляк, Полонский, Якир, Учебник
Номер 1228, Мерзляк, Полонский, Якир, Учебник
Номер 1268, Мерзляк, Полонский, Якир, Учебник
Задание 365, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1595, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 753, Мерзляк, Полонский, Якир, Учебник
Номер 980, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 433, Мерзляк, Полонский, Якир, Учебник
Номер 453, Мерзляк, Полонский, Якир, Учебник
Номер 456, Мерзляк, Полонский, Якир, Учебник
Номер 459, Мерзляк, Полонский, Якир, Учебник
Треугольники / Основы геометрии / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Треугольники
Треугольник — это ломаная линия, которая состоит из трёх звеньев-отрезков.
У треугольника три стороны.
У треугольника три вершины.
Бывают треугольники, у которых все стороны равны. Они называются равносторонними.
Бывают треугольники, у которых две стороны равны. Они называются равнобедренными.
Равносторонний треугольник тоже можно отнести к равнобедренным.
А это прямоугольный треугольник.
Советуем посмотреть:
Круг. Шар. Овал
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
1 класс
Страница 93, Моро, Волкова, Степанова, Учебник, часть 1
Страница 101, Моро, Волкова, Степанова, Учебник, часть 1
Страница 107, Моро, Волкова, Степанова, Учебник, часть 2
Страница 17.
Урок 10,
Петерсон, Учебник, часть 1
Страница 62. Урок 38, Петерсон, Учебник, часть 1
Страница 3. Урок 2, Петерсон, Учебник, часть 2
Страница 31. Урок 16, Петерсон, Учебник, часть 2
Страница 13. Урок 7, Петерсон, Учебник, часть 3
Страница 45. Урок 23, Петерсон, Учебник, часть 3
Страница 73. Урок 37, Петерсон, Учебник, часть 3
2 класс
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 50, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 65, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 80, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 8.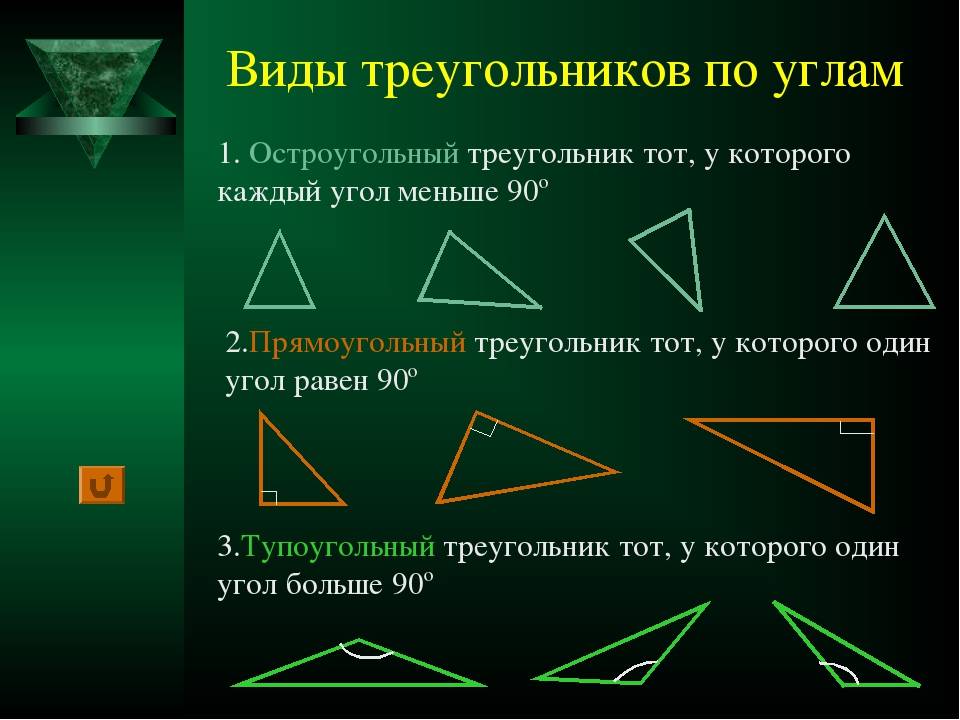
Урок 2,
Петерсон, Учебник, часть 2
Страница 16. Урок 5, Петерсон, Учебник, часть 3
Страница 25. Урок 9, Петерсон, Учебник, часть 3
3 класс
Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 86, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 25.
Урок 8,
Петерсон, Учебник, часть 1
Страница 41. Урок 15, Петерсон, Учебник, часть 1
Страница 24. Урок 11, Петерсон, Учебник, часть 2
Страница 43. Урок 17, Петерсон, Учебник, часть 2
Страница 45. Урок 18, Петерсон, Учебник, часть 2
4 класс
Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 37, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 17, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 112, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Треугольники в геометрии — определение, форма, типы, свойства
Что такое треугольники?
Треугольник — это замкнутая двумерная фигура с 3 сторонами, 3 углами и 3 вершинами.
Треугольник также является многоугольником.
На приведенном выше рисунке изображен треугольник, обозначенный буквой △ABC.
Родственные игры
Примеры треугольниковНекоторые примеры треугольников из реальной жизни включают бутерброды, дорожные знаки, вешалки для одежды и стойку для бильярда.
Связанные рабочие листы
Непримеры треугольниковПриведенные выше цифры не являются примерами треугольников. Эти фигуры нельзя назвать треугольниками, так как –
- Первая фигура четырехсторонняя.
- Вторая фигура представляет собой открытую форму.
- Третья фигурка имеет изогнутую сторону.
Части треугольника
- Треугольник имеет 3 стороны. В треугольнике АВС стороны равны АВ, ВС и СА.
- Угол, образованный любыми двумя сторонами треугольника, является углом треугольника, обозначаемым символом ∠. Треугольник имеет три угла. Три угла треугольника ABC равны ∠ABC, ∠BCA и ∠CAB.
Эти углы также называются ∠B, ∠C и ∠A соответственно. - Точка пересечения любых двух сторон треугольника называется вершиной. Треугольник имеет три вершины. В треугольнике ABC вершинами являются A, B и C.
Эти углы также называются ∠B, ∠C и ∠A соответственно.Свойства треугольника
- Сумма всех трех внутренних углов треугольника всегда равна 180⁰.
- Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны.
- Площадь треугольника равна половине произведения его основания на высоту.
Типы треугольников
Треугольники можно классифицировать на основе длины сторон или измерения их углов.
Чтобы классифицировать треугольники по их углам, мы измеряем каждый из их внутренних углов. Треугольники можно классифицировать по углам, как:
- Остроугольный треугольник или остроугольный треугольник
- Прямоугольный треугольник или прямоугольный треугольник
- Тупоугольный треугольник или тупоугольный треугольник
Типы треугольников в зависимости от длины сторон –
- Разносторонний треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Чтобы классифицировать треугольники по углам и сторонам, мы измеряем внутренние углы и длину сторон треугольника.
Треугольники, классифицируемые как по углам, так и по сторонам: –
- Остроугольный равносторонний треугольник
- Прямоугольный равнобедренный треугольник
- Тупоугольный разносторонний треугольник
Площадь треугольника
Площадь треугольника — это область, которую треугольник занимает в двумерном пространстве. Площадь разных треугольников различается в зависимости от их размера. Зная длину основания и высоту треугольника, мы можем определить его площадь. Выражается в квадратных единицах.
Итак, площадь треугольника = ½ (произведение основания и высоты треугольника)
В треугольнике PQR стороны PQ, QR и RP. QR — основание треугольника, а PS — высота треугольника. PS перпендикулярен из вершины P к стороне QR. Итак, чтобы найти площадь △PQR, мы используем следующую формулу:
Площадь △PQR = ½ (произведение основания и высоты треугольника)
Или площадь △PQR = ½ (QR X PS)
Периметр треугольника
Периметр треугольника равен сумме длин всех сторон треугольника.
Итак, периметр треугольника = сумма всех трех сторон.
В треугольнике PQR периметр будет суммой трех сторон, то есть PQ, QR и RP.
Итак, периметр △PQR = PQ + QR + RP.
Решенные примеры на треугольнике
В. Найдите площадь треугольника с основанием 10 см и высотой 8 см.
Ответ. Для данного треугольника основание = 10 см и высота = 8 см
Мы знаем, что
Площадь треугольника = ½ (Произведение основания и высоты треугольника)
Итак, площадь данного треугольника = ½ (10 x 8) = ½ (80) = 40 см 2
В. Используя рисунок ниже, найдите периметр треугольника ABC.
Ответ. Мы знаем, что Периметр треугольника = (Сумма всех сторон треугольника)
На данном рисунке длины сторон треугольника ABC равны
AB= 5 см, CA= 5 см и BC= 7 см. .
Итак, периметр △ABC= AB + BC + CA = 5 + 7 + 5 = 17 см.
В. Определите, является ли данная фигура треугольником, а также объясните причины.
Б.
В.
Ответ. А. Данная фигура является треугольником, так как имеет три прямые стороны и является замкнутой фигурой.
B. Форма не является треугольником, так как имеет четыре стороны.
C. Форма не является треугольником, так как это открытая фигура с тремя открытыми сторонами.
Q. Периметр треугольника PQR равен 16 см, а стороны PQ и QR равны 4 см и 6 см. Найдите длину третьей стороны треугольника.
Ответ. Мы знаем, что периметр треугольника = (сумма всех сторон треугольника)
Итак, периметр △PQR= PQ + QR + RP
16 = 4 + 6 + RP
RP= 16 – 10 = 6см
Итак, длина третьей стороны 6см.
Q. Углы A и B треугольника ABC равны 70⁰ и 60⁰ соответственно. Найдите третий угол C.
Ответ. Мы знаем, что сумма всех углов треугольника равна 180⁰.
Итак, ∠A + ∠B + ∠C = 180⁰
70⁰ + 60⁰ + ∠C = 180⁰
∠C = 180⁰ – 130⁰ = 50⁰ 900 05
Третий угол треугольника равен 50⁰.
В. Можно ли составить треугольник со сторонами 2 см, 3 см и 6 см?
Ответ.
Чтобы образовался треугольник, сумма любых двух сторон всегда должна быть больше третьей стороны.
Для данных размеров 3 см + 6 см = 9 см больше 2 см, 6 см + 2 см = 8 см больше 3 см, но 2 см + 3 см = 5 см меньше 6 см. Таким образом, данные меры не могут образовывать треугольник.
В. Если площадь треугольника 20 см, а длина его основания 5 см, найдите высоту треугольника.
Ответ. Мы знаем, что площадь треугольника = ½ x основание x высота
Итак, 20 = ½ x 5 x высота
Высота треугольника = (20 x 2) / 5 = 8 см
Практические задачи на треугольник
1
Выберите лишнее.
Разносторонний треугольник
Остроугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Правильный ответ: Остроугольный треугольник углы. 9{2}$.
Заключение
Геометрия — важный аспект математики, требующий углубленного изучения. Концепция треугольников является фундаментальной темой в геометрии для маленьких детей.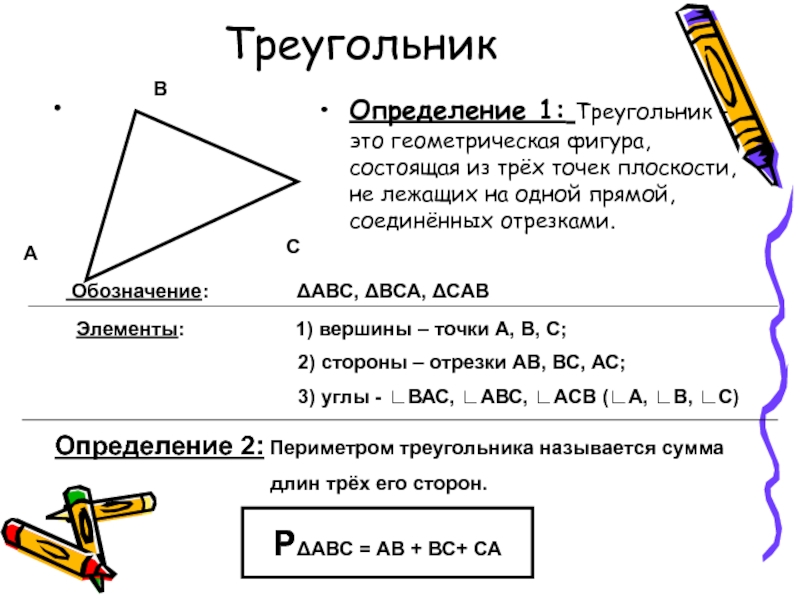
Благодаря интерактивному обучению с помощью подробных материалов курса от SplashLearn ваш ребенок узнает о треугольниках, их типах и свойствах, а также попрактикуется в играх и рабочих листах.
Треугольник
Треугольник — это трехсторонний многоугольник.
Части треугольника
Все треугольники состоят из трех сторон и трех углов. Точка, в которой встречаются две стороны треугольника, называется вершиной. Вершины треугольников обычно помечаются, как показано на рисунке ниже:
Три стороны показанного выше треугольника ABC, обозначенные символически как △ABC, представляют собой отрезки AB, BC и AC. A образуется при пересечении двух сторон треугольника. △ABC имеет вершины в точках A, B и C. В каждой вершине образован внутренний угол. Углы A, B и C являются тремя внутренними углами для △ABC.
Отрезок от вершины треугольника до стороны, противоположной вершине, которая перпендикулярна противоположной стороне, называется высотой. Сторона, перпендикулярная высоте, называется основанием треугольника.
В треугольнике ABC ниже отрезок CD является высотой, а сторона AB является основанием.
Стороны треугольника принято называть по противолежащему углу. Это часто включает использование прописных и строчных букв для обозначения угла и его противоположной стороны. В качестве примера см. △ABC выше. Сторона ВС противоположна углу А, поэтому она обозначена как сторона а.
Типы треугольников
Треугольники часто классифицируют по их углам и сторонам, как показано в таблицах ниже.
По уголкам:
| Тип | Уголки | Фигура |
|---|---|---|
| Острая | все внутренние углы < 90° | |
| Тупой | 1 внутренний угол > 90° | |
| Справа | 1 угол = 90° | |
| Равноугольный | каждый внутренний угол = 60° |
По сторонам:
| Тип | Стороны | Фигура |
|---|---|---|
| Scalene | нет двух равных сторон | |
| Равнобедренный | 2 конгруэнтные стороны | |
| Равносторонний | все стороны конгруэнтны |
Свойства треугольника
Ниже приведены некоторые свойства треугольника, на которые стоит обратить внимание.
Сумма углов
Используя свойства параллельных прямых и чередующихся внутренних углов, мы можем показать, что сумма внутренних углов треугольника равна 180°.
- Для △ABC, показанного выше, пусть линия DE, содержащая вершину C, параллельна стороне AB. Поскольку ∠DCE — прямой угол, ∠ECA + ∠DCB + ∠BCA = 180°.
- Кроме того, поскольку DE параллелен AB, это образует два набора конгруэнтных альтернативных внутренних углов, так что ∠ECA≅∠A и ∠DCB≅∠B.
- Подставив углы A и B в наше предыдущее уравнение, ∠A + ∠B + ∠BCA = 180°, где ∠BCA = ∠C.
Внешние углы
Для треугольника внешний угол представляет собой угол, образованный одной стороной треугольника и линией, продолжающейся от другой его стороны. Мера внешнего угла треугольника равна сумме двух удаленных друг от друга внутренних углов.
Для △ABC, показанного выше, ∠CAD — внешний угол для ∠A и ∠B, а ∠C — два отдаленных внутренних угла. Мы знаем, что ∠CAB + ∠B + ∠C = 180°..jpg)