Задачи тысячелетия по математике: Задачи тысячелетия. Просто о сложном / Хабр

Задачи тысячелетия. Просто о сложном / Хабр

Привет, хабралюди!

Сегодня я бы хотел затронуть такую тему как «задачи тысячелетия», которые вот уже десятки, а некоторые и сотни лет волнуют лучшие умы нашей планеты.

После доказательства гипотезы (теперь уже теоремы) Пуанкаре Григорием Перельманом, основным вопросом, который заинтересовал многих, был: «А что же он собственно доказал, объясните на пальцах?» Пользуясь возможностью, попробую объяснить на пальцах и остальные задачи тысячелетия, или по крайней мере подойти в ним с другой более близкой к реальности стороны.

Равенство классов P и NP

Все мы помним из школы квадратные уравнения, которые решаются через дискриминант. Решение этой задачи относится к классу P (Polynomial time) — для нее существует быстрый (здесь и далее под словом «быстрый» подразумевается как выполняющийся за полиномиальное время) алгоритм решения, который и заучивается.

Также существуют NP-задачи (Non-deterministic Polynomial time), найденное решение которых можно быстро проверить по определенному алгоритму. Для примера проверка методом перебора компьютером. Если вернуться к решению квадратного уравнения, то мы увидим, что в данном примере существующий алгоритм решения проверяется так же легко и быстро как и решается. Из этого напрашивается логичный вывод, что данная задача относится как к одному классу так и ко второму.

Таких задач много, но основным вопросом является, все или не все задачи которые можно легко и быстро проверить можно также легко и быстро решить? Сейчас для некоторых задач не найдено быстрого алгоритма решения, и неизвестно существует ли такой вообще.

На просторах интернета также встретил такую интересную и прозрачную формулировку:

Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации.

В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей.

В данном случае вопрос стоит все тот же, есть ли такой алгоритм действий, благодаря которому даже не имея информации о том, где находится человек, найти его так же быстро, как будто зная где он находится.

Данная проблема имеет большое значение для самых различных областей знаний, но решить ее не могут уже более 40 лет.

Гипотеза Ходжа

В реальности существуют множество как простых так и куда более сложных геометрических объектов. Очевидно, что чем сложнее объект тем более трудоемким становится его изучение. Сейчас учеными придуман и вовсю применяется подход, основная идея которого заключается в том, чтобы вместо самого изучаемого объекта использовать простые

«кирпичики» с уже известными свойствами, которые склеиваются между собой и образуют его подобие, да-да, знакомый всем с детства конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта.

Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков» так и объектов.

Гипотеза Римана

Всем нам еще со школы известны простые числа которые делятся только на себя и на единицу (2,3,5,7,11…). С давних времен люди пытаются найти закономерность в их размещении, но удача до сих пор так никому и не улыбнулась. В результате ученые применили свои усилия к функции распределения простых чисел, которая показывает количество простых чисел меньше или равных определенного числа. Например для 4 — 2 простых числа, для 10 — уже 4 числа.

Гипотеза Римана как раз устанавливает свойства данной функции распределения.

Многие утверждения о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности этой гипотезы.

Теория Янга — Миллса

Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения, объединяющие теории электромагнитного, слабого и сильного взаимодействий. Одно время теория Янга-Миллса рассматривалась лишь как математический изыск, не имеющий отношения к реальности. Однако, позже теория начала получать экспериментальные подтверждения, но в общем виде она все еще остается не решенной.

На основе теории Янга-Миллса построена стандартная модель физики элементарных частиц в рамках которой был предсказан и не так давно обнаружен нашумевший бозон Хиггса.

Существование и гладкость решений уравнений Навье — Стокса

Течение жидкостей, воздушные потоки, турбулентность. Эти, а также множество других явлений описываются уравнениями, известными как уравнения Навье — Стокса. Для некоторых частных случаев уже найдены решения, в которых как правило части уравнений отбрасываются как не влияющие на конечный результат, но в общем виде решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать.

Гипотеза Бёрча — Свиннертон-Дайера

Для уравнения x² + y² = z² в свое время еще Эвклид дал полное описание решений, но для более сложных уравнений поиск решений становится чрезвычайно трудным, достаточно вспомнить историю доказательства знаменитой теоремы Ферма, чтобы убедиться в этом.

Данная гипотеза связана с описанием алгебраических уравнений 3 степени — так называемых

эллиптических кривых и по сути является единственным относительно простым общим способом вычисления ранга, одного из важнейших свойств эллиптических кривых.

В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.

Гипотеза Пуанкаре

Думаю если не все, то большинство точно о ней слышали. Чаще всего встречается, в том числе и на центральных СМИ, такая расшифровка как «резиновую ленту натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». На самом деле эта формулировка справедлива для гипотезы Тёрстона, которая обобщает гипотезу Пуанкаре, и которую в действительности и доказал Перельман.

Частный случай гипотезы Пуанкаре говорит нам о том, что любое трехмерное многообразие без края (вселенная, например) подобно трехмерной сфере. А общий случай переводит это утверждение на объекты любой мерности. Стоит заметить, что бублик, точно так же как вселенная подобна сфере, подобен обычной кофейной кружке.

Заключение

В настоящее время математика ассоциируется с учеными, имеющими странный вид и говорящие о не менее странных вещах. Многие говорят о ее оторванности от реального мира. Многие люди как младшего, так и вполне сознательного возраста говорят, что математика ненужная наука, что после школы/института, она нигде не пригодилась в жизни.

Но на самом деле это не так — математика создавалась как механизм с помощью которого можно описать наш мир, и в частности многие наблюдаемые вещи. Она повсюду, в каждом доме. Как сказал В.О. Ключевский: «Не цветы виноваты, что слепой их не видит».

Наш мир далеко не так прост, как кажется, и математика в соответствии с этим тоже усложняется, совершенствуется, предоставляя все более твердую почву для более глубокого понимания существующей реальности.

7 ЗАДАЧ ТЫСЯЧЕЛЕТИЯ — I-NURE

Кто из вас хочет стать миллионером? Для этого не нужно покупать лотерейный билет или грабить банк. Математический институт Клэя в США готов с радостью выплатить миллион тем, кто просто решит хотя бы одну из их математических задач. Звучит настолько просто, что вы уже готовы  набросать решение любой из них? А давайте-ка сначала узнаем так ли просты эти задачки…

 

Как обычно, немного истории…

В начале 20 века знаменитый немецкий математик Давид Гильберт на одной из конференций представил миру  26 открытых математических проблем, требующих хорошенько пораскинуть мозгами. К концу столетия 20 из них были решены математиками всего мира. Последней, кстати, была теорема Ферма, знакомая многим из курса линейной алгебры и аналитической геометрии.

Новый список задач, представленный американским институтом Клэя в 1998 году, стал в  несколько раз «скромнее» — всего 7 задач – но, как видно, и намного сложнее, ведь за 21 год существования, лишь одна из них была решена…

 

 

Так что собой представляют эти 7 задач?

Каждая из них касается какой-либо из областей математики: от теории алгоритмов до топологии и математической физики. И пусть некоторые на первый взгляд могут показаться простыми, но не просто же так за решение любой из них присуждается 1 миллион долларов! Но, пожалуй, начнем описание с той самой единственной решенной задачи. Итак…

 

1. Гипотеза Пуанкаре

Область изучения – топология.

Эта гипотеза доказана в 2002 году российским математиком Григорием Перльманом. Очень часто можно встретить и другое название этой знаменитой задачи – «проблема бублика». Гипотеза утверждает следующее: всякий трёхмерный объект, обладающий некоторыми свойствами  трёхмерной сферы, обязан быть сферой с точностью до деформации. Сама же история решения этой задачи тысячелетия прямо-таки, как сюжет фильма: гениальный математик из Санкт-Петербурга на несколько лет обрывает все связи с внешним миром, а потом триумфально возвращается с решением одной из 7 задач, навсегда занося своё имя в историю мировой науки! Что ещё более любопытно: от награды в 1 миллион долларов Григорий Перльман отказался.

 

 

2. Равенство классов P и NP

Область изучения – теория алгоритмов.

Перед вами два класса: P и NP. P – это множество задач, которые компьютер может решить за полиномиальное время, т.е. довольно быстро. NP – это класс задач, правильность ответа, которых можно быстро проверить.

Для простоты понимания вот вам пример: у вас есть по одной монетке номиналом 2, 3, 5, 6 и 7.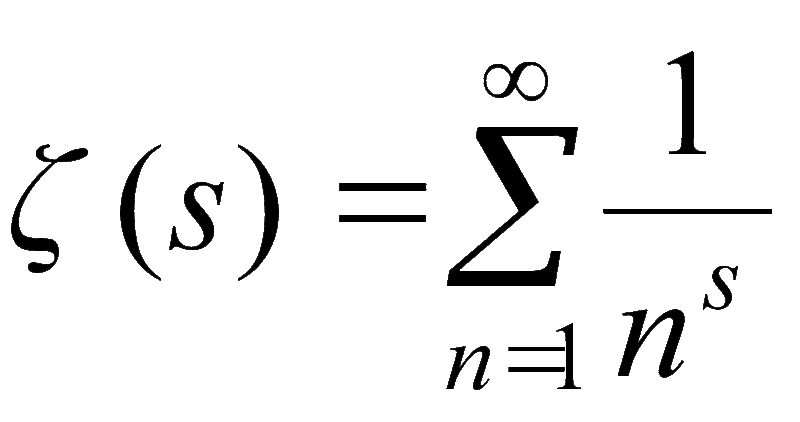 Ваша задача – оплатить покупку без сдачи на сумму 21 денежной единицы. Можно ли набрать из этих монет сумму, равную 21? Задача решается методом перебора, и вот плавно мы подходим к вопросу одной из задач тысячелетия: равны ли классы N и NP? Многие ученые уверены в отрицательном ответе, но доказать свою точку зрения так пока никто и не смог. Только вот что будет, если окажется, что P=NP?..

 

3. Уравнение Навье-Стокса

Область – гидродинамика.

Задача, которая может быть известна некоторым по фильму «Одарённая». В решении данного уравнения заложена одна из сложнейших проблем современной физики – проблема турбулентности.  Турбулентность хоть и является довольно распространённым явлением, но до сих пор остаётся почти неизученной, отчего и совершенно непредсказуемой.

 

 

Помимо самого уравнения, задача ставит перед нами и такой вопрос: если известно состояние жидкости в определённый момент  времени и характеристики её движения – существует ли решение, которое  будет верно для всего будущего времени? Так что, помимо проблемы турбулентности, решение этой задачи помогло бы метеорологам делать более точные прогнозы погоды, а нам – всегда вовремя брать с собой зонтик.

 

4. Гипотеза Римана

Область – теория чисел.

Задача, посвященная нашим любимым простым числам. Если проследить их последовательность в общем строю всех чисел, то можно прийти к тому, что какой-либо закономерности их распределения нет. 

Немецкий математик Бернхард Риман предложил гипотезу, которая утверждает, что все нетривиальные нули дзета-функции распределения простых чисел лежат на прямой линии. Гипотеза Римана уже была проверена для 10 триллионов  решений, но полное доказательство ещё не было подтверждено, но математики утверждают, что уже совсем близко подошли к решению этой задачи тысячелетия.

 

5. Гипотеза Ходжа

Область – алгебраическая геометрия.

«На любом невырожденном проективном  комплексном  алгебраическом  многообразии любой класс Ходжа представляет собой рациональную линейную комбинацию  классов алгебраических циклов». Так звучит формулировать данной гипотезы. Немного запутанно, да?

 

 

Суть в чем: в мире нас окружают простые и сложные объекты. И, вполне логично, что сложные объекты можно описать с помощью определённого количества простых. Основная идея гипотезы состоит в том, чтобы выяснить, до какой степени мы можем приближаться к форме  сложного объекта, склеивая вместе  простые тела  возрастающей размерности.

 

6. Теория Янга-Миллса

Область – физика элементарных частиц.

Физики Янг Чжэньнин и Роберт Миллс обнаружили связь между  геометрией и физикой элементарных частиц и написали уравнения, объединяющие теории электромагнитного,  слабого и сильного воздействия, что до этого казалось невозможным. По сути, уравнения теории Янга-Миллса пытаются предсказать поведение элементарных частиц и дать общее описание 3 из 4  фундаментальных взаимодействий. Проведённые эксперименты полностью подтверждают выдвинутую теорию, однако полное обоснование до сих пор так и не найдено.

И наконец…

 

7. Гипотеза Бёрча-Свиннертон-Дайера

Область – алгебраическая геометрия. Снова.

Гипотеза связана с описанием  алгебраических уравнений 3 степени – эллиптических кривых – и является единственным простым общим  способом  ранга эллиптических кривых.

Суть задачи такова: множество решений эллиптической кривой связано с поведением L-функции, которая вычисляется, как и дзета-функция гипотезы Римана, и количество рациональных решений бесконечно тогда, когда функция равна 0.

 

 

Главный вопрос: возможно ли вообще решить все задачи тысячелетия?

Как говорится: нет ничего невозможного! Терпение, труд и отличная математическая база всё перетрут. Кто знает, дорогие студенты ХНУРЭ, может быть именно вы благодаря своим знаниям разрешите оставшиеся 6 задач тысячелетия? И это касается не только тех, кто обучаться по профилю «Прикладная математика», а студентов всех факультетов ВУЗа. Так что, достаём листочки и начинаем решать – за кем будущее, как не за нами?

 

По материалам: Wikipedia.org, naked-science. ru, habr.com

 

Карина Темчур        

 

7 нерешенных задач. Сможет ли с ними справиться молодое поколение?

30 ноября 2017

Современная наука решает сложные задачи: ищет лекарства от тяжелых заболеваний, разбирается в устройстве «черных дыр» и пытается понять, как зародилась жизнь на Земле. Теоретические вопросы кажутся многим малозначительными, ведь непонятно, какую практическую пользу принесут их ответы. Однако именно они и расширяют понимание закономерностей, по которым живет окружающий мир. Поняв эти законы, человечество найдет новые способы улучшить жизнь на Земле и приспособиться к среде обитания на других планетах. Мы собрали семь примеров нерешенных задач из области естественных наук — математики, физики, химии и биологии.

№1. Теорема Римана и математические проблемы тысячелетия

Из школьной программы мы помним о существовании простых чисел: они делятся только на единицу и самих себя. Некоторые из них образуют пары с разницей в 2 (11 и 13, 59 и 61), а иногда — целые скопления (101, 103, 107, 109 и 113). Однако никто точно не знает, сколько таких скоплений существует и какой закономерности они подвержены. Эта задача называется теоремой Римана. Она входит в список нерешенных математических задач тысячелетия. Тому, кто ее решит, Математический институт Клэя выплатит вознаграждение в 1 млн долларов. Кроме того, подтверждение или опровержение теоремы Римана докажет стойкость протоколов на основе открытых кодов шифрования — например, RSA или HTTPS. От их целостности зависит, получат ли злоумышленники информацию пользователей.  

Больше информации о задаче — на сайте.  

№2. Можно ли выбраться из черной дыры?

 

Менее абстрактные задачи предстоит решить современным физикам. Одна из них — о существовании излучения, названного в честь известного физика и популяризатора науки Стивена Хокинга. Согласно его гипотезе, учитывающей квантовую теорию гравитации, черная дыра способна испускать элементарные частицы-фотоны, хотя сама обладает колоссальной силой притяжения. Исходя из этого, у любого объекта в космосе есть шанс выбраться из черной дыры, в том числе и у космического корабля при достаточной мощности двигателей. Однако теория пока не получила окончательного подтверждения и остается гипотезой.  

О деталях этой задачи можно узнать по ссылке.  

№3. Природа шаровой молнии  

Многие видели шаровую молнию, однако ученые так и не разобрались с причинами ее появления. Поняв, по каким законам существуют шаровые молнии, ученые смогут разработать дешевое средство противовоздушной обороны и приблизиться к созданию рабочего термоядерного реактора.  

Подробнее о шаровых молниях и их практическом применении можно узнать по ссылкам.  

№4. 137-й элемент периодической системы — последний?  

С момента первой публикации Дмитрием Менделеевым в 1871 году, таблица химических элементов пополнилась множеством новых. Последний из них — Оганессон — впервые был синтезирован в 2002 году и стал 118-м по счету. Теоретически ученые могут создавать новые химические элементы вплоть до 137-го. После этого скорость вращения электрона вокруг ядра атома на первом энергетическом уровне превысит скорость света. Этот факт нарушает законы физики и ставит под сомнение синтез 138 гипотетического элемента. Синтез новых химических элементов докажет или опровергнет нынешние представления о строении атомов, а также предоставит более совершенное сырье для выработки электроэнергии.  

Узнать больше о задаче можно на сайте.  

№ 5. Истоки жизни на Земле  

В биологии, которая граничит с химией, ученые также бьются над нерешенными вопросами. Одна из наиболее фундаментальных проблем — вопрос о происхождении жизни на Земле. Существующую теорию «первичного бульона», согласно которой органические вещества появились под воздействием солнечного света, молний и других факторов, экспериментально подтвердили американские химики Стэнли Миллер и Гарольд Юри. Однако эта теория не объясняет, как из хаотичного скопления примитивных органических веществ появилась сложная и «элегантная» молекула ДНК — основа большинства известных живых организмов на земле. Помимо ответа на один из фундаментальных вопросов, понимание истоков происхождения жизни даст людям шанс самим стать «творцами» и синтезировать новые живые существа. Этот факт станет не только прорывом в биологии: он поможет в генной инженерии и биотехнологиях.  

Подробнее о задаче можно узнать по ссылке.  

Задача №6. В чем секрет живучести тихоходок?  

Тихоходки — животные, отдаленно напоминающие медведок и организмы, близкие к членистоногим. Их размер не превышает 1,5 мм, а свое название они оправдывают невероятной медлительностью: средняя скорость их передвижения не превышает 3 мм в минуту. Такой неспешный образ жизни, а также способность высушивать собственное тело позволяют тихоходкам выживать в самых экстремальных условиях: при крайне низких температурах (-273 С), в кипящей воде и даже в открытом космосе под воздействием радиации. В то же время, ученые пока не знают, как механизмы выживания тихоходок можно использовать для человеческих нужд. Открытия в этой области могут помочь ученым создать скафандры, защищающие космонавтов от опасных температур и высокого давления. Кроме того, существование тихоходок на Земле дает исследователям надежду найти похожие формы жизни на других планетах.  

Подробное описание — на сайте.  

№7. Точные долгосрочные прогнозы погоды  

Прошедшее лето в центральной России показало, насколько непредсказуемой и разрушительной может быть природа: череда ураганов тому подтверждение. Службы спасения требуют от метеорологов точных прогнозов погоды, но специалисты уверяют, что здесь всегда возможен элемент случайности. Еще больший вопрос представляют долговременные климатические прогнозы, глобально влияющие на жизнь во всем мире. Сохранившиеся в северном полушарии озера, фьорды и другие геологические образования — лишь незначительное подтверждение изменений, которые могут изменить мир. Ученые знают, что на климат влияет множество факторов: от вулканической активности до интенсивности солнечного излучения. В то же время, исследователи не могут создать комплексную модель, которая смогла бы дать относительно точный прогноз на ближайшие 25 или 50 лет. Такая модель могла бы уберечь людей от стихийных бедствий и подготовить их к переменам в образе жизни.  

В чем проблема долгосрочных прогнозов погоды можно узнать из видео по ссылке.  

Александр Токарев,
Медиалаборатория Университета Талантов

Проблемы тысячелетия понятным языком: imit_omsu — LiveJournal

«Кажется, что-то слышал об этом» — самый популярный ответ от собеседников на вопрос о задачах тысячелетия. Хотите немного разобраться в запутанной сети математических проблем, чтобы не сгорать от стыда в разговоре с преподавателями? Тогда смелее читайте дальше!

Первое, о чем стоит вам сообщить: список из 7 проблем был определен Математическим институтом Клэя в 2000 году, а за решение каждой из них американский институт готов выплатить 1 миллион долларов.  

Свое историческое начало задачи берут еще 1900 году, когда в Париже на II Международном конгрессе математиков Давид Гильберт выступил с докладом, в котором сформулировал 23 проблемы, нуждающиеся, по его мнению, в разрешении. Именно они в дальнейшем и определили многие ключевые направления развития математики в XX веке. Случилось так, что к началу XXI века многие проблемы из списка были либо решены, либо вычернуты из-за нечёткой постановки задачи. 

После Гильберта обновлением списка занялся математик Стивен Смейл. На тот момент он состоял из 18 нерешенных задач, однако более широкой огласке предалась его альтернативная версия, составленная институтом Клэя, о которой далее и пойдет речь.   

Второе, о чем стоит знать, так это о том, что задач всего 7, одна из них уже считается решенной, а 6 остальных, соответственно, находятся в «подвешенном» состоянии. К примеру, гипотеза Римана перекочевала ещё из списка 1900 года, и с тех самых пор остается нерешенной. 

Ну а теперь предлагаю начать знакомство с каждой из них!

Гипотеза Пуанкаре (1904 г. ) 

На сегодняшний день гипотеза Пуанкаре считается единственной решенной задачей тысячелетия из списка. Она была сформулирована еще в 1904 году математиком Анри Пуанкаре. Данная задача — одна из наиболее известных проблем топологии. Её суть состояла в том, что если каждая замкнутая петля стягивается в точку, то ваша поверхность представляет собой деформированную сферу. Возьмём тор (тот же бублик). Если мы начнем чуть-чуть мять и растягивать резиновую сферу, тор мы никак не получим. 

Почему нет? Потому что с бубликами не всё так просто. Чтобы из сферы получить тор, её надо или порвать, или растянуть и склеить, а значит, тор — не деформированная сфера. По итогу имеем, что на поверхности сферы все петли стягиваются в точку, а на поверхности тора — нет.

После того, как в 2002-2003 годах задача была решена Григорием Перельманом, автором серии работ, подтверждающих справедливость данной гипотезы, проблема предалась широкой огласке. Многие СМИ объясняли суть задачи простыми словами: «резиновую ленту, натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». Однако, данная формулировка больше подходит для описания гипотезы Тёрстона — обобщения гипотезы Пуанкаре. Но это уже совсем другая история. 🙂 

Если возвращаться к истории петербургского математика Григория Перельмана, то выясняется, что премия института Клэя за доказательство гипотезы Пуанкаре была присуждена ему только в 2010 году. Однако, после того, как у него попытались отобрать лавры первооткрывателя, Перельман отказался от получения денежного вознаграждения.

Григорий Перельман

Равенство классов P и NP (1971 г.)

В узких кругах эта задача известна как «Пробема Кука» и «Проблема перебора». Отношения между классами P и NP рассматриваются в разделе теории алгоритмов, и вот уже почти полвека как великие умы человечества не могут найти чёткого доказательства для этой проблемы. Может быть это получится у вас? 🙂 А для того, чтобы разобраться в постановке задачи, вам нужно знать, что из себя представляют классы P и NP.  

Итак, в теории алгоритмов класс P (polynomial) опеределяют как множество задач, имеющих быстрые алгоритмы решения, время работы которых напрямую зависит от размера входных данных. Главное, что осуществляется такой алгоритм за полиномиальное время. Примерами задач из класса P являются известные ещё со школьной скамьи такие простейшие арифметические операции, как сложение, умножение, деление, взятие остатка от деления (естественно, все операции целочисленные). 

Класс NP (not-deterministic polinomial) в свою очередь включает в себя множество задач разрешимости, решение которых можно проверить на машине Тьюринга за время, не превосходящее значения некоторого многочлена, зависящего, опять же, от размера входных данных. 

Подобных задач разрешимости очень много, но основной вопрос они поднимают, по большей части, один и тот же: «все ли задачи, которые можно быстро проверить, можно столь же быстро решить?» На данный момент, для некоторых задач не найдено не то что быстрого алгоритма решения, даже неизвестно существует ли такой алгоритм вообще! 

Если данная проблема когда-нибудь обретёт аргументированное доказательство, то это здорово улучшит качество нашей жизни, ведь она имеет большое значение для самых различных областей знаний. Однако, на данный момент времени предполагается, что классы P и NP не равны, поскольку далеко не все задачи, решения которых легко проверяемы, могут быть легко решаемы.

P = NP?

Гипотеза Римана (1859 г.)

Эта задача из области теории чисел, уже третья из списка проблем тысячелетия, была сформулирована немецким математиком Бернхардом Риманом еще в XIX веке, но по сей день так и остается нерешенной. 

Чтобы поближе познакомиться с сутью гипотезы, вам придется вновь обратиться к школьным знаниям. На этот раз придётся вспомнить, что такое простые числа. Итак, это те самые числа, которые делятся только на себя и на единицу (2, 3, 5, 7, 11, 13, 17…).  Мощность множества простых чисел — алеф-ноль. Если, к примеру, нанести все простые числа на числовую ось, то сразу станет ясно, что распределены они на ней вовсе не равномерно, а значит, их поиск не подчиняется какой-либо закономерности. Где и когда обнаружится следующее простое число — загадка. s + … — обращается в ноль.
А нам известно, что нулевое значение она имеет, когда s — отрицательное четное число. В таких случаях мы получаем, так называемые, «тривиальные» нули дзета-функции. Кроме того, благодаря некоторым выкладкам Римана стало известно, что другие нули появляются, если s — комплексное число, действительная часть которого равна 1/2. 

Что сейчас известно о ходе решения задачи: расчёты, проведённые с использованием суперкомпьютеров и для невероятно громадных простых чисел, подтверждают справедливость гипотезы Римана. Она доказана примерно для 10 трлн первых решений, но в общем виде пока нет. А поскольку простые числа играют немаловажную роль в работе криптографических алгоритмов, то после доказательства данной гипотезы нас ожидает значительный прогресс в сфере шифрования и безопасности интернета.

Действительная (красная) и мнимая (синяя) компоненты дзета-функции

Существование и гладкость решений уравнений Навье — Стокса (1822 г. )

Спешу познакомить вас с ещё одной проблемой тысячелетия, но на сей раз из области математической физики (гидродинамики). Эта задача известна миру на протяжении практически 200 лет, но до сих пор остается нерешенной. Суть загадки состоит в том, чтобы доказать, что решение данных уравнений существует и является гладкой функцией. 

Задача, возникшая на стыке математики и классической физики, вырастает из научных трудов XIX в., в которых учёные стали формулировать строгие законы, описывающие движение жидкостей. Полученные уже тогда уравнения Навье — Стокса остаются одними из важнейших в гидродинамике и аэродинамике. С их помощью можно вычислить скорость потока с учётом вязкости, сжимаемости, плотности, давления, потому сами уравнения используются повсеместно. 

На первый взгляд может показаться, будто всё уже на своих местах и доказывать нечего, однако решить уравнения Навье — Стокса в общем виде до сих пор никому не удалось, а все расчёты, которые ведутся на данный момент, рассматривают лишь отдельные, частные случаи.  

Эта проблема особенно актуальна в наше время, ведь решение уравнений помогло бы раскрыть многие тайны о природе течения жидкостей, воздушных потоков и турбулентности. Современные технологии, от самолетов и подлодок до ветряных электростанций и автомобилей, повсеместно сталкиваются с последним явлением, и тот факт, что оно остается плохо изученным, делает турбулентость плохо просчитываемой и практически непредсказуемой. 

Из последних новостей о проблеме тысячелетия известно, что в 2014 году к решению приблизился казахстанский математик Мухтарбай Отелбаев, однако в его расчётах была найдена ошибка.

Дифференциальные уравнения движения Навье-Стокса

Гипотеза Ходжа (1941 г.)

Одна из самых важных задач алгебраической геометрии, сформулированная в 1941 году, заключается в том, что для проективных алгебраических многообразий (неприводимых замкнутых подмножеств многомерного проективного пространства над алгебраически замкнутым полем, ну это 1-й курс точно уже знает!) класс Ходжа представляет собой рациональную линейную комбинацию классов алгебраических циклов. Все равно ничего не понятно… 

Иными словами, в реальности существуют множество как простых, так и сложных геометрических объектов, и чем сложнее объект, тем более трудоёмким становится процесс его изучения. Но для простоты исследования свойств различных сложных геометрических объектов, ученые отдельно изучают свойства частички одного целого. Данный метод активно используется математиками ещё с XX века. 

Гипотеза Ходжа непосредственно связана как со свойствами составных частей, так и со свойствами целых объектов. На сегодняшний день в алгебраической геометрии это является достаточно серьёзной проблемой. Ещё бы, отыскать точные методы для анализа сложных предметов и форм на основании анализа его простых частей, а после склеивания вместе таких частиц (по возрастающей размерности) составить некий «портрет» о свойствах самого объекта. 

Метод оказался эффективным при описании разнообразных объектов, встречающихся в математике. При этом геометрические обоснования метода оставались весьма смутными: в некоторых случаях возникала необходимость в прибавлении частей, не имеющих никакого геометрического истолкования.  

Известно, что на данный момент времени удалось доказать гипотезу Ходжа удалось только для некоторых частных случаев. Более общее доказательство пока не найдено, впрочем, как и не найдено доказательство обратного — что гипотеза неверна.

Гипотеза Бёрча — Свиннертон-Дайера (1960 г.)

Список проблем тысячелетия продолжает ещё одна задача из области алгебраической геометрии, которая была выдвинута в начале 1960-х английскими учёными из Кембриджского университета. Её суть заключается в том, чтобы описать все возможные решения алгебраических уравнений с несколькими переменными, сложнее, чем уравнение школьной параболы. 

Юрий Матиясевич

Кроме того, не стоит забывать о том, что переменные в них обязательно должны быть целочисленными, как и решения, а значит, сами уравнения могут считаться диофантовыми. Однако, ещё в 1970 году советский математик Юрий Матиясевич, будучи аспирантом, показал, что универсального решения диофантовых уравнений не существует, сделав финальный шаг в доказательстве неразрешимости задачи о существовании решений у произвольного диофантова уравнения, ответив тем самым на вопрос десятой проблемы Гильберта.  

При рассмотрении частного случая, когда решения уравнений образуют абелево многообразие, Бёрч и Свиннертон-Дайер выдвинули предположение о том, что множество решений эллиптической кривой связано с поведением L-функции в окрестности единицы. 

Что же такое L-функция? Это некоторая комплексная функция L(s), заданная при условии, что вещественная часть числа s > 1. Свойства данной функции на всей комплексной плоскости в основном определяются свойствами уже известной нам дзета-функции (см. «Гипотеза Римана»).  То есть, в случае, если дзета-функция в точке 1 принимает значение равное нулю, мы получаем бесконечное число решений. Если же значение L(1) не равно нулю, то получаем конечное число рациональных решений, и это доказал математик Виктор Колывагин.

Есть некоторая вероятноятность, что ответы на гипотезу Бёрча – Свиннертон-Дайера будут получены только в частном виде, поскольку первый случай так и остается неподкрепленным какой-либо доказательной базой. 3 + 877*x

Теория Янга — Миллса (1954 г.)

Перейдем к заключающей проблеме тысячелетия, пришедшей из слияния таких областей науки как физика элементарных частиц и геометрия. Еще в 1954 году физики Янг и Миллс написали уравнения, применимые в области квантовой физики, объединяющие в себе описание нескольких фундаментальных взаимодействий природы — электромагнитного, слабого и сильного. 

На данный момент теория Янга — Миллса подтвердилась экспериментальным путем только для электрослабого и сильного взаимодействий. Но все попытки решить уравнения, описывающие все три взаимодейстия одновременно, оборачивались неудачей, однако рассчётные эксперименты показывают, что шанс всё-таки есть. 

Известно, что на основе теории Янга-Миллса была построена стандартная модель физики элементарных частиц — некий «код» нашей Вселенной, состоящий из кварков, лептонов и калибровочных бозонов, из которых, в свою очередь, слеплено всё, что существует во Вселенной.

Таблица частиц стандартной модели

Ещё 50 лет назад была предсказана последняя частица из стандартной модели и в течение последних 20 лет великие умы современности охотились за ней — недостающим бозоном Хиггса, и, наконец, поймали. (-24) доли секунды, в Швейцарии построили Большой Адронный Коллайдер. В нем разгоняют банчи (иными словами, сгустки) протонов и сталкивают друг с другом. Подробнее эту тему лучше изучать самостоятельно, но ни в коем случае не пытайтесь повторить это дома!

Сейчас же уравнения Янга — Миллса приняты учеными-физиками во всем мире. Несмотря на это, предсказать массы элементарных частиц экспериментальным путем в рамках их теории так и не удалось, ровно как и решить проблему в общем виде.   

Специально для ЖЖ матфака, с большим желанием пробудить в вас стремление к новому, ранее неизведанному, Садуллаева Надежда.

Математика. Задачи тысячелетия. Как заработать миллион!

В данной статье команда INTBOARD™ попыталась рассказать понятно о сложном. А именно, о 7 Проблем или Задач тысячелетия (Millennium Prize Problems).

Как с помощью математики, ее глубокого изучения, можно заработать миллионы.

И как говорится в высказывании, приписываемом Эйнштейну, «объяснение должно быть максимально простым, но не проще». Итак начнем.

Задачи тысячелетия (также Задачи тысячелетия; англ. Millennium Prize Problems) — это семь математических проблем, определенных Математическим институтом Клэя 2000 года, охарактеризованы как «важные классические задачи, решение которых не найдено на протяжении многих лет». За решение каждой из этих проблем институтом Клэя предложен приз в размере 1000000 долларов США. Анонсируя приз, институт Клэя провел параллель с проблемами Гильберта, которые были определены 1900 и повлекших существенное влияние на математику XX века.

1900 на Международном математическом конгрессе в Париже Давид Гильберт объявил 23 математические проблемы, которые, по его мнению, следовало бы решить в ХХ веке. На сегодня 21 проблему из этого списка уже решена, и только часть 8-й проблемы — гипотеза Римана — вошла в перечень Проблем тысячелетия.

В конце XX века математики пытались сформулировать подобные стратегические задачи на следующее, XXI века. Так, в мае 2000 года эксперты Математического института Клэя (Кембридж, Массачусетс, США) отобрали семь важнейших проблем современной математики. Количество проблем в перечне (семь) было выбрано исходя из того, что основатель института, бостонский миллионер Клей, выделил на премии семь миллионов долларов — по миллиону за решение каждой проблемы.

Равенство классов P и NP

Подробнее: Равенство классов P и NP

Вопрос заключается в том, для всех задач, для которых компьютер может быстро проверить заданный алгоритм (то есть, в течение полиномиального времени), он также может быстро найти это решение. Проблема равенства классов сложности P и NP является одной из важнейших проблем теории алгоритмов и имеет много далеко идущих последствий в математике, философии и криптографии (см.

Последствия равенства классов P и NP). Официальная постановка задачи принадлежит Стивену Куку.
Все мы помним из школы квадратные уравнения, решаемые через дискриминант. Решение этой задачи относится к классу P (Polynomial time) — для нее существует быстрый (здесь и далее под словом «быстрый» подразумевается как выполняется за полиномиальное время) алгоритм решения, который и заучивается.

Также существуют NP-задачи (Non-deterministic Polynomial time), найденное решение которых можно быстро проверить по определенному алгоритму. Например проверка методом перебора компьютером. Если вернуться к решению квадратного уравнения, то мы увидим, что в данном примере существующий алгоритм решения проверяется так же легко и быстро как и решается. С этого напрашивается логический вывод, что данная задача относится как к одному классу так и ко второму.

Таких задач много, но основным вопросом является, все или не все задачи, которые можно легко и быстро проверить можно легко и быстро решить? Сейчас для некоторых задач не найдено быстрого алгоритма решения, и неизвестно существует ли такой вообще.

На просторах интернета также встречается такое интересное и прозрачное формулировку:

«Предположим, что вы, находясь в большой компании, хотите убедиться, что там находится и ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. При отсутствии этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. «

В данном случае вопрос стоит такое же, есть такой алгоритм действий, благодаря которому даже не имея информации о том, где находится человек, найти его так же быстро, как будто зная где он находится.

Данная проблема имеет большое значение для самых разных областей знаний, но решить ее не могут уже более 40 лет.

Гипотеза Ходжа
Подробнее: Гипотеза Ходжа

Важная проблема алгебраической геометрии. Гипотеза описывает классы когомологий на комплексных проективных многообразиях, реализуемые алгебраическими подмноговидов.

В реальности существуют множество как простых так и куда более сложных геометрических объектов. Очевидно, что чем сложнее объект тем более трудоемким становится его изучения. Сейчас учеными придуман и вовсю применяется подход, основная идея которого заключается в том, чтобы вместо самого исследуемого объекта использовать простые «кирпичики» с уже известными свойствами, которые склеиваются между собой и образуют его подобие, да-да, знакомый всем с детства конструктор . Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта.
Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков» так и объектов.

Гипотеза Пуанкаре (доказана)
Подробнее: Гипотеза Пуанкаре

Считается самой известной проблемой топологии. Неформально говоря, она утверждает, что всякий «трехмерный объект», что обладает некоторыми свойствами трехмерной сферы (в частности, каждая петля внутри него взимается), должен хотя бы ути сферой с точностью до деформации. 2002 российский математик Григорий Перельман опубликовал работу, из которой следует справедливость гипотезы Пуанкаре.

Чаще всего встречается такая расшифровка как «резиновую ленту натянутую на сферу можно плавно взыскать в точку, а натянутую на бублик — нельзя». На самом деле эта формулировка справедливо для гипотезы Терстона, которая обобщает гипотезу Пуанкаре, и которую в действительности и доказал Перельман.
Частный случай гипотезы Пуанкаре говорит нам о том, что любой трехмерное многообразие без края (вселенная, например) подобно трехмерной сфере. А общий случай переводит это утверждение на объекты любой размерности. Стоит заметить, что бублик, точно так же, как вселенная подобный сфере, подобный обычной кофейной кружки.

Гипотеза Римана
Подробнее: Гипотеза Римана

Гипотеза утверждает, что все нетривиальные нули дзета-функции Римана имеют действительную часть 1/2. Ее доказательства или опровержения будет иметь далеко идущие последствия для теории, особенно в части распределения простых чисел. Гипотеза Римана была частью восьмой проблемы Гильберта.

Всем нам еще со школы известны простые числа которые делятся только на себя и на единицу (2, 3, 5, 7, 11, …). С давних времен люди пытаются найти закономерность в их размещении, но удача пока так никому и не улыбнулась. В результате ученые применили свои усилия к функции распределения простых чисел, которая показывает количество простых чисел меньше или равных определенного числа. Например, для 4 — 2 простых числа, для 10 — уже 4 числа. Гипотеза Римана раз устанавливает свойства данной функции распределения.
Многие утверждения о вычислительную сложность некоторых целочисленных алгоритмов, доказаны в предположении верности этой гипотезы.

Теория Янга — Миллса
Подробнее: Квантовая теория Янга — Миллса

Задача происходит из области физики элементарных частиц. Нужно доказать, что для любой простой компактной калибровочной группы G квантовая теория Янга — Миллса для пространства R4 существует и имеет ненулевой дефект массы. Это утверждение соответствует экспериментальным данным и численному моделированию, однако доказать его до сих пор не удалось.

Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения, объединяющие теории электромагнитного, слабого и сильного взаимодействия. В свое время теория Янга-Миллса рассматривается лишь как математическое изыскания, не имеет отношения к реальности. Однако позже теория начала получать экспериментальные подтверждения, но в общем виде она все еще остается нерешенной.

На основе теории Янга-Миллса построена стандартная модель физики элементарных частиц в рамках которой был предусмотрен и обнаружен именно бозон Хиггса.

Уравнения Навье — Стокса
Подробнее: Уравнение Навье — Стокса

Уравнения Навье — Стокса — это система уравнений, описывающих движение вязкой жидкости, одна из важнейших задач гидродинамики.

Несмотря на важность задачи, существование гладких решений с конечным кинетической энергией математически не доказан.
Поток жидкостей, воздушные потоки, турбулентность. Эти, а также множество других явлений описываются уравнениями, известными как уравнения Навье — Стокса. Для некоторых частных случаев уже найденные решения, в которых как правило части уравнений отбрасываются как, не влияющие на конечный результат, но в общем виде решение этих уравнений неизвестны, и при этом даже неизвестно, как их решать.

Гипотеза Берча и Свиннертона-Дайера
Подробнее: Гипотеза Берча и Свиннертона-Дайера

Гипотеза связана с уравнениями эллиптических кривых и множеством их рациональных решений.

Для сложных уравнений поиск решений становится чрезвычайно трудным, достаточно вспомнить историю доказательств знаменитой теоремы Ферма, чтобы убедиться в этом.

Данная гипотеза связана с описанием алгебраических уравнений 3 степени — так называемых эллиптических кривых. И по сути является единственным, относительно простым, общим способом вычисления ранга, одного из важнейших свойств эллиптических кривых.
В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые стандарты цифровой подписи.
•••
В настоящее время математика ассоциируется с учеными, имеют странный вид и говорят о не менее странные вещи. Многие говорят о ее оторванности от реального мира. Многие люди, как младшего, так и вполне сознательного возраста говорят, что математика не нужна наука, после школы / института, она нигде не пригодилась в жизни.
Но на самом деле это не так — математика создавалась как механизм с помощью которого можно описать наш мир, и в частности много наблюдаемых вещей. Она везде, в каждом доме. Как сказал Василий Осипович Ключевский: «Не цветы виноваты, что слепой их не видит».
Наш мир далеко не так прост, как кажется, и математика соответственно, тоже усложняется, совершенствуется, предоставляя все больше твердую почву для более глубокого понимания существующей реальности.
•••
По данным материалов Википедия и статьи «Задача тысячелетия. Просто о составе

Следующая >

7 математических загадок тысячелетия. Просто о сложном

Только для мыслящих людей!

«Я знаю только то, что ничего не знаю, но другие не знают и этого»
(Сократ, древнегреческий философ)

НИКОМУ не дано владеть вселенским разумом и знать ВСЁ. Тем не менее, у большинства ученых, да и тех, кто просто любит размышлять и исследовать, всегда есть стремление узнать больше, разгадать загадки. Но остались ли еще неразгаданные темы у человечества? Ведь, кажется, все уже ясно и нужно только применять полученные веками знания?

НЕ стоит отчаиваться! Еще остались нерешенные проблемы из области математики, логики, которые в 2000 году эксперты Математического института Клэя в Кембридже (Массачусетс, США) объединили в список, так называемые, 7 загадок тысячелетия (Millennium Prize Problems). Эти проблемы волнуют ученых всей планеты. С тех пор и по сей день любой человек может заявить, что нашел решение одной из задач, доказать гипотезу и получить от бостонского миллиардера Лэндона Клэя (в честь которого и назван институт) премию. Он уже выделил на эти цели 7 миллионов долларов. К слову сказать, на сегодняшний день одна из проблем уже решена.

Итак, вы готовы узнать о математических загадках?

Уравнения Навье — Стокса (сформулированы в 1822 году)

Область: гидроаэродинамика

Уравнения о турбулентных, воздушных потоках, а также течении жидкостей известны как уравнения Навье — Стокса. Если, к примеру, плыть по озеру на чем-либо, то неизбежно вокруг возникнут волны. Это касается и воздушного пространства: при полете на самолете в воздухе также будут образовываться турбулентные потоки.
Данные уравнения как раз производят описание процессов движения вязкой жидкости и являются стержневой задачей всей гидродинамики. Для некоторых частных случаев уже найдены решения, в которых части уравнений отбрасываются, как не влияющие на конечный результат, но в общем виде решения этих уравнений не найдены.
Необходимо найти решение уравнениям и выявить гладкие функции.

Гипотеза Римана (сформулирована в 1859 году)

Область: теория чисел

Известно, что распределение простых чисел (Которые делятся только на себя и на единицу: 2,3,5,7,11…) среди всех натуральных чисел не подчиняется никакой закономерности.
Над этой проблемой задумался немецкий математик Риман, который сделал свое предположение, теоретически касающееся свойств имеющейся последовательности простых чисел. Уже давно известны так называемые парные простые числа — простые числа-близнецы, разность между которыми равна 2, например 11 и 13, 29 и 31, 59 и 61. Иногда они образуют целые скопления, например, 101, 103, 107, 109 и 113.
Если такие скопления будут найдены и выведен определенный алгоритм, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.

Проблема Пуанкаре (сформулирована в 1904 году. Решена в 2002 году.)

Область: топология или геометрия многомерных пространств

Суть проблемы заключается в топологии и состоит в том, что если натягивать резиновую ленту, к примеру, на яблоко (сферу), то будет теоретически возможным сжать ее до точки, медленно перемещая без отрыва от поверхности ленту. Однако если эту же ленту натянуть вокруг бублика (тора), то сжать ленту без разрыва ленты или разлома самого бублика не представляется возможным. Т.е. вся поверхность сферы односвязна, в то время как тора – нет. Задача состояла в том, чтобы доказать, что односвязной является только сфера.

Представитель ленинградской геометрической школы Григорий Яковлевич Перельман является лауреатом премии тысячелетия математического института Клэя (2010 г.) за решение проблемы Пуанкаре. От знаменитой Фильдсовской премии он отказался.

Гипотеза Ходжа (сформулирована в 1941 году)

Область: алгебраическая геометрия

В реальности существуют множество как простых, так и куда более сложных геометрических объектов. Чем сложнее объект, тем труднее его изучать. Сейчас учеными придуман и вовсю применяется подход, основанный на использовании частей одного целого («кирпичики») для изучения этого объекта, как пример — конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта. Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков», так и объектов.
Это очень серьезная проблема алгебраической геометрии: найти точные пути и методы анализа сложных объектов с помощью простых «кирпичиков».

Уравнения Янга — Миллса (сформулированы в 1954 году)

Область: геометрия и квантовая физика

Физики Янг и Миллс описывают мир элементарных частиц. Они, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения в области квантовой физики. Тем самым был найден путь к объединению теорий электромагнитного, слабого и сильного взаимодействий.
На уровне микрочастиц возникает «неприятный» эффект: если на частицу действуют несколько полей сразу, их совокупный эффект уже нельзя разложить на действие каждого из них поодиночке. Это происходит по причине того, что в этой теории друг к другу притягиваются не только частицы материи, но и сами силовые линии поля.
Хотя и уравнения Янга — Миллса приняты всеми физиками мира, экспериментально теория, касающаяся предсказывания массы элементарных частиц, не доказана.

Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)

Область: алгебра и теория чисел

Гипотеза связана с уравнениями эллиптических кривых и множеством их рациональных решений. В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.
Задача в том, что нужно описать ВСЕ решения в целых числах x, y, z алгебраических уравнений, то есть уравнений от нескольких переменных с целыми коэффициентами.

Проблема Кука (сформулирована в 1971 году)

Область: математическая логика и кибернетика

Ее еще называют «Равенство классов P и NP», и она является одной из наиболее важных задач теории алгоритмов, логики и информатики.
Может ли процесс проверки правильности решения какой-либо задачи длиться дольше, чем время, затраченное на само решение этой задачи (независимо от алгоритма проверки)?
На решение одной и той же задачи, порой, нужно разное количество времени, если изменить условия и алгоритмы. К примеру: в большой компании вы ищете знакомого. Если вы знаете, что он сидит в углу или за столиком — то вам понадобится доли секунд, чтобы его увидеть. Но если вы не будете знать точно, где находится объект, то затратите больше времени на его поиски, обходя всех гостей.
Основным вопросом является: все или не все задачи, которые можно легко и быстро проверить, можно также легко и быстро решить?

Математика, как может показаться многим, не так далека от реальности. Она является тем механизмом, с помощью которого можно описать наш мир и многие явления. Математика всюду. И прав был В.О. Ключевский, который изрек: «Не цветы виноваты, что слепой их не видит».

И в заключение….

Одну из самых популярных теорем математики — Великую (Последнюю) теорему Ферма: аn + bn = cn — не могли доказать 358 лет! И только в 1994 году британец Эндрю Уайлз смог дать ей решение.

Так что, дерзайте, великие умы!

Теги: математические загадки , тайны тысячелетия , Перельман , 7 математических проблем , нерешенные загадки человечества , математика , неразгаданное , физические явления , математические головоломки

задач премии тысячелетия | Brilliant Math & Science Wiki

Содержание

• Гипотеза Пуанкаре
• П против НП
• Гипотеза Ходжа
• Гипотеза Римана
• Существование Янга-Миллса и массовый разрыв
• Существование и гладкость Навье-Стокса
• Гипотеза Берча-Суиннертона-Дайера

Единственная проблема тысячелетия, которая была решена на сегодняшний день, — это гипотеза Пуанкаре, поставленная в 1904 году задача о топологии объектов, называемых многообразиями .

Многообразие размерности nnn — это геометрический объект, снабженный топологической структурой, так что каждая точка имеет окрестность, которая выглядит (гомеоморфна) nnn-мерному евклидову пространству для некоторого n. н.п. Стандартный пример — сфера, поверхность шара, погруженная в трехмерное пространство. Муравей на поверхности сферы думает, что он стоит на ровной поверхности, так как кривизна сферы не наблюдается локально. Итак, сфера — это 222-многообразие; плоская земля выглядит как 222-мерное евклидово пространство.

Другим примером 222-многообразия является тор (с одним отверстием) .

Два коллектора считаются разными, если один не может непрерывно деформироваться в другой. Один из способов увидеть, что тор отличается от 222-сферы, состоит в том, что все петли на сфере можно стянуть на сфере в точку (представьте себе резиновую ленту на поверхности сферы — ее можно натянуть вверх). сферы, не разрывая полосу и не выходя из сферы), но петли на торе не могут (например, петля на вершине тора или одна из черных петель на рисунке).

Фундаментальным вопросом теории многообразий является проблема классификации : есть ли способ охарактеризовать, когда два многообразия одинаковы, без необходимости явно записывать карту, которая их идентифицирует? То есть существует ли такой набор свойств, что любые два многообразия, обладающие всеми этими свойствами, должны быть одинаковыми?

Гипотеза Пуанкаре утверждает, что любое замкнутое (безграничное) n nn-многообразие, гомотопически эквивалентное nnn-сфере, должно быть nnn-сферой. (Гомотопическая эквивалентность — это понятие, которое строго слабее, чем тождество вообще.) Это относительно легко для n=1,2.n=1,2.n=1,2. Это было доказано для n≥5 n\ge 5n≥5 Стивеном Смейлом в 1960-х годов, а для n = 4 n = 4 n = 4 Майклом Фридманом в 1982 году. Оба математика были награждены медалями Филдса — высшей наградой, которую может получить математик.

Случай n=3n=3n=3 эквивалентен следующему утверждению:

Любое односвязное замкнутое трехмерное многообразие — это то же самое, что и трехмерная сфера.

Здесь односвязный интуитивно означает, что коллектор не имеет отверстий; петлю на его поверхности всегда можно стянуть в точку. Поскольку n = 3n = 3n = 3 был единственным случаем, который нужно было доказать, это было утверждение гипотезы Пуанкаре, когда она была поставлена ​​​​как проблема тысячелетия.

Гипотеза была доказана в 2003 году российским математиком Григорием Перельманом с использованием идей Ричарда Гамильтона начала 1980-х годов. Гамильтон предложил использовать поток векторного поля, названный потоком Риччи , для решения проблемы и продемонстрировал его эффективность, доказав частные случаи гипотезы Пуанкаре. Перельман объявил о своем решении проблемы в серии статей в 2002 и 2003 годах. Рецензирование подтвердило правильность его доказательства, и в 2006 году ему предложили Филдсовскую медаль за свою работу.

Перельман отказался от Филдсовской медали, а также отказался принять Премию тысячелетия Клэя, когда она была официально предложена ему в 2010 году, заявив, что его вклад не более значителен, чем вклад Гамильтона. Его работа, по общему мнению, весьма оригинальна и совершенна; несмотря на его кажущуюся скромность и избегание внимания, его доказательство гипотезы Пуанкаре будет известно еще очень долго.

Основная статья: P против NP

Проблема определения того, является ли P=NP{\mathbf P} = \mathbf{NP}P=NP, является самой важной открытой проблемой в теоретической информатике. Вопрос заключается в том, могут ли вычислительные задачи, решения которых могут быть быстро проверены, также быть быстро решены. Большинство экспертов в этой области сходятся во мнении, что в общем случае это неверно, т. е. P≠NP, {\mathbf P}\ne \mathbf{NP},P​=NP, но прогресс в направлении доказательства очень незначителен. . 9k cnk для некоторых положительных чисел c,k c,kc,k, не зависящих от n. н.п.

Задача вычисления наибольшего общего делителя двух целых чисел a,b a,ba,b находится в P; \mathbf П;П; на самом деле алгоритм Евклида работает за время ≤5n, \le 5n,≤5n, где nnn — количество десятичных цифр любого из целых чисел.

Обратите внимание, что константы c cc и kkk в приведенном выше определении полиномиального времени на практике могут быть недопустимо большими. Например, совсем недавно было показано, что задача проверки простоты находится в P {\mathbf P}P; доказательство продемонстрировало явный алгоритм, но этот алгоритм не является самым быстрым алгоритмом для практических целей.

Класс задач в NP \mathbf{NP}NP — ​​это множество задач, решение которых можно проверить за полиномиальное время. То есть задача зависит от положительного целого числа nn n, представляющего количество входных данных (более формально, информацию в задаче и предполагаемом решении можно перевести в строку длины n nn), и она находится в NP \mathbf {NP}NP, если существует алгоритм, который принимает предполагаемое решение в качестве входных данных и возвращает «да» или «нет» в зависимости от того, действительно ли предполагаемое решение является решением проблемы, так что время работы алгоритма меньше чем cnk cn^kcnk для некоторых положительных чисел c,k c,kc,k, не зависящих от n. н.п.

Проблема определения того, существует ли гамильтонов путь на данном графе, находится в NP. \mathbf{НП}.НП. То есть довольно легко проверить, является ли конкретный путь на графе гамильтоновым; просто проверьте, проходит ли он через каждую вершину ровно один раз. Однако проблема нахождения гамильтонова пути (предположительно) намного сложнее. Даже проблема определения существования гамильтонова пути относится к классу задач, известных как NP\mathbf{NP}NP-полные задачи; то есть любую задачу из NP \mathbf{NP}NP можно за полиномиальное время свести к задаче о гамильтоновых путях. Таким образом, если задача Гамильтона о путях находится в P, \mathbf P,P, отсюда следует, что P=NP. \mathbf{P}=\mathbf{NP}.P=NP. Расширением задачи о гамильтоновых путях является знаменитая задача коммивояжера.

Доказательство того, что P=NP {\mathbf P} = {\mathbf{NP}} P=NP имело бы далеко идущие последствия, поскольку показало бы, что многие проблемы считаются сложными, включая проблемы, на которых многие криптосистемы основаны, могут быть решены за полиномиальное время. Многие проблемы теоретической математики также находятся в NP {\ mathbf {NP}} NP, поэтому P = NP {\ mathbf P} = {\ mathbf {NP}} P = NP будет означать, что они могут быть доказаны или опровергнуты «механически». » за полиномиальное время. Следует отметить, что это не обязательно означает, что эти решения будут практичными, и на самом деле доказательство того, что P = NP {\ mathbf P} = {\ mathbf {NP}} P = NP, может быть неконструктивным; то есть можно было бы доказать, что эти проблемы могут быть решены за полиномиальное время, с помощью доказательства, которое не дает никаких указаний на построение явного алгоритма, который выполняет это.

Гипотеза Ходжа — это утверждение о геометрических фигурах, вырезанных полиномиальными уравнениями над комплексными числами. Они называются комплексными алгебраическими многообразиями . Чрезвычайно полезным инструментом при изучении этих многообразий было построение групп, называемых группами когомологий , которые содержали информацию о структуре многообразий. Группы построены довольно абстрактно, но имеют много полезных отношений: например, отображение между многообразиями соответствует отображениям между группами когомологий. Поскольку вычисления над группами часто более просты, чем вычисления над многообразиями, это дает возможность классифицировать и изучать свойства комплексных алгебраических многообразий. 92=1×2+y2=1 в плоскости xyxyxy. Это экватор сферы и подмногообразие.

Гипотеза Ходжа утверждает, что некоторые группы когомологий, изученные Ходжем над некоторыми хорошими комплексными многообразиями, порождены классами подмногообразий. Рассматриваемые группы когомологий часто называют группами классов Ходжа, а классы, порожденные подмногообразиями, часто называют алгебраическими. Таким образом, в этих терминах гипотеза становится

.

Каждый класс Ходжа на проективном комплексном многообразии является алгебраическим.

Гипотеза была сформулирована Ходжем в 1950 г. Она известна для многообразий размерности ≤3, \le 3,≤3 и известны некоторые другие частные случаи. Успешное доказательство дало бы полезное указание на взаимодействие между алгеброй и геометрией. Соответствия между геометрическими структурами (многообразиями) и алгебраическими структурами (группами) часто приводят к очень важным результатам: в качестве другого примера этого явления см. Доказательство Уайлса последней теоремы Ферма, в котором использовалась гипотеза Таниямы-Шимуры, связывающая эллиптические кривые с модулярными формами. 9с}. ζ(s)=n=1∑∞​ns1​. Можно показать, что ζ \zeta ζ аналитически продолжается до функции, которая определена и дифференцируема всюду на комплексной плоскости, кроме простого полюса при s=1. с=1.с=1. Эта функция имеет тривиальные нули на отрицательной вещественной прямой в точках s=−2,−4,−6,…. s=-2,-4,-6,\ldots.s=-2,-4,-6,…. Расположение других его нулей более загадочно; предположение, что

Нетривиальные нули дзета-функции лежат на прямой Re s=12. \text{Re }s=\frac12.Re s=21​. 9{\frac12 + \epsilon}\big)n≤x∑​µ(n)=O(x21​+ϵ) для любого ϵ>0, \epsilon > 0,ϵ>0, где µ\muµ — функция Мёбиуса . (Объяснение правой части уравнения см. в вики, посвященной нотации большого O.)

обобщенная гипотеза Римана — это утверждение о нулях некоторых функций, известных как L LL-функции, определяемые рядами Дирихле, которые являются обобщениями дзета-функции Римана. Обобщенная гипотеза Римана может быть использована для доказательства многих открытых вопросов теории чисел, в том числе гипотезы Артина о первообразных корнях и так называемых 9{13} 1013 нетривиальных нулей, упорядоченных по размеру мнимой части, находятся на критической прямой. Саму гипотезу Римана по-прежнему трудно подвергнуть осмысленной критике.

A Теория Янга-Миллса в квантовой физике представляет собой обобщение работы Максвелла об электромагнитных взаимодействиях для сильных и слабых ядерных взаимодействий. Это ключевой компонент так называемой Стандартной модели физики элементарных частиц. Стандартная модель обеспечивает основу для объяснения электромагнитных и ядерных сил и классификации субатомных частиц. До сих пор было доказано, что он согласуется с экспериментальными данными, но остаются вопросы относительно его внутренней согласованности.

В частности, успешное применение теории к экспериментам и упрощенным моделям включало «массовый разрыв», который формально определяется как разница между энергией по умолчанию в вакууме и следующим за ним состоянием с самой низкой энергией. Таким образом, эта величина является массой самой легкой частицы в теории. Решение проблемы тысячелетия будет включать как набор формальных аксиом, характеризующих теорию и показывающих, что она внутренне логически непротиворечива, так и доказательство того, что существует некоторая строго положительная нижняя граница масс частиц, предсказываемых теорией.

Вообще говоря, нынешнее состояние проблемы таково, что исследователи успешно получают результаты, согласующиеся с экспериментальными данными, используя идеи и модели, исходящие из теории Янга-Миллса, но нет строгой, аксиоматизированной теории, которая связно объясняет экспериментальные данные и успешно предсказывает результаты о ядерных силах. 3 },Z3R3​, трехмерный тор — это так называемый периодический случай. Одним из распространенных объяснений сложности этой проблемы является то, что решения этих уравнений включают турбулентность, малоизученную область гидродинамики. 93 R3 стремится к бесконечности.

Кажется, об ответе на этот вопрос известно немногое. Для аналогичной задачи в двух измерениях существуют гладкие решения (известные с 1960-х годов), но это не дает большого представления о том, как действовать в трех измерениях. Известно, что в трех измерениях существуют гладкие решения, если v0 v_0 v0 в определенном смысле «маленькое», и известно, что существуют гладкие решения, в общем случае определенные для значений временного параметра t t t в [0,T), [ 0,T),[0,T), где T TT — конечное время, зависящее от v0 v_0v0, называемое «временем разрушения». Задача требует решения, определенного для всех t∈[0,∞), t \in [0,\infty),t∈[0,∞), что является более строгим.

Был достигнут некоторый прогресс в отношении слабых решений уравнения, которые являются функциями скорости v(x,t) v({\mathbf x},t) v(x,t), удовлетворяющими уравнениям «в среднем, «, а не для всех точек x. {\mathbf х}.x. Но это еще не привело к созданию убедительной программы для поиска решений общих уравнений.

Гипотеза Берча-Суиннертона-Дайера касается рациональных точек (точки со всеми координатами рациональными числами) на эллиптических кривых. Эллиптические кривые, с диофантовой точки зрения, на сегодняшний день являются наиболее интересными кривыми. С каждой плоской кривой связано неотрицательное целое число, называемое родом. Кривые рода 0 хорошо изучены, а их точки легко параметризуются. Кривые рода ≥2 \ge 2 ≥2 имеют только конечное число рациональных точек по чрезвычайно глубокой теореме из 1980-х из-за Фальтингса. Кривые рода 1 с рациональной точкой — это в точности эллиптические кривые, имеющие множество применений и очень интересную структуру на своих множествах рациональных точек. Подробнее см. вики по эллиптическим кривым.

В частности, фактом является то, что для данной эллиптической кривой E, E,E существует неотрицательное целое число n nn и множество рациональных точек P1,…,Pn P_1,\ldots,P_nP1​,…,Pn​ на EEE такой, что каждая рациональная точка на EEE может быть однозначно записана как целочисленная линейная комбинация Pi P_i Pi​ плюс точка кручения T. T.T. Точки кручения — это точки конечного порядка, и их конечное число. Здесь линейная комбинация включает в себя групповой закон на эллиптической кривой, который нетривиально записать в явном виде (но заметим, что это , а не — то же самое, что сложение по координатам). Целое число n nn называется рангом E, E, E, и половина гипотезы Берча-Суиннертона-Дайера касается вычисления этого ранга.

Существует функция L(E,s) L(E,s)L(E,s), определяемая некоторым рядом Дирихле, которая аналогична дзета-функции Римана. Порядок обращения в нуль L(E,s) L(E,s) L(E,s) при s=1 s=1s=1 называется аналитическим рангом E, E,E, а первая половина гипотезы Берча-Суиннертона-Дайера состоит в том, что 9r (s−1)r в ряд Тейлора для L(E,s) L(E,s)L(E,s) в районе s=1. с=1.с=1. Этот коэффициент предположительно равен выражению, включающему произведения и частные нескольких фундаментальных констант, относящихся к эллиптической кривой (например, одна из них — число точек кручения).

Первая половина гипотезы доказана в случае, когда аналитический ранг равен 0 0 0 или 1. 1.1. Вторая половина доказана для некоторых специальных классов эллиптических кривых с аналитическим рангом 0.0.0. Существует довольно много компьютерных доказательств этой гипотезы (некоторые из них восходят к компьютерным вычислениям, выполненным Берчем и Суиннертоном-Дайером в 19 веке).60s), но прогресс в общем доказательстве невелик. Установление гипотезы помогло бы с теоретическими результатами о структуре точек на эллиптических кривых, а также с практическими приложениями, включая нахождение образующих P1,…,Pn P_1,\ldots,P_nP1​,…,Pn​ множества рациональных точек.

Процитировать как: Проблемы Премии Тысячелетия. Brilliant.org . Извлекаются из https://brilliant.org/wiki/millennium-prize-problems/

Проблемы премии тысячелетия

Проблемы премии тысячелетия Значок поискаУвеличительное стекло. Это означает: «Нажмите, чтобы выполнить поиск». Логотип InsiderСлово «Инсайдер».

Рынки США Загрузка… ЧАС М С В новостях

Значок шевронаОн указывает на расширяемый раздел или меню, а иногда и на предыдущие/следующие параметры навигации.ДОМАШНЯЯ СТРАНИЦА

Стратегия

Значок «Сохранить статью» Значок «Закладка» Значок «Поделиться» Изогнутая стрелка, указывающая вправо.

Скачать приложение

IMDB / Представьте себе развлечения

• На рубеже 21 века Математический институт Клэя объявил список из семи наиболее важных нерешенных математических задач.
• Все задачи имеют приз в размере 1 миллиона долларов, который присуждается тому, кто их решит.
• Одна из семи задач решена, остальные шесть остаются открытыми вопросами.
• В сентябре 2018 года математик Майкл Атия заявил, что у него есть решение еще одной проблемы, но достоверность его решения еще предстоит выяснить.

В 2000 году Математический институт Клэя объявил задачи Премии тысячелетия. Это был сборник из семи наиболее важных математических задач, которые до сих пор остаются нерешенными.

Отражая важность проблем, Институт предложил приз в размере 1 миллиона долларов любому, кто сможет предоставить тщательное, прошедшее экспертную оценку решение любой из проблем.

В то время как одна из задач, гипотеза Пуанкаре, была успешно решена в 2006 году (а математик, решивший ее, Григорий Перельман, столь же лихо отказался как от премии в миллион долларов, так и от заветной Филдсовской медали), остальные шесть проблем остаются нерешенными. .

В сентябре 2018 года математик Майкл Атья заявил, что у него есть доказательство гипотезы Римана, одной из шести оставшихся нерешенных проблем. Однако математическому сообществу потребуется время, чтобы оценить утверждения Атьи.

Вот шесть математических задач, настолько важных, что решение любой из них стоит 1 миллион долларов.

P против NP

ФОТОГРАФИЯ: мужчина печатает на клавиатуре компьютера перед отображаемым киберкодом на этой иллюстрации. Томсон Рейтер

Некоторые задачи простые, а некоторые сложные.

В мире математики и компьютерных наук существует множество задач, которые мы знаем, как запрограммировать компьютер для «быстрого» решения — элементарная арифметика, сортировка списка, поиск в таблице данных. Эти проблемы могут быть решены за «полиномиальное время», сокращенно «P». Это означает, что количество шагов, необходимых для добавления двух чисел или сортировки списка, увеличивается управляемо с увеличением размера чисел или длины списка.

Но есть и другая группа задач, для которых легко проверить правильность возможного решения задачи, но мы не знаем, как эффективно найти решение. Нахождение простых множителей большого числа — это такая проблема — если у меня есть список возможных множителей, я могу их перемножить и посмотреть, вернусь ли я к исходному числу. Но не существует известного способа быстро найти множители произвольно большого числа. Действительно, безопасность Интернета зависит от этого факта.

По историческим и техническим причинам задачи, решение которых можно быстро проверить, называются решаемыми за «недетерминированное полиномиальное время» или «NP».

Любая проблема в P автоматически попадает в NP — если я могу быстро решить проблему, я могу так же быстро проверить возможное решение, просто решив проблему и посмотрев, соответствует ли ответ моему возможному решению. Суть вопроса P vs NP заключается в том, верно ли обратное: если у меня есть эффективный способ проверить решения проблемы, существует ли эффективный способ найти эти решения?

Большинство математиков и компьютерщиков считают, что ответ отрицательный. Алгоритм, который мог бы решать задачи NP за полиномиальное время, имел бы умопомрачительные последствия для большей части математики, естественных наук и технологий, и эти последствия настолько не от мира сего, что они дают основания сомневаться в том, что это возможно.

Конечно, доказательство того, что такого алгоритма не существует, само по себе является невероятно сложной задачей. Для того чтобы сделать такое заявление о такого рода проблемах, вероятно, потребуется гораздо более глубокое понимание природы информации и вычислений, чем мы имеем сейчас, и почти наверняка это будет иметь глубокие и далеко идущие последствия.

Прочтите официальное описание P vs NP от Математического института Клэя здесь.

Уравнения Навье-Стокса

Дэн Лачер/Flickr

Удивительно сложно объяснить, что происходит, когда вы добавляете сливки в свой утренний кофе.

Уравнения Навье-Стокса представляют собой гидродинамическую версию трех законов движения Ньютона. Они описывают, как будет развиваться поток жидкости или газа при различных условиях. Точно так же, как второй закон Ньютона дает описание того, как скорость объекта будет изменяться под действием внешней силы, уравнения Навье-Стокса описывают, как скорость потока жидкости будет изменяться под действием внутренних сил, таких как давление и вязкость, а также внешних сил. силы, подобные гравитации.

Уравнения Навье-Стокса представляют собой систему дифференциальных уравнений. Дифференциальные уравнения описывают, как конкретная величина изменяется во времени при заданных начальных начальных условиях, и они полезны при описании всех видов физических систем. В случае уравнений Навье-Стокса мы начинаем с некоторого начального потока жидкости, а дифференциальные уравнения описывают, как этот поток развивается.

Решение дифференциального уравнения означает нахождение некоторой математической формулы, позволяющей определить, какой на самом деле будет интересующая вас величина в любой конкретный момент времени, на основе уравнений, описывающих изменение величины. Многие физические системы, описываемые дифференциальными уравнениями, такие как вибрация гитарной струны или поток тепла от горячего объекта к холодному, имеют хорошо известные решения этого типа.

Однако уравнения Навье-Стокса сложнее. С математической точки зрения инструменты, используемые для решения других дифференциальных уравнений, оказались здесь бесполезными. Физически жидкости могут вести себя хаотично и турбулентно: дым, исходящий от свечи или сигареты, обычно течет плавно и предсказуемо, но быстро превращается в непредсказуемые вихри и завихрения.

Возможно, такое турбулентное и хаотичное поведение означает, что уравнения Навье-Стокса не могут быть точно решены во всех случаях. Возможно, удастся сконструировать некую идеализированную математическую жидкость, которая, следуя уравнениям, в конце концов станет бесконечно турбулентной.

Любой, кто сможет построить способ решения уравнений Навье-Стокса во всех случаях или показать пример, в котором уравнения не могут быть решены, получит Премию тысячелетия за эту задачу.

Прочтите здесь официальное описание уравнений Навье-Стокса Института математики Клэя.

Теория Янга-Миллса и квантовая массовая щель

Публичный Доман

Математика и физика всегда были взаимовыгодны. Развитие математики часто открывало новые подходы к физической теории, а новые открытия в физике стимулировали более глубокие исследования лежащих в их основе математических объяснений.

Квантовая механика была, пожалуй, самой успешной физической теорией в истории. Материя и энергия ведут себя совершенно по-разному в масштабе атомов и субатомных частиц, и одним из величайших достижений 20-го века стало теоретическое и экспериментальное понимание этого поведения.

Одной из основных основ современной квантовой механики является теория Янга-Миллса, которая описывает квантовое поведение электромагнетизма, а также слабых и сильных ядерных взаимодействий в терминах математических структур, возникающих при изучении геометрических симметрий. Предсказания теории Янга-Миллса были подтверждены бесчисленными экспериментами, и эта теория является важной частью нашего понимания того, как собираются атомы.

Несмотря на этот физический успех, теоретические математические основы теории остаются неясными. Одна из представляющих особенный интерес проблема — это «массовый разрыв», который требует, чтобы определенные субатомные частицы, в некотором роде аналогичные безмассовым фотонам, имели положительную массу. Разрыв масс является важной частью того, почему ядерные силы чрезвычайно сильны по сравнению с электромагнетизмом и гравитацией, но имеют чрезвычайно короткие радиусы действия.

Таким образом, задача Премии Тысячелетия состоит в том, чтобы показать общую математическую теорию, стоящую за физической теорией Янга-Миллса, и получить хорошее математическое объяснение разрыва масс.

Прочтите официальное описание Математического института Клэя теории Янга-Миллса и проблемы массового разрыва здесь.

Гипотеза Римана

Бернхард Риманн Викисклад

Возвращаясь к древним временам, простые числа — числа, которые делятся только сами на себя и на 1 — были объектом восхищения математиков. На фундаментальном уровне простые числа являются «кирпичиками» целых чисел, поскольку любое целое число можно однозначно разбить на произведение простых чисел.

Учитывая центральную роль простых чисел в математике, вопросы о том, как простые числа распределяются вдоль числовой прямой, то есть насколько далеко друг от друга простые числа, являются активными областями интереса.

К 19 веку математики открыли различные формулы, дающие приблизительное представление о среднем расстоянии между простыми числами. Однако остается неизвестным, насколько близко к этому среднему остается истинное распределение простых чисел, то есть есть ли части числовой прямой, где «слишком много» или «слишком мало» простых чисел согласно этим средним формулам.

Гипотеза Римана ограничивает эту возможность, устанавливая границы того, насколько далеко от среднего может отклоняться распределение простых чисел. Гипотеза эквивалентна и обычно формулируется в терминах того, лежат ли все решения уравнения, основанного на математической конструкции, называемой «дзета-функцией Римана», вдоль определенной линии в плоскости комплексных чисел. Действительно, изучение таких функций, как дзета-функция, стало отдельной областью математических интересов, что делает гипотезу Римана и связанные с ней проблемы еще более важными.

Как и в некоторых других задачах Премии Тысячелетия, существуют убедительные доказательства того, что Гипотеза Римана верна, но строгое доказательство остается неуловимым. На сегодняшний день вычислительные методы показали, что около 10 триллионов решений уравнения дзета-функции укладываются в требуемую линию, а контрпримеры не найдены.

Конечно, с математической точки зрения, 10 триллионов примеров истинности гипотезы абсолютно не заменяют полного доказательства этой гипотезы, оставляя гипотезу Римана одной из открытых проблем Премии тысячелетия.

В сентябре 2018 года уважаемый математик профессор Майкл Атья заявил, что нашел доказательство гипотезы Римана в лекции на Гейдельбургском форуме лауреатов. Однако несколько математиков выразили скептицизм по поводу результата, и теперь начнется тщательный процесс рассмотрения и оценки аргументов Атьи.

Прочтите официальное описание гипотезы Римана Института математики Клэя здесь.

Гипотеза Берча и Суиннертона-Дайера

Flickr/Оззи Делани

Одним из старейших и широчайших объектов математического изучения являются диофантовые уравнения, или полиномиальные уравнения, для которых мы хотим найти целочисленные решения. Классический пример, который многие могут вспомнить из школьной геометрии, — это пифагорейские тройки, или наборы из трех целых чисел, которые удовлетворяют теореме Пифагора x ²  + у ²  = г ² .

В последние годы алгебраисты уделяют особое внимание изучению эллиптических кривых, которые определяются особым типом диофантовых уравнений. Эти кривые имеют важные приложения в теории чисел и криптографии, и поиск целочисленных или рациональных решений для них является основной областью исследований.

Одним из самых ошеломляющих математических достижений за последние несколько десятилетий стало доказательство Эндрю Уайлса классической Великой теоремы Ферма, утверждающее, что версий пифагорейских троек с большей степенью не существует. Доказательство этой теоремы Уайлсом явилось следствием более широкого развития теории эллиптических кривых.

Гипотеза Берча и Суиннертона-Дайера предоставляет дополнительный набор аналитических инструментов для понимания решений уравнений, определяемых эллиптическими кривыми.

Прочтите официальное описание гипотезы Берча и Суиннертона-Дайера, данное Институтом математики Клэя.

Гипотеза Ходжа

Клаудио Роккини через Wikimedia Commons

Математическая дисциплина алгебраической геометрии — это, в широком смысле, изучение многомерных форм, которые могут быть определены алгебраически как множества решений алгебраических уравнений.

В качестве чрезвычайно простого примера вы можете вспомнить из школьного курса алгебры, что уравнение y = x ² приводит к параболической кривой, когда решения этого уравнения вычерчиваются на листе миллиметровой бумаги. Алгебраическая геометрия имеет дело с многомерными аналогами такого рода кривых, когда рассматриваются системы множественных уравнений, уравнения с большим количеством переменных и уравнения на плоскости комплексных чисел, а не действительные числа.

20-й век стал свидетелем расцвета сложных методов для понимания кривых, поверхностей и гиперповерхностей, которые являются предметом алгебраической геометрии. Сложные для воображения формы можно сделать более понятными с помощью сложных вычислительных инструментов.

Гипотеза Ходжа предполагает, что некоторые типы геометрических структур имеют особенно полезный алгебраический аналог, который можно использовать для лучшего изучения и классификации этих форм.

Прочтите официальное описание гипотезы Ходжа Институтом математики Клэя здесь.

Читать далее

LoadingЧто-то загружается. Функции Математика

Проблемы тысячелетия

Задача Давида Гильберта
Чуть более века назад математик Давид Гильберт (1862–1942) совершил настоящий прорыв на Международном конгрессе математиков в Париже. В 9 часов утра 8 августа 1900 года в главном лекционном зале ГЛАВНОЕ 23 проблемы Дэвида Гильберта. 0023

Кто не был бы счастлив, если бы смог приподнять завесу, скрывающую будущее, чтобы взглянуть на прогресс нашей науки и тайны ее дальнейшего развития в грядущие века? В такой богатой и обширной области, как математика, каковы будут цели и что будет руководством для мысли математиков в будущем? Какими будут новые разработки и новые методы в новом столетии?

Лекция Гильберта включала длинную преамбулу, в которой он обсуждал природу математики и ее роль в развитии других наук. Хотя в его списке было 23 задачи, он успел представить только 10 из них.

В то время Гильберт, профессор Геттингенского университета, считался ведущим математиком Германии. В полученном им приглашении прочесть инаугурационную лекцию в Париже его коллега Герман Коски (1864-1909) попросил его заглянуть в будущее. Но Гильберт закончил готовить свою лекцию в последнюю минуту и ​​замешкался с заглавием, не подошедшим вовремя к программе, в результате чего его лекция наконец состоялась на третий день Конгресса.

Курт Гёдель.

Усилия Гильберта соответствовали точке зрения математиков 19-го века о необходимости привнести в здание математики строгость и определенность. Действительно, в своей лекции Гильберт прямо упомянул природу математических проблем и роль математики в науке. Гильберт утверждал, что в математике нет ничего непознаваемого, «невежества». Все можно обосновать и логически объяснить. Если есть проблема, математики смогут найти ее решение. В Париже Гильберт столкнулся с другим видением, взглядом героев того времени, французского математика Анри Пуанкаре, который предпочитал более интуитивный подход (Пуанкаре называл теорию множеств Кантора «болезнью, от которой математика со временем излечится»). )

В любом случае никто не хотел быть изгнанным из рая теории множеств, созданной Джорджем Кантором (1845-1918) и его замечательной концепцией различных бесконечностей. Много лет спустя, 8 сентября 1930 года в Кенигсберге, на съезде Ассоциации немецких ученых и врачей Давид Гильберт прочитал лекцию, четыре минуты которой транслировались по радио. Гилберт закончил своим заявлением: «В противовес невежеству мы предлагаем наш лозунг: мы должны знать, мы будем знать».

Одной из вех в этой истории является работа итальянского математика Джузеппе Пеано (1858-1932), который заложил основы арифметики с помощью набора аксиом и правил. Но вопрос, возникший после Парижского конгресса, был простым, но сокрушительным: полна ли и непротиворечива ли эта система? Парадокс парикмахера Бертрана Рассела (1872-1970) поставил это под сомнение: в городе есть парикмахер, который бреет только городских жителей, которые не бреются сами: кто бреет парикмахера?

Парадокс связан с представлением о множестве всех множеств, не являющихся членами самих себя. Такое множество, если оно существует, будет членом самого себя тогда и только тогда, когда оно не является членом самого себя. В кажущемся прочным математическом здании образовалась брешь, поскольку никакая демонстрация не может быть надежной, если она основана на этой логике. Начался один из самых захватывающих периодов в истории дисциплины.

Так называемая программа Гильберта, целью которой было создание формальной системы математики, содержащей демонстрацию непротиворечивости (т. е. не приводящей к противоречиям), полноты (т. вывести формулу из аксиом, применяя правильные алгоритмы), был прерван почти в то же самое время, когда он произнес свой боевой клич против невежд в 1930. Другой гений математики, Курт Гёдель (1906–1970), доказал, что любая непротиворечивая аксиоматическая система арифметики обязательно неполна, то есть должны существовать истинные свойства, которые никогда нельзя будет продемонстрировать. Джон фон Нейман (1903–1957) сказал после презентации Гёделем своих открытий: «Все кончено».

Тем не менее, это еще не конец. Скорее, после этих драматических событий другие героические математики, такие как сам фон Нейман и Алан Тьюринг (1912–1954), основывались на этом новом подходе к разработке компьютеров и научных вычислений, какими мы их знаем сегодня.

Дэвид Гильберт.

100 лет спустя
С тех пор как Дэвид Гильберт составил свой знаменитый список, было предпринято несколько попыток его обновить. К сожалению, сегодня уже нет математиков, способных освоить все области математики, как это сделал в свое время Гильберт. Не потому, что больше нет математиков его уровня, а из-за невероятного развития, которое эта дисциплина претерпела за последнее столетие.

В 1992, Международный математический союз (IMU) в своей так называемой Декларации Рио-де-Жанейро решил вспомнить легендарный Международный конгресс математиков 1900 года в Париже и предложил, столетие спустя, чтобы математики со всего мира проводили мероприятия в течение всего столетия. год. В декларации изложены три основные цели:

• Определить самые большие математические проблемы 21-го века.
• Провозгласить математику ключом к развитию.
• Улучшить имидж математики за счет высококачественного распространения.

ЮНЕСКО также присоединилась к декларации ИДУ, и на своем пленарном заседании 11 ноября 1997 г. Генеральная конференция ЮНЕСКО последовала рекомендациям Комиссии III и одобрила проект резолюции 29 C/DR126 о Всемирном математическом 2000 г. (WMY 2000), подчеркнув образовательные аспекты математика.

Празднование WMY в 2000 году привело к организации многочисленных мероприятий по всему миру, проводимых национальными комитетами, а также породило различные инициативы, направленные на определение математических задач 21-го века.

Одной из таких инициатив является книга Бьёрна Энгквиста «Вильфрид Шмидт: математика без границ-2001 и далее». Springer-Verlag, Berlin, 2001, 1238 + XVI страниц, на которые около 90 математиков со всего мира поделились своими знаниями в соответствующих областях в виде 58 статей и пяти интервью. Это не энциклопедия и не синтезированный труд, но очевидно, что чтение дает общее представление о состоянии дисциплины в то время.

Еще одна экстраординарная попытка, более близкая к целям WMY 2000, была сделана В. И. Арнольдом: Математика: границы и перспективы. Американское математическое общество, 2000, 459.страницы. Эта книга была опубликована под эгидой IMU и была частью мероприятий Всемирного математического года 2000. Текст включает 30 статей, написанных некоторыми из самых влиятельных математиков мира; на самом деле, 15 из них написаны медалистами различных областей, в том числе К. Ф. Ротом (обладателем Филдсовской медали 1958 г.) и У. Т. Гауэрсом (обладателем Филдсовской медали 1998 г.). Некоторые статьи определяют некоторые из наиболее важных проблем для математиков в 21 веке, другие рассматривают различные проблемы, поставленные Гильбертом, а некоторые представляют собой статьи, в которых исследуются мотивы математиков того времени.

Проблемы тысячелетия
Однако, без сомнения, инициатива, которая оказала самое сильное влияние на общественное мнение — и начинает оказывать влияние на математическое сообщество, — это список так называемых проблем тысячелетия.

Эта инициатива была запущена Институтом математики Клэя (CMI), частным некоммерческим фондом, зарегистрированным по номеру
. в Кембридже, штат Массачусетс. CMI был создан в 1998 году по инициативе бостонского бизнесмена Лэндона Т. Клея и его жены Лавинии Д. Клэй. Цели института:

• Для увеличения и распространения математических знаний.
• Информировать математиков и других ученых о новых открытиях в области математики.
• Для поощрения одаренных студентов к выбору математической карьеры.
• Для признания выдающихся достижений и достижений в области математических исследований.

Первым президентом CMI был Артур Джаффе, известный математик из Гарвардского университета. Институт организует многочисленные мероприятия, включая конференции, лекции для широкой публики и семинары.

Институт хотел отметить математику в новом тысячелетии, учредив семь премий тысячелетия. Цель состояла в том, чтобы выявить наиболее сложные нерешенные проблемы и в то же время подчеркнуть, что математика является живым предметом, границы которого все еще открыты, и указать на важность работы по поиску решений проблем, имеющих историческое значение. Эти семь задач были выбраны научным комитетом Института после долгих размышлений. За решение каждой из задач предусмотрен приз в размере 1 миллиона долларов.

Проблемы тысячелетия были представлены в Париже 24 мая 2003 г. в Коллеж де Франс с лекциями Тимоти Гауэрса, Майкла Атьи и Джона Тейта.
Список следующий:

Гипотеза Берча и Суиннертона-Дайера
Одной из самых известных математических задач является поиск целых решений уравнений типа

x ² + y ² = z ²

Решение таких уравнений может быть очень трудным, и было показано, что не существует общего метода решения таких уравнений для целых чисел (это была десятая проблема Гильберта). Однако есть частичные решения. И гипотеза Берча и Суиннертона-Дайера верна, что в области алгебраических многообразий размер группы рациональных точек связан с поведением дзета-функции ζ(s) вблизи точки s=1.

Гипотеза Ходжа
Математики изучают сложные объекты, аппроксимируя их более простыми геометрическими блоками, которые соответствующим образом склеены, чтобы можно было их классифицировать. Это одна из традиционных задач дисциплины. Гипотеза Ходжа утверждает, что для математических объектов, известных как проективные алгебраические многообразия, части, называемые циклами Ходжа, на самом деле являются линейными комбинациями простых геометрических объектов, называемых алгебраическими циклами.

Уравнение Навье-Стокса
Уравнения Навье-Стокса восходят к 19 веку, и мы все чувствуем их действие, когда путешествуем на самолете, особенно если во время полета сталкиваемся с турбулентностью. Математики хотят их понять, а для этого им нужно больше знать об их решении. Однако, несмотря на значительные усилия на протяжении десятилетий, они все еще относительно плохо изучены.

Проблема P и NP
Одной из наиболее важных проблем информатики является определение того, существуют ли вопросы, ответ на которые можно легко проверить, но которые требуют невероятно много времени для решения какой-либо прямой процедурой (алгоритмом). P-задачи — это те, решение которых легко найти, а NP-задачи — это те, в которых легко проверить, действительно ли данное потенциальное решение таково.

Эта проблема была сформулирована независимо Стивеном Куком и Леонидом Левиным в 1971 году.

Гипотеза Пуанкаре
Резиновую ленту на поверхности сферы можно делать все меньше и меньше, пока она не сожмется в точку. Но если представить, что лента натянута в правильном направлении вокруг поверхности бублика (который в математике называется тором), сделать это будет невозможно. Таково происхождение алгебраической топологии, которая связывает алгебраические объекты с топологическими объектами и позволяет их изучать и классифицировать. Говорят, что сфера «односвязна», а тор — нет. Пуанкаре задавался вопросом столетие назад (1904), если то, что он смог продемонстрировать в двух измерениях, имело силу в более высоких измерениях, особенно в трех измерениях. Решение пришло сто лет спустя, когда Грегори Перельман опубликовал две статьи в 2002 и 2003 годах, объявив, что нашел ответ, используя новаторскую работу Ричарда Гамильтона о потоке Риччи. На самом деле то, что доказал Перельман, было более общим результатом, который содержал гипотезу Пуанкаре как частный случай, доказав также гипотезу геометризации Уильяма Тёрстона, тем самым решив одну из семи проблем тысячелетия. Перельман был награжден медалью Филдса на ICM в Мадриде в 2006 году за выдающиеся достижения, хотя, как известно, он отказался и от медали, и от чека на миллион долларов.

Гипотеза Римана
Простые числа можно рассматривать как строительные блоки, из которых формируются все остальные целые числа. Евклид доказал, что они бесконечны, но закономерность их распределения остается нерешенной проблемой. Георг Фридрих Бернхард Риман (1826-1866) заметил, что их частота связана с так называемой дзета-функцией Римана.

ζ(s) = 1 + 1/2s + 1/3s + 1/4s + …

Гипотеза Реймана утверждает, что интересные решения уравнения

ζ(с) = 0

(нули функции) лежат на некоторой вертикальной прямой. Это, несомненно, одна из самых сложных проблем, которые математики хотят решить сегодня.

Ян-Миллс и Масс Гэп
Элементарные частицы в физике описываются геометрически с использованием теории Чен-Нинга Янга и Роберта Л. Миллса. В отличие от электромагнитных сил, поля ядерного взаимодействия должны иметь массу, что выражается в том, что существует массовая щель. Но в классической теории Янга-Миллса частицы не имеют массы. Таким образом, задача состоит в том, чтобы математически строго продемонстрировать квантовую теорию Янга-Миллса и существование массовой щели.

Достижение этого, несомненно, потребует внедрения принципиально новых идей в физику и математику.

Анри Пуанкаре.

Испания и границы математики
Во времена Давида Гильберта математические исследования в Испании практически не проводились, несмотря на определенные индивидуальные усилия и тот факт, что Испания была домом для блестящих арабских и еврейских математиков во времена мусульманского господства, или что Испания была пионером в создании Королевской академии. математики в 1582 году при Филиппе II.

Стремление к «возрождению» в начале 20-го века привело к созданию в 1915 году Laboratorio Seminario Matematico под эгидой Junta de Ampliación de Estudios, предшественницы сегодняшнего CSIC, но этот расцвет математики был прерван Гражданская война. В 1980 году количество статей в журналах ISI, опубликованных испанскими математиками, составляло 0,3% от общего числа, по сравнению с 5% сегодня. В последние годы испанская математика бурно развивалась, о чем свидетельствует тот факт, что ICM впервые был проведен в Мадриде в 2006 г.

В упомянутых выше книгах не было ни одного испанского автора, и даже количество цитируемых испанцев было ничтожно мало. Однако сегодня ситуация была бы иной, и испанские математики заслужили признание за свою работу над такими проблемами, как обобщенные множества Сидона (Хавьер Силлеруэло и Карлос Винуэса), а также гипотезы Джона Нэша (Хавьер Фернандес де Бобадилья и Мария Пе) и В.И. Арнольд (Альберто Энцисо и Даниэль Перальта Салас),
Таким образом, мы можем сказать, что мы способны не только понять проблемы тысячелетия, но и работать над ними, и это чрезвычайно важное качественное изменение.

Георг Фридрих Бернхард Риман.

Прочие границы
Упомянутые здесь проблемы относятся в основном к внутренним границам математики, но в этом столетии эта дисциплина сталкивается с многочисленными проблемами из других областей науки, промышленности и технологического развития.

Неоспоримая парадигма, возникшая в последние десятилетия, — это возможность обработки больших объемов данных, ставшая возможной благодаря экспоненциальному росту вычислительной мощности современных компьютеров. Выявление закономерностей в бесчисленных данных, предоставленных астрономией, сейсмологией, генетикой и экспериментами на БАК, требует математических инструментов и, возможно, некоторых новых и более мощных. Более того, построение новых, еще более сложных математических моделей является ключом к решению серьезных проблем, стоящих перед нашим обществом, таких как устойчивое развитие или изменение климата.
Математика выглядит как абстрактная конструкция, которая может существовать вне физического мира. Однако его границы иногда опережают его потенциальные применения, иногда сопровождают их, а иногда отстают, но без этой дисциплины мы не смогли бы понять эту вселенную… понять эту вселенную, которая, как сказал Галилео Галилей, написана математическим языком. язык, который, как сказал Галилео Галилей, написан математическим языком. Эта двойственность и придает ему величие и делает его привлекательным.

Недоступность современной математики

Недоступность современной математики ноябрь 2002 г. В конце октября вышла моя новая книга The Проблемы тысячелетия: семь величайших нерешенных Математические загадки нашего времени поступил в продажу по всей стране, и в этом месяце видит, как я читаю обычные публичные лекции, книжные магазины и журналы, радио и телевидение интервью, которые в эти дни сопровождают публикацию любой новой книги, по мнению издателя, имеет даже призрак шанса стать следующим популярным научный бестселлер.

Из всех книг, которые я написал для генерала аудитории, этот последний представленный на сегодняшний день самая большая проблема в попытке сделать его как можно более доступным насколько это возможно для нематематиков. Семь нерешенных проблемы, которые я обсуждаю — глиняные проблемы тысячелетия — были выбраны небольшой звездной международной комитет ведущих математиков, назначенный Глиняная математика Институт, который предлагает денежный приз в размере 1 миллиона долларов. тому, кто первым решит любую из задач. Задача комиссии состояла в том, чтобы выбрать наиболее трудные и наиболее значимые нерешенные проблемы на конце второго тысячелетия, проблемы, которые долгие годы сопротивлялись усилиям некоторых величайшие математики мира, чтобы найти решение.

Никто, кто вообще знаком с современной математикой удивится, обнаружив, что ни один из семи выбранные проблемы, скорее всего, будут решены элементарными методы, и даже утверждение большинства проблемы не могут быть полностью поняты тем, кто не закончил математическую специальность в университете.

При написании книги мне пришлось игнорировать часто повторяющиеся утверждение, что каждая математическая формула, которую вы вводите книга снижает продажи на 50%. (лично я не думаю, что это буквально правда, но я верю, что Наличие страниц формул откладывает большой потенциал читателей.) Хотя моя книга в основном прозаическая, есть формулы, а некоторые главы имеют технические приложения это не что иное, как формулы.

Теперь, когда я готовлюсь к рекламной кампании, я сталкиваюсь с снова тот же вызов. С книгой, я думаю, я нашел способ представить историю Тысячелетия Задачи на 250 страниц текста. Но что я могу сказать о содержании книги в двадцатиминутном разговоре в книжный магазин или десятиминутное интервью на радио показывать? Мысли об этом заставили меня задуматься еще раз о природе современной математики. Проще говоря: Почему «Проблемы тысячелетия» так трудно понять?

Представьте на мгновение, что Лэндон Клей — богатый магнат взаимного фонда, который основал Институт Клэя и предоставил 7 миллионов долларов призовых для семи проблемы — решил установить свой приз конкурса не для математики, а для какой-то другой науки, скажем физики, или химии, или биологии. Это точно не потребовалась целая книга, чтобы объяснить заинтересованному мирской аудитории семь основных проблем в одной из этих дисциплины. Объяснительная статья на трех-четырех страницах в Scientific American или 1500 слов в New Scientist , вероятно, будет достаточно. Верно, когда Нобелевские премии присуждаются каждый год, газеты и журналам часто удается передать суть из отмеченного наградами исследования в нескольких абзацах. В общем, вы не можете сделать это с математикой. Математика другая. Но как?

Часть ответа можно найти в наблюдении сначала сделанный (кажется) американским математиком Рональдом Грэм, который большую часть своей карьеры возглавлял математические исследования в AT&T Bell Laboratories. По словам Грэма, математик — единственный ученый, который может с полным основанием утверждать: «Я ложусь на кушетку, закрой глаза и работай».0023

Математика почти полностью интеллектуальна. работа выполняется не в лаборатории, не в офисе или завод, а в голове. Конечно, эта голова прикреплен к телу, которое вполне может находиться в офисе — или на кушетке — но сама математика идет в мозгу, без какой-либо прямой связи с что-то в физическом мире. Это не для подразумевают, что другие ученые не занимаются умственной работой. Но в физике, химии или биологии объект мысль ученого – это вообще какое-то явление в физический мир. Хотя мы с тобой не можем получить внутри разума ученого и испытать ее мысли, мы живем в одном мире, и это обеспечивает ключевая связь, начальная основа для ученого объясните нам ее мысли. Даже в случае физики, пытающиеся понять кварки или биологи боремся с ДНК, хотя у нас нет повседневных опыт этих объектов, даже ненаучный тренированный ум без труда думает о них. В глубокий смысл, типичные художественные изображения кварки в виде скоплений цветных бильярдных шаров и ДНК как винтовая лестница вполне могла бы быть (на самом деле) «неправильно», а как мысленные образы, которые позволяют нам визуализируйте науку, они прекрасно работают.

В математике этого нет. Даже когда это можно нарисовать картинку, чаще всего иллюстрация может ввести в заблуждение настолько, насколько она помогает, в результате чего толкователю приходится придумывать словами то, чего не хватает или вводит в заблуждение в картина. Но как может нематематический читатель понять эти слова, когда они, в свою очередь, не ссылка на что-нибудь в повседневном опыте?

Даже для преданного любителя математики эта задача усложняется по мере роста предмета и более абстрактные и объекты математика обсуждения становятся все дальше и дальше от повседневный мир. Действительно, для некоторых современных проблемы, такие как гипотеза Ходжа — одна из семь проблем тысячелетия — возможно, мы уже дошел до того, что посторонний просто не может установить связь. Дело не в том, что человеческий разум требуется время, чтобы приспособиться к новым уровням абстракция. Так было всегда. Скорее, степень и темп абстракции могут иметь наконец достигли стадии, когда только эксперт может успевать.

Две с половиной тысячи лет назад молодой последователь Пифагора доказал, что квадратный корень из 2 равен не рациональное число, то есть не может быть выражено как дробь. Это означало, что то, что они приняли за чисел (целые числа и дроби) недостаточно для измерения длины гипотенуза прямоугольного треугольника с шириной и высотой оба равны 1 единице (что говорит теорема Пифагора будет иметь длину квадратный корень из 2). Это открытие стало таким потрясением для пифагорейцев, что их прогресс в математике фактически остановился. В конце концов, математики нашли выход из дилемму, изменив свое представление о том, что такое число — это то, что мы сегодня называем реальными числами.

Для греков числа начинались со счета (т. натуральных чисел ) и для измерения длин вы распространили их на более богатую систему ( рациональных числа ), объявив, что результат деления одно натуральное число другим было числом. Открытие того, что рациональных чисел нет в факт, достаточный для измерения длины, привел позже математиков отказаться от этой картины и вместо объявить, что числа просто — это точек на линия! Это было серьезное изменение, и потребовалось два тысяч лет, чтобы все детали были проработаны. Только к концу XIX в. математики наконец разработали строгую теорию действительных чисел. Даже сегодня, несмотря на простоту изображение действительных чисел в виде точек на линии, студенты университетов, изучающие математику, всегда имеют проблемы с пониманием формального (и очень абстрактного) Развитие действительных чисел.

Числа меньше нуля представляли собой еще одну борьбу. В наши дни мы думаем об отрицательных числах просто как о точки на числовой прямой, лежащие слева от 0, но математики сопротивлялись их внедрению, пока конец семнадцатого века. Точно так же большинство люди с трудом справляются со сложными числа — числа, содержащие квадратный корень из отрицательные величины — хотя существует простое интуитивное представление о комплексных числах как точки на двумерной плоскости.

В наши дни даже многие нематематики считают удобно использовать действительные числа, комплексные числа и отрицательные числа. Это несмотря на то, что это в высшей степени абстрактные понятия, мало что значащие связь со счетом, процесс, с которым нумерация началась около десяти тысяч лет назад, и даже хотя в повседневной жизни мы никогда не сталкиваемся с конкретный пример иррационального действительного числа или число, включающее квадратный корень из -1.

Точно так же и в геометрии открытие в восемнадцатого века, что были другие геометрии помимо того, что описал Евклид в своей знаменитая книга Элементы вызвала у обоих экспертов а у нематематиков огромные концептуальные проблемы. Только в девятнадцатом веке появилась идея «неевклидовы геометрии» получили широкое признание. Это признание пришло, несмотря на то, что мир нашего непосредственный, повседневный опыт полностью евклидов.

С каждым новым концептуальным скачком даже математики нужно время, чтобы свыкнуться с новыми идеями, принять их как часть общего фона на фоне которым они выполняют свою работу. До недавнего времени темп прогресс в математике был таков, что большой, заинтересованный наблюдатель мог догнать одно новое продвижение до того, как появилось следующее. Но становится все труднее. Чтобы понять что говорит Гипотеза Римана, первая проблема в списке Тысячелетия, ты должен был понять, и чувствовать себя комфортно не только с комплексными числами (и их арифметика), но и расширенное исчисление, и что значит сложить вместе бесконечно много (комплексные) числа и умножать бесконечно много (комплексных) чисел.

Теперь такого рода знания ограничены почти полностью для людей, которые специализировались в области математики в университете. Только они в состоянии видеть гипотезу Римана как простое утверждение, а не значительно отличается от среднего человек рассматривает теорему Пифагора. Моя задача в Написание моей книги, таким образом, заключалось не только в том, чтобы объяснить, что Гипотеза Римана говорит, но обеспечить все также предварительный материал. Ясно, я не могу сделать это в десятиминутном радиоинтервью!

Корень проблемы в том, что в большинстве случаев подготовительный материал не может быть объяснен в терминах повседневных явлений, так, как физики, для пример, может объяснить последние, самые глубокие, передовые Теория Вселенной — Теория Суперструн — в с точки зрения интуитивно простой картины крошечного, вибрирующие петли энергии («струны» теории).

Большинство математических понятий строятся не из повседневных явлений, а из более ранних математических концепции. Это означает, что единственный путь к получению даже поверхностное понимание этих понятий состоит в том, чтобы следовать всей цепочке абстракций, приводит к ним. Мои читатели решат, насколько хорошо я преуспеть в книге. Но этот проспект не доступно мне в коротком разговоре.

Возможно, тогда вместо того, чтобы пытаться описать Сами Проблемы Тысячелетия, я расскажу аудитории почему их так трудно понять. Я объясню, что концепции, связанные с Проблемы тысячелетия не столько по своей сути трудно — потому что они не — так как они очень, очень незнакомый. Так же, как идея комплексных чисел или неевклидова геометрия показалась бы непостижимо странным для древних греков. Сегодня, познакомившись с этими идеями, мы можем видеть, как они естественным образом вырастают из понятий греки знали как обычную математику.

Возможно, лучший способ приблизиться к тысячелетию Проблемы, я скажу, это думать о семи задачи как обычная математика 25 век.

И, возможно, так и окажется.

---

Угол Девлина обновлен в начале каждого месяца.

---

Математик Кит Девлин (англ. [электронная почта защищена]) Исполнительный директор Центра Изучение языка и информации в Стэнфорде Университет и «Парень-математик» на NPR Выпуск выходного дня. Его книга Проблемы тысячелетия: семь величайших Нерешенные математические загадки нашего времени был только что опубликован Basic Books. Большая часть приведенное выше обсуждение взято из введения к той книге.

---

Приз тысячелетия: P vs NP

СЕРИЯ ПРИЗОВ ТЫСЯЧЕЛЕТИЯ: Задачи тысячелетия — это семь математических задач, сформулированных Математическим институтом Клэя в 2000 году. в результате институт присуждает премию в размере 1 000 000 долларов США.

Российский математик Григорий Перельман был удостоен премии 18 марта прошлого года за решение одной из задач — гипотезы Пуанкаре — пока единственной решенной проблемы. Известно, что он отказался от премии тысячелетия в размере 1 000 000 долларов.

В ближайшие недели каждая из этих проблем будет освещена экспертами из организаций-членов Австралийского института математических наук (AMSI).

Здесь Марсель Джексон объясняет задачу P vs NP. Наслаждаться.

В 1930-х годах Алан Тьюринг показал, что существуют основные задачи, которые невозможно решить с помощью алгоритмических средств. Говоря современным языком, он показал, что не может быть общей компьютерной программы, которая отвечала бы да или нет на вопрос, остановится ли в конечном итоге другая компьютерная программа при ее запуске.

Удивительная неразрешимость этой проблемы остановки содержит еще одну загадочную тонкость. Хотя у нас нет способа узнать заранее, остановится ли программа, в принципе есть очевидный способ продемонстрировать, что она останавливается, если это останавливающаяся программа: запустите ее, подождите и посмотрите, как она остановится!

Другими словами, Тьюринг показал, что на самом широком уровне решить, является ли утверждение истинным, вычислительно сложнее, чем продемонстрировать, что оно истинно, когда оно истинно.

Вопрос эффективности

Работа Тьюринга стала поворотным моментом в истории вычислений. Примерно 80 лет спустя компьютерные устройства проникли почти во все сферы жизни общества. Оригинальный вопрос Тьюринга «что вычислимо?» вопрос был в основном заменен более подходящим: «Что является эффективно вычислимым?»

Но в то время как проблема остановки Тьюринга может быть доказана неразрешимой в нескольких волшебных строках, граница между «эффективным» и «неэффективным» кажется гораздо более неуловимой. P против NP — самый известный из множества нерешенных вопросов, возникших в результате этого современного взгляда на вопрос Тьюринга.

Так что же это за НП?

Грубо говоря, P (обозначающее «полиномиальное время») соответствует набору вычислительных задач, которые имеют эффективное решение. Это всего лишь абстрактная формулировка «эффективности», но на практике она работает довольно хорошо.

Класс NP соответствует задачам, для которых при ответе «да» имеется эффективная демонстрация положительного ответа («N» означает «недетерминированный», но приведенное здесь описание более интуитивно понятно) . P vs NP просто спрашивает, являются ли эти два класса вычислительных задач одинаковыми.

Это просто проблема «решить против демонстрации» в оригинальной задаче Тьюринга о остановке, но с дополнительным условием эффективности.

Головоломка

P явно не похожа на NP. Головоломки — хороший пример общей интуиции. Кроссворды популярны, потому что найти решение сложно, а люди любят вызовы. Но никто не тратит свое обеденное время на проверку уже решенных кроссвордов: проверка чужого решения не представляет такой же сложности.

Судоку еще понятнее: опять же, это настоящая задача для решения, но проверка существующего решения на правильность настолько рутинна, что лишена развлекательной ценности.

Возможность P=NP подобна обнаружению того, что «найти» часть этих головоломок имеет ту же сложность, что и «проверить». В это трудно поверить, но правда в том, что мы не знаем наверняка.

Та же самая интуиция пронизывает огромное количество важных вычислительных задач, для которых у нас в настоящее время нет эффективных алгоритмов. Одна особенно заманчивая особенность заключается в том, что чаще всего эти задачи могут быть показаны как максимально сложные среди NP-задач.

Эти так называемые «NP-полные» задачи являются тестовыми примерами для сравнения P и NP: если какая-либо из них имеет эффективное алгоритмическое решение, то оно есть и у всех (эффективная проверка не сложнее, чем эффективный поиск).

Но если можно показать, что хотя бы одно решение не имеет эффективного решения, то P не равно NP (а эффективное нахождение, вообще говоря, сложнее, чем эффективная проверка).

Вот несколько классических примеров NP-полных задач.

• Перегородка (дилемма инопланетных карманников) . На чужой планете два карманника крадут бумажник. Чтобы разделить выручку, они должны поровну разделить деньги: смогут ли они это сделать? Стандартные земные валюты эволюционировали, чтобы иметь стоимость монет, предназначенную для облегчения этой задачи, но в целом эта задача является NP-полной. Это в NP, потому что, если есть равное деление монет, это можно легко продемонстрировать, просто показав деление. (Сложнее всего найти!)

• Расписание . Выяснение того, существует ли расписание без коллизий, является NP-полным. Проблема в NP, потому что мы можем эффективно проверить правильное расписание без конфликтов.

• Коммивояжер . Коммивояжер должен посетить каждый из некоторого количества городов. Чтобы сократить расходы, продавец хочет найти кратчайший маршрут, проходящий через все города. Для некоторого заданного целевого расстояния «n» существует ли маршрут длиной не более «n»?

• Краткие цветопробы . Есть ли короткое доказательство для вашего любимого математического утверждения (возможно, задачи тысячелетия)? При подходящей формулировке «короткий» это NP-полное. Это в NP, потому что проверка формальных доказательств может быть выполнена эффективно: трудная часть — найти их (по крайней мере, мы думаем, что это сложная часть!).

В каждом случае нам неизвестен эффективный точный алгоритм, и отсутствие такого алгоритма эквивалентно доказательству того, что P не равно NP.

Итак, мы близки к решению? Кажется, лучшее, что мы знаем, это то, что мы мало знаем! Возможно, наиболее существенные достижения в саге о P и NP носят любопытный отрицательный характер: они в основном показывают, что мы не можем надеяться разрешить P как отличное от NP с помощью знакомых методов.

Мы знаем, что подход Тьюринга не работает. В 2007 году Александр Разборов и Стивен Рудич были удостоены премии Гёделя (часто называемой Нобелевской премией по компьютерным наукам) за свою работу, показывающую, что никакое «естественное доказательство» не может доказать, что P не равно NP.

Конечно, будем искать!

Это третья часть серии наград тысячелетия. Чтобы прочитать другие части, перейдите по ссылкам ниже.

• Часть первая: Премия тысячелетия: проблема существования и единственности Навье–Стокса
• Часть вторая: Премия тысячелетия: гипотеза Ходжа

Понимание того, как разные учащиеся учатся

1. Бабетта Меллер
2. http://www. edc.org/babette-moeller
3. Заслуженный ученый
4. Математика для всех: расширение и поддержание эффективного профессионального развития учителей для поддержки строгого персонализированного обучения математике для особо нуждающихся учащихся в классах K–5
5. http://mathforall.cct.edc.org/
6. Центр развития образования (EDC)

1. Андреа Бротман
2. https://www.linkedin.com/in/andrea-brothman-56a67218/
3. Старший специалист по учебной программе и учебному дизайну
4. Математика для всех: расширение и поддержание эффективного профессионального развития учителей для поддержки строгого персонализированного обучения математике для особо нуждающихся учащихся в классах K–5
5. http://mathforall.cct.edc.org/
6. Центр развития образования (EDC)

1. Тереза ​​Дункан
2. https://www.linkedin.com/in/teresagarciaduncan/
3. Президент
4. Математика для всех: расширение и поддержание эффективного профессионального развития учителей для поддержки тщательного персонализированного обучения математике для особо нуждающихся учащихся в классах K–5
5. http://mathforall. cct.edc.org/
6. Исследовательская ассоциация Дикона Хилла

1. Неста Маршалл
2. https://graduate.bankstreet.edu/academics/faculty-profile/nesta-marshall/
3. Инструктор-консультант-соруководитель программы
4. Математика для всех: расширение и поддержание эффективного профессионального развития учителей для поддержки строгого персонализированного обучения математике для особо нуждающихся учащихся в классах K–5
5. http://mathforall.cct.edc.org/
6. Педагогический колледж Бэнк-Стрит

1. Мэтт Маклеод
2. http://ltd.edc.org/people/matt-mcleod
3. Директор проекта
4. Математика для всех: расширение и поддержание эффективного профессионального развития учителей для поддержки строгого персонализированного обучения математике для особо нуждающихся учащихся в классах K–5
5. http://mathforall.cct.edc.org/
6. Центр развития образования (EDC), Университет Северо-Восточного Иллинойса

1. Питер Тирни-Файф
2. https://www. edc.org/staff/peter-tierney-fife
3. Старший специалист по учебной программе/педагогическому дизайну
4. Математика для всех: расширение и поддержание эффективного профессионального развития учителей для поддержки строгого персонализированного обучения математике для особо нуждающихся учащихся в классах K–5
5. http://mathforall.cct.edc.org/
6. Центр развития образования (EDC)

Фасилитаторов
Выбор

• Абстрактный
• Похожие видео
• Поделиться
• Карта

«Математика для всех: расширение и поддержка эффективного профессионального развития учителей» удовлетворить потребности широкого круга учащихся, в том числе с ограниченными возможностями.

Программа «Математика для всех» была разработана Центром развития образования в сотрудничестве с Педагогическим колледжем Бэнк-Стрит и при финансовой поддержке Национального научного фонда. Исследовательский грант от Института педагогических наук позволил нам установить обещание «Математика для всех» положительно повлиять на знания, убеждения и методы работы учителей, а также на успеваемость учащихся по тестам успеваемости по математике. В настоящее время финансирование в рамках Программы образовательных инноваций и исследований Министерства образования США поддерживает наши исследования по широкомасштабному внедрению «Математика для всех» в различных условиях и с различными группами населения с высокими потребностями в трех разных штатах.

В отличие от других программ профессионального обучения математике, которые сосредоточены на содержании математики или стратегиях обучения, «Математика для всех» направлена ​​на то, чтобы помочь учителям лучше понять, как отдельные учащиеся изучают математику, и помочь учителям использовать это понимание для планирования более доступных уроков математики.

No related posts.