|
элементарная теория чисел — мод [= остаток] операция (и отношение), имя и значение
По запросу я публикую свои комментарии в качестве ответа и добавляю некоторые дополнительные замечания.
$\rm\color{#c00}{операция}$ $\,a\bmod b\,$ обозначает остаток при делении $\,a\,$ на $\,b\,$ по алгоритму деления , например $\, a\bmod 2 = 1\,$ означает $\,a = 2n+1\,$ для целого числа $\,n,\,$, т. е. $\,a\,$ нечетно. $ $ Альтернативно, $\,a\:\!\%\:\!b\, :=\, a\bmod b\,$ — это нотация, иногда встречающаяся в языках программирования (см. ниже). 92\!+\!1)\bmod x\!-\!i$.
Также $\!\bmod\!$ используется как троичная $\rm\color{#c00}{relation}$ (в отличие от описанной выше бинарной операции) в отношениях конгруэнтности, например. $\ а\экв б\pmod{\! n}\iff n\mid a-b\,$ ( отношение эквивалентности для фиксированного модуля $\,n). $
$
Эти два обозначения $\!\bmod\!$ связаны следующим образом (ср. доказательства здесь или здесь)
$$ \begin{align} a\color{#90f}\equiv b\!\!\!\pmod{\!n}&\iff a\bmod n\, \color{#0a0 }=\, b\bmod n\\[.3em] \color{#90f}{\text{т.е. $\ $ эквивалент}} &\iff \text{$\rm\color{#0a0}{equal}$ нормальные формы}\end{align}\qquad\qquad$$
, так что $\,a\bmod n\,$ служит нормальной формой или каноническим представителем всего класса эквивалентности $\,[a]_n = a + n\:\!\Bbb Z\,$ все целые числа $\,\equiv a\!\pmod{\!n}.\,$ Стрелка выше означает, что проверка соответствия $\rm\color{#90f}{эквивалентности}$ целых чисел аналогична проверке $\rm \color{#0a0}{равенство}$ их нормальных форм (= остатки $\!\bmod n),\,$ так же, как мы можем проверить эквивалентность дробей, проверяя равенство их нормальных форм с наименьшими членами. Точно так же мы можем рассматривать остаток как rep «наименьших условий»: это наименьшее неотрицательное целое число в классе $[a]_n$ всех целых чисел, сравнимых с $\,a\,$ по модулю $\,n. \,$
\,$
операционное использование mod часто более удобно в вычислительных контекстах, тогда как реляционное использование часто дает большую гибкость в теоретических контекстах. Разница заключается в том, удобнее ли работать с общими классами эквивалентности по сравнению с их каноническими/обычными представителями («представителями»). Например, было бы довольно громоздко сформулировать законы арифметики дробей, если бы мы требовали, чтобы все дроби были в нормальной (приведенной) форме, т. е. в низших членах. Вместо этого оказывается более удобным иметь возможность работать с произвольными эквивалентными дробями. Например, это позволяет нам сформулировать правило сложения дробей в очень простой форме, выбрав сначала 9{\large k}\equiv \pm1,\,$, который включает выбор представителя наименьшей величины $\,\color{#c00}{\bf -1}\,$ против $\,\color{# 0a0}{10}\in [10]_{11}\! = \{\ldots,\, -23,-12,\color{#c00}{\bf -1},\color{#0a0}{10},21,\,\ldots\}.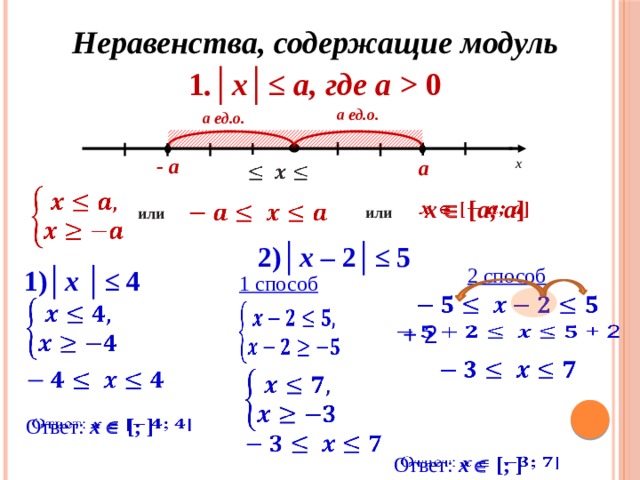 \,$ Или , так как здесь мы можем выбрать повторения, которые удобно сделать частное точным при вычислении модульных дробей, например. $\!\bmod 11\!:\,\ 9/13\экв -2/2\экв -1.\,$
Следовательно, аналогично сложению дробей, мы выбрали повторения, которые упростили арифметику . Использование повторений с наименьшей величиной часто упрощает и другие вычисления, например. это может вдвое сократить количество шагов в алгоритме Евклида. Таким образом, использование конгруэнтности 9Классы 0009 (по сравнению с каноническими повторениями) обеспечивают гораздо большую гибкость, что может привести к большим упрощениям — не только в вычислительном, но и в теоретическом плане, что становится яснее, когда изучаешь частных колец , которые дают (алгебраические) структур реификаций правила конгруэнтности = совместимость конгруэнтностей сложения и умножения).
\,$ Или , так как здесь мы можем выбрать повторения, которые удобно сделать частное точным при вычислении модульных дробей, например. $\!\bmod 11\!:\,\ 9/13\экв -2/2\экв -1.\,$
Следовательно, аналогично сложению дробей, мы выбрали повторения, которые упростили арифметику . Использование повторений с наименьшей величиной часто упрощает и другие вычисления, например. это может вдвое сократить количество шагов в алгоритме Евклида. Таким образом, использование конгруэнтности 9Классы 0009 (по сравнению с каноническими повторениями) обеспечивают гораздо большую гибкость, что может привести к большим упрощениям — не только в вычислительном, но и в теоретическом плане, что становится яснее, когда изучаешь частных колец , которые дают (алгебраические) структур реификаций правила конгруэнтности = совместимость конгруэнтностей сложения и умножения).
Остерегайтесь , что некоторые авторы опускают круглые скобки в $\, a\equiv b\pmod{\!n}$ вместо того, чтобы писать следующим образом: $\,a\equiv b\mod n\ $ или $\ a = b \mod n,\ $ используя \mod против \pmod в $\TeX$. Их легко спутать с $\,a = b\bmod n\,$, т. е. $\,a = (b\bmod n),\,$, поэтому следует иметь в виду такие возможные неоднозначности в контекстах, где обе формы $ \!\bmod\!$ используются. Подробнее об этом см. здесь.
Их легко спутать с $\,a = b\bmod n\,$, т. е. $\,a = (b\bmod n),\,$, поэтому следует иметь в виду такие возможные неоднозначности в контекстах, где обе формы $ \!\bmod\!$ используются. Подробнее об этом см. здесь.
Насколько я могу судить, имя % для операции $\!\bmod\!$ в нормальной форме (как в языке программирования C) не проникло в математическое сообщество. Я помню много вопросов по sci.math относительно значения $\rm\, a\:\!\%\:\! b.\, $ Таким образом, если вы используете это обозначение на математическом форуме, я рекомендую вам указать его значение. Это не было бы необходимо для $\!\bmod\!$, так как это обозначение повсеместно в математике (в настоящее время больше для конгруэнтности, чем для операторной формы). Имейте в виду, однако, что некоторые математики смотрят свысока на операционное использование mod в случае, когда было бы более естественно использовать форму конгруэнтности. По-видимому, боги математики делают то же самое, поскольку это может значительно усложнить некоторые доказательства (намного сложнее, чем приведенный выше простой случай сложения дробей).
Оператор модификации — Visual Basic
Редактировать
Твиттер LinkedIn Фейсбук Электронная почта
- Статья
- 3 минуты на чтение
Делит два числа и возвращает только остаток.
Синтаксис
результат = число1 Номер модификации2
Детали
результат
Требуется. Любая числовая переменная или свойство.
номер 1
Обязательно. Любое числовое выражение.
номер2
Обязательно. Любое числовое выражение.
Поддерживаемые типы
Все числовые типы. Сюда входят типы без знака и с плавающей запятой, а также Decimal .
Результат
Результат: остаток после деления число1 на число2 . Например, выражение 14 Mod 4 оценивается как 2.
Примечание
Существует разница между остатком и по модулю в математике, с разными результатами для отрицательных чисел. Оператор Mod в Visual Basic, оператор .NET Framework op_Modulus и базовая инструкция rem IL выполняют операцию остатка.
Результат операции Mod сохраняет знак делимого, число1 , поэтому оно может быть положительным или отрицательным. Результат всегда находится в диапазоне (- номер2 , номер2 ), исключая. Например:
Пример общего модуля
Публичная подсистема ()
Console.WriteLine($" 8 Mod 3 = {8 Mod 3}")
Console.WriteLine($"-8 Mod 3 = {-8 Mod 3}")
Console.WriteLine($" 8 Mod -3 = {8 Mod -3}")
Console.WriteLine($"-8 Mod -3 = {-8 Mod -3}")
Конец сабвуфера
Конечный модуль
' Пример отображает следующий вывод:
' 8 Мод 3 = 2
'-8 мод 3 = -2
8 Мод -3 = 2
'-8 Mod -3 = -2
Если либо число1 , либо число2 является значением с плавающей запятой, возвращается остаток от деления с плавающей запятой. Тип данных результата — это наименьший тип данных, который может содержать все возможные значения, полученные в результате деления на типы данных
Тип данных результата — это наименьший тип данных, который может содержать все возможные значения, полученные в результате деления на типы данных число1 и число2 .
Если номер 1 или номер 2 оценивается как Ничего, он считается нулевым.
Связанные операторы включают следующее:
Оператор \ (Visual Basic) возвращает целое частное от деления. Например, выражение
14 \ 4оценивается как 3.Оператор / (Visual Basic) возвращает полное частное, включая остаток, в виде числа с плавающей запятой. Например, выражение
14 / 4оценивается как 3,5.
Попытка деления на ноль
Если число2 оценивается как ноль, поведение Оператор Mod зависит от типа данных операндов:
- Целочисленное деление вызывает исключение DivideByZeroException, если
число2не может быть определено во время компиляции и генерирует ошибку времени компиляцииBC30542 Деление на ноль произошло при оценке этого выражение, есличисло2оценивается как ноль во время компиляции.
- Деление с плавающей запятой возвращает значение Double.NaN.
Эквивалентная формула
Выражение a Mod b эквивалентен любой из следующих формул:
a - (b * (a \ b))
a - (b * Fix(a / b))
С плавающей запятой imprecision
При работе с числами с плавающей запятой помните, что они не всегда имеют точное десятичное представление в памяти. Это может привести к неожиданным результатам некоторых операций, таких как сравнение значений и оператор Mod . Дополнительные сведения см. в разделе Устранение неполадок с типами данных.
Перегрузка
Оператор Mod может быть перегружен , что означает, что класс или структура могут переопределить свое поведение. Если ваш код применяет Mod к экземпляру класса или структуры, которая включает такую перегрузку, убедитесь, что вы понимаете ее переопределенное поведение. Для получения дополнительной информации см. Процедуры оператора.
Процедуры оператора.
Пример 1
В следующем примере оператор Mod используется для деления двух чисел и возврата только остатка. Если какое-либо число является числом с плавающей запятой, результатом будет число с плавающей запятой, представляющее остаток.
Debug.WriteLine(10 Mod 5) ' Вывод: 0 Debug.WriteLine(10 Mod 3) 'Вывод: 1 Debug.WriteLine(-10 Mod 3) ' Выход: -1 Debug.WriteLine(12 Mod 4.3) ' Выход: 3,4 Debug.WriteLine (12.6 Mod 5) ' Выход: 2,6 Debug.WriteLine (47.9 Mod 9.35) ' Выход: 1,15
Пример 2
В следующем примере демонстрируется потенциальная неточность операндов с плавающей запятой. В первом операторе операндами являются Double , а 0,2 — бесконечно повторяющаяся двоичная дробь с сохраненным значением 0,200000000000000001. Во втором утверждении символ буквального типа D приводит оба операнда к Decimal , а 0,2 имеет точное представление.
первый результат = 2.



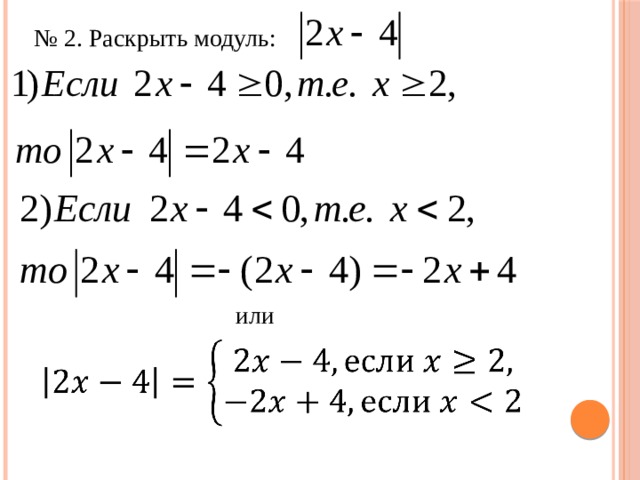 Того материала, который мы проходим в общеобразовательной школе не всегда достаточно для решения. И поэтому я решил собрать более подробный материал в своей, так называемой, «шпаргалке» по теме «Модуль».
Того материала, который мы проходим в общеобразовательной школе не всегда достаточно для решения. И поэтому я решил собрать более подробный материал в своей, так называемой, «шпаргалке» по теме «Модуль».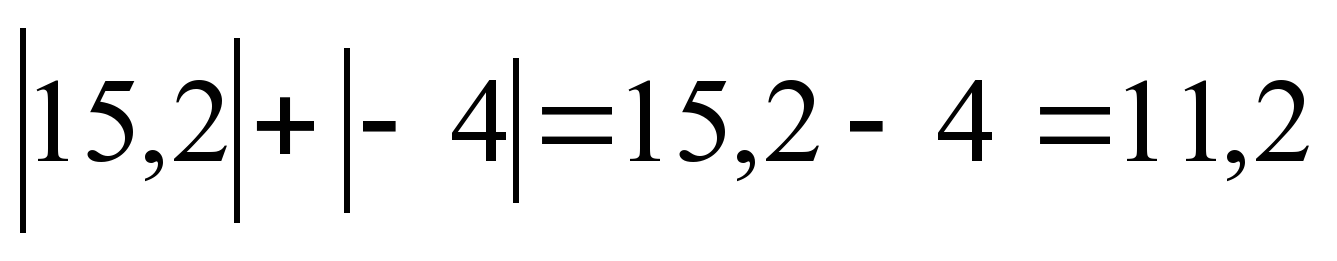 Исследован объём выполняемого домашнего задания в 5-8-х классах. Оформлен буклет-памятка для учеников и родителей с рекомендациями по выполнению домашнего задания.
Исследован объём выполняемого домашнего задания в 5-8-х классах. Оформлен буклет-памятка для учеников и родителей с рекомендациями по выполнению домашнего задания.
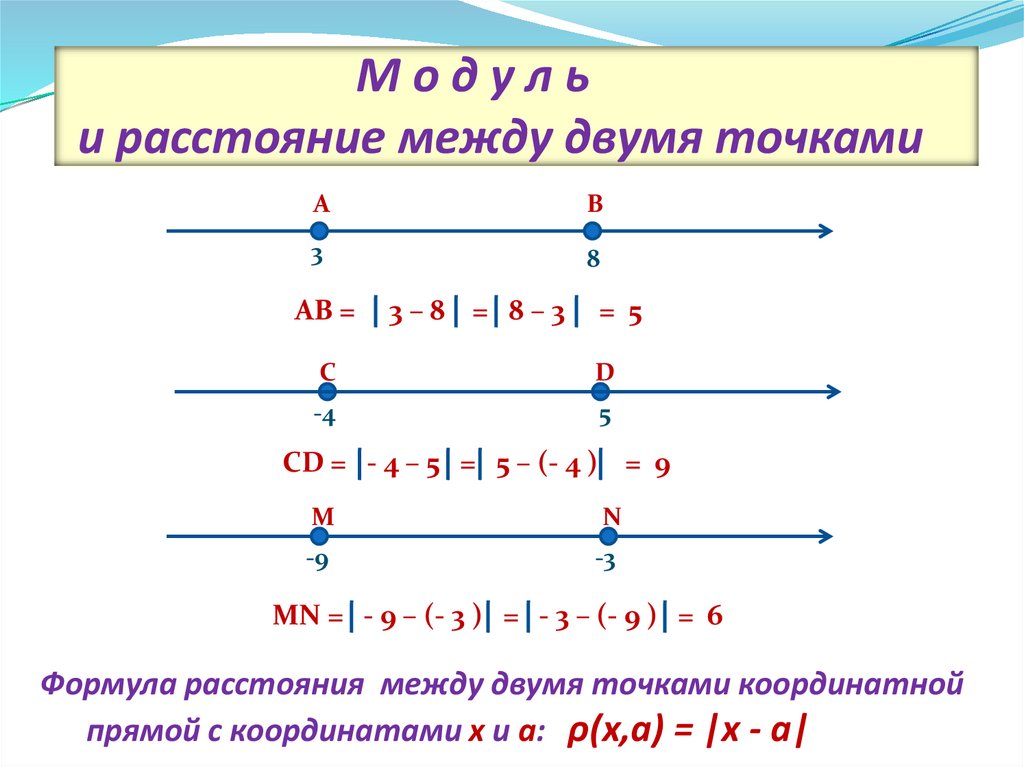 д.
д.
 Действия с натуральными числами и десятичными дробями». Работа представлена презентациями, которые содержат не только задачи и их решения, но и интересную информацию к сюжету задачи.
Действия с натуральными числами и десятичными дробями». Работа представлена презентациями, которые содержат не только задачи и их решения, но и интересную информацию к сюжету задачи. В ней представлены математические задачи краеведческого содержания по теме «Проценты». Задачи можно использовать на уроках, факультативных занятиях, кружках в качестве дополнительного дидактического материала.
В ней представлены математические задачи краеведческого содержания по теме «Проценты». Задачи можно использовать на уроках, факультативных занятиях, кружках в качестве дополнительного дидактического материала.

