УГОЛ — это… Что такое УГОЛ?
— геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало — вершиной У. Пусть [ ВА),[ ВС) — стороны угла, В — его вершина, — плоскость, определяемая сторонами У. Фигура делит плоскость на две фигуры Фигура i==l, 2, также наз. У. или плоским углом, наз. внутренней областью плоского У.
Два угла наз. равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины. От любого луча на плоскости в данную сторону от него можно отложить единственный У., равный данному У. Сравнение У. осуществляется двумя способами. Если У. рассматривается как пара лучей с общим началом, то для выяснения вопроса, какой из двух У. больше, необходимо совместить в одной плоскости вершины У. и одну пару их сторон (см. рис. 1). Если вторая сторона одного У. окажется расположенной внутри другого У., то говорят, что первый У. меньше, чем второй. Второй способ сравнения У. основан на сопоставлении каждому У. нек-рого числа. Равным У. будет соответствовать одинаковое число градусов или радиан (см.
Два У. наз. смежными, если у них общая вершина и одна сторона, а две другие стороны образуют прямую (см. рис. 2). Вообще, У., имеющие общую вершину и одну общую сторону, наз. прилежащими. У. наз. вертикальными, если стороны одного являются продолжениями за вершину сторон другого У. Вертикальные У. равны между собой. У., у к-рого стороны образуют прямую, наз. развернутым. Половина развернутого У. наз. прямым У. Прямой У. можно эквивалентно определить иначе: У., равный своему смежному, наз. прямым. Внутренняя область плоского У., не превосходящего развернутого, является выпуклой областью на плоскости. За единицу измерения У. принимается 90-я доля прямого У., наз. градусом.
Используется и т. мера У. Числовое значение радианной меры У. равно длине дуги, высекаемой сторонами У. из единичной окружности. Один радиан приписывается У., соответствующему дуге, длина к-рой равна ее радиусу. Развернутый У. равен радиан.
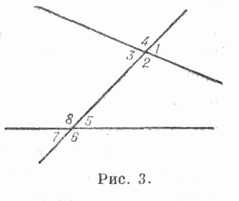
При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются У. (см. рис. 3): 1 и 5, 2 и 6, 4 и 8, З и 7 — наз. соответственными; 2 и 5, 3 и 8 — внутренними односторонними; 1 и 6, 4 и 7 — внешними односторонними; 3 и 5, 2 и 8- внутренними накрест лежащими; 1 и 7, 4 и 6 — внешними накрест лежащими.
В практич. задачах целесообразно рассматривать У. как меру поворота фиксированного луча вокруг его начала до заданного положения. В зависимости от направления поворота У. в этом случае можно рассматривать как положительные, так и отрицательные. Тем самым У. в этом смысле может иметь своей величиной любое действительное число. У. как мера поворота луча рассматривается в теории тригонометрич. функций: для любых значений аргумента (У.) можно определить значения тригонометрич. функций. Понятие У. в геометрич. системе, в основу к-рой положена точечно-векторная аксиоматика, в корне отличается от определений У. как фигуры — в этой аксиоматике под У. понимают определенную метрич. величину, связанную с двумя векторами с помощью операции скалярного умножения векторов. Именно, каждая пара векторов аи bопределяет нек-рый угол — число, связанное с векторами формулой
где (a, b) — скалярное произведение векторов.
Понятие У. как плоской фигуры и как нек-рой числовой величины применяется в различных геометрич. задачах, в к-рых У. определяется специальным образом. Так, под У. между пересекающимися кривыми, имеющими определенные касательные в точке пересечения, понимают У., образованный этими касательными.
За угол между прямой и плоскостью принимается У., образованный прямой и ее прямоугольной проекцией на плоскость; он измеряется в пределах от 0
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Угол. Измерение угла — урок. Математика, 5 класс.
Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.
Общая точка называется вершиной угла, а лучи — сторонами угла.
Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.
Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.
Иногда угол можно назвать только одной буквой, которая находится у вершины.
Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.
Чаще используют: α,β,γ,δ,ϵ,η,ϕ,ω — и другие.
Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.
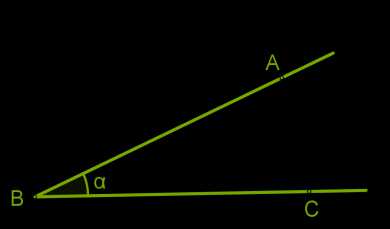
Пример:
описание рисункa:
1. на рисунке показан угол ∡ABC, ∡B или ∡α;
2. также нарисован развёрнутый угол ∡KLM.
Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.
За единицу измерения углов принимают градус, что является 1180 частью развёрнутого угла.
Величина развёрнутого угла — \(180°\).
Углы измеряют транспортиром.

Особый угол, половина развёрнутого угла — прямой угол.
Прямой угол обозначают маленьким квадратиком внутри угла.
Величина прямого угла равна \(90°\).
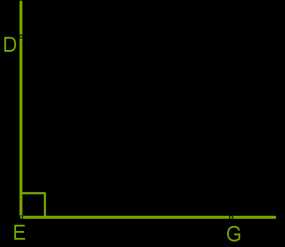
Углы, величина которых меньше \(90°\), называются острыми.
Углы, величина которых больше \(90°\), называются тупыми.
www.yaklass.ru
Величина угла — это… Что такое Величина угла?
«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
Смежные углы — острый (a) и тупой ( b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:
Невыпуклый угол
Прямой угол
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на , считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation. 2010.
dic.academic.ru
Математическая энциклопедия — значение слова Угол
— геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало — вершиной У. Пусть [ ВА),[ ВС) — стороны угла, В — его вершина, — плоскость, определяемая сторонами У. Фигура делит плоскость на две фигуры Фигура i==l, 2, также наз. У. или плоским углом, наз. внутренней областью плоского У. Два угла наз. равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины. От любого луча на плоскости в данную сторону от него можно отложить единственный У., равный данному У. Сравнение У. осуществляется двумя способами. Если У. рассматривается как пара лучей с общим началом, то для выяснения вопроса, какой из двух У. больше, необходимо совместить в одной плоскости вершины У. и одну пару их сторон (см. рис. 1). Если вторая сторона одного У. окажется расположенной внутри другого У., то говорят, что первый У. меньше, чем второй. Второй способ сравнения У. основан на сопоставлении каждому У. нек-рого числа. Равным У. будет соответствовать одинаковое число градусов или радиан (см. ниже), большему У.- большее число, меньшему -меньшее. Два У. наз. смежными, если у них общая вершина и одна сторона, а две другие стороны образуют прямую (см. рис. 2). Вообще, У., имеющие общую вершину и одну общую сторону, наз. прилежащими. У. наз. вертикальными, если стороны одного являются продолжениями за вершину сторон другого У. Вертикальные У. равны между собой. У., у к-рого стороны образуют прямую, наз. развернутым. Половина развернутого У. наз. прямым У. Прямой У. можно эквивалентно определить иначе: У., равный своему смежному, наз. прямым. Внутренняя область плоского У., не превосходящего развернутого, является выпуклой областью на плоскости. За единицу измерения У. принимается 90-я доля прямого У., наз. градусом. Используется и т.
Смотреть значение Угол в других словарях
Угол — м. перелом, излом, колено, локоть, выступ или залом (впадина) об одной грани. линейный, всякие две встречные черты и промежуток их; угол плоскостной или в плоскостях, встреча……..
Толковый словарь Даля
Угол — угла, об угле, на (в) углу и (мат.) в угле, м. 1. Часть плоскости между двумя прямыми линиями, исходящими из одной точки (мат.). Вершина угла. Стороны угла. Измерение угла градусами………
Толковый словарь Ушакова
Подчинить Рынок, Устраивать На Рынке Корнер (corner — Угол — Спекулятивный Контроль Рынка)
Экономический словарь
Угол — (сленг.) — монопольное поведение компании, состоящее в контролировании
объема совокупного
предложения
товара;
цена при этом может расти вплоть до появления……..
Экономический словарь
Comer («угол», Корнер) — Монополия, которая устанавливается организацией, преуспевающей в контролировании объема совокупного предложения какого-либо товара или услуги (часто называется спекулятивным……..
Экономический словарь
Угол — угла́, предлож. об угле́, в углу́, (матем.) в угле́; м.
1. Матем. Часть плоскости между двумя прямыми линиями, исходящими из одной точки. Измерение угла. Прямой у. (равный……..
Толковый словарь Кузнецова
Угол — Общеславянское слово индоевропейской природы. В латинском находим angulus («угол»), в греческом – agkylos («кривой»), в английском angle («угол») и т. д.
Этимологический словарь Крылова
Беннетта Угол — (N. G. Bennett, 1870-1947, англ. стоматолог) угол, на который отклоняются суставная головка и ветвь нижней челюсти при переходе из центральной окклюзии в боковую; в среднем равен 15-17
Большой медицинский словарь
Угол — (сленг.) — монопольное поведение компании, состоящее в контролировании объема совокупного предложения товара; цена при этом может расти вплоть до появления на рынке……..
Юридический словарь
Венозный Угол — (angulus venosus; син. Пирогова венозный угол) место слияния подключичной и внутренней яремной вен, образующих плечеголовную вену.
Большой медицинский словарь
Гиса Угол — (W. His, 1863-1934, нем. анатом) угол между стенками пищевода и желудка; величина Г. у. сказывается на скорости перехода пищи из пищевода в желудок.
Большой медицинский словарь
Критический Угол — , угол, при котором происходит заметный перелом в каком-либо процессе. Например, в оптике это — УГОЛ ПАДЕНИЯ в среде, в которой происходит полное внутренне ОТРАЖЕНИЕ………
Научно-технический энциклопедический словарь
Защитный Угол Светильника — показатель экранирования источника света осветительной арматурой, выражаемый величиной угла между горизонталью и прямой, соединяющей крайнюю точку светящего тела……..
Большой медицинский словарь
Зрительный Угол — (angulus opticus; син. угол зрения) угол, вершиной которого является узловая точка оптической системы глаза, а сторонами — линии, проведенные из нее к противоположным крайним……..
Большой медицинский словарь
Илеоцекальный Угол — (angulus ileocecalis; син. подвздошно-слепокишечный угол) область перехода подвздошной кишки в слепую.
Большой медицинский словарь
Телесный Угол — , пространственный угол, образованный в центре сферы ВЕРШИНОЙ КОНУСА, основание которого находится на поверхности сферы. Телесные углы измеряются в стерадианах и определяются……..
Научно-технический энциклопедический словарь
Угол — , мера наклона между двумя прямыми линиями или плоскостями, а также величины вращательного движения. Полный круг делится на 360° (градусов) иди на 2p радиан. Прямой угол……..
Научно-технический энциклопедический словарь
Угол Отражения — , в оптике — угол, под которым луч света отходит от отражающей поверхности. Угол измеряется между лучом и перпендикуляром — линией, расположенной под прямым углом к поверхности……..
Научно-технический энциклопедический словарь
Угол Падения — , в оптике — угол, под которым луч света падает на зеркало или другую поверхность. Угол измеряется между лучом и перпендикуляром — линией, расположенной под прямым углом……..
Научно-технический энциклопедический словарь
Угол Преломления — , в оптике — угол, под которым происходит преломление луча света от поверхности раздела между двумя разными прозрачными средами. Угол измеряется между преломляемым……..
Научно-технический энциклопедический словарь
Камерный Угол — см. Радужно-роговичный угол.
Большой медицинский словарь
Костовертебральный Угол — угол, образованный поясничным отделом позвоночника и нижним краем XII ребра.
Большой медицинский словарь
Внешний Угол — треугольника (многоугольника) — угол, образованный одной изего сторон и продолжением смежной стороны.
Большой энциклопедический словарь
Вписанный Угол — угол, образованный двумя хордами (СА и СВ), исходящими изодной точки (С) окружности.
Большой энциклопедический словарь
Лицевой Угол Общий — антропологический показатель: угол между глазнично-ушной горизонталью и линией, соединяющей верхненосовую точку и простион.
Большой медицинский словарь
Лобный Угол Брегматический — угол, образованный линиями глабелла-инион и глабелла-брегма; определяется по контурному изображению черепа; используется в антропометрии.
Большой медицинский словарь
Метровый Угол — см. Метроугол.
Большой медицинский словарь
Мозжечково-мостовой Угол — см. Мостомозжечковый угол.
Большой медицинский словарь
Мостомозжечковый Угол — (trigonum pontocerebellare, PNA; син. мостомозжечковый треугольник) участок головного мозга, ограниченный задним краем моста, мозжечком и оливой продолговатого мозга: место выхода VII и VIII черепных нервов.
Большой медицинский словарь
Двугранный Угол — фигура, образованная двумя полуплоскостями (гранямидвугранного угла), исходящими из одной прямой, называемой ребромдвугранного угла. измеряется линейным углом, т………
Большой энциклопедический словарь
Посмотреть еще слова :
slovariki.org
Математика: Геометрия. Угол
Углом называется фигура, которая состоит из точки (вершины угла) и двух лучей (стороны угла), исходящих из этой точки.Угол обозначается тремя точками «угол AOB»: берется одна любая точка на одном из лучей угла (точка А), вершина угла (точка О) и одна любая точка на другом луче угла (точка В). Можно обозначить это угол как «угол ВОА». Запись «угол АОВ» и «угол ВОА» обозначают один и тот же угол. В место слова угол употребляют знак ∠. Угол АОВ можно записать так:
1. ∠АОВ, ∠ВОА ;
2. ∠О – точка О вершина угла;
3. ∠(ab) – a и b лучи угла.
Угол разбивает плоскость на две части. Каждая часть называется плоским углом. Дополнительными углами называются плоские углы с общими сторонами.
Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. Угол СОD – развернутый угол с вершиной О.
Говорят, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. Луч с исходит из точки О, проходит между сторонами угла ab и пересекает отрезок АВ.
Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Углы измеряются в градусах.
Угол (ab) равен сумме углов (ac) и (cb). ∠(ab) = ∠(ac) + ∠(cb).
От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
mathematics-time.blogspot.com
Урок математики. Угол. Виды углов — Мои файлы — Каталог файлов
Урок математики во 2 классе
Тема урока:
Угол. Виды углов.
Вид урока: урок изучения и первичного закрепления новых знаний.
Цель: формирование общего понятия об угле, видах углов.
Задачи:
— учить различать прямой, острый и тупой угол;
— учить строить прямой угол;
— развивать познавательный интерес, умение сравнивать, обобщать;
— развивать внимание, воображение учащихся.
Оборудование:
компьютер;
мультимедиа проектор;
презентация Power Point.
Ход урока:
I. Организационный момент.
II. Устный счёт.
1) Игра «Гусеница-растеряша».
(Слайд 2)
— Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому правилу можно продолжить ряд чисел. (Дети называют правило: это чётные числа; каждое последующее число на 2 больше предыдущего).
— Какие же числа растеряла гусеница? (2,4,6,8,10,12,14,16) 2) Игра «Математический баскетбол».
(Слайд 3)
— Любой из вас забьёт гол, если правильно решит пример. (Дети по цепочке решают примеры). 30 + 7 25 + 5 32 – 12 66 + 4 80 – 7 28 – 10 45 – 45 53 + 7 59 – 9 90 + 9
3) Игра «Четвёртый лишний».
(Слайд 4)
— Посмотрите на фигуры в каждой рамке. Какая из них лишняя? Почему? (Учащиеся называют лишние фигуры, обосновывают свой выбор).
— Разделите все оставшиеся фигуры на две группы. Как это можно сделать? (Оставшиеся фигуры можно разделить на две группы: линии и многоугольники.)
— Назовите виды линий и многоугольников, известные вам. (Линии: прямая, ломаная, кривая. Многоугольники: квадрат, трапеция, прямоугольник, четырёхугольник, пятиугольник, шестиугольник, многоугольник).
III. Актуализация знаний. Повторение изученного.
4) Игра «Самый внимательный».
(Слайд 5)
— Посмотрите внимательно на рисунок, части всех предметов похожи на какие-то фигуры.
— Самый внимательный из вас найдёт на рисунке нужные фигуры. Подсказку ищите в верхнем правом углу рисунка. (Дети указкой показывают треугольники и квадраты).
(Слайд 6 -7)
IV. Работа над новым материалом.
1) — Тему урока вам подскажет кроссворд. Кроссворд «Геометрический».
(Слайд 8)
1) Часть прямой, у которой есть начало, но нет конца. (Луч).
2) Геометрическая фигура, не имеющая углов. (Круг).
3) Самая маленькая геометрическая фигура. (Точка).
4) Геометрическая фигура, имеющая форму вытянутого круга. (Овал).
— Тема нашего урока спряталась по вертикали. Найдите её. (Угол).
— На уроке мы познакомимся с разными видами углов, их свойствами, научимся их обозначать буквами.
2) Игра «Им угол имя подарил».
(Слайд 9)
— Угол важная фигура. Многим фигурам он помог дать имя. Назовите фигуры.
— Что общего в названиях фигур? Почему первая часть слов везде разная?
(Слайд 10)
— Углы окружают нас и в повседневной жизни. Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван.
— Обернитесь, рассмотрите наш класс. Приведите свои примеры, где можно найти углы вокруг нас.
3) Определение угла.
— На листе тетради отметьте точку и обозначьте её буквой А. Проведите из точки А два луча. На сколько частей лучи разделили плоскость? Меньшую часть заштрихуйте цветным карандашом. Какую фигуру вы заштриховали? (Угол). *** Динамическая пауза ***
(Слайд 11)
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
4) Обозначение углов.
(Слайд 11)
(Учитель комментирует флэш-ролик «Обозначение углов»).
— Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда?
— В таких случаях если называть разные углы одной буквой, то будет непонятно, о каком угле идёт речь. Что этого не произошло, на каждой стороне угла можно отметить по одной точке, поставить около неё букву и обозначить угол тремя буквами, при этом всегда в середине записывают букву, обозначающую вершину угла. Угол АОВ. Лучи АО и ОВ – стороны угла.
5) Практическая работа. Построение модели прямого угла.
(Слайд 12)
— Углы бывают разные, но сначала мы познакомимся с самым главным углом. Возьмите лист бумаги. Сложите лист пополам, а потом ещё раз пополам. Обведите линии сгиба карандашом. На сколько частей прямые линии разделили плоскость? (На четыре).
— Сколько углов получилось? (Четыре).
— Это особенные углы. Может быть, кто-то знает название этих углов? (Эти углы прямые).
— На пересечении линий сгиба поставьте точку. Обозначьте один прямой угол буквами. Заштрихуйте цветным карандашом его внутреннюю часть.
6) Определение и построение прямого угла.
(Слайд 13)
— Посмотрите на рисунок, я выделила на нём некоторые углы. Вы найдите и покажите только прямые углы. (На слайде отмечены для проверки некоторые из них).
(Слайд 14)
— Не всегда удобно определять прямой угол на глаз. Для этого используют линейку-угольник. Чтобы определить прямой угол или нет угла, нужно совместить вершину и одну сторону угла с вершиной и стороной прямого угла на линейке-угольнике.
— Какой же угол из трёх предложенных прямой? (Нижний; сиреневый).
— Почему вы так решили? (Вершина и стороны угла совпали с прямым углом на линейке-угольнике). Работа по учебнику. Задание Используя модель прямого угла, найди прямые углы и выпиши их номера. (Дети выполняют задание самостоятельно, затем один ученик называет свой вариант ответа, все проверяют работу).
— С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол, каждый сам назовёт его одной или тремя буквами. (Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется взаимопроверка в парах). *** Динамическая пауза ***
7) Виды углов.
(Слайд 14)
— На рисунке видно, что бывают и другие углы не прямые. Каким цветом выделен угол больше прямого? (Голубым).
— Меньше прямого? (Зелёным).
(Слайд 15)
— Каждый из углов имеет своё название. Острый угол – это угол, который меньше прямого. Тупой угол – это угол, который больше прямого.
— Рассмотрите рисунки. Какое правило работы важно помнить, при определении вида угла с помощью линейки-угольника? (Нужно совмещать вершину и одну сторону угла с вершиной и стороной прямого угла на линейке-угольнике). Работа в тетради.
— Начертите в тетради острый и тупой угол, подпишите их. Острый угол заштрихуйте зелёным карандашом, а тупой угол синим.
— Чем похожи и чем различаются эти углы? (Похожи: есть вершина, две стороны. Различаются: один больше, другой меньше прямого угла; разные названия).
— С помощью линейки-угольника проверьте работу друг друга в парах. Определить угол сначала «на глаз», потом проверить с помощью угольника. Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике. Если вторая сторона окажется внутри прямого угла, то угол острый, а если вторая сторона окажется снаружи – то тупой.
8) «Проверь себя!»
(Слайд 16)
Угол – это … (Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом).
(Слайд 17)
Стороны угла – это … а) отрезки; б) лучи; в) прямые. (Стороны угла – это лучи). На рисунке изображён угол … а) КОМ; б) ОМК; в) КМО. (Угол КОМ). Острый угол … прямого, а тупой угол … прямого. (Острый угол меньше прямого, а тупой угол больше прямого). (Слайд 18) Какого вида эти углы? (Тупой, острый, прямой).
V. Итог урока. Рефлексия.
-Кто доволен своей работой на уроке? Прикрепите на нашей полянке красный цветочек.
-Кто считает, что работал не во всю силу и хотел бы на следующий раз работать лучше – желтый цветочек.
-Кто не доволен своей работой – синий цветочек.
-Посмотрите, какая полянка у нас получилась Я вижу, что в основном дети старались и работали хорошо.
— Что вы узнали нового, интересного?
— Какое задание понравилось больше всего? Домашнее задание. Игра «Весёлый конструктор»
(Слайд 19)
— Придумайте и нарисуйте различные предметы, используя круги, овалы, точки, лучи и углы.
detkimal.ucoz.ru
