1 100 прямого угла 3 буквы: 1/100 прямого угла, 3 (три) буквы

alexxlab / / Разное

1/100 прямого угла, 3 (три) буквы

Вопрос с кроссворда

Ответ на вопрос «1/100 прямого угла «, 3 (три) буквы:
гон

Альтернативные вопросы в кроссвордах для слова гон

Охота с борзыми

внесист. единица плоского угла

Внесистемная метрическая единица плоского угла

Пора звериной любви

Преследование зайца егерями

Травля зверя на охоте

Зверский период брачных игр

Преследование зайца

Определение слова гон в словарях

Толковый словарь русского языка. Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
гона, м. (обл.). только ед. Действие по глаг. гнать. Большой был гон лошадям. Место охоты на нек-рых зверей (охот. ). Бобровый гон. Старинная мера расстояния.

Википедия Значение слова в словаре Википедия
Гон : Гон — поведение зверей в брачный период. Гон — устаревшая российская единица измерения расстояния. Гон — право на въезд в чужую или общую дачу для рубки леса или охоты. Гон — внесистемная единица измерения углов . Гон, Карлос — президент и генеральный …

Примеры употребления слова гон в литературе.

Таким образом, борзые предназначались для гона, доги — для резерва, а волкодавы — для генерального сражения.

По сведениям Министерства обороны России в Гоном Бадахшане было создано шесть перевалочных пунктов, принадлежащих автономно действующим группировкам, имевшим свои каналы переброски наркотических средств через границу и транспортировки их на рынки сбыта.

И верю, если только доезжачий С выжлятниками, лихо отдаря Борзятников, нежданною удачей Порадует, и гончих гон горячий Поднимет с лога волка-гнездаря,- То вы сумеете его повадку Перехитрить, живьем, сострунив, взять Иль в шерсть седеющую под лопатку Ему вонзить кинжал по рукоять.

Начинаются соболиные гоны, много оленя, лося, бортевой пчелы, глухаря, рябка, тетерева, медведей и волков.

Теперь Широколобый не любил ни одной из буйволиц в чегемском стаде, а когда приходило время гона, он, как и остальные буйволы, делал то, что положено природой, и тут же забывал буйволицу, с которой свел его случай.

Терпеливое облаивание сидящей на сосне белки, горячее гавканье при гоне зайца, неистово яростный, заливистый лай при виде крупного зверя, безудержно радостный лай со срывами в визг на высоких нотах при встрече с хозяином, громкое рычание на внезапно появившегося врага, предупреждающе звонкое тявканье, встречающее чужака возле хозяйского дома, ленивый брех — перекличка с деревенскими псами темной осенней ночью — все это были разные голоса Буяна, отражающие разное настроение.

Источник: библиотека Максима Мошкова

1/100 Прямого Угла 3 Буквы

Решение этого кроссворда состоит из 3 букв длиной и начинается с буквы Г

Ниже вы найдете правильный ответ на 1/100 прямого угла 3 буквы, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.

ответ на кроссворд и сканворд

Четверг, 9 Мая 2019 Г.

ГОН

предыдущий следующий

ты знаешь ответ ?

ответ:

связанные кроссворды

  1. Гон
    1. Брачный период зверя
    2. Время драться из-за самки
  2. Гон
    1. Длина участка пашни 3 буквы
    2. Особое состояние многих животных накануне спаривания 3 буквы
    3. Поведение животных в брачный период 3 буквы
    4. Поведение и состояние зверей в брачный период 3 буквы

Свойства треугольника — типы и формулы [Видео и практика]

7 минут чтения

В этой статье мы узнаем о простейшей форме многоугольника, треугольника . Все многоугольники можно разбить на треугольники, или другими словами, они образуются путем объединения двух или более треугольников. Таким образом, понимание основных свойств треугольника и его типов имеет важное значение.

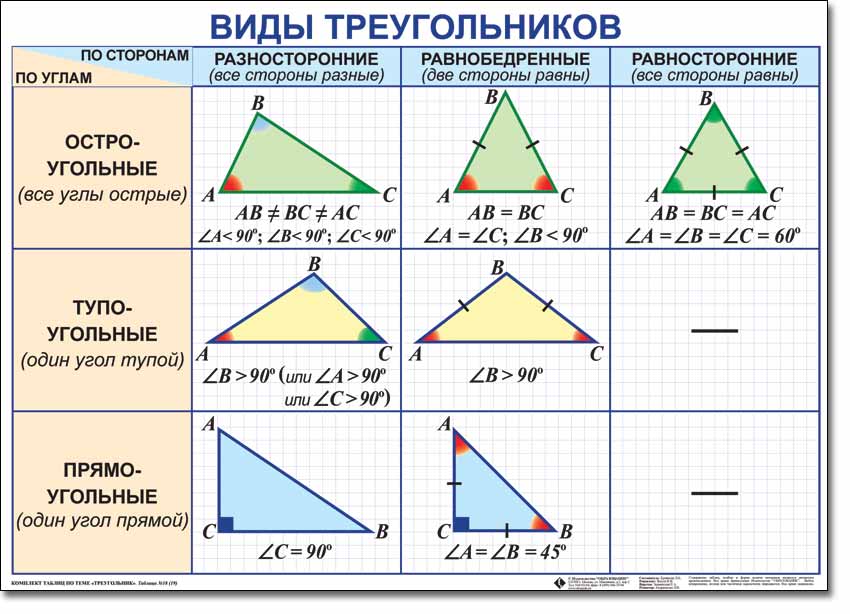
Всего существует шесть типов треугольников – равнобедренный, разносторонний, равносторонний, косой, остроугольный и прямоугольный. Исходя из классификации по внутренним углам, различают три типа – равнобедренные, равнобедренные и разносторонние. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, являются прямоугольным, остроугольным и косоугольным. Вот типы треугольников:

Based on the Angle Based on the Sides
Acute Angled Triangle Equilateral Triangle
Oblique angled Triangle Scalene Triangle
Right Angle Triangle Равнобедренный треугольник

Посмотрите это видео, чтобы узнать основные свойства треугольника:

Вот краткое изложение тем, которые мы рассмотрим в этой статье:

 [скрыть]

Что такое треугольник?

Как следует из названия, треугольник представляет собой многоугольник с тремя углами. Итак, когда замкнутая фигура имеет три угла?

Когда он состоит из трех сегментов линии, соединенных встык.

Таким образом, можно сказать, что треугольник — это многоугольник, у которого три стороны, три угла, три вершины, а сумма всех трех углов любого треугольника равна 180°.

Свойства треугольника

Свойства треугольника:

  1. Треугольник имеет три стороны, три угла и три вершины.
  2. Сумма всех внутренних углов треугольника всегда равна 180 °. Это называется свойством суммы углов треугольника.
  3. Сумма длин любых двух сторон треугольника больше длины третьей стороны.
  4. Сторона, лежащая напротив наибольшего угла треугольника, является наибольшей стороной.
  5. Любой внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.

Типы треугольников

Треугольники можно классифицировать двумя основными способами:

  • Классификация по внутренним углам (Прямой, Острый, Косой)
  • Классификация по длине сторон (Равносторонний, Равнобедренный, Разносторонний)

Рассмотрим подробно шесть типов треугольников:

  1. Остроугольный треугольник
  2. Прямоугольный треугольник
  3. Косоугольный треугольник
  4. Разноугольный треугольник
  5. Равнобедренный угловой треугольник
  6. Равнобедренный угловой треугольник

Остроугольный треугольник

Треугольник, у которого все три угла меньше 90 °, является остроугольным треугольником.

  • Итак, все углы остроугольного треугольника называются острыми углами

Ниже приведен пример остроугольного треугольника.

Прямоугольный треугольник

Треугольник, у которого один угол равен 92

Это известно как Теорема Пифагора

И наоборот, мы можем сказать, что если треугольник удовлетворяет условию Пифагора, то это прямоугольный треугольник.

Тупоугольный/косоугольный треугольник

Треугольник, у которого один угол больше 90 °, является тупоугольным треугольником.

Ниже приведен пример треугольника с тупым/косым углом.

Вопросы о треугольниках очень часто задают на GMAT. Ace GMAT Quant, подписавшись на нашу бесплатную пробную версию и получив доступ к более чем 400 вопросам. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2400 отзывами на GMATClub.

Сэкономьте более 60 часов подготовки к GMAT, составив четкий план обучения всего за 3 шага:

Разносторонний треугольник

Треугольник, у которого все три стороны разной длины — это разносторонний треугольник.

  • Поскольку все три стороны имеют разную длину, три угла также будут разными.

Ниже приведен пример разностороннего треугольника

Равнобедренный треугольник

Треугольник, у которого две стороны одинаковой длины, а третья сторона разной длины , является равнобедренным треугольником.

  • Углы, противоположные равным сторонам, имеют одинаковую меру.

Ниже приведен пример равнобедренного треугольника.

Равносторонний треугольник

Треугольник, у которого все три стороны имеют одинаковую длину , является равносторонним треугольником.

  • Поскольку все три стороны имеют одинаковую длину, все три угла также будут равны.
  • Каждый внутренний угол равностороннего треугольника = 60° треугольник,

    • Два угла равны 45°, а третий угол прямой.
    • Стороны этого треугольника будут в соотношении – 1:1:√2 соответственно.
    • Этот треугольник также называется равнобедренным прямоугольным треугольником , так как два угла равны.

    30-60-90 треугольник

    В этом треугольнике

    • Это прямоугольный треугольник, так как один угол = 90°
    • Углы этого треугольника находятся в соотношении – 1:2:3, и
    • Стороны , противоположные этим углам , будут в отношении – 1: √3: 2 соответственно
    • Это разносторонний прямоугольный треугольник , так как все три угла разные.

    Площадь треугольника

    • Площадь любого треугольника = ½ * основание * высота
    • Площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон Подытожим некоторые важные свойства треугольника.

      • Сумма всех внутренних углов любого треугольника равна 180 °
      • Сумма всех внешних углов любого треугольника равна 360 °
      • Внешний угол треугольника равен сумме двух его внутренних противоположных углов
      • Сумма длины любых двух сторон треугольника всегда больше длины третьей стороны
      • Аналогично, разность длин любых двух сторон треугольника всегда меньше длины третьей стороны
      • Сторона, противоположная наименьшему внутреннему углу, является самой короткой стороной, и наоборот.
      • Точно так же сторона, противоположная наибольшему внутреннему углу, является самой длинной стороной, и наоборот.
        • В случае прямоугольного треугольника эта сторона называется гипотенузой
      • Высота треугольника равна длине перпендикуляра, опущенного из вершины на противоположную ему сторону, и эта сторона равна считается базовым

      Если вам понравилась эта статья, вы также можете прочитать следующие статьи продвинутого уровня о треугольниках

      • Геометрические понятия и формулы GMAT для треугольников (часть 1)
      • Свойства треугольников: практические вопросы (часть 2)
      • Особые свойства треугольников (часть 3)

      Начинаете подготовку к GMAT? Вот пятиэтапный план подготовки к GMAT:

      Свойства треугольника: практический вопрос

      Вопрос: 1

      В равнобедренном треугольнике DEF, если внутренний угол ∠D = 100°, то какова величина ∠F?

      1. 20 °
      2. 40 °
      3. 60 °
      4. 80 °
      5. 100 °

      Раствор

      Шаг 1: дано

      • oref ASOSF IS AOSTEF IS ASOSF IS ASOSF IS AOSTEF IS AOSTEF IS AOSTEF IS AOSTEF IS AOSTEF IS AOSTEF ASOSC.

    Шаг 2: Найти

    • Значение ∠F

    Шаг 3: Подход и расчет

    • Мы знаем, что сумма всех внутренних углов треугольника = 180°
    • Отсюда следует, что ∠D + ∠E + ∠F = 180° = 80°
    • Поскольку треугольник ∆DEF равнобедренный; два его угла должны быть равны.
    • И единственная возможность ∠E = ∠F
    • Следовательно, 2∠F = 80°
    • Подразумевает, ∠F = 40°

    Отсюда правильный ответ Вариант Б.

  • 0004 В прямоугольном треугольнике ∆ABC, BC = 26 единиц и AB = 10 единиц. Если ВС — самая длинная сторона треугольника, то какова площадь ∆ABC?

    1. 120
    2. 130
    3. 240
    4. 260
    5. 312

    Решение

    Шаг 1: дано

    • ∆Abc is rought-ant-ant-ant-
      • ВС = 26 шт.
      • АВ = 10 шт.
      • до н.э. — самая длинная сторона треугольника
        • .

    Шаг 2: Нахождение

    • Площадь треугольника ∆ABC

    Шаг 3: Подход и вычисление hypotenuse

Thus, according to Pythagoras rule:

  • BC 2 = AB 2 + AC 2
  • 26 2 = 10 2 + AC 2
  • AC 2 = 676 – 100 = 576
  • Следовательно, AC = 24 единицы
  • Мы знаем, что площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон = ½ * AB * AC = ½ * 10 * 24 = 120 квадратных единиц

Следовательно, правильный ответ: Вариант А .

Вот еще несколько статей, которые вы можете прочитать:

  • Свойства четырехугольника
  • Свойства чисел: четные/нечетные, простые, HCF и LCM
  • Свойства круга
  • Свойства линий и углов

Если вы планируете сдавать GMAT, мы можем помочь вам составить индивидуальный план обучения и предоставить доступ к качественному онлайн-контенту для подготовки.   Напишите нам по адресу [email protected]. Мы являемся самой популярной компанией по подготовке к GMAT в gmatclub с более чем 2400 отзывами и единственной компанией по подготовке, которая набрала более 700+ баллов, чем любой другой партнер клуба GMAT .   Почему бы вам не воспользоваться бесплатной пробной версией и не судить самостоятельно?

Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.

FAQ – Свойства треугольника

Что такое треугольник и его свойства?

Треугольник – замкнутая фигура с тремя сторонами, тремя вершинами, тремя углами и суммой внутренних углов 180°

Какие бывают типы треугольников?

Треугольники можно классифицировать двумя способами: по внутренним углам и по длине сторон. По внутреннему углу треугольники бывают трех типов: остроугольные, прямоугольные и тупоугольные. В зависимости от длины сторон треугольники можно разделить на 3 категории: разносторонние, равнобедренные и равнобедренные.

Что такое разносторонний треугольник?

Треугольник, у которого все три стороны разной длины, является разносторонним треугольником.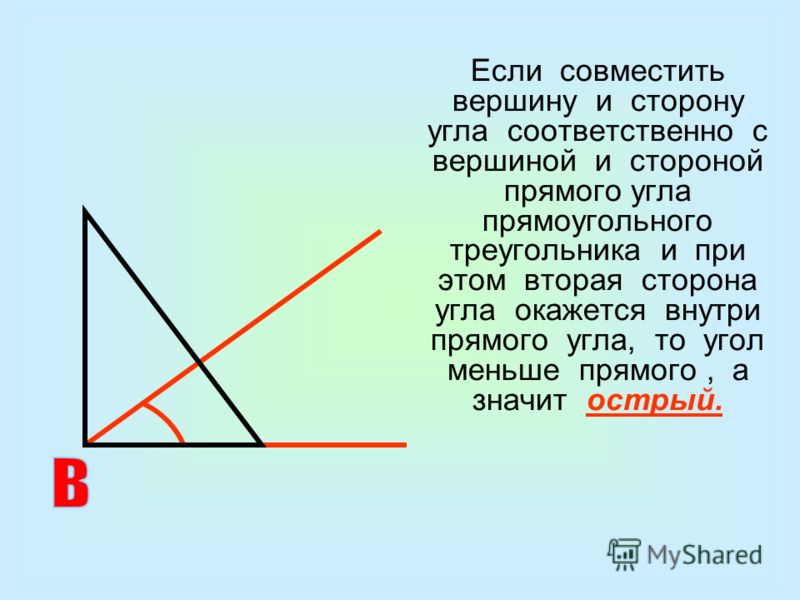

Что такое равнобедренный треугольник?

Треугольник, у которого две стороны одинаковой длины, а третья сторона разной длины, является равнобедренным треугольником.

Что такое равносторонний треугольник?

Треугольник, у которого все три стороны имеют одинаковую длину, является равносторонним треугольником.

 

Теорема Пифагора

Теорема Пифагора

На этом уроке мы узнаем, что такое теорема Пифагора и как ее использовать. найти недостающую сторону прямоугольного треугольника.

Тысячи лет назад греческая организация под названием пифагорейцы, возглавляемая человек по имени Пифагор, исследовал геометрию. Самое главное их достижение связано с открытием соотношения между длинами сторон правой треугольник. Это соотношение, называемое теоремой Пифагора, рассматривается самая важная формула в математике.

Сначала напомним некоторую терминологию. Напомним, что Прямоугольный треугольник – это треугольник, один из углов которого 90 градусов. Для прямоугольного треугольника сторона противоположный прямому углу называется гипотенуза. Эта сторона всегда будет самой длинной стороной справа. треугольник. Две другие (более короткие) стороны называются ноги.

Теорема Пифагора утверждает, что если сложить квадраты длин из двух катетов прямоугольного треугольника вы всегда получите квадрат длины гипотенузы.

 

Теорема Пифагора

Пусть и b — длины двух катетов прямоугольного треугольника и пусть c быть длиной гипотенузы. Затем

а 2 + б 2   =  в 2

 

 

Пример 1

Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .

 

Раствор

Сначала обратите внимание, что длины двух ног равны 4. и 3. Длина гипотенузы равна х . Используя буквы из Теорема Пифагора, имеем

        а   =  4

        б   =  3

        c   =  x

Теперь воспользуемся теоремой Пифагора

        а 2 + б 2   =  в 2

или

        4 2 + 3 2   =  x 2

Теперь возведите числа в квадрат

        16 + 9  =  90 574 x 90 575 2

Добавьте, чтобы получить

        25 =  х 2

Наконец, найдите положительное число, квадрат которого равен 25.

        х   =  5

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.

Упражнение 1

Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .

Ответить

Иногда в CAHSEE задача дает длины одной ноги и гипотенуза прямоугольного треугольника. Задача попросит вас найти третий нога. Вот пример.

Пример 2

Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .

 

Раствор

Сначала обратите внимание, что длина двух ног равна х и 6. Длина гипотенузы равна 10.  Использование буквы из теоремы Пифагора, имеем

        а   =  х

        б   =  6

        с   =  10

Теперь воспользуемся теоремой Пифагора

        а 2 + б 2   =  в 2

или

        х 2 + 6 2  =  10 2

Теперь возведите числа в квадрат

        х 2 + 36  =  100

Вычесть, чтобы получить

        x 2 = 100 — 36

=  64

Наконец, найдите положительное число, квадрат которого равен 64.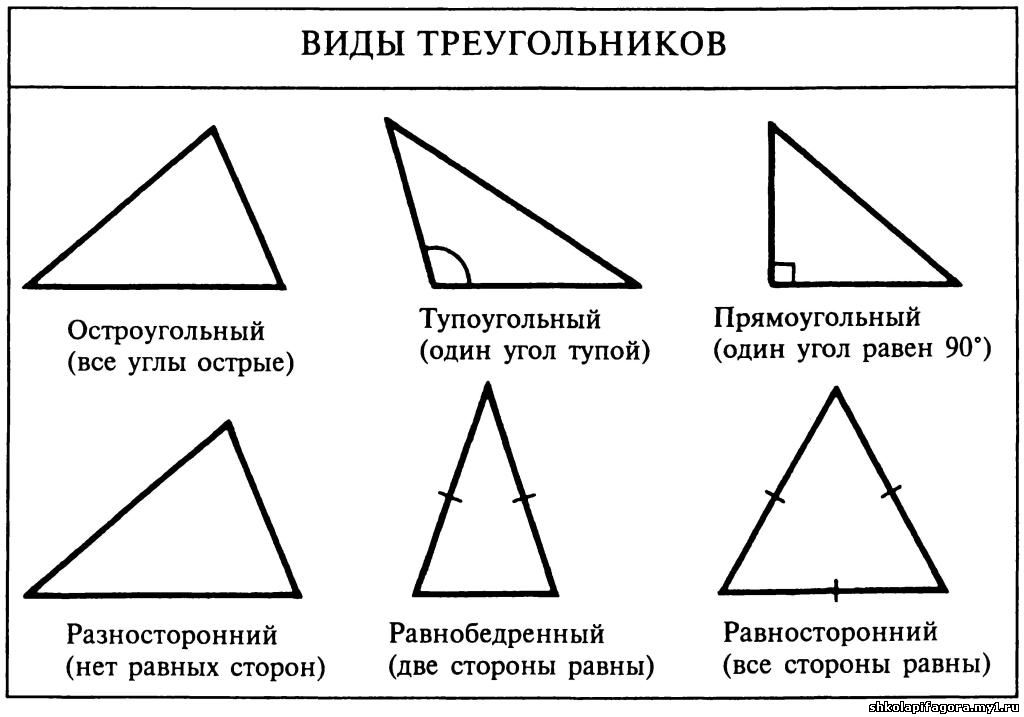

        х   =  8

 

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.

Упражнение 2

Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .

Ответить

Пример 3

Компания сотовой связи рекламирует такую ​​длину своего прямоугольного экрана. (между противоположными углами) составляет 5 дюймов. высота экрана 4 дюйма. Что ширина экрана?

Раствор

Схема экрана сотового телефона показана ниже

Верхняя часть образует прямоугольный треугольник с длиной двух сторон х и 4. Длина гипотенузы равна 5. Используя буквы из теоремы Пифагора, имеем

        а   =  x

        б   =  4

        с   =  5

Теперь воспользуемся теоремой Пифагора

        а 2 + б 2   =  в 2

или

        х 2 + 4 2   =  5 2

Теперь возведите числа в квадрат

        х 2 + 16  =  25

Вычесть, чтобы получить

        x 2 =  25–16

=  9

Наконец, найдите положительное число, квадрат которого равен 9.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *