Итоговое повторение по курсу «Алгебра и начала анализа» 10 класс
Похожие презентации:
Тригонометрические формулы. (10 класс)
Тригонометрия. Примеры на применение формул
Формулы понижения степени
Решение уравнения cosx = a. Понятие арккосинуса числа
Формулы преобразования суммы тригонометрических функций в произведение
Решение уравнения cosx = a. Понятие арккосинуса числа
Формулы сложения Синус, косинус, тангенс суммы и разности аргументов
Решение уравнения cosx = a. Понятие арккосинуса числа
Методы решения тригонометрических уравнений. (Урок-лекция)
Задание В7, открытого банка ЕГЭ по математике
1. Итоговое повторение по курсу «Алгебра и начала анализа» 10 класс
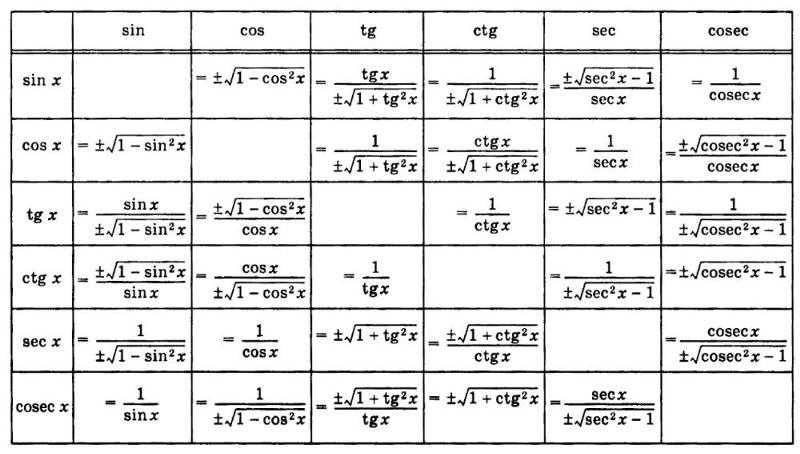
2. Основные тригонометрические формулы
sin 2 cos 2 1sin 2 1 cos 2
cos 2 1 sin 2
tg ctg 1
tg
1
ctg
1
ctg
tg
sin
cos
1 ctg 2
1
sin 2
cos
ctg
sin
1 tg 2
1
cos 2
tg
4.
 Упростите выраженияа)
Упростите выраженияа)sin 2
cos 1
б)
cos 2
sin 1
2
2
2
в)1 sin ctg sin
1 cos
1 sin
2 cos 2
1 sin 2
tg ctg
г)
2
1 cos
1
sin 2
д)(1 cos 2 )tg 2 1 tg 2
cos 2
5. Вычислите
sinа)
4
cos tg
3
2 sin sin
6
2
б) cos
6
cos
4
cos
3
2
4
4
cos
2
3
в)sin( ) cos( ) sin(
)
2
2
0
1
6. Формулы сложения
cos( ) cos cos sin sincos( ) cos cos sin sin
sin( ) sin cos cos sin
sin( ) sin cos cos sin
tg tg
tg ( )
1 tg tg
ctg ctg
ctg ( )
1 ctg ctg
tg tg
tg ( )
1 tg tg
ctg ctg
ctg ( )
1 ctg ctg
7. Вычислите
sin 105а)
б) cos105
3tg87 3tg 42
в)
1 tg87 tg 42
1
а) sin(
) sin
3
2
б)
sin( ) sin( ) cos( )
6 2
4
2 6
4
3
3
cos
2
cos sin
8.
 Формулы приведения
Формулы приведения9. Упростите выражение
а)tg ( )tg (
3
) sin( ) cos( )
2
2
б) ctg ( )ctg (
3
) tg (2 )ctg ( )
2
2
3
cos ( )
2
cos
( )
2
в)
2
tg ( 2 ) tg 2 ( 3 )
2
cos 2
1
cos 2
2
5
3 5
4
sin
tg
cos
г) ctg
3
4
6
3
д)
tg 225 cos 330 ctg120 sin 240
1
2
12
0,25
10. Формулы преобразования суммы тригонометрических функций в произведение
sin sin 2 sinsin sin 2 sin
2
cos
cos cos 2 cos
cos cos 2 sin
2
cos
2
2
2
cos
sin
2
2
2
sin( )
tg tg
cos cos
sin( )
tg tg
cos cos
sin( )
ctg ctg
sin sin
sin( )
ctg ctg
sin sin
cos( )
tg ctg
cos sin
cos( )
tg ctg
cos sin
12. Упростите выражение
sin 2 sin 6cos 2 cos 6
cos 2 cos 4
б)
cos 2 cos 4
а)
tg 4
tg3 tg
2 sin 40 cos 70
в)
cos 20
3
3 cos 5
г)
sin 35 cos 65
3
sin sin 3 sin 5 sin 7
д)
cos cos 3 cos 5 cos 7
tg 4
sin sin 2 sin 3
е)
cos cos 2 cos 3
tg 2
13.
 Формулы Преобразования произведения в сумму тригонометрических функций.1
Формулы Преобразования произведения в сумму тригонометрических функций.1sin sin cos( ) cos( )
2
1
cos cos cos( ) cos( )
2
1
sin cos sin( ) sin( )
2
14. Упростите выражение
а)2 sin sin 2 cos 3
б) sin 2 sin 15 cos 15
2
2
в)2 2 sin 83 sin 38
1
sin 31
2
1
6
2
sin
28
sin
17
sin
79
г)
2
д) 2 sin
sin cos 2
е) cos cos
4
4
cos
1
2
1
3
cos 2
1
cos 2
2
15. Формулы двойного угла
sin 2 2 sin coscos 2 cos sin 1 2 sin 2 cos 1
2
2tg
tg 2
2
1 tg
2
2
2
ctg 1
ctg 2
2ctg
2
16. Формулы тройного угла
sin 3 3 sin 4 sin 3cos 3 4 cos3 3 cos
3tg tg 3
tg3
2
1 3tg
ctg 3 3ctg
ctg3
2
3ctg 1
17. Формулы половинного угла
1 cossin
2
2
1 cos
cos
2
2
1 cos
sin
1 cos
tg
2
1 cos 1 cos
sin
1 cos
sin
1 cos
ctg
2
1 cos 1 cos
sin
18.
 Формулы понижения степени1 cos 2
Формулы понижения степени1 cos 2 cos
2
2
1 cos 2
sin
2
2
19. Упростите выражение
а)1 cos 4
ctg 2 2 3
1 cos 4
3
б)
1 cos 8
tg 2 4 2
1 cos 8
2
в)
1 cos 2 sin 2
tg
1 cos 2 sin 2 2
1
2
г)
tg ctg
д)
ctg tg sin 2
sin 2 2 sin
е)
cos 1
sin 2
2 cos 2
2 sin
20. Вычислите
а)cos
2
sin
2
2
2
8
8
cos
б) 2 sin
12
12
1
2
5
4 5
в) cos
sin
12
12
4
г) cos
д)
12
sin
sin
cos
12
12
12
3
2 cos 2 45 sin 2
3
3
2
3 3
8
1
21. Упростите выражение
1 cos 2sin 2
1 cos 2
б)
1 cos 2
tg
а)
в) ctg
г)
ctg 2
1 cos 2
sin 2
sin cos cos
2(1 cos )
4
4
2
1 cos 2
д)
tg
cos 2
1 cos
2
2
cos
2
sin 2
22.
 простейшие тригонометрические уравнения.sin x a
простейшие тригонометрические уравнения.sin x ax arcsin a 2 n, п Z
x arcsin a 2 n, n Z .
Частные
sin x 0
x n, n Z
случаи:
sin x 1
x
2
2 n, n Z
sin x 1
x
2
2 n, n Z
23. Решите уравнение
а) sin x1
2
x
2 n, n
6
x 7 2 n, n
6
2
б) sin x
2
x
2 n, n
4
x 3 2 n, n
4
в)
sin x 3
г)
sin x 1
нет решения
x
2
2 n, n
24. простейшие тригонометрические уравнения.
cos x ax arccos a 2 n, n Z
Частные
cos x 0
x
2
n, n Z
случаи:
cos x 1
cos x 1
x 2 n, n Z
x 2 n, n Z
25. Решите уравнение
2а) cos x
2
1
б) cos x
2
x 0
в) cos
г)
cos x 2
x
4
2 n, n
2
x
2 n, n
3
x
2
n, n
нет решения
26. простейшие тригонометрические уравнения.
tgx ax arctga n, n Z
Частные
tgx 1
tgx 0
x n, n Z
случаи:
x
4
n, n Z
tgx 1
x
4
n, n Z
27.
 Решите уравнениеа)
Решите уравнениеа)tgx 3
x
3
n, n
3
б)tgx
3
x
1
в) tg 4 x
3
x
x
г) tg 1
4 2
x 2 n, n
6
n, n
24
n
4
,n
28. простейшие тригонометрические уравнения.
ctgx ax arcctga n, n Z
Частные
ctgx 0
x
2
n, n Z
случаи:
ctgx 1
x
4
n, n Z
ctgx 1
3
x
n, n Z
4
29. Решите уравнение
а)ctgx 3
3
б) ctgx
3
x
в) ctg 1
2
г) ctg3 x
0
x
6
n, n
3
x
n, n
4
x
x
3
2 n, n
2
6
n
3
,n
30. Тригонометрические уравнения
Решитеуравнения преобразовав их к
квадратным
а)
3 cos x 10 cos x 3 0
2
б) 2 cos
в) 5 sin
2
2
x 2 sin x
x 4 sin x 4
2
г) tgx 3ctgx 4
д) ctg
2
x
3 1 ctgx 3 0
1
x arccos 2 n, n
3
x
2
2 n, n
x 2 n, n
x arccos 1 2 n, n
5
x
n, n
4
x arctg 3 n, n
x
n, n
4
x n, n
6
Решите
уравнения методом
разложения на множители
а) 3 cos x sin 2 x cos x
б)sin 2x 2 sin x
в) cos 7 x cos x 0
г) sin
д)
2
x sin 2 x 1
cos 3x 1 cos 6x
x
2
n, n
x n, n
x 2 n, n
4
n
x
,n
8 4
x n , n
6 3
x
n, n
2
x arctg 1 n, n
2
n
x
,n
6 3
x 2 n , n
9
3
Решите
уравнения, преобразовав их к
однородным
а) sin
x 3 cos x 0
x
б)3 sin x 4 sin x 0
2
x arctg
в) 6 sin x cos x 5 cos 2x
x
г) sin
2
x 14 sin x cos x 15 cos x
2
2
д)7 sin x 4 sin 2 x 7 cos x
2
3
n, n
4
n, n
3
1
5 n
arctg , n
2
3 2
x
n, n
4
x arctg15 n, n
x
1
7 n
arctg , n
2
4 2
33.
 Подготовка к егэ Задание:
Подготовка к егэ Задание:а)Решить уравнение
б)Указать корни уравнения,
удовлетворяющие условию.
x
x
x
x
;
1.а) 3 sin cos cos sin sin 2 x , б)
2
2
2
2
2
x
2.а) 4 cos
1 sin x sin 2 x,
2
3
,
2
3.а) 3 sin x cos
x
2
2
13
12 0 ,
4.а) 6tg x
2
5.а)
3
cos
2 x cos x 0,
2
б)
3
2 ; 2
;
2
б) 2
б)
3 7
2 ; 2
б)
2
;
2
6.а)
3sin 2x 13sin x 9 0 ,
б)
5
2 ; 2
cos
x
2
sin
2
x
1
4
cos
x
7.а)
,
2
б)
5
2 ; 2
8.а) 6 cos 2 x 13 sin
б)
5 9
2 ; 2
9.а) 6 sin
x 2 0,
x cos 2x 4 8sin x 3cos 2x , б) 2 ;0
3
x 0 ,
10.а) 2 cos x 1 sin
2
б) 2 ;5
English Русский Правила
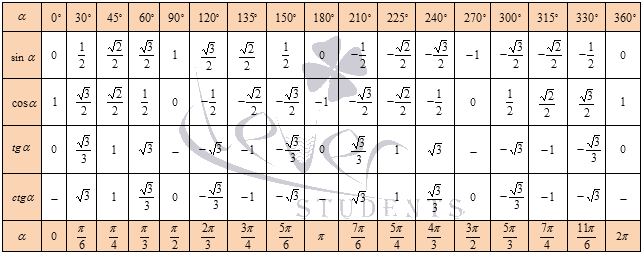
Внеклассный урок — Тригонометрические функции числового и углового аргументов
Тригонометрические функции числового и углового аргументовТригонометрические функции числового аргумента.
Тригонометрические функции числового аргумента t – это функции вида y = cos t,
y = sin t, y = tg t, y = ctg t.
С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.
Пояснения.
1) Возьмем формулу cos2 t + sin2 t = 1 и выведем с ее помощью новую формулу.
Для этого разделим обе части формулы на cos2 t (при t ≠ 0, то есть t ≠ π/2 + πk). Итак:
cos2 t sin2 t 1
——— + ——— = ———
cos2 t cos2 t cos2 t
Первое слагаемое равно 1. Мы знаем, что отношение синуса к конисусу – это тангенс, значит, второе слагаемое равно tg2 t. В результате мы получаем новую (и уже известную вам) формулу:
1 π |
2) Теперь разделим cos2 t + sin2 t = 1 на sin2 t (при t ≠ πk):
cos2 t sin2 t 1
——— + ——— = ———, где t ≠ πk + πk, k – целое число
sin2 t sin2 t sin2 t
Отношение косинуса к синусу – это котангенс. Значит:
1 |
Зная элементарные основы математики и выучив основные формулы тригонометрии, вы легко сможете самостоятельно выводить большинство остальных тригонометрических тождеств. И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:
И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:
sin2 t 1 sin2 t cos2 t + sin2 t 1
1 + tg2 t = 1 + ——— = — + ——— = —————— = ———
cos2 t 1 cos2 t cos2 t cos2 t
Точно так же легко можно найти сумму единицы и квадрата котангенса, как и многие другие тождества.
Тригонометрические функции углового аргумента.
В функциях у = cos t, у = sin t, у = tg t, у = ctg t переменная t может быть не только числовым аргументом. Ее можно считать и мерой угла – то есть угловым аргументом.
Ее можно считать и мерой угла – то есть угловым аргументом.
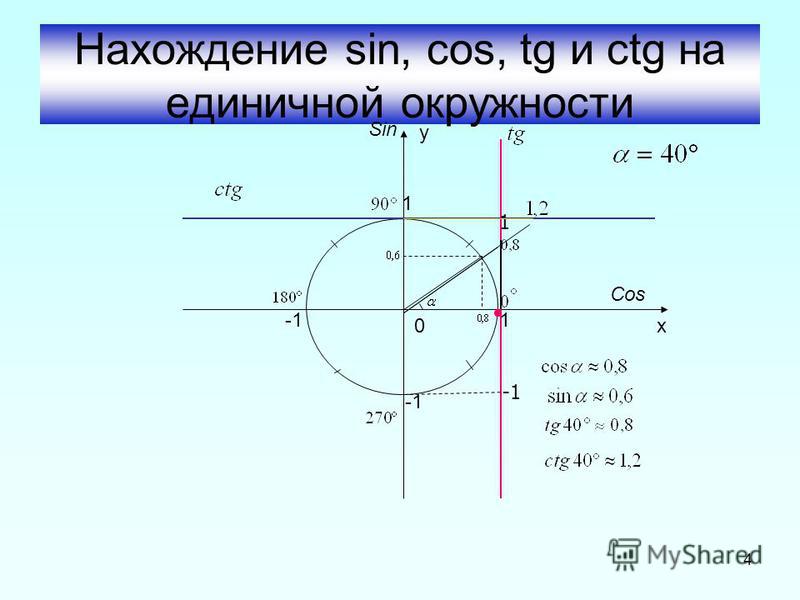
С помощью числовой окружности и системы координат можно легко найти синус, косинус, тангенс, котангенс любого угла. Для этого должны быть соблюдены два важных условия:
1) вершиной угла должен быть центр окружности, который одновременно является центром оси координат;
2) одной из сторон угла должен быть положительный луч оси x.
В этом случае ордината точки, в которой пересекаются окружность и вторая сторона угла, является синусом этого угла, а абсцисса этой точки – косинусом данного угла.
Пояснение. Нарисуем угол, одна сторона которого – положительный луч оси x, а вторая сторона выходит из начала оси координат (и из центра окружности) под углом 30º (см.рисунок). Тогда точка пересечения второй стороны с окружностью соответствует π/6. Нам известны ордината и абсцисса этой точки. Они же являются косинусом и синусом нашего угла:
√3 1
——; ——
2 2
А зная синус и косинус угла, вы уже легко сможете найти его тангенс и котангенс.
Таким образом, числовая окружность, расположенная в системе координат, является удобным способом найти синус, косинус, тангенс или котангенс угла.
Но есть более простой способ. Можно и не рисовать окружность и систему координат. Можно воспользоваться простыми и удобными формулами:
πα | πα |
Пример: найти синус и косинус угла, равного 60º.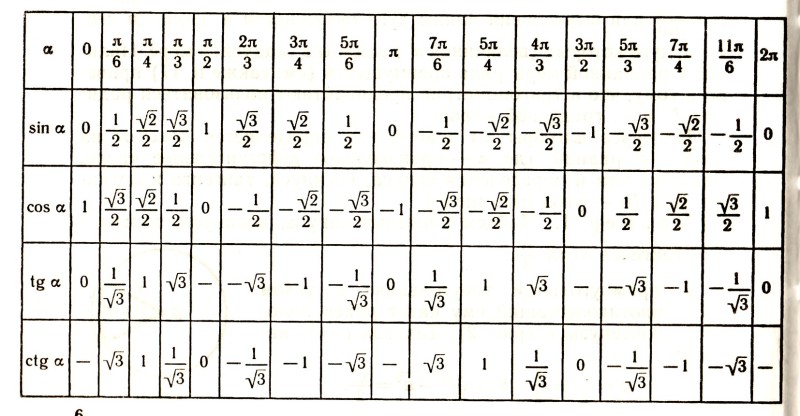
Решение:
π · 60 π √3
sin 60º = sin ——— = sin —— = ——
180 3 2
π 1
cos 60º = cos —— = —
3 2
Пояснение: мы выяснили, что синус и косинус угла 60º соответствуют значениям точки окружности π/3. Далее просто находим в таблице значения этой точки – и таким образом решаем наш пример. Таблица синусов и косинусов основных точек числовой окружности – в предыдущем разделе и на странице «Таблицы».
тригонометрическая функция в Zoran Skoda
Тригонометрическая функция по синусовому, косинусному, тангенсному и котангенсному, с ознакомлением койе су редом sin,cos,tg,ctgsin, cos, tg, ctg. У англоамериканской литературы za tangens i kotangens često koriste dulje oznake tan,cotantan, cotan. Аргумент тригонометрических функций, интерпретация као mjeru kuta, pa je njegova vrijednost ista ako dodamo ili oduzmemo 2π2\pi (u radijanima).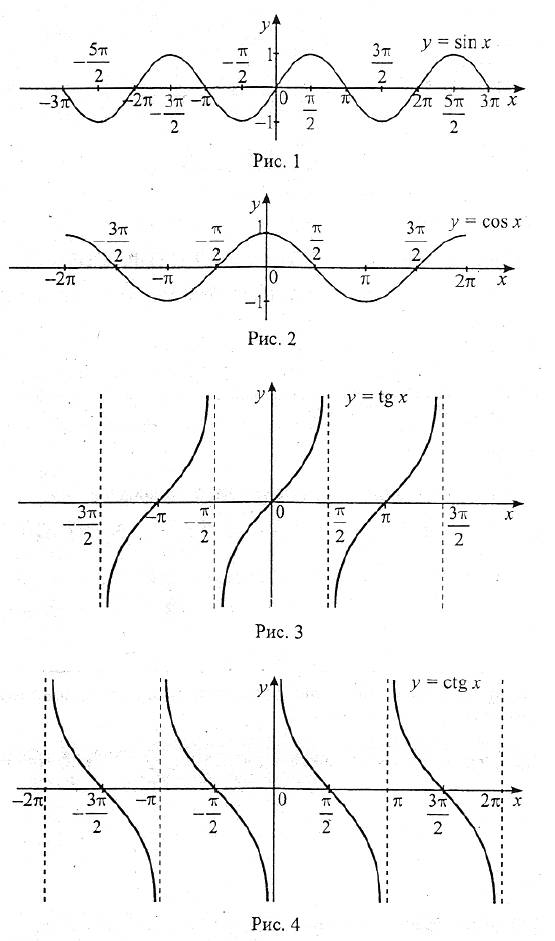
Trigonometrijske funkcije šiljastog kuta (tj. između 00 i π/2\pi/2) se mogu definirati tako da promatramo ma koji pravokutni trokut kojem je taj kut jedan od šiljastih kuteva, i definiramo
sinus kao omjer duljine kutu nasuprotne katete i duljine hipotenuze
kosinus kao omjer duljine kutu priležeće katete i duljine hipotenuze
tangens kao omjer duljine nasuprotne i duljine priležeće katete (эквивалентно, sinus kroz kosinus)
kotangens kao omjer duljine priležeće i duljine nasuprotne katete (эквивалентно, kosinus kroz sinus)
Избор правокутног трокута ний битан джер сви трокути с правым кутэм и единым заданием шилястим кутем имаю дакле 2 иста кута (па онда имаю иста и сва три кута, джер е зброй свих кутева у трокуту ту увийек испрут), teorema o sličnosti trokuta slični, slični trokuti imaju proporcionalne duljine stranica pa su omjeri duljina stranica jednaki. 9\круг). Формула Rezimiramo
cos(π/2−α)=sin(α),sin(π/2−α)=cos(α).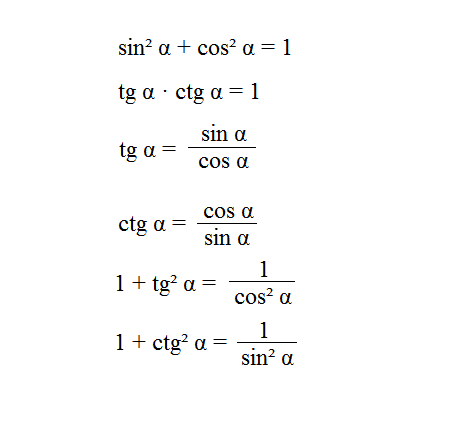 cos(\pi/2 — \alpha) = sin(\alpha),\,\,\,\,
sin(\pi/2 — \alpha) = cos(\alpha).
cos(\pi/2 — \alpha) = sin(\alpha),\,\,\,\,
sin(\pi/2 — \alpha) = cos(\alpha).
Definicije pamoću pravokutnog trokuta nemaju smisla za tupe kuteve, negativne kuteve etd. жер правокутных трокута с тупим или негативным кутевима нема. Zato se gornje definicije proširuju na sve brojeve tako da se promatra «trigonometrijska kružnica», (najčešće jedinična, tj. s polumjerom 11) kružnica sa središtem u ishodištu. Kut koji promatramo se nacrta tako da je prvi krak kuta pozitivna poluos osi xx. Promatramo bilo koju točku PP на другом kraku kuta – tu se obično uzima sjecište trigonometrijske kružnice i tog otherog kraka. Радиусвектор те точки je dakle вектор od ishodišta сделать тог sjecišta. Тада дефинирамо
sinus kao yy koordinata točke PP podijeljena s udaljenošću od ishodišta tj. duljinom radijus vektora rr (dakle samo yy ako je trigonometrijska kružnica jedinična kružnica)
косинус као х/рх/р
tangens kao y/xy/x, što je definirano samo kad je x≠0x\neq 0 (tj.
 \окр. 92} к je |x/r|≤1|x/r|\leq 1. Dakle coscos prima vrijednosti cos(x)cos(x) između −1-1 i 11, a isto vrijedi i za sinus, sin(x )∈[−1,1]sin(x)\in[-1,1]. Минимальная вредность −1-1 и максимальная вредность 11 Функция синуса и косинуса, которая достигается за счет полезности вредности: cos(0)=cos(±2π)=cos(2kπ)=1cos(0) = cos(\pm 2\pi) = cos(2k\pi) = 1 za sve k∈Zk\in\mathbf{Z} i cos(±π)=cos((2k+1)π)=−1cos(\pm\pi) = cos((2k +1)\pi) = -1, sin(2k+12π)=1sin(\frac{2k+1}{2}\pi) = 1, sin(2k−12π)=-1sin(\frac{2k- 1}{2}\pi) = -1 за sve k∈Zk\in\mathbf{Z} (проанализируйте тригонометрическую кружку!). Kako kosinus (za točke na jediničnoj kružnici) читается на оси xx, чтобы нам ориентировать kuta nije važna pa je cos(−x)=cos(x)cos(-x) = cos(x), tj. kosinus je parna funkcija. Slično Tome, Sinus čitamo na osi yy pa dok postavimo prvu o kuta na os xx orijentacija u kojem smjeru ćemo rotirati da dobijememo drumbi krak utiče na promenu predznaka koordinate na os -ozerusta aprinusta oosusta -u -u -ustrut -us Dakle sin(-x)=-sin(x)sin(-x) = -sin(x), другой действующий sinus je neparna funkcija realne varijable.
\окр. 92} к je |x/r|≤1|x/r|\leq 1. Dakle coscos prima vrijednosti cos(x)cos(x) između −1-1 i 11, a isto vrijedi i za sinus, sin(x )∈[−1,1]sin(x)\in[-1,1]. Минимальная вредность −1-1 и максимальная вредность 11 Функция синуса и косинуса, которая достигается за счет полезности вредности: cos(0)=cos(±2π)=cos(2kπ)=1cos(0) = cos(\pm 2\pi) = cos(2k\pi) = 1 za sve k∈Zk\in\mathbf{Z} i cos(±π)=cos((2k+1)π)=−1cos(\pm\pi) = cos((2k +1)\pi) = -1, sin(2k+12π)=1sin(\frac{2k+1}{2}\pi) = 1, sin(2k−12π)=-1sin(\frac{2k- 1}{2}\pi) = -1 за sve k∈Zk\in\mathbf{Z} (проанализируйте тригонометрическую кружку!). Kako kosinus (za točke na jediničnoj kružnici) читается на оси xx, чтобы нам ориентировать kuta nije važna pa je cos(−x)=cos(x)cos(-x) = cos(x), tj. kosinus je parna funkcija. Slično Tome, Sinus čitamo na osi yy pa dok postavimo prvu o kuta na os xx orijentacija u kojem smjeru ćemo rotirati da dobijememo drumbi krak utiče na promenu predznaka koordinate na os -ozerusta aprinusta oosusta -u -u -ustrut -us Dakle sin(-x)=-sin(x)sin(-x) = -sin(x), другой действующий sinus je neparna funkcija realne varijable.
Другие вишекратники от π/6\pi /6 uvijek imaju other krak koji zatvara π/6\pi/6 s nekom od poluosi (+x+x, −x-x, +y+y, −y-y) pa se lako stanovi koje se od vrijednosti ±1/2\pm 1/2, ±3/2\pm\sqrt{3}/2 pojave kao sinus или kosinus. Энергетический ядерный реактор. ako je α=47π/6\alpha = 47\pi/6 onda ga najprije svedemo na kut između 00 i 2π2\pi (или između −π-\pi i π\pi ako nam je tamo lakše određivati određivati trigonometrijske funkcije). Дакле, 47=2×6×4−147 = 2\times 6\times 4 — 1 или 47=2×6×3+1147 = 2\times 6 \times 3 + 11 pa je 47π/6=−π/ 6(mod2π)=11π/6(mod2π)47\pi/6 = -\pi/6\,\,(mod\,\,2\pi) = 11\pi/6\,\,(mod\, \,2\пи). Чтобы je kut u etvrtom kvadrantu, kojem other krak zatvara π/6\pi/6 s +x+x poluosi, dakle cos(−π/6)=3/2cos(-\pi/6) = \sqrt{3} /2, т.е. затвара кут π/3\pi/3 s −y-y pluosi, iz čega slijedi da je sin(−π/6)=−1/2sin(-\pi/6) = -1/2 (nacrtajte sliku da se uvjerite). Чтобы можно было добиться успеха и исправить парность функции косинуса и непарность функции синуса.
9\circ, kad tako uvrštavamo omjer pozitivne i negativne koordinate или negativne i pozitivne iste apsolutne vrijednosti pa je rezultat negativan i isti.
Тригонометрическая функция, не связанная с определением, не может быть инверзной функцией в дословном смысле. Međutim, možemo suziti (restringirati) trigonometrijske funkcije na interval duljine π\pi koji sadrži prvi kvadrant i još jedan susjedni kvadrant, tako da je suženje (restrikcija) trigonometrijske funkcije na ta dva kvadranta bijedna bijedna. Чтобы можно было направить на единства начин. Другим риечима, добивамо суда
sin|[−π/2,π/2],cos|[0,π],tg|(−π/2,π/2)ictg|(0,π) sin|_{[-\pi/2,\pi/2]},\,\,\,\, cos|_{[0,\pi]},\,\,\,\, tg|_{ (-\pi/2,\pi/2)}\,\,\,\, i\,\,\,\,ctg|_{(0,\pi)}
Inverz te bijekcije, inverz tog suženja, zovemo inverzna trigonometrijska funkcija ili arkus funkcija.
arcsin:[−1,1]→[−π/2,π/2]arccos:[−1,1]→[0,π]arctg:R→(−π/2,π/2)arcctg :R→(0,π)\массив{ arcsin : [-1,1]\to [-\pi/2,\pi/2] \\ arccos : [-1,1]\to [0,\pi] \\ arctg : \mathbf{R}\to (-\pi/2,\pi/2) \\ arcctg : \mathbf{R}\to (0,\pi) }
Функция sin|[−π/2,π/2]sin|_{[-\pi/2,\pi/2]}, tg|(−π/2,π/2)tg|_{( -\pi/2,\pi/2)}, pa dakle i njima inverzne funkcije arcsinarcsin, arctgarctg, su strogo rastuće funkcije (a
Функция arcsin(-1)=-π/2arcsin(-1) = -\pi/2. Функция arccosarcos по первому минимуму arccos(1)=0arccos(1) = 0 и максимуму arccos(-1)=πarccos(-1) = \pi. Infimum vrijednosti funkcija arctgarctg i arcctgarcctg je −1-1, a supremum je 11. Kako tangens ima vertikalne asimptote x=±π/2x = \pm\pi/2 (i općenitije, x=(2k+1)π/2x= (2k+1)\pi/2, k∈Zk\in\mathbf{Z}) к дуге с горизонтальной асимптотой y=±π/2y = \pm\pi/2 kojima se približava u ±∞\pm\infty . Kako kotangens ima vertikalne asimptote za x=kπx = k\pi, to arcctgarcctg ima dvije horizontalne asimptote, y=0y = 0 (kojoj se pližava kad x→∞x\to\infty) i y=πy = \pi (kojoj se približava kad x→−∞x\to-\infty).Латинский arcus označava luk. Naime mjera (u radijanima) šiljastog kuta sa središtem u ishodištu je jednaka jednaka duljini luka kojeg taj kut izrezuje na jediničnoj kružnici sa središtem u ishodištu. Inverzna funkcija gornjih suženja sinusa, kosinusa, tangensa ili kotangensa stoga vraća luk zadanoj vrijednosti geometrijskog omjera koji predstavlja vrijednost trigonometrijske funkcije kuta/luka.
 {-1}.
{-1}.Называнием тригонометрической функции зовемо и инвертирование за множество функций косинуса и синуса, на вс:
сек, сек(α)=1/cos(α)сек(\alpha) = 1/cos(\alpha) i
косекана, cosec(α)=1/sin(α)cosec(\alpha) = 1/sin(\alpha).
Te nazive se danas rijetko koristi, jer je zacijelo lakše pisati 1/cos(α)1/cos(\alpha) nego uvoditi novu oznaku sec(α)sec(\alpha). Тригонометрическими функциями зовемо и разне нжихове комбинации, нпр. функцию α↦cos(α)+3sin(α)\alpha\mapsto cos(\alpha)+ 3 sin(\alpha).
За неке первой тригонометрии у планиметрии, я нахожу за синусами и косинусами поучак, види странику трокут.
категория: задармат3
Последняя редакция: 1 октября 2021 г., 09:31:41. См. историю этой страницы для получения списка всех вкладов в нее.
Мэтуэй | Популярные проблемы
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найдите точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек (30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение соз(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 Преобразование градусов в радианы 45 33 Найдите точное значение 92 35 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт.  )/3
)/342 Найти точное значение sin((5pi)/3) 43 Найти точное значение грех((3pi)/4) 44 Найти точное значение желтовато-коричневый (пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение cos(30) 47 Найти точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение cos(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найти точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение желтовато-коричневый ((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 шт. 


 \окр. 92} к je |x/r|≤1|x/r|\leq 1. Dakle coscos prima vrijednosti cos(x)cos(x) između −1-1 i 11, a isto vrijedi i za sinus, sin(x )∈[−1,1]sin(x)\in[-1,1]. Минимальная вредность −1-1 и максимальная вредность 11 Функция синуса и косинуса, которая достигается за счет полезности вредности: cos(0)=cos(±2π)=cos(2kπ)=1cos(0) = cos(\pm 2\pi) = cos(2k\pi) = 1 za sve k∈Zk\in\mathbf{Z} i cos(±π)=cos((2k+1)π)=−1cos(\pm\pi) = cos((2k +1)\pi) = -1, sin(2k+12π)=1sin(\frac{2k+1}{2}\pi) = 1, sin(2k−12π)=-1sin(\frac{2k- 1}{2}\pi) = -1 за sve k∈Zk\in\mathbf{Z} (проанализируйте тригонометрическую кружку!). Kako kosinus (za točke na jediničnoj kružnici) читается на оси xx, чтобы нам ориентировать kuta nije važna pa je cos(−x)=cos(x)cos(-x) = cos(x), tj. kosinus je parna funkcija. Slično Tome, Sinus čitamo na osi yy pa dok postavimo prvu o kuta na os xx orijentacija u kojem smjeru ćemo rotirati da dobijememo drumbi krak utiče na promenu predznaka koordinate na os -ozerusta aprinusta oosusta -u -u -ustrut -us Dakle sin(-x)=-sin(x)sin(-x) = -sin(x), другой действующий sinus je neparna funkcija realne varijable.
\окр. 92} к je |x/r|≤1|x/r|\leq 1. Dakle coscos prima vrijednosti cos(x)cos(x) između −1-1 i 11, a isto vrijedi i za sinus, sin(x )∈[−1,1]sin(x)\in[-1,1]. Минимальная вредность −1-1 и максимальная вредность 11 Функция синуса и косинуса, которая достигается за счет полезности вредности: cos(0)=cos(±2π)=cos(2kπ)=1cos(0) = cos(\pm 2\pi) = cos(2k\pi) = 1 za sve k∈Zk\in\mathbf{Z} i cos(±π)=cos((2k+1)π)=−1cos(\pm\pi) = cos((2k +1)\pi) = -1, sin(2k+12π)=1sin(\frac{2k+1}{2}\pi) = 1, sin(2k−12π)=-1sin(\frac{2k- 1}{2}\pi) = -1 за sve k∈Zk\in\mathbf{Z} (проанализируйте тригонометрическую кружку!). Kako kosinus (za točke na jediničnoj kružnici) читается на оси xx, чтобы нам ориентировать kuta nije važna pa je cos(−x)=cos(x)cos(-x) = cos(x), tj. kosinus je parna funkcija. Slično Tome, Sinus čitamo na osi yy pa dok postavimo prvu o kuta na os xx orijentacija u kojem smjeru ćemo rotirati da dobijememo drumbi krak utiče na promenu predznaka koordinate na os -ozerusta aprinusta oosusta -u -u -ustrut -us Dakle sin(-x)=-sin(x)sin(-x) = -sin(x), другой действующий sinus je neparna funkcija realne varijable.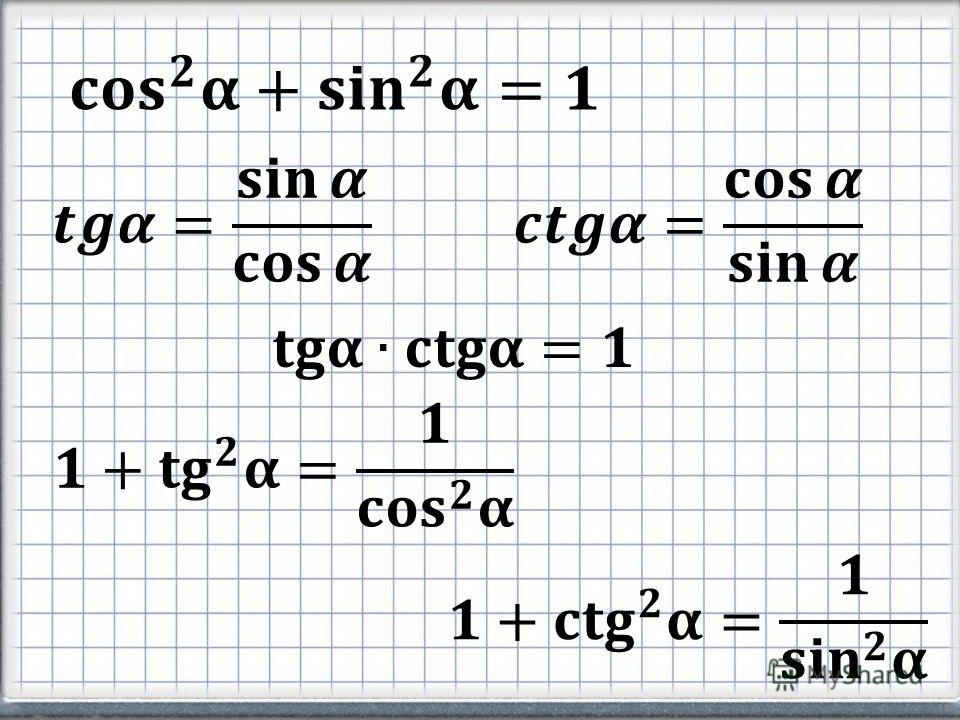

 {-1}.
{-1}. )/3
)/3