| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град.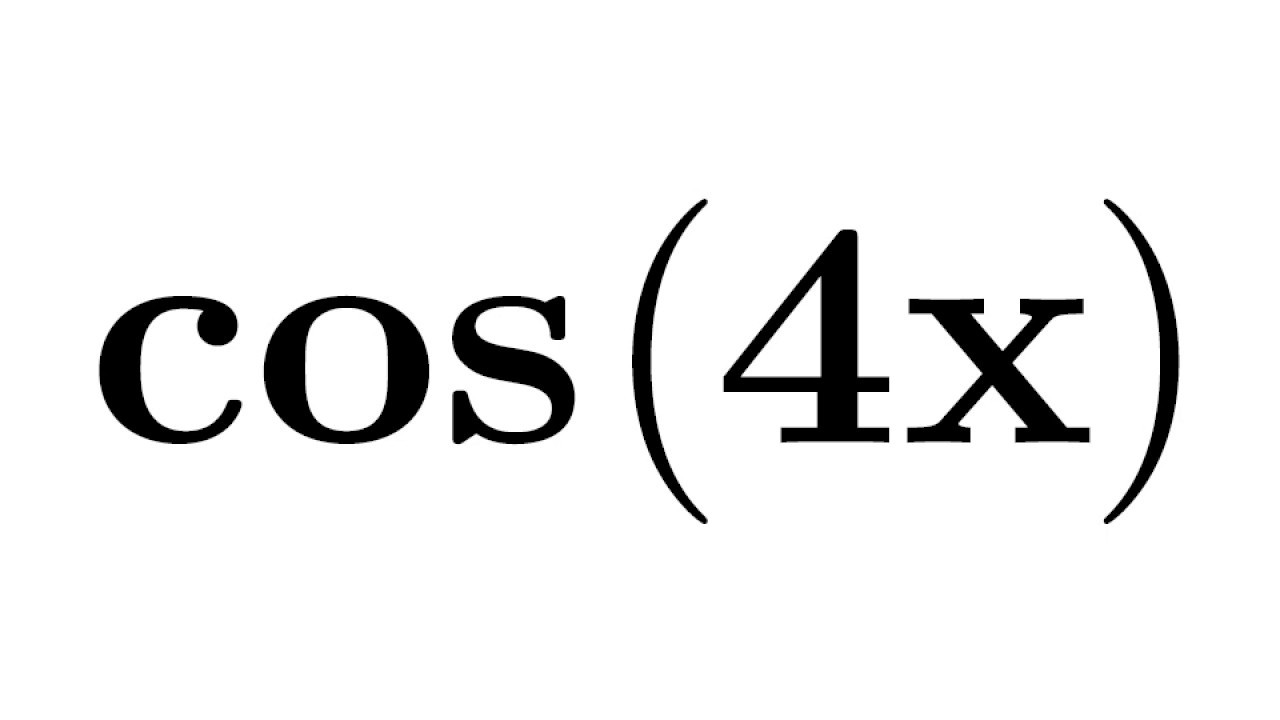 ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.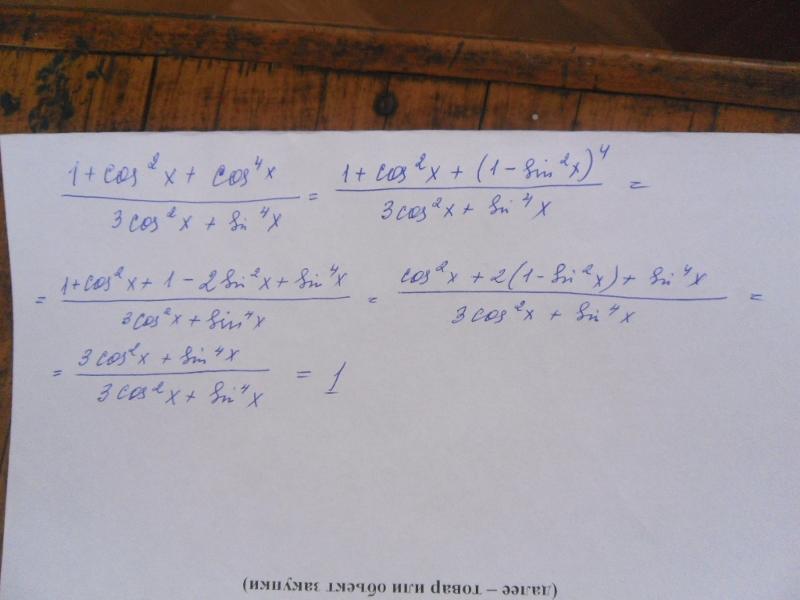 ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.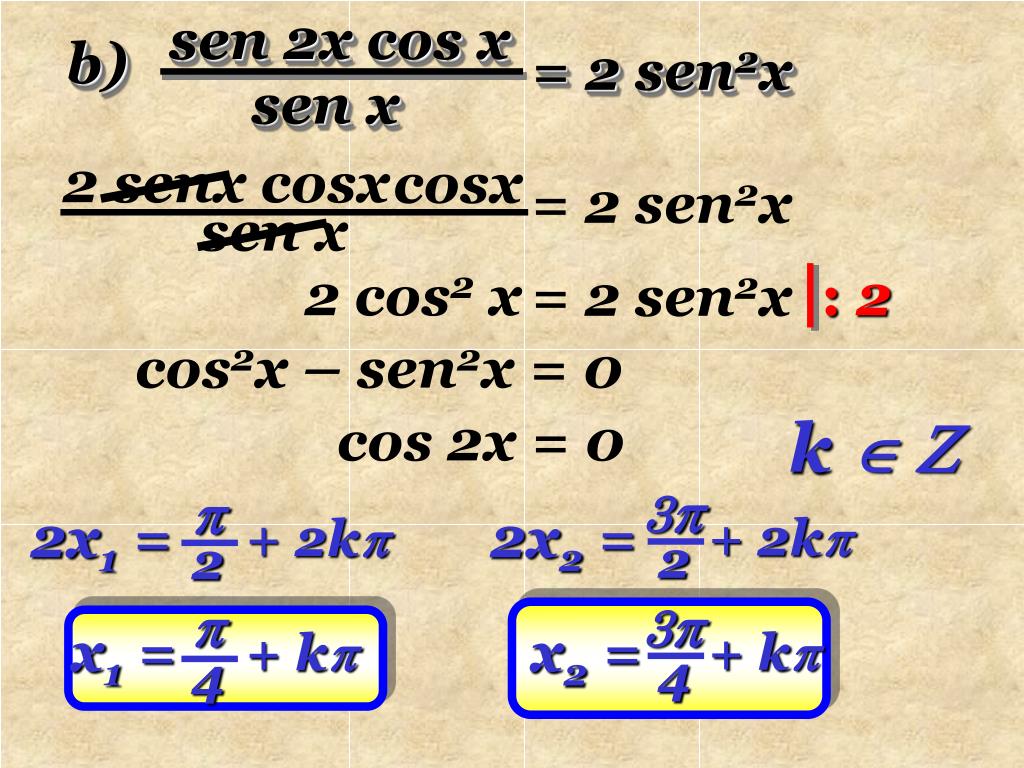 ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.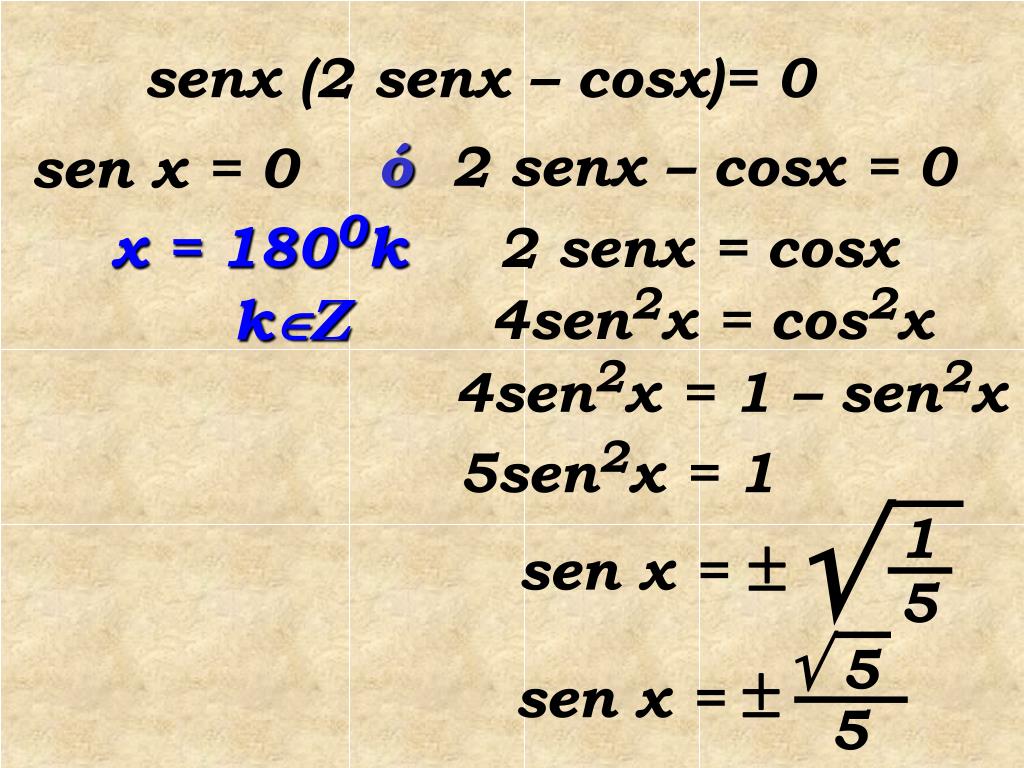 ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.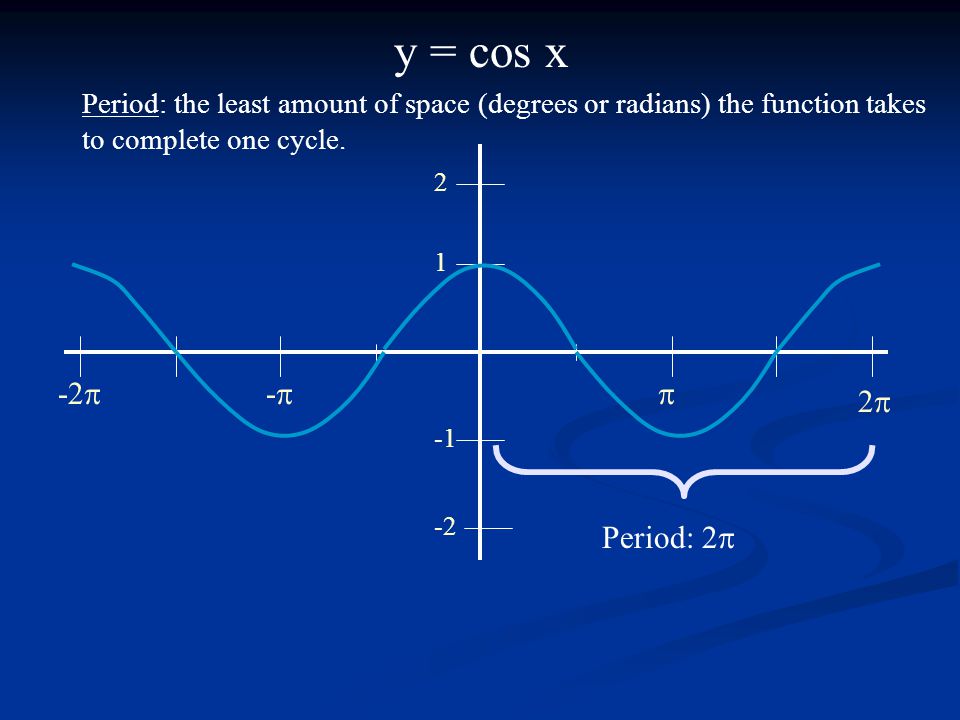 ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. 3 3 |
|
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) 2+n-72)=1/(n+9) |
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Найти cos x, если sin x cot x = 4
Ибрагим М.
Марк М. ответил • 28.05.20
Учитель математики — Высшая квалификация NCLB
(sin x / 1) (cos x / sin x) = 4
cos x = 4
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
Определение производной от 1 / cos (x) — стенограмма видео и урока
Решение
Хорошо, приступим.
Шаг 1. Первое, что мы хотим сделать, это определить функцию в числителе 1 / cos ( x ). Мы видим, что это 1, поэтому мы говорим f ( x ) = 1. Теперь мы хотим найти производную этой функции. Поскольку 1 является константой, мы знаем, что производная равна 0 из нашего списка фактов. Следовательно, f ‘( x ) = 0.
Шаг 2: Наш следующий шаг — определить функцию в знаменателе 1 / cos ( x ). Функция в знаменателе — cos ( x ), поэтому мы полагаем g ( x ) = cos ( x ).Теперь мы находим производную cos ( x ), которая, согласно нашему списку фактов, равна -sin ( x ). Таким образом, g ‘( x ) = -sin ( x ).
Шаг 3: Наш последний шаг — вставить f, g, f ‘и g’, которые мы нашли на шагах 1 и 2, в правило частного.
Наконец, мы упрощаем. Для этого мы будем использовать два наших факта: 1 / cos ( x ) = sec ( x )
и sin ( x ) / cos ( x ) = tan ( x ).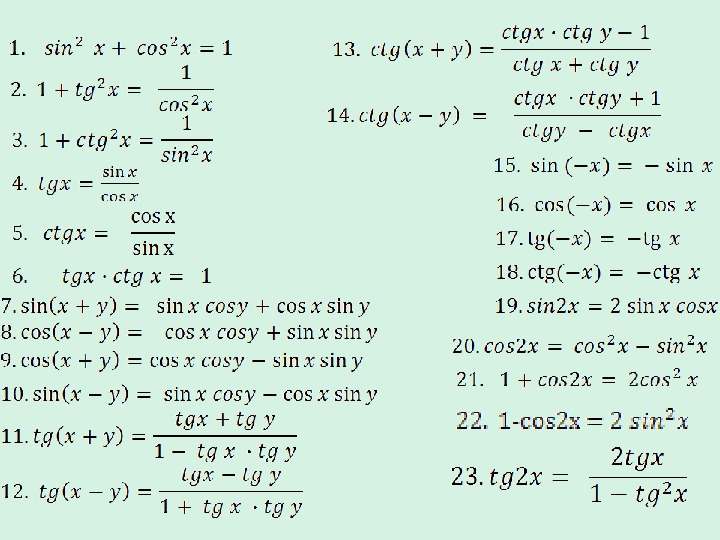 .
.
Мы видим, что производная 1 / cos ( x ) равна sec ( x ) tan ( x )
Тригонометрические функции
Как мы только что видели, будучи знакомыми с тригонометрическими тождествами и производными тригонометрические функции необходимы при поиске более сложных производных, включающих тригонометрические функции. Еще одна причина, по которой следует ознакомиться с этими двумя концепциями, заключается в том, что они действительно могут сократить объем работы, необходимой для поиска производной.В нашем примере мы можем найти производную 1 / cos ( x ) за два простых шага, если мы знаем некоторые простые тождества и производные тригонометрических функций.
Давайте посмотрим, как это возможно, но сначала давайте рассмотрим производные тригонометрических функций и некоторые тригонометрические тождества. Производные тригонометрических функций показаны на экране:
| Функция | Производная |
|---|---|
| sin ( x ) | cos ( x ) |
| cos ( x ) | -sin ( x ) |
| желто-коричневый ( x ) | сек 2 ( x ) |
| csc ( x ) | -csc ( x ) детская кроватка ( x ) |
| сек ( x ) | сек ( x ) желто-коричневый ( x ) |
| детская кроватка ( x ) | -csc 2 ( x ) |
Теперь давайте посмотрим на взаимные тригонометрические тождества.
Обратите внимание, что взаимные тригонометрические тождества дают, что sec ( x ) = 1 / cos ( x ), а производные тригонометрических функций дают, что производная sec ( x ) равна sec ( x ) желто-коричневый ( x ). В совокупности имеем следующее.
Этот способ нахождения производной намного проще, чем использование правила частного! Мы видим, что очень полезно знать различные тригонометрические тождества и производные тригонометрических функций.Это может сэкономить нам много времени.
В качестве еще одного быстрого примера предположим, что вам нужно найти производную sin ( x ) / cos ( x ). Вы можете найти производные числителя и знаменателя, а затем использовать правило частного, или вы можете узнать, что sin ( x ) / cos ( x ) = tan ( x ), а производная tan () x ) — это sec 2 ( x ).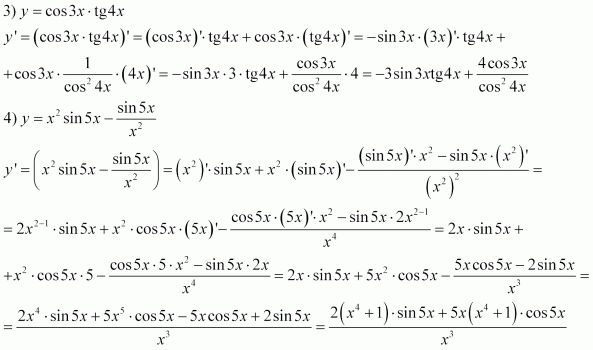 Последний процесс требует гораздо меньше работы!
Последний процесс требует гораздо меньше работы!
Резюме урока
Чтобы найти производную 1 / cos ( x ), мы можем использовать правило частного для производных, чтобы найти эту производную.Для этого мы выполняем следующие шаги:
1.) Определите функцию в числителе, f ( x ), и найдите ее производную, f ‘( x ).
2.) Найдите функцию в знаменателе, g ( x ), и найдите ее производную, g ‘( x ).
3.) Подключите эти функции к правилу частного и упростите.
Вы также можете использовать тождества и производные тригонометрических функций, чтобы найти производную 1 / cos ( x ). Однако взаимные идентичности — это лишь верхушка айсберга, когда дело доходит до тригонометрических идентичностей.Их гораздо больше, и запомнить их все было бы непросто. Таким образом, хорошо знать, что мы всегда можем найти производные, используя несколько методов, и хорошо знать все эти методы.
Производные тригонометрических функций
Три самых полезных производных в тригонометрии:
d dx sin (x) = cos (x)
d dx cos (x) = −sin (x)
d dx tan (x) = sec 2 (x)
Они просто упали с неба? Можем ли мы как-нибудь их доказать?Доказательство производной синуса
Нам нужно вернуться, прямо к первым принципам, к основной формуле для деривативов:
dy dx = lim Δx → 0 f (x + Δx) −f (x) Δx
Поп в грехе (x):
d dx sin (x) = lim Δx → 0 sin (x + Δx) −sin (x) Δx
Затем мы можем использовать это тригонометрическое тождество: sin (A + B) = sin (A) cos (B) + cos (A) sin (B), чтобы получить:
lim Δx → 0 sin (x) cos (Δx) + cos (x) sin (Δx) — sin (x) Δx
перегруппировать:
lim Δx → 0 sin (x) (cos (Δx) −1) + cos (x) sin (Δx) Δx
Разделен на два предела:
lim Δx → 0 sin (x) (cos (Δx) −1) Δx + lim Δx → 0 cos (x) sin (Δx) Δx 9090
И мы можем вывести sin (x) и cos (x) за пределы, потому что они являются функциями x, а не Δx
sin (x) lim Δx → 0 cos (Δx) −1 Δx + cos (x) lim Δx → 0 sin (Δx) Δx
Теперь все, что нам нужно сделать, это оценить эти два маленьких предела. Легко, правда? Ха!
Легко, правда? Ха!
Предел
sin (θ) θНачиная с
lim θ → 0 sin (θ) θ
с помощью некоторой геометрии:
Можем посмотреть на области:
Площадь треугольника AOB < Площадь сектора AOB < Площадь треугольника AOC
1 2 r 2 sin (θ) < 1 2 r 2 θ < 1 2 r 2 tan8 (θ) 90
Разделите все члены на 1 2 r 2 sin (θ)
1 < θ
Возьмем обратные:
1> sin (θ) θ > cos (θ)
Теперь, когда θ → 0, тогда cos (θ) → 1
Итак, sin (θ) θ лежит между 1 и чем-то, что стремится к 1
Итак, если θ → 0, тогда sin (θ) θ → 1 и так:
lim θ → 0 sin (θ) θ = 1
(Примечание: мы также должны доказать, что это верно с отрицательной стороны, как насчет того, чтобы вы попробовали с отрицательными значениями θ?)
Предел
cos (θ) −1 θИтак, теперь мы хотим узнать это:
lim θ → 0 cos (θ) −1 θ
Когда мы умножаем верх и низ на cos (θ) +1, получаем:
(cos (θ) −1) (cos (θ) +1) θ (cos (θ) +1) = cos 2 (θ) −1 θ (cos (θ) + 1)
Теперь мы используем это тригонометрическое тождество, основанное на теореме Пифагора:
cos 2 (x) + sin 2 (x) = 1
Преобразовано в эту форму:
cos 2 (x) — 1 = −sin 2 (x)
И предел, с которого мы начали, может стать:
lim θ → 0 −sin 2 (θ) θ (cos (θ) +1)
Это выглядит хуже! Но действительно лучше, потому что мы можем превратить это в два предела, умноженные вместе:
lim θ → 0 sin (θ) θ × lim θ → 0 −sin (θ) cos (θ) +1
Мы знаем первый предел (мы разработали его выше), а второй предел не требует особой работы, потому что при θ = 0 мы знаем напрямую, что −sin (0) cos (0) +1 = 0, поэтому:
lim θ → 0 sin (θ) θ × lim θ → 0 −sin (θ) cos (θ) +1 = 1 × 0 = 0
Собираем вместе
Так что мы снова пытались сделать? О, верно, мы действительно хотели это решить:
d dx sin (x) = sin (x) lim Δx → 0 cos (Δx) −1 Δx + cos (x) lim Δx → 0 sin (Δx) Δx
Теперь мы можем ввести значения, которые мы только что разработали, и получить:
d dx sin (x) = sin (x) × 0 + cos (x) × 1
И так (та да!):
d dx sin (x) = cos (x)
Производная косинуса
Теперь косинус!
d dx cos (x) = lim Δx → 0 cos (x + Δx) −cos (x) Δx
На этот раз мы будем использовать формулу угла cos (A + B) = cos (A) cos (B) — sin (A) sin (B) :
lim Δx → 0 cos (x) cos (Δx) — sin (x) sin (Δx) — cos (x) Δx
Изменить на:
lim Δx → 0 cos (x) (cos (Δx) −1) — sin (x) sin (Δx) Δx
Разделен на два предела:
lim Δx → 0 cos (x) (cos (Δx) −1) Δx — lim Δx → 0 sin (x) sin (Δx) Δx 9090
Мы можем вывести cos (x) и sin (x) за пределы, потому что они являются функциями от x, а не от Δx
cos (x) lim Δx → 0 cos (Δx) −1 Δx — sin (x) lim Δx → 0 sin (Δx) Δx
И используя наши знания сверху:
d dx cos (x) = cos (x) × 0 — sin (x) × 1
И так:
d dx cos (x) = −sin (x)
Производная тангенса
Чтобы найти производную tan (x), мы можем использовать это тождество:
tan (x) = sin (x) cos (x)
Итак, начнем с:
d dx tan (x) = d dx ( sin (x) cos (x) )
Теперь мы можем использовать правило частных производных:
( f г ) ’= gf’ — fg ’ г 2
И получаем:
d dx tan (x) = cos (x) × cos (x) — sin (x) × −sin (x) cos 2 (x)
d dx tan (x) = cos 2 (x) + sin 2 (x) cos 2 (x)
Тогда используйте этот идентификатор:
cos 2 (x) + sin 2 (x) = 1
Чтобы получить
d dx tan (x) = 1 cos 2 (x)
Готово!
Но большинству людей нравится использовать тот факт, что cos = 1 сек , чтобы получить:
d dx tan (x) = sec 2 (x)
Примечание: мы также можем сделать это:
d dx tan (x) = cos 2 (x) + sin 2 (x) cos 2 (x)
d dx tan (x) = 1 + sin 2 (x) cos 2 (x) = 1 + tan 2 (x)
(И, да, 1 + загар 2 (x) = sec 2 (x) в любом случае, см. Magic Hexagon)
Magic Hexagon)
Тейлор серии
Просто забавное примечание, мы можем использовать расширения серии Тейлора и дифференцировать термин за термином.
Пример: sin (x) и cos (x)
Расширение ряда Тейлора для sin (x) равно
sin (x) = x — x 3 3! + x 5 5! — …
дифференцировать по срокам:
d dx sin (x) = 1 — x 2 2! + x 4 4! — …
Что идеально соответствует разложению в ряд Тейлора для cos (x)
cos (x) = 1 — x 2 2! + x 4 4! -…
Давайте также дифференцируем , что по срокам:
d dx cos (x) = 0 — x + x 3 3! — . ..
..
Что является отрицательным из разложения в ряд Тейлора для sin (x), с которого мы начали!
Но это «круговое рассуждение», потому что в исходном разложении ряда Тейлора уже используются правила «производная sin (x) равна cos (x)» и «производная cos (x) равна −sin (x)» .
Тригонометрические идентичности
| Тригонометрические идентичности |
| (Математика | Триггер | Личности) |
| sin (theta) = кондиционер | csc (тета) = 1 / sin (тета) = c / a |
| cos (тета) = b / c | сек (тета) = 1 / cos (тета) = c / b |
| тангенс (тета) = грех (тета) / соз (тета) = а / б | кроватка (тета) = 1 / загар (тета) = b / a |
sin (-x) = -sin (x)
csc (-x) = -csc (x)
cos (-x) = cos (x)
sec (-x) = sec (x)
tan (-x ) = -tan (x)
детская кроватка (-x) = -cot (x)
| sin ^ 2 (x) + cos ^ 2 (x) = 1 | загар ^ 2 (x) + 1 = сек ^ 2 (x) | детская кроватка ^ 2 (x) + 1 = csc ^ 2 (x) | |
| sin (x y) = sin x cos y cos х грех у | |||
| cos (x y) = cos x уютный грех х грех у | |||
загар (x y) = (загар х загар у) / (1 загар х загар у)
sin (2x) = 2 sin x cos x
cos (2x) = cos ^ 2 (x) — sin ^ 2 (x) = 2 cos ^ 2 (x) — 1 = 1-2 грех ^ 2 (x)
загар (2x) = 2 загар (x) / (1 — загар ^ 2 (x))
sin ^ 2 (x) = 1/2 — 1/2 cos (2x)
cos ^ 2 (x) = 1/2 + 1/2 cos (2x)
sin x — грех y = 2 sin ((x — y) / 2) cos ((x + y) / 2)
cos x — cos y = -2 sin ((x — y) / 2) sin ((x + y) / 2)
| угол | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| грех ^ 2 (а) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| cos ^ 2 (а) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| загар ^ 2 (а) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
Данный треугольник abc с углами A, B, C; a противоположно A, b напротив B, c напротив C:
a / sin (A) = b / sin (B) = c / sin (C) (Закон Синусов)
| (Закон косинусов) |
(a — b) / (a + b) = tan [(A-B) / 2] / tan [(A + B) / 2] (Закон касательных)
Пример 5 — Выражение tan-1 cosx / (1 — sinx)
Последнее обновление: 12 мая 2021 г. , автор: Teachoo
, автор: Teachoo
Выписка
Пример 5
Выразите tan − 1 cosx / (1 — sinx), — π / 2
Sin nx cos nx
Roznásobením levé strany a porovnáním reálných a imaginárních částí je možno odvodit vztahy pro vyjádření cos (nx) a sin (nx) pomocí cos (x). Moivreovu větu lze také použít k vyjádření n-té odmocniny jedničky, tedy k nalezení takového komplexního čísla z, pro které platí z n = 1.
こ の ペ ー ジ 「物理 数学 II フ ー リ エ 解析」 は, ま だ 書 き か け で す. 加 筆 · 訂正 な ど, 協力 い た だ け る 皆 様 の 編 集 を 心 か ら お …
Roznásobením lève strany porovnáním reálných imaginárních Casti JE možno odvodit vztahy про vyjádření cos (nx) a sin (nx) pomocí cos (x) a sin (x). Moivreovu větu lze také použít k vyjádření n-té odmocniny jedničky, tedy k nalezení takového komplexního čísla z, pro které platí zn = 1.
. функции sin (nx) и cos (nx), где n принимает значения одного или нескольких натуральных чисел.2) cos (nx) + (x + π) * (1 / n) sin (nx) + c │x 從 –π ~ 0
| sin (nx | inférieur ou égal à n | sin x |: упражнение де mathématiques de niveau terminale — Forum de mathématiques
wir sollen das Integral von 0 bis 2pi bestimmen von sin (nx) cos (mx) Bitte um Hilfe 🙂
Тогда каждый интеграл будет иметь среднее значение нуля, если границы интегрирования являются целым числом периодов, если только этот интеграл не является cos (nx — nx) = cos (0) = 1 — термин, который вы получаете, если бы у вас были два одинаковых синуса или косинуса.И период cos (x) совпадает с (некоторым количеством) периодов nx и mx, поэтому эти члены будут равны нулю.
傅里叶 级数 课程 及 习题 讲解 ..pdf, 第 1 5 章 傅 里 叶 级 数 § 傅里叶 级数 一 基本 内容 一 、 nf (x) axn 在 幂级数 讨论中 n 1 , 可 视为 f (x) 经 函数 系 2 n 线性 表出 而得. 不妨 称 {1, x, x, L, x, L} 为 基 , 则 不同 的 基 就有 不同 的 级数. 今 用 三角函数 系 作为 基 , 就 得到 傅里叶 级数. 1 三角函数 系 …
Поля наклона вычисления AP Имя Применение интегрирования День 6 1. Покажите, что + e является решением дифференциального уравнения y ‘+ 2y = 2ex. aeg 2. Убедитесь, что y = —tcost — t является решением проблемы начального значения t——
Покажите, что + e является решением дифференциального уравнения y ‘+ 2y = 2ex. aeg 2. Убедитесь, что y = —tcost — t является решением проблемы начального значения t——
нет хорошего (простого) способа упростить эти sin (Nx), чтобы получить что-то, что является функцией от просто х.Я могу построить и найти всю эту информацию с помощью MATLAB, но я хотел бы знать, возможно ли найти аналитическую форму.
‘sin 2 2 cos 2 nx v nx vn SSS 60 Случай 1: 2 111 000 22 sin cos cos 2 2 2 nnxnxx xdx dx nn SSS SS ª º § · …
数学 に お い て 関 数 (ち ょ っこ う か ん す う れ つ 、 英: ортогональные функции) は 互 い に 直交 列 の 事 で る
cos (nx) = sin (N +1) x дополнительно ¨ N ∈ N. 2x) = 2cosx sinx; dies ist die Behauptung f¨ur N = 1.
(sin) cos (cos) sin (tan) sec dd cx nxnn dx dx dd xxxx dx dx d xx dx (cot) csc 2 (sec) sec tan (csc) csc cot d dx dd xxxxxx dx dx Вопрос: что такое Fx ‘(), если F xx () (1) 22? Ответ: () (1) (2 1) 4 42 2 4 2 3 d d d F x x x x x x
(Opera postuma, т.
