10 класс квадратные уравнения: «Решение уравнений» (10 класс, повторение)

Содержание

Кейс «Квадратные уравнения с параметром» для учащихся 10 класса

Кейс «Квадратные уравнения в гостях у параметра»

учителя математики МАОУ «Гимназия №87»

Ленинского района города Саратова

Заико Ильи Валерьевича

с 4 февраля по 27 марта 2020 года

Кейс «Квадратные уравнения в гостях у параметра»

Уравнения для меня важнее потому, что

политика – для настоящего,

а уравнения – для вечности.

Альберт Эйнштейн

Что такое параметр?

В повседневной жизни мы очень часто сталкиваемся с понятием параметра: параметры загрузки Windows 10, параметры бытовых приборов, параметры автомобиля. Рассмотрение параметров — это всегда выбор. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и многое другое. Перед выбором мы стоим и в различных жизненных ситуациях. Вспомним сказку: В чистом поле стоит столб, а на столбу написаны слова: «Кто поедет от столба сего прямо, тот будет голоден и холоден; кто поедет в правую сторону, тот будет здрав и жив, а конь его будет мертв; а кто поедет в левую сторону, тот сам будет убит, а конь его жив и здрав останется!» Иван-царевич прочел эту надпись и поехал в правую сторону, держа на уме: хоть конь его и убит будет, зато сам жив останется и со временем сможет достать себе другого коня.

(“Иван-царевич и серый волк” Русская народная сказка). Здесь от выбора зависит жизнь Ивана-царевича.

Но это в сказке, а что же собой представляет параметр в математике? Какую роль он играет при решении уравнений? Какими методами решаются уравнения с параметрами?

Что такое параметр в математике?

Параметр (от греческого – отмеривающий) в математике – величина, числовые значения которой позволяют выделить определённый элемент из множества элементов того же рода. (Большой энциклопедический словарь)

Так, например, в декартовых прямоугольных координатах уравнением определяется множество всех окружностей радиуса 1 на плоскости xOy; полагая, например, ,

выделяют из этого множества вполне определённую окружность единичного радиуса с центром в точке , — и, следовательно, являются параметрами окружности в рассматриваемом множестве элементов того же рода.

История возникновения уравнений с параметром

Задачи на уравнения с параметром встречались уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другим индийским ученым, Брахмагупта в VII веке было изложено общее правило решения квадратных уравнений, приведенных к единой канонической форме: . В уравнении коэффициенты, кроме параметра a, могут быть и отрицательными. В теоретической части книги «Китаб аль-джебр ва-ль-мукабала» Аль-Хорезми дает классификацию линейных и квадратных уравнений с параметрами. Автор выделяет 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е.

2) «Квадраты равны числу», т. е. .

3) «Корни равны числу», т. е. .

4) «Квадраты и числа равны корням», т. е. .

5) «Квадраты и корни равны числу», т. е. .

6) «Корни и числа равны квадратам», т. е. .

Формулы решения квадратных уравнений по Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Вывод формулы решения квадратного уравнения с параметром в общем виде имеется у Виета, однако он признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принял современный вид.

1) Определение. Квадратным уравнением называется уравнение вида:

где коэффициенты a, b, c – любые действительные числа, причем .

2) Решение квадратного уравнения по формулам.

3) Теорема обратная теореме Виета. Если числа таковы, что их произведение равно , а сумма равна , то эти числа являются корнями квадратного уравнения .

4) Графиком квадратичной функции является парабола с вершиной в точке , ветви которой направлены вверх, если или вниз, если . Абсциссы, обозначим их , общих точек параболы и оси Ox являются нулями квадратичной функции.

5) Поскольку корнем квадратного уравнения можно считать значение переменной x, при котором соответствующий квадратный трёхчлен принимает значение равное нулю, то каждый корень такого уравнения является нулём квадратичной функции и наоборот.

Поэтому, количество корней квадратного уравнения равно количеству нулей соответствующей квадратичной функции, а значит и количеству общих точек параболы и оси абсцисс.

Таблица количества общих точек параболы и оси абсцисс в зависимости от дискриминанта D соответствующего квадратного уравнения .

Таблица 1^*.

* здесь — абсциссы общих точек параболы и оси Ox, — абсцисса вершины параболы.

6) Теорема 1 (о равносильной замене неравенства). Неравенство равносильно совокупности систем и

7) Теорема 2 (о равносильной замене неравенства). Неравенство равносильно совокупности систем и

Исследовать расположение корней квадратного уравнения относительно точки в зависимости от значений его параметров-коэффициентов, решая подходящие для этого задания.

Задание 1. Найдём все значения параметра a, при которых только один корень квадратного уравнения больше 2.

Решение. Перепишем уравнение следующим, привычным для нас, образом

Так как свободный член этого уравнения можно представить в виде произведения , то есть , а второй коэффициент, взятый с противоположным знаком, можно представить в виде суммы , то есть , то, по теореме обратной теореме Виета, числа 3 и являются корнями заданного уравнения. Поскольку, согласно условию задачи, только один корень должен быть больше 2, и таким корнем уже является число 3, то второй корень должен, либо совпадать с первым, то есть , либо не превосходить число 2, то есть , поэтому искомыми значениями параметра a являются решения совокупности

Решим эту совокупность, имеем

Таким образом, интересующие нас значения параметра a образуют множество .

Ответ. .

Задание 2 (для самостоятельного решения). Найдите все значения параметра m, при которых один из корней уравнения находится между числами 0 и 2, а второй – между числами 3 и 5.

Решение.

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

________________________________________________________________________

Ответ. __________________________________________________________________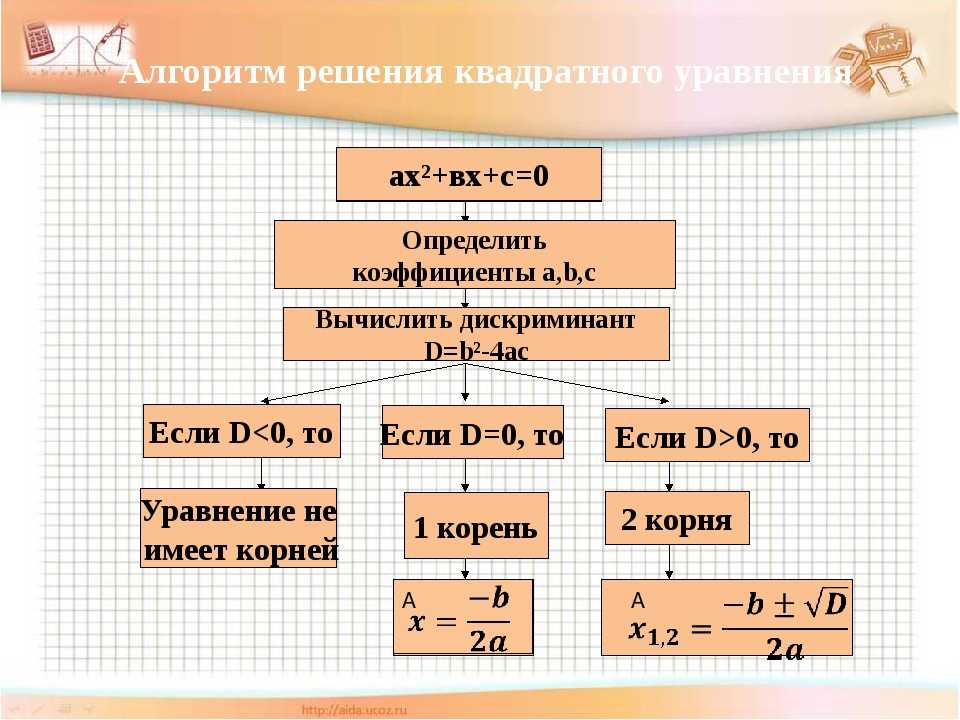

Указание: если не удалось подобрать корни с опорой на теорему обратную теореме Виета, решите это уравнение по формулам, то есть найдите его дискриминант и корни.

Задание 3. При каких значениях параметра a число 2 находится между корнями квадратного уравнения ?

Решение. В двух предыдущих заданиях поиск корней квадратного уравнения был связан либо с привлечением теоремы обратной теореме Виета, либо с нахождением дискриминанта. Поэтому поступим аналогичным образом и в этом задании, то есть найдём действительные корни заданного уравнения, если они существуют, например, по формулам.

Имеем, .

И далее,

Так как условие: «число 2 находится между корнями квадратного уравнения» прямо указывает на существование двух различных корней, то дискриминант должен быть положительным. Кроме того, в силу очевидного соотношения , должны выполняться неравенства: . А стало быть, искомыми значениями параметра a являются решения системы неравенств:

Вы никогда не сумеете решить возникшую проблему, если сохраните то же мышление и тот же подход, который привёл вас к этой проблеме.

Альберт Эйнштейн

Совершенно очевидно, что решение этой системы связано с немалыми техническими трудностями. Поэтому для настоящей задачи выбранный приём не оправдан. Однако способом преодоления возникшей трудности может стать изменение подхода к толкованию условия нашей задачи.

И такой подход основан на простой геометрической интерпретации. Графиком левой части заданного уравнения, то есть графиком квадратного трёхчлена , является парабола, ветви которой направлены вверх. Поскольку, согласно условию задачи, число 2 находится между корнями заданного квадратного уравнения, то парабола должна пересекать ось абсцисс в точках, расположенных по разные стороны от точки этой оси с координатой 2 (смотри рисунок 1). А значит, рисунок 1 – перевод условия данной задачи на графический язык.

Составим аналитическую запись приведённого рисунка, то есть найдём описывающие его соотношения (уравнения, неравенства). Для этого, рассматривая всевозможные параболы (с ветвями, направленными вверх), пересекающие ось абсцисс в точках, расположенных по разные стороны от точки 2 (постройте на рисунке 1 ещё такие параболы), будем сравнивать с нулём значение квадратичной функции при x=2. В результате мы заметим, что в каждом таком случае , поэтому требование будет как необходимым, так и достаточным для того, чтобы число 2 находилось между корнями заданного уравнения. А значит, искомыми значениями параметра a являются решения неравенства , то есть неравенства . Решите это неравенство самостоятельно

Итак, интересующие нас значения параметра a образуют множество .

Ответ. .

Задание 4 (для самостоятельного решения). При каких значениях параметра a корни уравнения расположены по разные стороны от числа (-1)?

Решение.

_______________________________

_________________________________

С понятийной точки зрения будет чрезвычайно полезным обобщить рассмотренные выше задачи, то есть найти условия, при которых число p лежит между нулями квадратичной функции . И снова обратимся к геометрической трактовке. Поскольку из условия задания следует, что дискриминант D больше нуля, то в зависимости от знака старшего коэффициента достаточно рассмотреть два случая: a>0 и a<0 (смотри рисунок 2).

Каждый из этих случаев полностью описывается следующими условиями: для рисунка 2(а) имеем, а для рисунка 2(б) — Заметим, что здесь нет необходимости требовать ещё выполнение условия D>0, это условие является лишним (избыточным), потому как неравенства системы гарантируют существование двух различных нулей квадратичной функции .

Поскольку совокупность этих двух систем, согласно теореме 2, равносильна неравенству , то справедливо следующее утверждение.

Утверждение 1. Для того, чтобы число p находилось между нулями квадратичной функции (корнями квадратного уравнения ), необходимо и достаточно выполнения неравенства .

Далее, попытаемся построить критерий, обеспечивающий положение заданного числа p вне корневого промежутка.

Для начала, заполняя пропуски, найдём условия, при которых нули квадратичной функции будут меньше числа p. И для этого снова обратимся к геометрическому толкованию поставленной задачи.

Графиком квадратичной функции является _____________, ветви которой направлены вверх, если ________ или вниз, если _______. Парабола может имеет с осью Ox либо одну общую точку и в этом случае дискриминант D, соответствующего квадратного трёхчлена, равен ____________, либо две общие точки и тогда дискриминант D будет _________________. Для удобства абсциссы общих точек параболы и оси Ox обозначим через ().

Теперь в декартовой прямоугольной системе координат xOy построим две параболы с ветвями направленными вверх: первую — имеющую с осью абсцисс одну общую точку, вторую – две общие точки, расположенные левее уже отмеченной на оси Ox точки с координатой p.

Из рисунка 3 видно, что:

1) старший коэффициент a ________;

2) дискриминанта D ______________; 3) и кроме того, согласно рисунку, значение квадратичной функции в точке x=p, в сравнении с нулём, будет __________________________, то есть .

Подумайте, достаточно ли этих условий, чтобы общие точки параболы и оси Ox располагались левее точки с абсциссой p? Для этого попытайтесь построить параболу, имеющую с осью Ox общие точки расположенные, наоборот, правее точки с абсциссой p, для которой выполнялось бы каждое из трёх условий 1) – 3).

Очевидно, что примером такой параболы может стать парабола, проходящая через точки оси Ox с абсциссами 5 и 10, поскольку для неё выполняются все вышеперечисленные условия 1) — 3). Однако, в этом случае, нули квадратичной функции будут больше числа p. А значит, выполнимость всех условий 1) – 3) не гарантирует расположение нулей квадратичной функции слева от точки p.

Окончательно зафиксировать точку p в нужном положении позволяет неравенство , где , то есть x₀ – абсцисса вершины параболы . А значит, следующая система полностью описывает рисунок 3.

Задание 5 (для самостоятельного решения). Рассуждая аналогичным образом, найдите условия, при которых нули квадратичной функции с отрицательным старшим коэффициентом будут меньше числа p.

Решение.

_______________________________

_________________________________

________________________________________________________________________________________________________________________________________________

________________________________________________________________________________________________________________________________________________

квадратичной функции с отрицательным старшим коэффициентом слева от точки p.

Как и ранее, согласно теореме 1 о равносильной замене неравенства, совокупность полученных систем и равносильна системе

Это и есть необходимое и достаточное условие того, что число p больше нулей квадратичной функций. Сформулируем его в таком виде.

Утверждение 2. Для того чтобы число p было больше нулей квадратичной функции (корней квадратного уравнения ), необходимо и достаточно выполнение следующей системы неравенств:

Задание 6 (для самостоятельного решения). Сформулируйте необходимое и достаточное условие того, что число p меньше нулей квадратичной функции .

Решение.

________________________________

_________________________________

_________________________________

Итак, результатом решения задания 6 является построенное необходимое и достаточное условие того, что число p меньше нулей квадратичной функции, которое можно сформулировать следующим образом.

Утверждение 3. Для того чтобы число p было меньше нулей квадратичной функции (корней квадратного уравнения ), необходимо и достаточно выполнение следующей системы неравенств:

Задание 7 (для самостоятельного решения). Найдите все значения параметра a, при которых все корни уравнения больше .

Задание 8 (для самостоятельного решения). Найдите все значения параметра а, при каждом из которых: 1) только один корень уравнения удовлетворяет неравенству ; 2) все корни уравнения удовлетворяет неравенству .

Выберите одно из двух заданий и решите его.

________________________________

_________________________________

_________________________________

________________________________________________________________________

____________________________________________________________________________________________________________________________________________

_______________________________________________________________________

Ответ. Искомые значения параметра a образуют множество__________________

В двух трёх предложениях опишите, чем Вы занимались на занятии, что Вам запомнилось? Какие результаты были Вами получены? Какой из этих результатов был в большей степени получен Вами самостоятельно?

________________________________________________________________________

________________________________________________________________________________________________________________________________________________

________________________________________________________________________

Заполните таблицу вариантов расположения нулей квадратичной функции на числовой прямой и соответствующих им условий.

Таблица.

Расположение нулей квадратичной функции на числовой прямой	Необходимое и достаточное условие

В заключении, с целью систематизации приобретённых знаний, будет чрезвычайно полезным исправить ошибки в первой блок-схеме – осмыслить их – запомнить – оформить свою мысль – применить знания на практике, заполнив вторую блок-схему.

О квадратных уравнениях в правильном порядке / Хабр

Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.

Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.

Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.

Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.

Начнем с конца

Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:

Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)
Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения

Гораздо проще начать с теоремы Виета.

Рассмотрим квадратный трехчлен

В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:

Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению , второе по построению).

Раскрывая скобки, мы получим следующее:

Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:

Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.

Геометрия параболы

Вершина

Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…

Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.

Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.

Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.

Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.

Парабола, вершина и ось симметрии

Тогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями

Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!

Потрясающий результат, который нам пригодится далее.

Ещё немного про корни

Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось . Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:

Корней нет, при этом
1. Либо значение в вершине больше нуля и старший коэффициент больше нуля
2. Либо значение в вершине меньше нуля и старший коэффициент меньше нуля
Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю
Корня два

Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:

И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.

Первый случай

Домножим первое неравенство на . Учитывая, что , знак неравенства сменится на противоположный:

Это условие, при котором корней нет.

Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.

Второй случай

Какая-то магия. Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.

На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.

Понятие дискриминанта

Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.

Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.

Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда

Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.

Все еще не видите? Воспользуемся снова теоремой Виета:

Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .

Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:

Или, немного преобразовав

Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.

В общем случае, дискриминант — более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.

Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.

Заключение

Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.

Как по мне, это именно то, как должны преподавать эту тему в школе.

4.3 Решение квадратных уравнений | Уравнения и неравенства

Квадратное уравнение — это уравнение, в котором показатель степени переменной не превышает \(\text{2}\). Следующее примеры квадратных уравнений:

Квадратные уравнения отличаются от линейных уравнений тем, что линейное уравнение имеет только одно решение, а квадратное уравнение имеет не более двух решений. Однако существуют особые ситуации, когда квадратное уравнение имеет либо одно решение, либо не имеет решений. 9{2} + bx + c = 0\) иметь вид \(\left(rx + s\right)\left(ux + v\right) = 0\).

Два решения: \(\left(rx + s\right) = 0\) или \(\left(ux + v\right) = 0\), поэтому \(x= -\dfrac{s}{r}\) или \(x = -\dfrac{v}{u}\) соответственно.

Проверьте ответ, подставив его обратно в исходное уравнение. 9{2} + Ьх + с = 0\)

Факторизовать

\[\влево(х + 1\вправо)\влево(3x — 1\вправо) = 0\]

Решите для обоих факторов

У нас есть

\начать{выравнивать*} х + 1 & = 0 \\ \поэтому х & = -1 \конец{выравнивание*}

ИЛИ

\начать{выравнивать*} 3х — 1 & = 0 \ \следовательно, x & = \frac{1}{3} \конец{выравнивание*} 9{2} & = 0 \конец{выравнивание*}

Квадратное уравнение является полным квадратом

Это пример особой ситуации, когда существует только одно решение квадратного уравнения. уравнения, потому что оба фактора одинаковы.

\начать{выравнивать*} х — 1 & = 0 \\ \поэтому х & = 1 \конец{выравнивание*}

Проверьте ответ, подставив обратно в исходное уравнение 9{2} — 6x — 8 & = 0 \\ (3x + 2)(3x — 4) & = 0 \\ 3х+2&=0\ х & = -\фракция{2}{3} \\ \текст{или} & \\ 3х — 4 & = 0 \ х & = \ гидроразрыва {4} {3} \\ \поэтому x = -\frac{2}{3} & \text{ или } x = \frac{4}{3} \end{выравнивание*}

9{2} — 9 & = 0 \\ (2у — 3)(2у + 3) & = 0 \\ 2у — 3&=0\ у & = \ гидроразрыва {3} {2} \\ \текст{или} & \\ 2у+3&=0\ y & = -\frac{3}{2} \\ \поэтому y = \frac{3}{2} & \text{ или } y = -\frac{3}{2} \end{выравнивание*}

\(4x^{2} + 16x — 9{2} + 16x — 9 & = 0 \\ (2х — 1)(2х + 9) & = 0 \\ 2х — 1 & = 0 \ х & = \ гидроразрыва {1} {2} \\ \текст{или} & \\ 2х+9&=0\ y & = -\frac{9}{2} \\ \следовательно, x = \frac{1}{2} & \text{ или } x = -\frac{9}{2} \end{выравнивание*}

9{2} + 58x — 48 & = 0 \\ (5х — 6)(3х — 8) & = 0 \\ 5х — 6 & = 0 \ х & = \ гидроразрыва {6} {5} \\ \текст{или} & \\ 3х — 8 & = 0 \ х & = \ гидроразрыва {8} {3} \\ \следовательно, x = \frac{6}{5} & \text{ или } x = \frac{8}{3} \end{выравнивание*}

9{2} + 5x — 6 & = 0 \\ (7x + 6)(2x — 1) & = 0 \\ 7х+6&=0\ х & = -\ гидроразрыва {6} {7} \\ \текст{или} & \\ 2х — 1 & = 0 \ х & = \ гидроразрыва {1} {2} \\ \поэтому x = -\frac{6}{7} & \text{ или } x = \frac{1}{2} \end{выравнивание*}

92 -17 лет + 4 &= 0\\ (4у-1)(у-4)&= 0\\ \поэтому y = \frac{1}{4} &\text{ или } y = 4 \конец{выравнивание*}

\(\dfrac{1}{2}(b — 1) = \dfrac{1}{3}\left(\dfrac{2}{b} + 4\right)\)

Примечание \(b \neq 0\)

\начать{выравнивать*} \frac{1}{2}(b — 1) &= \frac{1}{3}\left(\frac{2}{b} + 4\right) \\ 3(b — 1) &= 2\влево(\frac{2}{b} + 4\вправо) \\ 3b — 3 &= \frac{4}{b} + 8 \\ 3b^2 — 3b &= 4 + 8b \\ 3b^2 — 11b — 4 &= 0 \\ (3b + 1)(b — 4) &= \\ \поэтому b = -\frac{1}{3}b &\text{ или } b = 4 \конец{выравнивание*} 92 — 9) &= 0 \\ (б-2)(б+2)(б-3)(б+3) &= 0 \\ \поэтому b = \pm 2 &\text{ или } b = \pm 3 \end{align*}

\(\dfrac{a + 1}{3a — 4} + \dfrac{9}{2a + 5} + \dfrac{2a + 3}{2a + 5} = 0\)

\begin{выравнивание*} \frac{a + 1}{3a — 4} + \frac{9}{2a + 5} + \frac{2a + 3}{2a + 5} & = 0 \\ \frac{(a + 1)(2a + 5) + 9(3a — 4) + (2a + 3)(3a — 4)}{(3a — 4)(2a + 5)} & = 0 \\ 2а^{2} + 7а + 5 + 27а — 36 + 6а^{2} + а — 12 & = 0 \\ 8а^{2} + 35а — 43 & = 0 \\ (8а + 43)(а — 1) & = 0 \\ 8а+43&=0\ а & = -\frac{43}{8} \\ \текст{или} & \\ а — 1 & = 0 \\ а & = 1 \\ \поэтому a = -\frac{43}{8} & \text{ или } a = 1 \end{выравнивание*} 92 — 2x — 3}{x+1} &= 0 \\ \frac{(x+1)(x-3)}{x+1} &= 0 \\ \поэтому х &= 3 \конец{выравнивание*}

\(x + 2 = \dfrac{6x -12}{x- 2}\)

Примечание \(x \neq 2\)

\начать{выравнивать*} х + 2 &= \frac{6x-12}{x- 2} \\ (х+2)(х-2) &= 6х — 12 \\ х^2 — 4 &= 6х — 12\\ х^2 — 6х + 8 & = 0 \\ (х — 2)(х — 4) & = 0 \\ \поэтому х &= 4 \конец{выравнивание*} 9{2} — 6а&=0\ 3а(3а — 2) & = 0 \\ 3а & = 0 \\ а & = 0 \\ \текст{или} & \\ 3а — 2&=0\ а & = \ гидроразрыва {2} {3} \\ \следовательно, a = 0 & \text{ или } a = \frac{2}{3} \конец{выравнивание*}

Решения

NCERT для математики класса 10 Глава 4 Квадратные уравнения Пример 4.

Решения NCERT Математика класса 10 Глава 4 Квадратные уравнения — Вот все решения NCERT по математике класса 10 Глава 4 Квадратные уравнения. Это решение содержит вопросы, ответы, изображения, пошаговое объяснение полной главы 4 под названием «Квадратные уравнения в классе 10». 4 Квадратные уравнения. После того, как вы изучили урок, вы должны искать ответы на его вопросы из учебника. Здесь вы можете получить полные решения NCERT для математики класса 10, глава 4, квадратные уравнения в одном месте.

Класс 10 Квадратные уравнения по математике Пример 4.1
प्रश्नावली 4.1 का हल हिंदी में
Квадратные уравнения по математике, класс 10, пр. 4.2
प्रश्नावली 4.2 का हल हिंदी में
Квадратные уравнения по математике, класс 10, пр. 4.3
प्रश्नावली 4.3 का हल हिंदी में
Квадратные уравнения по математике, класс 10, пр. 4.4
प्रश्नावली 4.4 का हल हिंदी में
Дополнительные вопросы по квадратным уравнениям 10 класса

Решения NCERT для математики класса 10 Глава 4 Квадратные уравнения Ex 4. 1 являются частью решений NCERT для математики класса 10. Здесь мы дали решения NCERT для математики класса 10, глава 4, квадратные уравнения, пример 4.1.

Доска	CBSE
Учебник	НЦЕРТ
Класс	Класс 10
Субъект	Математика
Глава	Глава 4
Название раздела	Квадратные уравнения
Упражнение	Пример 4.1
Количество решенных вопросов	2
Категория	Решения NCERT

Упр. 4.1 Класс 10 Математика Вопрос 1.
Проверьте, являются ли следующие уравнения квадратными: ) (3-x)
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x (x + 5)
(в) (2х – 1) (х – 3) = (х + 5) (х – 1)
(vi) x ² + 3x + 1 = (x – 2) ²
(vii) (x + 2) ³ = 2x(x ² – 1)
(viii) x ³ -4x ² -x + 1 = (x-2) ³
Решение:

Решения NCERT Класс 10 Математика Глава 4 Квадратные уравнения — Видео

Решения NCERT Класса 1 Математика глава 4 Квадратные уравнения здесь.

Упражнение 4.1 Класс 10 Математика Вопрос 2.
Представьте следующие ситуации в виде квадратных уравнений:
(i) Площадь прямоугольного участка составляет 528 м ² . Длина участка (в метрах) более чем в два раза превышает его ширину. Нам нужно найти длину и ширину участка.
(ii) Произведение двух последовательных положительных целых чисел равно 306. Нам нужно найти целые числа.
(iii) Мать Рохана старше его на 26 лет. Произведение их возраста (в годах) через 3 года будет равно 360. Мы хотели бы найти нынешний возраст Рохана.
(iv) Поезд проехал расстояние 480 км с постоянной скоростью. Если бы скорость была на 8 км/ч меньше, то на преодоление того же расстояния ушло бы на 3 часа больше. Нам нужно найти скорость поезда.
Решение:

Неправильный результат NCVT 2019

Решения NCERT, класс 10, математика, глава 4, квадратные уравнения

, класс 10, математика, глава 4, решения квадратных уравнений приведены ниже в формате PDF. Вы можете просмотреть их в Интернете или загрузить PDF-файл для дальнейшего использования.

или сохраните изображения решений и распечатайте их, чтобы они всегда были под рукой при подготовке к экзамену. Нажмите здесь, чтобы загрузить решения NCERT для класса 10 по математике, глава 4, квадратные уравнения.

NCERT Solutions для класса 10 Математика Глава 4 Квадратичные уравнения (Hindi Medium) EX 4,1

Класс 10 Математические квадратичные уравнения. переменная x представляет собой уравнение вида ax2 + bx + c = 0, где a, b, c — действительные числа, а a ≠ 0.

Любое уравнение вида P(x) = 0, где P(x) — это многочлен степени 2, является квадратным уравнением.

Нуль(и)/корень(и) квадратного уравнения

Вещественное число α называется корнем квадратного уравнения ax ² + bx + c = 0, a ≠ 0, если aα ² + bα + c = 0,
Можно сказать, что x = α является решением квадратного уравнения или что α удовлетворяет квадратному уравнению.
Нули квадратного полинома ax ² + bx + c = 0 и корни уравнения ax ² + bx + c = 0 совпадают. Квадратное уравнение имеет не более двух корней/нулей.

Связь между нулями и коэффициентом квадратного уравнения

Если α и β — нули квадратного уравнения ax ² + bx + c = 0, где a, b, c — действительные числа и a ≠ 0, то

Методы решения квадратных уравнений

Ниже приведены методы, используемые для решения квадратных уравнений:

(i) Факторизация
(ii) Заполнение квадрата
(iii) Квадратная формула

Методы факторизации

В этом

62 методом находим корни квадратного уравнения (ax

² + bx + c = 0) путем разложения LHS на два линейных множителя и приравнивания каждого множителя к нулю, например,
6x ² – x – 2 = 0
⇒ 6x ² + 3x – 4x – 2 = 0 …(i)
⇒ 3x (2x + 1) – 2(2x + 1) = 0
⇒ (3x – 2) (2x + 1) = 0
⇒ 3x – 2 = 0 или 2x + 1 = 0

Необходимое условие : Произведение 1-го и последнего членов уравнения.

(i) должно быть равно произведению 2-го и 3-го членов того же уравнения.

Метод завершения квадрата

Это метод преобразования L.H.S. квадратного уравнения, не являющегося полным квадратом, в сумму или разность полного квадрата и константы путем сложения и вычитания подходящих постоянных членов. например,
(1) x ² + 4x – 5 = 0
⇒ x ² + 2(2)(x) -5 = 0
⇒ x ² + 2(2)(x) + (2) ² – (2) ² – 5 = 0
⇒ (х + 2) ² – 4 – 5 = 0
⇒ (х + 2) ² – 9 = 0
⇒ х + 2 ± 3
⇒ x = -5, 1
(2) 3x ² – 5x + 2 = 0

Квадратная формула

Рассмотрим квадратное уравнение: ax ² + bx + c = 0.
Если b ² – 4ac ≥ 0, то корни приведенного выше уравнения имеют вид:

Природа корней

Для квадратного уравнения ax ² + bx + c = 0
(a ≠ 0), значение (b ² – 4ac) называется дискриминантом уравнения и обозначается как D.

Кейс «Квадратные уравнения с параметром» для учащихся 10 класса

О квадратных уравнениях в правильном порядке / Хабр

Начнем с конца

Геометрия параболы

Вершина

Ещё немного про корни

Понятие дискриминанта

Заключение

4.3 Решение квадратных уравнений | Уравнения и неравенства

Факторизовать

Решите для обоих факторов

Квадратное уравнение является полным квадратом

NCERT для математики класса 10 Глава 4 Квадратные уравнения Пример 4.

Решения NCERT Класс 10 Математика Глава 4 Квадратные уравнения — Видео

Решения NCERT, класс 10, математика, глава 4, квадратные уравнения

NCERT Solutions для класса 10 Математика Глава 4 Квадратичные уравнения (Hindi Medium) EX 4,1

Класс 10 Математические квадратичные уравнения. переменная x представляет собой уравнение вида ax2 + bx + c = 0, где a, b, c — действительные числа, а a ≠ 0.

Нуль(и)/корень(и) квадратного уравнения

Связь между нулями и коэффициентом квадратного уравнения

Методы решения квадратных уравнений

Методы факторизации

62 методом находим корни квадратного уравнения (ax

Метод завершения квадрата

Квадратная формула

Природа корней

Добавить комментарий Отменить ответ