Виды и степени нарушений Слуха
Виды и степени нарушений Слуха
Около 10% всего населения Земного шара в той или иной степени имеют нарушения Слуха.
Тугоухость определяют как снижение Cлуха, при котором затруднено общение с окружающими людьми по причине недостаточного восприятия чужой речи. С нарушением восприятия звуков можно столкнуться в любом возрасте. Тугоухость может варьировать по степени тяжести — от легкой до глубокой.
Степень нарушения Слуха определяется в ходе специального исследования, называемого Аудиометрией. Суть исследования состоит в измерении порога Слухового восприятия человека почастотно.
Если человек слышит Звуки на всех Частотах до 25 Децибелл (дБ), то его Слух считается нормальным.
Если он слышит только Звуки громче, чем 25 дБ, говорят о снижении Слуха.
Чем большая громкость Звука требуется для того, чтобы человек услышал подаваемый в наушники сигнал, тем большая у него степень Тугоухости.
Согласно Международной классификации Тугоухости:
1. Слух в норме означает, что человек слышит Звуки на всех частотах от 0 до 25 дБ и не испытывает проблем с общением.
2. 1-я степень Тугоухости (слабая) означает, что человек слышит Звуки только громче 26-40 дБ. У него появляются трудности в восприятии тихой и отдаленной речи.
3. 2-я степень Тугоухости (средняя) означает, что человек слышит Звуки только громче 41-55 дБ. У него имеются трудности в восприятии тихой и отдаленной речи, диалога.
4. 3-я степень Тугоухости (средне-тяжелая) означает, что человек слышит Звуки только громче 56-70 дБ. Он воспринимает только громкую речь и испытывает затруднение при коллективном общении и разговоре по телефону.
5. 4-я степень Тугоухости (тяжелая) означает, что человек слышит Звуки только громче 71-90 дБ. Он с трудом воспринимает даже громкую речь. Понятен только крик или усиленная наушниками речь.
Разговор по телефону не возможен.
6. Глухота (глубокая) означает, что человек может услышать звуки только громче 91 дБ и испытывает трудности в понимании даже усиленной наушниками речи.
Снижение Слуха может возникать в следствии различных причин.
Кондуктивная Тугоухость
Эта Тугоухость, вызываемая препятствиями на пути проведения звуковой волны. Такая Тугоухость хорошо лечится либо консервативным, либо хирургическим путем.
Основными причинами развития данного вида Тугоухости являются: скопления ушной серы, средний отит, отосклероз и др.
Нейросенсорная (сенсоневральная) Тугоухость.
Эта Тугоухость связана с нарушением преобразования механических колебаний в электрические импульсы. Причинами ее развития являются нарушения во внутреннем ухе или улитке. Поражение рецепторов звукового анализатора может быть вызвано акустическими травмами, ототоксическим действием антибиотиков, сосудистыми нарушениями кровоснабжения улитки и др.
причинами, приводящими к гибели волосковых клеток внутреннего уха.
Данный вид Тугоухости очень тяжело поддается лечению и может быть компенсирован только Слухопротезированием.
Смешанная Тугоухость.
Эта Тугоухость представляет собой сочетание двух вышеупомянутых типов нарушения Слуха
Степени 10
Горячая математикасилы 10 легко запомнить, потому что мы используем база 10 система счисления.
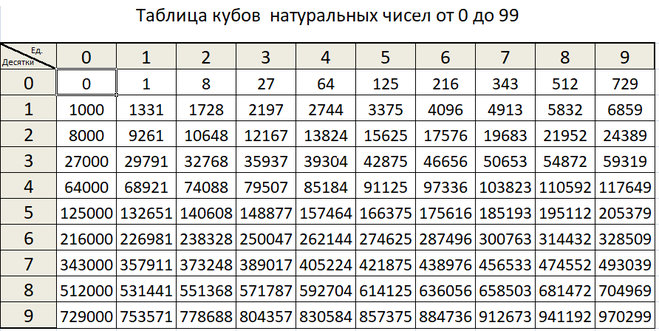
Для 10 н с н положительное целое число, просто напишите » 1 » с н нули после него. Для отрицательные силы 10 − н , писать » 0 .» с последующим н − 1 нули, а затем 1 .
Полномочия 10 широко используются в научная нотация , так что это хорошая идея, чтобы освоиться с ними.
Полномочия 10 | |
| 10 1 «=» 10 | 10 1 «=» 1 |
| 10 2 «=» 100 | 10 -1 «=» 0,1 |
| 10 3 «=» 1000 | 10 -2 «=» 0,01 |
| 10 4 «=» 10 000 | 10 -3 «=» 0,001 |
10 5 «=» 100 000 (сто тысяч) | 10 -4 «=» 0,0001 (одна десятитысячная) |
10 6 «=» 1 000 000 (один миллион) | 10 -5 «=» 0,00001 (стотысячный) |
10 7 «=» 10 000 000 (десять миллионов) | 10 -6 «=» 0,000001 (одна миллионная) |
10 8 «=» 100 000 000 (сто миллионов) | 10 -7 «=» 0,0000001 (одна десятимиллионная) |
10 9 «=» 1 000 000 000 (один миллиард) | 10 -8 «=» 0,00000001 (стомиллионный) |
10 10 «=» 10 000 000 000 (десять миллиардов) | 10 -9 «=» 0,000000001 (одна миллиардная) |
Нажмите
здесь
для большего количества имен для
очень большие и очень маленькие числа
.
Степени числа 10
Степени числа 10Далее: Научное обозначение Вверх: ES 10 Дополнение Раздаточный материал 1 Предыдущий: ES 10 Дополнительный раздаточный материал 1 Десятичная система, основанная на числе 10, является используемой системой счисления. больше всего в мире. Другие системы счисления, с которыми вы знакомы, являются двоичными. числа, которые основаны на нуле и 1 и используются в компьютерах, и время, который делится (в основном) на единицы, кратные 60 — есть Например, 60 секунд в минуте и 60 минут в часе. Поскольку десятичная система и степени 10 настолько важны в науке, что я немного расскажу о них здесь.
- 1.1 Что такое 10 x ?
- 1.2 Умножение и деление степеней 10
- 1.3 Что насчет «журналов»?
- 1.4 Делаем все это на своем калькуляторе
1.1 Что такое 10
x ? Не паникуйте по поводу фразы «степени 10» — вы уже привыкли использовать
их, даже если вы не знаете об этом.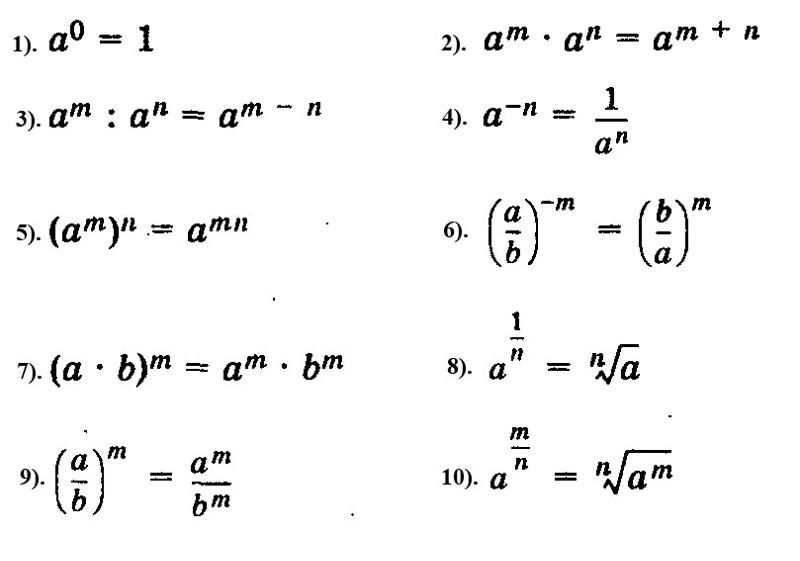
Степени десяти записываются как 10 х , где x — это мощность, о которой я говорю, и называется «экспонента». 10 x означает «10 × 10, x » раз.» 10 -x означает «1/10 × 1/10, x раз.» В математике, а не в словах, это выглядит так
Вот пара примеров, чтобы было немного понятнее:
Таблица 1 перечисляет числа как в общей нотации, так и в математической нотации. Некоторые степени десяти часто используются в науке и имеют специальные «префиксы», которые перечислены также. Кроме того, некоторым степеням числа десять были даны имена, некоторые из которых не знакомые вам сомнения; Я внес имена в таблицу.
Если вы посмотрите на Таблицу 1,
вы можете заметить кое-что полезное: показатель степени для каждой записи в таблице равен
равно количеству нулей в соответствующем числе, записанном «нормально».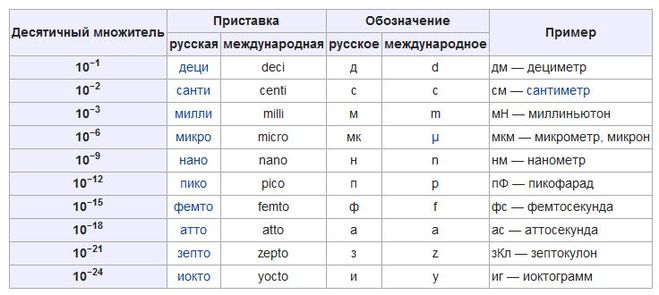
«Префикс» в пятой колонке в Таблица 1 используется как сокращение, когда речь идет о количестве вещей. Например, память компьютера обычно измеряется в мегабайтах или миллионах байтов, а память на жестком диске компьютера теперь часто измеряется гигабайтами или миллиардами байт. Кроме того, вы можете получить рецепт на лекарство от простуды, которое, скажем, 20 миллиграммов какого-то наркотика. Это сокращенный способ сказать 20 тысячных грамма.
Наверх
1.2 Умножение и деление степеней 10
Возможно, вы не уверены, что полезно иметь возможность записывать числа в
степени десяти.
Что ж, степени десяти полезны и при выполнении математических операций.
Скажем, я спрашиваю вас: «Сколько будет 10 раз по 1000?».
сделка — это всего 10000. Но что, если я спрошу вас: «Сколько будет в триллион раз
один квадриллион?
Оказывается, умножать действительно большие числа легко со степенями десять. Все, что вам нужно сделать, это сложить показатели, и все готово. Давайте использовать пример, который я только что дал вам. Сколько будет один триллион умножить на один квадриллион? Во-первых, используя Таблицу 1, вы можете увидеть один триллион 10 12
, и один квадриллион 10 15 . Итак, ответ 10 27 . что является действительно большим числом — и вы можете увидеть это почти сразу, без нужен калькулятор или лист бумаги, чтобы сделать это от руки. Вот еще несколько Примеры: Деление работает аналогично, за исключением того, что вы вычитаете степени.
Сколько будет один триллион, разделенный на один квадриллион? Ну, это
10 12 ÷
10 15 ,
так что ответ 10 -3 , или одна тысячная.
Здесь
еще несколько примеров:
Опять же, хотя это может показаться бесполезным для небольших чисел, представьте деление один триллион триллионов триллионов, то есть 10 36 , на один миллиард миллиардов миллиардов, что 10 18 , от руки. Это займет у вас некоторое время. (Кстати, ответ 10 18 .)
Наверх
1.3 Что насчет «журналов»?
Вам может быть интересно, есть ли противоположность степеням числа 10; что-нибудь
как деление противоположно умножению или вычитанию
напротив добавления. Оказывается, есть как раз такая штука:
логарифмы, или «журналы». Раньше логи были очень важны для
умножение
и деление, и все время использовались при выполнении арифметических действий с использованием логарифмических линеек.
Теперь, когда ручные калькуляторы стали обычным явлением, использование логарифмов
для базовых расчетов исчезает, но все еще может быть полезным.
И хотя использование логарифмов для простых арифметических операций встречается редко, есть и другие
использует логарифмы во многих областях науки, и мы можем увидеть некоторые из этих
использует позже в классе.
Где бревна действительно полезны, так это в выполнении умножения и деления числа. Из предыдущего раздела вы знаете, что для умножения чисел, которые являются степенями десяти, вы добавляете показатели степени, и чтобы разделить такие числа, вы вычесть показатели. Ну, так как логарифм числа, который является степенью 10 — это всего лишь показатель степени этой степени, чтобы выполнить умножение, вы просто прибавляете журналы. Чтобы сделать деление, просто вычтите бревна. Пример:
Вы могли видеть ответ из раздела 1.2,
но вы можете видеть, как легко это сделать с помощью журналов.
Наверх
1.4 Делаем все это на своем калькуляторе
Если у вас есть простой научный калькулятор, на нем будет кнопка что-то похожее на «10 х ». Это кнопка для возведения в степень числа 10. Вы просто вводите число, скажем, 5, и нажмите кнопку «10 x », и число вы получите обратно будет 10 5 или 100 000. В некоторых случаях, если вы введете большое число, например 50, и нажмете 10 x кнопка, вы не увидите последующую цифру 1 50 нулей, но что-то похожее на «1 E 50» или «1 EE 50». Не паника — это всего лишь версия вашего калькулятора экспоненциальной записи , о которых мы поговорим в следующем разделе.
Также на научных калькуляторах вы найдете кнопку для ведения журналов — это
обычно пишется как «журнал» и часто находится очень близко к кнопке для выполнения
10 х .