Математика Чётные и нечётные числа
Материалы к уроку
Конспект урока
7. Чётные и нечётные числа
|
Организационный этап
Посмотрите друг на друга. Улыбнитесь соседу справа, а теперь соседу слева. Улыбка творит чудеса и поднимает настроение. Но не только улыбка творит чудеса, а и дружба. Дружные Смешарики пришли к нам на урок. Сегодня мы повторим таблицу умножения и деления на 2. Узнаем, какие числа называются чётными, а какие – нечётными.
|
|
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Ну-ка в сторону карандаши. Ни счетных палочек. Ни ручек. Ни мела. Устный счёт! Мы творим это дело Только силой ума и души!
Задание 1 Нюша расставила банки с вареньем в погребе на 2 полки. Она поставила по 5 банок на каждую полку. Сколько банок с вареньем заготовила Нюша? 10 банок
Задание 2 Ёжик любит яблоки. Он приносил себе 2 дня по 8 яблок. Сколько яблок он принёс? 16 яблок
|
|
|
|
Этап усвоения новых знаний
Задание 3 Бараш положил в погреб на зиму 8 штук свёклы. Всю свёклу он разложил в 2 корзины поровну. Сколько штук свёклы лежит в каждой корзине? Мы видим, что в каждую корзину положили по 4 свёклы.
Решите еще одну задачу. Бараш положил в погреб на зиму 11 штук тыквы. Всю тыкву он разложил на 2 полки поровну. Сколько штук тыквы лежит на каждой полке? Мы видим, что 11 не можем разделить на 2, т. к. на каждую полку можно положить по 5 тыкв, и одна еще останется. Значит, есть числа, которые мы можем разделить на 2 без остатка, и числа, которые без остатка на 2 не делятся. Числа, которые делятся на 2 без остатка, называются чётными. 2, 4, 6, 8, 10…- четные числа Числа, которые не делятся на 2 без остатка, называются нечётными. 1, 3, 5, 7, 9…- нечетные числа |
|
|
|
Этап закрепления новых знаний
Задание Перед вами улица, на которой живут Смешарики. 1 3 _ _ 9 нечётные 2 _ _ 8 _ чётные
Проверьте себя. Четные номера домов: 2, 4, 6, 8, 10. Нечетные номера домов: 1, 3, 5, 7, 9 Задание Решите задачу.На улице Смешариков 8 домов с чётными номерами, а с нечётными на 1 дом больше. Сколько всего домов на улице Смешариков? Проверьте себя. В первом действии найдем, сколько домов с нечетными номерами: 1) 8 + 1 = 9 домов Во втором действии ответим на вопрос задачи: сложим количество домов с чётными номерами и количество домов с нечётными номерами: 2) 8 + 9 = 17 домов Запишем ответ: 17 домов на улице Смешариков.
Задание Определите, какой номер дома последний? Последний дом номер 17. 17 разделим на 2. Получится по 8 и остается еще 1. Так как 17 нельзя разделить на 2 без остатка, значит это число нечётное Двузначное чётное число можно отличить от нечётного по последней цифре. Если последняя цифра в записи числа делится на 2, то всё число делится на 2, значит, оно чётное |
|
|
|
Задание Решите числовые выражения. 57-13 60-32 33+16 23+46 73-58 Проверьте себя. 57-13=44 60-32=28 33+16=49 23+46=69 73-58=15 Найдите среди результатов нечётные числа и подчеркните их. Проверьте себя. Нечётные числа – 49, 69, 15.
|
|
|
|
Самостоятельная работа
Задание Запишите числа по порядку от 10 до 19. Обведите кружками четные числа – красным карандашом, а нечетные – синим. Проверьте себя и оцените свои успехи. Четные числа – 10, 12, 14 , 16, 18 Нечетные числа – 11, 13, 15, 17, 19
|
|
|
|
Итог урока
Мы сегодня вместе со Смешариками познакомились с чётными и нечётными числами. Какие числа называются чётными? Числа, которые делятся на 2 без остатка, называются чётными. 2, 4, 6, 8, 10…- чётные числа Какие числа называются нечётными? Числа, которые не делятся на 2 без остатка, называются нечётными. 1, 3, 5, 7, 9…- нечётные числа
Рефлексия
Выберите смайлик, который более всего соответствует вашему пониманию изученных сегодня на уроке правил и нарисуйте его у себя в тетради. Спасибо за работу! |
||
Значит 8 делится на 2 без остатка.
Ветер сорвал номера на некоторых домиках, давайте поможем их восстановить. Домики у Смешариков круглые, поэтому в своей тетради вы будете рисовать кружки на 2 строчках. Первая сторона улицы – нечетная, вторая — чётная. Пронумеруйте домики.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Главная → Видеоуроки → Математика. Описание видеоурока: Четные и нечетные числа — это целые числа. Если число может быть разделено на 2 без остатка, то число чётное. Если же целое число разделить на 2 и в итоге мы получим число с остатком, то значит число нечетное. Валерий Волков 13 17.09.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
5 класс. Натуральные числа.
5 класс.
10 — 11 класс.
нечетных и четных чисел | Определение, примеры, свойства, отличия
Введение Математика — это мир чисел. У нас есть различные типы чисел, такие как натуральные числа, целые числа, десятичные числа и дроби, которые основаны на определенных характеристиках чисел.
У всех этих типов чисел есть одна общая черта. Все они имеют нечетные числа и четные числа. Итак, что такое нечетные числа и четные числа и как мы их классифицируем? Давайте узнаем.
Рассмотрим числа 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10. Это полностью натуральные числа. Если вы посмотрите на них внимательно, некоторые из чисел, такие как 2, 4, 6, 8 и 10, делятся на 2, а остальные числа 1, 3, 5, 7 и 9 не делятся на 2. Итак, можем ли мы составить группа чисел по признаку их делимости на 2? Да, именно так мы определяем нечетные числа и четные числа.
Четные числа — это числа, которые делятся на 2, оставляя в остатке 0. Например, в приведенном выше примере 2 , 4 , 6 , 8 и 10 — четные числа.
Нечетные числа — это числа, которые не делятся на 2 и всегда дают в остатке 1 при делении на 0. Например, в приведенном выше примере 1 , 3 , 5 , 7 и 9 являются нечетными числами.
Нечетные и четные числа от 1 до 100 Ниже приведена таблица четных и нечетных чисел.
Он показывает числа до 100. Числа, заштрихованные синим цветом, являются четными числами, а числа, заштрихованные желтым цветом, — нечетными числами.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Do we always have look at the number table to identify whether the number is нечетное число или четное число, или мы можем определить число любым другим способом? Давайте узнаем.
Теперь мы знаем, что число, которое делится на 2 и дает в остатке 0, называется четным числом. С другой стороны, нечетное число — это число, которое не делится на 2. Также остаток в случае нечетного числа всегда равен «1». Итак, можем ли мы определить, является ли число четным или нечетным, просто взглянув на само число?
Рассмотрим числа от 1 до 10. У нас есть 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10. Из них мы знаем, что числа 1, 3, 5, 7 и 9 — нечетные числа, а числа 2, 4, 6, 8, 10 — четные числа. Аналогично рассмотрим теперь числа от 11 до 20. У нас есть 11, 12, 13, 14, 15, 16, 17, 18, 18 и 20. Из них 11, 13, 15, 17 и 19 нечетные числа. а числа 12, 14, 16, 18 и 20 четные? Вы видите здесь закономерность? Запишем отдельно нечетные и четные числа. У нас будет
Нечетные числа – 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Четные числа – 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
Посмотрите на последние цифры нечетных чисел.
Нечетные числа заканчиваются любой из пяти цифр 1, 3, 5, 7 и 9. Следовательно, мы можем сказать, что все нечетные числа имеют любую из пяти цифр 1, 3, 5, 7 и 9 на своих единицах. Следовательно, мы можем сказать, что числа, имеющие любую из пяти цифр 1, 3, 5, 7 и 9, являются нечетными числами.
Теперь посмотрите на последние цифры четных чисел. Четные числа заканчиваются любой из пяти цифр 0, 2, 4, 6 и 8. Следовательно, мы можем сказать, что все четные числа имеют любую из пяти цифр 0, 2, 4, 6 и 8 на своем месте единиц. Следовательно, мы можем сказать, что числа, имеющие любую из пяти цифр 0, 2, 4, 6 и 8, являются четными числами.
Давайте теперь посмотрим на свойства нечетных и четных чисел.
Свойства нечетных чисел- Когда мы складываем два нечетных числа, всегда получается четное число. Например, если мы сложим 7 и 15, мы получим 7 + 15 = 22. Точно так же, когда мы сложим 13 и 17, мы получим 13 + 17 = 30, что является четным числом.
- Когда мы вычитаем два нечетных числа, результатом всегда будет нечетное число. Например, когда мы вычитаем 9из 17 мы получим 17 – 9 = 8. Точно так же, когда мы вычтем 21 из 37, мы получим 37 – 21 = 16, что является четным числом.
- При умножении двух нечетных чисел всегда получается нечетное число. Например, если мы умножим 3, которое является нечетным числом, на 5, которое также является нечетным числом, результатом будет 3 x 5 = 15, что также является нечетным числом. Точно так же, если мы умножим 7, которое является нечетным числом, на 9, которое также является нечетным числом, результатом будет 7 x 9 = 63, что также является нечетным числом.
- Когда мы умножаем четное число на нечетное, всегда получается четное число. Например, если мы умножим 3, являющееся нечетным числом, на 6, являющееся четным числом, результатом будет 3 x 6 = 18, что является четным числом. Точно так же, если мы умножим 9, которое является нечетным числом, на 4, которое является четным числом, результатом будет 9 x 4 = 36, что является четным числом.
- Когда мы складываем два четных числа, всегда получается четное число. Например, если мы сложим 8 и 6, то получим 8 + 6 = 14, то есть четное число. Точно так же, если мы сложим 24 и 12, мы получим 24 + 12 = 36, что является четным числом.
- Когда мы вычитаем два четных числа, всегда получается четное число. Например, если мы вычтем 8 из 14, мы получим 14 – 8 = 6. Точно так же, когда мы вычтем 24 из 36, мы получим 36 – 24 = 12.
- Когда мы складываем четное число и нечетное число, результат всегда нечетное число. Например, если мы добавим 3, что является нечетным числом, и 6, которое является четным числом, мы получим 3 + 6 = 9, что является нечетным числом. Точно так же, если мы добавим 9, что является нечетным числом, и 16, что является четным числом, мы получим 9.+ 16 = 25, что является нечетным числом.
- Когда мы вычитаем четное число из нечетного, всегда получается нечетное число. Например, если мы вычтем 3, которое является нечетным числом, из 6, которое является четным числом, мы получим 6 — 3 = 3, которое является нечетным числом. Точно так же, если мы вычтем 12, что является четным числом, из 17, которое является нечетным числом, мы получим 17 — 12 = 5, что является нечетным числом.
- Когда мы умножаем два четных числа, всегда получается четное число. Например, если мы умножим 6, что является четным числом, на 12, что также является четным числом, результатом будет 6 x 12 = 78, что также является четным числом. Точно так же, если мы умножим 4, которое является четным числом, на 8, которое также является четным числом, результатом будет 4 x 8 = 32, что также является четным числом.
- Ноль — четное число. Ноль — четное число, потому что оно кратно 2, а именно 0 × 2.
Точно так же, если мы вычтем 12, что является четным числом, из 17, которое является нечетным числом, мы получим 17 — 12 = 5, что является нечетным числом.Теперь, когда мы узнали, что мы подразумеваем под нечетными и четными числами, можем ли мы обобщить их в операторе, чтобы представить их в форме построителя множества? Давайте узнаем.
Для представления нечетных и четных чисел в обобщенной форме важно понимать условие, определяющее нечетные и четные числа.
Мы знаем, что основным условием для того, чтобы число было четным, является то, что оно делится на 2. Поэтому, если мы хотим обобщить его и представить в форме построителя множеств, мы будем иметь
Набор четных чисел = { x : x = 2k, где k — любое целое число }
Точно так же мы знаем, что основное условие для того, чтобы число было нечетным, состоит в том, что оно не делится на 2. Также , мы знаем, что любое число, которое не делится на 2, оставит в остатке 1 при делении на 2. Следовательно, такое число должно иметь вид 2x + 1, где x — целое число. Поэтому, если мы хотим обобщить его и представить в форме построителя набора, мы будем иметь
Множество нечетных чисел = { x : x = 2k + 1, где k любое целое число }
Решенные примерыПример 1 Найдите сумму
а) Первые 5 нечетных натуральных чисел.
б) Первые 5 четных натуральных чисел
Решение Нас попросили найти
а) Первые 5 нечетных натуральных чисел.
б) Первые 5 четных натуральных чисел
Выполним их последовательно.
Чтобы получить сумму первых пяти нечетных натуральных чисел, мы должны сначала перечислить первые 5 нечетных натуральных чисел. Мы знаем, что натуральные числа начинаются с 1 и продолжаются 1, 2, 3, 4, 5 и так далее.
Следовательно, первые 5 нечетных натуральных чисел — это 1, 3, 5, 7 и 9. Сумма этих чисел будет равна 1 + 3 + 5 + 7 + 9 = 25
Следовательно, сумма первых 5 нечетных натуральные числа = 25
Далее найдем сумму первых 5 четных натуральных чисел.
Первые 5 четных натуральных чисел 2, 4, 6, 8 и 10.
Сумма этих чисел будет 2 + 4 + 6 + 8 + 10 = 30
Следовательно, сумма первых 5 нечетных натуральные числа = 25
Пример 2 Перечислите все нечетные числа больше 3 и меньше 30.
Решение Нас попросили перечислить все нечетные числа больше 3 и меньше 30. Давайте сначала перечислим все числа больше than 3 and less than 30 in the table below –
| 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Далее мы выделим нечетные числа в этой таблице и пометим их желтым цветом.
Получим,
| 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Therefore, all odd numbers greater than 3 and smaller than 30 are
Пример 3 Решение а) Нам даны цифры – 3 , 4 6 и 7. Нам нужно найти трехзначное наименьшее четное число. Наименьшее трехзначное четное число будет 3 4 6. б) Опять же, нам даны цифры — 3 , 4 6 и 7 нам нужно найти наименьшее четырехзначное четное число, где 6 стоит на разряде тысяч. 4-значное наименьшее четное число с 6 в разряде тысяч равно 6 3 7 4. в) Нам даны цифры – 3 , 4 6 и 7. Нам нужно найти двузначное число нечетное число меньше 40. Двузначное нечетное число меньше 40 равно 3 7. г) Нам даны цифры – 3 , 4 6 и 7. Нам нужно найти 4-значное наибольшее нечетное число с 3 на месте сотен. 4-значное самое большое нечетное число с 3 на разряде сотен будет 6 3 4 7 e) Нам даны цифры – 3 , 4 6 и 7. Нам нужно найти наименьшее четное число, используя все 4 цифры. Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку! В начальной школе мы изучаем четные и нечетные числа. Итак, что такое четные числа и нечетные числа? И как мы можем отличить четные числа от нечетных? Понятия четных и нечетных чисел часто используются в нашей повседневной жизни. Например, в программировании мы используем четные и нечетные числа. Четные и нечетные числа имеют свойства. Итак, мы должны не только уметь различать четные и нечетные числа, но и уметь вычислять, каким будет ответ после сложения, вычитания и умножения. Мы объясним, как различать четные и нечетные числа и как их вычислять. Соглашение Первые, что даже нечетные и нечетные числа, которые являются. ? Поняв определения слов, вы сможете понять, что это за числа. Четные и нечетные числа определяются следующим образом. Если число делится на 2, то это четное число. Если число не делится на 2, то оно нечетное. Например, 32 — четное или нечетное число? Как показано ниже, 32 можно разделить на 2. Следовательно, 32 — четное число. Кроме того, поскольку число, которое делится на 2, является четным числом, если число увеличивается на 2 на 2, оно всегда будет четным числом. Другими словами, числа, кратные 2, являются четными числами. Все эти числа четные. С другой стороны, число 17 четное или нечетное? 17 не делится на 2. Ответ будет с остатком. Следовательно, 17 — нечетное число. Вы можете определить, является ли число четным или нечетным, по тому, делится ли оно на два или нет. Другими словами, любое число, которое увеличивается на 2 вместо 1, является нечетным числом. Все эти номера нечетные. И четные, и нечетные числа увеличиваются на два. Как мы можем эффективно различать четные и нечетные числа? Как упоминалось выше, число является четным, если оно делится на два. Любое другое число является нечетным числом. Итак, давайте сосредоточимся на месте единиц. Мы можем различать четные числа и нечетные числа следующим образом. Независимо от того, насколько велико число, если разряд единиц равен 0, 2, 4, 6 или 8, это четное число. Кроме того, независимо от того, насколько велико число, если разряд единиц равен 1, 3, 5, 7 или 9, это нечетное число. Вы можете определить, является ли число четным или нечетным, проверив разряд единиц. Неважно, четное или нечетное число на десятом или сотом месте. Например, 395374 — четное или нечетное число? Если вы проверите 395374, то увидите, что разряд единиц равен 4. 4 — четное число, поэтому 395374 — четное число. Фактически, 395374 можно разделить на 2. Чтобы узнать, четное это число или нечетное, проверьте разряд единиц. Теперь давайте подумаем, будет ли результат сложения или вычитания четным или нечетным. Когда мы делаем сложение, существуют следующие свойства. Объясняя причину, мы должны доказать это с помощью средней школы математика. Поэтому причину мы опустим, но она всегда будет выглядеть так, как указано выше. Итак, давайте рассмотрим простые целые числа следующим образом. Поймите, какой ответ получается при сложении четных или нечетных чисел. Что же происходит при вычитании? Как и при сложении, вычитание дает тот же результат, как показано ниже. При рассмотрении четных и нечетных чисел, если числа с одинаковыми свойства (нечетные и нечетные или четные и четные) добавляются или вычитаются, ответ будет четным. Что происходит при умножении? При умножении, если вы умножаете на четное число, ответ всегда будет четным числом. Если бы вы узнали о кратных в начальной школе по математике, вы бы поняли, почему это происходит. Как упоминалось выше, число, которое делится на два, является четным числом. Четное число тоже кратно 2. При умножении на 2, конечно, ответ всегда будет кратен 2. Кроме того, если вы умножаете не только на 2, но и на четное число, ответ всегда будет четным числом. Это потому, что четное число кратно 2. Единственный случай, когда при умножении получается нечетный результат, — это перемножение нечетных чисел. Итак, при умножении мы получить следующее. В отличие от сложения и вычитания, умножение имеет высокую вероятность того, что ответ будет четным числом. Чтобы ответ был нечетным, нужно нечетные числа перемножить. Одним из наиболее часто используемых понятий являются четные и нечетные числа. Поскольку в повседневной жизни мы часто используем четные и нечетные числа, важно понимать, как различать четные и нечетные числа. Если число делится на 2, то это четное число. Кроме того, если вы разделите на 2 и получите остаток, число будет нечетным.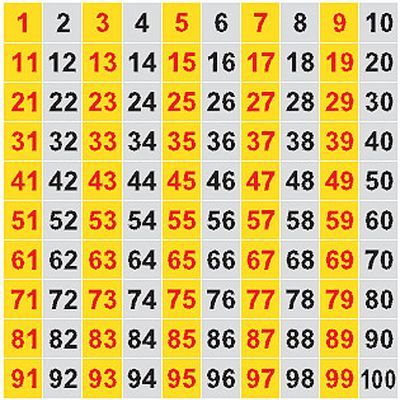
Наименьшее четное число при использовании всех 4 цифр будет 3 4 7 6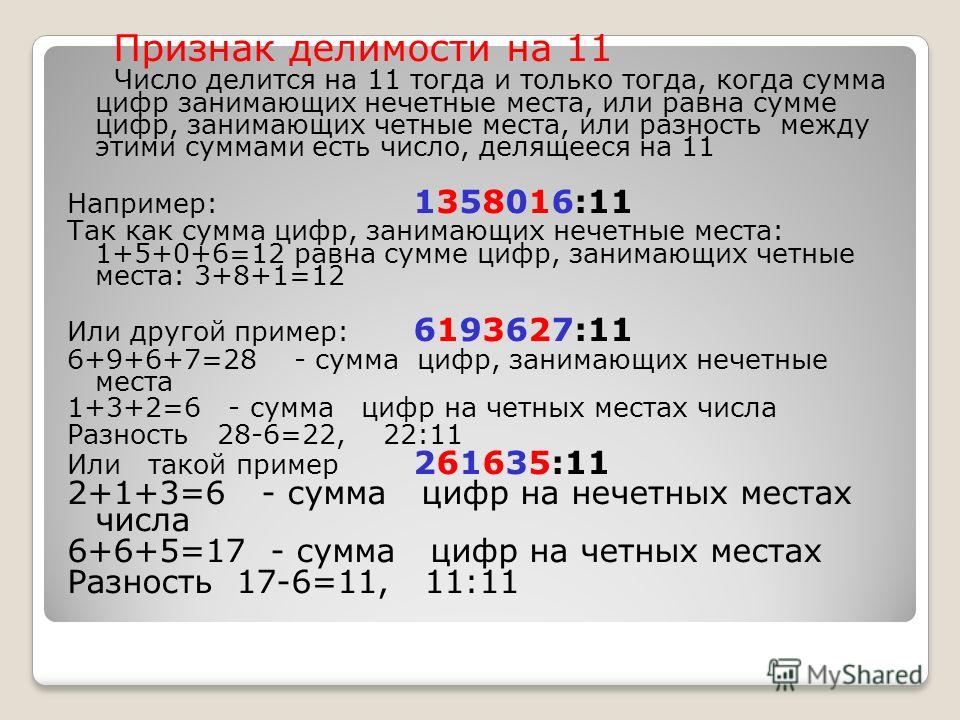 
Как различать и запоминать в математике ｜ Хацуди
Кроме того, мы часто используем четные и нечетные числа при совершении покупок. Каковы и нечетные цифры: определение и смысл
Как различать и запоминать четные и нечетные числа
Другими словами, числа, кратные двум, являются четными числами. С другой стороны, если оно не кратно двум, то это нечетное число.
Является ли ответ на сложение или вычитание четным или нечетным числом?
С другой стороны, при сложении или вычитании чисел с разными свойствами (четными и нечетными) ответ будет нечетным. Это свойство верно и для больших чисел. В умножении ответ: четное или нечетное число?
Как показано ниже, при умножении нечетного числа на нечетное число получается нечетное число. Понимание свойств четных и нечетных чисел
