дифференциальные-уравнения
задан 8 Апр ’13 11:59
Alex7
1●2●8
0% принятых
изменен 8 Апр ’13 18:57
Angry Bird
91●2●5
старыеновыеценные
|
У меня получилось так ссылка отвечен 8 Апр ’13 17:48 ссылка отвечен 8 Апр ’13 12:30 falcao |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.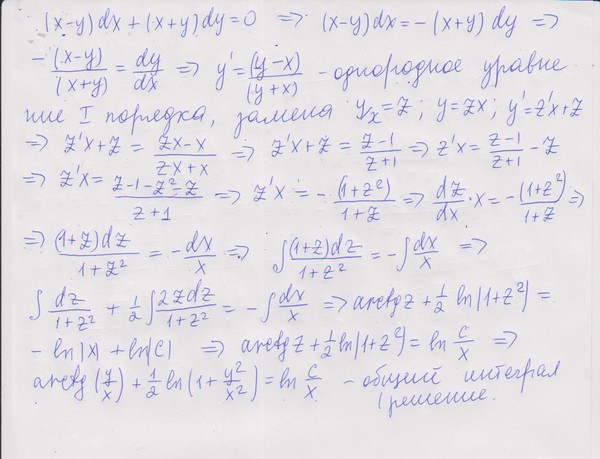
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
регистрация »
отмечен:
дифференциальные-уравнения
×1,199
задан
показан
3086 раз
обновлен
8 Апр ’13 19:26
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
алгебраическое предварительное исчисление — $xy=1 \ подразумевает $минимум $x+y=$?
$\begingroup$
Если $x,y$ — действительные положительные числа, такие что $xy=1$, как я могу найти минимум для $x+y$?
- алгебра-предварительное исчисление
$\endgroup$
0
$\begingroup$
Среднее арифметическое $\ge$ Среднее геометрическое
$\frac{x+y}{2} \ge \sqrt{xy} $ 92\стрелка вправо\mathbb{R}; \ (x,y)\mapsto x+y$ с дополнительным условием $x\cdot y = 1$.
Теперь вы используете множитель Лагранжа и минимизируете функцию $$g(x,y)=x+y+\lambda (xy-1)$$ Теперь вы берете частные производные, которые должны быть равны нулю как минимум \начать{выравнивать*} \frac{\partial g}{\partial x} &= 1+ \lambda y\\ \frac{\partial g}{\partial y} &= 1+ \lambda x\\ \frac{\partial g}{\partial \lambda} &= xy-1 \конец{выравнивание*} Теперь осталось решить систему \начать{выравнивать*} 0&=1+\лямбда у\\ 0&= 1+\лямбда х \\ 0&=ху — 1 \end{выравнивание*} 92+4\cdot x\cdot \frac{1}{x}\geq4$$ Следовательно, $x+y\geq 2$. Также для $x=y=1$ у вас есть $x+y=2$, следовательно, $2$ действительно минимальное значение.
$\endgroup$
$\begingroup$
Приведенный выше ответ делает это полностью.
Однако вы можете представить эту проблему графически. Представьте три оси $x,y,z$ и первый квадрант кривой $xy=1$, проведенные на плоскости $xy$.
{-3}$$
При $x=1$ это $2$. Поскольку это больше 0, мы знаем, что это минимум. Обратите внимание, что в данном случае это только поворотная точка в пределах диапазона, поэтому должен быть глобальный минимум , но в целом вам придется проверять каждую поворотную точку.
Итак, ваш минимум $2$, при $x=1, y=1$.
Некоторые ссылки для новичков в производных:
- http://www.mathsrevision.net/alevel/pages.php?page=45
- http://www.mathsrevision.net/alevel/pages.php?page=43
$\endgroup$
3
$\begingroup$
Вот еще один подход. У нас есть $ x, y > 0 $ и
$$ xy=1 \ подразумевает y=\frac{1}{x}. $$
Подстановка $ y=\frac{1}{x} $ в уравнение $f(x,y)=x+y$ дает
$$ F(x)= x+\frac{1}{x }.$$
Теперь у нас есть функция одной переменной, которую можно минимизировать с помощью методов одномерного исчисления как 92}=0\подразумевает х = 1>0.