3 в разных степенях. Возведение в иррациональную степень. Максимальное число со знаком
На канал на youtube нашего сайта сайт, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2 х = 2 3
Такой пример можно решить даже в уме.
А теперь посмотрим как нужно это решение оформить:
2 х = 2 3
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
3 3х — 9 х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n) m = a nm .
3 3х = (3 2) х+8
Получим 9 х+8 =(3 2) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10 4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n) m = a nm .
4 х = (2 2) х = 2 2х
И еще используем одну формулу a n a m = a n + m:
2 2х+4 = 2 2х 2 4
Добавляем в уравнение:
2 2х 2 4 — 10 2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2:
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2) х = 3 2х
Получаем уравнение:
3 2х — 12 3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены . Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t 1 = 9
t 2 = 3
Возвращаемся к переменной x .
Берем t 1:
t 1 = 9 = 3 х
Стало быть,
3 х = 9
3 х = 3 2
х 1 = 2
Один корень нашли. Ищем второй, из t 2:
t 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу
Основная цель
Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.
Тема “ Степень и её свойства ”
- Определение степени с натуральным показателем.
- Умножение и деление степеней.
- Возведение в степень произведения и степени.
Контрольные вопросы
- Сформулируйте определение степени с натуральным показателем, большим 1. Приведите пример.
- Сформулируйте определение степени с показателем 1. Приведите пример.
- Каков порядок выполнения действий при вычислении значения выражения, содержащего степени?
- Сформулируйте основное свойство степени. Приведите пример.
- Сформулируйте правило умножения степеней с одинаковыми основаниями. Приведите пример.
- Сформулируйте правило деления степеней с одинаковыми основаниями. Приведите пример.
- Сформулируйте правило возведения в степень
произведения.
 Приведите пример. Докажите
тождество (ab) n = a n b n .
Приведите пример. Докажите
тождество (ab) n = a n b n . - Сформулируйте правило возведения степени в степень. Приведите пример. Докажите тождество (а m) n = а m n .
Определение степени.
Степенью числа a с натуральным показателем n , большим 1, называется произведение n множителей, каждый из которых равен а . Степенью числа а с показателем 1 называется само число а .
Степень с основанием а и показателем n записывается так: а n . Читается “ а в степени n ”; “ n- я степень числа а ”.
По определению степени:
а 4 = а а а а
. . . . . . . . . . . .
Нахождение значения степени называют возведением в степень .
1. Примеры возведения в степень:
3 3 = 3 3 3 = 27
0 4 = 0 0 0 0 = 0
(-5) 3 = (-5) (-5) (-5) = -125
25 ; 0,09 ;
25 = 5 2 ; 0,09 = (0,3) 2 ; .
27 ; 0,001 ; 8 .
27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .
4. Найти значения выражений:
а) 3 10 3 = 3 10 10 10 = 3 1000 = 3000
б) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7
Вариант 1
а) 0,3 0,3 0,3
в) b b b b b b b
г) (-х) (-х) (-х) (-х)
д) (ab) (ab) (ab)
2. Представьте в виде квадрата числа:
3. Представьте в виде куба числа:
4. Найти значения выражений:
в) -1 4 + (-2) 3
г) -4 3 + (-3) 2
д) 100 — 5 2 4
Умножение степеней.
Для любого числа а и произвольных чисел m и n выполняется:
a m a n = a m + n .
Доказательство:
Правило : При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.
a m a n a k = a m + n a k = a (m + n) + k = a m + n + k
а) х 5 х 4 = х 5 + 4 = х 9
б) y y 6 = y 1 y 6 = y 1 + 6 = y 7
в) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11
г) 3 4 9 = 3 4 3 2 = 3 6
д) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5
а) 2 3 2 = 2 4 = 16
б) 3 2 3 5 = 3 7 = 2187
Вариант 1
1. Представить в виде степени:
Представить в виде степени:
а) х 3 х 4 е) х 2 х 3 х 4
б) а 6 а 2 ж) 3 3 9
в) у 4 у з) 7 4 49
г) а а 8 и) 16 2 7
д) 2 3 2 4 к) 0,3 3 0,09
2. Представить в виде степени и найти значение по таблице:
а) 2 2 2 3 в) 8 2 5
б) 3 4 3 2 г) 27 243
Для любого числа а0 и произвольных натуральных чисел m и n, таких, что m>n выполняется:
a m: a n = a m — n
Доказательство:
a m — n a n = a (m — n) + n = a m — n + n = a m
по определению частного:
a m: a n = a m — n .
Правило : При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице :
т.к. а n: a n = 1 при а0 .
а) х 4:х 2 = х 4 — 2 = х 2
б) у 8:у 3 = у 8 — 3 = у 5
в) а 7:а = а 7:а 1 = а 7 — 1 = а 6
г) с 5:с 0 = с 5:1 = с 5
а) 5 7:5 5 = 5 2 = 25
б) 10 20:10 17 = 10 3 = 1000
в)
г)
д)
Вариант 1
1.
2. Найдите значения выражений:
Возведение в степень произведения.
Для любых а и b и произвольного натурального числа n:
(ab) n = a n b n
Доказательство:
По определению степени
(ab) n =
Сгруппировав отдельно множители а и множители b, получим:
=
Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.
Например:
(a b c) n = a n b n c n ;
(a b c d) n = a n b n c n d n .
Правило : При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают.
1. Возвести в степень:
а) (a b) 4 = a 4 b 4
б) (2 х у) 3 =2 3 х 3 у 3 = 8 х 3 у 3
в) (3 а) 4 = 3 4 а 4 = 81 а 4
г) (-5 у) 3 = (-5) 3 у 3 = -125 у 3
д) (-0,2 х у) 2 = (-0,2) 2 х 2 у 2 = 0,04 х 2 у 2
е) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4
2. Найти значение выражения:
Найти значение выражения:
а) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000
б) (3 5 20) 2 = 3 2 100 2 = 9 10000= 90000
в) 2 4 5 4 = (2 5) 4 = 10 4 = 10000
г) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1
д)
Вариант 1
1. Возвести в степень:
б) (2 а с) 4
д) (-0,1 х у) 3
2. Найти значение выражения:
б) (5 7 20) 2
Возведение в степень степени.
Для любого числа а и произвольных натуральных чисел m и n:
(а m) n = а m n
Доказательство:
По определению степени
(а m) n =
Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают .
1. Возвести в степень:
(а 3) 2 = а 6 (х 5) 4 = х 20
(у 5) 2 = у 10 (b 3) 3 = b 9
2. Упростите выражения:
а) а 3 (а 2) 5 = а 3 а 10 = а 13
б) (b 3) 2 b 7 = b 6 b 7 = b 13
в) (х 3) 2 (х 2) 4 = х 6 х 8 = х 14
г) (у у 7) 3 = (у 8) 3 = у 24
а)
б)
Вариант 1
1.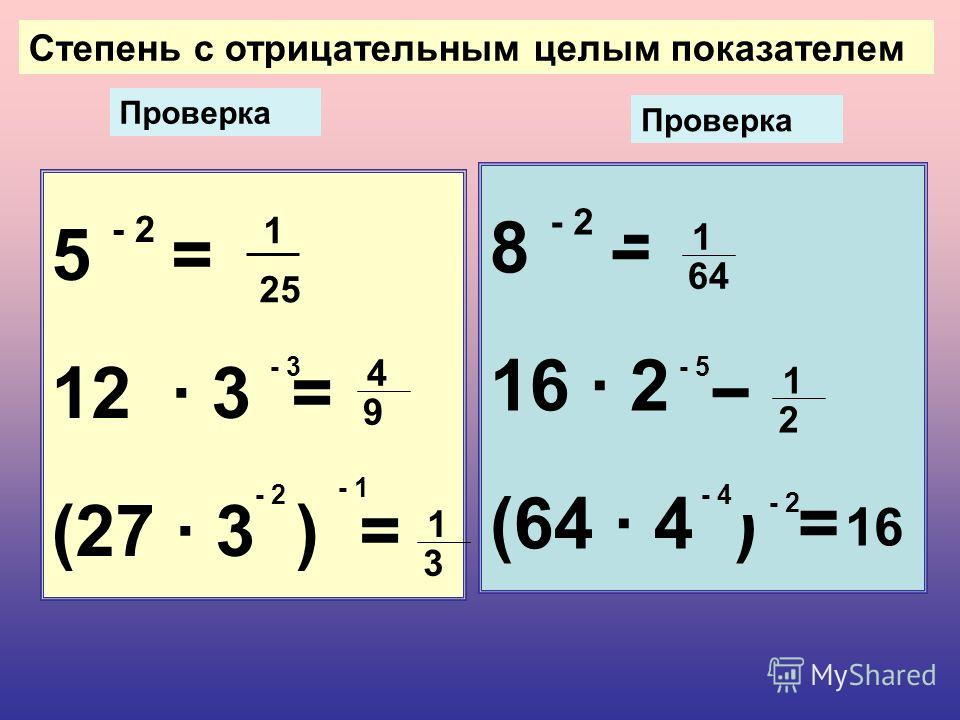 Возвести в степень:
Возвести в степень:
а) (а 4) 2 б) (х 4) 5
в) (у 3) 2 г) (b 4) 4
2. Упростите выражения:
а) а 4 (а 3) 2
б) (b 4) 3 b 5+
в) (х 2) 4 (х 4) 3
г) (у у 9) 2
3. Найдите значение выражений:
Приложение
Определение степени.
Вариант 2
1ю Запишите произведение в виде степени:
а) 0,4 0,4 0,4
в) а а а а а а а а
г) (-у) (-у) (-у) (-у)
д) (bс) (bс) (bс)
2. Представьте в виде квадрата числа:
3. Представьте в виде куба числа:
4. Найти значения выражений:
в) -1 3 + (-2) 4
г) -6 2 + (-3) 2
д) 4 5 2 – 100
Вариант 3
1. Запишите произведение в виде степени:
а) 0,5 0,5 0,5
в) с с с с с с с с с
г) (-х) (-х) (-х) (-х)
д) (ab) (ab) (ab)
2. Представьте в виде квадрата числа: 100 ; 0,49 ; .
3. Представьте в виде куба числа:
4. Найти значения выражений:
в) -1 5 + (-3) 2
г) -5 3 + (-4) 2
д) 5 4 2 — 100
Вариант 4
1. Запишите произведение в виде степени:
а) 0,7 0,7 0,7
в) х х х х х х
г) (-а) (-а) (-а)
д) (bс) (bс) (bс) (bc)
2. Представьте в виде квадрата числа:
3. Представьте в виде куба числа:
4. Найти значения выражений:
в) -1 4 + (-3) 3
г) -3 4 + (-5) 2
д) 100 — 3 2 5
Умножение степеней.
Вариант 2
1. Представить в виде степени:
а) х 4 x 5 е) х 3 х 4 х 5
б) а 7 а 3 ж) 2 3 4
в) у 5 у з) 4 3 16
г) а а 7 и) 4 2 5
д) 2 2 2 5 к) 0,2 3 0,04
2. Представить в виде степени и найти значение по таблице:
а) 3 2 3 3 в) 16 2 3
б) 2 4 2 5 г) 9 81
Вариант 3
1. Представить в виде степени:
Представить в виде степени:
а) а 3 а 5 е) у 2 у 4 у 6
б) х 4 х 7 ж) 3 5 9
в) b 6 b з) 5 3 25
г) у у 8 и) 49 7 4
д) 2 3 2 6 к) 0,3 4 0,27
2. Представить в виде степени и найти значение по таблице:
а) 3 3 3 4 в) 27 3 4
б) 2 4 2 6 г) 16 64
Вариант 4
1. Представить в виде степени:
а) а 6 а 2 е) х 4 х х 6
б) х 7 х 8 ж) 3 4 27
в) у 6 у з) 4 3 16
г) х х 10 и) 36 6 3
д) 2 4 2 5 к) 0,2 2 0,008
2. Представить в виде степени и найти значение по таблице:
а) 2 6 2 3 в) 64 2 4
б) 3 5 3 2 г) 81 27
Деление степеней.
Вариант 2
1. Представьте в виде степени частное:
2. Найдите значения выражений.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Все определения будут проиллюстрированы примерами.
Yandex.RTB R-A-339285-1
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1
Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени (0 , 5) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Приведем примеры.
Пример 1
Условие: возведите — 2 в степень 4 .
Решение
Используя определение выше, запишем: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Пример 2
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Пример 3
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ (3 , 14) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .
Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи .
От основания степени это не зависит.
Пример 4
Так, (− 9) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
Пример 5
5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1
0 0 — не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Пример 6
Возведите 3 в степень — 2 .
Решение
Используя определение выше, запишем: 2 — 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8: 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8
Пример 7
Возведите 1 , 43 в степень — 2 .
Решение
Переформулируем: 1 , 43 — 2 = 1 (1 , 43) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1 , 43) — 2 = 1 (1 , 43) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1 , 43) — 2 = 10000 20449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .
Пример 8
Пример: 3 − 1 = 1 / 3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Определение 2
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а, потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Пример 9
Вычислите 8 — 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2
После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Пример 10
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь — 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11
Вычислите приближенное значение 21 , 174367 ….
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Когда число умножается само на себя , произведение называется степенью .
Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.
Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.
И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a
Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.
Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения.
Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель . Это число или буква называется показателем степени или степенью числа. Так, а 2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a 3 означает aaa, то есть здесь a повторяется три раза как множитель.
Также, a 3 означает aaa, то есть здесь a повторяется три раза как множитель.
Показатель первой степени есть 1, но он обычно не записывается. Так, a 1 записывается как a.
Вы не должны путать степени с коэффициентами . Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a. Но a 4 = a.a.a.a
Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква . В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a x , показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень . Так, b m и d n возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b m = b 3 ; но если m = 5, тогда b m =b 5 .
Так, b m и d n возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b m = b 3 ; но если m = 5, тогда b m =b 5 .
Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d) 3 есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a 3 + 3a 2 b + 3a 2 d + 3ab 2 + 6abd + 3ad 2 + b 3 + d 3 .
Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель , и этот множитель или делитель есть первоначальным числом, которое возводится в степень.
Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a 5 , a 4 , a 3 , a 2 , a 1 ;
показатели, если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножать на a, мы успешно получим несколько значений.
Если мы начнем справа умножать на a, мы успешно получим несколько значений.
Tак a.a = a 2 , второй член. И a 3 .a = a 4
a 2 .a = a 3 , третий член. a 4 .a = a 5 .
Если мы начнем слева делить на a,
мы получим a 5:a = a 4 и a 3:a = a 2 .
a 4:a = a 3 a 2:a = a 1
Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.
Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.
Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.
Или a 5 , a 4 , a 3 , a 2 , a, 1, 1/a, 1/a 2 , 1/a 3 .
Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.
Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a 3) = a 3 .
Тот же самый план записи может применяться к многочленам . Так, для a + b, мы получим множество,
(a + b) 3 , (a + b) 2 , (a + b), 1, 1/(a + b), 1/(a + b) 2 , 1/(a + b) 3 .
Для удобства используется еще одна форма записи обратных степеней.
Согласно этой форме, 1/a или 1/a 1 = a -1 . И 1/aaa или 1/a 3 = a -3 .
1/aa или 1/a 2 = a -2 . 1/aaaa или 1/a 4 = a -4 .
А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a 0 .
Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a 4 , a 3 , a 2 , a 1 , a 0 , a -1 , a -2 , a -3 , a -4 .
Или a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.
Корень степени может выражен более чем одной буквой.
Так, aa.aa или (aa) 2 есть второй степенью aa.
И aa.aa.aa или (aa) 3 есть третьей степенью aa.
Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.
Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:
Правило возведения в степень:
Умножайте величину саму на себя столько раз, сколько указано в степени числа.
Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.
Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.
Четвертая степень a есть a 4 или aaaa. (Art. 195.)
Шестая степень y есть y 6 или yyyyyy.
N-ая степень x есть x n или xxx….. n раз повторенное.
Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.
Tак (ay) 2 =a 2 y 2 ; (ay) 2 = ay.ay.
Но ay.ay = ayay = aayy = a 2 y 2 .
Так, (bmx) 3 = bmx.bmx.bmx = bbbmmmxxx = b 3 m 3 x 3 .
Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.
Пример 1. Четвертая степень dhy есть (dhy) 4 , или d 4 h 4 y 4 .
Пример 2. Третья степень 4b, есть (4b) 3 , или 4 3 b 3 , или 64b 3 .
Пример 3. N-ая степень 6ad есть (6ad) n или 6 n a n d n .
Пример 4. Третья степень 3m.2y есть (3m.2y) 3 , или 27m 3 .8y 3 .
Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,
(a + b) 1 = a + b, первая степень.
(a + b) 1 = a 2 + 2ab + b 2 , вторая степень (a + b).
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 , третья степень.
(a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 , четвертая степень.
Квадрат a — b, есть a 2 — 2ab + b 2 .
Квадрат a + b + h есть a 2 + 2ab + 2ah + b 2 + 2bh + h 2
Упражнение 1. Найдите куб a + 2d + 3
Упражнение 2. Найдите четвертую степень b + 2.
Упражнение 3. Найдите пятую степень x + 1.
Упражнение 4. Найдите шестую степень 1 — b.
Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.
Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a 2 + 2ah + h 2 также, (a — h)(a — h) = a 2 — 2ah + h 2 .
Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.
Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.
Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.
Пример 1. Квадрат 2a + b, есть 4a 2 + 4ab + b 2 .
Пример 2. Квадрат ab + cd, есть a 2 b 2 + 2abcd + c 2 d 2 .
Пример 3. Квадрат 3d — h, есть 9d 2 + 6dh + h 2 .
Пример 4. Квадрат a — 1 есть a 2 — 2a + 1.
Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.
Во многих случаях является эффективным записывать степени без умножения.
Так, квадрат a + b, есть (a + b) 2 .
N-ая степень bc + 8 + x есть (bc + 8 + x) n
В таких случаях, скобки охватывают все члены под степенью.
Но если корень степени состоит из нескольких множителей , скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.
Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)] 2 или (a + b) 2 .(c + d) 2 .
Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.
Куб a.(b + d), есть 3 , или a 3 .(b + d) 3 .
Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.
Вторая степень (- a) есть +a 2
Третья степень (-a) есть -a 3
Четвёртая степень (-a) есть +a 4
Пятая степень (-a) есть -a 5
Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a 2
И -a.-a = +a 2
Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.
Третья степень a 2 есть a 2.3 = a 6 .
Для a 2 = aa; куб aa есть aa.aa.aa = aaaaaa = a 6 ; что есть шестой степенью a, но третьей степенью a 2 .
Четвертая степень a 3 b 2 есть a 3.4 b 2.4 = a 12 b 8
Третья степень 4a 2 x есть 64a 6 x 3 .
Пятая степень (a + b) 2 есть (a + b) 10 .
N-ая степень a 3 есть a 3n
N-ая степень (x — y) m есть (x — y) mn
(a 3 .b 3) 2 = a 6 .b 6
(a 3 b 2 h 4) 3 = a 9 b 6 h 12
Правило одинаково применяется к отрицательным степеням.
Пример 1. Третья степень a -2 есть a -3.3 =a -6 .
Для a -2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a 6 = a -6
Четвертая степень a 2 b -3 есть a 8 b -12 или a 8 /b 12 .
Квадрат b 3 x -1 , есть b 6 x -2 .
N-ая cтепень ax -m есть x -mn или 1/x .
Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.
Пример 1. Квадрат -a 3 есть +a 6 . Квадрат -a 3 есть -a 3 .-a 3 , которое, согласно правилам знаков при умножении, есть +a 6 .
2. Но куб -a 3 есть -a 9 . Для -a 3 .-a 3 .-a 3 = -a 9 .
3. N-ая степень -a 3 есть a 3n .
Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.
Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.
Квадрат a/b есть a 2 /b 2 . Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a 2 b 2
Вторая, третья и n-ая степени 1/a есть 1/a 2 , 1/a 3 и 1/a n .
Примеры двочленов , в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2) 2 = x 2 + 2.x.(1/2) + 1/2 2 = x 2 + x + 1/4
(x — 1/2) 2 = x 2 — 2.x.(1/2) + 1/2 2 = x 2 — x + 1/4
2. Квадрат a + 2/3 есть a 2 + 4a/3 + 4/9.
3. Квадрат x + b/2 = x 2 + bx + b 2 /4.
4 Квадрат x — b/m есть x 2 — 2bx/m + b 2 /m 2 .
Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени .
Так, в дроби ax -2 /y, мы можем переместить x из числителя в знаменатель.
Тогда ax -2 /y = (a/y).x -2 = (a/y).(1/x 2 = a/yx 2 .
В дроби a/by 3 мы можем переместить у из знаменателя в числитель.
Тогда a/by 2 = (a/b).(1/y 3) = (a/b).y -3 = ay -3 /b.
Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель. 2
2
Текстовый документ по теме «Степень числа»
Степень числа.
Введение.
Один раз мне на олимпиаде по математике попался вопрос:
„Какой цифрой оканчивается значение выражения 2 в 2013 степени?“
Определение степени я уже знала. Со свойствами степени я была знакома. Но ответить на данный вопрос не смогла. И я поставила перед собой цель:
узнать, какой цифрой оканчивается значение выражения чисел в разных степенях.
Задачи:
выяснить, какой цифрой оканчивается значения выражения от 2 до 10 в степени 2015;
заметить закономерность появления цифр на конце степени числа;
сделать выводы.
Оказывается, это очень просто узнать…
Если возводить в степень цифру 2,можно кое-что заметить:
2 в первой степени- 2
2 во второй степени- 4
2 в третьей степени- 8
2 в четвёртой степени- 16
2 в пятой степени- 32
2 в шестой степени- 64
2 в седьмой степени- 128
2 в восьмой степени- 256
2 в девятой степени- 512
2 в десятой степени- 1024
В какую бы степень мы не возводили 2, окончания будет только цифры: 2,4,6,8 — четыре числа
Из наблюдений можно составить таблицу:
Показатель степени | Последняя цифра | Остаток от деления на 4 показателя |
1 | 2 | 1 |
2 | 4 | 2 |
3 | 8 | 3 |
4 | 6 | 0 |
5 | 2 | 1 |
6 | 4 | 2 |
7 | 8 | 3 |
8 | 6 | 0 |
9 | 2 | 1 |
10 | 4 | 2 |
Какой же цифрой оканчивается значение выражения 2 в 2013 степени?
Для этого нужно разделить 2013 на 4 с
остатком.
После деления в столбик,2013/4=503(ост.1)
Остаток от деления на 4 показателя, будет
1.
Смотрим на таблицу.
И так получаем, что 2 в 2013 степени будет оканчиваться цифрой 2.
Узнаем, какой же цифрой оканчивается
значение выражения 2 в 2015 степени.
Делим 2015 на 4.
2015/4 = 503 (ост. 3)
Из таблицы получаем, что значение выражения 2 в 2015 степени будет оканчиваться цифрой 8.
Степень числа 3.
Итак, будем возводить в степень цифру 3:
3 в первой степени-
3 во второй степени-9
3 в третей степени-27
3 в четвёртой степени-81
3 в пятой степени- 243
3 в шестой степени-729
3 в седьмой степени-2187
3 в восьмой степени-6561
3 в девятой степени-19683
3 в десятой степени-54049
Если цифру 3 возводить в степень, число будет оканчиваться только на: 3,7,9,1 — четыре числа
Показатель степени | Последняя цифра | Остаток от деления на 4 показателя |
1 | 3 | 1 |
2 | 9 | 2 |
3 | 7 | 3 |
4 | 1 | 0 |
5 | 3 | 1 |
6 | 9 | 2 |
7 | 7 | 3 |
8 | 1 | 0 |
9 | 3 | 1 |
10 | 9 | 2 |
„Какой цифрой оканчивается значение выражения 3 в 2015 степени?“
Решим точно так же. 2015 делим на 4 с
остатком
2015 делим на 4 с
остатком
Остаток 3. Смотрим в таблицу.
И так получаем, что 3 в 2015 степени, будет оканчиваться цифрой 7.
Степень числа 4.
Рассмотрим ещё и 4 в степени от 1до 10. Имеем:
4 в первой степени: 4
4 во второй степени: 16
4 в третей степени: 64
4 в четвертой степени: 256
4 в пятой степени: 1024
4 в шестой степени: 4096
4 в седьмой степени: 16384
4 в восьмой степени: 65636
4 в девятой степени: 262144
4 в десятой степени: 10485
Если цифру 4 возводить в степень, число будет оканчиваться только на: 4, 6.
Здесь уже 2 числа
Показатель степени | Последняя цифра | Остаток от деления на 2 показателя |
1 | 4 | 0 |
2 | 6 | 1 |
3 | 4 | 0 |
4 | 6 | 1 |
5 | 4 | 0 |
6 | 6 | 1 |
7 | 4 | 0 |
8 | 6 | 1 |
9 | 4 | 0 |
10 | 6 | 1 |
„Какой цифрой оканчивается значение выражения 4 в 2015 степени?“
Делим 2015 уже на 2. 2015/2 = 1007 (ост:
1)
2015/2 = 1007 (ост:
1)
Значение выражения 4 в 2015 степени будет оканчиваться цифрой 6
Степень числа 5,6, 10.
Число 5:
5 во второй степени: 25
5 в третьей степени: 125
5 в четвёртой степени: 625
5 в пятой степени: 3125
5 в шестой степени: 15625
5 в седьмой степени: 78125
5 в восьмой степени: 390625
5 в девятой степени: 1953125
5 в десятой степени: 9765625
Если цифру 5 возводить в степень, число будет оканчиваться только на: 5
В какую бы мы степень не возводили цифру 5. Число всё равно будет оканчиваться на 5.
Так же число 6.
В какую бы степень не возводили 6, значение выражения будет оканчиваться на
6.
Ещё число 10, тоже имеет одну цифру на конце.
Продолжим возводить в степень число7.
7 в первой степени: 7
7 во второй степени: 49
7 в третьей степени: 343
7 в четвёртой степени: 2401
7 в пятой степени: 16807
7 в шестой степени: 117649
7 в седьмой степени: 823543
7 в восьмой степени: 5764801
7 в девятой степени: 40353607
7 в десятой степени: 282475249
Окончанием степени числа 7 могут быть только числа — 7, 9, 3, 1 — 4 числа
Показатель степени | Последняя цифра | Остаток от деления на 4 показателя |
|
1 | 7 | 3 | 74т+п имеет последней ту же цифру, что число 7п |
2 | 9 | 1 | |
3 | 3 | 3 | |
4 | 1 | 1 | |
5 | 7 | 3 | |
6 | 9 | 1 | |
7 | 3 | 3 | |
8 | 1 | 1 | |
9 | 7 | 3 | |
10 | 9 | 1 |
„Какой цифрой оканчивается значение выражения 7 в 2015 степени?“
Делим 2015 на 4.
2015/4 = 503 (ост: 3). А остатки от деления только 1и 3. Что делать?
Значение выражения 7 в 2015 степени оканчивается той же цифрой, что и 7 в третьей степени, то есть цифрой 3
Возводим в степень число 8.
8 в первой степени: 8
8 во второй степени: 64
8 в третьей степени: 512
8 в четвёртой степени: 4096
8 в пятой степени: 32768
8 в шестой степени: 262144
8 в седьмой степени: 2097152
8 в восьмой степени: 16777216
8 в девятой степени: 134217728
8 в десятой степени: 1073741824
На конце выражения степени числа8 стоят цифры- 8, 4,2,6 –всего 4 цифры.
Показатель степени | Последняя цифра | Остаток от деления на 4 показателя |
а4т+п имеет последней ту же цифру, что число 8п |
1 | 8 | 0 | |
2 | 4 | 0 | |
3 | 2 | 2 | |
4 | 6 | 2 | |
5 | 8 | 0 | |
6 | 4 | 0 | |
7 | 2 | 2 | |
8 | 6 | 2 | |
9 | 8 | 0 | |
10 | 4 | 0 |
Какой цифрой оканчивается значение выражения 8 в 2015 степени?“
Делим 2015 на 4.
2015/3 =671 (остаток 2) . Значит, 8в 2015 степени оканчивается на ту же цифру,
что и число 8во второй, то есть — 4
Степень числа 9.
9 в первой степени: 9
9 во второй степени: 81
9 в третьей степени: 729
9 в четвёртой степени: 6561
9 в пятой степени: 59049
9 в шестой степени: 531441
9 в седьмой степени: 4782969
9 в восьмой степени: 43046721
9 в девятой степени:4782969
9 в десятой степени: 43046721
Окончание степени числа 9 только 2 числа: 9 и 1
Как быть?
Показатель степени | Последняя цифра | Нечётный показатель степени – на конце степени числа — цифра 9 Чётный показатель степени – на конце степени числа — цифра 1
|
1 | 9 | |
2 | 1 | |
3 | 9 | |
4 | 1 | |
5 | 9 | |
6 | 1 | |
7 | 9 | |
8 | 1 | |
9 | 9 | |
10 | 1 |
Выражение 9 в 2015 степени оканчивается
цифрой 9, так как: 2015 показатель степени нечетный.
Примеры задач.
Примеры задач взяты из интернета « Методическая разработка занятия с одаренными детьми
«Степень с натуральным показателем. Сравнение степеней», составленной
учителями:
Алекаева Наталья Александровна, учитель математики
Веденеева Ирина Викторовна, учитель математики
Лазарян Елена Сергеевна, учитель математики
Задача 1
Найти последнюю цифру числа 82006.
Решение:
если число оканчивается на 8, то его степени оканчиваются на 8,4,2,6. Повторение через 4.
а4т+п имеет последней ту же цифру, что число ап.
2006=501 х 4 +2.
82006=84 х 501+2, значит, это число имеет ту же цифру, что и 82, т.е. оканчивается на 4.
Задача 2
На какую цифру оканчивается число 32004+42005?
Решение:
32004 | оканчивается на 1. |
41=4 | Если степень числа 4 – нечётное число, то число оканчивается на “4”, если степень чётная, на “6”. 2005 – нечётное число, значит, 42005 оканчивается на “4”. |
32004+42005 | оканчивается на “5” (1+4=5). Ответ. Данное выражение оканчивается на “5” |
Задача 3
Доказать, что разность 9999931999 – 7777771997 кратна 5.
Решение:
Если оканчивается цифрой 3, то степени оканчиваются 3,9,7,1. Повторение через 4. в нашем случае 1999:4=499+3, 1999=4 х 499 +3. Значит число 9999931999 оканчивается на ту же цифру, что число 33, т.е. на 7.
Если число
оканчивается на 7, то степень числа оканчивается на 7,9,3,1. повторение через
4.
повторение через
4.
71=7
72=49
73=343
74=2401
75=16807
1997:4=499+4
1997 = 4 х 499+1, значит, 7777771997 оканчивается на туже цифру, что и число 71, т.е. на 7.
Разность данных чисел оканчивается на 0 (7–7=0), 0:5, следовательно, разность кратна “5”.
Ответ. Разность кратна 5.
Задача 4.
Какой цифрой оканчивается число ((9999999)99)9 .
Решение:
91=9
92=81
93=729
Если степень четная, то число оканчивается на 1, если степень нечетная, то на 9.
999 оканчивается на 9, т.к. 9 – нечетное число
число 999 – нечетное, т.к. оканчивается на 9.
((99999)9 оканчивается на 9, т.е. оно нечётное.
((999999)99)9 оканчивается на 9, т.к. степень нечетная.
Ответ. 9.
9.
Задача 5
776776+777777+778778. Какой цифрой оканчивается сумма и кратна ли она 5.
Решение:
776776 оканчивается 6 .
777777 оканчивается
7. если число оканчивается на 7, то его степени оканчиваются на 7,9,3,1,
повторение через 4.
777=4 х 194+1.
Значит, 777777 имеет последней ту же цифру, что и 71,
т.е. оканчивается на 7.
778778
81=8 82=64
83=512 84=4096
85=32768 Степени оканчиваются на 8,4,2,6. Повторение через 4. 778778 оканчивается на ту же цифру что и 83, т.е. на 2. 778=4 х 194+3.
Наша сумма оканчивается на 5 (6+7+2=15).
Ответ. Сумма оканчивается на 5, кратна 5.
Задача 5
Число 3 возвели в 23-ю степень. Полученное число вновь возвели в 23-ю степень и так далее. Возведение повторено2013 раз. Определить последнюю цифру полученного
числа.
Решение №3. Натуральные степени числа 3 оканчиваются на 3, 9, 7, 1, 3, 9, 7, 1, … . Остаток от деления 23 на 4 равен 3, поэтому 23-я степень числа 3 оканчивается на 7. Натуральные степени числа 7 оканчиваются на 7, 9, 3, 1, 7, 9, 3, 1, … . Остаток от деления 23 на 4 равен 3, поэтому 23-я степень 23-ей степени числа 3 оканчивается на 3. Продолжая рассуждать аналогичным образом, получим, что искомое число оканчивается на 7.
Ответ. Число оканчивается на 7.
Вывод: Я заметила закономерность появления цифр на конце степени числа. Узнала, какой цифрой оканчивается значение выражения чисел от 2 до 10 в степени 2015
Полученные знания можно применять: в
математике, в логических задачах, на олимпиадах.
Литература.
« Методическая разработка занятия с одаренными детьми «Степень с натуральным показателем. Сравнение степеней», составленная учителями:
Алекаева Наталья Александровна, учитель математики
Веденеева Ирина Викторовна, учитель математики
Лазарян Елена Сергеевна, учитель математики
Содержание
Введение ………………………………………………………………………. 1
1
Степень числа 2 1-2
Степень числа 3 3-4
Степень числа 4 4-5
Степень числа 5,6,10. 6
Степень числа 7 6-7
Степень числа 8 8-9
Степень числа 9 9-10
Примеры задач. 10-13
Заключение. 14
14
Литература. 15
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
3 радиана в градус
3 радиана равняются 171,887 градусам
Универсальный конвертер единиц измерения
| ⇆ | ||
Пожалуйста, выберите физическую величину, две единицы, затем введите значение в любом из полей выше. | ||
Чтобы вычислить значение до соответствующего значения в градусах, просто умножьте количество в радианах на 57,29.5779513082 (коэффициент пересчета). Вот формула :
Значение в градусах = значение в радианах × 57,295779513082
Предположим, вы хотите преобразовать 3 радиана в градусы. Используя приведенную выше формулу преобразования, вы получите:
Значение в градусах = 3 × 57,295779513082 = 171,887 градусов
Этот конвертер может помочь вам получить ответы на такие вопросы, как:
- Сколько радиан в 3 градусах?
- 3 радиана скольким градусам равны?
- Сколько в градусах 3 радиана?
- Как преобразовать радианы в градусы?
- Какой коэффициент преобразования радиан в градусы?
- Как перевести радианы в градусы?
- По какой формуле можно перевести радианы в градусы? Среди прочих.
Таблица преобразования радиан в градусы
В таблице ниже содержатся пары значений из радиан в градусы в диапазоне от одной до ста тысяч.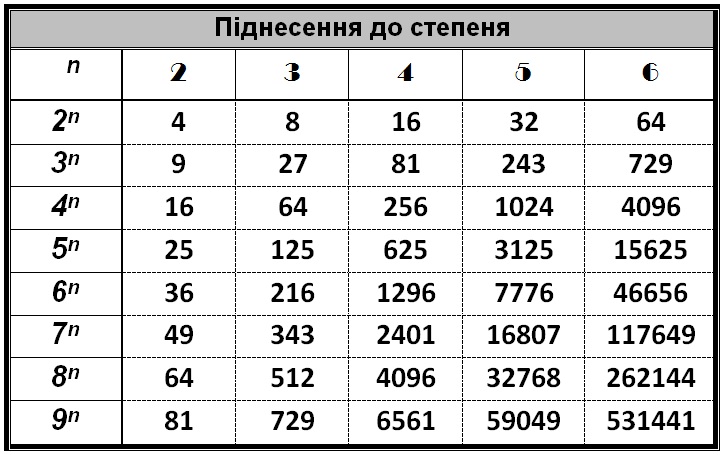
Radians to degrees table
0 to 1
| Radians to degrees |
|---|
| 0 rad = 0 deg |
| 0.001 rad = 0.0573 deg |
| 0.002 rad = 0.115 deg |
| 0.003 rad = 0,172 град |
| 0,004 RAD = 0,229 град |
| 0,005 RAD = 0,286 град |
| 0,006 RAD = 0,344 DEG |
| 0,007 RAD = 0,401 DEG | 0,007 RAD = 0,401 DEG | 9000 0,008 0,008 0,008.0005 |
| 0,009 RAD = 0,516 град |
| 0,01 RAD = 0,573 град |
| 0,02 RAD = 1,15 DEG |
| 0,03 RAD = 1,72 град |
| 0,04 RAD = 2,2939.03 RAD = 1,72 град |
| 04 0,039 0,03 RAD = 1,72 градуса |
| 0,06 RAD = 3,44 град |
| 0,07 RAD = 3,44 град |
| 0,08 RAD = 4,58 DEG |
| 0,09 RAD = 5,16 DEG |
0. 0.0.09 0,09 RAD = 5,16 DEG 0.0.09 0,09 RAD = 5,16 DEG |
| 0,10,10,104 0,09 DAD = 5,16 DEG |
| 0,09.0005 |
| 1 / 5 rad = 11.5 deg |
| 0.3 rad = 17.2 deg |
| 0.4 rad = 22.9 deg |
| 1 / 2 rad = 28.6 deg |
| 0.6 rad = 34.4 deg |
| 0.7 rad = 40.1 deg |
| 0.8 rad = 45.8 deg |
| 0.9 rad = 51.6 deg |
| 1 rad = 57.3 deg |
Radians to degrees table
1 to 10000
| Radians to degrees |
|---|
| 1 rad = 57.3 deg |
| 2 rad = 115 deg |
| 3 rad = 172 deg |
| 4 rad = 229 град |
| 5 RAD = 286 DEG |
| 6 RAD = 344 DEG |
| 7 RAD = 401 DEG |
| 8 RAD = 458 DEG |
| 9 RAD = 516 DEG |
| 9 RAD = 516 DEG |
| 10 RAD = 573 град |
| 20 RAD = 1150 DEG |
| 30 RAD = 1720 DEG |
| 40 RAD = 2290 DEG |
| 50 RAD = 2860 DEG |
| 60 RAD = 34404 град |
| 70 RAD = 4010 град |
| 80 RAD = 4580 DEG |
| 90 RAD = 5160 DEG |
| 100 RAD = 5730 DEG |
200 RAD = 11500 DEG111111111119 |
200 RAD = 11500 DEG1111111111111111111111111111119 |
| 200 300 рад = 17200 град |
| 400 rad = 22900 deg |
| 500 rad = 28600 deg |
| 600 rad = 34400 deg |
| 700 rad = 40100 deg |
| 800 rad = 45800 deg |
| 900 RAD = 51600 DEG |
| 1000 RAD = 57300 DEG |
| 10000 RAD = 573000 градусов |
градусов до радиан.
 Таблица
Таблица от 0 до 100
| 666666666666666666.0977 |
|---|
| 0 DEG = 0 RAD |
| 0,1 DEG = 0,00175 RAD |
| 1 / 5 DEG = 0,00349 RAD |
0,3 DEG = 0,00524 RAD1 |
| 0,3 DEG. RAD |
| 1 / 2 DEG = 0,00873 RAD |
| 0,6 DEG = 0,0105 RAD |
| 0,7 град = 0,0122 RAD |
| 0,8 DEG = 0,014 RAD 9000 9000 9000 9000 |
| 0,8 DEG = 0,014 RAD 9000 9000 9000 |
| 0,8 DEG = 0,014 RAD 9000 9000 |
| .0004 0.9 deg = 0.0157 rad |
| 1 deg = 0.0175 rad |
| 2 deg = 0.0349 rad |
| 3 deg = 0.0524 rad |
| 4 deg = 0.0698 rad |
| 5 deg = 0.0873 RAD |
| 6 DEG = 0,105 RAD |
| 7 DEG = 0,105 RAD |
| 8 DEG = 0,14 RAD |
| 9 DEG = 0,157 RAD |
10 DEG = 0,175 RAD1111119 |
10 DEG = 0,175 RAD1111111111111111119 |
10 DEG. 0004 20 градусов = 0,349 рад 0004 20 градусов = 0,349 рад |
| 30 DEG = 0,524 RAD |
| 40 DEG = 0,698 RAD |
| 50 DEG = 0,873 RAD |
| 60 DEG = 1,05 RAD |
| 60 DEG = 1,05 RAD |
| 80 deg = 1.4 rad |
| 90 deg = 1.57 rad |
| 100 deg = 1.75 rad |
Degrees to radians table
100 to 1000000
| Degrees to radians | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 deg = 1.75 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 200 deg = 3.49 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 300 deg = 5.24 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 400 deg = 6.98 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 500 deg = 8.73 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 600 DEG = 10,5 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 700 DEG = 12,2 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 800 DEG = 14 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 900 DEG = 15,7 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1000 DEG = 17,5 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2000 DEG. 0005 0005 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3000 DEG = 52,4 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4000 DEG = 69,8 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5000 DEG = 87,3 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6000 DEG = 105 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7000 DEG. DEG = 140 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9000 DEG = 157 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10000 DEG = 175 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20000 DEG = 349 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30000 DEG = 524 RAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40000 DEG = 6900 DEG.8 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50000 deg = 873 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60000 deg = 1050 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70000 deg = 1220 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80000 deg = 1400 rad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Радианы до градусов переоборудования от 1 до 100Radians до градусов Таблицы1–25 Radians до градусов.0973
Радиан до градусов Таблица51 до 75
Radians to degrees table76 to 100
Clean Energy Consulting — Renewable Energy PartnerOur Story For over 15 years, our renewable energy, transportation decarbonization, and climate Решения позволили предприятиям и коммунальным службам откликнуться на призыв к немедленным и значимым действиям по борьбе с изменением климата. ПИОНЕРЫ В ОБЛАСТИ КЛИМАТИЧЕСКИХ РЕШЕНИЙПоддержка запуска первых добровольных общественных программ солнечной энергетики в США Ведение переговоров по созданию первого в США зеленого тарифа Содействовал крупнейшей совокупной сделке по возобновляемым источникам энергии Инициировал некоторые из первых сделок с возобновляемыми источниками природного газа Целеустремленность Стив Макдугал и Дэн Калафатас основали компанию 3Degrees, полагая, что бизнес должен служить интересам всех заинтересованных сторон и играть центральную роль в решении глобального климатического кризиса. Наше название было вдохновлено целями глобального потепления, которые ставились в то время для предотвращения катастрофического изменения климата. Несмотря на то, что цели изменились с момента нашего основания, мы по-прежнему стремимся добиваться максимально возможного воздействия на климат. Я горжусь тем, что работаю в 3Degrees. Глубокий опыт и таланты компании поражают… Для меня большая честь быть частью этого». — ДЭН КАЛАФАТАС, СОУЧРЕДИТЕЛЬ И ПРЕДСЕДАТЕЛЬ ПРАВЛЕНИЯ UNITED FOR CLIMATE ACTIONВ 2017 году компания 3Degrees объединилась с Origin Climate — инициатором разработки углеродных проектов и доверенным консультантом по корпоративной стратегии и закупкам в области возобновляемых источников энергии, чья совместная сертификация B Corp и согласованные ценности представляют собой идеальное партнерство и возможность добиться большего влияния на наших клиентов. ПОДДЕРЖКА ЛИДЕРОВ В ОБЛАСТИ УСТОЙЧИВОГО РАЗВИТИЯ Сегодня 3Degrees помогает нашему постоянно растущему числу клиентов достигать целей в области возобновляемых источников энергии и обезуглероживания. Прежде всего, 3Degrees обязана своей устойчивостью, ростом и успехом отстаиванию наших основных ценностей. Каждый сотрудник 3Degrees несет ответственность за знание и соблюдение этих принципов. Выберите значение ниже, чтобы узнать больше.
Страстьза принятие срочных мер по борьбе с изменением климата.Сейчас больше, чем когда-либо, миру нужны деловые и общественные лидеры для принятия мер по борьбе с изменением климата. Мы гордимся тем, что принимаем меры в рамках нашей собственной деятельности и предоставляем исключительные услуги нашим клиентам для решения этой проблемы. УВАЖЕНИЕдля всех людей.Мы стремимся привнести равенство и справедливость в нашу повседневную деятельность и создать корпоративную культуру, основанную на уважении и включении всех людей, где голоса с различным опытом, опытом и точками зрения слышны и ценны на всех уровнях нашей организации. ОБЯЗАТЕЛЬСТВОдобиваться результатов за счет новаторских работ. Суть для нас в том, чтобы как можно быстрее и эффективнее продвигать значимые меры по борьбе с изменением климата. Мы не уклоняемся от сложных заданий или первой в своем роде работы. Наши предложения услуг и взаимодействие с сотрудниками постоянно развиваются, поскольку мы стремимся оказывать максимальное влияние на наши сообщества и окружающую среду. ЧЕСТНОСТЬруководит нашими действиями. Всегда.Дело не только в том, что вы делаете, но и в том, как вы это делаете. Мы стараемся всегда поступать правильно, даже когда никто не смотрит. В своей деятельности мы руководствуемся мнением всех заинтересованных сторон нашего бизнеса, и мы возлагаем ответственность друг на друга за нашу откровенность, преданность нашей миссии и честность в нашей работе. Узнайте больше о нашей приверженности ответственным закупкам: Политика закупок 3Degrees РАЗНООБРАЗИЕвдохновляет нас на новые подходы к ведению бизнеса. Действия по борьбе с изменением климата должны признавать, исследовать и продвигать равенство и интеграцию в маргинализированные сообщества. Узнайте больше о наших обязательствах по борьбе с расизмом и DEI здесь. Я увлечен нашей средой, и в 3Degrees я могу напрямую связать то, что я делаю, с тем, что я люблю. — КАРЛИНА ВУ, КОНСУЛЬТАНТ ПО ЭНЕРГЕТИЧЕСКОЙ И КЛИМАТИЧЕСКОЙ ПРАКТИКЕ Узнайте больше о работе в 3Degrees и ознакомьтесь с текущими вакансиями. Работайте с нами ВОЛОНТЕРСТВОСотрудникам предлагается использовать оплачиваемые часы работы волонтеров, чтобы отдавать свое время и талант организациям в своих местных сообществах.
БЛАГОТВОРИТЕЛЬНЫЕ ПОжертвования Кроме того, наша программа 3DGives предоставляет пожертвования и подбор подарков соответствующим критериям некоммерческим организациям, номинированным нашими сотрудниками на основании их влияния на общество и соответствия миссии 3Degrees.
Наша страсть к борьбе с изменением климата начинается рядом с домом. Устойчивое развитие является неотъемлемой частью нашей собственной деятельности, а также работы с нашими клиентами. ВОЗОБНОВЛЯЕМАЯ ЭНЕРГЕТИКАМы подтверждаем 100-процентное использование электроэнергии в масштабах всей компании сертификатами возобновляемой энергии ПУТЕШЕСТВИЯ И КОММУТИНИРОВАНИЕ Мы компенсируем все выбросы, возникающие в результате деловых поездок сотрудников и поездок на работу, а также субсидируем оплату проезда в общественном транспорте для штатных сотрудников. |

 Приведите пример. Докажите
тождество (ab) n = a n b n .
Приведите пример. Докажите
тождество (ab) n = a n b n .



 3 deg
3 deg
 0004 51 RAD = 2920 DEG
0004 51 RAD = 2920 DEG deg
deg
 После того, как 3Degrees стала ключевым игроком на рынке REC и компенсации выбросов углерода, а также новатором программ экологически чистой энергетики, Дэн и Стив осознали необходимость развития наших услуг для удовлетворения растущего спроса на более комплексные консалтинговые решения в области энергетики и климата.
После того, как 3Degrees стала ключевым игроком на рынке REC и компенсации выбросов углерода, а также новатором программ экологически чистой энергетики, Дэн и Стив осознали необходимость развития наших услуг для удовлетворения растущего спроса на более комплексные консалтинговые решения в области энергетики и климата. Мы гордимся тем, что сотрудничаем с этими лидерами отрасли, чтобы решить неотложную проблему изменения климата и создать устойчивое и справедливое будущее для всех.
Мы гордимся тем, что сотрудничаем с этими лидерами отрасли, чтобы решить неотложную проблему изменения климата и создать устойчивое и справедливое будущее для всех. Всегда.
Всегда.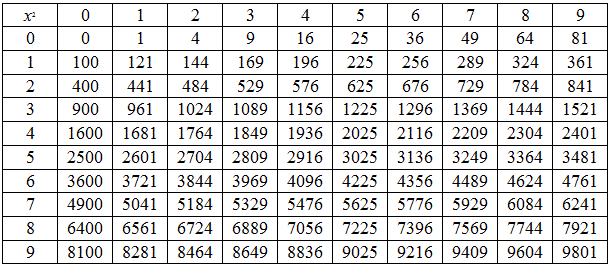 3Degrees стремится выявлять и устранять барьеры и модели поведения, которые мешают организациям, включая нашу собственную, представлять и продвигать эти сообщества на всех уровнях организации. Мы понимаем, что у нас много работы, и она требует постоянного внимания и заботы.
3Degrees стремится выявлять и устранять барьеры и модели поведения, которые мешают организациям, включая нашу собственную, представлять и продвигать эти сообщества на всех уровнях организации. Мы понимаем, что у нас много работы, и она требует постоянного внимания и заботы.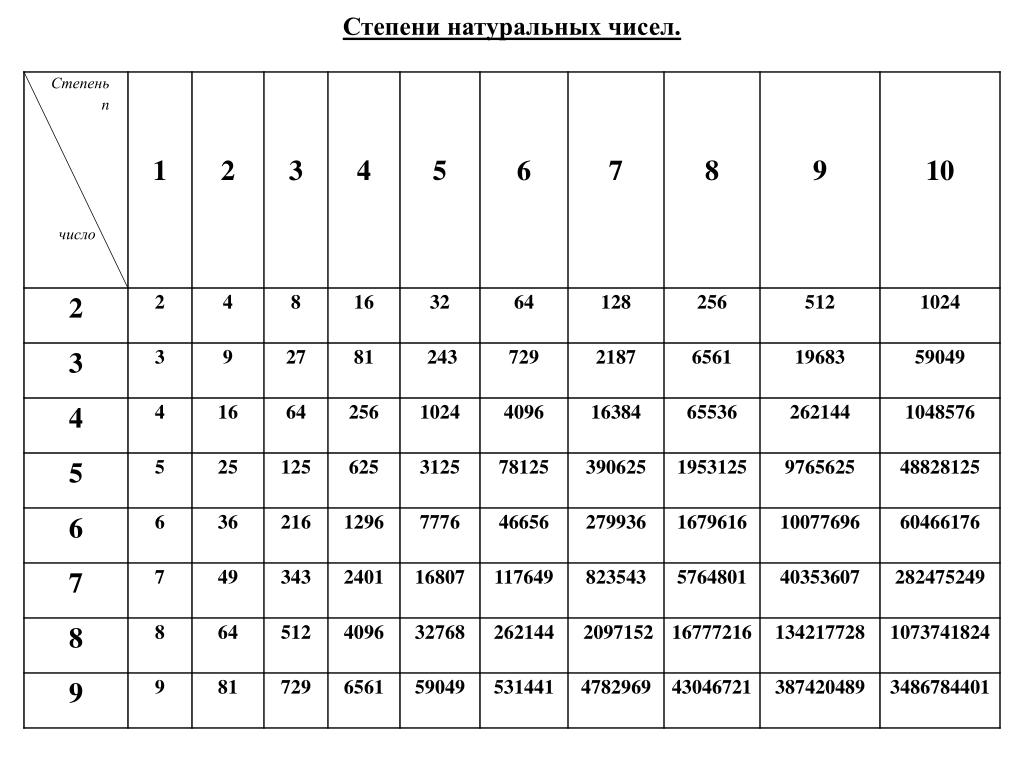 3Degrees поддержала множество проектов, в том числе:
3Degrees поддержала множество проектов, в том числе: