3Х 2 5х решить уравнение: Решите уравнение 3х^2 +5х=0 — Школьные Знания.com

Содержание

Тест «Полные,неполные квадратные уравнения» 6 вариантов

тест по теме: » Полные и неполные квадратные уравнения. В-1

А1. Решите уравнение 5х² -10=0. Если корней несколько, найдите их произведение.

1) -2 3)решений нет

2) 2 4)

А2. Укажите уравнение, которое не имеет корней.

1) 2,7х² -1,5x=0 3) 2,7х² — 1,5=0

2) 2,7x²+1,5х=0 4) 2,7х² +1,5=0

А3. Вычислите дискриминант квадратного уравнения 2х²-7х+3=0

1) 5 3) 625

2) 73 4) 25

А4. Решите уравнение х² +3х -4=0

1) 1;-3 3) -4;1

2) решений нет 4) 1;-4

А5. Найдите сумму корней квадратного уравнения х² -6х +2=0

1) решений нет 3) 6

2) 2 4)- 6

А6. Найдите произведение корней квадратного уравнения х² -7х -6=0

1) -6 3) 6

2) решений нет 4) 7

А7. Решите уравнение 3х² -5х -12=0

1) 1; 3) -6;

2) 5; 0 4) 3; —

А8. Решите уравнение х² -7х=0

1) -7; 0 3) 0;7

2) -1;1 4) -7;0

А9.Укажите неполное квадратное уравнение

1) 3х² -4х-7=0 3)х²-7х-8=0

2) 3х²-7х=0 4) 5х² -3х-140=0

В1. Решите уравнение. (х-2)(х+2)=7х-14

В-2

А1. Решите уравнение 7х² -35=0. Если корней несколько, найдите их произведение.

1) 5 3) решений нет

2) -5 4)

А2. Укажите уравнение, которое не имеет корней.

1)6,9х² +3,4x=0 3) 6,9х² -3,4x=0

2) 6,9х² +3,4=0 4) 6,9х

2 -3,4=0

А3. Вычислите дискриминант квадратного уравнения 2х²+7х+5=0

1) 89 3) 3

2) 81 4) 9

А4. Решите уравнение х² -5х +6=0

1)2;-3 3) 3;2

2)решений нет 4) -2;-3

А5. Найдите сумму корней квадратного уравнения х² +7х +4=0

1) 7 3) решений нет

2) -7 4) 4

А6. Найдите произведение корней квадратного уравнения х² +5х +2 =0

1)– 2,5 3) -2

2)решений нет 4) 2

А7. Решите уравнение 3х² -2х — 40 =0

1) 4 ; 3) 4 ; —

2) 10 ;0 4) -4 ; —

А8. Решите уравнение х² -14х=0

1) 0; 14 3) -14; -1

2)-14;1 4) 0; -14

А9.Укажите полное квадратное уравнение

1) 5х² -4х-10=0 3)х²-25 =0

2) х²+15х +14 =0 4) 3х² -3х=0

В1. Решите уравнение. (х-2)²= 3х-8

В-3

А1. Решите уравнение 3х

2 -9=0. Если корней несколько, найдите их произведение.

1) 3) 3

2) решений нет 4) -3

А2. Укажите уравнение, которое не имеет корней.

1)5,9х² -2,3x=0 3) 5,9х² +2,3=0

2) 5,9х² +2,3x=0 4) 5,9х² -2,3=0

А3. Вычислите дискриминант квадратного уравнения 6х²-11х+3=0

1) 7 3) 193

2) 49 4) 2041

А4. Решите уравнение х² +7х +10=0

1)2; 5 3) -2; -5

2)решений нет 4) -2; 5

А5.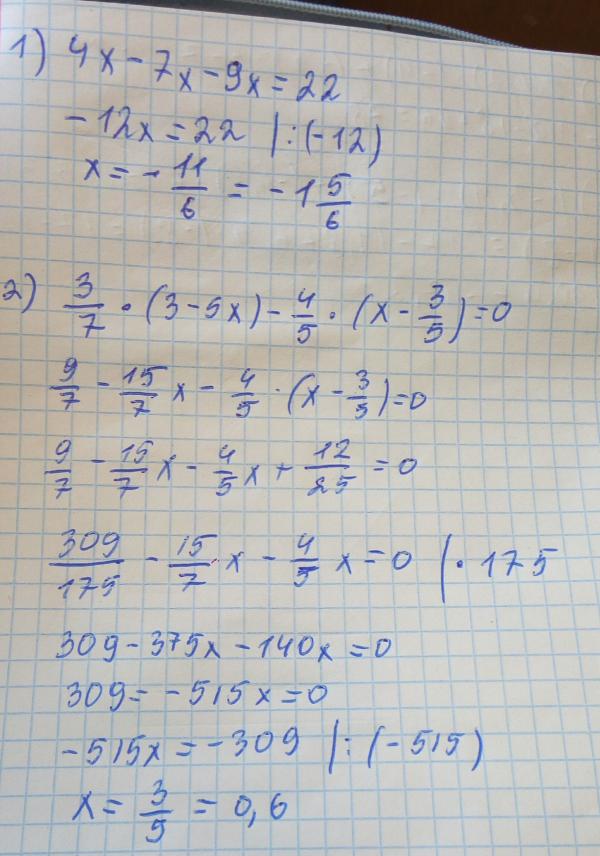 Найдите сумму корней квадратного уравнения х² -11х +5=0

1) решений нет 3) — 11

2) 11 4) 5

А6. Найдите произведение корней квадратного уравнения х² +5х -2 =0

1)– 2 3) -5

2) 2 4) решений нет

А7. Решите уравнение 4х² +36х +81 =0

1) 4 3) 4,5; 0

2) — 4,5 4) решений нет

А8. Решите уравнение х² -9х=0

1) 0; -9 3) 0;9

2)1; 9 4) -1; -9

А9.Укажите полное квадратное уравнение

1) 5х² -25х=0 3)х²-36 =0

2)3х²+5х +28 =0 4) 3х²=0

В1.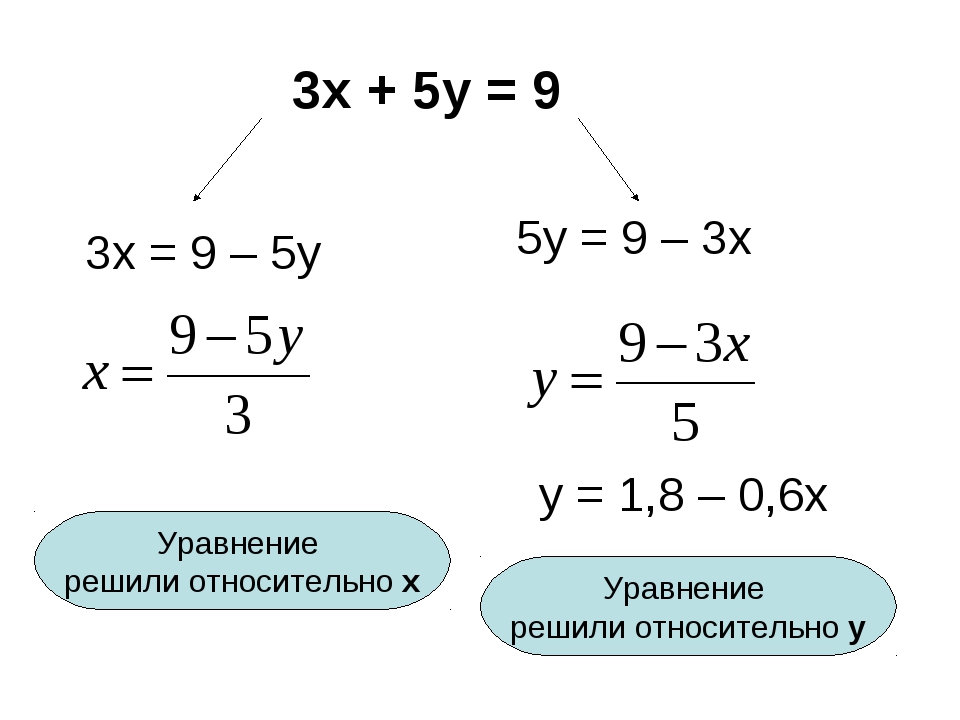 Решите уравнение.

(х-1)²= 29 -5х

В-4

А1. Решите уравнение 4х² -28=0. Если корней несколько, найдите их произведение.

1) 7 3)решений нет

2) -7 4)

А2. Укажите уравнение, которое не имеет корней.

1)9,1х² — 4,5=0 3) 9,1х² + 4,5х=0

2) 9,1х

2 + 4,5=0 4) 9,1х² — 4,5х=0

А3. Вычислите дискриминант квадратного уравнения 6х²+7х-3=0

1) 121 3) 529

2) 11 4) -23

А4. Решите уравнение х² -5х +4=0

1)-4;-1 3) 1;4

2)решений нет 4)- 1; 4

А5. Найдите сумму корней квадратного уравнения х² +12х +5=0

1) -12 3) 5

2) решений нет 4) 12

А6. Найдите произведение корней квадратного уравнения х² +9х -7=0

1) 7 3) решений нет

2) -7 4) -9

А7. Решите уравнение 5х² +14х -3=0

1) -2; 3) -2;

2) решений нет 4)- 3;

А8. Решите уравнение х² -4х=0

1) 0;4 3) 0;-4

2) -1;4 4) -4; -1

А9.Укажите полное квадратное уравнение с чётным вторым коэффициентом

1) 5х² -4х-17=0 3)2 х²=0

2) 6х²-7х +8 =0 4) 5х² -9х-14=0

В1. Решите уравнение.

(х-3)(х+3)= 5х-13

В-5

А1. Решите уравнение 9х² -54=0. Если корней несколько, найдите их произведение.

1)решений нет 3) 6

2) — 6 4)

А2. Укажите уравнение, которое не имеет корней.

1)8,6х² + 1.5=0 3) 8,6х² – 1.5х =0

2) 8,6х² — 1.5=0 4) 8,6х² + 1.5х =0

А3. Вычислите дискриминант квадратного уравнения 3х²-5х +2=0

1) 18 3) 1

2) -91 4) 101

А4. Решите уравнение х²

-9х +20=0

1) -5;-4 3) -4;5

2) 4; 5 4)- 5; 4

А5. Найдите сумму корней квадратного уравнения х² -17х +4=0

1) -40 3) -17

2) Решений нет 4) 17

А6. Найдите произведение корней квадратного уравнения х² -29х +27=0

1) 29 3) нет корней

2) -29 4) 27

А7. Решите уравнение 7х² +8х +1 =0

1) -; -1 4) -2; -1

2) решений нет 4)- 1;

А8. Решите уравнение х² -6х=0

1) 0;1 3) 0;-6

2) 0;6 4) 0; -1

А9. Укажите неполное квадратное уравнение

1) 6х² +14х+8=0 3) 9х²=0

2) х²-7х +9 =0 4) 5х² -25х +6=0

В1. Решите уравнение.

(х+3)²= 2х+6

В-6

А1. Решите уравнение 10х² -100=0. Если корней несколько, найдите их произведение.

1) 0 3)

2) -10 4) 10

А2. Укажите уравнение, которое не имеет корней.

1)10,2х² — 13,4=0 3) 10,2х² + 13,4=0

2) 10,2х² + 13,4х=0 4) 10,2х² — 13,4х=0

А3. Вычислите дискриминант квадратного уравнения 9х²-2х -21=0

1.728 3)- 157

2)760 4) 265

А4. Решите уравнение х² -19х +88=0

1) 8; 11 3) -11; 8

2) -8; -11 4)- 8; 11

А5. Найдите сумму корней квадратного уравнения х² +25х +44=0

1)25 3) -25

2) 44 4) решений нет

А6. Найдите произведение корней квадратного уравнения х² -8х +22=0

1)корней нет 3) 22

2) 8 4)- 22

А7. Решите уравнение 5х² +8х -4 =0

1) — ; 2 3) решений нет

2) 2; 5 4)- 2;

А8. Решите уравнение х² -8х=0

1)-8;0 3) -1; 8

2) 1;8 4) 0; 8

А9.Укажите приведённое квадратное уравнение

1) х² -14х+7=0 3) 27х²=0

2) 3х²-9х =0 4) 5х² -10х +36=0

В1. Решите уравнение (х-4)(х+4)= -14х -49

Ответы:

№ варианта	А1	А2	А3	А4	А5	А6	А7	А8	А9	В1
1	1	4	4	4	3	1	4	3	2	2;5
2	2	2	4	3	2	4	3	1	2	3;4
3	4	3	2	3	2	1	2	3	2	-7;4
4	2	2	1	3	1	2	4	1	1	1;4
5	2	1	3	2	4	4	1	2	3	-3;-1
6	2	3	2	1	3	3	4	4	1	-11;-3

Тест с ответами по теме: «Квадратные уравнения»

1. Какое из предложенных уравнений является квадратным уравнением?
а) 8х2 — 5х + 7 + 3х3 = 0.
б) 8х2 + 3х — 2\х + 4 = 0.
в) 2х + 1\7*х2 + 5 =9. +

2. Какое из чисел -2, -1, 0, 1, 2 является корнем уравнения 3х2 -5х +2 = 0?
а) 1. +
б) -1.
в) 0.

3. Решите неполное квадратное уравнение 2х2 – 18 = 0.
а) 2 и 3.
б) -1 и 9.
в) -3 и 3. +

4. Решите неполное квадратное уравнение х2 + 2х = 0.
а) -1 и 2
б) 0 и -2. +
в) 0 и 2.

5. Решите неполное квадратное уравнение 2х2 = 0.
а) 0. +
б) -1 и 0.
в) 2 и 0.

6. Найдите корни уравнения х2 -7х + 6 = 0.
а) — 1 и — 6.
б) 1 и 6. +
в) 0 и 6.

7. Найдите корни уравнения х2 + 6х + 5 = 0.
а) 1 и 5.
б)-1 и -6.
в) -1 и -5. +

8. Найдите корни уравнения х2 + 8х + 16 = 0.
а) — 4 и 4.
б) 8 и — 8.
в) — 4. +

9. Решите уравнение 7х2 — х – 8 = 0.
а) 1 и 7.
б) -1 и — 7.
в) -1 и 7. +

10. Найдите сумму корней уравнения х2 — 16х + 2 8 = 0.
а) -16.
б) 16. +
в) 28.

11. Найдите сумму корней уравнения 3 х2 — 15х -2 8 = 0.
а) 5.
б) 15.
в) 5. +

12. Найдите произведение корней уравнения 2 х2 — 15х — 2 8 = 0.
а) 14.
б) -14. +
в) 28.

13. Решите уравнение (2х – 3) (3х + 6) = 0.
а) 3 и 6.
б) 1,5 и 0,5.
в) — 2 и 1,5. +

14. Решите уравнение (х – 2)2 = 3х — 8.
а) 1 и 7.
б) 2 и 0,5.
в) 3 и 4. +

15. Один из корней квадратного уравнения равен 3. Найдите второй корень уравнения х2 — 21х + 54 = 0.
а) 18. +
б) — 18.
в) 27.

16. Один из корней квадратного уравнения равен -3. Найдите коэффициент р уравнения х2 + рх + 18 = 0.
а) — 9.
б) — 8.
в) 9. +

17. Какое из чисел -3, -1, 0, 1, 3 является корнем уравнения 3х2 -5х -8 = 0?
а) 1.
б) -3.
в) 0.
г) -1.
д) 3. +

18. Решите неполное квадратное уравнение 4х2 – 64 = 0.
а) нет корней.
б) -1 и 16.
в) 2 и ??. +

19. Решите неполное квадратное уравнение — х2 + 2х = 0.
а) -1 и 0.
б) 0 и -2.
в) 1 и 2. +

20. Решите неполное квадратное уравнение 2х2 = 0.
а) 1,5
б) -1 и 2.
в) 2. +

21. Найдите корни уравнения х2 — 4х + 3 = 0.
а) 2 и 1,5.
б)-1 и 1.
в) 0 и 3. +

22. Найдите корни уравнения х2 + 8х + 7 = 0.
а) 1 и 7.
б) -1 и 7.
в) -1 и -7. +

23. Найдите корни уравнения х2 + 10х + 25 = 0.
а) — 5 и 5.
б) — 5.
в) — 5 и 5. +

24. Решите уравнение 3х2 — 8х + 5 = 0.
а) 1 и 5.
б) -2 и 3,5.
в) 1*2\3 и 1. +

25. Найдите сумму корней уравнения х2 — 17х + 2 8 = 0.
а) -17.
б) 14. +
в) 28.

ГБОУ средняя школа № 259 имени М.Т. Лорис-Меликова

Все, что важно знать выпускнику, в памятках от Рособрнадзора

Друзья, #МузейУИстока предлагает написать комментарии к этому посту свои любимые стихи Пушкина. https://vk.com/wall-187421469_1270 Поехали! 6 июня 2021 года исполняется 222 года со дня рождения выдающегося русского поэта и писателя Александра Сергеевича Пушкина. Ко дню рождения Александра Сергеевича Пушкина в школьной #библиотеке подготовлена тематическая выставка «Всё ли Читать дальше …

Добрый день! #большаяперемена Коллеги, мы подготовили мотивационный ролик о конкурсе и возможностях, которые он дает ttps://disk.yandex.ru/i/NRF3AnSArtfANg #Школа259СПБ

Уважаемые родители! Приглашаем вас принять участие в опросе мнения о том, справедлива ли система ЕГЭ при поступлении в вузы. Проголосовать можно по ссылке — https://vk.com/wall615914394_80 Проголосовать можно по ссылке — https://vk.com/irina_potehina В этом году единому государственному экзамену исполнилось 20 лет. Удалось ли Читать дальше …

️Дети — маленькие частички большого счастья, чудо, которое наполняет жизнь каждого взрослого неподдельной радостью и теплотой. Дети так нуждаются в любви и заботе, в родительской ласке и хочется, чтобы каждое детское сердце не было обделено этим маленьким счастьем. ️В День защиты детей Читать дальше …

Чтобы помочь школьникам справиться с эмоциональным напряжением, эксперты Института воспитания подготовили небольшую памятку о том, как взять себя в руки перед ЕГЭ и успешно сдать его.

Поздравление с Днем города Санкт-Петербурга! Лучший город на Земле прими поздравления от #Школа259СПб #ДЕНЬГОРОДА2021 для вас выступают учащиеся начальных классов ГБОУ средней школы N259 им. М.Т. Лорис-Меликова Адмиралтейского района Санкт-Петербурга на празднике посвященный Дню города. Желаем всем хорошего, праздничного настроения, мира, добра Читать дальше …

Церемония награждения нагрудным знаком «Почетный работник воспитания и просвещения Российской Федерации» Уважаемая Астгик Телемаковна! Сердечно поздравляю Вас с получением заслуженной награды, которая является прямым подтверждением Ваших высоких профессиональных и личностных качеств. Примите искренние пожелания крепкого здоровья и благополучия и дальнейших Читать дальше …

26 мая 2021 года на базе ГБОУ средней школы №259 им. М. Т. Лорис-Меликова Адмиралтейского района состоялся семинар учителей на тему «Социализация и обучение детей-инофонов в среде доминирующей русскоязычной культуры в современной петербургской школе». В работе семинара приняли участие учителя Читать дальше …

Уважаемые родители! Ежегодно с началом летне-весеннего сезона регистрируются случаи гибели детей при выпадении из окна! Как правило, во всех случаях падения дети самостоятельно забирались на подоконник, используя в качестве подставки различные предметы мебели, и, опираясь на противомоскитную сетку, выпадали из Читать дальше …

Алгебраическое решение уравнений

Содержание: Эта страница соответствует § 2.4 (с. 200) текста.

Предлагаемые задачи из текста:

с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87, 88, 95, 97

Квадратные уравнения
Уравнения с участием радикалов
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения

Квадратичные уравнения

Квадратное уравнение имеет вид ax ² + bx + c = 0, где a, b и c — числа, а a — не равно 0.

Факторинг

Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое. Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста.

Пример 1.

2x ² — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2 или x = 4.

Принцип квадратного корня

Если x ² = k, то x = ± sqrt (k).

Пример 2.

x ² — 9 = 0.
x ² = 9.
x = 3 или x = -3.

Пример 3.

Пример 4.

x ² + 7 = 0.
х ² = -7.
х = ±.
Обратите внимание, что = =, так что решения
x = ±, два комплексных числа.

Завершение площади

Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат корневой принцип.

Пример 5.

x ² + 6x — 1 = 0.
x ² + 6x = 1.
x ² + 6x + 9 = 1 + 9.
9, добавленная к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) ² = 9. Причина выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами). Поэтому эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это истина, учитывая (x + a) ² = x ² + 2ax + a ². Чтобы получить «а» нужно всего лишь разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x ² + 2ax, нужно добавить ².]
(x + 3) ² = 10.
Теперь мы можем применить принцип квадратного корня и затем решить относительно x.
x = -3 ± sqrt (10).

Пример 6.

2x ² + 6x — 5 = 0.
2x ² + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент (коэффициент x ²) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив обе части уравнения на 2.
x ² + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат, (3/2) ² = 9/4. Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
x ² + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(х + 3/2) ² = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2

До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере.

Пример 7.

x ² = 16.

x ² — 16 = 0.

(x + 4) (x — 4) = 0.

x = -4 или x = 4.

В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна.

Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие: всегда одинаковы, поэтому их можно применить к общему квадратному уравнению

ах ² + bx + c = 0.

Результатом квадрата этого общего уравнения является формула для решений уравнения называется квадратной формулой.

Квадратичная формула

Решения уравнения ax ² + bx + c = 0 равны

Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае, где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.

Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как сделай это!

Примеры использования квадратичной формулы:

Пример 8.

2x ² + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика функции f (x) = 2x ² + 6x — 5.

Пример 9.

4x ² + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует обратить внимание на две вещи.
Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
Решение упрощено, так что квадратный корень не используется. Это означает, что уравнение могло быть решается факторингом. (Все квадратные уравнения могут быть решены путем факторизации! Я имею в виду, что это могло быть решено легко факторингом.)
4x ² + 4x + 1 = 0.
(2x + 1) ² = 0.
х = -1/2.

Пример 10.

х ² + х + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов. функции f (x) = x ² + x + 1. Таким образом, решения сложны, поскольку график y = x ² + x + 1 не имеет пересечений по x.

Выражение под радикалом в квадратичной формуле, b ² — 4ac, называется дискриминантом уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.

1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.

Примечания к проверке растворов

Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример 3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения, потому что при решении уравнений очень легко сделать невнимательные ошибки.
Алгебраический метод, который состоит из обратной подстановки числа в уравнение и проверки того, что полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда решение предполагает радикальное.
Например, в нашем предпоследнем примере 4x ² + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) ² +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере, 2x ² + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2. Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический проверить или использовать калькулятор для алгебраической проверки быстрее.
Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту для построения графика y = 2x ² + 6x — 5 и проследите график, чтобы приблизительно определить, где х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения. Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно не точное решение.
Обратите внимание, что если вы начали с уравнения 2x ² + 6x — 5 = 0 и сразу перешли к графику утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя (алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень близко к найденным вами числам, значит, вы, наверное, правы!

Упражнение 1:

Решите следующие квадратные уравнения.
(а) 3x ² -5x — 2 = 0. Ответ
(б) (x + 1) ² = 3. Ответ
(в) x ² = 3x + 2. Ответ

Вернуться к содержанию

Уравнения с участием радикалов

Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения необходимо проверить.

Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы радикальный член сам по себе на одной стороне уравнения.

Пример 11.

Теперь, когда мы изолировали радикальный член в правой части, возводим обе части в квадрат и решаем полученное уравнение для x.
Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно раствор .
Решение : x = 3.
Примечание: Решением является x-координата точки пересечения графиков y = x и у = sqrt (х + 1) +1.

Посмотрите, что бы произошло, если бы мы возводили обе части уравнения в квадрат до , выделив радикал срок.

Это хуже, чем мы начали!

Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью возведение в степень один раз. Однако мы можем уменьшить количество радикальных членов на , возведя их в степень.

Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и возвести в степень. Затем мы повторяем этот процесс.

Пример 12.

Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат снова обе стороны.
Чек:
Подстановка x = 5/4 в исходное уравнение дает
sqrt (9/4) + sqrt (1/4) = 2.
3/2 + 1/2 = 2.
Это утверждение верно, поэтому решение x = 5/4.

Примечание по проверке решений:

В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение — координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).

Упражнение 2:

Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ

Вернуться к содержанию

Полиномиальные уравнения высшей степени

Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее.Когда мы встречаемся такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать решения с графической утилитой.

Нулевая постоянная

Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий x, чтобы начать задачу.

Пример 13.

2x ³ + 3x ² -5x = 0.
x (2x ² + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения.
x = 0 или 2x ² + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом. Примечание: Если бы мы не смогли разложить квадратичный коэффициент во втором уравнении, то мы могли бы прибегнуть к к использованию квадратичной формулы.[Убедитесь, что вы получили те же результаты, что и ниже.]
x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится при пересечении графиков f (x) = 2x ³ + 3x ² -5x.

Фактор

по группировке

Пример 14.

x ³ -2x ² -9x +18 = 0.
Коэффициент при x ² в 2 раза больше, чем при x ³, и такое же соотношение существует между коэффициенты при третьем и четвертом членах. Группа слагает один и два, а также три и четыре.
x ² (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители.
(x — 2) (x ² — 9) = 0.
Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.
x — 2 = 0 или x ² — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся на пересечении графика f (x) = x ³ -2x ² -9x +18.

Квадратичная форма

Пример 15.

x ⁴ — x ² — 12 = 0.
Этот многочлен неквадратичный, он имеет четвертую степень. Однако его можно рассматривать как квадратичный по x ².
(x ²) ² — (x ²) — 12 = 0.
Это может помочь вам фактически заменить z на x ².
z ² — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на x ² и решите полученные уравнения.
x ² = 4.
х = 2, х = -2.
х ² = -3.
x = i , или x = — i.
Итак, есть четыре решения, два реальных и два комплексных.
Примечание: Эти решения находятся на пересечении графика f (x) = x ⁴ — х ² — 12.
График f (x) = x ⁴ — x ² — 12 и увеличение, показывающее его локальное экстремумы.

Упражнение 3:

Решите уравнение x ⁴ — 5x ² + 4 = 0. Ответ

Вернуться к содержанию

Уравнения, содержащие дробные выражения или абсолютные значения

Пример 16.

Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков. из y = 1 и y = 2 / x-1 / (x + 2).

Пример 17.

5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности, и все решения должны быть проверены.
Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (x — 1) = x + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.
Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот точка часто сбивает студентов с толку, потому что кажется, что мы говорим, что абсолютное значение выражения отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное.
Теперь наше уравнение принимает вид
-5 (x — 1) = x + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по x, или вы можете найти решение как x-координаты точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).

Упражнение 4:

(а) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ

Вернуться к содержанию

Математическая сцена — Уравнения III — Урок 2

Математическая сцена — Уравнения III — Урок 2 — Квадратные уравнения

2008 Rasmus ehf и Jhann sak Ptursson

Уравнения III

Урок 2 Уравнения кубической и четвертой степени

Как мы можем решить такие уравнения, как кубическое уравнение показано здесь?

x ³ — x ² 4x + 4 = 0

Существует чрезвычайно сложная формула для решения кубические уравнения.Некоторые калькуляторы имеют встроенную формулу и поэтому могут использоваться для решения кубических уравнений.

Мы собираемся узнать, как эти уравнения могут быть решены с помощью факторизация. Если уравнение имеет решения, которые являются целыми числами a, b и c, то мы можем разложить уравнение на множители следующим образом:

x ³ — x ² 4x + 4 = (x — а) (х — б) (х — в) = 0

Умножая скобки, видим, что константа член 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе.

abc = 4

Все решения a, b и c должны быть множителями 4, поэтому не так много целых чисел, которые нам нужно учитывать.

У нас есть только следующие возможности:

1, 2 и 4

Хорошо изучите каждое из этих чисел, чтобы найти, какие из них являются решениями уравнения.

f (1) = 1 ³ — 1 ² 4 × 1 + 4 = 0 1 — решение

f (−1) = (−1) ³ — (−1) ² 4 × (-1) + 4 = 6 900 · 10

f (2) = 2 ³ — 2 ² 4 × 2 + 4 = 0 2 — решение

f (−2) = (−2) ³ — (−2) ² 4 × (−2) + 4 = 0 −2 — решение

Мы нашли три решения, поэтому нам не нужно попробуйте 4 и −4 как кубический уравнение имеет максимум три решения.

Эти три числа дают нам значения a, b и c и мы можем факторизовать уравнение.

x ³ — x ² 4x + 4 = (x — 1) (x — 2) (x + 2) = 0

Этот метод включает поиск целых чисел, которые являются множителями (можно разделить на) постоянный член, а затем проверить, действительно ли эти целые числа являются решениями уравнения.
К сожалению, мы не можем предполагать, что решения уравнения третьей степени являются все целые числа.
Однако, если мы можем найти одно целочисленное решение, допустим, что это x = a, тогда по Теорема остатка, мы знаем, что (x — a) является фактором уравнения. Мы можно найти другой множитель, квадратичный множитель, делением. Затем мы можем решить квадратное уравнение, используя формула для решения квадратиков.

Пример 1

Решите уравнение x ³ — 3x ² 2x + 4 = 0

Ставим числа, кратные 4 в уравнение, чтобы увидеть, верны ли какие-либо из них.

f (1) = 1 ³ — 3 × 1 ² 2 × 1 + 4 = 0 1 — решение

f (−1) = (−1) ³ — 3 × (−1) ² 2 × (-1) + 4 = 2 900 · 10

f (2) = 2 ³ — 3 × 2 ² 2 × 2 + 4 = −4

f (−2) = (−2) ³ — 3 × (−2) ² 2 × (−2) + 4 = −12

f (4) = 4 ³ — 3 × 4 ² 2 × 4 + 4 = 12 900 · 10

f (−4) = (−4) ³ — 3 × (−4) ² 2 × (−4) + 4 = −100

Единственное целочисленное решение — x = 1.Когда мы нашли одно решение, нам действительно не нужно проверять другие числа, потому что теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить квадратичный получаем из деления.

Теперь мы можем разложить наши выражение следующим образом:

x ³ — 3x ² 2x + 4 = (х — 1) (х ² — 2х — 4) = 0

Теперь нам остается решить квадратичную уравнение.

x ² — 2x — 4 = 0

Воспользуемся формулой квадратичной системы с a = 1, b = −2 и c = −4.

Мы нашли все три решения уравнение x ³ — 3x ² 2x + 4 = 0. Это: эфтирфаранди:

х = 1

x = 1 + 5

x = 1 — 5

Пример 2

Мы можем легко использовать тот же метод для решения уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f (x) = x ⁴ — x ³ — 5x ² + 3x + 2 = 0.

Сначала мы находим целые множители постоянный член, 2. Целочисленные множители 2 равны 1 и 2.

f (1) = 1 ⁴ — 1 ³ — 5 × 1 ² + 3 × 1 + 2 = 0 1 — решение

f (−1) = (−1) ⁴ — (−1) ³ — 5 × (−1) ² + 3 × (−1) + 2 = −4

f (2) = 2 ⁴ — 2 ³ — 5 × 2 ² + 3 × 2 + 2 = −4

f (−2) = (−2) ⁴ — (−2) ³ — 5 × (−2) ² + 3 × (−2) + 2 = 0 ср. нашли вторую решение.

Два найденных нами решения 1 и −2 означают, что мы можем разделить на x — 1 и x + 2 и остатка не будет. Сделайте это в два этапа.
Сначала разделим на x + 2

Теперь разделите полученное кубический коэффициент по x — 1.

Теперь мы разложили на множители
f (x) = x ⁴ — x ³ — 5x ² + 3x + 2 в
f (x) = (x + 2) (x — 1) (x ² — 2x — 1) и только Осталось решить квадратное уравнение

x ² — 2x — 1 = 0.Мы используем формула с a = 1, b = −2 и c = −1.

Всего найдено четыре решения. Их:

х = 1

х = -2

х = 1 +

х = 1-

Иногда мы можем решить уравнение третьей степени, заключив в скобки члены два на два и найдя множитель что у них общего.Давайте посмотрим на это на примере.

Пример 3.

Решите уравнение x ³ — 2x ² — 4x + 8 = 0

x ³ — 2x ² — 4x + 8 = 0

(x ³ — 2x ² ) — (4x — 8) = 0

[x ² (x — 2) — 4 (x — 2)] = 0

(x — 2) [x ² — 4] = 0

(х — 2) (х — 2) (x + 2) = 0

Здесь скобка (x — 2) является общим множителем и может быть вынесена за пределы общая скобка.

Обратите внимание, что скоба (x — 2) происходит дважды, когда мы закончили факторизацию. x = 2 — это поэтому двойное решение, и у нас есть только два разных. Это:

х = 2 и х = -2 .

Лауснир: x = 2 og x = −2 .

Все примеры, которые мы рассмотрели до сих пор, уравнения, в которых член с наибольшей степенью имеет коэффициент 1.

Как мы иметь дело с уравнениями, где этот коэффициент — какое-то другое число?

Общая форма — f (x) = ax ³ + bx ² + cx + d, где a, b, c и d — целые числа.

Мы можем искать целочисленные решения в том же как и раньше, проверяя множители постоянного члена d. Если мы найдем целочисленное решение, тогда мы можем разделить и найти другие решения, как и раньше.

Если ни один из факторов d не дает нам решения затем мы ищем решения, которые являются дробями.
Предположим, есть дробное решение, и назовем его решение x = t / n.

Это означает, что x — t / n является фактором f (x), или, если мы умножаем на n, то xn — t является множителем.

Теперь предположим, что мы разделили f (x) на xn. — t и нашли квадратичный множитель, мы можем назвать его
Ax ² + Bx + C.

Теперь у нас есть результат, что

ax ³ + bx ² + cx + d = (xn — t) (Ax ² + Bx + C)

сравнивая коэффициенты x ³ на обе стороны уравнения мы видим, что a = nA и, следовательно, n должно быть множителем а.
Аналогично, сравнивая постоянные члены, мы видим, что d = −tC и, следовательно, t является множителем d.

Мы заключаем, что любая дробь является решением кубическое уравнение ax ³ + bx ² + cx + d должен иметь вид t / n, где t — множитель числа d, а n — фактор числа a.

Обобщение для функции степени n:

ф (х) = a _n x ⁿ + a _{n − 1} x ^{n − 1} + × × × × + а ₁ х + ₀

с коэффициентами a ₀ , а ₁ , а ₂ , × × × × × а _{n − 2} , _{n − 1} и _n .

Если эта функция имеет рациональное решение, скажем, t / n, тогда t — коэффициент ₀ , а n — коэффициент _n .

Пример 4

Решите уравнение f (x) = 2x ³ — 7x ² + 4x + 3 = 0.

Возможные целые корни f (x) — это делители 3, они равны 1 и 3. Дроби, которые могут быть корнями, — это эти четыре числа, разделенные на множители 2.Итак, полный список рациональных чисел, которые нам нужно рассмотреть, — это , 1, ³ / ₂ и 3.

Сразу видно, что нам не нужно рассмотрите любые отрицательные значения, поскольку все они будут давать отрицательные значения для f (x), а не 0.

Теперь попробуем другие возможности

f () = 2 () ³ — 7 () ² + 4 × + 3 = 3

f (1) = 2 × 1 ³ — 7 × ² + 4 × 1 + 3 = 2

ф (³/₂) = 2 (³/₂) ³ — 7 (³/₂) ² + 4 × ³/₂ + 3 = 0, поэтому мы нашли решение.

x = ³/₂ — решение, поэтому (x — ³/₂) — фактор. Разделение на (x — ³/₂) может быть трудным. Поэтому мы умножаем на 2 и вместо этого делим на (2x — 3). Если (x — ³/₂) является фактор

, то (2x — 3).

Теперь нам нужно решить уравнение x ² — 2x — 1 = 0.Мы уже решили это уравнение в примере 2. Решения: 1 + 2 og 1 — 2.

Итак, мы нашли три решения. Их:

x = ³/₂ = 1

х = 1 + 2

х = 1 — 2

Попробуйте пройти тест 2 по уравнениям III.

Не забудьте использовать контрольный список для следите за своей работой.

систем линейных уравнений

Часто бывает необходимо посмотреть на несколько функций одного и того же независимого Переменная.Рассмотрим предыдущий пример, где x — количество произведенных товаров. и продано, была независимой переменной в трех функциях: функции затрат, функция дохода и функция прибыли.

В целом там может быть:

n уравнений

v переменные

Решение систем уравнений

Есть четыре метода решения систем линейных уравнений:

а.графическое решение

б. алгебраическое решение

c. метод исключения

d. метод замещения

Графическое решение

Пример 1

даны являются два следующих линейных уравнения:

f (x) = y = 1 + 0,5x

f (x) = y = 11 — 2x 900 · 10

Изобразите первое уравнение , найдя две точки данных.Установив сначала x, а затем y равны нулю, можно найти точку пересечения y на вертикальная ось и точка пересечения x на горизонтальной оси.

Если x = 0, тогда f (0) = 1 + .5 (0) = 1

Если y = 0, тогда f (x) = 0 = 1 + 0,5x

-,5x = 1

х = -2

Результирующий точки данных: (0,1) и (-2,0)

Постройте график второго уравнения , найдя две точки данных.От установив сначала x, а затем y равными нулю, можно найти точку пересечения y по вертикальной оси и точка пересечения x по горизонтальной оси.

Если x = 0, тогда f (0) = 11-2 (0) = 11

Если y = 0, тогда f (x) = 0 = 11 — 2x

2x = 11 900 10

х = 5,5

Результирующий точки данных: (0,11) и (5.5,0)

В точке пересечения двух уравнений x и y имеют одинаковые значения. На графике эти значения можно прочитать как x = 4 и y = 3.

Пример 2

даны являются два следующих линейных уравнения:

f (x) = y = 15 — 5x 900 · 10

f (x) = y = 25 — 5x 900 · 10

Если x = 0, тогда f (0) = 15-5 (0) = 15

Если y = 0, тогда f (x) = 0 = 15 — 5x

5x = 15

х = 3

Результирующий точки данных: (0,15) и (3,0)

Если x = 0, тогда f (0) = 25-5 (0) = 25

Если y = 0, тогда f (x) = 0 = 25 — 5x

5x = 25

х = 5

Результирующий точки данных: (0,25) и (5,0)

Из графика видно, что эти линии не пересекаются.Они параллельны. У них одинаковый наклон. Нет однозначного решения.

Пример 3

даны являются два следующих линейных уравнения:

21x — 7y = 14

-15x + 5y = -10

Rewrite уравнения, поместив их в форму пересечения наклона.

Первый уравнение становится

7y = -14 + 21x

у = -2 + 3х

Второй уравнение становится

5y = -10 + 15x

у = -2 + 3х

Изобразите любое уравнение, найдя две точки данных.Установив сначала x, а затем y равный нулю, можно найти точку пересечения y по вертикали ось и точку пересечения x на горизонтальной оси.

Если x = 0, тогда f (0) = -2 +3 (0) = -2

Если y = 0, тогда f (x) = 0 = -2 + 3x

3x = 2

х = 2/3

Результирующий точки данных: (0, -2) и (2 / 3,0)

Из графика видно, что эти уравнения эквивалентны.Там — бесконечное количество решений.

Алгебраическое решение

Этот метод будет проиллюстрирован с помощью анализа спроса и предложения. Этот Тип анализа заимствован из работ великого английского экономиста Альфреда Маршалл.

Q = количество и P = цена

P (s) = функция предложения и P (d) = функция спроса

При построении графика цена откладывается на вертикальной оси. Таким образом, цена — это зависимая переменная.Было бы логичнее рассматривать количество как зависимая переменная, и этот подход использовал великий французский экономист, Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя Анализ Маршалла, который называют крестом Маршалла.

Цель состоит в том, чтобы найти равновесную цену и количество, т. Е. Решение где цена и количество будут иметь одинаковые значения в функции предложения и функция цены.

Q _E = равновесная величина P _E = равновесная цена

Для равновесия
предложение = спрос
или P (s) = P (d)

Учитывая следующие функции

П (т) = 3Q + 10 и P (d) = -1 / 2Q + 80

Приравняйте уравнения друг к другу и решите относительно Q.

P (т) = 3Q + 10 = -1 / 2Q + 80 = P (d)

3.5Q = 70 900 · 10

Q = 20 Равновесное количество 20.

Подставьте это значение вместо Q в любое уравнение и решите для P.

P (т) = 3 (20) + 10

П (т) = 70

П (г) = -1/2 (20) + 80

П (г) = 70 Цена равновесия — 70.

Метод исключения

Этот метод включает удаление переменных из уравнений. Переменные удаляются последовательно, пока не останется только одна последняя переменная, т.е. пока не будет одно уравнение с одним неизвестным. Затем это уравнение решается для одного неизвестного. Затем решение используется для нахождения второго последняя переменная. Процедура повторяется, добавляя обратно переменные в качестве их решений. найдены.

Пример 1

2х + 3у = 5

-5x — 2y = 4

Порядок действий: удалить y.Коэффициенты при y не совпадают в два уравнения, но если бы они были, можно было бы сложить два уравнения и члены y будут сокращаться. Однако это возможно через умножение каждого уравнения, чтобы заставить члены y иметь одинаковые коэффициенты в каждом уравнении.

Шаг 1: Умножьте первое уравнение на 2, а второе уравнение умножьте на 3. Это дает

4х + 6у = 10

-15x — 6y = 12

Шаг 2: Сложите два уравнения.Это дает

-11x = 22

х = -2

Шаг 3: Решить относительно y в любом из исходных уравнений

2 (-2) + 3у = 5
3 года = 9
г = 3 или
-5 (-2) — 2y = 4
10 — 2y = 4
2y = 6
г = 3

Альтернативная процедура: удалить x.Коэффициенты при x не совпадают в двух уравнениях, но если бы они были, можно было бы добавить два уравнения и члены y будут сокращаться. Однако возможно путем умножения каждого уравнения, чтобы заставить члены x равняться имеют одинаковые коэффициенты в каждом уравнении.

Шаг 1: Умножьте первое уравнение на 5, а второе уравнение умножьте на 2. Это дает

10x + 15y = 25 900 · 10

-10x — 4y = 8

Шаг 2: Сложите два уравнения.Это дает

11лет = 33

y = 3

Шаг 3: Решить относительно x в любом из исходных уравнений

2x + 3 (3) = 5
2x = -4
х = -2 или
-5x — 2 (3) = 4
— 5x = 10
х = -2

Пример 2

2x ₁ + 5x ₂ + 7x ₃ = 2

4x ₁ — 4x ₂ — 3x ₃ = 7

3x ₁ — 3x ₂ — 2x ₃ = 5

В этом примере есть три переменные: x ₁, x ₂ и х ₃.Одна из возможных процедур — удалить первый x ₁, , чтобы исключить следующие x ₂, а затем найти x ₃. Значение, полученное для x ₃, используется для решения x ₂ и наконец, значения, полученные для x ₃ и x ₂, используются для решить относительно x ₁.

Процедура Часть A Сначала удалите x ₁.

Шаг 1 Умножение первое уравнение на 2 и вычтите второе уравнение из первого уравнение.Это дает

4x ₁ + 10x ₂ + 14x ₃ = 4 первое уравнение

4x ₁ — 4x ₂ — 3x ₃ = 7 второе уравнение

14x ₂ + 17x ₃ = -3 второе уравнение вычитается из первого

Шаг 2 Умножение первое уравнение на 3, третье уравнение умножьте на 2 и вычтите третье уравнение из первого уравнения.Это дает

6x ₁ + 15x ₂ + 21x ₃ = 6 первое уравнение

6x ₁ — 6x ₂ — 4x ₃ = 10 третье уравнение

21x ₂ + 25x ₃ = -4 третье уравнение вычитается из первого

Процедура, часть B Второе удаление x ₂. Из Части А осталось два уравнения. Из этих двух уравнений исключить х ₂.

14x ₂ + 17x ₃ = -3 первое уравнение

21x ₂ + 25x ₃ = -4 второе уравнение

Шаг 1 Умножение первое уравнение на 21, второе уравнение умножьте на 14. и вычтите второе уравнение из первого уравнения.Это дает

294x ₂ + 357x ₃ = -63 первое уравнение

294x ₂ + 350x ₃ = -56 второе уравнение

7x ₃ = -7 второе уравнение вычитается из первого

х ₃ = -1

Часть C Решите относительно x ₂, вставив значение, полученное для x ₃ в любое уравнение из части B.

14x ₂ + 17 (-1) = -3

1 4x ₂ = 14

х ₂ = 1 или

21x ₂ + 25 (-1) = -4

21x ₂ = 21

х ₂ = 1

Часть D Решите относительно x ₁, вставив полученные значения x ₂ andx ₃ в любом из трех исходных уравнений.

2x ₁ + 5x ₂ + 7x ₃ = 2 первое исходное уравнение

2x ₁ + 5 (1) + 7 (-1) = 2

2x ₁ = 4

x ₁ = 2 или

4x ₁ — 4x ₂ — 3x ₃ = 7 секунд исходное уравнение

4x ₁ — 4 (1) — 3 (-1) = 7

4x ₁ = 8

х ₁ = 2 или же

3x ₁ — 3x ₂ — 2x ₃ = 5 третье исходное уравнение

3x ₁ — 3 (1) -2 (-1) = 5 900 10

3x ₁ = 6

х ₁ = 2

Метод замещения

Это включает выражение одной переменной через другую до тех пор, пока не будет одно уравнение с одним неизвестным.Затем это уравнение решается для этого один неизвестный. Затем результат используется для поиска переменной, которая была выражается через переменную, решение которой было только что найдено.

Пример

12x — 7лет = 106 первое уравнение

8x + У = 82 второе уравнение

Решите второе уравнение для y, а затем подставьте полученное значение y в первое уравнение.

г = 82 — 8x второе уравнение, решенное относительно y

12x — 7 (82 — 8х) = 106 первое уравнение переписано в x

12x — 574 + 56x = 106

68x = 680

х = 10

Подставьте полученное значение x в любое из исходных эквивалентов.

12x — 7лет = 106 первое уравнение

12 (10) — 7лет = 106

7лет = 14

г = 2

8 (10) + У = 82 второе уравнение

г = 2

[индекс]

Для квадратного уравнения 3×2 5x + 2 0 Как вы учитесь математике 10 CBSE

Подсказка: Мы дали квадратное уравнение вида $ a {x ^ 2} + bx + c = 0 $.2} — 4 \ left (3 \ right) \ left (2 \ right)}}} {{2 \ left (3 \ right)}} $
Шаг 3: Упростив приведенное выше уравнение, мы получаем
$ x = \ dfrac {{5 \ pm \ sqrt {25–24}}} {2} $
Шаг 4. При дальнейшем упрощении получаем
$ x = \ dfrac {{5 \ pm \ sqrt 1}} {2} $
. $ x = \ dfrac {{5 \ pm 1}} {2} $
Шаг 5: Сначала, учитывая положительный знак, получаем
$ x = \ dfrac {{5 + 1}} {2} $
$ \ Rightarrow x = 3 $
Шаг 6: Теперь, учитывая отрицательный знак, мы получаем
$ x = \ dfrac {{5-1}} {2} $
$ \ Rightarrow x = 2 $

Следовательно, решение приведенного выше уравнения равно $ x = 2 $ и $ x = 3 $

Примечание:
При решении квадратного уравнения существуют два корня.2} — 4ac $.
Если значение дискриминанта больше нуля, то мы получаем два разных корня, если дискриминант равен нулю, то мы получаем одинаковые корни, а если дискриминант меньше нуля, то мы получаем мнимые корни.

Вы в одном шаге от ответа!

Подпишитесь бесплатно!

Регистрируясь, вы также получаете доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам БЕСПЛАТНО!

Решите квадратные уравнения по квадратичной формуле — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

Решите квадратные уравнения, используя квадратную формулу
Используйте дискриминант, чтобы предсказать количество решений квадратного уравнения
Определите наиболее подходящий метод для решения квадратного уравнения

Прежде чем начать, пройдите тест на готовность.

Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).

Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз предпринимали одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ — «да». В этом разделе мы выведем и воспользуемся формулой, чтобы найти решение проблемы. квадратное уровненеие.

Мы уже видели, как решить формулу для конкретной переменной «в целом», чтобы мы проделали алгебраические шаги только один раз, а затем использовали новую формулу, чтобы найти значение конкретной переменной. Теперь мы рассмотрим этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x . Возможно, будет полезно взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение формы, когда вы читаете алгебраические шаги ниже, поэтому вы видите их как с числами, так и со словом «в целом».’

Последнее уравнение — квадратичная формула.

Квадратичная формула

Решения квадратного уравнения вида даются формулой:

Чтобы использовать квадратичную формулу, мы подставляем значения в выражение в правой части формулы. Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения.

Как решить квадратное уравнение с помощью квадратичной формулы