4 найдите корень уравнения: Найдите корень уравнения: 1) 2x − 7 = x + 4; 2) −0,7(5 − x) = −4,9.

alexxlab / / Разное

Тренировочный вариант ЕГЭ. Задание 7. Найдите корень уравнения sqrt(x-1)=4

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.

При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Главная → Видеоуроки →  ЕГЭ по математике. Профильный уровень. Задание 7.

Описание видеоурока:

Решите уравнение: Найдите корень уравнения sqrt(x-1)=4

Иррациональным называется уравнение, в котором неизвестное (переменная) содержится под знаком корня или под знаком операции возведения в рациональную (дробную) степень.

Валерий Волков 10 08.04.2016

Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!

Новости образования

ЕГЭ по математике

Профильный уровень

Задание 1     Задание 2

Задание 3     Задание 4

Задание 5     Задание 6

Задание 7     Задание 8

Задание 9     Задание 10

Задание 11     Задание 12

Задание 13     Задание 14

Задание 15     Задание 16

Задание 17     Задание 18

Задание 19     Задание 20

Задание 21

ГИА по математике

Задача 1     Задача 2

Задача 3     Задача 4

Задача 5     Задача 6

Задача 7     Задача 8

Задача 9     Задача 10

Задача 11     Задача 12

Задача 13     Задача 14

Задача 15     Задача 16

Задача 17     Задача 18

Задача 19     Задача 20

Задача 21     Задача 22

Задача 23     Задача 24

Задача 25     Задача 26

Демонстрационные варианты ОГЭ по математике

Математика. 5 класс.

Натуральные числа

Обыкновенные дроби

Десятичные дроби

Проценты

Математика. 6 класс.

Делимость чисел

Сложение и вычитание дробей с разными знаменателями

Умножение и деление обыкновенных дробей

Отношения и пропорции

Положительные и отрицательные числа

Измерение величин

Математика. 7 класс.

Преобразование выражений

Многочлены

Формулы сокращенного умножения

Математика. 8 класс.

Модуль числа. Уравнения и неравенства.

Квадратные уравнения

Квадратные неравенства

Уравнения с параметром

Задачи с параметром

Математика. 9 класс.

Функции и их свойства

Прогрессии

Векторы

Комбинаторика, статистика и теория вероятностей

Математика. 10 — 11 класс.

Числовые функции

Тригонометрические функции

Тригонометрические уравнения

Преобразование тригонометрических выражений

Производная

Степенные функции

Показательная функция

Логарифмические функции

Первообразная и интеграл

Уравнения и неравенства

Комбинаторика

Создаёте видеоуроки?

Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.

Актуально

Физкультминутки для школьников и дошкольников

Подготовка к ЕГЭ Подготовка к ОГЭ

Самостоятельная работа по теме: «Уравнения»

 

Задание № 7

 

1.     Иррациональные уравнения

 

1. Най­ди­те ко­рень урав­не­ния .

 

2. Най­ди­те ко­рень урав­не­ния .

 

3. Най­ди­те ко­рень урав­не­ния .

 

4. Най­ди­те ко­рень урав­не­ния:  

Если урав­не­ние имеет более од­но­го корня, ука­жи­те мень­ший из них.

 

5. Най­ди­те ко­рень урав­не­ния .

 

6. Най­ди­те ко­рень урав­не­ния .

 

7. Ре­ши­те урав­не­ние .

 

8. Ре­ши­те урав­не­ние .

 

9. Ре­ши­те урав­не­ние .

Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

 

10. Най­ди­те ко­рень урав­не­ния 

 

11. Ре­ши­те урав­не­ние 

 

12. Ре­ши­те урав­не­ние:

 

13. Най­ди­те ко­рень урав­не­ния 

 

14. Най­ди­те ко­рень урав­не­ния 

 

 

 

 

 

2.     Линейные, квадратные, ку­би­че­ские уравнения

                                                                                                     

1. Най­ди­те ко­рень урав­не­ния: .

 

2. Най­ди­те ко­рень урав­не­ния 

3. Най­ди­те ко­рень урав­не­ния  Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

 

4. Ре­ши­те урав­не­ние  Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

 

5. Най­ди­те ко­рень урав­не­ния 

 

6. Най­ди­те ко­рень урав­не­ния 

 

7. Ре­ши­те урав­не­ние 

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

 

8. Ре­ши­те урав­не­ние 

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

 

9. Най­ди­те ко­рень урав­не­ния 

 

10. Най­ди­те ко­рень урав­не­ния  Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

11. Най­ди­те ко­рень урав­не­ния: .

 

12. Най­ди­те ко­рень урав­не­ния 

 

13. Най­ди­те ко­рень урав­не­ния .

 

14. Най­ди­те ко­рень урав­не­ния:  Если урав­не­ние имеет более од­но­го корня, ука­жи­те мень­ший из них.

 

15. Ре­ши­те урав­не­ние .

16. Ре­ши­те урав­не­ние .

17. Ре­ши­те урав­не­ние .

 

18.. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

 

19. Най­ди­те ко­рень урав­не­ния . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

20. Най­ди­те ко­рень урав­не­ния .

 

21. Най­ди­те ко­рень урав­не­ния .

 

3.     Логарифмические уравнения

 

 

 

1. Най­ди­те ко­рень урав­не­ния .

 

2. Най­ди­те ко­рень урав­не­ния .

 

3. Най­ди­те ко­рень урав­не­ния .

 

4. Най­ди­те ко­рень урав­не­ния .

 

5. Най­ди­те ко­рень урав­не­ния .

 

6. Най­ди­те ко­рень урав­не­ния .

 

7. Най­ди­те ко­рень урав­не­ния .

 

8. Ре­ши­те урав­не­ние .

 

9. Ре­ши­те урав­не­ние .

 

10. Ре­ши­те урав­не­ние .

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

 

11. Най­ди­те ко­рень урав­не­ния .

 

12. Най­ди­те ко­рень урав­не­ния .

 

13. Най­ди­те ко­рень урав­не­ния 

 

14. Най­ди­те ко­рень урав­не­ния 

 

15. Най­ди­те ко­рень урав­не­ния 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.      Показательные уравнения

 

1. Най­ди­те ко­рень урав­не­ния .

 

2. Най­ди­те ко­рень урав­не­ния .

 

3. Най­ди­те ко­рень урав­не­ния .

 

4. Най­ди­те ко­рень урав­не­ния .

5. Най­ди­те ко­рень урав­не­ния .

 

6. Най­ди­те ко­рень урав­не­ния .

 

7. Най­ди­те ко­рень урав­не­ния: .

 

8. Най­ди­те ко­рень урав­не­ния: 

 

9. Най­ди­те ре­ше­ние урав­не­ния: 

 

10. Ре­ши­те урав­не­ние .

 

11. Ре­ши­те урав­не­ние .

 

12. Най­ди­те ко­рень урав­не­ния 

 

13. Най­ди­те ко­рень урав­не­ния 

14. Най­ди­те ко­рень урав­не­ния 

 

15. Най­ди­те ко­рень урав­не­ния 

16. Най­ди­те ко­рень урав­не­ния 

17. Най­ди­те ко­рень урав­не­ния 

 

 

5.     Рациональные уравнения

 

 

1. Най­ди­те ко­рень урав­не­ния: 

 

2. Най­ди­те ко­рень урав­не­ния: . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

 

3. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

 

4. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

 

5. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

 

 

6. Най­ди­те ко­рень урав­не­ния: .

 

7. Най­ди­те ко­рень урав­не­ния: .

 

8. Най­ди­те ко­рень урав­не­ния 

 

9. Най­ди­те ко­рень урав­не­ния .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.     Тригонометрические уравнения

1.     Най­ди­те корни урав­не­ния:  

В ответ за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

 

2.     Ре­ши­те урав­не­ние .

В от­ве­те на­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

 

3.     Ре­ши­те урав­не­ние .

В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы:

1.      Иррациональные уравнения.

 

 

1. Най­ди­те ко­рень урав­не­ния .

Воз­ве­дем в квад­рат:

 

Ответ: 3.

 

Воз­ве­дем в квад­рат:

Ответ: 87.

 

3. Най­ди­те ко­рень урав­не­ния .

Воз­ве­дем в квад­рат:

.

Ответ: 35.

 

4. Най­ди­те ко­рень урав­не­ния:  

Если урав­не­ние имеет более од­но­го корня, ука­жи­те мень­ший из них.

Воз­ве­дем в квад­рат:

Ответ: −9.

 

5. Най­ди­те ко­рень урав­не­ния .

Воз­ве­дем в квад­рат:

.

Ответ: 11.

 

6. Най­ди­те ко­рень урав­не­ния .

Воз­ве­дем обе части урав­не­ния в тре­тью сте­пень:

Ответ: 31.

 

7. Ре­ши­те урав­не­ние .

Воз­ве­дем в квад­рат:

 

Ответ:  −2,5.

 

8. Ре­ши­те урав­не­ние .

Воз­ве­дем в квад­рат:

Ответ:  −2.

 

 

9. Ре­ши­те урав­не­ние .

Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

Воз­ве­дем в квад­рат:

Урав­не­ние имеет един­ствен­ный ко­рень, он и яв­ля­ет­ся от­ве­том.

 

Ответ: 6.

 

10. Най­ди­те ко­рень урав­не­ния 

Воз­ве­дем в квад­рат обе части урав­не­ния:

 

 

Ответ:6.

 

11. Ре­ши­те урав­не­ние 

Воз­ве­дем в квад­рат обе части урав­не­ния:

 

 

Ответ:−17.

12. Ре­ши­те урав­не­ние:

Воз­ве­дем в квад­рат:

Ответ:  −7.

 

13. Най­ди­те ко­рень урав­не­ния 

Воз­ве­дем в квад­рат:

Ответ: 1.

 

14. Най­ди­те ко­рень урав­не­ния 

Воз­ве­дем в квад­рат:

 

Ответ: 8.

2.     Линейные, квадратные, ку­би­че­ские уравнения(пояснения)

 

 

1. Най­ди­те ко­рень урав­не­ния: .

 

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 13.

 

2. Най­ди­те ко­рень урав­не­ния 

По­сле­до­ва­тель­но по­лу­ча­ем:

 

 

Ответ: 0,2.

3. Най­ди­те ко­рень урав­не­ния  

Решим квад­рат­ное урав­не­ние:

 

Ответ: −8.

 

4. Ре­ши­те урав­не­ние  

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

Решим квад­рат­ное урав­не­ние:

Ответ: −9.

 

5. Най­ди­те ко­рень урав­не­ния 

Найдём ко­рень урав­не­ния:

 

 

Ответ: −4.

 

6. Най­ди­те ко­рень урав­не­ния 

Найдём ко­рень урав­не­ния:

 

 

Ответ: 2.

 

7. Ре­ши­те урав­не­ние 

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

. Таким об­ра­зом, наи­боль­ший ко­рень 

Ответ: 4.

 

8. Ре­ши­те урав­не­ние 

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

. Таким об­ра­зом, наи­боль­ший ко­рень 

Ответ: 2.

 

9. Най­ди­те ко­рень урав­не­ния 

По­сле­до­ва­тель­но по­лу­чим:

 

 

Ответ: −2.

 

10. Най­ди­те ко­рень урав­не­ния  

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

. По тео­ре­ме Виета для квад­рат­но­го урав­не­ния: . Таким об­ра­зом, . Наи­мень­ший ко­рень 

Ответ: 3.

11. Най­ди­те ко­рень урав­не­ния: .

По­сле­до­ва­тель­но по­лу­ча­ем:

.

Ответ: −5.

 

12. Най­ди­те ко­рень урав­не­ния 

Рас­кро­ем скоб­ки:

 

Ответ: −9.

 

13. Най­ди­те ко­рень урав­не­ния .

Пе­ре­несём вы­ра­же­ния с пе­ре­мен­ной в левую часть, а числа — в пра­вую, по­лу­чим:  от­ку­да 

 

Ответ: −0,5.

14. Най­ди­те ко­рень урав­не­ния:  

Если урав­не­ние имеет более од­но­го корня, ука­жи­те мень­ший из них.

Решим квад­рат­ное урав­не­ние:

По тео­ре­ме, об­рат­ной тео­ре­ме Виета, сумма кор­ней урав­не­ния равна 17, а их про­из­ве­де­ние равно 72. Тем самым, это числа 8 и 9.

 

Ответ: 8.

 

15. Ре­ши­те урав­не­ние .

Вы­пол­ним пре­об­ра­зо­ва­ния, ис­поль­зуя фор­му­лы  и :

Ответ: −1,5.

 

16. Ре­ши­те урав­не­ние .

Ис­поль­зу­ем фор­му­лы квад­ра­та раз­но­сти и квад­ра­та суммы:

Ответ: −6.

17. Ре­ши­те урав­не­ние .

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ:  −4.

18. Ре­ши­те урав­не­ние .

Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

 

Пе­ре­ве­дем число в пра­вой части урав­не­ния в не­пра­виль­ную дробь и умно­жим обе части урав­не­ния на 3, по­лу­ча­ем:

 

Ответ:  −7.

 

19. Най­ди­те ко­рень урав­не­ния .

Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

За­пи­шем квад­рат­ное урав­не­ние в стан­дарт­ном виде:  от­ку­да  В ответ за­пи­шем мень­ший из кор­ней.

 

Ответ: −1.

 

 

 

 

20. Най­ди­те ко­рень урав­не­ния .

 

Из­вле­кая ку­би­че­ский ко­рень из обеих ча­стей урав­не­ния, по­лу­ча­ем , от­ку­да .

21. Най­ди­те ко­рень урав­не­ния .

Из­вле­кая ку­би­че­ский ко­рень из обеих ча­стей урав­не­ния, по­лу­ча­ем , от­ку­да .

 

3.     Логарифмические уравнения

 

1. Най­ди­те ко­рень урав­не­ния .

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: −124.

 

2. Най­ди­те ко­рень урав­не­ния .

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 21.

 

3. Най­ди­те ко­рень урав­не­ния .

По­сле­до­ва­тель­но по­лу­ча­ем:

.

 

Ответ: 2.

 

4. Най­ди­те ко­рень урав­не­ния .

По­сле­до­ва­тель­но по­лу­ча­ем:

.

Ответ: −12.

 

5. Най­ди­те ко­рень урав­не­ния .

Ло­га­риф­мы двух вы­ра­же­ний равны, если сами вы­ра­же­ния равны и при этом по­ло­жи­тель­ны:

 

 

Ответ: 6.

6. Най­ди­те ко­рень урав­не­ния .

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: −42.

 

7. Най­ди­те ко­рень урав­не­ния .

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: −4.

 

8.Ре­ши­те урав­не­ние .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: 5.

 

9. Ре­ши­те урав­не­ние .

За­ме­тим, что  и ис­поль­зу­ем фор­му­лу  Имеем:

 

 

 

Ответ: 2.

10. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

На ОДЗ пе­рей­дем к урав­не­нию на ос­но­ва­ние ло­га­риф­ма:

Итак, на ОДЗ урав­не­ние имеет толь­ко один ко­рень.

 

Ответ: 12.

11. Най­ди­те ко­рень урав­не­ния .

Ис­поль­зу­ем фор­му­лу :

 

или

Ответ:2.

 

12. Най­ди­те ко­рень урав­не­ния .

Ис­поль­зуя фор­му­лу , по­лу­ча­ем:

 

 

Ответ: 6.

 

Внимание:

Сле­ду­ет от­ли­чать это урав­не­ние от по­хо­же­го, но дру­го­го: . В этом слу­чае имеем:

 

 

13. Най­ди­те ко­рень урав­не­ния 

Поль­зу­ясь опре­де­ле­ни­ем ло­га­риф­ма, имеем:

 

 

Ответ:−11.

 

14.Най­ди­те ко­рень урав­не­ния 

Найдём ко­рень урав­не­ния:

 

 

Ответ: 22,4.

 

15. Най­ди­те ко­рень урав­не­ния 

По­сле­до­ва­тель­но по­лу­ча­ем:

 

 

Ответ: 4,5.

 

4.     Показательные уравнения

 

 

1. Най­ди­те ко­рень урав­не­ния .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: −1.

 

2. Най­ди­те ко­рень урав­не­ния .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

 

 

Ответ: 4.

 

 

3. Най­ди­те ко­рень урав­не­ния .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

 

 

Ответ: 10.

4. Най­ди­те ко­рень урав­не­ния .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

 

 

Ответ: 4.

 

5. Най­ди­те ко­рень урав­не­ния .

 

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: 8,75

6. Най­ди­те ко­рень урав­не­ния .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

.

Ответ: 12,5.

7. Най­ди­те ко­рень урав­не­ния: .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

.

Ответ: 8.

8. Най­ди­те ко­рень урав­не­ния: 

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: 0.

 

9. Най­ди­те ре­ше­ние урав­не­ния: 

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: 4.

10. Ре­ши­те урав­не­ние .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: 3.

 

11. Ре­ши­те урав­не­ние .

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: −2.

12. Най­ди­те ко­рень урав­не­ния 

По­сколь­ку 81 равно 34, имеем:

 

Ответ: 7.

13. Най­ди­те ко­рень урав­не­ния 

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

 

 

Ответ: 8.

 

14. Най­ди­те ко­рень урав­не­ния 

 При­рав­ни­ва­ем по­ка­за­те­ли в сте­пе­нях: 

 

Ответ: 9

 

15. Най­ди­те ко­рень урав­не­ния 

 При­рав­ни­ва­ем по­ка­за­те­ли в сте­пе­нях: 

 

Ответ: -2

16. Най­ди­те ко­рень урав­не­ния 

 

При­рав­ни­ва­ем по­ка­за­те­ли в сте­пе­нях: 

 

Ответ: 3

17. Най­ди­те ко­рень урав­не­ния 

По­сле­до­ва­тель­но по­лу­ча­ем:

 

 

При­рав­ни­ва­ем по­ка­за­те­ли в сте­пе­нях: 

 

Ответ: 1.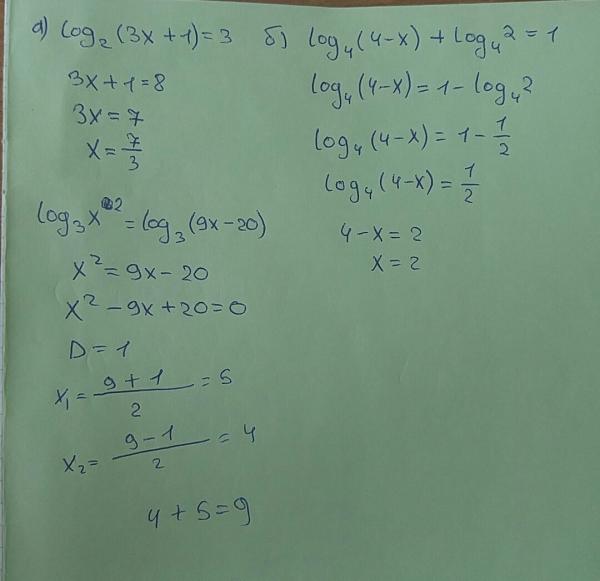

 

 

5. Рациональные уравнения

1. Най­ди­те ко­рень урав­не­ния: 

Из­ба­вим­ся от зна­ме­на­те­ля:

.

Ответ: 14.

2. Най­ди­те ко­рень урав­не­ния: . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

Об­ласть до­пу­сти­мых зна­че­ний: .

 

При  до­мно­жим на зна­ме­на­тель:

 

 

Оба корня лежат в ОДЗ. Боль­ший из них равен 5.

 

 

Ответ: 5.

3. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 5.

4. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

Об­ласть опре­де­ле­ния урав­не­ния за­да­ет­ся со­от­но­ше­ни­ем . На об­ла­сти опре­де­ле­ния имеем:

Оба най­ден­ный ре­ше­ния удо­вле­тво­ря­ют усло­вию , мень­ший из них равен −0,5.

Ответ: −0,5.

 

5. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

 

За­ме­тим, что чис­ли­те­ли дро­бей равны. Имеем:

Ответ: 1.

 

6. Най­ди­те ко­рень урав­не­ния: .

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 1.

 

7. Най­ди­те ко­рень урав­не­ния: .

По­сле­до­ва­тель­но по­лу­ча­ем:

.

Ответ: 0,3.

 

8. Най­ди­те ко­рень урав­не­ния 

Если две дроби с рав­ным чис­ли­те­лем равны, то равны их зна­ме­на­те­ли. Имеем:

 

Ответ:7.

 

9. Най­ди­те ко­рень урав­не­ния .

Если две дроби с рав­ным чис­ли­те­лем равны, то равны их зна­ме­на­те­ли. Имеем

 

Ответ:−6.

 

6.Тригонометрические уравнения

 

 

1.      Най­ди­те корни урав­не­ния: 

 

В ответ за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

 

По­сле­до­ва­тель­но по­лу­ча­ем:

 

 

Зна­че­ни­ям  со­от­вет­ству­ют по­ло­жи­тель­ные корни.

 

Если , то  и .

 

Если , то  и .

 

Зна­че­ни­ям  со­от­вет­ству­ют мень­шие зна­че­ния кор­ней.

 

Сле­до­ва­тель­но, наи­боль­шим от­ри­ца­тель­ным кор­нем яв­ля­ет­ся число .

 

Ответ: −4.

 

2. Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

Решим урав­не­ние:

 

 

Зна­че­нию  со­от­вет­ству­ет . По­ло­жи­тель­ным зна­че­ни­ям па­ра­мет­ра со­от­вет­ству­ют по­ло­жи­тель­ные зна­че­ния кор­ней, от­ри­ца­тель­ным зна­че­ни­ям па­ра­мет­ра со­от­вет­ству­ют мень­шие зна­че­ния кор­ней. Сле­до­ва­тель­но, наи­боль­шим от­ри­ца­тель­ным кор­нем яв­ля­ет­ся число −1.

 

Ответ:  −1.

 

 

3. Ре­ши­те урав­не­ние .

В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

Решим урав­не­ние:

 

Зна­че­ни­ям  со­от­вет­ству­ют боль­шие по­ло­жи­тель­ные корни.

Если , то  и .

Если , то  и .

Зна­че­ни­ям  со­от­вет­ству­ют мень­шие зна­че­ния кор­ней.

Наи­мень­шим по­ло­жи­тель­ным ре­ше­ни­ем яв­ля­ет­ся 0,5.

Ответ: 0,5.

 

 

 

 

логарифмов — Найдите корни уравнения с квадратичными, линейными и логарифмическими членами?

Задавать вопрос

спросил

Изменено 7 лет, 10 месяцев назад

Просмотрено 2к раз

$\begingroup$ 92 + bx + c\log x=0. $

с учетом натурального $\log$. Wolfram alpha подводит меня к выражениям, включающим функцию Ламберта W (логарифм произведения), когда я включаю либо квадратичный член, либо линейный член (но не оба), и аналитические аппроксимации, когда я указываю реальные значения для коэффициентов.

Это нормально, но существует ли более общее решение с точки зрения коэффициентов?

спасибо!

  • логарифмы
  • квадратичные уравнения
  • трансцендентные уравнения 9{n-1} H_{n-1}\left( \sqrt\frac{na}{c} \frac{b}{2a}\right) }{n!}$$

    Ссылки

    » Обобщение $W$-функции Ламберта, многочлены Бесселя и трансцендентные уравнения», Джорджо Мугнаини, http://arxiv.org/pdf/1501.00138

    $\endgroup$

    $\begingroup$

    Любое уравнение, которое можно записать в виде $$A+B x+C \log(D+Ex)=0$$, имеет решение, которое может быть выражено через функцию Ламберта.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *