Абсолютное значение — MathCracker.com
Алгебра Учебники
Абсолютное значение числа соответствует его величине без учета знака, если он есть. Геометрически это соответствует расстоянию от точки \(x\) до начала координат \(0\) на реальной прямой.
Математически абсолютное значение числа \(x\) представляется как \(|x|\).
Из-за геометрической природы его интерпретации абсолютное значение широко используется в алгебре и других областях математики, и оказывается, что вычислить абсолютное значение данного числа очень легко: все, что вам нужно сделать, это отбросить знак, если есть знак.
ПРИМЕР 1
Вычислите абсолютное значение \(-8\).
ОТВЕЧАТЬ:
Как мы упоминали выше, абсолютное значение числа — это его величина без учета знака. В этом случае, отбрасывая знак, мы понимаем, что абсолютное значение \(-8\) равно \(8\). Математически мы пишем \(|-8| = 8\).
ПРИМЕР 2
Вычислите абсолютное значение \(4\).
ОТВЕЧАТЬ:
Мы знаем, что абсолютное значение числа — это его величина без учета знака. В этом случае нет знака, который нужно отбрасывать, поэтому получите абсолютное значение \(4\) просто \(4\). Итак, математически мы пишем \(|4| = 4\).
В этом случае нет знака, который нужно отбрасывать, поэтому получите абсолютное значение \(4\) просто \(4\). Итак, математически мы пишем \(|4| = 4\).
Математическое определение абсолютного значения
Этой идеи «отбрасывать знак» было бы достаточно, если бы все, что мы делали, — это вычислять абсолютное значение чисел. Но на самом деле мы делаем больше вещей, которые немного сложнее, такие как уравнения абсолютных значений и неравенства.
Математически формальное определение \(|x|\) дается ниже.
\ [| х | = \ left \ {\ begin {array} {cc} x \ text {} & \, \, \, \ text {for} x \ ge 0 \\ \\ -x & \, \, \ text {for} x <0 \\ \ end {array} \ right. \]
\]
Без паники проанализируем данное определение. Он просто говорит: «Проверьте данное число \(x\). Если \(x\) больше или равно нулю, то абсолютным значением числа будет само число. В противном случае, если данное число \(x\) отрицательно, абсолютное значение числа будет \(-x\), что соответствует умножению первоначально заданного числа на \(-1\).
Итак, в случае \(-8\) это число отрицательное, поэтому абсолютное значение получается умножением его на \(-1\), поэтому мы получаем \(|-8|\) = (-1) \ times (-8) = 8. Вот и все.
Это определение может показаться излишним. В конце концов, почему бы не придерживаться метода «уронить знак»? Для этого есть причина, и это просто потому, что такой способ определения абсолютного значения помогает нам справляться с более сложными ситуациями, связанными с абсолютным значением.
Хотел только указать, почему мы беремся за формальное определение абсолютного значения, и это потому, что в какой-то момент оно нам понадобится, когда мы будем обрабатывать более сложные операции с абсолютными значениями.
Свойства абсолютного значения
Это основные свойства:1) \(|0| = 0\)
2) \(|ab| = |a||b|\), для вещественных чисел \(a\) и \(b\)
3) \(|a+b| \le |a|+|b|\), для вещественных чисел \(a\) и \(b\)
Ошибка квадратного корня квадрата
Наконец, я хотел бы отдать должное абсолютному значению отсутствующей ссылки.
и вот вам одно из звездных проявлений абсолютной ценности. Со временем вы поймете, что это проявляется чаще, чем вы думаете.
Подробнее об абсолютном значении
Абсолютное значение — это простая концепция, и она действительно полезна, поскольку имеет четкую геометрическую интерпретацию в реальной линии: она представляет собой расстояние от любой точки до начала координат.
Хотя вычислить его для числа просто, существуют более сложные операции, которые включают абсолютные значения, такие как уравнения и неравенства абсолютных значений. Для их решения требуется четкая стратегия, иначе вы можете попасть в тупик.
Как найти абсолютное значение?
Обычно найти абсолютное значение заданного числа не так уж и сложно: все, что вам нужно сделать, это получить величину числа без учета знака. Другими словами, чтобы было проще, просто посмотрите, есть ли знак, и бросьте его.
Процедура менее очевидна, когда вы вычисляете абсолютное значение алгебраического выражения, и в этом случае вам нужно сначала уменьшить выражение до числа, а затем отбросить любой знак, если он есть.
Приложения абсолютной ценности
Использование абсолютного значения выходит за рамки простого вычисления абсолютного значения чисел. 2} = x\), что неверно, когда \(x\) отрицательно.
2} = x\), что неверно, когда \(x\) отрицательно.
Абсолютное значение также появляется в геометрии (поскольку абсолютное значение разницы представляет собой расстояние между двумя точками), при интегрировании и для тех случаев, когда нам нужно решить неравенства по абсолютной величине .
Кроме того, вы можете использовать это
калькулятор абсолютного значения
чтобы попрактиковаться в концепциях, изученных в этом руководстве. Или для более общих расчетов вы можете использовать это
калькулятор алгебраических выражений
.
Или для более общих расчетов вы можете использовать это
калькулятор алгебраических выражений
.
Абсолютная величина Учебники по алгебре
Абсолютное значение серии Pandas
Python — это язык программирования высокого уровня, который отлично подходит для аналитиков данных, поскольку Pandas в Python предоставляет потрясающую экосистему пакетов, ориентированных на данные. Pandas в Python предоставляет потрясающие пакеты, которые упрощают и упрощают анализ данных.
Pandas в Python предоставляет потрясающие пакеты, которые упрощают и упрощают анализ данных.
В Python абсолютное значение числа почти такое же, как и в математике. Когда вы находите абсолютное значение числа с помощью любой функции Python, она также возвращает неотрицательное значение этого числа. Язык программирования Python предоставляет встроенные функции и пакеты panda для нахождения абсолютного значения числа или ряда. В этой статье мы собираемся подробно обсудить эту тему.
Что такое абсолютное значение в Python?
Если вы не знакомы с абсолютным значением ряда, давайте познакомим вас с определением абсолютного значения или ряда. Если вы уже знакомы с ним, давайте просто дадим вам краткий обзор, чтобы напомнить вам об основных понятиях.
Независимо от знака числа, абсолютная функция возвращает свое неотрицательное значение, и она также широко известна как функция модуля. Например, абсолютное значение или модуль числа 2 равно 2, как и абсолютное значение или модуль числа -2. Функция absolute() обычно используется для нахождения расстояния от до положительной стороны этого конкретного предоставленного числа без учета знака числа.
Функция absolute() обычно используется для нахождения расстояния от до положительной стороны этого конкретного предоставленного числа без учета знака числа.
Как получить абсолютную ценность в серии Pandas?
Как мы упоминали ранее, Python предоставляет пакеты panda для поиска абсолютного значения числа или ряда. В пакетах Pandas есть несколько функций для вычисления абсолютного значения, и series.abs() — одна из таких функций. Series.abs() используется для поиска абсолютного значения каждого числа в наборе данных.
abs() — это встроенная функция Python, доступная в стандартной библиотеке. Когда ему передается число, он возвращает неотрицательное значение этого числа без учета знака числа. Число может быть комплексным числом, действительным числом, числом с плавающей запятой или просто целым числом.
Однако величина возвращается в случае предоставления комплексного числа. Принимая во внимание, что абсолютное целое число возвращается для целого числа, абсолютное действительное число для действительного числа и абсолютное число с плавающей запятой для числа с плавающей запятой, независимо от их знака.
Каков синтаксис метода abs()?
Синтаксис abs() очень прост, он принимает только один параметр; число, из которого он должен вычислить абсолютное значение и вернуть его абсолютное значение. Вот синтаксис abs():
«Число» — это снова любое действительное, комплексное, число с плавающей запятой или простое целое число, заданное в качестве входных данных для получения абсолютного значения. Теперь давайте рассмотрим несколько примеров, чтобы узнать, как использовать функцию abs().
Пример 1:
В этом примере мы возьмем 6 чисел; целое число, отрицательное целое число, вещественное число, число с плавающей запятой, отрицательное число с плавающей запятой и комплексное число, чтобы показать, какие различные типы абсолютных значений будут возвращаться функцией abs(). См. код функции abs (0) ниже:
Пинтегер =5
Девять = -5
реальное число =2
PFloat =3.8
NFloat = -3.8
ComplexNum =5+9j
Распечатать(«Абсолютное значение положительного целого числа равно =»,пресс(Пинтегер))
Распечатать(«Абсолютное значение отрицательного целого числа равно =»,пресс(Девять))
Распечатать(«Абсолютное значение действительного числа равно =»,пресс(реальное число))
Распечатать(«Абсолютное значение положительного числа с плавающей запятой:»,пресс(PFloat))
Распечатать(«Абсолютное значение отрицательного числа с плавающей запятой:»,пресс(NFloat))
Распечатать(«Абсолютное значение комплексного числа равно:»,пресс(ComplexNum))
Как вы можете видеть, вместо целого числа возвращается целое число, вместо действительного числа возвращается действительное число. с плавающей запятой возвращается для числа с плавающей запятой, а величина возвращается для комплексного количество. Однако абсолютное число для отрицательных значений также одинаково.
с плавающей запятой возвращается для числа с плавающей запятой, а величина возвращается для комплексного количество. Однако абсолютное число для отрицательных значений также одинаково.
Пример 2:
Теперь, когда мы знаем, как работает функция abs() и как она вычисляет абсолютное значение числа, давайте узнаем, как использовать функцию abs() для нахождения абсолютного значения ряда. Как мы уже обсуждали ранее, Pandas в Python предоставляет функцию Series.abs() для нахождения абсолютного значения ряда, поэтому мы будем использовать ее в этом примере.
Разница между функциями abs() и Series.abs() заключается в том, что Series.abs() не принимает никаких параметров и возвращает абсолютное значение полного набора данных, а не просто число. Во-первых, вам нужно создать набор данных для передачи в серию, а затем применить функцию abs(). Функция abs() просматривает каждое число в наборе данных и находит его абсолютное значение. Посмотрите простой код ниже, чтобы узнать, как использовать функцию Series. abs().
abs().
импорт панды в виде пд
список1 =[1,2,3, -4, -10.3,4+6j]
серия1 = пд.Ряд(список1)
Распечатать(серия1.пресс())
Стоит отметить, что список включает как комплексные, так и действительные числа. Ниже приведен вывод приведенного выше кода:
Теперь вы можете видеть, что abs() и series.abs() имеют одинаковую функциональность и возвращают один и тот же результат.
Пример 3:
Передача полного массива в abs() заставляет abs() возвращать абсолютное значение каждого числа. Однако в этом примере мы научим вас вычислять абсолютное значение определенного числа или строки в наборе данных. Первый шаг — создать DataFrame, а затем указать имя строки, в которой вы хотите найти абсолютное значение, а затем, наконец, примените функцию abs(), чтобы найти абсолютное значение этого конкретного ряд.
импорт панды в виде пд
дф = пд.кадр данных({‘Имя’: [‘Херри’,’Дженни’,’Питер’,’Марс’],
«Математика»: [53,29, -92, -56. 3],
3],
‘Физика’: [-58, -97,62,48]})
дф[«Абсолютная математика»]=(дф.Математика).пресс()
дф
Посмотрите на вывод ниже и обратите внимание, что abs() вычисляет только абсолютное значение математической строки, в то время как другая строка остается неизменной.
Вывод
В этой статье мы изучили общую концепцию абсолютного значения в математике, а затем увидели, как найти абсолютное значение в Python. Пакеты Pandas для нахождения абсолютного значения числа доступны на языке программирования Python. Метод abs() в кадре данных используется для нахождения абсолютного значения числа, ряда или отдельной строки.
Функция abs() в Python, абсолютное значение числа.
Функция abs() в Python, абсолютное значение числа.Сообщить об ошибке.
Синтаксис:abs(x)Параметры:
x— число, может быть целым числом, числом с плавающей запятой или комплексным числом.
- абсолютное значение числа
x, переданного в качестве аргумента.
Функция abs() используется для возврата абсолютного значения числа.
abs() принимает только один аргумент, число, абсолютное значение которого должно быть возвращено. Аргумент может быть целым числом, числом с плавающей запятой или комплексным числом.
- Если аргумент представляет собой целое число или число с плавающей запятой,
abs()возвращает абсолютное значение в виде целого числа или числа с плавающей запятой. - В случае комплексного числа
abs()возвращает только часть величины, которая также может быть числом с плавающей запятой.
# Число с плавающей точкой (запятой)
>>> f = -54.26
>>> print('=>', abs(f))
# => 54.26
# Целое число
>>> i = -94
>>> print('=>', abs(i))
# => 94
# Комплексное число
>>> c = (3 - 4j)
>>> print('=>', abs(c))
# => 5. 0
0
- ОБЗОРНАЯ СТРАНИЦА РАЗДЕЛА
- Функция abs(), абсолютное значение числа.
- Функция all(), все элементы True.
- Функция any(), хотя бы один элемент True.
- Функция ascii(), преобразует строку в ASCII.
- Функция bin(), число в двоичную строку.
- Класс bool(), логическое значение объекта.
- Функция breakpoint(), отладчик кода.
- Класс bytearray(), преобразует в массив байтов.
- Класс bytes(), преобразует в строку байтов.
- Функция callable(), проверяет можно ли вызвать объект.
- Функция chr(), число в символ Юникода.
- Класс classmethod, делает функцию методом класса.
- Функция compile() компилирует блок кода Python.
- Класс complex(), преобразует в комплексное число.
- Функция delattr(), удаляет атрибут объекта.
- Класс dict() создает словарь.
- Функция dir(), все атрибуты объекта.
- Функция divmod(), делит числа с остатком.
- Функция enumerate(), счетчик элементов последовательности.

- Функция eval(), выполняет строку-выражение с кодом.
- Функция exec(), выполняет блок кода.
- Функция filter(), фильтрует список по условию.
- Класс float(), преобразует в вещественное число.
- Функция format(), форматирует значение переменной.
- Класс frozenset(), преобразует в неизменяемое множество.
- Функция getattr(), значение атрибута по имени.
- Функция globals(), переменные глобальной области.
- Функция hasattr(), наличие атрибута объекта.
- Функция hash(), хэш-значение объекта.
- Функция help(), справка по любому объекту.
- Функция hex(), число в шестнадцатеричную строку.
- Функция id(), идентификатор объекта.
- Функция input(), ввод данных с клавиатура.
- Класс int(), преобразует в тип int.
- Функция isinstance(), принадлежность экземпляра к классу.
- Функция issubclass(), проверяет наследование класса.
- Функция iter(), создает итератор.
- Функция len(), считает количество элементов.

- Класс list(), преобразовывает в список.
- Функция locals(), переменные локальной области.
- Функция map(), обработка последовательности без цикла.
- Функция max(), максимальное значение элемента.
- Класс memoryview(), ссылка на буфер обмена.
- Функция min(), минимальное значение элемента.
- Функция next(), следующий элемент итератора.
- Класс object(), возвращает безликий объект.
- Функция oct(), число в восьмеричную строку.
- Функция open(), открывает файл на чтение/запись.
- Функция ord(), число символа Unicode.
- Функция pow(), возводит число в степень.
- Функция print(), печатает объект.
- Класс property(), использует метод класса как свойство.
- Класс range(), генерирует арифметические последовательности.
- Функция repr(), описание объекта.
- Функция reversed(), разворачивает последовательность.
- Функция round(), округляет число.
- Класс set(), создает или преобразовывает в множество.

- Функция setattr(), создает атрибут объекта.
- Класс slice(), шаблон среза.
- Функция sorted(), выполняет сортировку.
- Декоратор staticmethod(), метод класса в статический метод.
- Класс str(), преобразует объект в строку.
- Функция sum(), сумма последовательности.
- Функция super(), доступ к унаследованным методам.
- Класс tuple(), создает или преобразует в кортеж.
- Класс type(), возвращает тип объекта.
- Функция vars(), словарь переменных объекта.
- Функция zip(), объединить элементы в список кортежей.
- Функция __import__(), находит и импортирует модуль.
- Функция aiter(), создает асинхронный итератор.
- Функция anext(), следующий элемент асинхронного итератора.
Как найти абсолютное значение? – Обзоры Вики
Абсолютное значение числа — это расстояние числа от нуля, которое всегда будет положительным значением. Чтобы найти абсолютное значение числа, отбросить отрицательный знак, если он есть, чтобы сделать число положительным. Например, минус 4 станет 4.
Например, минус 4 станет 4.
Отсюда, каково абсолютное значение? Абсолютное значение (или модуль) | х | действительного числа x неотрицательное значение x без учета его знак. Например, абсолютное значение 5 равно 5, и абсолютное значение u22125 также равно 5. Абсолютное значение числа можно рассматривать как его расстояние от нуля по линии действительных чисел.
Каково абсолютное значение числа 4? Например, абсолютное значение 4 записывается как | 4 |. Кроме того, абсолютное значение -4 записывается как |-4|. Как мы обсуждали ранее, абсолютное значение всегда дает неотрицательное значение. Следовательно, |4|=|-4| =4.
Дополнительно Каково абсолютное значение -| 11? Правильный ответ:
Объяснение: абсолютное значение любого положительного числа — это само число, поэтому 11 имеет 11 как абсолютная величина. Кроме того, абсолютное значение отрицательного числа является его (положительной) противоположностью, поэтому также имеет абсолютное значение 11.
Каково абсолютное значение числа 45? Абсолютное значение любого числа также рассматривается как его расстояние от нуля. По определению мы знаем, что абсолютное значение любого действительного числа — это его положительное значение, и только положительное значение. не что иное, как 45 45 — положительное число.
Какое абсолютное значение 42?
Абсолютное значение — это расстояние между числом и нулем. Расстояние между −42 и 0 равно 42 .
Каково абсолютное значение числа 54? Абсолютное значение — это расстояние между числом и нулем. Расстояние между 0 и 54 равно 54.
Что означает |- 7 и каково его значение? Примеры алгебры
Абсолютное значение — это расстояние между числом и нулем. Чай расстояние между −7 и 0 равно 7.
Какое абсолютное значение 1 3?
Абсолютное значение числа — это одна из двух вещей. Если число не отрицательное, то абсолютное значение числа равно самому себе. Таким образом, абсолютное значение 6 равно 6, абсолютное значение 1/3 равно 1/3 и абсолютное значение 0 равно 0.
Также каково абсолютное значение |- 9? Абсолютное значение −9 равно 9.
Чему равно абсолютное значение (- 3?
Например, абсолютное значение 3 равно 3, а абсолютное значение −3 также равно 3. Абсолютное значение числа можно рассматривать как его расстояние от нуля.
Каково значение |- 21? Абсолютное значение -21, | – 305| , – 21. = абсолютное значение – 21 = 21.
Каково абсолютное значение числа 9 и отрицательного числа 9?
Абсолютное значение отрицательной девятки — это количество единиц, от которых отсчитывается -9. нуль. Это девять единиц от нуля. Таким образом, абсолютное значение -9 равно 9. Расстояние от 0 всегда является положительной величиной.
Какое абсолютное значение 25?
Расстояние от 25 до 0 равно 5 единиц . Это означает, что абсолютное значение 25 равно 5.
Каково абсолютное значение 8 |? Абсолютное значение 8 равно 8.
Каково абсолютное значение минус 4? Абсолютный (обозначается вертикальными чертами) означает, что все, что находится между ними, преобразуется в неотрицательное. Так что |−4|=4 и так |4|=4 .
Так что |−4|=4 и так |4|=4 .
Каково абсолютное значение | — 8?
Абсолютное значение -8 равно 8; |−8|=8 . Абсолютное значение любого числа всегда положительно.
Каково абсолютное значение -|- 12? Примеры алгебры
Абсолютное значение — это расстояние между числом и нулем. Расстояние между −12 и 0 равно 12 .
Каково абсолютное значение -|- 13?
Абсолютное значение — это расстояние между числом и нулем. Расстояние между −13 и 0 равно 13 .
Каково абсолютное значение |- 17? Абсолютное значение -17 равно +17.
Каково абсолютное значение /-6?
Абсолютное значение определяется как расстояние от числа до 0 , поэтому оно всегда положительно. Таким образом, абсолютное значение −6 будет расстояние от −6 до 0 на числовой строке, а это 6.
Каково абсолютное значение -(- 6? Абсолютное значение – 6 также равно 6. Абсолютное значение имеет особое обозначение в математических выражениях. Например, абсолютное значение 6 обозначается двумя вертикальными линиями: |6|. А абсолютное значение -6 обозначается как -6 с линиями по обеим сторонам, как и раньше: |−6|.
А абсолютное значение -6 обозначается как -6 с линиями по обеим сторонам, как и раньше: |−6|.
Какое абсолютное значение 8?
Абсолютное значение 8 равно 8.
Каково абсолютное значение числа 20? |20| знак равно 20; Абсолютное значение 20 равно 20.
Какое абсолютное значение 15?
Мы видим, что расстояние между этим числом и нулем равно $15$ единице, и согласно определению абсолютного значения мы знаем, что это расстояние от нуля до целого числа. Следовательно, абсолютное значение $ — 15 $ равно $15$, что также можно представить как $left| {– 15} вправо| = 15 долларов.
Каково абсолютное значение |- 9 |=?
Абсолютное значение −9 равно 9.
Каково абсолютное значение минус 18? Абсолютное значение |−18|=18 .
Абсолютное значение (алгебра)
Эта статья посвящена обобщению основной концепции. Для базовой концепции см. Абсолютная величина. Для использования в других целях см. Абсолютное значение (значения).
В алгебра, абсолютная величина (также называемый оценка, величина, или же норма,[1] несмотря на то что «норма «обычно относится к определенному типу абсолютного значения на поле ) это функция который измеряет «размер» элементов в поле или область целостности. Точнее, если D является областью целостности, то абсолютная величина есть любое отображение | x | из D к действительные числа р удовлетворение:
Точнее, если D является областью целостности, то абсолютная величина есть любое отображение | x | из D к действительные числа р удовлетворение:
| • | |Икс|≥0{displaystyle left | xight | geq 0} | (неотрицательность) | ||
| • | |Икс|=0{displaystyle left | xight | = 0} если и только если Икс=0{displaystyle x = 0} | (положительная определенность ) | ||
| • | |Иксу|=|Икс||у|{displaystyle left | xyight | = left | xight | left | yight |} | (мультипликативность) | ||
| • | |Икс+у|≤|Икс|+|у|{displaystyle left | x + yight | leq left | xight | + left | yight |} | (неравенство треугольника ) |
Из этих аксиом следует, что | 1 | = 1 и | -1 | = 1. Кроме того, для любого положительного целое число п,
- |п| = |1 + 1 + … + 1 (п раз) | = | −1 — 1 — … — 1 (п раз) | ≤п.

Классический «абсолютная величина «- это функция, в которой, например, | 2 | = 2, но многие другие функции удовлетворяют указанным выше требованиям, например квадратный корень классической абсолютной величины (но не ее квадрата).
Абсолютное значение вызывает метрика (и, следовательно, топология ) к d(ж,грамм)=|ж−грамм|.{displaystyle d (f, g) = | f-g |.}
Содержание
- 1 Примеры
- 2 Типы абсолютного значения
- 3 Места
- 4 Оценки
- 5 Завершено
- 6 Поля и области целостности
- 7 Примечания
- 8 Рекомендации
Примеры
- Стандартное абсолютное значение целых чисел.
- Стандартное абсолютное значение на сложные числа.
- В п-адическое абсолютное значение на рациональное число.
- Если р это область рациональные функции над полем F и п(Икс){displaystyle p (x)} фиксированный неприводимый элемент из р, то следующее определяет абсолютное значение на р: за ж(Икс){displaystyle f (x)} в р определять |ж|{displaystyle | f |} быть 2−п{displaystyle 2 ^ {- n}}, куда ж(Икс)=п(Икс)пграмм(Икс)час(Икс){Displaystyle f (x) = p (x) ^ {n} {гидроразрыв {g (x)} {h (x)}}} и граммcd(грамм(Икс),п(Икс))=1=граммcd(час(Икс),п(Икс)).
 {displaystyle gcd (g (x), p (x)) = 1 = gcd (h (x), p (x)).}
{displaystyle gcd (g (x), p (x)) = 1 = gcd (h (x), p (x)).}
Типы абсолютного значения
В банальный абсолютное значение — это абсолютное значение с |Икс| = 0, когда Икс= 0 и |Икс| = 1 в противном случае.[2] Каждая область целостности может иметь хотя бы тривиальное абсолютное значение. Тривиальное значение — единственно возможное абсолютное значение на конечное поле потому что любой ненулевой элемент можно возвести в некоторую степень, чтобы получить 1.
Если абсолютное значение удовлетворяет более сильному свойству |Икс + у| ≤ макс (|Икс|, |у|) для всех Икс и у, тогда |Икс| называется ультраметрический или же неархимедово абсолютное значение, а в противном случае Абсолютная величина архимеда.
Места
Если |Икс|1 и |Икс|2 два абсолютных значения в одной и той же области целостности D, то два абсолютных значения равны эквивалент если |Икс|1Икс|2Икс. Если два нетривиальных абсолютных значения эквивалентны, то для некоторой экспоненты е у нас есть |Икс|1е = |Икс|2 для всех Икс. Увеличение абсолютного значения до степени меньше 1 приводит к другому абсолютному значению, но повышение до степени больше 1 не обязательно приводит к абсолютному значению. (Например, возведение в квадрат обычного абсолютного значения действительных чисел дает функцию, которая не является абсолютным значением, потому что она нарушает правило |Икс+у| ≤ |Икс|+|у|.) Абсолютные значения с точностью до эквивалентности, или, другими словами, класс эквивалентности абсолютных значений, называется место.
Если два нетривиальных абсолютных значения эквивалентны, то для некоторой экспоненты е у нас есть |Икс|1е = |Икс|2 для всех Икс. Увеличение абсолютного значения до степени меньше 1 приводит к другому абсолютному значению, но повышение до степени больше 1 не обязательно приводит к абсолютному значению. (Например, возведение в квадрат обычного абсолютного значения действительных чисел дает функцию, которая не является абсолютным значением, потому что она нарушает правило |Икс+у| ≤ |Икс|+|у|.) Абсолютные значения с точностью до эквивалентности, или, другими словами, класс эквивалентности абсолютных значений, называется место.
Теорема Островского утверждает, что нетривиальные места рациональное число Q обычные абсолютная величина и п-адическое абсолютное значение для каждого прайма п.[3] Для данного простого числа п, любое рациональное число q можно записать как пп(а/б), куда а и б целые числа не делятся на п и п целое число. {- n}.}
{- n}.}
Поскольку обычное абсолютное значение и п-adic абсолютные значения — это абсолютные значения в соответствии с определением выше, они определяют места.
Оценки
Основная статья: Оценка (алгебра)
Если для некоторого ультраметрического абсолютного значения и любого основания б > 1, определим ν(Икс) = −logб|Икс| за Икс ≠ 0 и ν(0) = ∞, где ∞ должно быть больше всех действительных чисел, тогда мы получаем функцию из D к р ∪ {∞} со следующими свойствами:
- ν(Икс) = ∞ ⇒ Икс = 0,
- ν(ху) = ν(Икс)+ν(у),
- ν(Икс + у) ≥ min (ν (Икс), ν(у)).
Такая функция известна как оценка в терминологии Бурбаки, но другие авторы используют термин оценка за абсолютная величина а затем скажи экспоненциальная оценка вместо оценка.
Завершено
Учитывая область целостности D с абсолютным значением, мы можем определить Последовательности Коши элементов D по модулю, требуя, чтобы для любого ε> 0 существовало положительное целое число N так что для всех целых чисел м, п > N есть |Иксм − Иксп| звенеть при поточечном сложении и умножении. Можно также определить нулевые последовательности как последовательности (ап) элементов D такой, что |ап| сходится к нулю. Нулевые последовательности — это главный идеал в кольце последовательностей Коши, а кольцо частного поэтому является областью целостности. Домен D является встроенный в этом кольце частных, называемом завершение из D по модулю |Икс|.
Поскольку поля являются областями целостности, это также конструкция для завершения поля по абсолютному значению. Чтобы показать, что результатом является поле, а не просто область целостности, мы можем либо показать, что нулевые последовательности образуют максимальный идеал, или же построить обратное напрямую. Последнее можно легко сделать, взяв для всех ненулевых элементов факторкольца последовательность, начинающуюся с точки за последним нулевым элементом последовательности. Любой ненулевой элемент факторкольца будет отличаться от такой последовательности на нулевую последовательность, и, выполняя поточечную инверсию, мы можем найти представительный обратный элемент.
Последнее можно легко сделать, взяв для всех ненулевых элементов факторкольца последовательность, начинающуюся с точки за последним нулевым элементом последовательности. Любой ненулевой элемент факторкольца будет отличаться от такой последовательности на нулевую последовательность, и, выполняя поточечную инверсию, мы можем найти представительный обратный элемент.
Другая теорема Александр Островский имеет это, что любое поле, полное относительно Архимедов абсолютное значение изоморфный к действительным или комплексным числам, и оценка эквивалентна обычному.[4] В Теорема Гельфанда-Торнхейма утверждает, что любое поле с архимедовой оценкой изоморфно подполе из C, оценка эквивалентна обычному абсолютному значению на C.[5]
Поля и области целостности
Если D является областью целостности с модулем |Икс|, то мы можем расширить определение абсолютного значения на поле дробей из D установив
- |Икс/у|=|Икс|/|у|.
 «Архивная копия». Архивировано из оригинал на 2008-12-22. Получено 2009-04-03.CS1 maint: заархивированная копия как заголовок (связь)
«Архивная копия». Архивировано из оригинал на 2008-12-22. Получено 2009-04-03.CS1 maint: заархивированная копия как заголовок (связь)Рекомендации
- Бурбаки, Николас (1972). Коммутативная алгебра. Эддисон-Уэсли.
- Касселс, J.W.S. (1986). Местные поля. Тексты студентов Лондонского математического общества. 3. Издательство Кембриджского университета. ISBN 0-521-31525-5. Zbl 0595.12006.
- Джейкобсон, Натан (1989). Базовая алгебра II (2-е изд.). W H Freeman. ISBN 0-7167-1933-9. Глава 9, пункт 1 «Абсолютные значения«.
- Януш, Джеральд Дж. (1996–1997). Поля алгебраических чисел (2-е изд.). Американское математическое общество. ISBN 0-8218-0429-4.
Модуль числа в математике — что это такое, как раскрыть абсолютную величину, решение уравнений
Термин (module) в буквальном переводе с латинского означает «мера».
 Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.Оглавление:
- Геометрическое значение
- Свойства абсолютной величины
- Особенности решения уравнений с модулем
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a|.
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.

Это интересно: умножение на 0 правило для любого числа.
Содержание
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
- Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
- Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
- В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
- Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.

Графически это можно выразить следующим образом: |a| = OA.
Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
- Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.
- Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем.
 Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|. - Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
- Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.

- Такое же правило распространяется и на показатель степени выражения.
Это интересно: что такое разность в математике?
Особенности решения уравнений с модулем
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5, если, А больше или равняется нулю.
5-А, если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка.
 Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Абсолютное значение — значение, знак, примеры
абсолютное значение переменной x представлено |x| который произносится как «Модуль х» или «Модуль х». «Модуль» — латинское слово, означающее «мера». Абсолютное значение обычно называют числовым значением или величиной. Абсолютное значение представляет собой только числовое значение и не включает знак числового значения. Модуль любой векторной величины всегда принимается положительным и является ее абсолютной величиной. Кроме того, такие величины, как расстояние, цена, объем и время, всегда представлены в виде абсолютных значений.
Например, абсолютное значение: |+5| = |-5| = 5. Абсолютному значению не присваивается знак. В этой статье мы рассмотрим концепцию абсолютного значения числа, его символа и того, как найти абсолютное значение.
 Мы будем решать различные примеры на основе концепции для лучшего понимания.
Мы будем решать различные примеры на основе концепции для лучшего понимания.1. Что такое абсолютное значение? 2. Определение абсолютного значения 3. Знак абсолютного значения 4. Абсолютное значение 0 5. Функция абсолютного значения 6. Часто задаваемые вопросы об абсолютном значении Что такое абсолютное значение?
Абсолютное значение числа — это его расстояние от начала координат 0. Мы знаем, что расстояние — всегда неотрицательная величина. Поскольку абсолютное значение — это расстояние, абсолютное значение числа всегда является неотрицательным числом. Иногда знак приписывается числовому значению, чтобы обозначить направление, в дополнение к значению. Увеличение или уменьшение количества, значения выше или ниже среднего значения, прибыли или убытка в сделке иногда объясняют присвоением числовому значению положительного или отрицательного значения.
 Но для абсолютного значения знак числового значения игнорируется и рассматривается только числовое значение.
Но для абсолютного значения знак числового значения игнорируется и рассматривается только числовое значение.Определение абсолютного значения
Абсолютное значение числа определяется как его величина независимо от знака числа. Чтобы найти абсолютное значение действительного числа, мы рассматриваем только число и удаляем знак. Это может быть только неотрицательное значение. Абсолютное значение положительного числа — это само число, отрицательное число — это число без отрицательного знака, а абсолютное значение 0 — это 0.
На приведенном выше рисунке мы можем наблюдать абсолютные значения на числовой ряд с помощью иллюстрации. Абсолютное значение представлено |x|, а на приведенном выше рисунке |4| = |-4| = 4,
Знак абсолютного значения
Чтобы представить абсолютное значение числа (или переменной), мы пишем вертикальную черту по обе стороны от числа, т. е. |x| где х — целое число. Например, абсолютное значение числа 4 записывается как |4|.
 Кроме того, абсолютное значение -4 записывается как |-4|. Как мы обсуждали ранее, абсолютное значение всегда дает неотрицательное значение. Следовательно, |4|=|-4| =4. То есть он превращает отрицательные числа также в положительные числа. На следующем рисунке представлен символ абсолютного значения.
Кроме того, абсолютное значение -4 записывается как |-4|. Как мы обсуждали ранее, абсолютное значение всегда дает неотрицательное значение. Следовательно, |4|=|-4| =4. То есть он превращает отрицательные числа также в положительные числа. На следующем рисунке представлен символ абсолютного значения.Абсолютное значение числа
Как обсуждалось выше, абсолютное значение числа всегда является неотрицательным значением. Чтобы определить абсолютное значение числа x, мы обозначаем его как |x| и его формула определяется выражением |x| = x, если x > 0 и |x| = -x, если x < 0 и |x| = 0, если x = 0. Некоторые примеры абсолютного значения числа:
- |2| = 2
- |-9| = 9
- |3.4| = 3,4
- |-1,23| = 1,23
Абсолютное значение 0
До сих пор мы обсуждали абсолютное значение положительных и отрицательных чисел. Теперь обсудим абсолютное значение нуля. Поскольку 0 не является ни положительным, ни положительным, поэтому абсолютное значение 0 равно 0.
 Расстояние числа 0 равно нулю от 0, поэтому мы можем сказать, что абсолютное значение 0 равно 0.
Расстояние числа 0 равно нулю от 0, поэтому мы можем сказать, что абсолютное значение 0 равно 0.Функция абсолютного значения
Функция абсолютного значения определяется как f(x) = |x|, { |x| = +x для x ≥ 0 и |x| = -x для x < 0} Используя определение абсолютного значения, мы знаем, что оно всегда приводит к неотрицательному числу. Таким образом, график функции f(x) = |x| выглядит следующим образом.
Из определения функции абсолютного значения значение |x| в зависимости от знака х. |х|= + х. Мы также знаем, что √ {x 2 } = + x. Следовательно, имеем √{x 2 } = | х |.
Важные примечания об абсолютном значении
- Абсолютное значение x представлено либо |x| или абс(х).
- Абсолютное значение любого числа всегда дает неотрицательное значение.
- Мы произносим |x| как «mod x» или «модуль x».
Think Tank
- Мы знаем, что абсолютное значение дает неотрицательное число.
 Тогда почему у нас есть -x в приведенном выше определении функции абсолютного значения?
Тогда почему у нас есть -x в приведенном выше определении функции абсолютного значения?
(Подсказка: какой знак у -x, если x<0 ? |-x|= x ИЛИ -x, если x<0 ?)
Похожие статьи
- Числа
- Калькулятор целых чисел
- Калькулятор вычитания целых чисел
- Калькулятор умножения целых чисел
- Добавление калькулятора целых чисел
Примеры абсолютных значений
Пример 1: Мохан хочет найти значения следующего. Поможем ей использовать определение абсолютной ценности? (I) |-13/5|, (II) — | -3|, (III) |2(-3) + 4|.
Решение:
Мы знаем, что абсолютное значение всегда дает неотрицательные значения. Таким образом, мы имеем следующие решения.
(Я) | -13/15| = 13/15
(II) — |-3| = -(3) = -3
(III) |2(-3) + 4| = |-6+4| = |-2| = 2
Ответ: Следовательно(I) | -13/15| = 13/15, (II) — | -3 | = -3, (III) |2(-3) + 4| = 2
Пример 2: Учитель поручил Рии решить следующее уравнение абсолютного значения, используя определение абсолютной функции.
 |х-2| = 4. Можем ли мы попытаться помочь ей?
|х-2| = 4. Можем ли мы попытаться помочь ей?Решение:
Данное уравнение имеет вид |x-2|=4. Используя определение функции абсолютного значения, когда мы удаляем знак абсолютного значения с одной стороны уравнения. Затем мы получаем знак + на другой стороне. x-2= + 4. Это приводит к двум уравнениям, которые мы решаем по отдельности.
х — 2 = +4
х = +4 + 2
х = +6
х — 2 = -4
х = -4 + 2
х = -2
Ответ: Следовательно, решения данного уравнения равны x = 6, x = -2.
Пример 3: Рохан хочет найти значение -|-x| когда x > 0. Как мы можем помочь Рохану найти абсолютное значение?
Решение:
Давайте поможем ему, используя определение функции абсолютного значения. Дано, что x > 0, тогда имеем -x < 0. Теперь по определению функции абсолютного значения имеем: |-x|= -(-x) = x.
 Следовательно, -|-х| = -х.
Следовательно, -|-х| = -х.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Абсолютное значение Вопросы
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы об абсолютном значении
Что такое абсолютное значение в алгебре?
Абсолютное значение числа определяется как его величина числа независимо от знака числа. Он дает расстояние числа от числа 0. Абсолютное значение числа всегда является неотрицательным числом.
Каково абсолютное значение -5?
Абсолютное значение -5 определяется выражением |-5| = 5, потому что абсолютное значение превращает отрицательные числа в положительные, т. е. |-5| = 5.

Что означает абсолютное значение?
Абсолютное значение дает только числовое значение и не показывает никакого знака. Абсолютное значение |5| равно 5, а абсолютное значение |-3| равно 3.
Как найти абсолютное значение отрицательного числа?
Абсолютное значение отрицательного числа также является положительным значением. Если число x < 0, то его абсолютное значение определяется выражением |x| = -х. Например, |-2| = 2. Независимо от знака числового значения абсолютное значение всегда неотрицательно.
Какая польза от абсолютного значения?
Абсолютное значение используется для информирования числового значения количества, независимо от знака количества. Многочисленные величины, такие как длина, цена и объем, не имеют для знака никакого значения и записываются без всякого знака. Здесь понятие абсолютного значения полезно для представления таких величин.
Каково абсолютное значение отрицательного целого числа?
Абсолютное значение отрицательного целого числа также является положительным значением.
 |-5| = 5. Например, значение смещения иногда записывают как -5 метров, но знак минус означает только направление, а расстояние всего 5 метров.
|-5| = 5. Например, значение смещения иногда записывают как -5 метров, но знак минус означает только направление, а расстояние всего 5 метров.Может ли абсолютное значение быть отрицательным?
Абсолютное значение всегда неотрицательно. Даже для положительного или отрицательного значения в пределах модуля абсолютное значение всегда положительно. | + Х| = X, если X > 0.
Могут ли два разных числа иметь одинаковое абсолютное значение?
Два разных числа могут иметь одинаковое абсолютное значение. Например, два числа -7 или +7 имеют одинаковое абсолютное значение 7. |-7| = |+7| = 7.
Почему абсолютное значение всегда положительное?
Абсолютное значение означает расстояние числа от начала координат 0. Число, представленное на числовой прямой, может быть отрицательным, но абсолютное значение всегда положительное, поскольку расстояние никогда не бывает отрицательным. Например, абсолютное значение -9 равно 9, что означает, что расстояние от числа -9 до начала координат 0 равно 9 единицам на числовой прямой.

Каково одно основное правило абсолютной ценности?
Основное правило абсолютного значения гласит, что абсолютное значение любого числа всегда неотрицательно. Если число является положительным целым числом, абсолютное значение числа положительно, т. е. |15| = 15. Если число является отрицательным целым числом, даже в этом случае абсолютное значение положительно, т. е. |-20| = 20,
Каково абсолютное значение 0?
Абсолютное значение 0 равно 0, так как расстояние от 0 до 0 равно 0.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по абсолютным значениям
Уравнения с абсолютными значениями — Обзор алгебры I (видео)
TranscriptFAQsPractice
Привет и добро пожаловать в это видео об абсолютной ценности! Мы рассмотрим, что такое абсолютное значение числа и как его вычислить, а также что такое абсолютная разница 9.
 0004 и как оно связано с абсолютным значением. Давайте начнем!
0004 и как оно связано с абсолютным значением. Давайте начнем!Абсолютное значение числа равно его расстоянию от 0 на числовой строке . Возьмем в качестве примера цифру 6. Используя числовую прямую, мы можем видеть, что 6 находится в шести единицах от 0.
Следовательно, абсолютное значение 6 равно 6. Отрицательное 6 также находится в шести единицах от 0. Абсолютное значение -6 также равно 6.
Абсолютное значение имеет специальное обозначение в математических выражениях. Например, абсолютное значение числа 6 обозначается двумя вертикальными линиями: \(|6|\). А абсолютное значение -6 обозначается как -6 с линиями по обеим сторонам, как и раньше: \(|-6|\).
Теперь, как мы только что видели, абсолютное значение 6 равно 6, а абсолютное значение -6 также равно 6.
Независимо от того, с каким числом вы имеете дело, большим или большим, положительным или отрицательным, операция абсолютного значения всегда дает положительное число.
 Это полезно помнить при вычислении выражений и решении уравнений, но также важно помнить почему.
Это полезно помнить при вычислении выражений и решении уравнений, но также важно помнить почему.Когда мы говорим о расстоянии, направление не имеет значения. На повседневном языке мы бы не сказали, например, «Продуктовый магазин находится в минус 1 миле от нас». Мы бы просто сказали: «Продуктовый магазин в миле отсюда».
Точно так же на числовой прямой мы просто считаем расстояние без указания направления. Таким образом, абсолютное значение числа семь равно семи буквально переводится как «отрицательное число 7 равно семи единицам от 0».
Когда мы вычисляем выражения и решаем уравнения, абсолютное значение скобки действуют так же, как круглые скобки в порядке операций. Сначала мы оцениваем то, что находится внутри скобок абсолютного значения.
Примеры абсолютных значений
Давайте рассмотрим простой пример.
\(1-|2+(-5)|\)
Сначала мы оцениваем то, что находится внутри скобок, поэтому 2 плюс -5 равно -3, что дает нам 1 минус абсолютное значение -3 .
 Отрицательное число 3 находится на расстоянии трех единиц от нуля, что означает, что абсолютное значение -3 равно 3. Это дает нам 1 минус 3, что равно -2.
Отрицательное число 3 находится на расстоянии трех единиц от нуля, что означает, что абсолютное значение -3 равно 3. Это дает нам 1 минус 3, что равно -2.Поскольку абсолютное значение — это вычисление расстояния числа от нуля, выражение абсолютного значения, такое как абсолютное значение 3, может быть записано как абсолютное значение 3-0. Другой способ интерпретировать это утверждение — сказать: «Расстояние между 3 и 0 равно 3». Запись таким образом дает тот же результат. Однако второе число здесь не обязательно должно быть 0. На самом деле мы можем вычислить расстояние между любыми двумя числами.
На числовой прямой расстояние между -2 и 8 равно 10. В качестве выражения мы можем записать его как абсолютное значение -2 минус 8 равно 10. Это называется абсолютной разностью .
Давайте кратко подведем итоги. Абсолютное значение числа — это его расстояние от нуля на числовой прямой, и независимо от того, с каким числом вы работаете, ответ всегда будет положительным числом.
 Абсолютная разница используется для вычисления расстояния между любыми двумя числами на числовой прямой, а не только между числом и нулем.
Абсолютная разница используется для вычисления расстояния между любыми двумя числами на числовой прямой, а не только между числом и нулем.Надеюсь, отзыв был полезен! Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Что такое абсолютное значение?
A
Абсолютное значение — это расстояние от нуля до числа.
Q
Как найти абсолютное значение?
A
Найдите абсолютное значение числа, определив, насколько оно далеко от нуля. Другими словами, сделайте число положительным.
пр. |-17| = 17Q
Как вы решаете уравнения абсолютного значения?
A
Решите уравнения абсолютного значения, выделив выражение абсолютного значения, а затем используйте как положительные, так и отрицательные ответы для решения переменной. Ваша переменная, скорее всего, будет равна двум разным значениям.
пр. 2|х – 3| = 14
Сначала изолируйте выражение абсолютного значения, разделив обе части на 2.
|x – 3| = 7
Затем решите x – 3 = ±7.
х – 3 = 7
х = 10
Или
х – 3 = -7
х = -4
Итак, х = 10 или х = -4.Q
Как вы решаете абсолютные неравенства?
A
Решите абсолютные неравенства, сначала изменив неравенство так, чтобы выражение абсолютного значения было изолировано с одной стороны. Затем удалите знаки абсолютного значения и поместите выражение между положительным и отрицательным ответом. Наконец, манипулируйте, чтобы изолировать переменную в середине.
пр. 4|2x – 3| |2x – 3| -7 -4 -2Q
Как построить график абсолютного значения?
A
Чтобы построить графики уравнений абсолютного значения, сначала нарисуйте выражение внутри знаков абсолютного значения. Затем все, что находится под осью x на этом графике, отразите по оси x, чтобы оно стало положительным.
пр. у = |х + 1|Практические вопросы
Вопрос № 1:
\ (| -2 | = \)-20
-2
2
20
Показать ответ
2
20 0005
.
 0005
0005Ответ:
Правильный ответ: 2. Абсолютное значение говорит вам, насколько далеко число от 0, поэтому это всегда положительное значение числа. \(|-2|=2\), потому что -2 на 2 позиции дальше от 0.
Скрыть ответ
Вопрос №2:
\(|-3-11|=\)-8
8
14
-14
Показать ответ
Ответ:
Правильный ответ: 14. Абсолютное значение делает любое число положительным, поскольку оно показывает, насколько далеко число от 0. Во-первых, упростите. выражение внутри полос абсолютного значения.
\(|-3-11|=|-14|\)
Затем возьмите абсолютное значение -14, \(|-14|=14\).HIDE Ответ
Вопрос № 3:
\ (| 4-7+8 | = \)5
-5
11
-11
Показать ответ
Ответ: Ответ: Ответ:
Правильный ответ: 5.
 Абсолютное значение делает любое число положительным, поскольку оно показывает, насколько оно далеко от 0. Во-первых, упростите выражение в столбцах абсолютного значения.
Абсолютное значение делает любое число положительным, поскольку оно показывает, насколько оно далеко от 0. Во-первых, упростите выражение в столбцах абсолютного значения.
\(|4-7+8|=|5|\)
Затем возьмите абсолютное значение 5, \(|5|=5\). 5 остается положительным, поскольку отстоит от 0 на 5 позиций. 8-8
Показать ответ
Ответ:
Правильный ответ: -8.
\(|6-7+2|-9\)
Сначала упростим выражение в столбцах абсолютных значений.
\(|1|-9\)
Затем возьмите абсолютное значение 1.
\(1-9\)
Наконец, вычтите.
\(1-9=-8\)Скрыть ответ
Вопрос №5:
\(4-|16+7-35|-21=\)-29
2 5
-5
5
Показать ответ
Ответ:
Правильный ответ: -29.

\(4-|16+7-35|-21\)
Сначала упростим выражение в столбцах абсолютных значений.
\(4-|-12|-21\)
Затем возьмите абсолютное значение -12.
\(4-12-21\)
Наконец, вычтите.
\(4-12-21=-29\)Скрыть ответ
Вернуться к видео по алгебре I
314669686316 Абсолютное значение
Что такое 9009 Абсолютное значение 9–0 Свойства и примеры01Абсолютное значение относится к расстоянию точки от нуля или начала координат на числовой прямой, независимо от направления. Абсолютное значение числа всегда положительно.
Абсолютное значение числа обозначается двумя вертикальными чертами, заключающими число или выражение. Например, абсолютное значение числа 5 записывается как |5| = 5. Это означает, что расстояние от 0 равно 5 единицам:
Точно так же абсолютное значение отрицательного числа 5 обозначается как |-5| = 5. Это означает, что расстояние от 0 равно 5 единицам:
Число не только показывает расстояние от начала координат, но также важно для построения графика абсолютного значения.

Рассмотрим выражение | х | > 5. Чтобы представить это на числовой прямой, вам нужны все числа, абсолютная величина которых больше 5. Это делается графически, помещая открытую точку на числовой строке.
Рассмотрим другой случай, когда | х | = 5. Сюда входят все абсолютные значения, которые меньше или равны 5. Это выражение изображается на графике путем помещения закрытой точки на числовую прямую. Знак равенства указывает, что все сравниваемые значения включены в график.
Простой способ представления выражений с помощью неравенств заключается в следовании следующим правилам.
- Для | х | < 5, -5 < x < 5
- Для | х | = 5, -5 = 90 592 x 90 593 = 5
- Для |x + 6| < 5, -5 < x + 6 < 5
Свойства абсолютного значения
Абсолютное значение обладает следующими фундаментальными свойствами:
- Неотрицательность |a| ≥ 0
- Положительная определенность |a| = 0a = 0
- Мультипликативность |ab| = |а| |б|
- Субаддитивность |a + b| ≤ |а| + |б|
- Идемпотентность ||a|| = |а|
- Симметрия |−a| = |а|
- Тождество неразличимого |a − b| = 0 ⇔ а = б
- Неравенство треугольника |a − b| ≤ |а — с| + |с — б|
- Сохранение деления |a/b|=|a|/|b| если b ≠ 0
Пример 1
Упростить -|-6|
Решение
- Преобразование символов абсолютного значения в круглые скобки
–| –6 | = – (6)
- Теперь я могу взять минус через скобки:
– (6) = – 6
Пример 2
Найдите возможные значения x.

|4x| = 16
Решение
В этом уравнении 4x может быть как положительным, так и отрицательным. Таким образом, мы можем написать его как:
4x = 16 или -4x = 16
Разделите обе стороны на 4.
x = 4 или x = -4
Следовательно, два возможных значения x равны -4 и 4.
Пример 3
Решите следующие задачи:
а) Решить | –9|
Ответить
| –9| = 9
б) Упростить | 0 – 8 |.
Ответить
| 0 – 8 | = | –8 | = 8
c) Решить | 9 – 3 |.
Ответить
| 9 – 3 | = | 6| = 6
d) Упростить | 3 – 7 |.
Ответить
| 3 – 7 | = | –4 | = 4
e) Тренировка | 0 (–12) |.
Ответить
| 0(–12) | = | 0 | = 0
f) Упростить | 6 + 2(–2) |.

Ответить
| 6 + 2(–2) | = | 6 – 4 | = | 2| = 2
g) Решить –| –6 |.
Ответить
–| –6| = – (6) = –6
ч) Упростить –| (–7) 2 |.
Ответить
–| (–7) 2 | = –| 49 | = –49
i) Вычислить –| –9| 2
Ответ
–| –9 | 2 = – (9) 2 = –(4) = –81
j) Упростить (–| –3|) 2 .
Ответ
( — | –3 |) 2 = ( — (3)) 2 = (–3) 2 = 9
Пример 4
: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка: Оценка -|-7 + 4|
Решение
- Прежде всего, начните с вычисления выражений в символах абсолютного значения:
-|-7 + 4| = -|-3| - Ввести круглые скобки
-|-3| = -(3) = -3 - Итак, ответ равен -3.

Пример 5
Морской водолаз находится на -20 футов ниже поверхности воды. Какое расстояние ему нужно проплыть, чтобы выбраться на поверхность?
Решение
Ему нужно поплавать |-20| = 20 футов.
Пример 6
Вычислите абсолютное значение 19 – 36(3) + 2(4 – 87)?
Решение
19 -36 (3) + 2 (4 -87)
= 19 -108 + 2 (-83)
= 19 -108 -166
= -255
Пример 7 4
Решите уравнение, определив абсолютные значения,
2 |-2 × – 2| – 3 = 13
Решение
Перепишите выражение со знаком абсолютного значения с одной стороны.
- Добавьте 3 к обеим частям выражения
2 | – 2 × – 2| – 3 + 3 = 13 + 3
2 | – 2 × – 2| = 16
- Разделите обе части на 2.
|- 2 × – 2| = 8
- Оставшееся уравнение такое же, как и для записи выражения в виде:
– 2 × – 2 = 8 или – 8
- a) -2 x – 2 = 8
Теперь найдите x
х = – 5- б) – 2 х – 2 = – 8
х = 3
- Правильный ответ: (-5, 3).

Пример 8
Вычислить действительные значения выражения с абсолютным значением.
|х – 1| = 2x + 1
Решение
Один из методов решения этого уравнения заключается в рассмотрении двух случаев:
a) Предположим, что x – 1 ≥ 0, и перепишем выражение в следующем виде:x – 1 = 2x + 1
Вычислить значение x
x = -2
b) Предположим, что x – 1 ≤ 0, и перепишем это выражение как
-(x – 1) = 2x + 1
– x + 1 = 2x + 1
найти x как
x = 0Важно проверить правильность решений уравнения, потому что все значения x были приняты.
Замена x на – 2 в обеих частях выражения дает.| (-2) – 1| = |-2 + 1| = 1 в левую часть и 2(-2) + 1 = – 3 в правую часть
Поскольку два уравнения не равны, следовательно, x = -2 не является ответом на это уравнение.
Проверка x = 0Замена x на 0 в обеих частях уравнения дает:
|(0) – 1| = 1 слева и 2(0) + 1 = 1 справа.

Два выражения равны, поэтому x = 0 является решением этого уравнения.
Что такое абсолютное значение числа?
Абсолютное значение числа означает, насколько далеко это число от нуля на числовой прямой.
Вопросы также используют такие термины, как «величина» или «модуль», чтобы представить абсолютное значение числа. «6» отличается от нуля на 6,
и «?6» также отличается от нуля на 6.Таким образом, абсолютное значение 6 равно 6,
и абсолютное значение ?6 также равно 6Это то же самое, что сказать….
Величина 6 равна 6 Модуль 6 равен 6 Величина ?6 также равна 6 Модуль ?6 также равен 6 Другие примеры:
- Абсолютное значение ?11 равно 11
- Абсолютное значение 5 равно 5
- Абсолютное значение 0 равно 0
- Абсолютное значение ?142 равно 142
Фактически, все отрицательные числа становятся положительными, а все неотрицательные числа (? 0) остаются неизменными.

Нет минусов!
Вы также можете представить абсолютное значение числа как расстояние этого числа от нуля на числовой прямой.
Поскольку расстояние не может быть отрицательным , это означает, что абсолютное значение всегда равно ? 0, то есть неотрицательный.
Абсолютное значение -67 – 33 + 100 равно?
Решение:
Во-первых, упростить.
-67 – 33 + 100 =
-100 + 100 =
0
Абсолютное значение 0 равно 0.
Попробуем еще.
Какова величина ?(69 ? 67) 2 ? 100?
- ?104
- ?96
- 0
- 96
- 104
Решение:
Сначала упростим выражение: ?(69? 67) 2 ? 100
Использование PEMDAS,
?(69 ? 67) 2 ? 100
?(2) 2 ? 100
?4 ? 100
?104
Величина ?104 равна 104.

Чтобы показать, что нам нужно абсолютное значение чего-либо, мы ставим «|» отмечает обе стороны, например |-5| = 5 или |5| = 5.
Возвращаясь к предыдущим примерам, мы можем переписать их, используя символ абсолютного значения, следующим образом:
- Абсолютное значение ?11 равно 11 ? |-11| = 11
- Абсолютное значение числа 5 равно 5 ? |5| = 5
- Абсолютное значение 0 равно 0 ? |0| = 0
- Абсолютное значение ?142 равно 142 ? |-142| = 142
Иногда абсолютное значение также записывается как «abs()», поэтому abs(?1) = 1 совпадает с |?1| = 1. Однако в вопросах почти всегда используется символ «|». метки для представления оператора абсолютного значения.
|?3×6| =
Решение:
Этот вопрос требует, чтобы вы нашли величину произведения ?3 и 6.
. Сначала мы возьмем произведение ?3 и 6, что равно ?18. Затем мы находим абсолютное значение ?18, которое равно 18,
Сначала мы возьмем произведение ?3 и 6, что равно ?18. Затем мы находим абсолютное значение ?18, которое равно 18,= |?3×6|
= |?18|
= 18
Ответ |8 ? 3| то же, что |3 ? 8|? - Да
- №
Решение:
Неважно, в какую сторону мы делаем вычитание, абсолютное значение всегда будет одним и тем же:
|8?3| = |5| = 5
|3?8| = |?5| = 5?|2?5| = - 3
- ?3
Решение:
?|2?5| = ?|?3| = ?3
Обратите внимание, что вне абсолютного значения есть отрицательное значение. Поскольку это внешнее абсолютное значение, оно не будет затронуто.
Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми.
 Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вам придется…
Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вам придется…читать дальше
Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; следовательно, низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот…
подробнее
Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…
читать далее
Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь.
 С…
С…подробнее
Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов…
читать дальше
Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…
подробнее
Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями.
 Мы здесь, чтобы убедиться, что вы знаете все…
Мы здесь, чтобы убедиться, что вы знаете все…читать дальше
Сформулируем правила сложения, вычитания, умножения и деления четных и нечетных чисел. Вот правила сложения/вычитания четных и нечетных чисел: Четные ± четные = четные (например, 2 + 2 = 4; -4 — 2 = -6) Нечетные ± нечетные = четные (например, 1 + 1 = 2; -31 — 1 = -32)…
подробнее
Начнем с основных определений: Четное: любое целое число, которое делится на 2. Примеры: 2, 4, 14. Нечетное: любое целое число, которое не делится на 2, т. е. оставляет в остатке 1 при делении на 2. Примеры: 1, 3, 5, 7, 9 Пока все хорошо. Рассмотрите этот потенциал…
подробнее
Найдите остаток от деления 5 142 376 298 на 9? Метод длинного деления точно скажет вам остаток от деления 5 142 376,29.8 на 9, но вы можете себе представить, сколько времени это займет. Хорошая новость заключается в том, что, как и делимость.
 ..
..читать дальше
Как найти абсолютное значение
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Алгебра 1 Помощь » Вещественные числа » Числовые строки и абсолютное значение » Как найти абсолютное значение
Какое число или числа имеют абсолютное значение ?
Возможные ответы:
Таких номеров не существует.
Правильный ответ:
Таких номеров не существует.
Объяснение:
Абсолютное значение каждого действительного числа неотрицательно, поэтому число с абсолютным значением не может существовать.

Сообщить об ошибке
Какое число или числа имеют абсолютное значение ?
Возможные ответы:
Таких номеров не существует.
Правильный ответ:
Таких номеров не существует.
Объяснение:
Абсолютное значение каждого действительного числа неотрицательно, поэтому число с абсолютным значением не может существовать.
Сообщить об ошибке
Какое число или числа имеют абсолютное значение 29?
Возможные ответы:
Такого номера не существует.
Правильный ответ:
Объяснение:
Абсолютным значением любого положительного числа является само число, поэтому 29 имеет 29 как абсолютное значение.
 Кроме того, абсолютное значение отрицательного числа является его (положительной) противоположностью, поэтому также имеет 29 в качестве абсолютного значения.
Кроме того, абсолютное значение отрицательного числа является его (положительной) противоположностью, поэтому также имеет 29 в качестве абсолютного значения.Сообщить об ошибке
Какое число или числа имеют абсолютное значение 11?
Возможные ответы:
Таких номеров не существует.
Правильный ответ:
Объяснение:
Абсолютным значением любого положительного числа является само число, поэтому 11 имеет 11 как абсолютное значение. Кроме того, абсолютное значение отрицательного числа является его (положительной) противоположностью, поэтому также имеет 11 в качестве абсолютного значения.
Сообщить об ошибке
Вычислить выражение.
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, упростите термины в скобках и абсолютное значение.

Помните, что абсолютное значение отрицательного члена положительно.
Умножай и упрощай.
Сообщить об ошибке
Решить для .
Возможные ответы:
Решение не существует.
Правильный ответ:
Объяснение:
Разделите обе части на .
Удалите скобки абсолютного значения, задав выражение, равное как положительным, так и отрицательным значениям 4:0002 Мистер Смит и его жена отправились в путешествие, они проехали много миль к месту назначения, однако по пути туда им пришлось развернуться и проехать много миль от места назначения, чтобы забрать кошелек мистера Смита из магазина. Получив его бумажник, они проехали еще несколько миль, чтобы добраться до места назначения. Каково общее количество миль, которое проехала семья?
Возможные ответы:
Недостаточно информации.

Правильный ответ:
Пояснение:
Несмотря на то, что Смиты путешествовали в обратном направлении, вам все равно нужно добавить в уравнение положительное число. Таким образом, выглядит следующим образом:
, что равно
Отчет о ошибке
Упростить следующее уравнение:
Возможные ответы:
Правильный ответ:
. Объяснение:
Важно понимать, что абсолютное значение — это расстояние от числа.
Чтобы упростить это уравнение, сначала необходимо упростить абсолютные значения.
, затем упростите функцию
Отчет о ошибке
Решение:
Возможные ответы:
Правильный ответ:
Правильный ответ:
6
.
 Объяснение:
Объяснение:Чтобы найти это абсолютное значение, нам нужно разделить абсолютное значение на его положительное и отрицательное решение.
Разбейте абсолютное значение и перепишите члены для положительного решения и найдите .
Для отрицательного решения разделите абсолютное значение и добавьте минус перед количеством, которое содержится в абсолютном значении.
Разделить на минус один с обеих сторон.
Вычесть три с обеих сторон.
Упростите обе стороны.
Ответы на этот вопрос:
Сообщить об ошибке
Упростите следующее выражение:
Возможные ответы:
Правильный ответ:
Объяснение:
Упростите следующее выражение:
Мы можем начать с изменения знака абсолютного значения на положительное 16.

Мы можем сделать это, потому что отрицательные числа внутри знака абсолютного значения всегда следует рассматривать как положительные числа.
Далее упростите дробь, чтобы получить
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление об авторских правах
2 90 Диагностика 03 Ресурсы 557 практических тестов Вопрос дня Карточки Learn by ConceptМожет ли абсолютное значение быть отрицательным? (3 вещи, которые нужно знать) – JDM Educational
Абсолютное значение часто встречается в алгебре и часто используется для представления расстояния. Это поднимает вопросы о том, как абсолютное значение относится к отрицательным числам.
Итак, может ли абсолютное значение быть отрицательным? Абсолютное значение не может быть отрицательным – выход абсолютного значения всегда положительный или нулевой. Однако мы можем использовать отрицательные входные данные для абсолютного значения, и мы можем вычитать внутри абсолютного значения.
 Мы также можем получить отрицательные решения для некоторых уравнений и неравенств с абсолютной величиной.
Мы также можем получить отрицательные решения для некоторых уравнений и неравенств с абсолютной величиной. Конечно, бывают случаи, когда уравнение или неравенство с абсолютной величиной не имеет решения или когда все решения будут положительными. Все зависит от задействованных чисел и знака неравенства,
В этой статье мы поговорим об абсолютных значениях и о том, как они связаны с отрицательными числами.
Начнем.
Может ли абсолютное значение быть отрицательным?
Абсолютное значение не может быть отрицательным. То есть вывод оператора абсолютного значения никогда не может дать отрицательное число.
Причина становится понятной, если мы посмотрим на определение абсолютного значения. Абсолютное значение (или модуль) действительного числа x обозначается |x| и он сообщает нам расстояние между 0 и x на числовой прямой.
Поскольку расстояние никогда не может быть отрицательным, также верно и то, что абсолютное значение никогда не может быть отрицательным.

Например, |3| (словами «абсолютное значение 3») равно 3, поскольку 3 — это расстояние в 3 единицы от 0 на числовой прямой (3 единицы справа от нуля).
Аналогично, |-3| (проще говоря, «абсолютное значение -3») равно 3, поскольку -3 — это расстояние в 3 единицы от 0 на числовой прямой (3 единицы слева от нуля).
Если у нас есть уравнение с абсолютной величиной, равной отрицательному числу, то у нас есть уравнение без решения.
Почему абсолютное значение никогда не бывает отрицательным?
Абсолютное значение никогда не бывает отрицательным, потому что оно сообщает нам величину числа, а не его направление относительно нуля.
Другими словами, абсолютное значение говорит нам, насколько далеко от нуля находится число. Он не говорит нам о направлении (находится ли число слева или справа от нуля на числовой прямой).
Есть три основных случая, когда мы берем абсолютное значение числа x:
- x отрицательное — в этом случае мы опускаем знак минус и берем оставшееся положительное значение.
 Например, абсолютное значение -3 (обозначается |-3|) равно 3.
Например, абсолютное значение -3 (обозначается |-3|) равно 3. - x положительное – в этом случае мы просто берем значение x как абсолютное значение, так как оно уже положительное. Например, абсолютное значение 3 (обозначается |3|) равно 3.
- x равно нулю – в этом случае абсолютное значение x равно нулю, так как расстояние между 0 и x равно нулю. То есть абсолютное значение нуля (обозначается |0|) равно 0,9.0078
This table суммирует входы и выходыSign
Of
InputSign
Of
OutputPositive Positive Zero Zero Negative Positive
для функции абсолютного значения
|x|.
Всегда ли абсолютное значение положительно?
Абсолютное значение не всегда положительное. Он также может быть равен нулю, но никогда не может быть отрицательным.
Абсолютное значение нуля равно нулю. Абсолютное значение любого отличного от нуля числа положительно.
Вместо этого мы можем использовать выражение «абсолютное значение всегда неотрицательно». Это означает, что абсолютное значение может быть положительным или нулевым, но не отрицательным.
Как сделать абсолютное значение отрицательным
Чтобы сделать абсолютное значение отрицательным, вы можете «принудительно» выполнить отрицание, поставив знак минус перед символом оператора абсолютного значения (слева от него).
Например, -|3| (отрицательное значение абсолютного значения 3) будет – 3 (отрицательное 3).
Аналогично, -|-3| (отрицательное абсолютное значение -3) также будет -3 (отрицательное 3).
Точно так же, как абсолютное значение x (обозначаемое |x|) всегда неотрицательно, мы также можем сказать, что отрицательное значение абсолютного значения x (обозначаемого -|x|) всегда неположительно (отрицательно или равно нулю).

Можно ли получить отрицательное значение в абсолютном значении?
Вы можете иметь отрицательное абсолютное значение (то есть отрицательное число в качестве аргумента, которое вы подставляете к абсолютному значению). Это может произойти несколькими способами.
Во-первых, вы можете использовать отрицательное значение в качестве аргумента оператора абсолютного значения. Например, |-3| = 3 имеет отрицательное значение по модулю.
Вы также можете вычитать числа из абсолютного значения. Например, |5 – 9| = |-4| = 4 имеет вычитание по модулю.
Наконец, у вас может быть переменное выражение с вычитанием абсолютного значения. Например, у вас может быть такое выражение, как |x – 2| или |x – y|, что говорит вам о расстоянии между двумя значениями на числовой прямой.
Вы также можете прочитать о концепции абсолютной разницы, которая говорит нам о расстоянии между двумя значениями на числовой прямой.
Может ли уравнение абсолютного значения равняться отрицательному числу?
Уравнение абсолютного значения может равняться отрицательному числу, но в этом случае решения не будет.

Помните: абсолютное значение неотрицательно, то есть оно либо равно нулю, либо положительно. Вывод оператора абсолютного значения никогда не бывает отрицательным.
Например, уравнение |x| = -2 не имеет решения. Независимо от того, какое значение x вы подставите, результат всегда будет как минимум 0 (для x = 0) или положительным (для любого ненулевого значения x).
Может ли решение абсолютного уравнения равняться отрицательному числу?
Решение уравнения абсолютного значения может равняться отрицательному числу. Вот несколько примеров.
Пример 1: уравнение абсолютного значения с отрицательным решением
Рассмотрим уравнение абсолютного значения |x + 4| = 5.
Помните, что абсолютное значение 5 будет равно 5, но абсолютное значение -5 также будет равно 5.
Таким образом, при решении этого уравнения необходимо учитывать две «половины»: положительное и отрицательное.
Тогда нам нужно решить 2 отдельных уравнения:
- (A) x + 4 = 5
- (B) x + 4 = -5
Решение дает первое уравнение (A) x = 1.

Решение второго уравнения (B) дает нам x = -9.
В этом конкретном примере одно из решений уравнения абсолютного значения отрицательно (x = -9), а другое положительно (x = 1).
Однако также возможно, что несколько решений уравнения абсолютного значения будут отрицательными.
Пример 2. Уравнение абсолютного значения с двумя отрицательными решениями
Рассмотрим уравнение абсолютного значения |x + 8| = 2.
Опять же, когда мы решаем это уравнение, нужно учитывать две «половины»: положительную и отрицательную.
Нам действительно нужно решить 2 отдельных уравнения:
- (A) x + 8 = 2
- (B) x + 8 = -2
Решая первое уравнение x (A) = -6.
Решение второго уравнения (B) дает нам x = -10.
В этом конкретном примере оба решения (x = -6 и x = -10) уравнения абсолютного значения отрицательны.
Пример 3. Уравнение абсолютного значения с тремя отрицательными решениями
Рассмотрим уравнение абсолютного значения |x 3 + 6x 2 + 11x + 6| = 0.

Чтобы решить это уравнение, нам нужно выяснить, какие значения x делают выражение внутри оператора абсолютного значения равным нулю.
Итак, мы хотим решить х 3 + 6х 2 + 11x + 6 = 0.
Это делит как:
(x+1)(x+2)(x+3) = 0
Что дает нам решения x = -1, x = — 2 и х = -3.
Может ли абсолютное неравенство быть отрицательным?
Неравенство абсолютного значения может быть отрицательным. Однако решений может быть, а может и не быть, в зависимости от знака неравенства.
Может ли решение абсолютного неравенства равняться отрицательному числу?
Решение абсолютного неравенства может равняться отрицательному числу.
Абсолютное неравенство может иметь отрицательные решения.Вот несколько примеров.
Пример 1: Абсолютное неравенство с отрицательными решениями
Рассмотрим абсолютное неравенство |2x – 3| > 9.
Для решения необходимо рассмотреть два отдельных неравенства:
- (A) 2x – 3 > 9
- (B) 2x – 3 < -9
 Для этой половины решения нет отрицательных значений.
Для этой половины решения нет отрицательных значений.Решение уравнения (B) дает нам 2x < -6 или x < -3. Все значения для этой половины решения отрицательны.
На самом деле любые значения меньше -3 (все они отрицательные) являются решениями этого неравенства абсолютных значений. Таким образом, существует бесконечно много отрицательных решений этого абсолютного неравенства.
Пример 2. Абсолютное неравенство с отрицательными решениями
Рассмотрим абсолютное неравенство |3x – 6| < 12.
Для решения необходимо рассмотреть цепочку неравенств:
-12 < 3x – 6 < 12
-6 < 3x < 18
-2 < x < 6 или (-2, 6).
В наборе (-2, 6) решений абсолютного неравенства есть бесконечно много отрицательных значений.
Заключение
Теперь вы знаете, как связаны отрицательные значения и абсолютное значение. Хотя абсолютное значение никогда не имеет отрицательного выхода, могут быть отрицательные решения уравнения или неравенства абсолютного значения.



 0
0

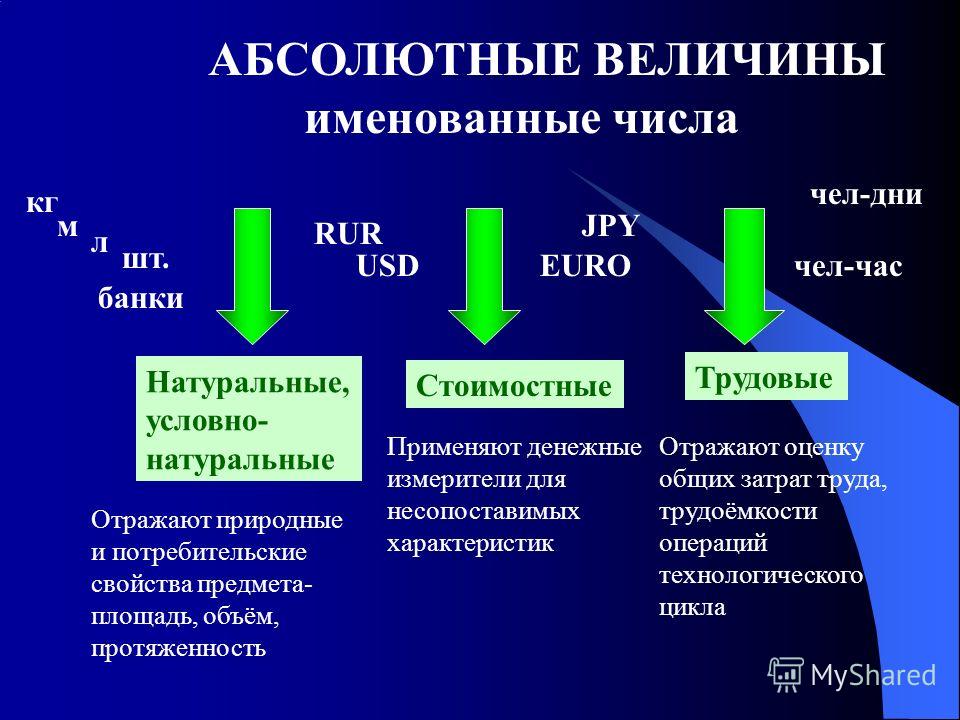


 {displaystyle gcd (g (x), p (x)) = 1 = gcd (h (x), p (x)).}
{displaystyle gcd (g (x), p (x)) = 1 = gcd (h (x), p (x)).} «Архивная копия». Архивировано из оригинал на 2008-12-22. Получено 2009-04-03.CS1 maint: заархивированная копия как заголовок (связь)
«Архивная копия». Архивировано из оригинал на 2008-12-22. Получено 2009-04-03.CS1 maint: заархивированная копия как заголовок (связь)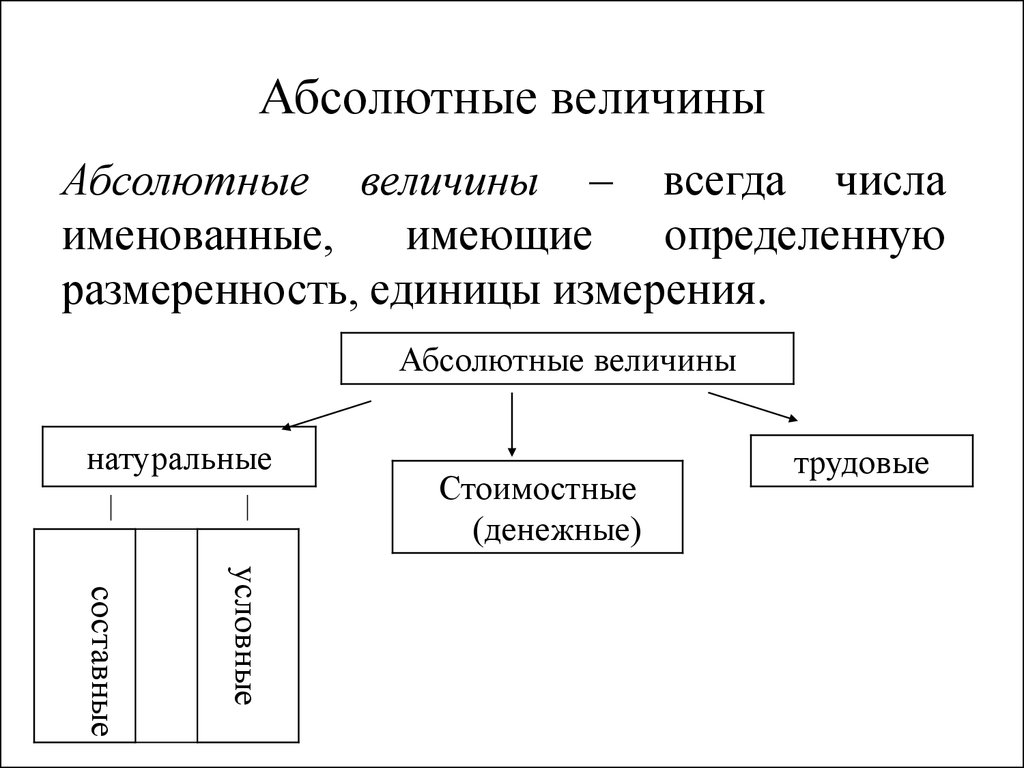 Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

 Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
 Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка. Мы будем решать различные примеры на основе концепции для лучшего понимания.
Мы будем решать различные примеры на основе концепции для лучшего понимания. Но для абсолютного значения знак числового значения игнорируется и рассматривается только числовое значение.
Но для абсолютного значения знак числового значения игнорируется и рассматривается только числовое значение. Кроме того, абсолютное значение -4 записывается как |-4|. Как мы обсуждали ранее, абсолютное значение всегда дает неотрицательное значение. Следовательно, |4|=|-4| =4. То есть он превращает отрицательные числа также в положительные числа. На следующем рисунке представлен символ абсолютного значения.
Кроме того, абсолютное значение -4 записывается как |-4|. Как мы обсуждали ранее, абсолютное значение всегда дает неотрицательное значение. Следовательно, |4|=|-4| =4. То есть он превращает отрицательные числа также в положительные числа. На следующем рисунке представлен символ абсолютного значения. Расстояние числа 0 равно нулю от 0, поэтому мы можем сказать, что абсолютное значение 0 равно 0.
Расстояние числа 0 равно нулю от 0, поэтому мы можем сказать, что абсолютное значение 0 равно 0. Тогда почему у нас есть -x в приведенном выше определении функции абсолютного значения?
Тогда почему у нас есть -x в приведенном выше определении функции абсолютного значения? |х-2| = 4. Можем ли мы попытаться помочь ей?
|х-2| = 4. Можем ли мы попытаться помочь ей? Следовательно, -|-х| = -х.
Следовательно, -|-х| = -х.
 |-5| = 5. Например, значение смещения иногда записывают как -5 метров, но знак минус означает только направление, а расстояние всего 5 метров.
|-5| = 5. Например, значение смещения иногда записывают как -5 метров, но знак минус означает только направление, а расстояние всего 5 метров.
 0004 и как оно связано с абсолютным значением. Давайте начнем!
0004 и как оно связано с абсолютным значением. Давайте начнем! Это полезно помнить при вычислении выражений и решении уравнений, но также важно помнить почему.
Это полезно помнить при вычислении выражений и решении уравнений, но также важно помнить почему. Отрицательное число 3 находится на расстоянии трех единиц от нуля, что означает, что абсолютное значение -3 равно 3. Это дает нам 1 минус 3, что равно -2.
Отрицательное число 3 находится на расстоянии трех единиц от нуля, что означает, что абсолютное значение -3 равно 3. Это дает нам 1 минус 3, что равно -2. Абсолютная разница используется для вычисления расстояния между любыми двумя числами на числовой прямой, а не только между числом и нулем.
Абсолютная разница используется для вычисления расстояния между любыми двумя числами на числовой прямой, а не только между числом и нулем.
 0005
0005 Абсолютное значение делает любое число положительным, поскольку оно показывает, насколько оно далеко от 0. Во-первых, упростите выражение в столбцах абсолютного значения.
Абсолютное значение делает любое число положительным, поскольку оно показывает, насколько оно далеко от 0. Во-первых, упростите выражение в столбцах абсолютного значения. 








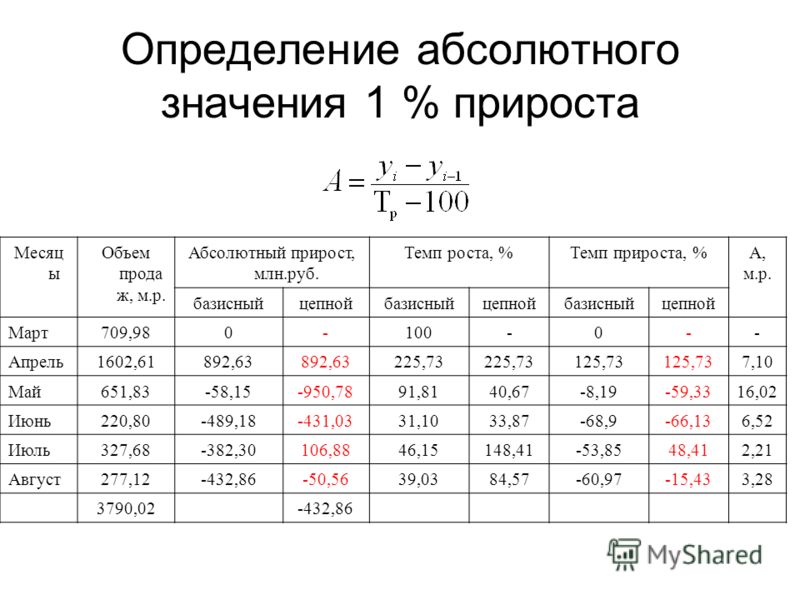 Сначала мы возьмем произведение ?3 и 6, что равно ?18. Затем мы находим абсолютное значение ?18, которое равно 18,
Сначала мы возьмем произведение ?3 и 6, что равно ?18. Затем мы находим абсолютное значение ?18, которое равно 18, Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вам придется…
Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вам придется… С…
С… Мы здесь, чтобы убедиться, что вы знаете все…
Мы здесь, чтобы убедиться, что вы знаете все… ..
..
 Кроме того, абсолютное значение отрицательного числа является его (положительной) противоположностью, поэтому также имеет 29 в качестве абсолютного значения.
Кроме того, абсолютное значение отрицательного числа является его (положительной) противоположностью, поэтому также имеет 29 в качестве абсолютного значения.

 Объяснение:
Объяснение:
 Мы также можем получить отрицательные решения для некоторых уравнений и неравенств с абсолютной величиной.
Мы также можем получить отрицательные решения для некоторых уравнений и неравенств с абсолютной величиной. 
 Например, абсолютное значение -3 (обозначается |-3|) равно 3.
Например, абсолютное значение -3 (обозначается |-3|) равно 3.




 Для этой половины решения нет отрицательных значений.
Для этой половины решения нет отрицательных значений.