Алгебраическое дополнение матрицы
Продолжаем изучать матрицы и мы добрались до такого понятия как алгебраическое дополнение. Что же оно представляет? Алгебраическое дополнения элемента матрицы — есть число, которое состоит из произведения определителя(детерминанта) матрицы (без строки и столбца на которой стоит элемент матрицы) и (-1) в степени суммы номера столбца и строки. Если это перевести в наглядный вид, то получим Исходная матрица
Для элемента 9, стоящего на 3 строке и 3 столбце, алгебраическое дополнение будет иметь вид
Наш бот, умеет рассчитывать алгебраическое дополнение в том числе и комплексных матриц. и вот один из примеров
Удачных расчетов!
|
||||||||||||||||
|
||||||||||||||||
2 cos(1+i)
|
Угол между ними.
| ||||||||||
Алгебраическое дополнение к элементу определителя матрицы: нахождение, свойства
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
ru Математика Алгебра Алгебраическое дополнение матрицы
В данной публикации мы рассмотрим определение и свойства алгебраического дополнения матрицы, приведем формулу, с помощью которой его можно найти, а также разберем пример для лучшего понимания теоретического материала.
- Определение и нахождение алгебраического дополнения
- Свойства алгебраического дополнения
Определение и нахождение алгебраического дополнения
Алгебраическое дополнение Aij к элементу aij определителя n-го порядка – это число Aij = (-1)i+j · Mij, где M – это минор матрицы.
Пример
Вычислим алгебраическое дополнение A32 к a32 определителя ниже:
Решение
Свойства алгебраического дополнения
1. Если просуммировать произведения элементов произвольной строки и алгебраических дополнений к элементам строки i определителя, то получится определитель, в котором вместо строки i стоит данная произвольная строка.
2. Если просуммировать произведения элементов строки (столбца) определителя и алгебраических дополнений к элементами другой строки (столбца), то получится ноль.
3. Сумма произведений элементов строки (столбца) определителя и алгебраических дополнений к элементам данной строки (столбца) равняется определителю матрицы.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Конвертер десятичных чисел в дополнение до двух — изучение двоичного числа
Десятичная дробь в дополнении до двух
Введите десятичное целое число (например, -123) (без запятых и пробелов) Преобразует в это двоичное целое число с дополнением до двух:Опции:
- Количество битов:
Дополнение до двух до десятичной дроби
Введите двоичное целое число в дополнении до двух (например, 00010110) (без запятых и пробелов) Преобразует в это десятичное целое число:Опции:
- Количество битов:
О конвертере десятичного числа/дополнения до двух
Это преобразователь десятичного числа в дополнение до двух и преобразователь числа в дополнении до двух в десятичное число .
Эти преобразователи не дополняют свой вход; то есть они не отрицают его. Они просто преобразуют его в форму дополнения до двух или из нее. Например, -7 преобразуется в 11111001 (в 8 бит), что равно -7 в дополнении до двух. (Если дополнить его, получится 7 или 00000111 до 8 бит.) Точно так же 0011 преобразуется в 3, а не в -3.
Как использовать конвертер десятичной дроби в дополнение до двух
Десятичная запятая в дополнение до двух
- Введите положительное или отрицательное целое число.
- Установите число битов для представления дополнения до двух (если оно отличается от значения по умолчанию).
- Нажмите «Конвертировать», чтобы конвертировать.
- Нажмите «Очистить», чтобы сбросить форму и начать с нуля.
Если вы хотите преобразовать другой номер, просто введите исходный номер и нажмите «Преобразовать» — нет необходимости сначала нажимать «Очистить».
Если введенное вами число слишком велико для представления в запрошенном количестве битов, вы получите сообщение об ошибке (в нем будет указано, сколько битов вам нужно).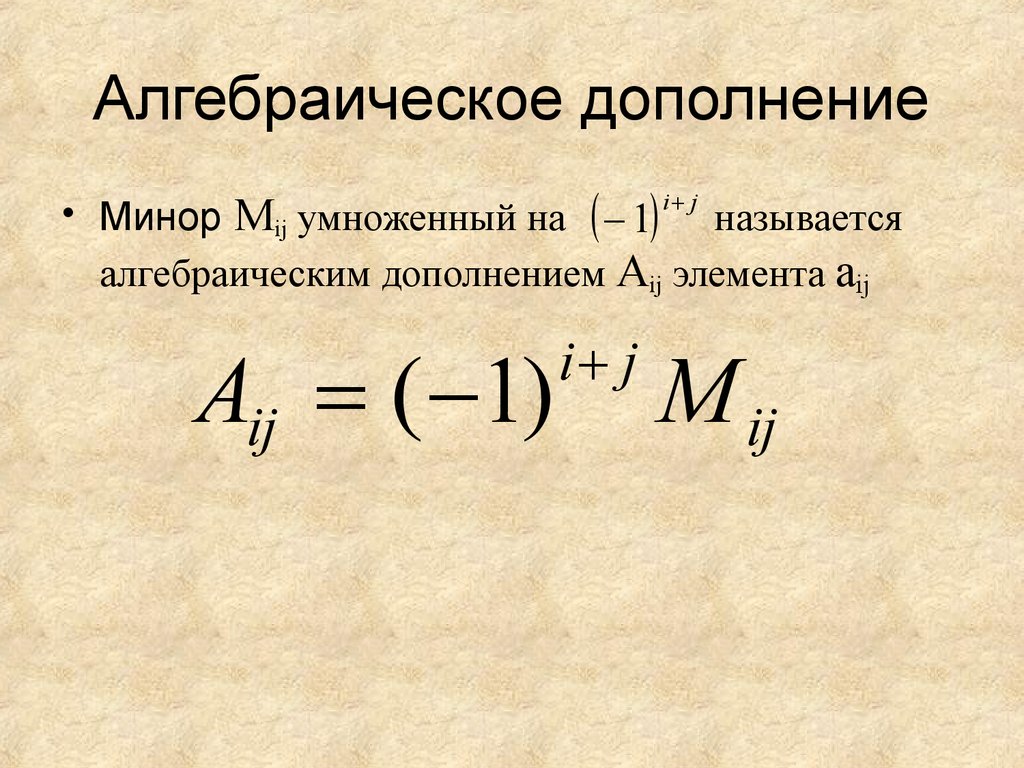
Дополнение до двух до десятичного числа
- Введите число в дополнении до двух — строку из нулей и единиц.
- Установите количество битов, соответствующее длине ввода (если оно отличается от значения по умолчанию).
- Нажмите «Конвертировать», чтобы конвертировать.
- Нажмите «Очистить», чтобы сбросить форму и начать с нуля.
Вывод будет положительным или отрицательным десятичным числом.
Изучение свойств преобразования с дополнением до двух
Лучший способ изучить преобразование с дополнением до двух — начать с небольшого количества битов. Например, давайте начнем с 4 битов, которые могут представлять 16 десятичных чисел в диапазоне от -8 до 7. Вот что возвращает конвертер десятичных чисел в дополнение до двух для этих 16 значений:
| Десятичное число | Дополнение до двух |
|---|---|
| -8 | 1000 |
| -7 | 1001 |
| -6 | 1010 |
| -5 | 1011 |
| -4 | 1100 |
| -3 | 1101 |
| -2 | 1110 |
| -1 | 1111 |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
Неотрицательные целые числа всегда начинаются с «0» и будут иметь столько начальных нулей, сколько необходимо, чтобы дополнить их до требуемого количества битов.
(Если вы уберете ведущие нули, вы получите чистое двоичное представление числа.) Отрицательные целые числа всегда начинаются с «1».
Если вы пропустите эти значения дополнения до двух через конвертер дополнения до двух в десятичную форму, вы подтвердите, что преобразование правильное. Вот та же таблица, но в двоичном лексикографическом порядке:
| Дополнение до двух | Десятичное число |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | -8 |
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
Независимо от того, сколько битов вы используете в представлении дополнения до двух, -1 десятичное число всегда представляет собой строку из 1 в двоичном формате.
Преобразование числа с фиксированной точкой в дополнении до двух в десятичное число
Вы можете использовать преобразователь числа с дополнением до двух в десятичное число для преобразования чисел, представленных в представлении с дополнением до двух с фиксированной точкой. Например, если у вас есть 16-битные числа в формате Q7.8, введите значение дополнения до двух, а затем просто разделите десятичный ответ на 2 8 . (Числа в формате Q7.8 находятся в диапазоне от -2 15 /2 8 = -128 до (2 15 -1)/2 8 = 127,99609375.) Вот несколько примеров: к 24405 и 24405/2 8 = 95,33203125
Реализация
Этот преобразователь реализован в десятичной арифметике произвольной точности. Вместо того, чтобы работать с двоичным представлением входных данных — обычным способом «перевернуть биты и добавить 1» — он выполняет операции с десятичным представлением входных данных, добавляя или вычитая степень двойки.
В частности, вот что было сделано и когда:
- Десятичное число в дополнении до двух
- Неотрицательный ввод: просто преобразовать в двоичный формат и дополнить ведущими нулями.
- Отрицательный ввод (знак «-»): добавьте 2 numBits , затем преобразуйте в двоичный код.
- Дополнение до двух до десятичной дроби
- Неотрицательный ввод (ведущий бит «0»): просто преобразовать в десятичное число.
- Отрицательный ввод (начальный бит «1»): преобразовать в десятичный, получив положительное число, затем вычесть 2 numBits .
Ограничения
Из практических соображений я установил произвольный предел в 512 бит для входных данных.
Дополнение 2 в цифровой электронике
следующий → ← предыдущая Как и дополнение до 1, дополнение до 2 также используется для представления двоичных чисел со знаком. Чтобы найти дополнение двоичного числа до 2, мы сначала найдем дополнение двоичного числа до 1, а затем добавим 1 к его младшему значащему биту. Например, если мы хотим вычислить дополнение до 2 числа 1011001, то сначала мы находим дополнение до 1 числа, равное 0100110, и добавляем 1 к младшему биту. Таким образом, прибавив 1 к младшему биту, число будет (0100110)+1=0100111. Мы также можем создать логическую схему, используя вентили ИЛИ, И и НЕ. Логическая схема для нахождения дополнения до 2 5-битного двоичного числа выглядит следующим образом: Пример 1: 110100 Чтобы найти дополнение до 2 данного числа, замените все 0 на 1 и все 1 на 0. Таким образом, дополнение числа 110100 до 1 равно 001011. Теперь добавьте 1 к младшему биту этого числа, т. е. (001011)+1= 001100. Пример 2: 100110 Чтобы найти дополнение данного числа до 1, замените все 0 на 1 и все 1 на 0. Таким образом, дополнение числа 100110 до 1 равно 011001. Теперь добавьте один младший бит этого числа, т. Е. (011001) + 1 = 011010. Таблица дополнения до 2
Использование дополнения до 2Дополнение 2 используется для представления чисел со знаком и выполнения арифметических операций, таких как вычитание, сложение и т. Пример 1: +6 и -6 Число +6 представлено так же, как двоичное число. Для представления обоих чисел используйте 5-битный регистр. Таким образом, +6 представлен в 5-битном регистре как 0 0110. -6 представлено в 5-битном регистре следующим образом:
|
д. Положительное число просто представлено как форма величины. Таким образом, для представления положительных чисел ничего не нужно делать. Но если мы представляем отрицательное число, то мы должны выбрать либо метод дополнения 1, либо метод дополнения 2. Дополнение до 1 — неоднозначный метод, а дополнение до 2 — однозначный метод. Давайте посмотрим на пример, чтобы понять, как мы можем вычислить дополнение до 2 в представлении двоичного числа со знаком.