Arcsin y x: Mathway | Популярные задачи

2

Арксинус — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

y
Повторим условие обратимой
функции.
Среди множества значений
функции не должно быть таких
значений, которые функция
принимает более чем в одной
точке области определения.
Например, для квадратичной
функции обратной не
существует, т.к. каждое свое
значение она принимает в двух

точках области определения.
O
-3 -2
1 2
x
y
Но если мы рассмотрим
квадратичную функцию на
промежутке 0 ;
то можно построить график
обратной функции.
Графики симметричны
относительно прямой у = х.
O
-3 -2
1 2
x
2
2
3
2
y = sin x
-1
D
E ( у ) : yх ;
2 2
y
2
1
1
-1
2
2
3
2
y = arcsin x
D
E( y) : yx 1;1
0; ;01; 1
22
x
1 ;01; 0
2 2
2
y = arcsin x
y
2
D( y) : x 1;1
-1
1
2
По определению
нечетной функции
f(-x) = – f(x)
x
E ( у ) : y ;
2 2
Функция нечетная
(график симметричен относительно точки О)
arcsin(-x) = – arcsinx
Функция возрастает
Функция непрерывна
y
2
arcsina
3
4
a 1;1
6
0
2
x
a
– это такое число
,
синус которого равен a
arcsin 0
1
arcsin
2
2
arcsin
2
3
arcsin
2
arcsin 1
a ;
2 2
arcsin 1,5
Не существует
arcsin 3
Не существует
arcsina
a
– это такое число
,
синус которого равен a
a 1;1
a ;
2 2
arcsin(-x) = – arcsinx
arcsin( 1)
1
arcsin( )
2
2
arcsin(
)
2
3
arcsin(
)
2
arcsin( 3 )
arcsin( 1,5)
Повторим
y = f(x)
y
y = f(x)
y = — f(x)
-1
x
1
y = — f(x)
y
y = — arcsin x
D( y) : x 1;1
E ( у ) : y ;
2 2
2
1
-1
2
x
Повторим
y = f(x)
y = f(-x)
y
y = f(x)
y = f(-x)
-1
1
x
y
y = arcsin (-x)
D( y) : y 1;1
E ( у ) : х ;
2 2
2
1
-1
2
x
y
y = 2arcsin x
D( y) : x 1;1
E( у) : y ;
2
1
-1
2
x
y
1
=
y — 2 arcsin x
D( y) : x 1;1
E ( у ) : y ;
4 4
2
1
-1
2
x
y
y = arcsin 12 x
D( y) : х 2; 2
E ( у ) : у ;
2 2
2
1
-1
2
x
y
y = arcsin 2x
1 1
D ( y ) : х ;
2 2
E ( у ) : у ;
2 2
2
1
-1
2
x
y
2
=
y 1,5arcsin x + 3
D( y) : х 1;1
17
E ( у ) : у ;
12
12
2
1
-1
2
x
Повторим
y = f(x)
y = f(x)
y
y = f(x)
1
x
y
Повторим
1
y = f(x)
y= f x
Функция четная
(график симметричен
относительно оси Оу)
x
y
y = arcsin x
D( y) : y 1;1
E ( у ) : х 0;
2
Функция четная
(график симметричен
относительно оси Оу)
2
1
-1
2
x
y
y = arcsin x –
6
D( y) : х 1;1
E ( у ) : у 0;
3
Функция четная
(график симметричен
относительно оси Оу)
2
1
-1
2
x
Можно сначала найти область
определения и множество значений,
а затем построить график.
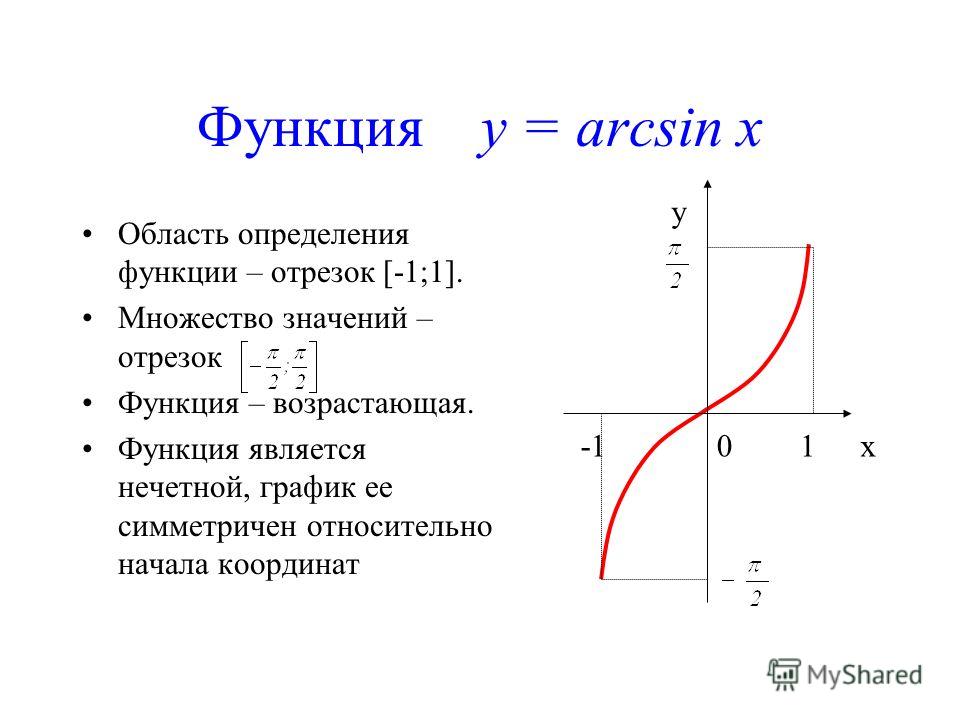
y
y = -2arcsin (x – 3)
1 x 3 1
2 x 4
2
D ( y ) : x 2; 4
2
arcsin( x 3)
x
2
2 arcsin( x 3)
y
E ( y ) : y ;
1
/ ( 2)
2
3
y
3
y = arcsin( x – )
4
3 3
D ( y ) : х 1 ;1
4 4
3
E ( у ) : у arcsin ;
4 2
Функция четная
(график симметричен
относительно оси Оу)
2
1
-1
2
x

English     Русский Правила

{-1}})'(x) = \dfrac{1}{f(x)’}$$

Следовательно, производная от $\arcsin(x)$ должна быть: $$\dfrac{1}{\cos(x)}$$

Но по какой-то причине это работает только для небольших $x$. Где я сделал ошибку?

Привет, Финн

• исчисление
• тригонометрия
• производные
• обратная функция

$\endgroup$

3

$\begingroup$ 92}},$$ из-за тождества Пифагора и $-\frac\pi2\le\arcsin x\le \frac\pi2$, поэтому косинус равен $\ge 0$.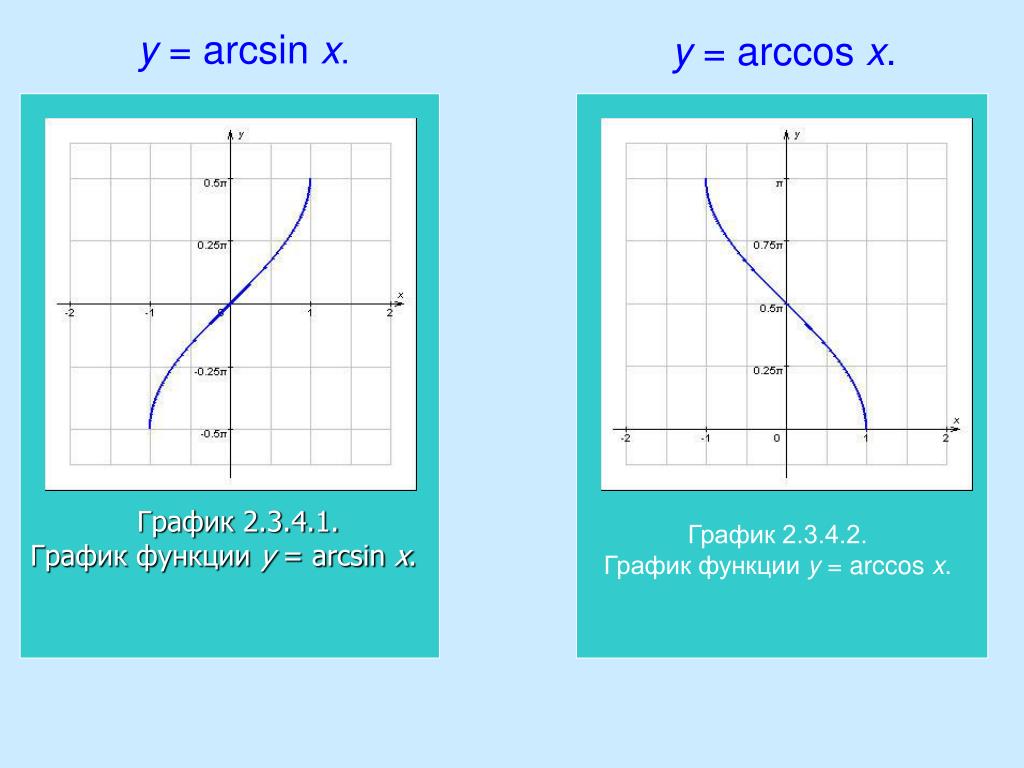

$\endgroup$

$\begingroup$

Может быть проще применить определение арксинуса: $$ х=\sin(\arcsin(x)) $$ «Правило инверсии» гарантирует, что производная арксинуса существует (с условием, о котором я расскажу позже), поэтому вы можете дифференцировать обе стороны, используя цепное правило: $$ 1=\cos(\arcsin(x))\arcsin'(x) $$ Следовательно $$ \ arcsin ‘(x) = \ frac {1} {\ cos (\ arcsin (x))} $$ Условие, о котором я упоминал выше, состоит, конечно же, в том, что $\cos(\arcsin(x))\ne0$. 92}}\qquad x\in(-1,1) $$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

исчисление — Почему $\arctan x$ не равно $\arcsin(x)/\arccos(x)$?

спросил 2 года 4 месяца назад

Изменено 1 год, 8 месяцев назад

Просмотрено 5к раз

$\begingroup$

Почему $\arctan x$ не равно $\frac{\arcsin(x)}{\arccos(x)}$? Есть ли контрпример, который я могу использовать, чтобы показать, что они не равны? Благодарить!

• исчисление
• тригонометрия
• обратная функция

$\endgroup$

7

$\begingroup$

Помимо $x=0$ и значения, близкого к $0,450116$, вы можете попробовать любое другое значение.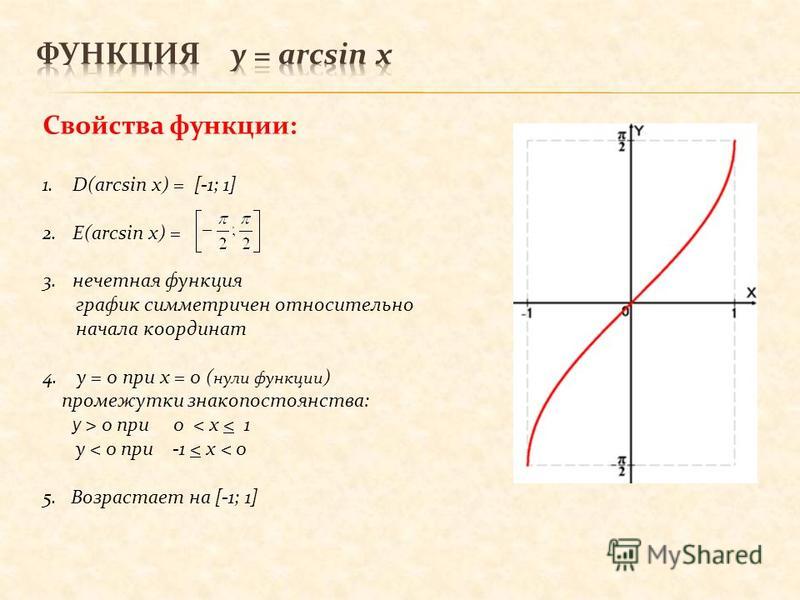

{-1}(x).$$

$\endgroup$

2

$\begingroup$

Конечно:

$$\arctan1=\frac\pi4\neq\frac{\cfrac\pi2}{0}=\frac{\arcsin 1}{\arccos 1}$$

$\endgroup$

$\begingroup$

Функции $f(x)=\arctan(x)$ и $g(x)=\frac{\arcsin(x)}{\arccos(x)}$ различаются по нескольким причинам:

1. As упомянутые в других ответах, они принимают разные значения во многих точках. Например, $f(1)=\frac{\pi}{4}$, а $g(1)=\frac{\pi/2}{0}$ не определено.
2. У них разные домены: домен $\arctan$ — $\mathbb R$, а домен $\arcsin$ и $\arccos$ — $[-1,1]$, поэтому домен $g$ равен включены в $[-1,1]$. Именно, поскольку $\arccos(x)=0 \iff x=1$, область определения $g$ равна $[-1,1)$.
3. Функция $\arctan$ нечетная, а $g$ нет. В самом деле, поскольку $\arcsin$ нечетно, $f=g$ означало бы, что $\arccos(x)=\arcsin(x)\arctan(x)$ четно, что, как известно, неверно.

   No related posts.