Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
11.21
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Боря купил 4 книги.
Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Решено
Два угла треугольника равны 60 градусов и 45 градусов,а сторона,лежащая против большего из них,равна 3корень квадратный из двух.Найдите сторону треугольника,лежащую против меньшего из данных углов.
Решено
Две стороны треугольника равны 7 см и 9 см,а медиана,проведенная к третьей,-4 см.Найдите неизвестную сторону треугольника.
Основание AD трапеции АВСD лежит в плоскости . Через точки В и С проведены параллельные прямые, пересекающие плоскость в точках Е и Fсоответственно.
https://vk.com/doc245577262_450343753?hash=070c1827ac04604427&dl=5341e6ab46d7f1837f 14-й вариант
Пользуйтесь нашим приложением
Практика_4 — Стр 2
Задача 14.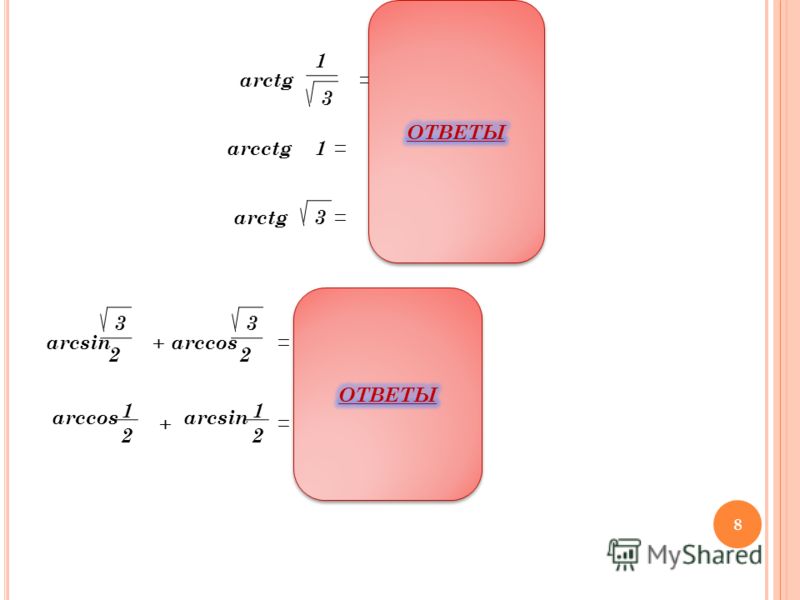
W(p) k . p(Tp 1)
Численные значения параметров T 0,1 с; k 100с 1.
Необходимо синтезировать систему с частотой среза 100с 1
и запасом по фазе, равном 60 . Общий коэффициент передачи разомкнутой системы должен быть сохранен тем же.
Рис. 10
Решение. Для исходной системы lgωсри 1,5 тогда
сри 10 10 31,6с 1 и запас по фазе:
и 180 90 arctg(ωсриT) 90 arctg(31,6 0,1) 17,5 .
Для синтезируемой системы запас по фазе:
11
|
| 90 arctg(ω |
|
| T ) arctg(ω | T ) arctg(ω |
| 1 | ) |
| |
|
|
|
|
|
| ||||||
| с |
|
| срс 1 | срс 1 | срс ω2 | , | ||||
|
|
| 1 |
|
|
|
|
|
| ||
90 arctg(ωсрс | ) |
|
|
|
|
|
| ||||
|
|
|
|
|
|
| |||||
|
|
| ω2 |
|
|
|
|
|
| ||
где ω1 1 – первая частота излома АЧХ корректирующего звена;
T
ω2 – вторая частота излома АЧХ корректирующего звена.
Так как с 60 , а срc 100с 1, то тогда может быть определена частота ω2:
60 90 arctg(100 1 ) 17,5, откуда
|
| 100 |
| 100 | ω2 | |
ω2 |
|
| 173,5с 1. | |||
tg30 | 0,577 | |||||
|
|
|
|
АЧХ корректирующего звена приведена на рис. 10 и соответствует последовательному соединению пассивного форсирующего звена и усилителя (рис. 11). Так как 20lgkу 26,7 дБ, то
kу 101,33 21,38.
Рис. 11
Передаточная функция корректирующего звена
Wпос(p) kуk T1p 1, T2 p 1
где k | у | k 1, k R | /(R R | 2 | ), k | 1 |
|
| R2 |
| 1 | , | ||||||||||||
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
| 2 |
| 1 |
|
| kу |
|
| R1 R2 | 21,38 | ||||||||||
| R1CR2 |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
T |
| 1 |
|
| 1 | , T R C | 1 |
| 1 | . |
|
|
| |||||||||||
R R |
|
| ω |
|
|
|
| |||||||||||||||||
1 |
| ω | 2 |
|
| 173,5 |
| 2 1 |
|
| 10 |
|
|
|
| |||||||||
|
| 1 | 2 |
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
| ||||
12
Отсюда определяются параметры корректирующего звена: R1, R2,C.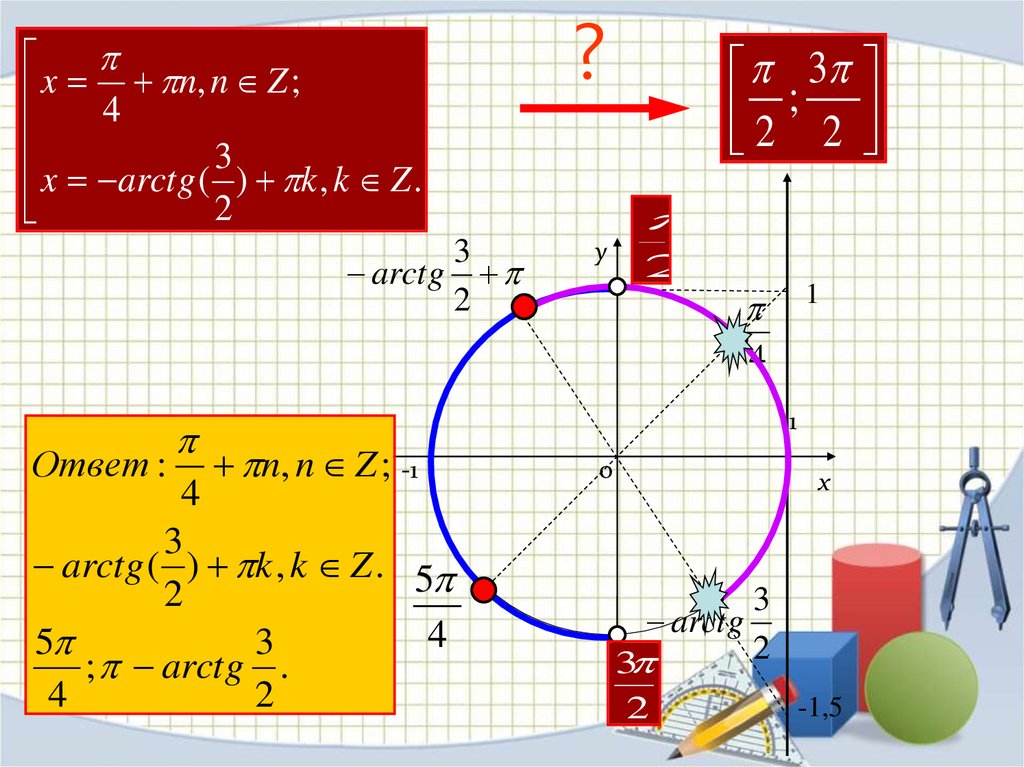
Задача 15. Дана нескорректированная система автоматического регулирования с передаточной функцией
Wисх(p) | 2 | . | |
p(0.25p 1)(0.0625p 1) | |||
|
|
Необходимо увеличить коэффициент усиления разомкнутой системы в 20 раз (26 дБ), не нарушая существенно качества переходного процесса системы. Допустимое снижение запаса по фазе составляет 5 .
Решение. Из построенной на рис. 12, а характеристики Lисх(ω) видно, что запас по фазе нескорректированной системы при частоте среза с 2с-1 составляет 56 .
Желаемая характеристика в области низких частот должна быть поднята на 26 дБ, а в области средних и высоких частот должна совпадать с Lисх(ω).
Фаза скорректированной системы может быть записана в виде
(рис. 12, а)
жел( ) 90 arctg ω arctg ω arctg0,25ω arctg0,0625ω.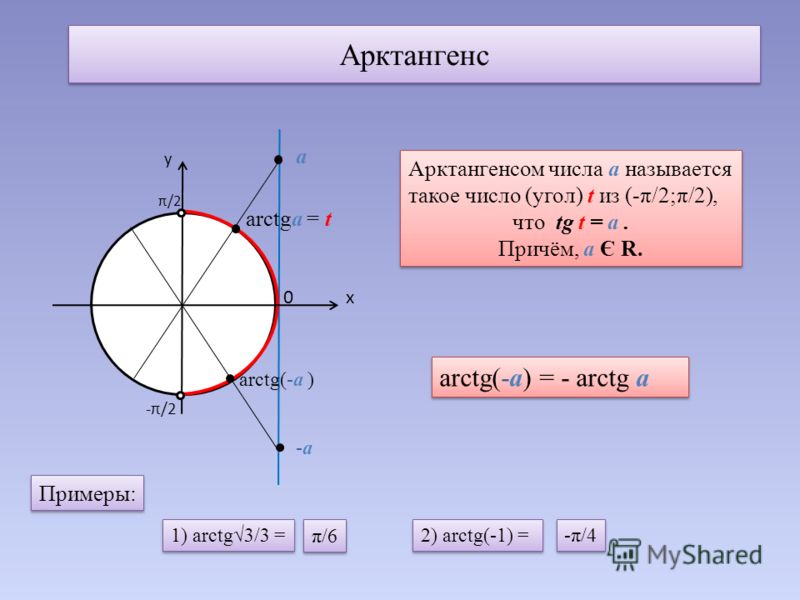
ω1 ω2
Подставив в это уравнение ω ωc 2c 1 и учитывая, что ω1 и ω2 связаны соотношением ω1 ω2 /20, а также
жел(ωc) 180 51 129 ,
получим
6 arctg2 20 arctg 2 . ω2 ω2
Из этого уравнения определим ω2 0.22с 1, ω1 0.011с 1. Ха-
рактеристика Lпос(ω) Lжел(ω) Lисх(ω) построена на рис. 12, б. Корректирующее устройство можно представить в виде после-
довательного соединения пассивно интегрирующего звена и дополнительного усилителя (рис. 13).
Передаточная функция корректирующего устройства
Wк(p) kк T2 p 1. T1p 1
13
Рис. 12
Рис. 13
Численные значения параметров определяются по характеристике Lпос(ω) согласно уравнениям:
1
T1 ω1 (R1 R2)C 90c;
14
1
T2 ω2 R2C 4,5c;
kк T1 R1 R2 20. T2 R2
Тогда при C 10 мкФ получаем: R1 8,55 МОм; R2 450 кОм.
15
c — Быстрый и точный алгоритм атан/арктан аппроксимации
Для своих нужд я разработал следующую функцию на основе аппроксимации Паде-Чебышёва.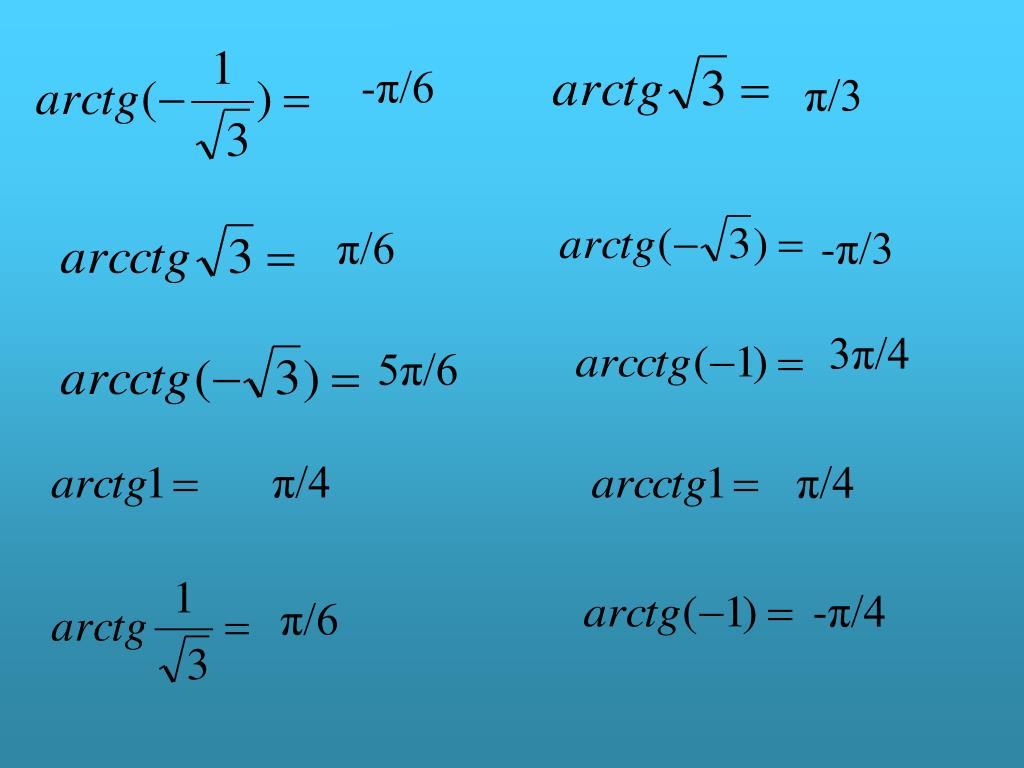
2 с пороговым значением
jnb arctg_end // Данные уже в формате xmm0, если |x|>=62919776
vfmsub132ss xmm0,xmm4,xmm1 // xmm0 = (pi-3)/2*|x|*Q-P
vdivss xmm0,xmm0,xmm1 // xmm0 = (pi-3)/2*sign(x)-P/(x*Q)
arctg_end: // Добавить к результату 3/2*sign(x)
vaddss xmm0,xmm0,[edx+4*eax+36] // xmm0 = pi/2*sgn(x)-P/(x*Q)
рет // Возврат
}
}
тригонометрия — $\operatorname{Arctg}(a) + \operatorname{Arctg}(b)$, когда $a b =1$
спросил
Изменено 3 года, 1 месяц назад
Просмотрено 153 раза
$\begingroup$
Как упоминалось здесь, известно, что можно написать $\operatorname{Arctg}(a) + \operatorname{Arctg}(b)$ как форму $\operatorname{Arctg}\frac{a+b}{1 — a\:b}$ плюс константа в случае, когда $a \:b<1$ или $a \:b>1$.
Мне интересно, что происходит, когда $a b=1$. Есть ли формула для этого случая?
- тригонометрия
$\endgroup$
3
$\begingroup$
Хорошо известно, что $$\arctan x+\arctan\frac1x= \begin{cases}\phantom{-}\dfrac\pi 2&\text{if } x>0,\\[0.5ex]-\dfrac\pi 2 &\text{ если } x<0.\end{cases}$$
$\endgroup$
2
$\begingroup$
Подсказка:
$ab = 1 \rightarrow a = b = 1$, поэтому
$$\arctan (1) + \arctan (1) = \dfrac {1+1}{1-1} \rightarrow \dfrac 2 0 $$
Так как $\dfrac 2 0$ не определено, то
$$\arctan \dfrac 2 0 = \dfrac \pi 2.$$
Кроме того, поскольку $\arctan 1 = \dfrac {\pi}{4}$,
$$\arctan 1 + \arctan 1 = \dfrac \pi 4 + \dfrac \pi 4 = \dfrac \pi 2.
