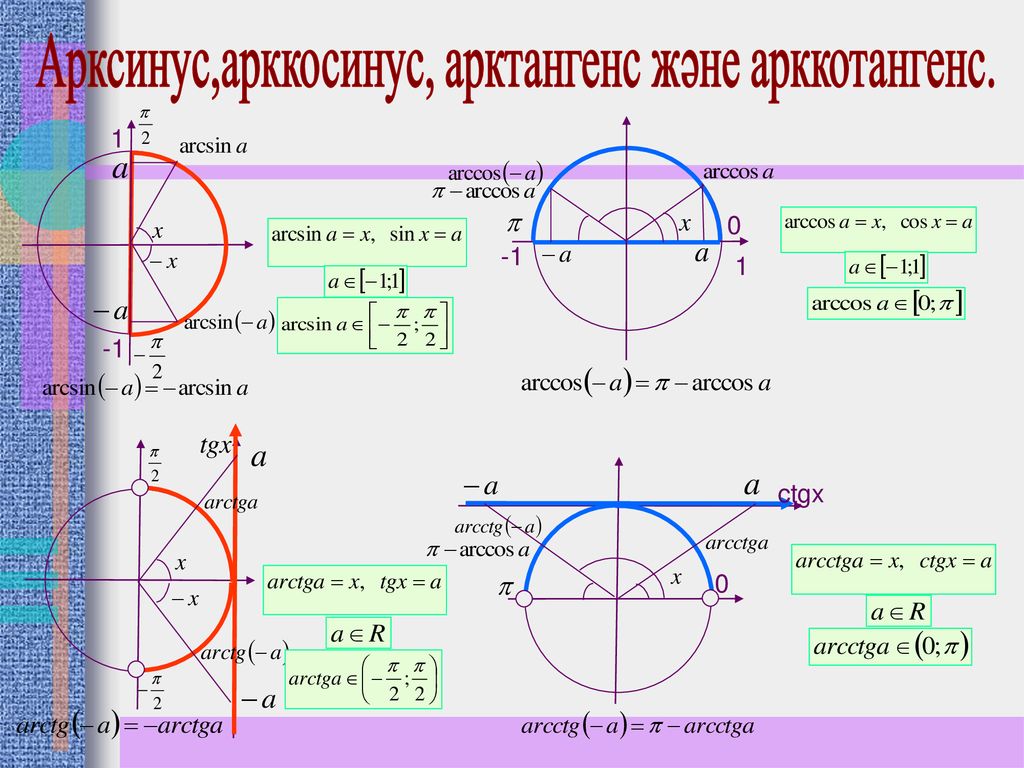
Арккосинус числа a. Функция y = arccos x, её свойства и график. Как найти арккосинус числа
12+
4 недели назад
Математика от Баканчиковой106 подписчиков
Тригонометрия 8-11 класс. Что такое арккосинус числа? Как найти арккосинус любого числа? Как построить график функции y = arccos x? Какие свойства есть у функции y = arccos x? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Функция y=arcsin x, её график и свойства» и «Обратная функция, её свойства и график», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, как получается график функции y = arccos x, и почему область определения функции y = arccos x ограничена отрезком [-1; 1], а область значений – отрезком [0; π]. Обратим особое внимание на то, что арккосинус – это угол поворота, а не просто число. Дадим Вам определение арккосинуса числа а, и поясним, какую задачу решает график функции y = arccos x. Особо отметим две характерные ошибки, которые допускают ученики при вычислении арккосинуса.
Как найти функции обратные данным и построить график. Алгебра 8-11 класс. https://youtu.be/Gr53TGYtBO8
Функция y = sin x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/a0f98530ee52e1303236e975c6a826f8/
Функция y = cos x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/79a7a2ce60eefcab7aea2ee136a00bb2/
Функция y = tg x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/054662ce7a2196ad6a2d199f1e895585/
Функция y = sin x, график функции и способы задания функции. Тригонометрия 8-11 класс. https://rutube.ru/video/f067b3cda83df006306963e40f30b5ab/
Определение синуса, косинуса, тангенса и котангенса на единичной окружности. Шпаргалка по тригонометрии. Алгебра 10 класс. https://rutube.ru/video/4a839b2f5c0a7656b8b41b6e5e67ddc4/
Определение тангенса и котангенса на единичной окружности. Алгебра 10 класс. https://rutube.ru/video/f2494d81bfa2dcc2e9562060c1f5690f/
Графический способ задания функции. График функции. Определение.
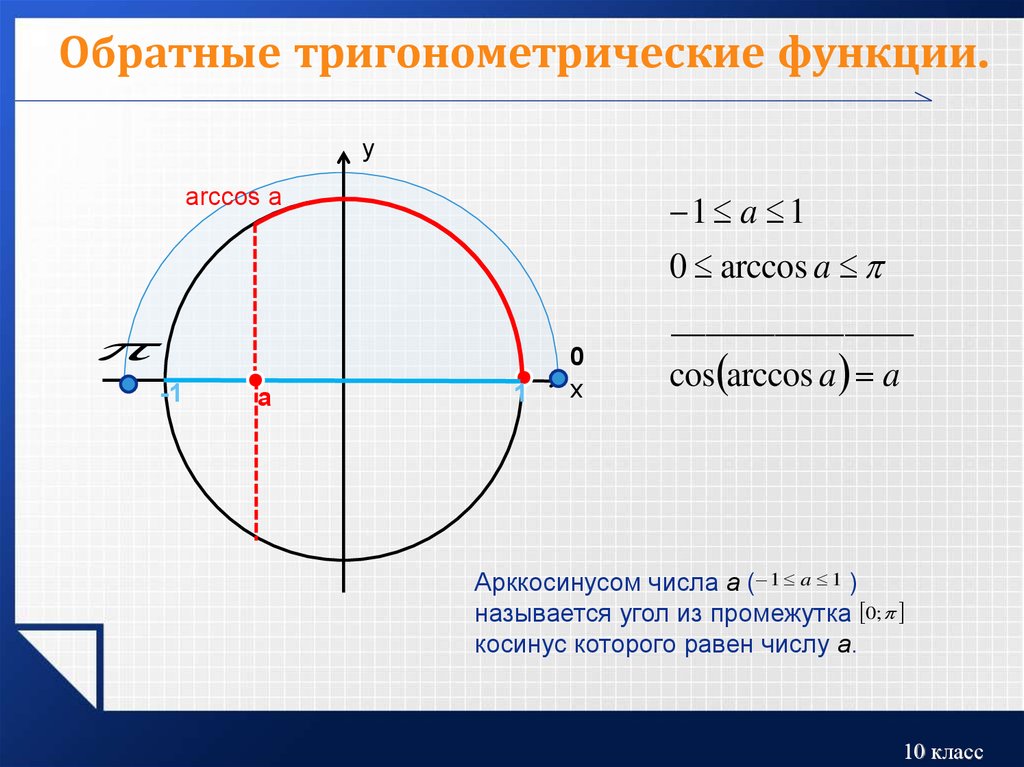
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса.
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами.
Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания.
А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да.
..) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать.
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой.
Учимся — с интересом!)
можно познакомиться с функциями и производными.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты.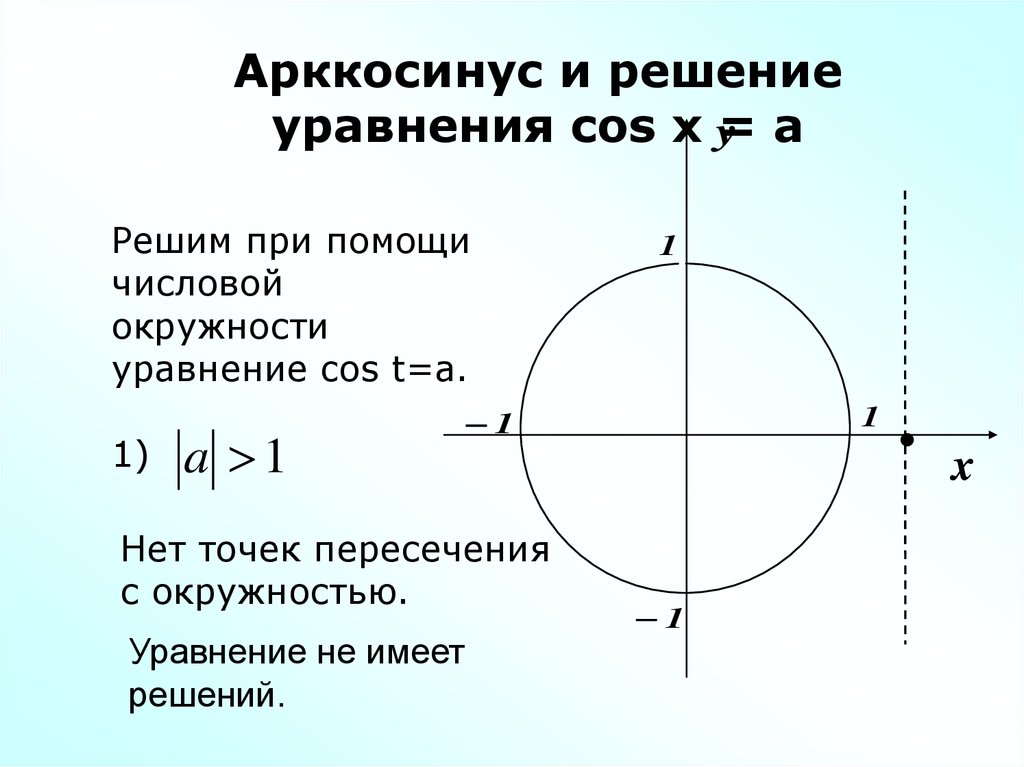
Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a
, arccos(−a)=π−arccos a
, arctg(−a)=−arctg a
и arcctg(−a)=π−arcctg a
.
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.
п.Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a равен π/10 , и нужно вычислить значение арктангенса этого числа a . Решить поставленную задачу можно так: по известному значению арккосинуса найти число a , после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.
— 96 с.: ил. ISBN 5-7107-2667-2
— 96 с.: ил. ISBN 5-7107-2667-2Урок и презентация на темы: «Арккосинус. Таблица арккосинусов. arccos(0), arccos(1), arccos(2)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Что такое арккосинус?
2. Обозначение арккосинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арккосинуса.
6. Примеры.
Что такое арккосинус?
Ребята, мы с вами уже изучили функцию Y=cos(X), построили ее график и решали некоторые уравнения, например cos(x)= 1/2. Для решения этого уравнения требовалось провести прямую x= 1/2 и посмотреть, в каких точках она пересекает числовую окружность.
Видно что прямая пересекает окружность в двух точках F и G.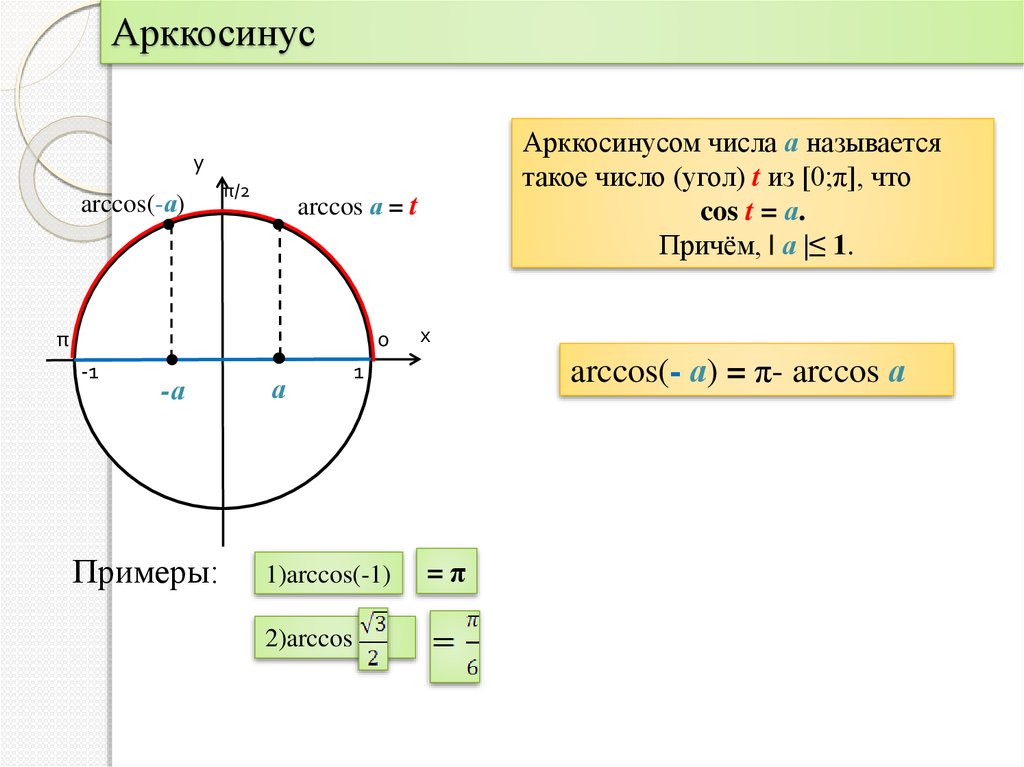
Эти точки и являются решением уравнения. Переобозначим F как x1, а G — как x2. Решение уравнения мы нашли довольно легко и определили, что x1 = π/3 + 2πk, а x2 = -π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение cos(x)=4/7. Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности?
Обозначение арккосинуса
Давайте внимательно посмотрим на уравнение cos(x)=4/7.
Как мы и говорили, решениями нашего уравнения будут две точки: F=x1+2πk и G=x2+2πk, но, что это за точки? Много лет назад столкнувшись с этой проблемой математики решили, что надо придумать некоторый способ описания решения на математическом языке. И был придуман новый символ – arccos(x). Будем читать как арккосинус.
Тогда решения нашего уравнения запишутся как: x1=arccos(4/7) и x2=-arccos(4/7). И решение в общем виде: x=arccos(4/7) + 2πk и x=-arccos(4/7) + 2πk. Арккосинус — это угол (длина дуги AF, AG), косинус которого равен 4/7.
Немного истории
Символ arccos появляется впервые в 18 веке в работах математика Шерфера и известного французского ученого Жозефа Луи Лагранжа, портрет которого вы видите на этой странице. Несколько ранее понятие арккосинус уже рассматривал Д. Бернули, но записывал его совсем другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия:
arccos x — это угол (можно сказать и дуга), косинус которого равен x.
Определение арккосинуса.
Если |а|≤ 1, то arccos(a) – это такое число из отрезка , косинус которого равен а.
Если |а|≤ 1, то уравнение cos(x)=a имеет решение: x=±arccos(a) + 2πk
Есть три случая, в которых предпочитают записывать решения более простым способом:
cos(x)=0, то x= π/2 + πk
cos(x)=1, то x= 2πk
cos(x)=-1, то x= π + 2πk
Также стоит записать важное равенство:
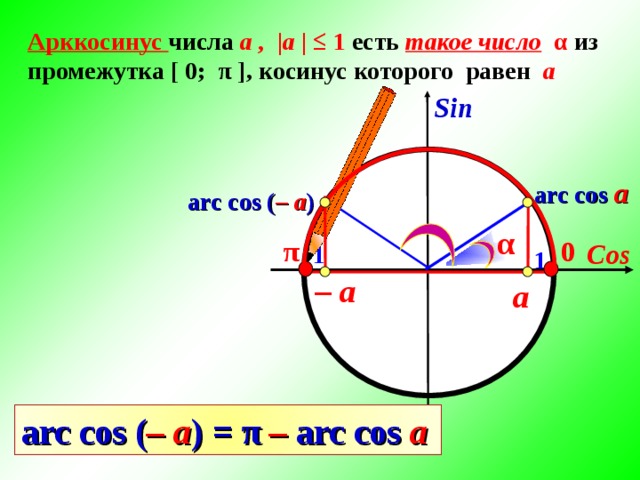
Для любого -1 ≤ а ≤ 1 выполняется равенство: arccos(a) + arccos(-a) = π ; при решение заданий удобнее использовать: arccos(-a) = π — arccos(a), где -1 ≤ а ≤ 1
Таблица значений арккосинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арккосинуса
Примеры
1.
Найти значение функции arccos(-√3/2).
Решение: Пусть arccos(-√3/2)=x, тогда cos(x)=-√3/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=5π/6, т.к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
Ответ: arccos(-√3/2)=5π/6
2. Найти значение функции arccos(√2/2).
Решение: Пусть arccos(√2/2) = x, тогда cos(x)= √2/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=π/4, т.к. cos(π/4)= √2/2 и 0 ≤ π/4 ≤ π.
Ответ: arccos(√2/2)=π/4
3. Найти значение функции arccos(1).
Решение: Пусть arccos(1) = x, тогда cos(x)= 1 и по определению 0≤ x ≤ π. Посмотрим значения косинуса в таблице: значит x=0, т.к. cos(0)= 1 и 0 ≤ 0 ≤ π.
Ответ: arccos(1)=0
4. Решить неравенство cos(x)> -0.3.
Решение: Косинус — это абсцисса точки числовой окружности. Значит необходимо найти такие точки, абсциссы которых больше -0.3. Нарисуем прямую x=-0.3. Она пересекает числовую окружность в двух точках: F и G. Неравенству x>-0.3 соответствуют точки дуги GF.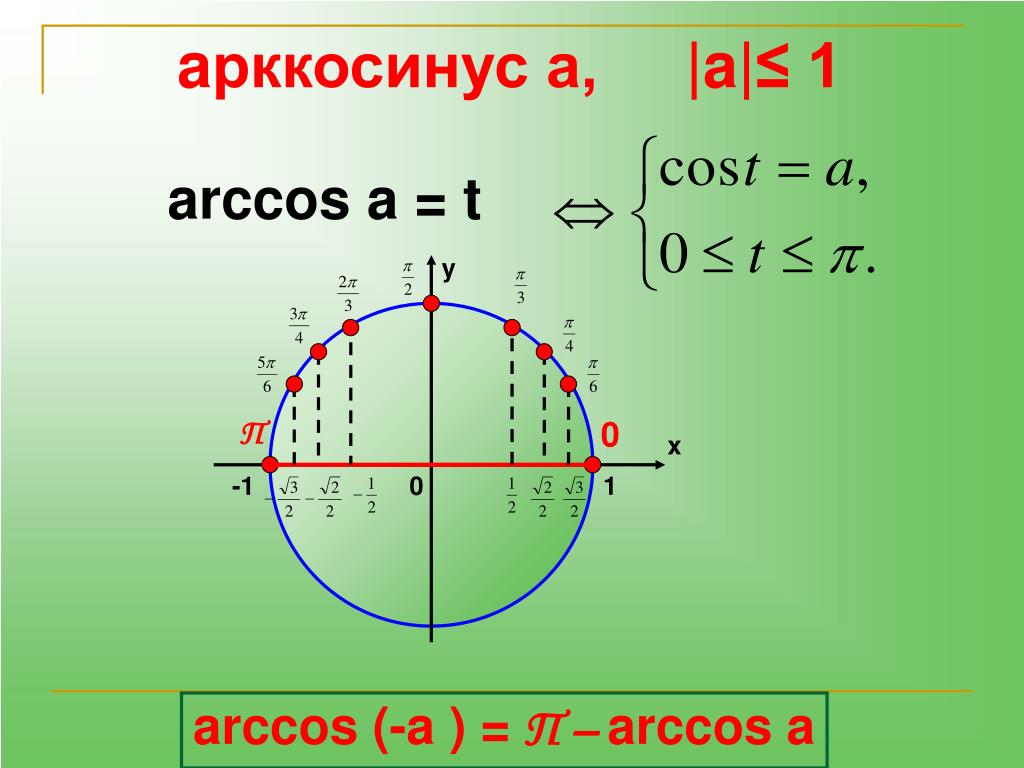
Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3)
Задачи для самостоятельного решения
1)Вычислить:
а) $arccos(\frac{\sqrt{3}}{2})$,
б) $arccos(-\frac{1}{2})$,
в) $arccos(0)$,
г) $arccos(-0,5)$.
2) Решить уравнения:
а) $cos(x)=-\frac{1}{2}$,
б) $cos(x)=1$,
в) $cos(x)=\frac{\sqrt{3}}{2}$,
г) $cos(x)=0,25$,
д) $cos(x)=-1,2$.
3) Решить неравенства:
а) $cos(x)>0,6$,
б) $cos(x)≤0,2$.
Тригонометрическая функция arccos() — арккосинус — определение математического слова
Тригонометрическая функция arccos() — арккосинус — определение математического слова — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Тематический указатель
Функция arccos обратна функции косинуса.
Возвращает угол, косинус которого равен заданному числу.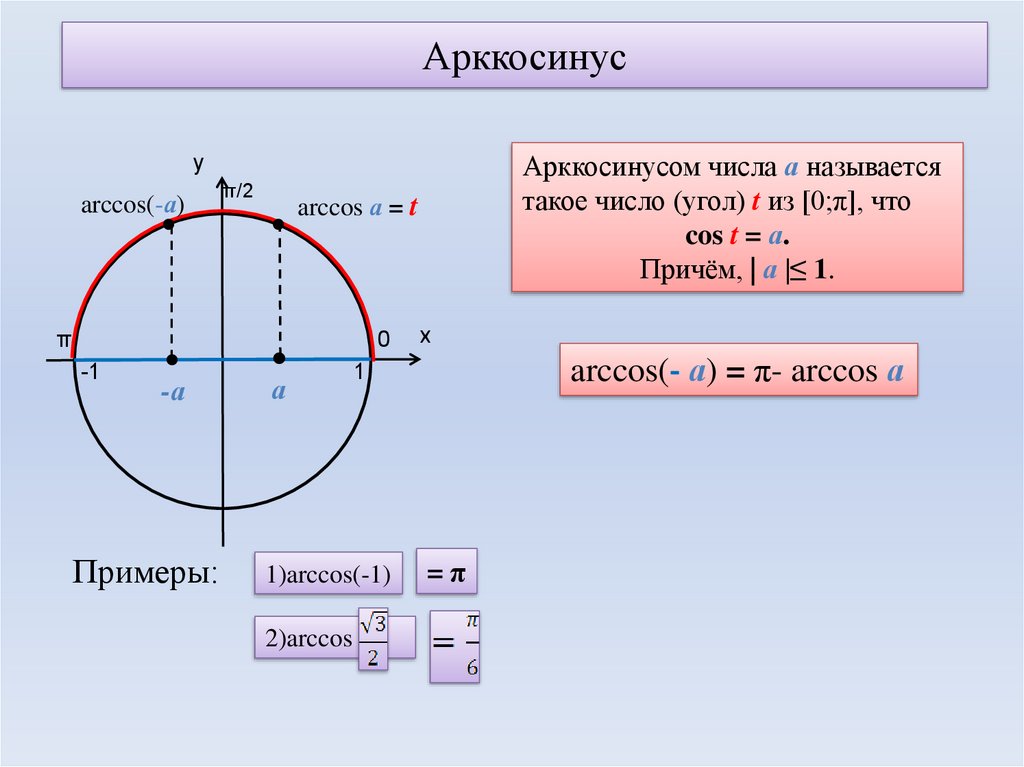
Попробуйте это Перетащите любой вершину треугольника и посмотрите, как вычисляется угол C с помощью функции arccos().
Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке. Эти обратные функции имеют то же имя, но с «дугой» впереди. (На некоторых калькуляторах кнопка arccos может быть помечена как acos, а иногда и cos -1 .) Таким образом, обратным значением cos является arccos и т. д. Когда мы видим «arccos x», мы понимаем это как «угол, косинус которого равен x».
| cos30 = 0,866 | Означает: косинус 30 градусов равен 0,866 |
| arccos 0,866 = 30 | Означает: угол, косинус которого равен 0,866, равен 30 градусам. |
См. также Обратные функции — тригонометрия
Пример — использование arccos для нахождения угла
На приведенном выше рисунке нажмите «Сброс».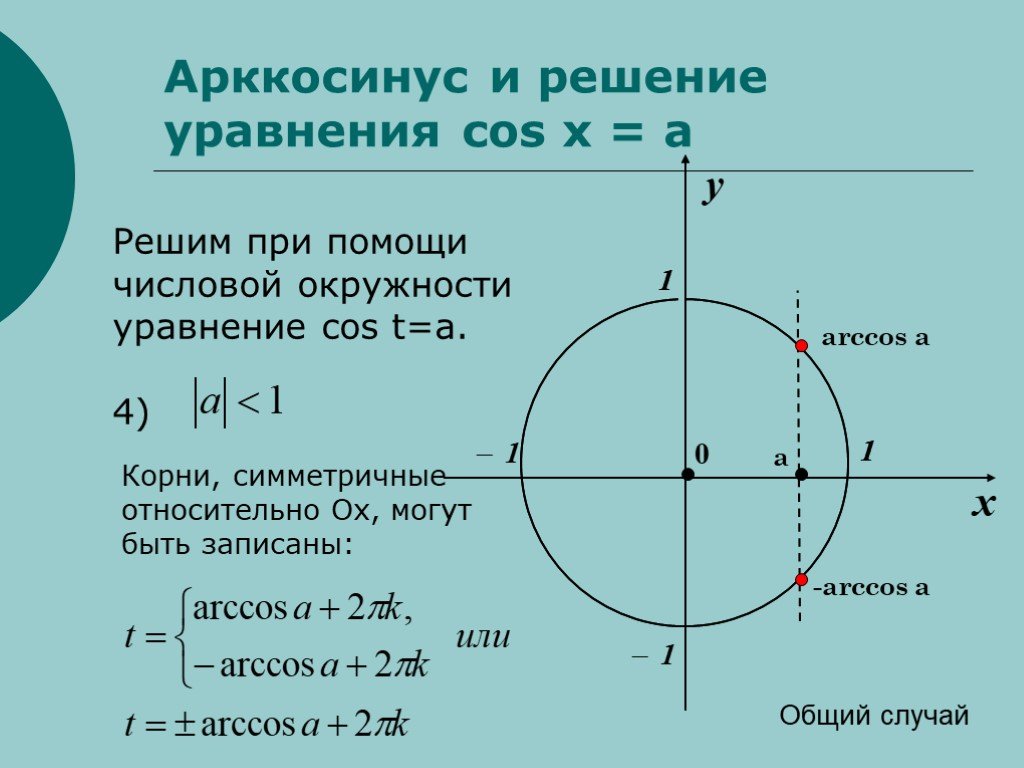
Мы знаем длины сторон, но нам нужно найти угол С.
Мы знаем, что
поэтому нам нужно знать угол, косинус которого равен 0,866, или формально:
Используя калькулятор, мы находим arccos 0,866 равным 30°.
Большие и отрицательные углы
Напомним, что мы можем подать заявку функции триггера на любой угол, включая большие и отрицательные углы. Но когда мы рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, имеющих одинаковый косинус. Например, 45° и 360+45° будут иметь одинаковый косинус. Подробнее об этом см. Обратные тригонометрические функции.
Чтобы решить эту проблему, диапазон обратных триггерных функций ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и домен arccos
Напомним, что область определения функции — это множество допустимых для нее входных данных. Диапазон — это набор возможных выходов.
Для y = arccos x :
| Диапазон | |
| Домен |
По соглашению диапазон arccos ограничен от 0 до +180°. Итак, если вы используете калькулятор, чтобы решить, скажем, arccos 0,55, из бесконечного числа возможностей он вернет 56,63 °, тот, что находится в диапазоне функции.
Что попробовать
- На рисунке выше нажмите «сбросить» и «скрыть подробности».
- Отрегулируйте треугольник до нового размера
- Используя функцию arccos, вычислите значение угла C из длин сторон
- Нажмите «показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
- Определение угла, свойства углов
- Стандартное положение на углу
- Начальная сторона угла
- Конечная сторона угла
- Четырехугольники
- Котерминальные уголки
- Базовый угол
Тригонометрические функции
- Знакомство с шестью триггерными функциями
- Функции больших и отрицательных углов
- Инверсные триггерные функции
- SOH CAH TOA Память
- Синусоидальная функция (sin) в прямоугольных треугольниках
- Функция обратного синуса (арксинус)
- График функции синуса
- Синусоидальные волны
- Функция косинуса (cos) в прямоугольных треугольниках
- Функция арккосинуса (arccos)
- График функции косинуса
- Касательная функция (тангенс) в прямоугольных треугольниках
- Функция арктангенса (арктангенс)
- График функции касательной
- Функция котангенса cot (в прямоугольных треугольниках)
- Функция секанса сек (в прямоугольных треугольниках)
- Функция косеканса csc (в прямоугольных треугольниках)
Решение задач по тригонометрии
- Общий подход
- Определение наклонного расстояния вдоль склона или пандуса
- Определение угла уклона или пандуса
Исчисление
- Производные тригонометрических функций
(C) 2011 Copyright Math Open Reference.
Все права защищены
numpy.arccos — NumPy v1.23 Руководство
- Numpy.arccos ( x , /, OUT = NONE , * , где = TRUE , CASTING = ‘SOME_KIND’ , Заказ = ‘K 9016, 9016, , 9016, 9016, 9016, 9016, 9016, 9016, , , , . subok=True [ подпись , extobj ]) =
Тригонометрический арккосинус, поэлементный.
Инверсия
cos, так что еслиy = cos(x), тоx = arccos(y).- Параметры
- x array_like
x -координата на единичной окружности. Для реальных аргументов доменом является [-1, 1].
- out ndarray, None или кортеж из ndarray и None, необязательный
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь форма, на которую транслируются входные данные.
Если не указано или Нет,
возвращается только что выделенный массив. Кортеж (возможен только как
аргумент ключевого слова) должен иметь длину, равную количеству выходов.- где array_like, необязательный
Это условие передается по входу. В местах, где условие равно True, массив из будет установлен в результат ufunc. В другом месте массив из сохранит исходное значение. Обратите внимание, что если неинициализированный массив из создается по умолчанию
out=None, места внутри него, где условие False, будут остаются неинициализированными.- **kwargs
Другие аргументы, содержащие только ключевые слова, см. документы ufunc.
- Возвращает
- угол ndarray
Угол луча, пересекающего единичную окружность при данной x -координата в радианах [0, пи]. Это скаляр, если x является скаляром.
См. также
-
cos,arctan,arcsin,emath.arccos
Примечания
arccos— многозначная функция: для каждого x существует бесконечно много чисел z таких, чтоcos(z) = x. Конвенция заключается в том, чтобы вернуться угол z , действительная часть которого лежит в [0, pi] .Для типов входных данных с действительным знаком
arccosвсегда возвращает действительные выходные данные. Для каждого значения, которое не может быть выражено как действительное число или бесконечность, это дает 9-1.Ссылки
М. Абрамовиц и И.А. Стегун, «Справочник по математическим функциям», 10-е издание, 1964, стр. 79. https://personal.math.ubc.ca/~cbm/aands/page_79.htm
Примеры
Мы ожидаем, что arccos 1 будет равен 0, а -1 будет равен pi:
>>> np.
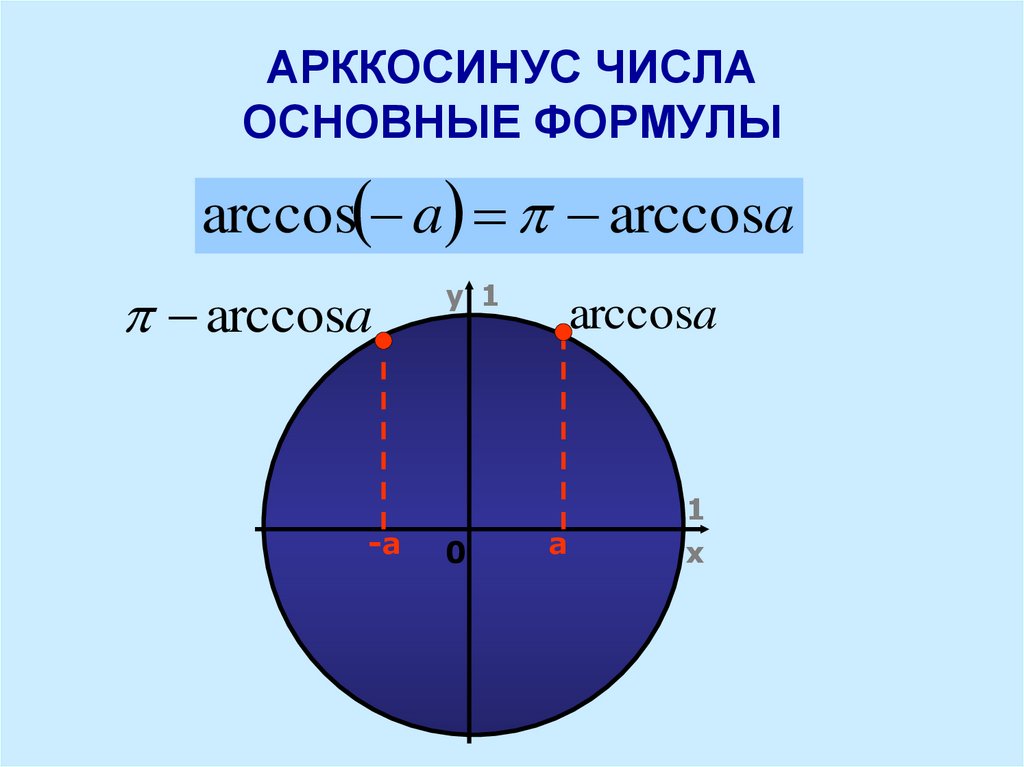Если не указано или Нет,
возвращается только что выделенный массив. Кортеж (возможен только как
аргумент ключевого слова) должен иметь длину, равную количеству выходов.
