Арксинус 2 3: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )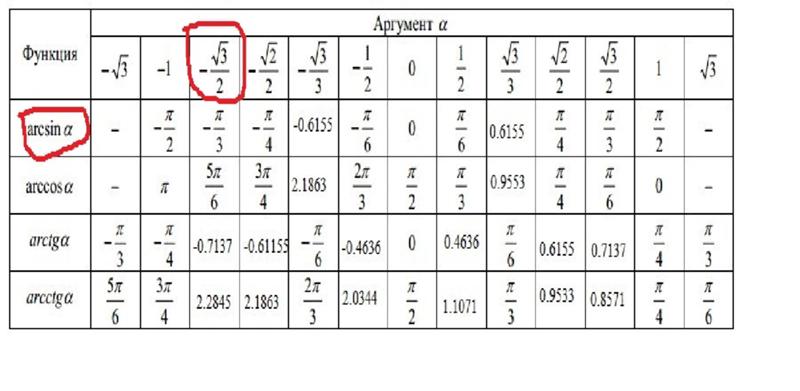
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )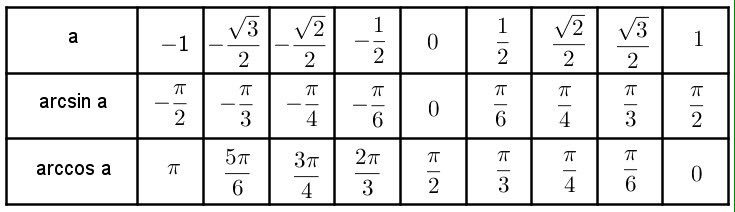
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )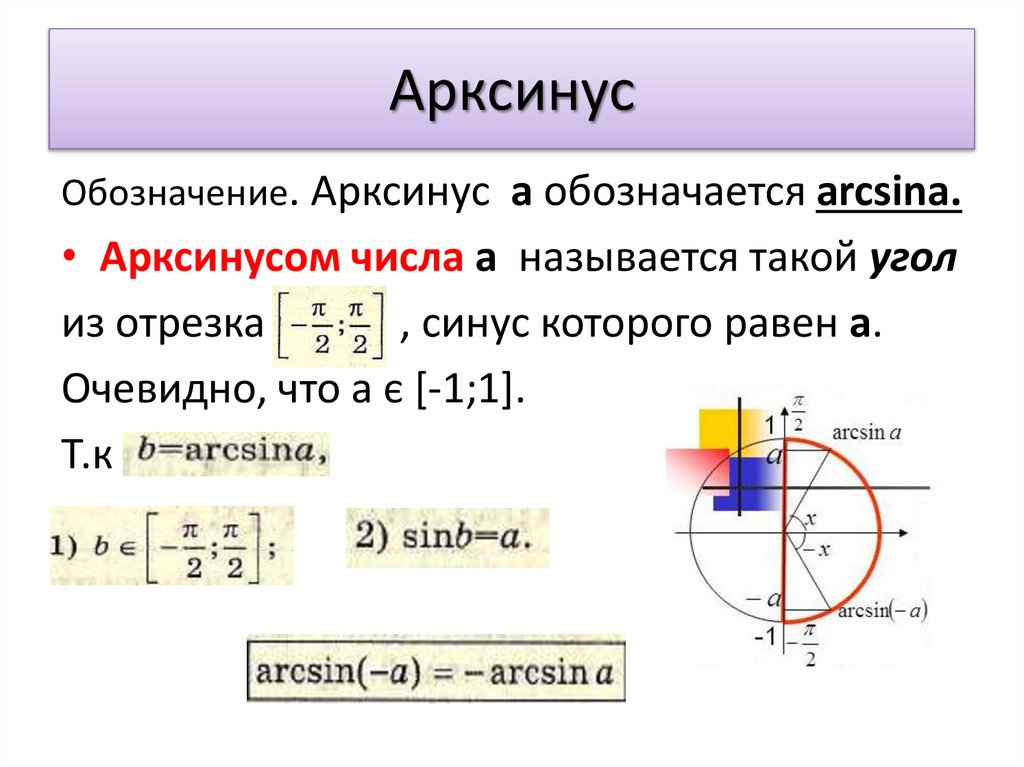
87
Найти точное значение		sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

Внеклассный урок — Простейшие тригонометрические уравнения cos t = a, sin t = a, tg x = a, ctg x = a

Простейшие тригонометрические уравнения 

Тригонометрическое уравнение – это уравнение, содержащее неизвестное под знаком тригонометрической функции.

Простейшими тригонометрическими уравнениями называют уравнения вида
sin x = a, cos x = a, tg x = a, ctg x = a, где a – действительное число (a ∈ R).

 

Уравнение cos x = a.

Принцип:

arccos a = x.

Следовательно, cos x = a.

Условия: модуль а не больше 1;  x не меньше 0, но не больше π

(| a | ≤ 1;  0 ≤ x  ≤ π)

 

Формулы:

                                        
                                           x = ± arccos a  +  2πk,     где k – любое целое число

                                           arccos (-a) = π – arccos a,    где 0 ≤ a ≤ 1

 

Пример 1: Решим уравнение

                √3
cos x  =  ——.
                 2

Решение.

Применим первую формулу:

                      √3
x = ± arccos —— + 2πk
                      2

Сначала находим значение арккосинуса:

             √3       π
arccos —— = —
              2        6

Осталось подставить этот число в нашу формулу:

            π
x = ± —— + 2πk
            6

Пример решен.

 

Пример 2: Решим уравнение

                  √3
cos x  =  – ——.
                   2

Решение.

Сначала применим первую формулу из таблицы:

                        √3
x = ± arccos (– —) + 2πk
                         2

Теперь с помощью второго уравнения вычислим значение арккосинуса:

                 √3                         √3                 π        π        π       6π       π         5π
arccos (– ——) = π – arcos ——  =  π  –  —  =  —  –  —  =  —  –  —  =  ——
                  2                           2                   6        1        6        6        6          6

Применяя формулу для —а, обращайте внимание на знак а: он меняется на противоположный.

Осталось подставить значение арккосинуса и решить пример:

           5π
x = ± —— + 2πk
            6

Пример решен.

 

Уравнение sin x = a.

Принцип:

arcsin a = x,

следовательно sin x = a.

Условия: модуль а не больше 1;  x в отрезке [-π/2; π/2]

(| a | ≤ 1;  –π/2 ≤ x  ≤ π/2)

 

Формулы.

(1 из 3)


x = arcsin a  +  2πk

x = π – arcsin a  +  2πk

 

Эти две формулы можно объединить в одну:
x = (–1)narcsin a + πn

 

(k – любое целое число;  n – любое целое число; | a | ≤ 1)

Значение четного n: n = 2k

Значение нечетного n: n = 2k + 1

Если n – четное число, то получается первая формула.

Если n – нечетное число, то получается вторая формула.

                                                                  √3
Пример 1: Решить уравнение sin x  =  ——
                                                                  2

Решение.

Применяем первые две формулы:

                        √3
1) x  =  arcsin —— + 2πk
                         2

                              √3
2) x  =  π – arcsin —— + 2πk
                               2

Находим значение арксинуса:

             √3        π
arcsin ——  =  —
             2          3

Осталось подставить это значение в наши формулы:

            π
1) x =  — + 2πk
           3

 

                 π                   2π
2) x =  π – —  + 2πk = —— + 2πk
                 3                    3

Пример решен.

 

Пример 2: Решим это же уравнение с помощью общей формулы.

Решение.

               π
x = (–1)n — + πn
               3

Пояснение: если n будет четное число, то решение примет вид № 1; если n будет нечетным числом – то вид №2.

Пример решен.

 

(2 из 3)
Для трех случаев есть и более простые решения:

Если sin x = 0,  то x = πk

Если sin x = 1,  то x = π/2 + 2πk

Если sin x = –1,  то x = –π/2 + 2πk

 

Пример 1: Вычислим arcsin 0.

Решение.

Пусть arcsin 0 = x.

Тогда sin x = 0, при этом x ∈ [–π/2; π/2].

Синус 0 тоже равен 0. Значит:

x = 0.

Итог:

arcsin 0 = 0.

Пример решен.

 

Пример 2: Вычислим arcsin 1.

Решение.

Пусть arcsin 1 = x.

Тогда sin x = 1.

Число 1 на оси ординат имеет имя π/2. Значит:

arcsin 1 = π/2.

Пример решен.

 

(3 из 3)


arcsin (–a) = –arcsin a

 

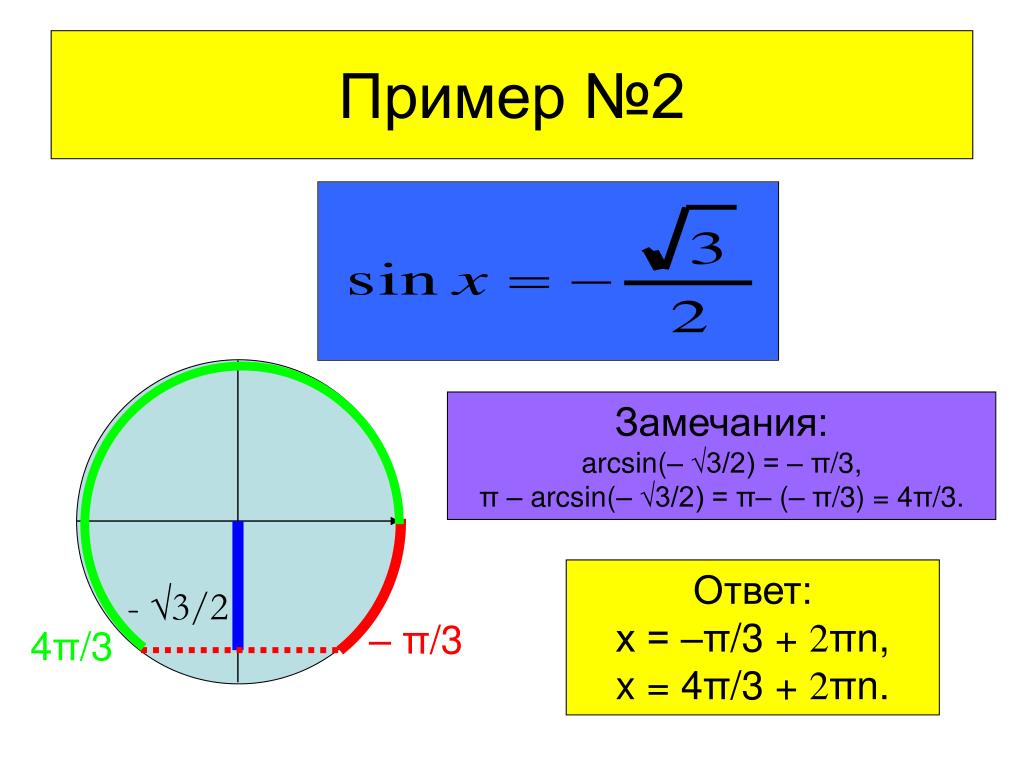
Пример: Решить уравнение

                √3
sin x = – ——
                2

Решение.

Применяем формулы:

                          √3
1) x = arcsin (– ——) + 2πk
                           2

                                √3
2) x = π – arcsin (– ——) + 2πk
                                 2

Находим значение арксинуса:

                 √3                        √3           π
arcsin (– ——) = – arcsin (——) = – —
                  2                          2             3

Подставляем это значение arcsin в обе формулы:

              π
1) x = – — + 2πk
              3
                     π                         π                    4π
2) x = π – (– —) + 2πk = π +  —  +  2πk = ——  +  2πk
                     3                         3                     3

Пример решен.

 

Уравнение tg x = a.

Принцип:

arctg a = x,

следовательно tg x = a.

Условие: x больше –π/2, но меньше π/2

(–π/2 < x < π/2)

 

Формулы.

(1)

 x = arctg a + πk

где k – любое целое число (k ∈ Z)

 

(2)


arctg (–a) = –arctg a


Пример 1: Вычислить arctg 1.

Решение.

Пусть arctg 1 = x.

Тогда tg x = 1,  при этом x ∈ (–π/2; π/2)

Следовательно:

       π                       π
x = —    при этом  — ∈ (–π/2; π/2)
       4                       4

                            π
Ответ: arctg 1 = —
                            4

 

Пример 2: Решить уравнение tg x = –√3.

Решение.

Применяем формулу:

x = arctg (–√3) + πk

Решаем:

arctg (–√3) = –arctg √3 = –π/3.

Подставляем:

x = –π/3 + πk.

Пример решен.

 

Уравнение ctg x = a.

Принцип:

arcctg a = x,

следовательно ctg x = a.

Условие: x больше 0, но меньше π

(0 < x < π)

 

Формулы.

(1)

x = arcctg a + πk

(k ∈ Z)

 

(2)


arcctg (–a) = π – arcctg а

                                                 
Пример 1: Вычислить arcctg √3.

Решение.

Следуем принципу:

arcctg √3 = х

ctg х = √3.

х = π/6.

Ответ: arcctg √3 = π/6

Пример 2: Вычислить arcctg (–1).

Решение.

Применяя формулу (2), обращайте внимание на знак а: он меняется на противоположный. В нашем примере –1 меняется на 1:

arcctg (–1) = π – arcctg 1 = π – π/4 = 3π/4.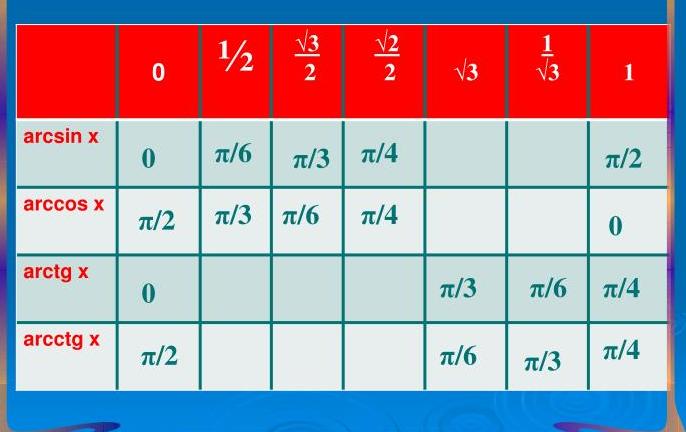

Пример решен.

 

Калькулятор — arcsin(-2/3) — Solumaths

Arcsin, расчет онлайн

Резюме:

Функция арксинуса позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.

арксинус онлайн

Описание:

Функция арксинус является обратной функцией синусоидальная функция, это позволяет вычисляет арксинус числа онлайн .

Число, к которому вы хотите применить функцию арксинуса, должно принадлежать диапазону [-1,1].

  1. Расчет арксинуса

    2. Чтобы вычислить арксинус числа, просто введите число и примените функция arcsin . Таким образом, для при вычислении арксинус числа следующего за 0.4, необходимо ввести арксинус(`0.

    4`) или сразу 0.4, если кнопка arcsin уже появляется, возвращается результат 0.411516846067. 92)`.

  2. Таблица замечательных значений
    3. 9005 5 9 0056 ` 0`
    arcsin(`-1`) `-pi/2`
    arcsin(`-sqrt(3)/2`) `-pi/3`
    угловой синус(`- sqrt(2)/2`) `-pi/4`
    arcsin(`-1/2`) `-pi/6`
    arcsin(`0`)
    arcsin(`1/2`) `pi/6`
    arcsin(`sqrt(2)/2`) `pi/4`
    arcsin(`sqrt(3)/2`) `pi/3`
    arcsin(`1`) `pi/ 2`
Синтаксис:

arcsin(x), где x — число.

Иногда используются другие обозначения: asin

Примеры:

arcsin(`0`) возвращает 0

Производная арксинуса :

Чтобы дифференцировать функцию арксинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арксинуса 92)`

Предел арксинуса :

Калькулятор предела позволяет вычислить пределы функции арксинуса.

предел арксинуса(x) is limit(`»arcsin»(x)`)

Обратная функция арксинуса :

обратная функция арксинуса представляет собой синусоидальную функцию, отмеченную как sin.

Графический арксинус :

Графический калькулятор может отображать функцию арксинуса в заданном интервале.

Свойство функции арксинуса:
Функция арксинуса является нечетной функцией.

Расчет онлайн с арксинусом (арксинусом)

См. также

Список связанных калькуляторов:

  • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
  • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
  • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
  • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
  • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
  • Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
  • Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
  • Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
  • Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
  • Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
  • Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
  • Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
  • Тангенс: тангенс. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Прочие ресурсы

  • Исправленные упражнения на числовые функции
  • Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
  • Научитесь считать с помощью обычных математических функций

 

тригонометрия — Как вычислить $\sin(2*\arcsin(3/5))$ вручную?

спросил

Изменено 6 лет, 3 месяца назад

Просмотрено 2к раз

$\begingroup$

Хотя достаточно просто зайти на Wolfram Alpha и убедиться, что ответ 24/25, я хотел бы узнать, как доказать это вручную, если это возможно.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *