Биномиальное распределение примеры | matematicus.ru
Skip to content
Artman Теория вероятностей
Биномиальный закон распределения случайной величины определяется при помощи формулы Бернулли:
Рассмотрим примеры применения формулы Бернулли для построения биномиальных законов распределения дискретной случайной величины X.
Пример 1
Написать биномиальный закон распределения дискретной случайной величины X –числа появлений «герба» при двух бросаниях монеты.
Решение
При бросании монеты вероятность выпадения «герба» равна 0.5, а «решки» q=1–p=1-0.5=0.5
Также случайная величина X — числа появлении «герба» принимает значения: 0, 1, 2
Найдём значения случайной величины X:
и в виде таблицы составим биномиальный закон распределения СВ X:
| X | 0 | 2 | |
| P | 0. 25 | 0.5 | 0.25 |
Пример 2
Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X — числа выпадений четного числа очков на двух игральных костях.
Решение
По условию задачи, кость бросается два раза — составим в виде таблицы всевозможные комбинации выпадения четного и нечетного числа очков
| Первая кость | Вторая кость |
| Четное число очков | Четное число очков |
| Четное число очков | Нечетное число очков |
| Нечетное число очков | Четное число очков |
| Нечетное число очков | Нечетное число очков |
В соответствии с таблицей, из четырёх комбинаций числа выпадений четного числа равна единице, следовательно, р=1/4=0.
25, а не выпадения — q=1–p=1-0.25=0.75
Дискретная случайная величина X принимает следующие значения: 0, 1, 2
По формуле Бернулли составим биномиальный закон распределения СВ X:
Сведём данные биномиального закона распределения X в таблицу:
| X | 0 | 1 | 2 |
| P | 0.5625 | 0.375 | 0.0625 |
Пример 3
В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X — числа нестандартных деталей среди четырех отобранных.
Из условия задачи p = 0.1, q=1–р=0.9
Возможные варианты значений СВ X: 0, 1, 2, 3, 4
По формуле Бернулли имеем:
Ряд распределения по биномиальному закону распределения случайной величины X имеет вид:
| X | 0 | 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||
| P | 0. {-5}$18172 Биномиальное распределение дискретной случайной величиныБиномиальное распределение — одно из важнейших распределений вероятностей дискретно изменяющейся случайной величины. Биномиальным распределением называется распределение вероятностей числа m наступления события А в n взаимно независимых наблюдениях. Часто событие А называют «успехом» наблюдения, а противоположное ему событие — «неуспехом», но это обозначение весьма условное. Условия биномиального распределения:
Вероятность того, что в n испытаниях событие А наступит именно m раз, можно вычислить по формуле Бернулли (на сайте рассказано более подробно о случаях использования формулы Бернулли): или , где p — вероятность наступления события А; q = 1 — Разберёмся, почему биномиальное распределение описанным выше образом связано с формулой Бернулли. Событие — число успехов при n испытаниях распадается на ряд вариантов, в каждом из которых успех достигается в m испытаниях, а неуспех — в n — m испытаниях. Рассмотрим один из таких вариантов — B1. По правилу сложения вероятностей умножаем вероятности противоположных событий: , а если обозначим q = 1 — p, то . Такую же вероятность будет иметь любой другой вариант, в котором m успехов и n — m неуспехов. Число таких вариантов равно — числу способов, которыми можно из n испытаний получить m успехов. Сумма вероятностей всех m чисел наступления события А (чисел от 0 до n) равна единице: где каждое слагаемое представляет собой слагаемое бинома Ньютона. На практике часто необходимо вычислять вероятности «не более m успехов в n испытаниях» или «не менее m успехов в n испытаниях». Для этого используются следующие формулы. Интегральную функцию, то есть вероятность F(m) того, что в n наблюдениях событие А наступит не более m раз, можно вычислить по формуле: . В свою очередь вероятность Иногда бывает удобнее вычислять вероятность того, что в n наблюдениях событие А наступит не более m раз, через вероятность противоположного события: . Какой из формул пользоваться, зависит от того, в какой из них сумма содержит меньше слагаемых. Характеристики биномиального распределения вычисляются по следующим формулам. Математическое ожидание: . Дисперсия: . Среднеквадратичное отклонение: . Биномиальное распределение и расчёты в MS ExcelВероятность биномиального распределения Pn(m) и значения интегральной функции F(m) можно вычислить при помощи функции MS Excel БИНОМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши). MS Excel требует ввести следующие данные:
Пример 1. Менеджер фирмы обобщил информацию о числе проданных в течение последних 100 дней фотокамер. В таблице обобщена информация и рассчитаны вероятности того, что в день будет продано определённое число фотокамер.
День завершён с прибылью, если продано 13 или более фотокамер. Вероятность того, что день будет отработан без прибыли: Пусть вероятность того, что день отработан с прибылью, является постоянной и равна 0,61, и число проданных в день фотокамер не зависит от дня. Тогда можно использовать биномиальное распределение, где событие А — день будет отработан с прибылью, — без прибыли. Вероятность того, что из 6 дней все будут отработаны с прибылью: . Тот же результат получим, используя функцию MS Excel БИНОМ.РАСП (значение интегральной величины — 0): P6(6) = БИНОМ.РАСП(6; 6; 0,61; 0) = 0,052. Вероятность того, что из 6 дней 4 и больше дней будут отработаны с прибылью: , где , , , . P6(≤3) = БИНОМ.РАСП(3; 6; 0,61; 1) = 0,435. Вероятность того, что из 6 дней все будут отработаны с убытками: , Тот же показатель вычислим, используя функцию MS Excel БИНОМ.РАСП: P6(0) = БИНОМ.РАСП(0; 6; 0,61; 0) = 0,0035. Решить задачу самостоятельно, а затем посмотреть решениеПример 2. В урне 2 белых шара и 3 чёрных. Из урны вынимают шар,
устанавливают цвет и кладут обратно. Попытку повторяют 5 раз. Число появления белых шаров — дискретная
случайная величина X, распределённая по биномиальному закону.
Составить закон распределения случайной величины. Определить моду, математическое ожидание и дисперсию. Правильное решение и ответ. Статистика — не Ваша специализация? Закажите статистическую обработку данных Продолжаем решать задачи вместеПример 3. Из курьерской службы отправились на объекты n = 5 курьеров. Каждый курьер с вероятностью p = 0,3 независимо от других опаздывает на объект. Дискретная случайная величина X — число опоздавших курьеров. Построить ряд распределения это случайной величины. Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение. Найти вероятность того, что на объекты опоздают не менее двух курьеров. Решение. Случайная величина X — число опоздавших курьеров — распределена по биномиальному закону. Под наблюдением понимается отправка курьера на объект, а под «успехом» удобнее понимать его опоздание. Найдём вероятности возможных значений случайной величины и округлим их до трёх знаков после запятой: Ряд распределения будет иметь вид:
Математическое ожидание случайной величины: . Дисперсия случайной величины: . Среднеквадратичное отклонение: . Найдём вероятность того, что на объекты опоздают не менее двух курьеров: Пример 4. Игральная кость бросается четыре раза. Найти вероятность того, что шестёрка появится а) ровно один раз; б) хотя бы один раз. Решение. Случайная величина X — число появлений шестёрки — имеет биномиальное распределение с параметрами n = 4; p = 1/6. а) . б)
Пройти тест по теме Теория вероятностей и математическая статистика К началу страницы Начало темы «Теория вероятностей» Действия над вероятностями Различные задачи на сложение и умножение вероятностей Формула полной вероятности Формула Байеса Независимые испытания и формула Бернулли Распределение вероятностей дискретной случайной величины Распределение вероятностей непрерывной случайной величины Математическое ожидание и дисперсия случайной величины Распределение Пуассона дискретной случайной величины Равномерное распределение непрерывной случайной величины Нормальное распределение непрерывной случайной величины Биномиальное распределение с примерами Биномиальное распределение — это распределение вероятностей, применимое к биномиальным экспериментам. Содержание Что такое биномиальное распределение? Биномиальное распределение — это дискретное распределение вероятностей, которое представляет вероятности биномиальных случайных величин в биномиальном эксперименте. Биномиальное распределение определяется как распределение вероятностей, связанное с биномиальным экспериментом, где биномиальная случайная величина указывает, сколько успехов или неудач произошло в этом пространстве выборки. Что такое случайная величина?Случайная величина представляет собой переменную, которая может принимать случайные значения в эксперименте. Скажем, случайная величина, представляющая количество бракованных изделий, найденных в 100 предметах, выбранных случайным образом. Здесь 100 элементов представляют 100 испытаний. Может быть несколько экспериментов, включающих случайную выборку 100 предметов и подсчет количества дефектных предметов.
В приведенном выше эксперименте количество дефектных элементов можно назвать СЛУЧАЙНОЙ переменной. Случайная величина также представлена буквой X. X принимает значения 5 и 9 в вышеупомянутых экспериментах. Когда значение случайной величины может принимать только конечные значения, случайную величину также можно назвать случайной дискретной величиной. Все возможные значения (или результаты), которые может принимать случайная величина, также называются выборочным пространством . Что такое биномиальная случайная величина?В биномиальном эксперименте результат каждого испытания в эксперименте может принимать одно из двух значений: успех или неудача. Каждое испытание в биномиальном эксперименте также можно назвать испытанием Бернулли . Для одного испытания биномиальное распределение можно также назвать Распределение Бернулли. Вы можете проверить мой пост о распределении Бернулли, объясненном на примерах Python. Другими словами, результат каждого испытания классифицируется в соответствии с двумя уровнями категориальной переменной. Вот несколько примеров испытаний Бернулли:
Результат интереса к испытанию эксперимента часто называют успехом . Биномиальная случайная величина может быть числом успехов в эксперименте, состоящем из N испытаний . Таким образом, ниже приведены некоторые примеры биномиальной случайной величины:
Что такое биномиальный эксперимент? Биномиальный эксперимент представляет собой биномиальную случайную величину X, которая подсчитывает число «n» успехов в N испытаниях, когда каждое испытание имеет только два результата: успех и неудачу. Требования для случайного эксперимента , чтобы он был биномиальным экспериментом , следующие:
Что такое биномиальное распределение? Биномиальное распределение — это тип дискретного распределения вероятностей, представляющий вероятности различных значений биномиальной случайной величины (X) в повторных независимых N испытаниях в эксперименте. Среднее значение и дисперсия биномиального распределения эксперимента с n числом испытаний и вероятностью успеха в каждом испытании p следует: Среднее значение = np Дисперсия = н.п.( 1-р) В биномиальном опыте, состоящем из N испытаний, все испытания независимы и выборка берется с заменой. Если выборка взята без замены, это называется гипергеометрическим распределением . Биномиальное распределение Пример PythonВот код Python для биномиального распределения. Обратите внимание на некоторые из следующих:
из scipy.stats импортировать бином
импортировать matplotlib.pyplot как plt
импортировать numpy как np
#
# X = дискретная случайная величина, представляющая количество успехов
# p = Вероятность успеха
#
X = np.arange (0,21)
р = 0,6
п = 20
#
# Рассчитать биномиальное распределение вероятностей
#
binom_pd = binom.pmf(X, n, p)
#
# Построить распределение вероятностей
#
рис, топор = plt.subplots(1, 1, figsize=(8, 6))
ax.plot(X, binom_pd, 'bo', ms=8, label='geom pmf')
plt.ylabel("Вероятность", fontsize="18")
plt.xlabel("X - количество успехов", fontsize="18")
plt.title("Биномиальное распределение — количество успехов по сравнению с вероятностью", fontsize="18")
ax.vlines(X, 0, binom_pd, colors='b', lw=5, alpha=0.Вот как будет выглядеть график биномиального распределения. Этот график является результатом выполнения приведенного выше кода. Рис. 1. График биномиального распределенияРеальные примеры биномиального распределенияВот несколько реальных примеров биномиального распределения:
Ссылки
ВыводыВот краткое изложение того, что вы узнали в этом посте в отношении Биномиальное распределение :
Аджитеш Кумар Недавно я работал в области анализа данных, включая науку о данных и машинное обучение / глубокое обучение. Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Ознакомьтесь с моей последней книгой, озаглавленной «Основы мышления: создание успешных продуктов с использованием первых принципов». Недавно я работал в области аналитики данных, включая науку о данных и машинное обучение/глубокое обучение. Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin. Ознакомьтесь с моей последней книгой под названием «Мышление на основе первых принципов: создание успешных продуктов с использованием мышления на основе первых принципов».0007 Опубликовано в ИИ, наука о данных, машинное обучение, статистика. Метки: Наука о данных, машинное обучение, статистика. Определение, формула, анализ и примерЧто такое биномиальное распределение?Биномиальное распределение — это статистическое распределение, которое обобщает вероятность того, что значение примет одно из двух независимых значений при заданном наборе параметров или предположений. Базовые предположения биномиального распределения заключаются в том, что в каждом испытании есть только один исход, каждое испытание имеет одинаковую вероятность успеха, и каждое испытание является взаимоисключающим или независимым друг от друга. Ключевые выводы
Понимание биномиального распределенияНачнем с того, что «биномиальное» в биномиальном распределении означает два термина — количество успехов и количество попыток. Каждый бесполезен без другого. Биномиальное распределение — это обычное дискретное распределение, используемое в статистике, в отличие от непрерывного распределения, такого как нормальное распределение. Это связано с тем, что биномиальное распределение учитывает только два состояния, обычно представляемые как 1 (успех) или 0 (неудача), учитывая количество испытаний в данных. Таким образом, биномиальное распределение представляет собой вероятность x успехов в n испытаниях при заданной вероятности успеха p для каждого испытания. Биномиальное распределение суммирует количество испытаний или наблюдений, когда каждое испытание имеет одинаковую вероятность достижения одного конкретного значения. Биномиальное распределение часто используется в статистике социальных наук в качестве строительного блока для моделей дихотомических переменных результатов, например, победит ли республиканец или демократ на предстоящих выборах, умрет ли человек в течение определенного периода времени и т. д. Он также имеет приложения в финансах, банковском деле и страховании, среди других отраслей. Анализ биномиального распределения Ожидаемое значение или среднее значение биномиального распределения рассчитывается путем умножения количества испытаний (n) на вероятность успеха (p) или n × p. Например, ожидаемое значение числа выпадений орла в 100 попытках выпадения орла или решки равно 50, или (100 × 0,5). Другим распространенным примером биномиального распределения является оценка шансов на успех игрока со штрафного броска в баскетболе, где 1 = попадание в корзину, а 0 = промах. Биномиальная функция распределения рассчитывается как: P ( x : n , p ) = n C x p x ( 1 — p ) n — x Где:
Среднее значение биномиального распределения равно np, а дисперсия биномиального распределения равна np (1 − p). Когда p = 0,5, распределение симметрично относительно среднего — например, при подбрасывании монеты, потому что шансы выпадения орла или решки составляют 50%, или 0,5. Биномиальное распределение представляет собой сумму серии нескольких независимых и одинаково распределенных испытаний Бернулли. В испытании Бернулли говорят, что эксперимент является случайным и может иметь только два возможных исхода: успех или неудачу. Например, подбрасывание монеты считается испытанием Бернулли; каждое испытание может принимать только одно из двух значений (орел или решка), каждый успех имеет одинаковую вероятность, и результаты одного испытания не влияют на результаты другого. Распределение Бернулли — это частный случай биномиального распределения, при котором число испытаний n = 1. Пример биномиального распределения Биномиальное распределение рассчитывается путем умножения вероятности успеха, возведенной в степень числа успехов, и вероятности неудачи, возведенной в степень разности между количеством успехов и числом испытаний. Затем умножьте произведение на комбинацию количества попыток и успехов. Например, предположим, что казино создало новую игру, в которой участники могут делать ставки на количество орлов или решек при определенном количестве подбрасываний монеты. Предположим, участник хочет сделать ставку в 10 долларов на то, что при 20 бросках монеты выпадет ровно шесть решек. Участник хочет вычислить вероятность этого события, и поэтому он использует расчет для биномиального распределения. Вероятность рассчитывалась как (20!/(6!×(20-6)!))×(0,50)(6)×(1-0,50)(20-6). Следовательно, вероятность того, что при 20 подбрасываниях монеты выпадет ровно шесть решек, равна 0,0369, или 3,7%. Математическое ожидание в этом случае равнялось 10 орлам, поэтому участник сделал неудачную ставку. На приведенном ниже графике показано, что среднее значение равно 10 (ожидаемое значение), а шансы на выпадение шести орлов выделены слева красным цветом. Вы можете видеть, что вероятность выпадения шести орлов меньше, чем семи, восьми, девяти, 10, 11, 12 или 13 орлов. Биномиальный калькулятор StatCrunch Так как же это можно использовать в финансах? Один пример: допустим, вы банк, кредитор, который хочет знать с точностью до трех знаков после запятой вероятность дефолта конкретного заемщика. Каковы шансы, что такое количество заемщиков не выполнит своих обязательств, что они сделают банк неплатежеспособным? Как только вы воспользуетесь функцией биномиального распределения для расчета этого числа, у вас будет лучшее представление о том, как оценивать страховку и, в конечном счете, сколько денег нужно ссудить и оставить в резерве. Что такое биномиальное распределение?Биномиальное распределение — это статистическое распределение вероятностей, которое устанавливает вероятность того, что значение примет одно из двух независимых значений при заданном наборе параметров или предположений. Как используется биномиальное распределение? Этот шаблон распределения используется в статистике, но имеет значение в финансах и других областях. Почему важно биномиальное распределение?Биномиальное распределение используется для расчета вероятности положительного или отрицательного исхода в опросе или многократном повторении эксперимента. Есть только два возможных результата для этого типа распределения. В более широком смысле, распределение является важной частью анализа наборов данных для оценки всех потенциальных результатов данных и того, как часто они происходят. Прогнозирование и понимание успеха или неудачи результатов имеет важное значение для развития бизнеса. Итог Биномиальное распределение является важным статистическим распределением, описывающим бинарные результаты (например, подбрасывание монеты, ответ «да/нет» или условие «включено/выключено»). Понимание его характеристик и функций важно для анализа данных в различных контекстах, которые включают результат, принимающий одно из двух независимых значений. |
Поэтому рассматриваемое
распределение и называется биномиальным распределением.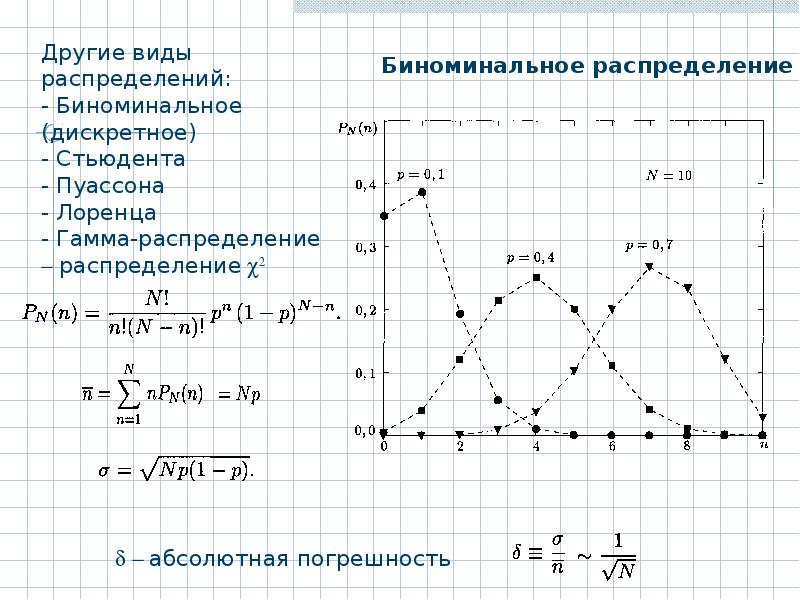
Вероятность, что день будет отработан с прибылью:
Это количество успешных попыток за определенное количество попыток. Биномиальное распределение можно представить как распределение вероятностей количества выпавших орлов при подбрасывании монеты в конкретном эксперименте, состоящем из фиксированного количества подбрасываний монеты. В этом сообщении блога мы изучим биномиальное распределение с помощью примеров 9.0004 . Если вы начинающий специалист по обработке и анализу данных, стремящийся лучше изучить биномиальное распределение или лучше понять его, этот пост может быть очень полезен.
Специалистам по данным и специалистам в других областях важно понимать эту концепцию, поскольку биномы часто используются в бизнес-приложениях.
Когда значение случайной величины может принимать бесконечные значения, случайную величину также можно назвать случайная непрерывная переменная .
Таким образом, эксперимент может состоять из 1 попытки, 5 попыток, 10 попыток, 20 попыток и т. д. На примере реального мира эксперимент может состоять в подбрасывании монеты 10 раз (10 попыток), взятии 10 предметов для проверки того, являются ли предметы дефектный и т. д. Если эксперимент состоит только из одного испытания, которое дает только два результата, таких как успех или неудача, испытание называется 9.0003 Суд над Бернулли. 
Таким образом, в эксперименте, включающем подбрасывание монеты 10 раз (N), биномиальная случайная величина (количество орлов, представленных как успехи) может принимать значение от 0 до 10, а биномиальное распределение вероятностей представляет собой распределение вероятностей, представляющее вероятности случайного переменная, принимающая значение 0-10. 9{(n-к)}\)
stats используется для определения распределения вероятностей с использованием функции pmf 
5)
Вероятность выпадения орла равна 1/2. Биномиальное распределение можно представить как B(50,0,5). На приведенной ниже диаграмме представлено биномиальное распределение для 100 экспериментов.
Вероятность найти человека, страдающего каким-либо заболеванием, говорит, с. Биномиальное распределение можно представить как B(100,p)
е. биномиальную модель) для описания этой конкретной переменной. Допустим, вероятность/доля пьющих с высоким риском составляет 0,35 или 35%. Биномиальное распределение можно представить как B(1000,0,35)
Биномиальное распределение можно представить как B(50,0,78)
Здесь случайная величина X – это количество «успехов», то есть количество серьезных последствий. Скажем, вероятность/доля серьезного эффекта составляет 1/5, или 0,2, или 20%. Биномиальное распределение может быть представлено как B(100,0.20)
Я хотел бы связаться с вами на Linkedin.
Биномиальное распределение определяет вероятность наблюдения определенного количества успешных результатов в определенном количестве испытаний.
При p > 0,5 кривая распределения скошена влево. При p < 0,5 кривая распределения скошена вправо.
Банки могут использовать его для оценки вероятности дефолта конкретного заемщика, суммы кредита и размера резерва. Он также используется в страховой отрасли для определения цен на полисы и оценки рисков.