Чему равен куб периметра квадрата площади 4: Чему равен куб периметра квадрата площади 4? — Знания.site

Содержание

Призма — Умскул Учебник

На этой странице вы узнаете

Чем упаковка стикеров похожа на призму?
Как можно попасть в призму в реальной жизни?
Как сложить игральные кости из листа бумаги?
Как найти объем воды в аквариуме?

Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.

Определение призмы
Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей.
Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу.
На самом деле, упаковка со стикерами является не чем иным, как призмой!
Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами.
Чем упаковка стикеров похожа на призму?
Упаковка стикеров является объемной фигурой, в основаниях которой лежат равные прямоугольники. А боковые стороны упаковки являются параллелограммом. Таким образом, упаковка стикеров полностью соответствует определению призмы.
Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы.
Строение призмы
Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы.
Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы.
Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому.
Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами».
Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы.
Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы.
В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы.
Рассмотрим элементы призмы.
Ребро — это линия пересечения двух плоскостей.
Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.
Ребра бывают двух видов:
ребра оснований,
боковые ребра.
Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям.
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны.
Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы.
Виды призм
Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.
Мы рассмотрим две классификации.
В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее.
В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:
треугольная призма,
четырехугольная призма,
шестиугольная призма.
Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма.
В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они.
С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:
прямые,
наклонные.
Разберемся в них чуть подробнее.
Прямая призма — призма, боковые ребра которой перпендикулярны основаниям.
В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник.
Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям.
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде.
Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами.
Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты?
Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм.
Свойство 1. Высота прямой призмы совпадает с её боковым ребром.
Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно?
Свойство 2. Все боковые грани прямой призмы — прямоугольники.
Как можно попасть в призму в реальной жизни?
Многие комнаты и помещения, особенно в типовой застройке, обладают формой призмы. Сидя в комнате, в классе, в столовой, даже в автобусе — мы как бы находимся внутри большой призмы.
Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.
Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
Например, в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник.
Определение параллелепипеда
Еще одной разновидностью прямоугольной призмы является параллелепипед.
Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами.
Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда.
Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга.
Нельзя не упомянуть про одно очень важное свойство параллелепипеда:
Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда.
Какие бывают параллелепипеды?
Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм.
Прямой параллелепипед
Рассмотрим несколько интересных свойств прямого параллелепипеда.
1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям.
2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра.
3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками.
Прямые параллелепипеды можно разделить еще на два вида:
Прямой параллелепипед: в основании лежит параллелограмм;
Прямоугольный параллелепипед: в основании лежит прямоугольник.
Рассмотрим свойства прямоугольного параллелепипеда.
1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками.
2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°. 2\)
225 = 35 + 46 + x²
x² = 144
x = 12
Ответ: 12.
У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:
Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник.
Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат.
При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники.
Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания.
В кубе все ребра равны, а все его грани будут квадратом.
Таким образом, мы рассмотрели все виды параллелепипеда.
Формулы для призмы
Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни.
Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить.
Как сложить игральные кости из листа бумаги?
Задумали вы вечером сыграть с семьей или друзьями в настольную игру. Но вот незадача: игральные кости опять куда-то запропастились. Не беда.Достаточно вычертить на листе бумаги несколько квадратов, вырезать получившуюся фигуру, согнуть по ребрам и склеить между собой с помощью клея. В итоге получатся кубики для игры.
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?
Нужно найти площади желтых квадратиков и сложить их.
Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней.
Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать.
Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой
S_бок. = P * h
В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани.
Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10.
Решение.
Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph.
Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12.
Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120. 2} = \sqrt{144 + 25} = \sqrt{169} = 13\).
Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30.
Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390.
Ответ: 390.
Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований.
Площадь полной поверхности призмы — сумма площадей всех граней.
Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу.
S = S_бок + 2S_осн
Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. 2} = \sqrt{36 + 64} = \sqrt{100} = 10\).
Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000.
Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.
Ответ: 1192
Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы.
Решение.
Шаг 1. Воспользуемся формулой S = S_бок + 2S_осн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25.
Шаг 2. Подставим известные величины в формулу:
1980 = S_бок + 2 * 25
S_бок = 1930
Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:
20h = 1930
h = 96,5
Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.
Ответ: 96,5.
Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?
Для этого достаточно воспользоваться формулой объема призмы.
V = S_осн. * h
Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты.
Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh.
Как найти объем воды в аквариуме?
Для этого достаточно перемножить ширину, длину аквариума и высоту воды. Тем самым мы найдем объем призмы, форму которой принимает вода в аквариуме.
Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы.
Решение.
Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой \(\frac{1}{2}ab\). Площадь равна \(\frac{1}{2} * 12 * 15 = 90\).
Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины:
V = 90 * 4 = 360.
Ответ: 360.
Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см³ воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика.
Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды.
Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема:
\(S = \frac{V}{h}\)
Тогда:
\(S = \frac{3000}{10} = 300\)
Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200.
Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.
Ответ: 1200.
Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию.
Фактчек
Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы.
Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы.
В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами.
Проверь себя
Задание 1.
Что такое диагональ призмы?
Отрезок, соединяющий две соседние вершины в призме.
Отрезок, соединяющий противоположные углы в боковой грани призмы.
Отрезок, соединяющий противоположные углы в основании призмы.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Задание 2.
Что такое прямая призма?
Призма, боковые ребра которой перпендикулярны основаниям.
Призма, боковые ребра которой расположены под острым углом относительно основания.
Призма, боковые ребра которой расположены под тупым углом относительно основания.
Призма, в основании которой лежит прямоугольник.
Задание 3.
Как найти высоту прямой призмы?
Высоту нужно найти с помощью оснований.
Высота совпадает с боковым ребром.
Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
В прямой призме невозможно найти высоту.
Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?
Параллелограмм с острыми углами.
Ромб с острыми углами.
Трапеция.
Прямоугольник.
Задание 5.
Как найти площадь полной поверхности призмы?
Нужно найти сумму площадей всех боковых граней.
Нужно сложить площадь боковой поверхности и площадь основания.
Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
Нужно сложить площади оснований.
Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3
Формула периметра треугольника
ФОРМУЛА ПЛОЩАДИ ЭЛЛИПСА:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
Формулы объема
Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом.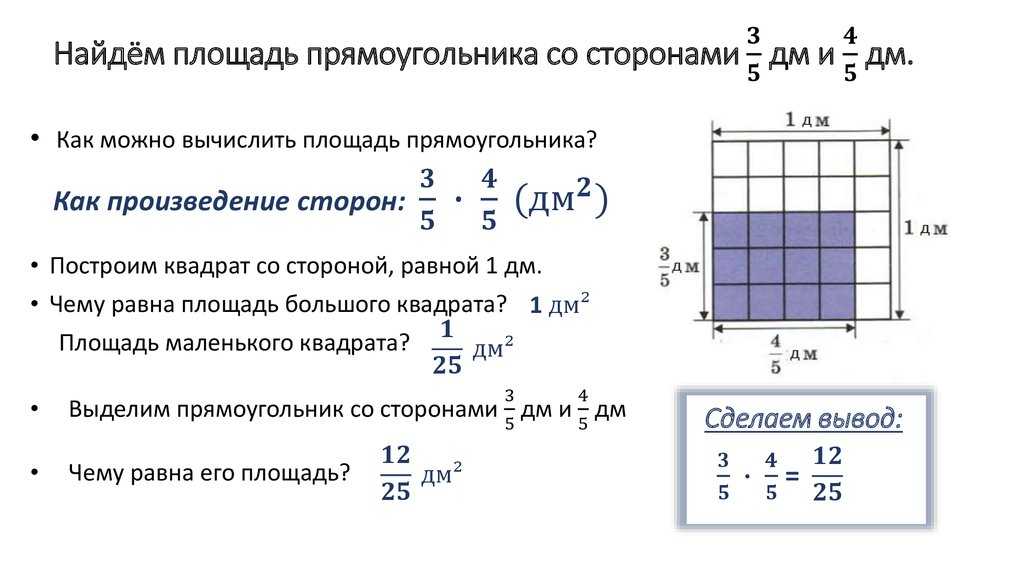 В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
ФОРМУЛА ОБЪЕМА КУБА:
1)
Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
ФОРМУЛА ОБЪЕМА ПИРАМИДЫ:
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
ФОРМУЛЫ ОБЪЕМА КОНУСА:
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3. 1415) на квадрат радиуса основания на высоту.
,
V — объем конуса
S
— площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
ФОРМУЛЫ ОБЪЕМА ЦИЛИНДРА:
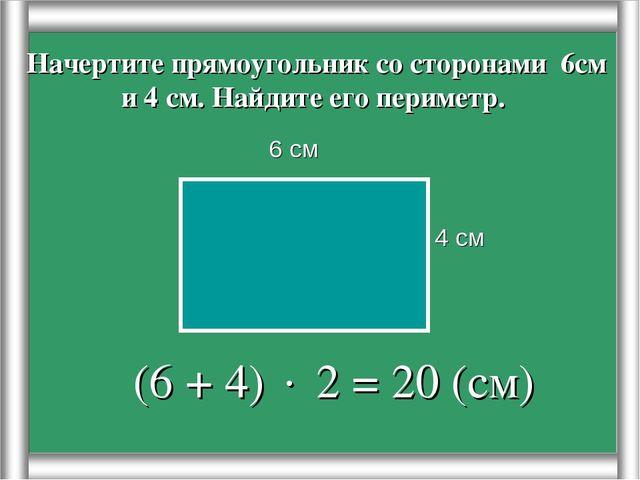
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
V — объем шара
π — число пи (3.1415)
R — радиус шара
ФОРМУЛА ОБЪЕМА ТЕТРАЭДРА:
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.

V — объем тетраэдра
a — длина ребра тетраэдра
Формулы треугольника
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади треугольника выражается числом заключающихся в него квадратных единиц.
1-АЯ ФОРМУЛА
S — площадь треугольника
a, b — длины 2-х сторон треугольника

С — угол между сторонами a и b
2-АЯ ФОРМУЛА
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ЬЯ ФОРМУЛА
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-АЯ ФОРМУЛА
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-АЯ ФОРМУЛА
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
Периметр геометрической фигуры
— суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).
P — периметр треугольника
a, b, c — длины сторон треугольника
Формулы круга и окружности
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Формула площади круга:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц.

1) Площадь круга равна произведению квадрата радиуса на число пи (3.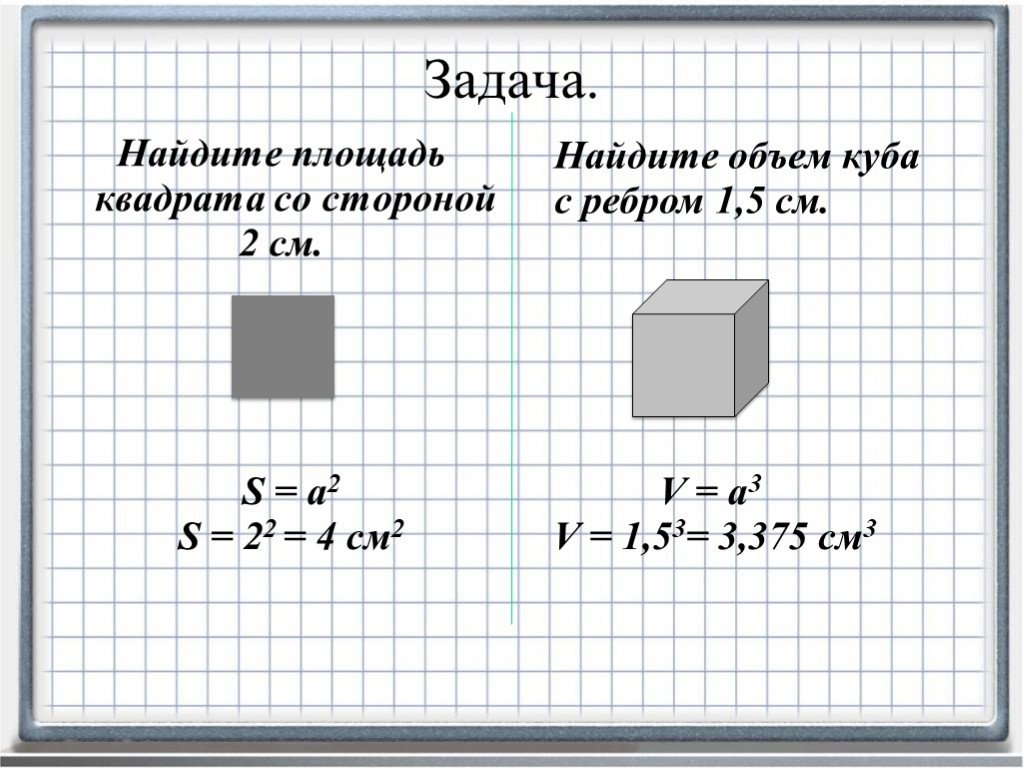 1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
ФОРМУЛА ПЕРИМЕТРА КРУГА (ДЛИНЫ ОКРУЖНОСТИ):
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр круга равен произведению радиуса на два пи (3.1415).
P — Периметр круга (длина окружности)

π — число пи (3.1415)
r — радиус круга (окружности)
Формулы трапеции
Трапеция — четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие — непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
ФОРМУЛА ПЛОЩАДИ ТРАПЕЦИИ:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади трапеции выражается числом заключающихся в него квадратных единиц.
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания

b — длина 2-ого основания
h — длина высоты трапеции
ФОРМУЛА ПЕРИМЕТРА ТРАПЕЦИИ:
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).
P — периметр трапеции
a, c — длины оснований трапеции
b, d — длины боковых сторон трапеции
Формулы квадрата
Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.

ФОРМУЛЫ ПЛОЩАДИ КВАДРАТА:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади квадрата выражается числом заключающихся в него квадратных единиц.
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S — площадь квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
ФОРМУЛЫ ПЕРИМЕТРА КВАДРАТА:
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.
P — периметр квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
Формулы прямоугольника
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b) называется квадратом.
ФОРМУЛА ПЛОЩАДИ ПРЯМОУГОЛЬНИКА:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади прямоугольника выражается числом заключающихся в него квадратных единиц.
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
ФОРМУЛА ПЕРИМЕТРА ПРЯМОУГОЛЬНИКА:
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
Видео-вопрос: Нахождение общей площади поверхности куба по периметру его основания
Стенограмма видео
Если периметр основания куба куб равен 54,4 см, найдите его полную поверхность.
В основе куба лежит квадрат. Вот основание и периметр этого квадрата составляет 54,4 сантиметра. Расстояние вокруг базы измеряет это много. Мы знаем, что основание куба квадрат и что у квадрата все стороны равны. Если сложить все четыре стороны, сторона плюс сторона плюс сторона плюс сторона, это будет 54,4 сантиметра.
Для решения проблемы однако нам нужно выяснить, сколько стоит одна сторона. Мы должны разделить 54,4 на четыре. Сколько раз четыре входят в пять? Один раз. Один раз четыре равно четырем. Пять минус четыре равно одному. Запишите следующую цифру. Сколько раз четыре входят в 14? Три раза. Трижды четыре равно 12. 14 минус 12 равно двум. Убедитесь, что мы выровняли нашу десятичную дробь точку для частного, а затем опустите следующую цифру.
Сколько раз можно ввести четыре 24? Шесть раз. Шесть раз четыре равно 24. 24 минус 24 равно нулю. Нет остатка. Это говорит нам о том, что каждый из наших сторона измеряет 13,6 см. Мы нашли длину только одного сторона, но какова наша цель здесь? Наша цель – найти общее площадь поверхности куба. Мы знаем, что площадь поверхности куб — это площадь всех шести граней, сложенных вместе. Начнем с нахождения площади база.
Помните, что основание квадратное, и мы знаем длину стороны. И чтобы найти площадь квадрата, возводим в квадрат длину его стороны. Умножайте рядом. Нам нужно возвести в квадрат 13,6. Для этого умножаем в 13,6 раз 13.6. Шесть раз шесть равно 36. Шесть раз три равно 18 плюс три, которые мы перенесли, равняется 21. Запишите единицу; нести два. Шесть раз один шесть, плюс два мы перенесли равные восемь.
Теперь мы начнем умножать на три. Трижды шесть равно 18. Запишите восьмерку; нести свой один. Трижды три равно девять плюс один равен 10. Запишите ноль; нести один. Три раза три это три, плюс один — четыре. Теперь умножаем на единицу. Один раз шесть равно шесть. Один раз три равно трем. Один раз один равно одному. Оттуда мы добавляем все частичные продукты.
Сбить шестерку. Один плюс восемь равно девять. Восемь плюс ноль плюс шесть равно 14. Запишите четыре; нести один. Один плюс четыре плюс три равно восемь. И тогда мы сбиваем один. Мы имеем дело с двумя десятичными места. Таким образом, мы помещаем наши десятичные знаки в два слева. И мы нашли площадь основание: 184,96 см в квадрате. Теперь, когда мы знаем площадь одного из стороны, мы можем найти полную площадь поверхности.
У куба шесть одинаковых граней, и это означает, что мы можем взять площадь одной из граней и умножить ее на шесть. Чтобы найти общую площадь поверхности, 184,96, умноженное на шесть, даст нам общую площадь поверхности. Шесть раз шесть равно 36. Шесть раз девять равно 54, плюс три равно 57. Шесть раз четыре равно 24, плюс пять равно 29. Шесть раз восемь равно 48, плюс два равно 50. Шесть раз один — шесть, плюс пять — 11.
Мы видим, что есть два десятичных знака. места в нашей задаче, а в решении будет два десятичных знака. Умножая площадь одного из граней на шесть, мы нашли общую площадь поверхности равной 1109,76 см. в квадрате.
Как найти площадь квадрата
Все математические ресурсы верхнего уровня SSAT
6 Диагностические тесты 311 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 Следующая →
Справка по математике верхнего уровня SSAT » Геометрия » Площади и периметры многоугольников » Площадь полигонов » Как найти площадь квадрата
Объем куба 1000 кубических сантиметров. Используя коэффициент преобразования 2,5 сантиметра = 1 дюйм, укажите площадь его поверхности в квадратных дюймах, округлив до ближайшего квадратного дюйма.
Возможные ответы:
75 квадратных дюймов
96 квадратных дюймов
108 квадратных дюймов
144 квадратных дюйма
100 квадратных дюймов
Правильный ответ:
96 квадратных дюймов
Пояснение:
Площадь поверхности куба в шесть раз больше квадрата его стороны, поэтому мы найдем длину стороны. Это кубический корень из объема 1000, поэтому
  сантиметров.
Чтобы переписать это в дюймах, разделите на 2,5:
    дюймы
Площадь поверхности куба в квадратных дюймах равна
   квадратных дюймов.
Сообщить об ошибке
Объем куба составляет 64 кубических дюйма. Найдите длину стороны куба и площадь его поверхности.
Возможные ответы:
Правильный ответ:
Пояснение:
Объем куба равен длине одного ребра, равно как и кубическому корню из объема:

У куба шесть граней, а площадь поверхности куба равна . Итак, мы можем написать:

Площадь поверхности =
Сообщить об ошибке
Квадрат имеет площадь 16 квадратных дюймов. Укажите диагональ квадрата.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы определить длину диагонали квадрата, воспользуемся теоремой Пифагора. Сначала нужно найти длину стороны:

Теперь «возведите в квадрат» длину одной стороны и умножьте на 2, затем извлеките квадратный корень из этого числа, чтобы получить длину диагонали:

Сообщить об ошибке
Джон собирается внести удобрение на его ферму размером 200 футов на 200 футов.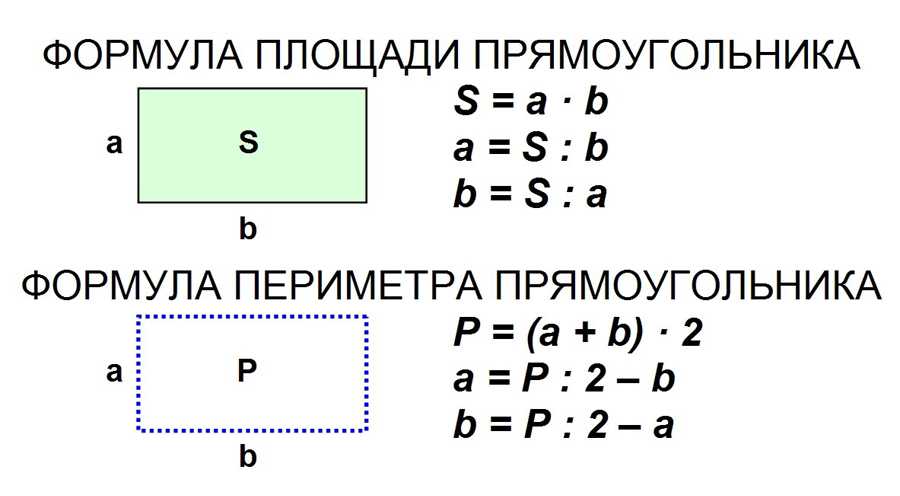 Каждый фунт удобрений, которые он собирается использовать, достаточен для 40 квадратных футов. Если удобрение стоит 2 доллара за фунт, сколько он должен потратить, чтобы удобрить свою ферму?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь фермы:

квадратных фута. Таким образом, количество необходимых ему удобрений можно рассчитать следующим образом:

фунтов

Каждый фунт удобрений стоит 2 доллара, поэтому ему нужно потратить доллары.
Сообщить об ошибке
Длина диагонали квадрата равна . Найдите площадь квадрата через .
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно использовать теорему Пифагора, чтобы решить эту задачу.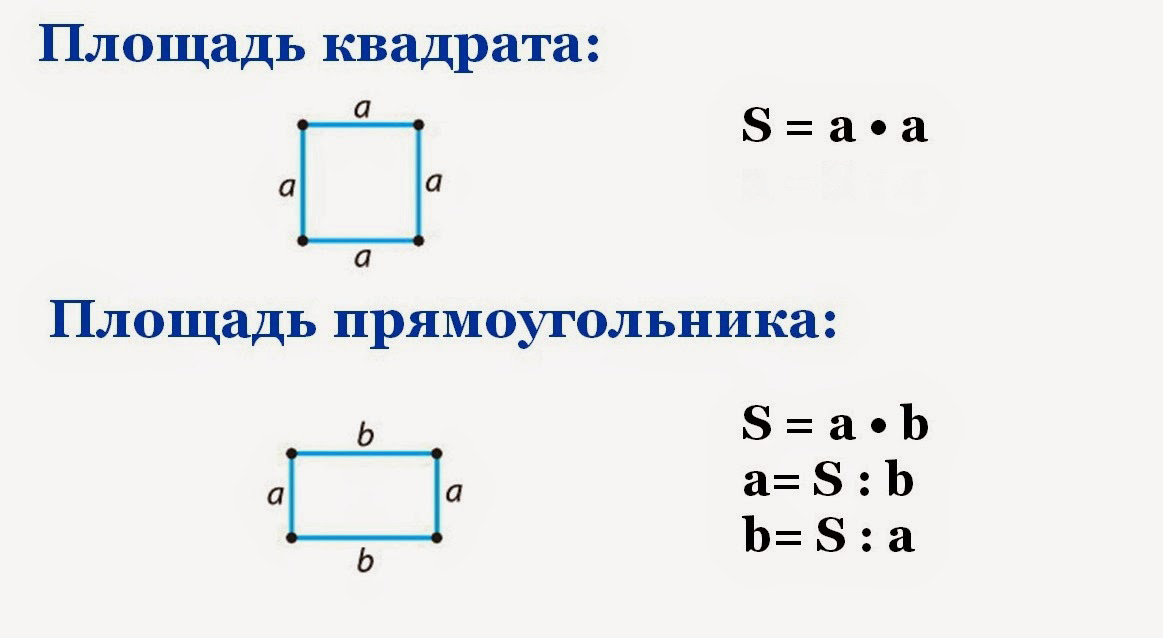 Мы можем написать:

где длина диагонали и длина стороны. Длина диагонали квадрата равна , поэтому мы можем написать:

Сообщить об ошибке
Квадрат вписан в круг, площадь которого равна квадратным дюймам. Какова площадь квадрата?
Возможные ответы:
Правильный ответ:
Пояснение:
Начните с вычисления площади круга в обратном направлении, чтобы найти его диаметр.
Площадь круга равна , и  (вы можете довольно быстро получить это методом проб и ошибок, так как вы знаете, что это число между 3 и 4, а поскольку 12.25 оканчивается на 5, вы теперь знаете, что речь идет о 5), поэтому диаметр круга равен 7. Это также диагональ квадрата. Д
Вы можете помнить, что катеты прямоугольного треугольника (из которых у нас есть два внутри квадрата, когда мы проводим диагональ) равны гипотенузе, деленной на .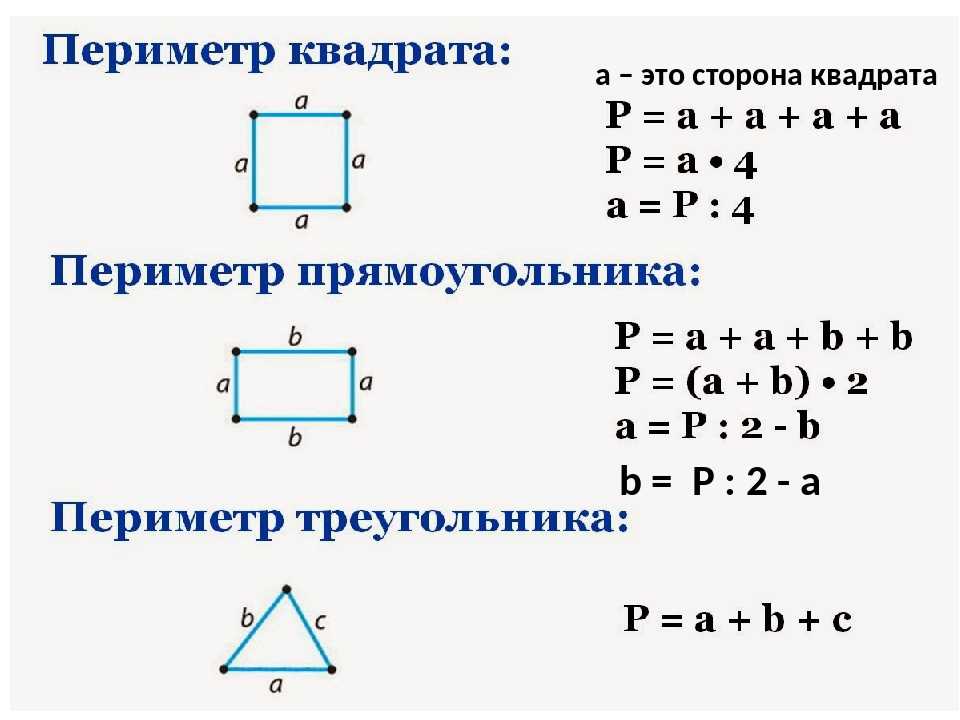 Но даже если вы забудете об этом, вам следует вспомнить теорему Пифагора, которая утверждает, что . В этом случае и равны, поэтому квадрат каждой стороны равен половине , или 24,5. И площадь одной стороны квадрата тоже равна площади квадрата.
Сообщить об ошибке
Периметр квадрата . Какова площадь квадрата?
Возможные ответы:
Правильный ответ:

Пояснение:
Используйте периметр, чтобы найти длину стороны квадрата.

Теперь, используя длину стороны, найдите площадь квадрата.

Сообщить об ошибке
Периметр квадрата равен . Какова площадь квадрата?
Возможные ответы:
Правильный ответ:

Пояснение:
Сначала используйте периметр, чтобы найти длины сторон квадрата.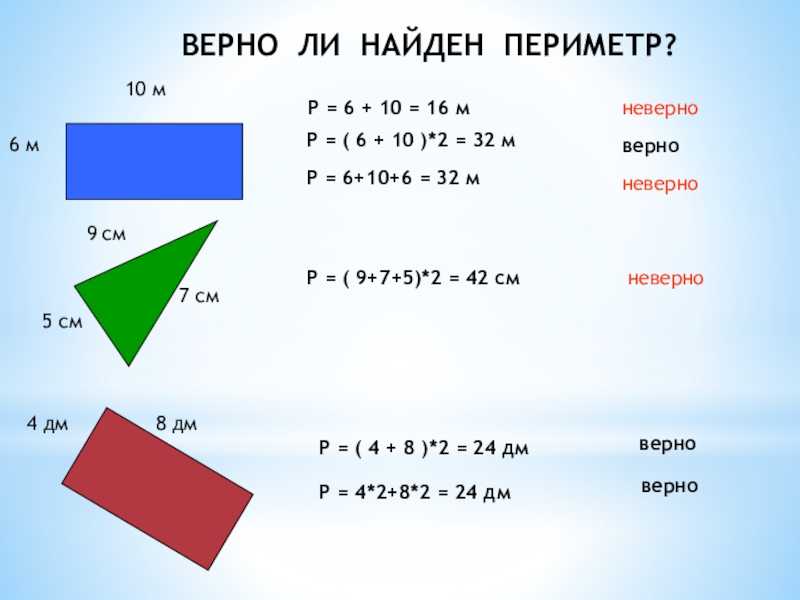
Используйте эту информацию, чтобы найти область.
Сообщить об ошибке
Периметр квадрата такой же, как у прямоугольного треугольника. Укажите площадь квадрата.
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку мы знаем длину одного катета и гипотенузы, мы можем вычислить длину другого катета, используя теорему Пифагора. Мы можем использовать такую форму:
Установка и равные длинам гипотенузы и катета — 13 и 5 соответственно:
Периметр равен сумме длин трех сторон:
Это также периметр квадрата, поэтому длина каждой стороны составляет одну четвертую от этого, или
Площадь равна площади этого квадрата, или
Сообщить об ошибке
Периметр квадрата равен длине окружности с площадью 4.
No related posts.