Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Завершение квадрата
» Завершение квадрата » вот где мы. ..
..
| … возьмем квадратное уравнение следующим образом: | и превратите его в это: | |
| топор 2 + Ьх + с = 0 | а(х+ d ) |
Для тех из вас, кто торопится, могу сказать, что: d = b 2a
и: e = c − b 2 4a
Но если у вас есть время, позвольте мне показать вам, как « Заполнить квадрат » самостоятельно.
Завершение квадрата
Допустим, у нас есть простое выражение вида x 2 + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?
Что ж, немного вдохновившись геометрией, мы можем преобразовать его вот так:
Как видите x 2 + bx можно переставить почти в квадрат. ..
..
… и мы можем завершить квадрат с помощью (b/2) 2
В алгебре это выглядит так:
| x 2 + шт | + (б/2) 2 | = | (х+b/2) 2 |
| «Завершить квадрат » |
Итак, сложив (b/2) 2 , мы можем завершить квадрат.
Результат (x+b/2) 2 имеет x только один раз , что проще в использовании.
Сохранение равновесия
Теперь… мы не можем просто прибавить (b/2) 2 без вычитания ! В противном случае меняется все значение.
Итак, давайте посмотрим, как это сделать правильно на примере:
| Начните с: | |
| («b» в данном случае равно 6) | |
| Заполните квадрат: | |
| Также вычесть новый термин |
Упростите и готово. | |
Результат:
x 2 + 6x + 7 = (x+3) 2 − 2
И теперь x появляется только один раз, и наша работа сделана!
Быстрый подход
Вот быстрый способ получить ответ. Вам может понравиться этот метод.
Сначала подумайте о желаемом результате: (x+d) 2 + e
После разложения (x+d) 2 получаем: x 2 + 2dx + d 2 + e
Теперь посмотрим, сможем ли мы превратить наш пример в эту форму, чтобы обнаружить d и e
Пример: попробуйте вписать x
2 + 6x + 7 в x 2 + 2dx + d 2 + eТеперь мы можем «форсировать» ответ:
- 911 33 Мы знаем, что 6х должно закончиться вверх как 2dx, поэтому d должно быть 3
- Далее мы видим, что 7 должно стать d 2 + e = 9 + e, поэтому e должно быть −2
И мы получаем тот же результат (x+3) 2 − 2, что и выше!
Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений.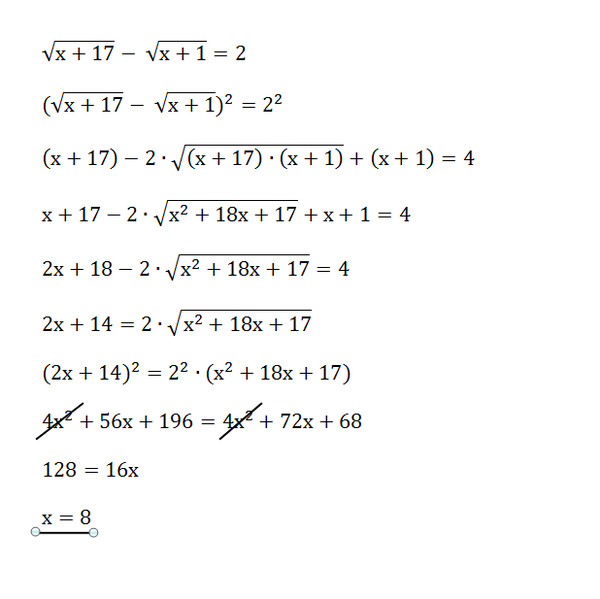 ..
..
Решение общих квадратных уравнений путем заполнения квадрата
Мы можем дополнить квадрат до , решить квадратное уравнение (найти, где оно равно нулю).
топор 2 + Ьх + с = 0
Но с этим легко справиться… просто разделите все уравнение сначала на «а», а затем продолжайте:
х 2 + (б/а)х + с/а = 0
шагов
Теперь мы можем решить квадратное уравнение за 5 шагов:
- Шаг 1 Разделите все члены на a (коэффициент x 2 ).
- Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
- Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.
Теперь у нас есть что-то похожее на (x + p) 2 = q, которое можно довольно легко решить:
- Шаг 4 Извлеките квадратный корень из обеих частей уравнения.

- Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .
Примеры
Хорошо, несколько примеров помогут!
Пример 1: решить x
2 + 4x + 1 = 0Шаг 1 можно пропустить в этом примере, так как коэффициент при x 2 равен 1
Шаг 2 Переместите числовой член в правую часть уравнения: 909 09
x 2 + 4x = -1
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правую часть уравнения.
(б/2) 2 = (4/2) 2 = 2 2 = 4
x 2 + 4x + 4 = -1 + 4
(x + 2) 2 = 3
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
х + 2 = ±√3 = ±1,73 (до 2 знаков после запятой)
Шаг 5 Вычтите 2 с обеих сторон:
x = ±1,73 – 2 = -3,73 или -0,27
А вот еще интересная и полезная штука. В конце шага 3 у нас было уравнение: (х + 2) 2 = 3 Это дает нам вершину (точка поворота) x 2 + 4x + 1: (-2, -3) |
Пример 2: решить 5x
2 – 4x – 2 = 0Шаг 1 Разделить все члены на 5
x 2 – 0,8x – 0,4 = 0
Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 – 0,8x = 0,4
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правой части уравнения:
(b/2) 2 = (0,8/2) 2 = 0,4 2 = 0,16
x 2 – 0,8x + 0,16 = 0,4 + 0,16
(x – 0,4) 2 = 0,56
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
x – 0,4 = ±√0,56 = ±0,748 (до 3 знаков после запятой)
Шаг 5 Вычтите (-0,4) из обеих частей (другими словами, добавьте 0,4 ):
x = ±0,748 + 0,4 = -0,348 или 1,148
Почему «Завершить квадрат»?
Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу, чтобы решить квадратное уравнение?
Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.
Бывают также случаи, когда форма ax 2 + bx + c может быть частью более крупного вопроса и переставлять его как a(x+ d ) 2 + 9092 8 e делает решение проще, потому что x появляется только один раз.
Например, «x» может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.
Также завершение квадрата является первым шагом в выводе квадратичной формулы
Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.
364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206
Сноска: значения «d» и «e»
Как я получил значения d и e из верхней части страницы?
| Начните с | |
| Разделить уравнение на a | |
| Положить c/a на другую сторону | |
| Добавить (b/2a) 2 на обе стороны | |
| «Заполните квадрат» | |
Теперь верни все назад. | |

 3
3 14159..
14159..

