1-2 класс. Прямой угол. Строительство. : my_mice — LiveJournal
1-2 класс. Прямой угол. Строительство. : my_mice — LiveJournal ?- Дети
- Cancel
Сейчас у меня серия геометрических уроков. С 1-2 классом мы разговаривали про углы вообще. К моему удивлению, практически никто из детей понятия «угол» не знал вообще. Ни в одной из групп. Единицы знали про бесконечность прямой и про то, что такое луч.
Для меня это очень базовые понятия. «Геометрию для малышей» Житомирского (https://sheba.
С некоторыми группами еще мы делали отвесы — из нитки и большой скрепки, и проверяли, где у нас вертикальные линии. И поговорили об относительности вертикальных линии. И даже немножко про силу тяжести. Я даже некоторым показала опыт с мятым листочком, раз уж зашла речь о том, тяжелые или легкие предметы падают быстрее и почему. Так что у нас не только математика, но иногда и физика бывает тоже. 🙂
Интересно было, что практически никто не смог правильно сказать, какими должны быть ножки стола, чтобы крышка была горизонтальной.
Так мы подошли к понятию прямого угла как угла между вертикалью и горизонталью. Я решила не грузить 1-2 класс градусными мерами пока.
Еще мы побегали с угольниками и поискали прямые углы в комнате, где занимались, а в конце сделали очень простой домик. (Подсмотрела его в блоге Банды умников.
) Tags: математический кружок, маткружок
Subscribe
Школьники. Домино.
Со всеми школьниками мы сегодня поговорили про домино. В начале немножко поиграли, потом обсуждали, сколько доминошек всего, как их считать, чтобы…
Дошкольники. 8 марта. Магазин.
На этой неделе я решила устроить праздничные уроки. Начали мы с игры Жени Кац (ее, кстати, можно скачать на ее сайте за небольшую денежку) которую я…
Школьники. Математика на шахматной доске.
Общая тема школьников была математика на шахматной доске. Хотя играли мы в начале в Мэтч. Прекрасная игра на пространственное мышление. Дальше со…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
- 11 comments
Школьники.
Домино.Со всеми школьниками мы сегодня поговорили про домино. В начале немножко поиграли, потом обсуждали, сколько доминошек всего, как их считать, чтобы…
Дошкольники. 8 марта. Магазин.
На этой неделе я решила устроить праздничные уроки. Начали мы с игры Жени Кац (ее, кстати, можно скачать на ее сайте за небольшую денежку) которую я…
Школьники. Математика на шахматной доске.
Общая тема школьников была математика на шахматной доске. Хотя играли мы в начале в Мэтч. Прекрасная игра на пространственное мышление. Дальше со…
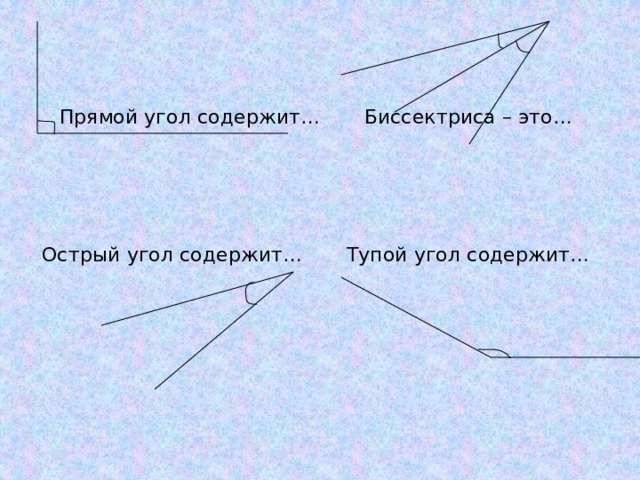
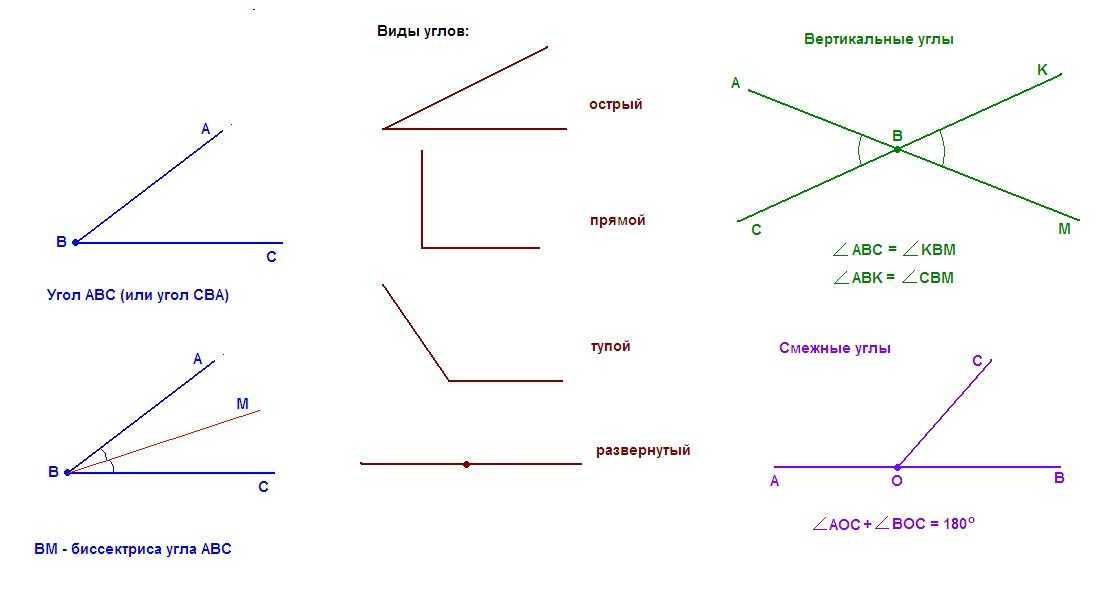
Домино.Острый угольник. Виды углов
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла.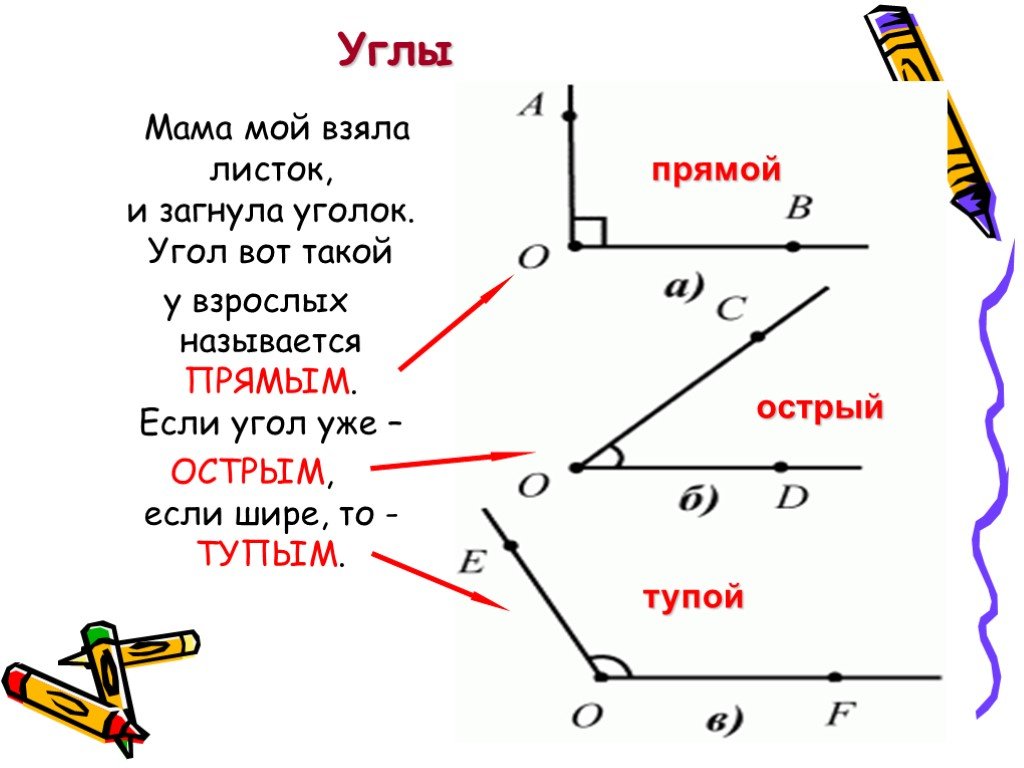
Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
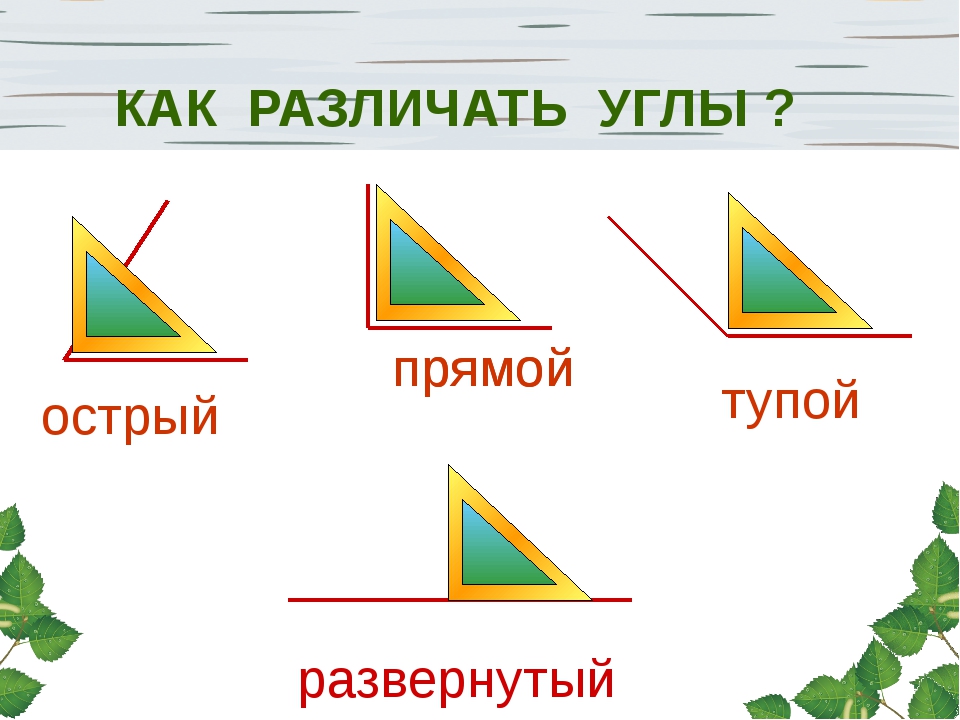
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы.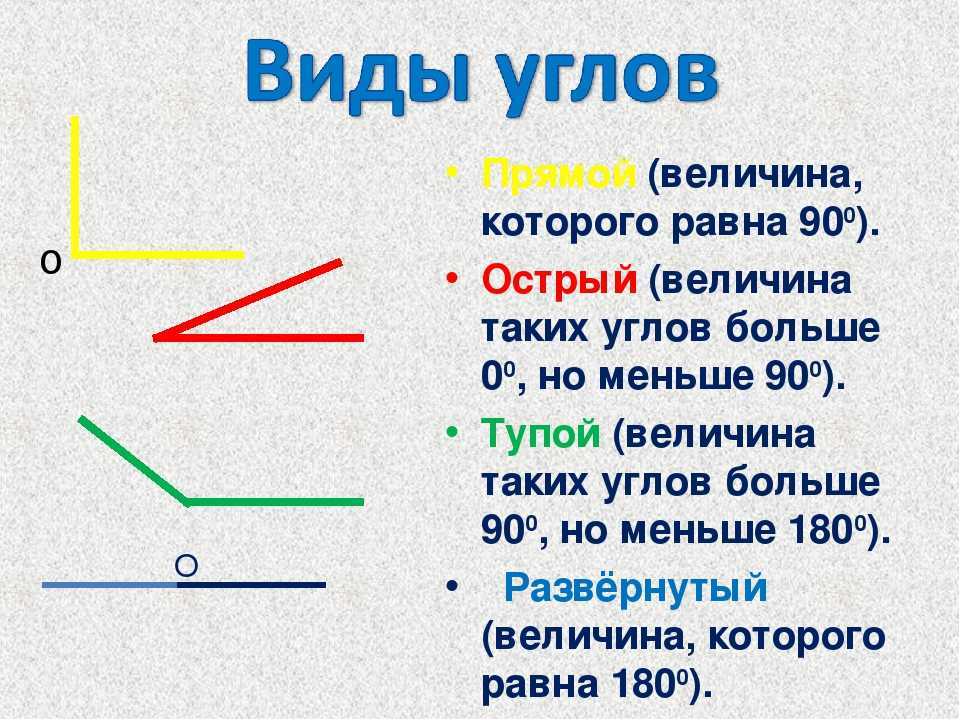
Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.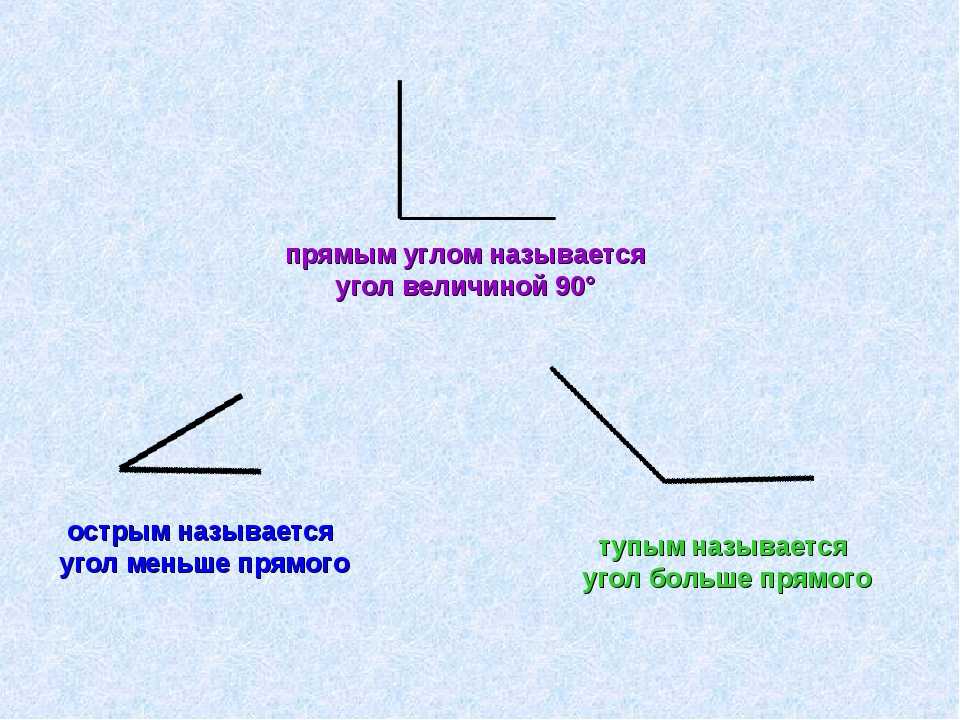
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Каждый угол, в зависимости от его величины, имеет своё название:
| Вид угла | Размер в градусах | |
|---|---|---|
| Острый | Меньше 90° | |
| Прямой | Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой. | |
| Тупой | Больше 90°, но меньше 180° | |
| Развёрнутый | Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла. | |
| Выпуклый | Больше 180°, но меньше 360° | |
| Полный | Равен 360° |
Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны — OM и ON составляют прямую.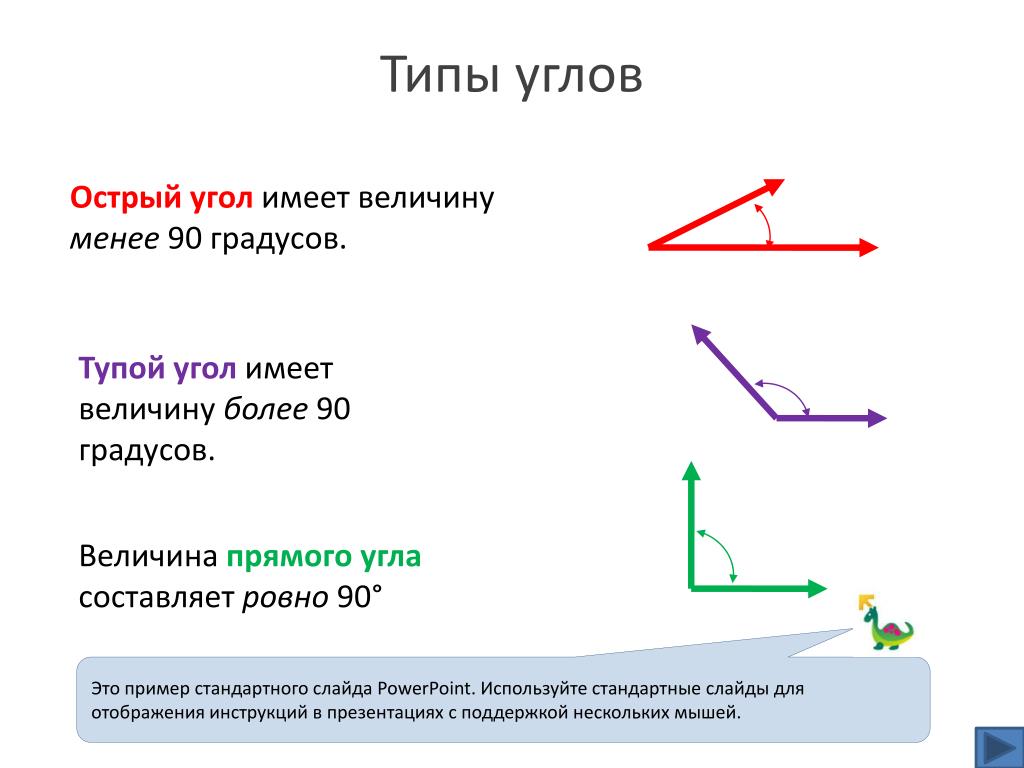
Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .
Сумма смежных углов равна 180°.
Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 — вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.
Острый угол- это тот угол, градусная мера которого меньше 90 градусов. Прямой угол- это тот угол, градусная мера которого 90 градусов.
Острый угол — от нуля до 90 градусов (не включительно).
Выглядят они вот так
Прямой угол равен 90 градусам, его стороны перпендикулярны друг другу.
Есть ещ тупые углы — от 90 градусов до 180, вот так они выглядят:
Какой перед вами угол, в общем-то, можно определить на глаз, но если нужны точные градусы, нужно пользоваться транспортиром.
Элементарно просто, берем уголок, или линейку или транспортир, можно и все вместе. С транспортиром все просто, уведите соответствующие отметки, то есть 90%- прямой угол; то что больше 90%-91,99,120,170 называется тупым углом; в свою очередь, то что меньше 90%-89, 75, 40,15 называется острым углом. Ошибиться практически невозможно.
Угол образованный пересечением двух перпендикулярных прямых называется прямым. Также прямой угол может возникнуть при делении окружности на ровные четыре части (1/4 окружности).
Прямой угол равен 90 градусам.
Когда стороны угла совпадают, такой угол называется нулевым
Нулевой угол равен 0 градусам.
Все углы, значения в градусах которых больше нулевого и меньше прямого называется острыми.
Острый угол — больше 0 градусов и меньше 90 градусов.
Если стороны угла лежат в противоположных направлениях и образуют прямую, такой угол называется развернутым и равен он 180 градусам.
Углы, значения в градусах которых больше прямого и меньше развернутого называются тупыми.
Тупой угол — больше 90 градусов и меньше 180 градусов.
Всех их объединяет одно:
острый, прямой и тупой углы — все они выпуклые .
Острым называется угол, величина которого меньше 90 градусов.
Прямой угол с раствором 90 градусов.
Тупым называется угол, величина которого больше 90 градусов, но меньше 180 градусов.
Прямой угол сразу видно на глаз.
Вс достаточно просто. Проведм аналогию с обычными часами.
Если одну из стрелок установить так, чтобы она указывала на двенадцать часов, а другою, чтоб указывала на три — то они образуют прямой угол в девяносто градусов. Если же начать двигать стрелку указывающую на три часа в обратном направлении(в двухчасовой отметки на циферблате) — то она будет образовывать, вместе со второй стрелкой, острые углы(менее 90 градусов). Когда же стрелки будут указывать в одну точку — они образуют нулевой угол в ноль градусов.А если вернуть вторую стрелку к исходной(трехчасовой отметке) и начать передвигать е вперед по циферблату — то вплоть до шестичасовой отметки она вместе с первой будут образовывать тупые углы(более 90 градусов). Когда стрелки будут указывать, одна на 12, а другая на 6 — это будет, так называемый, разврнутый угол в 180 градусов.
В этом вопросе нужно отталкиваться от прямого угла:
1.Прямой угол равен 90 градусов
2.Все углы которые меньше прямого угла, то есть меньше 90 градусов, считаются острыми.
К примеру, углы 89 градусов, 60 градусов, 30 градусов.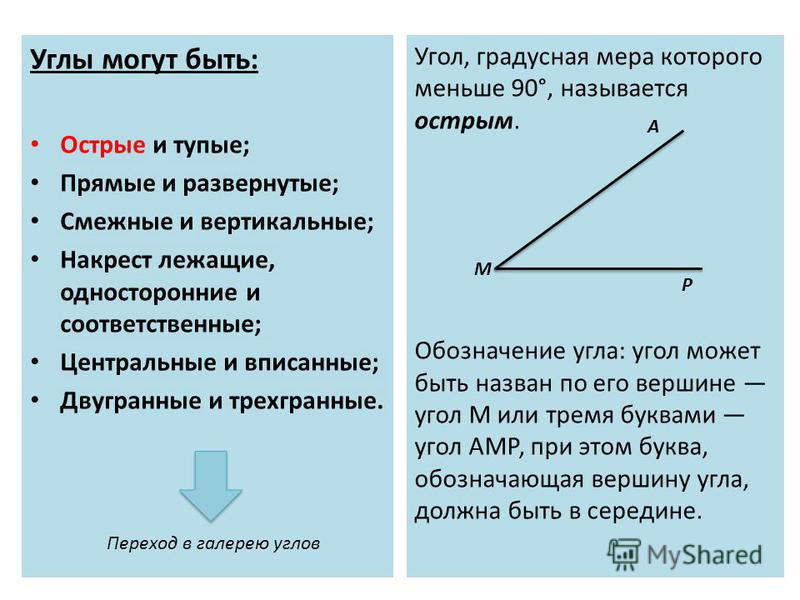
3.Все углы, которые больше прямого угла, то есть больше 90 градусов, считаются тупыми.
К примеру, 91 градус, 120 градусов, 179 градусов -тупые углы
Еще нужно учесть, что угол равный 180 градусов называется развернутым .
Это геометрия 7-го класса. Возможно даже и раньше в школе проходят, точно не помню. Для измерения величины угла используют транспортир. Так вот, прямой угол равен 90 градусов, острый угол всегда меньше 90 градусов (даже на 1 градус), а тупой угол всегда больше 90 градусов.
Острый угол — это угол меньше 90.
Тупой угол — это угол больше 90, но меньше 180.
Прямой угол — это угол 90.
Есть ещ разврнутый угол, то есть угол, находящийся в диапазоне между 180 и 360.
Если угол больше 360, то чтобы узнать, какой угол, следует отнять от значения этого угла 360 и посмотреть, что останется. Если вс равно больше, то повторить эту операцию нужное число раз.
Угол 0, также как и 180 с одной стороны используются в расчтах как угол, но фактически являются началом отрезка или линии, а не углом.
Если брать треугольники, то их углы должны находиться в диапазоне между 0 и 180, так как при таких углах треугольника (0 и 180) это будет уже не треугольник, а отрезок, а при бльших углах треугольника не получится.
Прямой угол — это угол 90 градусов, встречается в таких четырехугольниках, как квадрат и прямоугольник.
Тупой угол — это угол, градусная мера которого больше 90 градусов, но меньше 180, встречается в ромбе, многоугольгике, произвольных параллелограммах.
Острый угол — это угол до 90 градусов, его, например, нет в квадрате.
видов углов | Учитесь на примерах из реальной жизни
Прежде чем мы приступим к изучению различных типов ракурсов, давайте сначала поймем, где и как мы используем ракурсы в нашей повседневной жизни.
Зачем нужны углы?
Уголки используются для создания конструкций, которые не развалятся.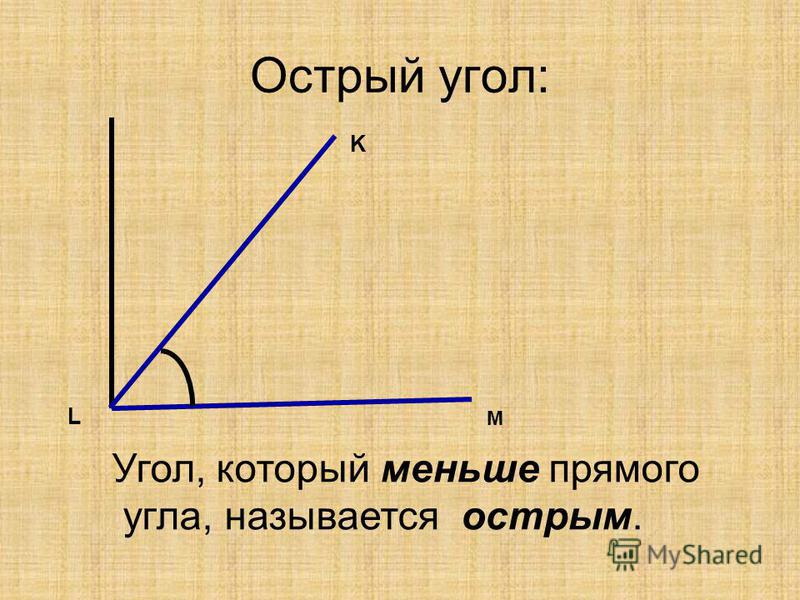
Даже для передачи мяча следующему игроку в футболе мы используем углы.
Художники каждый день используют ракурсы для создания реалистичных картин.
Архитекторы не могут обойтись без них при проектировании дорог и мостов.
Это просто для того, чтобы дать вам мимолетное представление о том, как углы проникают почти во все сферы жизни, делая изучение углов в два раза более важным. Давайте теперь углубимся в урок!
Какие бывают типы углов?
Углы можно разделить на различные типы в зависимости от их размеров.
Острый угол
Возьмем эти два луча. Мы зафиксируем один луч и повернем другой. Мы показали лучи разными цветами, так что вращение легко понять.
Нажмите, чтобы посмотреть, как луч превращается в острый угол.
Этот угол, размеры которого больше 0° и меньше 90°, известен как острый угол.
Острые углы в реальной жизни
Просто прогуляйтесь, и вы обязательно получите богатый список примеров острых углов.
Прямой угол
На этот раз мы повернем наш луч, пока он не будет направлен прямо вверх и не будет перпендикулярен другому лучу. В этом случае угол составляет ровно 90°.
Нажмите, чтобы посмотреть, как образуется прямой угол.
Это называется прямым углом и обозначается квадратиком, а не дугой.
Прямые углы в реальной жизни
Просто посмотрите немного, и вы можете найти сотни примеров, которые можно добавить к вашему списку прямых углов.
Тупой угол
Теперь повернем наш луч на 90°.
Нажмите, чтобы увидеть, как два луча образуют тупой угол.
Как видите, угол больше 90°, но меньше 180°. Это тупой угол.
Тупые углы в реальной жизни
Это всего лишь несколько примеров из десятков сотен тупых углов, которые окружают вас; осмотритесь в поисках хороших примеров.
Прямой угол
Давайте повернем луч так, чтобы он указывал в направлении, противоположном другому лучу, помогая обоим лучам составить прямую линию.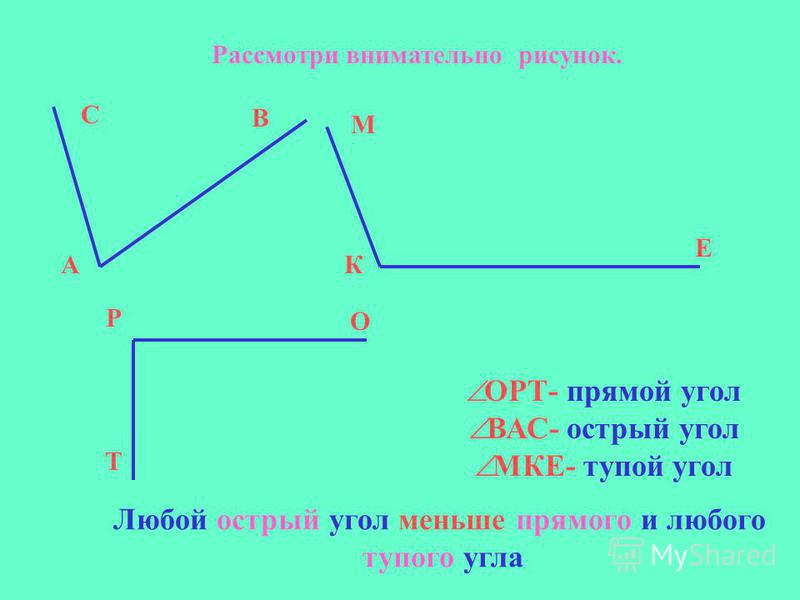
Нажмите, чтобы посмотреть, как луч превращается в прямой угол.
Угол, образованный здесь, является прямым углом. Он измеряет 180 °, что делает довольно очевидным, откуда он получил свое название. Прямой угол может быть образован сложением двух прямых углов.
Прямые углы в реальной жизни
Рефлекторные и полные углы
Угол, образованный, когда луч выходит за пределы 180° и лежит между 180° и 360°, называется рефлекторным углом.
Нажмите, чтобы посмотреть, как формируется рефлекторный угол.
Угол, образованный, когда луч совершает один полный оборот, составляет 360° и называется полным углом.
Нажмите, чтобы увидеть, как формируется полный угол.
Рефлекс и полные углы в реальной жизни
Рефлекс угол
Полный угол
Объединяем все виды углов!
Нажмите, чтобы мельком увидеть типы углов — все сразу!
Развлекайся с углами!
Подсчитайте количество острых и прямых углов в каждой букве слова «MATH».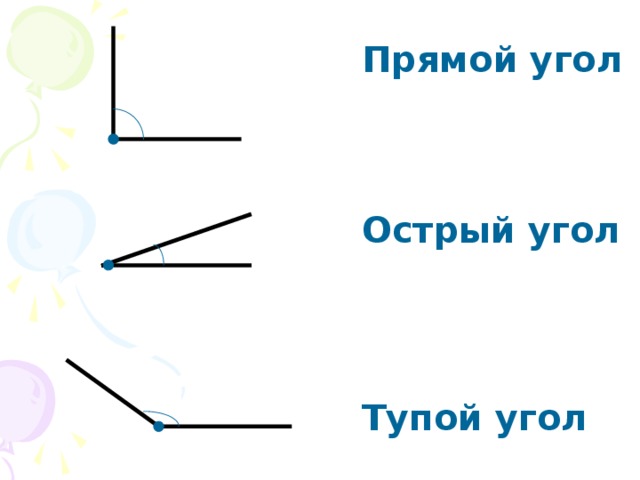
Нажмите на каждую букву, чтобы увидеть положение углов.
Вы насчитали 12? Математика действительно меняет правила игры, не так ли?
Прогулка по типам
Острые углы измеряются между 0° и 90°.
Прямые углы равны ровно 90°.
Тупые углы больше 90°, но меньше 180°.
Прямые углы измеряют 180°.
Углы рефлекса составляют от 180° до 360°.
Угол, образованный одним полным оборотом, составляет 360° и называется полным углом.
Пройди тест на типы углов прямо сейчас!
Прогресс
Перезапустить тест
Извините, ваш ответ неверен.
Ответ:
Острый угол, прямой угол и тупой угол
Предоставил:
Диего Чт, 27 января 2022 г., 12:05 UTC
Этот pdf-файл содержит: —
Наименование углов
Внутренние и внешние углы
Измерение
Биссектрисы
1.
Ч 3
2.
3.1
3.
Противоположные лучи
Противоположные лучи –
Лучи, являющиеся частью одной линии и имеющие только общие
конечные точки
XY и XZ
Также называются прямым углом
4.
Другой случай, когда два луча имеют общую конечную точку…
Угол –
Фигура, образованная двумя неколлинеарными лучами, имеющими
общий конец
Вершина – общий конец
Стороны – лучи, составляющие угол
Три способа названия:
Три точки (вершина посередине)
Только вершина
Число
5.
Назовите угол четырьмя способами. Затем определите его вершину
и стороны.
6.
Именование углов
Если несколько углов имеют общую вершину, назовите 9 углов.0178 угол с тремя точками или номер
7.
Назовите все углы, имеющие вершину D.
8.
Угол делит плоскость на три области
Внутренняя часть угла
Внешняя сторона угла
Сам угол
9.
Укажите, находится ли каждая точка внутри,
снаружи или на углу.
10.
P92: 1 – 32 (пропустить 30)
21 – 23: если неверно, объяснить, почему
Прочтите P95, #1–3
11.
3-2
Измеритель угла
12.
Угловая мера
Градус –
Единица измерения углов
1/360 окружности
Символ: °
мPQR читается как «мера угла PQR»
Причина, по которой нет знака градуса, потому что это мера
, а не мера
13.
Постулат 3-1: Углы измеряются
14.
Транспортир –
Геометрический инструмент для измерения углов и зарисовки
углов заданной величины
15.
Используйте транспортир для измерения угла KLM.
16.
Используйте транспортир, чтобы Найдите меру
меры ∠CDF. ∠PQR, ∠PQS и
∠PQT.
17.
Постулат 3-2: Транспортир Постулат
Значение: из данного луча можно
провести два угла с заданной мерой угла
18.
С помощью транспортира начертите угол с мерой
, равной 35.
С помощью транспортира начертите угол с мерой
, равной 65.
19.
Классификация углов
Типы углов:
Прямой угол – мера 90
Острый угол – мера меньше 90
Тупой угол – мера больше 90
20.
Классифицируйте каждый угол как острый, тупой или прямой
21.
Мера угла A равна 100. Найдите x.
Угол B равен 138. Найдите x.
22.
P100: 1, 2 (используйте P99), 4 – 25, 31 – 37
3.1/3.2 Wkst
23.
Глава 3 Расследование
Волшебная Середина
P102: 1 – 2
24.
3-3
Постулат сложения углов
25.
Практическая геометрия
P104: Следуйте инструкциям, ответьте на вопросы
26.
Постулат 3-3: Сложение углов Постулат
(Постулат АА)
29.
Найдите m∠ABC, если
м∠ABD = 70 и
м∠DBC = 43.
Если m∠EBC = 55 и
м∠EBD = 20, найдите
м∠2.
Найдите m∠ABD, если
m∠ABC = 110 и
m∠2 = 36.
30.
Биссектриса угла
33.
Практическая геометрия
P107: выполните шаги, ответьте на вопросы
34.
P108: 1 – 24, 26 – 30
35.
3-4
СМЕЖНЫЕ УГЛЫ И ЛИНЕЙНЫЕ
ПАРЫ УГЛОВ
36.
Смежные углы
38.
Линейная пара
39.
Назовите угол, под которым
образует линейную пару
с ∠TCM.
Образуют ли ∠1 и ∠TCE
линейную пару?
Обоснуйте свой ответ
.
40.
В Центре Джона Хэнкока в Чикаго, штат Иллинойс,
, представлены различные виды ракурсов. Опишите
выделенных углов.
41.
P112: 1, 3 – 21, 23 – 27
Читать P115
1–3
42.
3-5
Дополнительные и дополнительные
Уголки
43.
Дополнительные уголки
44.
Дополнительные уголки
45.
Дополнительные уголки
46.
Дополнительные уголки
47.
Назовите две пары дополнительных углов.
Назовите пару смежных углов.
48.
Назовите пару несмежных дополнительных углов
.
Найдите градусную меру угла, который
является дополнительным к углу BGC.
49.
Углы C и D являются дополнительными. Если m∠C =
12x и m∠D = 4(x + 5), найдите x. Затем найдите
м∠C и м∠D.
50.
Постулат 3-4: Дополнение Постулат
51.
Если m∠3 = 115 и ∠3 и ∠4 образуют линейную пару,
найти m∠4.
52.
P119: 1 – 37
53.
3-6
Равные углы
54.
Равные углы
55.
Вертикальные уголки
56.
Теорема 3-1: Теорема о вертикальном угле
57.
Найдите х.
60.
Предположим, что ∠A ≅ ∠B На рисунке ниже
и m∠B = 47. Найти ∠1 является дополнительным
мерой an к ∠2, ∠3 является
угол, который является дополнительным к ∠2,
дополнительный к ∠A. и m2∠ = 105.
Найдите m∠1 и m∠3.
63.
P125: 1 (с компасом), 4 – 22, 24 – 28
64.
3-7
Перпендикулярные линии
65.