Что такое упрощение выражений? — Ваша онлайн-энциклопедия
Содержание
- — Что значит упростить выражение 7 класс?
- — Как упростить выражение при умножении дробей?
- — Что значит упростить многочлен?
- — Как упрощать выражение в математике?
- — Как упростить целое выражение?
- — Что такое выражение в математике 4 класс?
- — Что такое найди значение выражение?
- — Что значит значение буквенного выражения?
- — Как правильно упрощать дроби?
- — Как можно сократить дробь?
- — Как можно упрощать дроби?
- — Как преобразовать многочлен в многочлен стандартного вида?
- — Что такое многочлен первой степени?
- — Что значит разложить многочлен на множители?
Распределительное свойство умножения позволяет упрощать буквенные выражения. Такие преобразования, в результате которых получаются более простые выражения, называют упрощением выражений.
Что значит упростить выражение 7 класс?
Упростить выражение – это значит уменьшить количество операций, которые необходимо сделать, чтобы вычислить его значение при конкретных значениях переменных.
Как упростить выражение при умножении дробей?
Упрощение дробно-рациональных выражений
- Дробь можно упростить, разложив на множители ее числитель и знаменатель и сократив одинаковые множители:
- Для сложения и вычитания дробей нужно привести их к общему знаменателю:
- Для умножения двух дробей нужно перемножить их числители и знаменатели.
Что значит упростить многочлен?
Преобразование (упрощение) произведения одночлена и многочлена Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена. … Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Как упрощать выражение в математике?
Упрощая выражения, складывают коэффициенты, а буквенные множители оставляют без изменения.
Как упростить целое выражение?
Целые выражения можно упрощать, используя правила сложения, вычитания и умножения многочленов. Вспомним их. Во-первых, произведение многочленов равно многочлену, членами которого являются произведения каждого члена одного многочлена и каждого члена другого многочлена Т.
Что такое выражение в математике 4 класс?
Числовое выражение – числа, соединенные знаками арифметических действий для выполнения вычисления. Значение выражения –число, которое получается после выполнения всех действий. Скобки в выражениях – знаки «( )», которые позволяют разграничить и определить порядок действий.
Что такое найди значение выражение?
Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1. Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений. К числу 10 прибавить разность чисел 8 и 3.
Значение данного выражения 1. Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений. К числу 10 прибавить разность чисел 8 и 3.
Что значит значение буквенного выражения?
Значение выражения – это число, полученное в результате выполнения всех действий в выражении. Буквенное выражение – выражение, составленное из чисел, букв, знаков математических действий и скобок. Переменная – это значение буквы в буквенном выражении.
Как правильно упрощать дроби?
Деление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.
- Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число. …
- Сократим дробь на 3 (делим числитель на 3; .
 ..
.. - Сокращаем дробь на 7.
3 июн. 2012 г.
Как можно сократить дробь?
Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы. В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.
Как можно упрощать дроби?
Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число. Это число является наибольшим общим делителем числителя и знаменателя данной дроби.
Как преобразовать многочлен в многочлен стандартного вида?
Чтобы привести многочлен к стандартному виду, нужно: Привести каждый одночлен многочлена к стандартному виду. Выполнить приведение подобных одночленов.
Как привести многочлен к стандартному виду
- Вначале приведём к стандартному виду все одночлены внутри многочлена. …
- Теперь приведём подобные.
 …
… - Запишем окончательное решение.
Что такое многочлен первой степени?
Степенью многочлена называют наивысшую степень входящих в него одночленов. ax + b , где буквами a и b обозначены произвольные числа, причем число a отлично от нуля, является многочленом первой степени.
Что значит разложить многочлен на множители?
Разложить многочлен на множители — это значит представить многочлен в виде произведения двух или нескольких множителей. (x + 5) (x + 9), где x + 5 и x + 9 являются множителями.
Интересные материалы:
Что такое инерция простыми словами?
Что такое искомое слово?
Что такое искусственный интеллект простыми словами?
Что такое история простыми словами?
Что такое измерение простыми словами?
Что такое календарь простыми словами?
Что такое Хабалка слова?
Что такое химия простыми словами?
Что такое ключевые слова на ютуб?
Что такое когерентность простыми словами?
как упростить выражение? (любое) — Спрашивалка
как упростить выражение? (любое) — СпрашивалкаЛК
Любашка Кислякова
- выражение
Georg
Научитесь вычислять степени с натуральными показателями. 2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий.
2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий.
Нередко в выражениях необходимо извлекать корни. Корни четной степени извлекаются только из неотрицательных выражений или чисел. Корни нечетной степени извлекаются из любых выражений.
Di
Dimarik
Упростить выражение — это значит раскрыть все скобки (если это возможно), совершить все возможные действие и в результате должно получится маленькое выражение, решаемое всего несколькими действиями или даже одним.
Например: х+(2*3+7)
Упрощаем: х+(6+7)
И еще: х+13
Все. Это уже максимально упрощенное выражение. Решить его можно, только зная значение х (это именно выражение, а не равенство или уравнение)
удачи
РИ
Рома Изотов
вынесением за скобки, сведением общих. 2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий.
2*в*с) =2/(а*с) . Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т. к. легче проверить результаты промежуточных действий.
4
Нередко в выражениях необходимо извлекать корни. Корни четной степени извлекаются только из неотрицательных выражений или чисел. Корни нечетной степени извлекаются из любых выражений.
Похожие вопросы
Как упростить выражение ?
Упростите выражение.
Как упростить выражение?
Упростите выражения:
как упростить выражение
Раскройте скобки и упростите выражения:
Упростите выражение)
Упростите выражение! Упростить выражение: sinacos2a+sin2acosa
помогите упростить выражение:
Ребятушки, поможете упростить выражение?
Урок 15.
 Упрощение выражений — гдз по математике для 6 класса Зубарева И.И., Мордкович А.Г.
Упрощение выражений — гдз по математике для 6 класса Зубарева И.И., Мордкович А.Г.Класс
1 класс
2 класс
- Математика
- Английский язык
3 класс
- Английский язык
- Русский язык
- Математика
4 класс
- Математика
- Русский язык
- Английский язык
5 класс
- Биология
- Английский язык
- Русский язык
- Математика
6 класс
- Математика
- Биология
- Английский язык
- Русский язык
7 класс
- Химия
- Английский язык
- Русский язык
- Физика
- Математика
- Биология
8 класс
- Английский язык
- Биология
- Химия
- Математика
- Физика
- Русский язык
9 класс
- Химия
- Биология
- Английский язык
- Физика
- Русский язык
- Математика
10 класс
- Биология
- Математика
- Физика
- Химия
- Английский язык
11 класс
- Химия
- Английский язык
- Биология
6 КЛАСС
Урок 15.
 Упрощение выражений
Упрощение выраженийВнимательно читайте условие задания.
Соседи числа — это число, которое предшествует этому числу при счете (предыдущее число), и число, которое при счёте следует за ним.
Увеличить число на несколько единиц - использовать действие сложение, знак"+" Уменьшить на несколько единиц- использовать действие вычитание, знак "-".
Сумма, разность, произведение рациональных чисел является рациональным числом (без деления на нуль).
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми.
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого и второго чисел плюс квадрат второго числа.
Непростые натуральные числа, больше 1, называют составными числами
Вычитание — обратное сложению арифметическое действие, посредством которого от одной величины отнимается другая величина.
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа и второго плюс утроенное произведение первого числа и квадрата второго плюс куб второго числа.
Чтобы определить, делиться ли одно натуральное число на другое, можно это делимое число разложить на множители.
Запомните: натуральные числа - те, которые используем при счете (когда нам необходимо посчитать людей или предметы).
Задача на нахождение суммы всегда решается действием сложения. Задача на нахождение остатка решается действием вычитания. знак "-"
Разность квадратов двух чисел равно произведению суммы этих чисел и их разности.
Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат их суммы.
Натуральные числа не могут быть отрицательными. Поэтому натуральное число получаем, если мы из большего отнимаем меньшее, но не наоборот.
Сантиметр (см) – единица измерения длины. Дециметр (дм) – более крупная единица измерения длины.1 дм = 10 см.
10 единиц какого−либо разряда, дает 1 единицу более высокого разряда.
Два действительных числа равны между собой, если они имеют одинаковые знаки и их абсолютные величины имеют одинаковые целые части и одинаковые цифры соответствующих разрядов.
Умножение обратно делению и наоборот деление обратное умножению. Так как в примерах первое число сначала делится(умножается) на одно число и умножается(делится) на это же число, то решением уравнения будет первое число из выражения.
Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности.
Правила: от перемены местами множителей произведение не меняется; чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель; чтобы найти неизвестное делимое, нужно частное умножить на делитель; чтобы найти неизвестный делитель, нужно делимое разделить на частное
Рациональные числа − это числа, которые можно записать в виде десятичной периодической дроби. Иррациональные числа − это числа, которые можно записать в виде бесконечной десятичной непериодической дроби. Действительные числа − это все рациональные и иррациональные числа.
Свойства многочленов: 1) Члены многочлена можно менять местами.2) Прибавление к многочлену нуля или нулевого многочлена не изменят его. 3) В многочлене можно приводить подобные члены.
Чтобы раскрыть скобки, перед которыми стоит знак "+", скобки можно опустить, не меняя знаки слагаемых в скобках. Чтобы раскрыть скобки, перед которыми стоит знак "−", скобки можно опустить, изменив знак каждого слагаемого в скобках, не противоположный. Чтобы заключить многочлен в скобки со знаком "+" перед ними, нужно записать в скобках все его члены с теми же знаками. Чтобы заключить многочлен в скобки со знаком "−" перед ними, нужно записать в скобках все его члены с противоположными знаками.
Алгебраическая дробь не определена, когда при подстановке числового значения вместо переменной получается деление на нуль.
Для разложения многочлена на множители можно использовать: 1) вынесение общего множителя за скобки; 2) применение формул сокращенного умножения; 3) способ группировки; 4) выделение полного квадрата;
Внимательно читайте условие задания.
Соседи числа — это число, которое предшествует этому числу при счете (предыдущее число), и число, которое при счёте следует за ним.
Ответ: 3 кг; 45 кг.
Увеличить число на несколько единиц - использовать действие сложение, знак"+" Уменьшить на несколько единиц- использовать действие вычитание, знак "-".
Сумма, разность, произведение рациональных чисел является рациональным числом (без деления на нуль).
Вопросники:
Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.
Ответ: 23·(42−12)=32.
Пример 2Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Пример 3Представьте выражение со степенями 9-b3·π-12 в виде произведения.
Решение
Представим число 9 как степень 32 и применим формулу сокращенного умножения:
9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1
Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
Определение 2- ar·as=ar+s;
- ar:as=ar−s;
- (a·b)r=ar·br;
- (a:b)r=ar:br;
- (ar)s=ar·s.
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.
Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Пример 4Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.
Ответ: a2,5·(a2)−3:a−5,5=a2.
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5Найти значение степенного выражения 313·713·2123.
Решение
Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.
Есть еще один способ провести преобразования:
313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21
Ответ: 313·713·2123=31·71=21
Пример 6
Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.
Решение
Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.
Ответ: t3−t−6.
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2
Ответ: 3·523·513-5-231+2·x2-3-3·x2=-122+x2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a0,3:
a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a
б) Обратим внимание на знаменатель:
x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162
Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т. е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12
Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.
Пример 9Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.
Получаем:
30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14
Ответ: а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10Выполните действия x12+1×12-1-x12-1×12+1·1×12.
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
Приведем их к общему знаменателю:
x12-1·x12+1
Вычтем числители:
x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12
Теперь умножаем дроби:
4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12
Произведем сокращение на степень x12, получим 4×12-1·x12+1.
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.
Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1
Пример 11Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение
Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.
Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.
Переходим от последнего произведения к дроби x138x2,7+1.
Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить на x3·(x+1)0,2.
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12Представьте выражение x19·x·x36 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x≥0 и x·x3≥0 , которые задают множество [0, +∞).
На этом множестве мы имеем право перейти от корней к степеням:
x19·x·x36=x19·x·x1316
Используя свойства степеней, упростим полученное степенное выражение.
x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13
Ответ: x19·x·x36=x13.
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.
Теперь поделим обе части равенства на 72·x. Это выражение на ОДЗ переменной x принимает только положительные значения:
Это выражение на ОДЗ переменной x принимает только положительные значения:
5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0
Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.
Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Вопрос.ру — «Как упрощать выражения правильно?»
Вопрос от #29447 1325 дней назад
Как упрощать выражения правильно?
Ответ от Дарья
1. Подобные члены. Это члены с переменной одного порядка, члены с одинаковыми переменными или свободные члены (члены, не содержащие переменную). Другими словами, подобные члены включают одну переменную в одной и той же степени, включают несколько одинаковых переменных или не включают переменную вовсе. Порядок членов в выражении не имеет значения.
Например, 3×2 и 4×2 — это подобные члены, так как они содержат переменную «х» второго порядка (во второй степени). Однако х и x2 не являются подобными членами, так как содержат переменную «х» разных порядков (первого и второго). Точно так же -3yx и 5хz не являются подобными членами, так как содержат разные переменные.
2.
Разложение на множители. Это нахождение таких чисел, произведение которых приводит к исходному числу. Любое исходное число может иметь несколько множителей. Например, число 12 может быть разложено на следующий ряд множителей: 1 × 12, 2 × 6 и 3 × 4, поэтому можно сказать, что числа 1, 2, 3, 4, 6 и 12 являются множителями числа 12.
Подобные члены. Это члены с переменной одного порядка, члены с одинаковыми переменными или свободные члены (члены, не содержащие переменную). Другими словами, подобные члены включают одну переменную в одной и той же степени, включают несколько одинаковых переменных или не включают переменную вовсе. Порядок членов в выражении не имеет значения.
Например, 3×2 и 4×2 — это подобные члены, так как они содержат переменную «х» второго порядка (во второй степени). Однако х и x2 не являются подобными членами, так как содержат переменную «х» разных порядков (первого и второго). Точно так же -3yx и 5хz не являются подобными членами, так как содержат разные переменные.
2.
Разложение на множители. Это нахождение таких чисел, произведение которых приводит к исходному числу. Любое исходное число может иметь несколько множителей. Например, число 12 может быть разложено на следующий ряд множителей: 1 × 12, 2 × 6 и 3 × 4, поэтому можно сказать, что числа 1, 2, 3, 4, 6 и 12 являются множителями числа 12. Множители совпадают с делителями, то есть числами, на которые делится исходное число.
Например, если вы хотите разложить на множители число 20, запишите это так: 4 × 5.
Обратите внимание, что при разложении на множители переменная учитывается. Например, 20x = 4(5x).
Простые числа не могут быть разложены на множители, потому что они делятся только на себя и на 1.
3. Запомните и соблюдайте порядок выполнения операций во избежание ошибок.
Скобки
Степень
Умножение
Деление
Сложение
Вычитание
4.Запишите выражение. Простейшие алгебраические выражения (которые не содержат дробей, корней и так далее) можно решить (упростить) всего за несколько шагов.
Например, упростите выражение 1 + 2x — 3 + 4x.
5. Определите подобные члены (члены с переменной одного порядка, члены с одинаковыми переменными или свободные члены).
Найдите подобные члены в этом выражении. Члены 2x и 4x содержат переменную одного порядка (первого). Кроме того, 1 и -3 — это свободные члены (не содержат переменную). Таким образом, в этом выражении члены 2х и 4x являются подобными, и члены 1 и -3 тоже являются подобными.
Множители совпадают с делителями, то есть числами, на которые делится исходное число.
Например, если вы хотите разложить на множители число 20, запишите это так: 4 × 5.
Обратите внимание, что при разложении на множители переменная учитывается. Например, 20x = 4(5x).
Простые числа не могут быть разложены на множители, потому что они делятся только на себя и на 1.
3. Запомните и соблюдайте порядок выполнения операций во избежание ошибок.
Скобки
Степень
Умножение
Деление
Сложение
Вычитание
4.Запишите выражение. Простейшие алгебраические выражения (которые не содержат дробей, корней и так далее) можно решить (упростить) всего за несколько шагов.
Например, упростите выражение 1 + 2x — 3 + 4x.
5. Определите подобные члены (члены с переменной одного порядка, члены с одинаковыми переменными или свободные члены).
Найдите подобные члены в этом выражении. Члены 2x и 4x содержат переменную одного порядка (первого). Кроме того, 1 и -3 — это свободные члены (не содержат переменную). Таким образом, в этом выражении члены 2х и 4x являются подобными, и члены 1 и -3 тоже являются подобными. 6. Приведите подобные члены. Это значит сложить или вычесть их и упростить выражение.
2x + 4x = 6х
1 — 3 = -2
7.
Перепишите выражение с учетом приведенных членов. Вы получите простое выражение с меньшим количеством членов. Новое выражение равно исходному.
В нашем примере: 1 + 2x — 3 + 4x = 6х — 2, то есть исходное выражение упрощено и с ним легче работать.
8. Соблюдайте порядок выполнения операций при приведении подобных членов. В нашем примере было легко привести подобные члены. Однако в случае сложных выражений, в которых члены заключены в скобки и присутствуют дроби и корни, привести подобные члены не так просто. В этих случаях соблюдайте порядок выполнения операций.
Например, рассмотрим выражение 5(3x — 1) + х((2x)/(2)) + 8 — 3x. Здесь было бы ошибкой сразу определить 3x и 2x как подобные члены и привести их, потому что сначала необходимо раскрыть скобки. Поэтому выполните операции согласно их порядку.
5(3x-1) + x((2x)/(2)) + 8 — 3x
15x — 5 + x(x) + 8 — 3x
15x — 5 + x2 + 8 — 3x. Теперь, когда в выражении присутствуют только операции сложения и вычитания, вы можете привести подобные члены.
6. Приведите подобные члены. Это значит сложить или вычесть их и упростить выражение.
2x + 4x = 6х
1 — 3 = -2
7.
Перепишите выражение с учетом приведенных членов. Вы получите простое выражение с меньшим количеством членов. Новое выражение равно исходному.
В нашем примере: 1 + 2x — 3 + 4x = 6х — 2, то есть исходное выражение упрощено и с ним легче работать.
8. Соблюдайте порядок выполнения операций при приведении подобных членов. В нашем примере было легко привести подобные члены. Однако в случае сложных выражений, в которых члены заключены в скобки и присутствуют дроби и корни, привести подобные члены не так просто. В этих случаях соблюдайте порядок выполнения операций.
Например, рассмотрим выражение 5(3x — 1) + х((2x)/(2)) + 8 — 3x. Здесь было бы ошибкой сразу определить 3x и 2x как подобные члены и привести их, потому что сначала необходимо раскрыть скобки. Поэтому выполните операции согласно их порядку.
5(3x-1) + x((2x)/(2)) + 8 — 3x
15x — 5 + x(x) + 8 — 3x
15x — 5 + x2 + 8 — 3x. Теперь, когда в выражении присутствуют только операции сложения и вычитания, вы можете привести подобные члены. x2 + (15x — 3x) + (8 — 5)
x2 + 12x + 3
9. Найдите наибольший общий делитель (НОД) всех коэффициентов выражения. НОД — это наибольшее число, на которое делятся все коэффициенты выражения.
Например, рассмотрим уравнение 9×2 + 27x — 3. В этом случае НОД=3, так как любой коэффициент данного выражения делится на 3.
10.
Разделите каждый член выражения на НОД. Полученные члены будут содержать меньшие коэффициенты, чем в исходном выражении.
В нашем примере разделите каждый член выражения на 3.
9×2/3 = 3×2
27x/3 = 9x
-3/3 = -1
Получилось выражение 3×2 + 9x — 1. Оно не равно исходному выражению.
11. Запишите исходное выражение как равное произведению НОД на полученное выражение. То есть заключите полученное выражение в скобки, а за скобки вынесите НОД.
В нашем примере: 9×2 + 27x — 3 = 3(3×2 + 9x — 1)
12. Упрощение дробных выражений с помощью вынесения множителя за скобки. Зачем просто выносить множитель за скобки, как это было сделано ранее? Затем, чтобы научиться упрощать сложные выражения, например дробные выражения.
x2 + (15x — 3x) + (8 — 5)
x2 + 12x + 3
9. Найдите наибольший общий делитель (НОД) всех коэффициентов выражения. НОД — это наибольшее число, на которое делятся все коэффициенты выражения.
Например, рассмотрим уравнение 9×2 + 27x — 3. В этом случае НОД=3, так как любой коэффициент данного выражения делится на 3.
10.
Разделите каждый член выражения на НОД. Полученные члены будут содержать меньшие коэффициенты, чем в исходном выражении.
В нашем примере разделите каждый член выражения на 3.
9×2/3 = 3×2
27x/3 = 9x
-3/3 = -1
Получилось выражение 3×2 + 9x — 1. Оно не равно исходному выражению.
11. Запишите исходное выражение как равное произведению НОД на полученное выражение. То есть заключите полученное выражение в скобки, а за скобки вынесите НОД.
В нашем примере: 9×2 + 27x — 3 = 3(3×2 + 9x — 1)
12. Упрощение дробных выражений с помощью вынесения множителя за скобки. Зачем просто выносить множитель за скобки, как это было сделано ранее? Затем, чтобы научиться упрощать сложные выражения, например дробные выражения. В этом случае вынесение множителя за скобки может помочь избавиться от дроби (от знаменателя).
Например, рассмотрим дробное выражение (9×2 + 27x — 3)/3. Воспользуйтесь вынесением множителя за скобки, чтобы упростить это выражение.
Вынесите множитель 3 за скобки (как вы делали это ранее): (3(3×2 + 9x — 1))/3
Обратите внимание, что теперь и в числителе, и в знаменателе присутствует число 3. Его можно сократить, и вы получите выражение: (3×2 + 9x – 1)/1
Так как любая дробь, у которой в знаменателе находится число 1, равна просто числителю, то исходное дробное выражение упрощается до: 3×2 + 9x — 1.
В этом случае вынесение множителя за скобки может помочь избавиться от дроби (от знаменателя).
Например, рассмотрим дробное выражение (9×2 + 27x — 3)/3. Воспользуйтесь вынесением множителя за скобки, чтобы упростить это выражение.
Вынесите множитель 3 за скобки (как вы делали это ранее): (3(3×2 + 9x — 1))/3
Обратите внимание, что теперь и в числителе, и в знаменателе присутствует число 3. Его можно сократить, и вы получите выражение: (3×2 + 9x – 1)/1
Так как любая дробь, у которой в знаменателе находится число 1, равна просто числителю, то исходное дробное выражение упрощается до: 3×2 + 9x — 1.
Вернуться к списку вопросов
Действия с числовыми и алгебраическими выражениями (Г.Г. Гаицгори) 7 класс онлайн-подготовка на Ростелеком Лицей |
Повторение (алгебраическое выражение)
Определение: алгебраическое выражение – это любая составленная со смыслом запись, которая может содержать только числа, буквы, знаки действия и скобки. Например, .
Например, .
Можно вычислить значение алгебраического выражения при заданных значениях переменных, для этого достаточно подставить значение в выражение и выполнить вычисления. Например, при значение выражения : .
Задача на вычисление значения алгебраического выражения при заданном значении переменной
Задача 1. Найдите значение выражения при .
Решение. Подставим значение в выражение и выполним вычисления:
Ответ: .
В задаче 1 получилось деление на 0. Можно попробовать поделить 3 на 0, например, на калькуляторе. Убедитесь сами, что калькулятор не смог найти значение этого выражения. Не получится и у нас. Деление на 0 не имеет смысла, не определено.
Почему деление на ноль не определено?
0 был введен как часть большого механизма под названием целые числа для обозначения отсутствия чего-то. 0 облегчает счет и запись чисел, но нулевого количества нет, на него не укажешь пальцем, поэтому сказать, сколько 0 содержится в другом числе нельзя.
0 облегчает счет и запись чисел, но нулевого количества нет, на него не укажешь пальцем, поэтому сказать, сколько 0 содержится в другом числе нельзя.
Разделить 3 на 0 означает сказать, сколько раз в 3 ничего нет. Ответить на вопрос, сколько в гараже квадратных метров можно, но ответить, сколько в нем пустоты, – нет.
Если бы был придуман какой-то смысл для выражения , то это противоречило бы некоторым известным свойствам и определениям, например свойствам умножения, поэтому деление на 0 не определяют.
Можно все же попробовать разделить 3 на 0. Деление – это действие, обратное умножению, т.е., если .
Но при умножении на 0 всегда получается 0, т.е. такого просто не существует.
Рассмотрим случай деления 0 на 0, чтобы не возникало ощущения, что он – особый и отличается от деления 3 на 0.
Равенство будет справедливым для любого , потому что Но результат деления должен быть конкретным числом. Снова получаем противоречие.
Поэтому деление на 0 в математике не определено.
Недопустимые значения переменных
Подставить в алгебраическое выражение можно любое число, но не всегда получится посчитать его значение.
Определение: такие значения переменной, при которых выражение не определено (нельзя вычислить его значение), называют недопустимыми значениями.
На данный момент мы знакомы только с одним таким случаем. Например, если в выражении есть дробь или деление , то мы не будем подставлять в выражение такие значения переменной, при которых знаменатель обращается в 0: .
Есть и другие случаи появления недопустимых значений переменных, но о них мы узнаем позже, по мере изучения различных функций.
Рассмотрим примеры на определение недопустимых значений переменных в выражениях.
Пример 1. Определить недопустимые значения переменной в выражении .
Решение. Выражение представляет собой дробь, поэтому её знаменатель не может обращаться в 0: .
Таким образом, недопустимым значением переменной является 0, т.е. выражение определено для любых .
Ответ: 0.
Пример 2. Определить недопустимые значения переменной в выражении .
Решение. Выражение представляет собой дробь, поэтому её знаменатель не может обращаться в 0: .
Таким образом, недопустимым значением переменной является 5, т.е. выражение определено для любых .
Ответ: 5.
Где еще можно встретить деление на ноль?
Докажем, что . Введем переменные , пусть .
Запишем:
Получим равенство:
Перегруппируем слагаемые и получим:
Вынесем общий множитель за скобки в каждой из частей равенства:
Разделим обе части равенства на и получим:
Получили, что . В чём подвох? Дело в том, что в наше «доказательство» вкралась ошибка: было выполнено деление на 0 при делении обеих частей равенства на выражение (по предположению эти числа равны: ).
Это пример математического софизма – утверждения с доказательством, в котором кроются ошибки. Софизмы бывают не только математическими, например, фраза «Ты не терял то, что у тебя есть. Ты не терял рога и хвост. Значит, у тебя есть рога и хвост» содержит логическую ошибку: из первой фразы не следует, что у тебя есть всё, что ты не терял.
Наиболее известными софизмами являются апории Зенона. Подробнее узнать о них вы можете по этой ссылке.
Действия с числовыми выражениями
Мы уже сталкивались с эквивалентными выражениями, когда приводили дроби к общему знаменателю. Мы записывали цепочки эквивалентных дробей и выбирали из них те, у которых одинаковый знаменатель:
и
Например, в данном случае это будут дроби: .
Эквивалентные выражения можно заменять друг другом, от этого смысл и значение записи не изменится.
Например, пусть есть выражение . Можно выполнить умножение и получить выражение . Оба эти числовых выражения равны, эквивалентны.
Можно выполнить умножение и получить выражение . Оба эти числовых выражения равны, эквивалентны.
Если же выполнить все действия в каком-то числовом выражении, то получится его значение: , т.е. – значение числового выражения . Выполнив все действия, мы упростили числовое выражение.
Действия с алгебраическими выражениями
Алгебраические выражения могут быть записаны по-разному, но означать одно и то же, например: и .
Можно ли сказать, что выражение упрощено? Обычно под упрощением подразумевают эквивалентную запись в таком виде, чтобы для вычисления значения выражения нужно было выполнить как можно меньше действий.
Например, чтобы вычислить значение выражения при заданном значении переменной необходимо выполнить 3 действия, а для выражения – одно действие. Конечно, разница в 2 действия невелика, но, если бы такую операцию нужно было бы проделать 50 раз, тогда разница была бы уже в целых 100 действий.
Задача 2. Докажите, что выражение эквивалентно выражению .
Докажите, что выражение эквивалентно выражению .
Доказательство
Дважды воспользуемся распределительным законом :
Задача 3. Упростите выражение: .
Решение. Воспользуемся формулой разности квадратов :
Ответ: .
Сравним количество действий, которое необходимо сделать, чтобы вычислить первое выражение и второе. В первом случае нужно было выполнить 5 действий, а во втором – только 1. В таких случаях говорят, что мы упростили алгебраическое выражение.
Недопустимые значение переменных
Найдем недопустимые значения переменных для выражения: .
Знаменатель дроби содержит переменные, определим, когда он обратится в 0:
Т.е. недопустимыми значениями переменных будут противоположные значения. Например, если , то .
Эквивалетность выражений
Выражения и не являются эквивалентными для любых и , т. к. первое выражение определено, когда , а второе выражение определено при любых значениях переменных и .
к. первое выражение определено, когда , а второе выражение определено при любых значениях переменных и .
Т.е. эти выражения будут эквивалентными только для таких и , которые не являются противоположными числами.
Примеры упрощения алгебраических выражений
Задача 4. Упростите выражение: .
Решение. Воспользуемся распределительным законом, чтобы раскрыть обе скобки:
Ответ: .
Задача 5. Упростите выражение: .
Решение: воспользуемся распределительным законом, чтобы раскрыть внутренние скобки, затем упростим полученное в скобках выражение и снова применим распределительный закон:
Ответ: .
Всегда ли лучше упрощать выражение
Задача 1. Найдите значение выражения , если , .
Решение.
Вычисление с упрощением выражения (воспользуемся формулой разности квадратов, которая была записана ранее):
Вычисление без упрощения выражения:
Ответ: 30.
В данном случае оказалось, что считать быстрее, если выражение не упрощать.
Таким образом, упрощать или не упрощать выражение, нужно решать в зависимости от условия и удобства решения конкретной задачи.
Задача 6. Пусть и – некоторые натуральные числа. Докажите, что разность чисел и делится на 4.
Доказательство
Рассмотрим разность чисел: .
Упростим выражение – раскроем скобки (помним, что минус перед скобками относится к обоим слагаемым в скобках):
делится на , значит, и эквивалентное ему исходное выражение делится на .
Доказано
Заключение
На этом уроке мы вспомнили, как работать с числовыми выражениями, и научились работать с алгебраическими выражениями. Мы научились находить допустимые и недопустимые значения переменных для выражений, содержащих дроби или деление, а также обсудили, что значит упростить алгебраическое выражение.
Мы научились находить допустимые и недопустимые значения переменных для выражений, содержащих дроби или деление, а также обсудили, что значит упростить алгебраическое выражение.
Список рекомендованной литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник. «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник. «Просвещение», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «edufuture.biz» (Источник)
- Интернет-портал «school-assistant.ru» (Источник)
Домашнее задание
- Найдите значение выражения при .
- Упростите выражение: .

- Раскройте скобки и докажите, что .
Упрощение выражений — определение, с показателями, примеры
Упрощение выражений означает переписывание одного и того же алгебраического выражения без похожих членов и в компактной форме. Для упрощения выражений мы объединяем все подобные члены и раскрываем все заданные скобки, если они есть, и тогда в упрощенном выражении у нас останутся только непохожие члены, которые не могут быть сокращены дальше. Давайте узнаем больше об упрощении выражений в этой статье.
| 1. | Как упростить выражения? |
| 2. | Упрощение выражений с показателями |
| 3. | Упрощение выражений с помощью распределительного свойства |
| 4. | Упрощение выражений с дробями |
| 5. | Часто задаваемые вопросы об упрощении выражений |
Как упростить выражения?
Прежде чем изучать упрощение выражений, давайте быстро рассмотрим значение выражений в математике. Выражения относятся к математическим утверждениям, содержащим как минимум два термина, содержащих либо числа, либо переменные, либо и то, и другое, соединенные оператором сложения/вычитания между ними. Общее правило для упрощения выражений — PEMDAS — означает Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. В этой статье мы больше сосредоточимся на том, как упростить алгебраические выражения. Давайте начнем!
Выражения относятся к математическим утверждениям, содержащим как минимум два термина, содержащих либо числа, либо переменные, либо и то, и другое, соединенные оператором сложения/вычитания между ними. Общее правило для упрощения выражений — PEMDAS — означает Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. В этой статье мы больше сосредоточимся на том, как упростить алгебраические выражения. Давайте начнем!
Нам нужно научиться упрощать выражения, так как это позволит нам более эффективно работать с алгебраическими выражениями и упростить наши вычисления. Чтобы упростить алгебраические выражения, выполните шаги, указанные ниже:
- Шаг 1: Решите скобки, добавляя/вычитая одинаковые члены внутри скобок и умножая члены в скобках на множитель, написанный снаружи. Например, 2x (x + y) можно упростить как 2x 2 + 2xy.
- Шаг 2: Используйте правила экспоненты, чтобы упростить термины, содержащие экспоненты.

- Шаг 3: Добавьте или вычтите одинаковые члены.
- Шаг 4: Наконец, запишите полученное выражение в стандартной форме (от высшей степени к низшей степени).
Для лучшего понимания возьмем пример. Упростите выражение: х (6 – х) – х (3 – х). Здесь есть две круглые скобки, каждая из которых содержит два разных термина. Итак, сначала мы будем решать скобки, умножая x на члены, написанные внутри. x(6 — x) можно упростить как 6x — x 2 и -x(3 — x) можно упростить как -3x + x 2 . Теперь объединение всех членов даст 6x — x 2 — 3x + x 2 . В этом выражении 6x и -3x подобны термам, а -x 2 и x 2 подобны термам. Таким образом, сложение этих двух пар одинаковых членов даст (6x — 3x) + (-x 2 + x 2 ). Путем дальнейшего упрощения мы получим 3x, что и будет окончательным ответом. Следовательно, х (6 – х) – х (3 – х) = 3х.
Посмотрите на приведенное ниже изображение, показывающее еще один пример упрощенного выражения.
Правила упрощения алгебраических выражений
Основное правило упрощения выражений состоит в том, чтобы объединять одинаковые термины вместе и писать непохожие термины как есть. Некоторые из правил упрощения выражений перечислены ниже:
- Чтобы добавить два или более одинаковых членов, добавьте их коэффициенты и запишите с ними общую переменную.
- Используйте распределительное свойство, чтобы открыть скобки в выражении, которое говорит, что a (b + c) = ab + ac.
- Если сразу за скобками стоит знак минус, измените знак всех терминов, написанных внутри этой скобки, чтобы упростить ее.
- Если за скобками стоит знак «плюс» или положительный знак, просто снимите скобку и напишите термины как есть, сохранив их первоначальные знаки.
Упрощение выражений с показателями
Упрощение выражений с показателями степени осуществляется путем применения правил показателей степени к терминам. Например, (3x 2 )(2x) можно упростить как 6x 3 . Таблица правил экспоненты, которую можно использовать для упрощения алгебраических выражений, приведена ниже:
Таблица правил экспоненты, которую можно использовать для упрощения алгебраических выражений, приведена ниже:
| Правило нулевой экспоненты | а 0 = 1 |
| Правило экспоненты идентичности | 1 = |
| Правило продукта | a м × a n = a m+n |
| Частное правило | a м /a n = a m-n |
| Отрицательные степени Правило | а -м = 1/а м ; (а/б) -м = (б/а) м |
| Сила силы Правило | (а м ) н = а мн |
| Сила продукта Правило | (ab) м = a м b м |
| Степень частного правила | (a/b) м = a м /b м |
Пример: Упростить: 2ab + 4b (b 2 — 2a).
Чтобы упростить это выражение, давайте сначала раскроем скобку, умножив 4b на оба слагаемых, написанных внутри. Отсюда следует, что 2ab + 4b (b 2 ) — 4б (2а). Используя правило произведения показателей, можно записать как 2ab + 4b 3 — 8ab, что равно 4b 3 — 6ab.
Вот как мы можем упростить выражения с показателями, используя правила показателей.
Упрощение выражений с помощью распределительного свойства
Распределительное свойство утверждает, что выражение, заданное в форме x (y + z), может быть упрощено как xy + xz. Это может быть очень полезно при упрощении выражений. Посмотрите на приведенные выше примеры и посмотрите, использовали ли мы это свойство для упрощения выражений и как. Возьмем еще один пример упрощения 4(2a + 3a + 4) + 6b с использованием дистрибутивного свойства.
Следовательно, 4(2a + 3a + 4) + 6b упрощается как 20a + 6b + 16. Теперь давайте узнаем, как использовать распределительное свойство для упрощения выражений с дробями.
Упрощение выражений с помощью дробей
Когда дроби даны в выражении, мы можем использовать распределительное свойство и правила экспоненты, чтобы упростить такое выражение. Например, 1/2 (x + 4) можно упростить как x/2 + 2. Давайте возьмем еще один пример, чтобы понять это.
Пример: Упростите выражение: 3/4x + y/2 (4x + 7).
Используя распределительное свойство, данное выражение можно записать как 3/4x + y/2 (4x) + y/2 (7). Теперь, чтобы умножить дроби, мы умножаем числители и знаменатели отдельно. Итак, y/2 × 4x/1 = (y × 4x)/2 = 4xy/2 = 2xy. И у/2 × 7/1 = 7у/2. Следовательно, 3/4x + y/2 (4x + 7) = 3/4x + 2xy + 7y/2. Все три не похожи друг на друга термины, поэтому это упрощенная форма данного выражения.
При упрощении выражений с дробями мы должны следить за тем, чтобы дроби были в простейшей форме и в упрощенном выражении присутствовали только непохожие члены. Например, (2/4)x + 3/6y не является упрощенным выражением, поскольку дроби не приводятся к наименьшей форме. С другой стороны, x/2 + 1/2y имеет упрощенную форму, так как дроби имеют сокращенную форму, и оба термина отличаются друг от друга.
С другой стороны, x/2 + 1/2y имеет упрощенную форму, так как дроби имеют сокращенную форму, и оба термина отличаются друг от друга.
► Похожие темы:
Ознакомьтесь с интересными статьями, посвященными концепции упрощения выражений в математике.
- Калькулятор упрощения выражений
- Упрощение рациональных выражений
- Упрощение подкоренных выражений
Часто задаваемые вопросы об упрощении выражений
Что такое упрощение выражений в математике?
В математике упрощение выражений — это способ записи выражения в самой низкой форме путем объединения всех похожих терминов вместе. Это требует от человека знакомства с понятиями арифметических операций над алгебраическими выражениями, дробями и показателями. Мы следуем тому же правилу PEMDAS для упрощения алгебраических выражений, что и для простых арифметических выражений. Наряду с PEMDAS, правила экспоненты и знания об операциях над выражениями также необходимо использовать при упрощении алгебраических выражений.
Какие математические понятия важны для упрощения выражений?
Математические понятия, важные для упрощения алгебраических выражений, приведены ниже:
- Знакомство с похожими и разными алгебраическими терминами.
- Требуется базовое знание алгебраических выражений.
- Сложение и вычитание алгебраических выражений.
- Умножение и деление выражений.
- Понимание терминов с показателями степени и правил степени.
- Алгебраические тождества и свойства.
Каковы правила упрощения выражений?
Ниже приведены правила упрощения выражений:
- Следуйте правилу PEMDAS, чтобы определить порядок упрощения терминов в выражении.
- Распределительное свойство можно использовать для упрощения умножения двух членов в алгебраическом выражении.
- Правила экспоненты можно использовать для упрощения терминов с экспонентами.
- Сначала раскрываем скобки, если они есть. Затем упростим члены, содержащие показатели.

- После этого соедините все подобные термины.
- Упрощенное выражение будет содержать только непохожие члены, связанные операторами сложения/вычитания, которые нельзя упростить дальше.
Как упростить выражения?
Следуйте приведенным ниже шагам, чтобы научиться упрощать выражения:
- Раскройте скобки, если они есть. Если за скобкой стоит положительный знак, то снять скобку и записать все термины, сохраняя их первоначальные знаки. Если за скобкой стоит знак минус, то снять скобку и поменять знаки всех написанных внутри терминов с + на -, а — на +. И если есть число или переменная, написанная сразу за скобкой, то умножьте ее на все члены внутри, используя распределительное свойство.
- Используйте правила экспоненты для упрощения терминов с экспонентами, если таковые имеются.
- Добавить/вычесть все одинаковые термины.
- Запишите упрощенное выражение в стандартной форме (от члена с наибольшей степенью к члену с наименьшей степенью).

Чем отличаются упрощение выражений и решение уравнений?
Уравнения относятся к операторам, которые имеют знак равенства «=» между терминами, написанными слева, и терминами, написанными справа. Решение уравнений означает нахождение значения заданной неизвестной переменной. С другой стороны, упрощение выражений означает только приведение выражения к самой низкой форме. Он не предназначен для нахождения значения неизвестной величины.
Что такое пример упрощения выражений?
Упрощение алгебраических выражений относится к процессу приведения выражения к наименьшей форме. Пример упрощения алгебраических выражений приведен ниже:
2x + 6x (y — 7) — 8
= 2x + 6xy — 42x — 8
= 6xy — 40x — 8
Упрощение выражений | Brilliant Math & Science Wiki
Эшли То, Ашиш Менон, Радж Магеш, а также
способствовал
Содержимое
- Объединение похожих терминов
- Умножение и деление мономов
- Экспоненты
- Смотрите также
«Похожие термины» относятся к терминам, переменные которых абсолютно одинаковы, но могут иметь разные коэффициенты. Например, термины 2xy 2xy2xy и 5xy5xy5xy похожи, поскольку имеют одну и ту же переменную xyxyxy. Термины 2xy 2xy2xy и 2x2x2x не одинаковы.
Например, термины 2xy 2xy2xy и 5xy5xy5xy похожи, поскольку имеют одну и ту же переменную xyxyxy. Термины 2xy 2xy2xy и 2x2x2x не одинаковы.
Объединение похожих терминов означает добавление (или вычитание) подобных терминов вместе, чтобы получить только один термин.
Что такое 2xy+5xy 2xy + 5xy 2xy+5xy?
Поскольку 2xy2xy2xy и 5xy5xy5xy подобны термам (с переменной xyxyxy), мы можем сложить их коэффициенты, чтобы получить 2xy+5xy=(2+5)xy=7xy 2xy + 5xy = (2+5) xy = 7 xy 2xy+5xy=(2+5)xy=7xy. □ _\квадрат □
Что такое 5xy-3xy5xy — 3xy5xy-3xy?
Поскольку 5xy5xy5xy и 3xy3xy3xy подобны слагаемым (с переменной xyxyxy), мы можем вычесть их коэффициенты вместе, чтобы получить 5xy−3xy=(5−3)xy=2xy5xy — 3xy = (5-3) xy = 2xy 5xy− 3xy=(5−3)xy=2xy. □ _\квадрат □ 92 -а -7. \ _\квадрат (2a3+a3)−4a2+(a−2a)−(5+2)=3a3−4a2−a−7. □
При сложении и вычитании полиномов дробной формы начните с нахождения общего знаменателя каждого члена.
Упростить 3a−12−a+24. \frac{3a — 1}{2} — \frac{a + 2}{4}. 23а−1−4a+2.
У нас есть
3а-12-а+24=(3а-12×22)-а+24=(6а-2)-(а+2)4=5а-44. □ \begin{выровнено} \frac{3a — 1}{2} — \frac{a + 2}{4} &= \left( \frac{3a — 1}{2} \times \frac{2}{2} \right) — \ гидроразрыв {а + 2} {4} \\ &= \frac{(6a — 2) — (a+2)}{4} \\ &= \frac{5a — 4}{4}. \ _\площадь \end{выровнено} 23a−1−4a+2=(23a−1×22)−4a+2=4(6a−2)−(a+2)=45a−4. □ 97. \ _\квадрат 3ab2×(−2a4b5)=(3×−2)×(a1×a4)×(b2×b5)=−6a5b7. □
При делении вы можете преобразовать деление в умножение с переменными точно так же, как с константами. Например:
2÷3=2×13x÷y=x×1y \begin{align} 2 \div 3 &= 2 \times \frac{1}{3} \\ х \ дел у &= х \ раз \ гидроразрыва {1} {у} \end{выровнено} 2÷3x÷y=2×31=x×y1
и
2÷13=2×3x÷1y=x×y. \begin{выровнено} 2 \div \frac{1}{3} &= 2 \times 3 \\ x \div \frac{1}{y} &= x \times y. \end{выровнено} 2÷31x÷y1=2×3=x×y. 9{\color{#624F41}a} 66+66+66+66+66+66=6a
Если a\color{#624F41} aa удовлетворяет приведенному выше уравнению, каково значение a\color{#624F41} аа?
- Дроби
- Рационализация знаменателей
- Решение уравнений
Цитировать как: Упрощение выражений. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/simplifying-expressions/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/simplifying-expressions/
TOP 9 что значит упростить выражение ЛУЧШИЙ и НОВЫЙ
Вы задаетесь вопросом , что значит упростить выражение , но в настоящее время нет ответа, поэтому позвольте kienthuctudonghoa.com обобщить и перечислить лучшие статьи с вопросом. ответьте на вопрос, что значит упростить выражение, что поможет вам получить наиболее точный ответ. Следующая статья надеется помочь вам сделать более подходящий выбор и получить больше полезной информации
Mục lục
- 10052
- 2 2. Упрощение выражений — определение, с показателями, примеры
- 3 3. Упрощение выражений — приемы и примеры
- 4 4. Что значит упростить выражение? – Quora
- 5 5.Упрощение выражений – YouTube
- 6 6.Что значит упростить рациональное выражение – YouTube
- 7 7.Упрощение выражений | Brilliant Math & Science Wiki
- 8 8.
 Упрощение в алгебре — математика — это весело
Упрощение в алгебре — математика — это весело - 9 9. Как упростить алгебраические выражения — видео и стенограмма урока
1.Simplifying Expressions – Varsity Tutors
- Author: www.varsitytutors.com
- Post date: 14 yesterday
- Rating: 4(1386 reviews)
- Highest rating: 3
- Низкий рейтинг: 3
- Резюме: Упростить выражение означает написать эквивалентное выражение, не содержащее похожих членов. Это означает, что мы перепишем выражение с …
См. Подробная информация
2. Ограничение выражений — Определение, с показателями, примеры
- Автор: www.cuemath.com
- Post Date: 9 вчера
- Rateing: 999999999999 гг.
- Высшая оценка: 5
- Низкая оценка: 3
- Резюме: Упрощение выражений означает переписывание одного и того же алгебраического выражения без похожих членов и в компактной форме.
 Чтобы упростить выражения, мы объединяем все …
Чтобы упростить выражения, мы объединяем все …
См. Подробная информация
3. Ограничение выражений — уловки и примеры
- Автор: www.storyofmathematics.com
- Post Date: 16 вчера
- Rate Самый высокий рейтинг: 3
- Низкий рейтинг: 1
- Сводка:
Подробнее
4.Что значит упростить выражение? – Квора
- Автор: www.quora.com
- Дата поста: 8 вчера
- . Резюме: Упрощать что-либо означает облегчить понимание или выполнение. Когда вы что-то упрощаете, вы разбиваете это на более мелкие, более управляемые части. Это может …
Подробнее
5. Упрощение выражений — YouTube
- Author: www.youtube.com
- Post date: 13 yesterday
- Rating: 2(1813 reviews)
- Highest rating: 3
- Low rated: 3
- Резюме:
Подробнее
6.
 Что значит упростить рациональное выражение – YouTube
Что значит упростить рациональное выражение – YouTube- Автор: www.youtube.com
- Дата публикации: 1 89049 вчера0052
- Рейтинг: 5 (653 обзоры)
- Высокий рейтинг: 3
- Низкий рейтинг: 3
- . Brilliant Math & Science Wiki
- Автор: Brilliant.org
- Пост Дата: 8 вчера
- Рейтинг: 3 (450 Обзоры)
- .0048 Низкий рейтинг: 2
- Резюме: Упростить математическое выражение означает представить его в наименее сложной форме. В общем, самая простая форма — это та, в которой используется …
Подробнее
8. Упрощение в алгебре — математика — это весело
- Автор: www.mathsisfun.com
- 520 Дата публикации: 2 9048 Вчера
- Рейтинг: 3(688 отзывов)
- Высший рейтинг: 4
- Низкий рейтинг: 1
- Резюме: Упрощение: сделать проще! упростить 4x+2x до 6x.
 Одна из важных задач, которую мы выполняем в алгебре, — это упрощение. Вас часто просят положить что -нибудь…
Одна из важных задач, которую мы выполняем в алгебре, — это упрощение. Вас часто просят положить что -нибудь…
См. Подробность
9. Как упростить алгебраические выражения — видео и стенограмма урока
- Автор: Исследование. Рейтинг:
- Высшая оценка: 3
- Низкая оценка: 2
- Резюме: Что значит упростить выражение? Упрощение числового выражения — это вопрос выполнения …
См. подробности
Приведенная выше информация о вопросе , что означает упрощение выражения , безусловно, помогла вам получить желаемый ответ, пожалуйста, поделитесь этой статьей со всеми . так что каждый может знать эту полезную информацию. Желаю тебе хорошего дня!
Top EN —Simplify Expressions With the Order of Operations
Learning Outcomes
- Recognize и объединить похожие термины в выражение
- Используйте порядок операций для упрощения выражений
Введение
Несколько важных терминов, прежде чем мы начнем:
- операции/операторы: В математике мы называем такие операции, как умножение, деление, сложение и вычитание.
 3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Это как сказать, что четыре яблока плюс три яблока равно семи яблокам. Но два яблока плюс шесть апельсинов не могут быть объединены и упрощены, потому что они не «подобны терминам». Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином. 92+3x-1[/latex]
3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Это как сказать, что четыре яблока плюс три яблока равно семи яблокам. Но два яблока плюс шесть апельсинов не могут быть объединены и упрощены, потому что они не «подобны терминам». Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином. 92+3x-1[/latex]Показать решение
В следующем видео вам будет показан еще один пример сочетания похожих терминов. Обратите внимание, почему у вас не получается объединить в примере все три термина.
youtube.com/embed/b9-7eu29pNM?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Порядок действий
Вы можете помнить или не помнить порядок действий для применения нескольких математических операций к одному выражению. Точно так же, как для нас является социальным соглашением ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для предоставления шаблонного плана, которому нужно следовать, когда вам необходимо использовать несколько математических операций для одного выражения. .
Порядок действий
- Сначала выполните все операции внутри группирующих символов. К символам группировки относятся круглые скобки ( ), квадратные скобки [ ], фигурные скобки { } и дроби.
- Вычисление показателей степени или квадратных корней.
- Умножение или деление слева направо.
- Сложение или вычитание слева направо.

Этот порядок операций верен для всех действительных чисел.
В следующем примере показано, как упростить выражение, содержащее как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также нужно будет вспомнить, как выполнять эти вычисления.
В следующем видеоролике показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание с элементами, содержащими дроби.
Экспоненты и квадратные корни
В этом разделе мы расширим наши навыки, применяя правила порядка операций к выражениям с экспонентами и квадратными корнями.
 Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] — это основание, а [latex]2[/latex] — это показатель степени — показатель степени определяет, сколько раз основание умножается само на себя.
Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] — это основание, а [latex]2[/latex] — это показатель степени — показатель степени определяет, сколько раз основание умножается само на себя.Экспоненты — это способ представления многократного умножения; порядок операций помещает его перед любым другим умножением, делением, вычитанием и сложением.
В следующем видео выражение с показателями в его терминах упрощается с помощью порядка операций.
При наличии группирующих символов внутри группирующих символов расчет производится изнутри наружу. То есть сначала начните упрощение внутри самых внутренних группирующих символов.
Помните, что круглые скобки также могут использоваться для обозначения умножения.
 В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения.
В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения.В следующем видеоролике показано, как использовать порядок операций для упрощения выражения с помощью группировки символов, показателей степени, умножения и сложения. 9{3}}\cdot \,32[/latex]
Используйте поле ниже, чтобы записать несколько мыслей о том, как упростить это выражение с помощью дробей и символов группировки.
Показать решение
Некоторые люди используют поговорку, чтобы запомнить порядок действий. Это высказывание называется PEMDAS или P лизинг E извините M y D ухо A unt S союзник. Первая буква каждого слова начинается с той же буквы арифметической операции.
P аренда [латекс] \displaystyle \Rightarrow [/латекс] P арензы (и другие символы группировки)
E xcuse [латекс] \displaystyle \Rightarrow [/латекс] E экспонентыM
y D ухо [латекс] \displaystyle \Rightarrow [/latex] M умножение и D ivision (слева направо)
A unt S союзник [латекс] \displaystyle \Rightarrow латекс] A дополнение и S вычитание (слева направо)Примечание: Несмотря на то, что в пословице умножение предшествует делению, деление может выполняться первым.
 Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке запутать ваше понимание этого!
Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке запутать ваше понимание этого!Сводка
Порядок операций дает нам согласованную последовательность для использования в вычислениях. Без порядка операций вы могли бы найти разные ответы на одну и ту же вычислительную задачу. (Некоторые из первых калькуляторов и некоторые недорогие НЕ используют порядок операций. Чтобы использовать эти калькуляторы, пользователь должен вводить числа в правильном порядке.)
Упрощение определения и значения | Dictionary.com.
[ sim-pluh-fahy ]
/ ˈsɪm pləˌfaɪ /
Сохранить это слово!
См. синонимы для: упрощать / упрощать / упрощать / упрощение на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
глагол (используется с дополнением), упрощенный, упрощенный.

сделать менее сложным или сложным; сделать проще или проще: упростить проблему.
ВИКТОРИНА
Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Происхождение упрощения
1645–55; <французский simplifier<средневековая латынь simplificāre to make simple, эквивалент латинского simpli- (объединение формы simplussimple) + -ficāre-fy
ДРУГИЕ СЛОВА ИЗ упрощение
sim·pli·fi·ca·tion, существительноеsim·pli·fi ·ca·tive, прилагательноеsim·pli·fi·er, sim·pli·fi·ca·tor, существительноеnon·sim·pli·fi·ca·tion, существительное
su·per·sim·pli·fy, глагол ( используется с объектом), суперупрощенный, суперупрощенный, упрощённый, прилагательноенеупрощающий, прилагательное
СЛОВА, КОТОРЫЕ МОГУТ СПУТАТЬ С Упрощение
простой, упрощенный , упрощённыйСлова рядом упрощают
симплекс, симплексный метод, симплицидентат, простота, Симплициус, упрощать, упрощать, упрощенный, Симплон, Симплон Пасс, просто
Dictionary.
 com Unabridged
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
com Unabridged
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022Слова, относящиеся к упрощению
уточнить, сократить, облегчить, уменьшить, сократить, упростить, сократить, проанализировать, наказать, расшифровать, распутать, разъяснить, объяснить, интерпретировать, упорядочить, расшифровать, уварить, сломать, сломать, очистить
Как использовать упрощение в предложении
Сообщение Обновленное фразовое соответствие Google упрощает ключевые слова и беспокоит рекламодателей, появившихся первыми в поисковой системе.
Обновленное сопоставление фраз Google упрощает ключевые слова и беспокоит рекламодателей|Джордж Нгуен|9 февраля 2021 г.|Search Engine Land
Чтобы разные устройства могли общаться друг с другом, этот тип системы связи должен был быть стандартизирован или упрощен, поэтому все единицы могут понимать друг друга.
Советы от Элоизы: простой способ проверить окупаемость инвестиций|Элоиза Элоиза|2 февраля 2021 г.
 |Washington Post
|Washington PostДля авторов эта функция упрощает процесс ответов на вопросы, поскольку позволяет им просматривать всех своих поклонников ‘ вопросы в одном месте.
Новая функция TikTok «Вопросы и ответы» позволяет авторам отвечать на вопросы фанатов с помощью текста или видео|Сара Перес|20 января 2021 г.|TechCrunch
К счастью, появились другие идеи, предлагающие способы продвижения полиномов более высокой степени, которые можно упростить с помощью замена.
Математики воскрешают 13-ю проблему Гильберта|Стивен Орнс|14 января 2021 г.|Журнал Quanta
Новые медицинские протоколы упростят расследования НБА в отношении игроков, которых снимают на камеру в общественных местах.
Ужесточенные протоколы НБА о коронавирусе ограничивают объятия перед игрой, постояльцев отелей и выходы на публику|Бен Голливер|12 января 2021 г.|Washington Post
«Он увел меня от джаза и помог мне упростить мое ремесло и начать писать коммерческие песни вещь, — говорит она.

Становление Киесы: от морского снайпера до королевы красоты и поп-дивы|Марлоу Стерн|20 октября 2014|DAILY BEAST
Но Эрдоган либо не знает об этом, либо пытается упростить историю.
Президент Турции объявляет Лоуренса Аравийского более сильным врагом, чем ИГИЛ|Джейми Деттмер|13 октября 2014 г.|DAILY BEAST
Они одновременно чрезмерно упрощают и разжигают конфликт, который и без того плохо изучен.
Троллинг в Твиттере усугубляет израильско-палестинский конфликт?|Эмили Шайр|22 июля 2014 г.|DAILY BEAST
Second Market предлагает решения для частных компаний и инвестиционных фондов, чтобы упростить рынки частного капитала.
Внутри японского ограбления биткойнов|Джейк Адельштейн|28 февраля 2014 г.|DAILY BEAST
Крупный бизнес требует комплексной налоговой реформы, которая упростит их жизнь.
Тайна раскрыта: вот почему крупный бизнес продолжает поддерживать республиканцев, даже когда республиканцы разрушают экономику|Дэниел Гросс|3 октября 2013 г.
 |DAILY BEAST
|DAILY BEASTИ этот факт, казалось, был наполнен свидетельством душевного состояния Гордона; похоже, это не упростило ситуацию.
Уверенность|Генри Джеймс
Он почти надеялся, что Наполеон все-таки применит силу, и что для упрощения ситуации придет война с Францией.
Жизнь Мадзини|Болтон Кинг
Люди, которые смотрят на вещи таким образом, упрощают дела для Ангела-Записывающего.
Рыжая корова и ее друзья|Питер Макартур
Очевидно, кого-то надо убрать, чтобы упростить этот клубок, но кого?
Немецкий Помпадур|Мари Хей
Но некоторые из нас могли бы упростить день и таким образом найти место для полного удовольствия вечером.
Girls and Women|Harriet E. Paine (AKA E. Chester}
Определения в британских словарях для упрощения
упрощения
/ (ˈsɪmplɪˌfaɪ) /
— verby
сделать менее сложным, ясным или простым
математику, чтобы привести (уравнение, дробь и т.
 д.) к более простой форме путем исключения общих множителей, перегруппировки терминов в одной переменной и т. д.
д.) к более простой форме путем исключения общих множителей, перегруппировки терминов в одной переменной и т. д.Производные формы упрощения
упрощение, существительное, прилагательное, упрощение, существительноеПроисхождение слова для упрощения
C17: через французский язык от средневековой латыни simplificāre, от латинского simplus simple + facere to make
Collins English Dictionary — Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Упрощение математического определения — Как обсудить
Упрощение математического определения
Что означает упрощение в математике? Упрощение в математике, как и в английском языке, означает максимальное упрощение. В примере = 36 + 10. Для простоты становится = 46, потому что максимально просто.
Что значит упростить в математическом примере?
Упрощение означает выполнение чего-то менее сложного или менее запутанного.
 Примером упрощения является объяснение сложного математического понятия с использованием терминов, которые очень легко понять ребенку.
Примером упрощения является объяснение сложного математического понятия с использованием терминов, которые очень легко понять ребенку.Есть ли «математическое» определение «упрощения»?
Упрощение алгебраического выражения можно определить как запись выражения в его наиболее эффективной и компактной форме без изменения значения исходного выражения. Процесс заключается в сборе похожих терминов, добавлении или вычитании терминов в предложении.
Что такое упрощение математики?
Например, упрощение — это процесс замены математического выражения более простым (обычно более коротким) эквивалентным выражением.
Что такое упрощенное 3/6?
Для этого сначала найдите наибольший общий делитель 3 и 6, который равен 3. Затем разделите 3 и 6 на наибольший общий делитель, чтобы получить следующую упрощенную дробь: 1/2. Следовательно, выполняется это равенство: 3/6 = 1/2. Если числитель больше или равен знаменателю дроби, то такая дробь называется неправильной.

Как упростить выражение в математике?
Знать метод. При упрощении математических выражений нельзя просто идти слева направо, умножать, складывать, вычитать и т. д. Некоторые математические операции имеют приоритет над другими и должны выполняться в первую очередь. На самом деле, переговоры вне очереди могут дать вам неверный ответ.
Что значит упростить выражение?
Ответ: Слово «упрощать» означает «упрощать». Чтобы упростить выражение, вам нужно исключить ненужные числа или термины, обычно путем их исключения или факторизации. Это может относиться к построению числовой задачи или более краткой группировке похожих терминов в алгебраическом выражении.
Математическое определение упрощения
Что такое упрощение? Определение, факты и пример. Сократите дробь до наименьшего числа, удалив наименьший общий знаменатель для числителя и знаменателя, или сократите алгебраическое выражение, группируя и комбинируя одинаковые члены.

Что означает простейшая форма в математике?
Простейшая форма числа или выражения состоит в том, чтобы записать его в основной форме. Например, простейшая форма дроби состоит в том, чтобы упростить дробь и записать дробь в ее простейшей или наименьшей форме путем деления числителя и знаменателя на их общий множитель.
Что означает упрощение в математике?
Что такое упрощение? Определение, факты и пример. Сократите дробь до наименьшего числа, исключив наименьший общий знаменатель для числителя и знаменателя, или сократите алгебраическое выражение, группируя и комбинируя одинаковые члены.
Что такое упрощение выражений в математике?
- Знай метод. При упрощении математических выражений нельзя просто идти слева направо, умножать, складывать, вычитать и т. д.
- Начните с решения всех терминов в скобках. В математике скобки указывают на то, что содержащиеся в них термины должны оцениваться отдельно от окружающего выражения.

- Определите экспонентов.
Как упростить выражение с помощью дробей?
Сложные регулярные выражения — это дроби, которые делятся на дроби. Как только вы нашли наименьший общий делитель, вам нужно умножить две дроби на общий делитель. При делении 4/х на 3/у общий делитель равен ху. Таким образом, вы должны умножить на xy вверху и внизу. Затем упростите выражение.
Что означает упрощение среднего в алгебре
Сократите дробь до наименьших членов, исключив наименьший общий знаменатель для числителя и знаменателя, или сжав алгебраическое выражение, группируя и комбинируя одинаковые члены. Упрощение облегчает понимание и решение алгебраических выражений.
Что значит упростить алгебраическое выражение?
Упрощая алгебраическое выражение, они относятся к наиболее компактному и эффективному написанию без изменения смысла выражения. В основном он собирает равные члены, то есть складывает все, что можно добавить.

Что означает «с точки зрения» в алгебре?
В алгебраическом выражении элементы терминов разделены знаками плюс или минус. В этом примере есть четыре терма: 3x 2, 2y, 7xy и 5. Термы могут состоять из переменных и коэффициентов или констант. Переменные В алгебраических выражениях буквы обозначают переменные. Эти буквы на самом деле являются замаскированными числами.
Что означает упрощение в математическом определении
1. Сделать проще, яснее или проще. 2. (Математика) Математика для приведения (уравнений, дробей и т. д.) к более простой форме путем устранения общих множителей, группировки членов в одной переменной и т. д.
Что означает самый простой математический термин?
Простейшая форма — это наименьшая возможная эквивалентная дробь числа. Шаги, чтобы найти простейшую форму: Найдите общие делители числителя и знаменателя.
Что означает термин в математике
В элементарной математике термин представляет собой число или переменную, или произведение нескольких чисел или переменных.
 Термины разделяются знаком + или в глобальном выражении. Например 3+4x+5yzw. 3, 4x и 5yzw — это три отдельных термина. В контексте полиномов этот термин может означать моном с одним коэффициентом.
Термины разделяются знаком + или в глобальном выражении. Например 3+4x+5yzw. 3, 4x и 5yzw — это три отдельных термина. В контексте полиномов этот термин может означать моном с одним коэффициентом.Что такое общий термин в математике?
Определение общего термина. — Математическое выражение переменных и констант, определяющее последовательные элементы последовательности или ряда, когда одна из переменных, часто обозначаемая как k, заменяется целыми числами.
Каковы основные математические термины?
Урок английского языка по основам математики. Это ДОБАВИТЬ, ПЛЮС, ДОБАВИТЬ, МИНУС, Вычесть, ВЫЧИСЛИТЬ, МНОЖЕСТВО, ВРЕМЯ, ДЕЛЕНИЕ, РАВНО, ЧЕТНОЕ И НЕЧЕТНОЕ, ДЕСЯТЫЙ, ДЕСЯТЫЙ, ПОЛОВИНА.
Каково определение термина в математике?
В элементарной математике термин представляет собой число или переменную, или произведение нескольких чисел или переменных. Термины разделяются знаком + или в глобальном выражении.
 Например внутри.
Например внутри.Что означает в математике?
По математике! означает «факультет». Факультет имеет множество приложений, таких как комбинаторика, алгебра и математический анализ. Факториал обозначается n! , где н!
Какое другое слово для упрощения?
Альтернативные синонимы для упрощения: Объяснение исключения учетной записи, Сокращение, Сокращение изменения.
Какая самая простая форма математики?
Простейшая форма (дроби) Простейшая форма дроби состоит в том, что верх и низ не могут быть меньше (и при этом быть целыми числами). Пример: 2/4 можно упростить до 1/2. Чтобы упростить дробь, разделите верхнюю и нижнюю часть на наибольшее число, которое можно разделить на два числа.
Что означает простое определение выражения?
Упрощение выражения часто означает удаление пары круглых скобок; разложение выражения часто означает его применение. Предположим, вы начинаете с выражения 5 x (2 x 2 3 x + 7).

Что значит упростить?
Определение упрощено. Переходный глагол. Короче: как. a: Верните его к основам. b: Уменьшить объем или сложность: необходима рационализация для упрощения административных процедур.
Что значит упростить в математических дробях
Что значит упростить дробь? Упростить или уменьшить дробь означает привести числитель и знаменатель к их наименьшему числу или как можно меньшему и сохранить одну и ту же часть целого. И почему вы хотите это сделать?
Как преобразовать дроби в простейшую форму?
Правила преобразования процентов в дроби в простейшей форме. Процент записывается в виде дроби со 100 в знаменателе. Например 30% = $\frac {30}{100}$ Эта дробь затем упрощается и сокращается до меньших значений. Пример: 30% = $\frac{30}{100}=\frac{3}{10}$.
Как записать дробь в простейшей форме?
Дроби в их простейшей форме. Есть два разных способа записать дробь в ее простейшей форме.
 1) Разделить на общие множители. 2) Поделиться с ЗКФ. Дробь находится в наименьшем члене, когда единственный общий знаменатель между числителем и знаменателем равен 1.
1) Разделить на общие множители. 2) Поделиться с ЗКФ. Дробь находится в наименьшем члене, когда единственный общий знаменатель между числителем и знаменателем равен 1.Как упростить сложную дробь?
Упрощение сложных дробей с помощью LCD-умножения Преобразование смешанных чисел в неправильные дроби. Сократите каждую фракцию, если это возможно. Найдите наименьший общий делитель (НОД) всех дробей в вашей сложной дроби. Умножьте числитель и знаменатель сложной дроби с помощью ЖК-дисплея.
Что такое 9 6 упрощенный?
Дробь 9 6 равна 1 1 2. Эта дробь не является допустимой дробью, поскольку абсолютное значение верхнего числа или числителя (9) больше абсолютного значения нижнего числа или знаменателя (6). Следовательно, эквивалентная дробь — это смешанное число, состоящее из целого числа (1) и правильной дроби (1 2).
Что означает упрощение в математических терминах, примеры
Math. Например, упрощение — это процесс замены математического выражения более простым (обычно более коротким) эквивалентным выражением.
 Упрощение дроби до разложимой дроби.
Упрощение дроби до разложимой дроби.Как упростить выражение?
Вот основные шаги, которые необходимо выполнить, чтобы упростить алгебраическое выражение: Удалите круглые скобки, умножив множители. Используйте правила экспоненты, чтобы удалить круглые скобки, относящиеся к метрикам. Объединяйте одинаковые термины, добавляя коэффициенты. комбинировать константы.
Как упростить выражения, комбинируя одинаковые термины?
Упростите алгебраическое выражение, комбинируя одинаковые термины. Подобные термины имеют одну и ту же переменную, возведенную в один и тот же показатель степени (или степени). Определите термины, которые имеют аналогичную форму, а затем объедините вероятности. Помните, что при объединении одних и тех же терминов объединяются только вероятности; форма переменной остается неизменной.
Что значит написать упрощенное математическое выражение, используя
Упрощение выражения — это еще один способ сказать, что вы можете решить математическую задачу.
 В основном, упрощая предложение, старайтесь писать его как можно проще. Ведь больше нельзя складывать, вычитать, умножать или делить. Возьмем, к примеру, это выражение:.
В основном, упрощая предложение, старайтесь писать его как можно проще. Ведь больше нельзя складывать, вычитать, умножать или делить. Возьмем, к примеру, это выражение:.Что означает запись упрощенного математического выражения в стандартной форме
Упрощение алгебраического выражения можно определить как запись выражения в его наиболее эффективной и компактной форме без изменения смысла исходного выражения. Процесс включает в себя сбор похожих терминов, добавление или вычитание терминов в предложении.
Когда выражение имеет простейшую форму?
Как правило, термин используется в самой простой форме, когда его проще всего использовать. Пример: 5x + x — 3 Это проще, чем: 6x — 3 Общие методы, которые помогут вам упростить: • Объедините одинаковые термины • Разложите на множители • Расширьте (в отличие от разложения на множители) • Удалите дроби путем умножения.
Какой пример числа в стандартной форме?
Записывайте их последовательно, чтобы облегчить чтение очень больших и малых чисел.
 Любое число, которое вы можете записать в виде десятичной дроби между числами и умножить на степень 10, называется стандартной формой. ✕ 10¹³ ✕ 10¹³ являются примерами чисел в стандартной форме. Учитесь с подробным учебником по математике K5.
Любое число, которое вы можете записать в виде десятичной дроби между числами и умножить на степень 10, называется стандартной формой. ✕ 10¹³ ✕ 10¹³ являются примерами чисел в стандартной форме. Учитесь с подробным учебником по математике K5.Как лучше всего упростить выражение?
Как упростить выражения? Упрощение алгебраического выражения можно определить как запись выражения в его наиболее эффективной и компактной форме без изменения смысла исходного выражения. Процесс включает в себя сбор похожих терминов, добавление или вычитание терминов в предложении.
Какая самая простая форма уравнения?
Как правило, термин используется в самой простой форме, когда его проще всего использовать. Пример: 5x + x — 3. Легче, чем: 6x — 3.
Как упростить рациональные выражения?
Действия по упрощению регулярных выражений. 1) Найдите множители, которые имеют общие числитель и знаменатель. 2) 3x — это общий множитель для числителя и знаменателя.
 Обратите внимание, что x ≠ 0 очевидно. 3) Исключить общий множитель. 4) Если возможно, поищите другие факторы, общие для числителя и знаменателя.
Обратите внимание, что x ≠ 0 очевидно. 3) Исключить общий множитель. 4) Если возможно, поищите другие факторы, общие для числителя и знаменателя.Что такое упрощение математических задач
Упростите вычисления, решая небольшие части задачи по одной, используя правило порядка действий. Сначала найдите числа в скобках. Затем вы решаете задачу на умножение, а затем на деление, всегда слева направо. Наконец, решите сложение и вычитание слева направо. 94 как х х х х. Затем сократите все в числителе и знаменателе. Затем умножьте оставшиеся переменные и константы. Результатом является выражение в его простейшей форме.
Что такое алгебраические выражения?
- Части алгебраического выражения. Алгебраическое выражение содержит переменную с коэффициентами или без них, математический оператор и иногда константу.
- Выражения и алгебраические термины.
- Типы алгебраических выражений.
- Упрощение алгебраических выражений.

- Алгебраические формулы для решения алгебраических выражений.
Каковы примеры упрощения выражений?
- Разделить числитель и знаменатель на множители. Единственный способ узнать, имеют ли числитель и знаменатель общие множители, — это разложить их на множители!
- Список ограниченных значений. Здесь полезно отметить ограничения.
- Устранить общие факторы. Теперь обратите внимание, что числитель и знаменатель имеют общий множитель.
- Окончательный ответ.
Какие есть примеры математических выражений?
- Алгебраическое мономиальное выражение.
- Биномиальное выражение
- Полиномиальное выражение.
- Числовое выражение: Математическое выражение включает в себя как числа, так и пилоты.
- Variable Expression: это выражение, которое содержит не только числа, но и переменные, такие как B.6x + y, 7xy + 6 и т. д.
Почему важно упростить математическую задачу?
Упрощение математической задачи — это стратегия, часто используемая в сочетании с другими стратегиями решения задач.
 Когда проблема слишком сложна, чтобы решить ее за один шаг, часто бывает полезно разбить ее на более простые задачи и решить каждую из них по отдельности. Чтобы построить более простую задачу из более сложной, может потребоваться переформулировать задачу с меньшими, более простыми числами или использовать более знакомый сценарий, чтобы понять проблему и найти решение.
Когда проблема слишком сложна, чтобы решить ее за один шаг, часто бывает полезно разбить ее на более простые задачи и решить каждую из них по отдельности. Чтобы построить более простую задачу из более сложной, может потребоваться переформулировать задачу с меньшими, более простыми числами или использовать более знакомый сценарий, чтобы понять проблему и найти решение.Определение термина по математике
Термин (математика) Математический термин, который может составлять отделимую часть уравнения, ряда или другого термина, используемого в математической логике, универсальной алгебре и системах парафраз. Термин – это математическое выражение.
Что означают термины в математике?
Найдите значение математических слов по модулю. : Всегда положительное число, абсолютное значение относится к расстоянию между числами от 0. Биссектриса угла. : линия, которая делит угол на два равных угла. Коробчатая и вискерная диаграмма / график. Дополнительные углы: два угла, сумма которых равна 9.
 0°. Наибольший общий фактор.
0°. Наибольший общий фактор.Какой термин определяется как математический?
Математика (от греческого: μάθημα, máthēma, знание, изучение, изучение) включает изучение таких тем, как количество (теория чисел), структура (алгебра), пространство (геометрия) и изменение (исчисление). Общепринятого определения нет.
Что означает математический термин?
Математика (прил.) Или относящаяся к природе математики. Книга по математике, состоящая из логарифмической линейки и других математических пособий, предлагает математическое решение математической задачи с доказательством. числовой, математический (прил.) по отношению к числам или способность думать или работать с числами.
Что означает оценка в алгебре?
Вычисление означает упрощение выражения. Когда вас попросят оценить алгебраическое выражение, вы должны вставить конкретное значение переменной в выражение и найти его. Например, вас могут попросить оценить 2x {\displaystyle 2x}, когда x = 2 {\displaystyle x=2}.

Как оценивать по математике?
- Определите переменную и ее значение. Эта информация должна быть предоставлена вам.
- Заменяет указанное значение переменной. Для этого вставьте указанное значение в выражение, где вы видите переменную.
- Произведите необходимые расчеты.
- Вычислите выражение с двумя переменными.
Что означает слово оценивать?
Оценка — это нахождение ценности чего-либо. Обычно это означает что-то рассказать. Иногда вы заменяете значения переменными и оцениваете или вычисляете полученные значения.
Что означает оценка в науке?
Оценка — это оценка того, на что был похож опыт, когда вы его решили, на что, по вашему мнению, он был похож и что можно было бы улучшить, если бы его пришлось повторить. Оценка является важной частью научного метода, и ваша письменная оценка находится в конце экспериментального письма, обычно как часть заявления.

Математическое определение коэффициента
Определение коэффициента — это число или символ, который позволяет получить математический результат. Примером коэффициента является 6 в следующем алгебраическом уравнении: 6 x 2. Число или символ, умноженный на неизвестную переменную или величину в алгебраическом термине.
Что такое коэффициент в математическом выражении?
- Всегда помните, что с переменной связан коэффициент.
- Переменные без номера имеют коэффициент 1 1.
- Знаете ли вы, почему переменная называется переменной?
Какое математическое определение коэффициента?
В математике коэффициент — это коэффициент умножения члена полинома, ряда или любого выражения. Обычно это число, но может быть и любое выражение.
Что означает слово «коэффициент» в математике?
В математике коэффициент — это коэффициент умножения члена полинома, ряда или любого выражения. Обычно это число, но может быть и любое выражение (включая такие переменные, как a, b и c).


 ..
..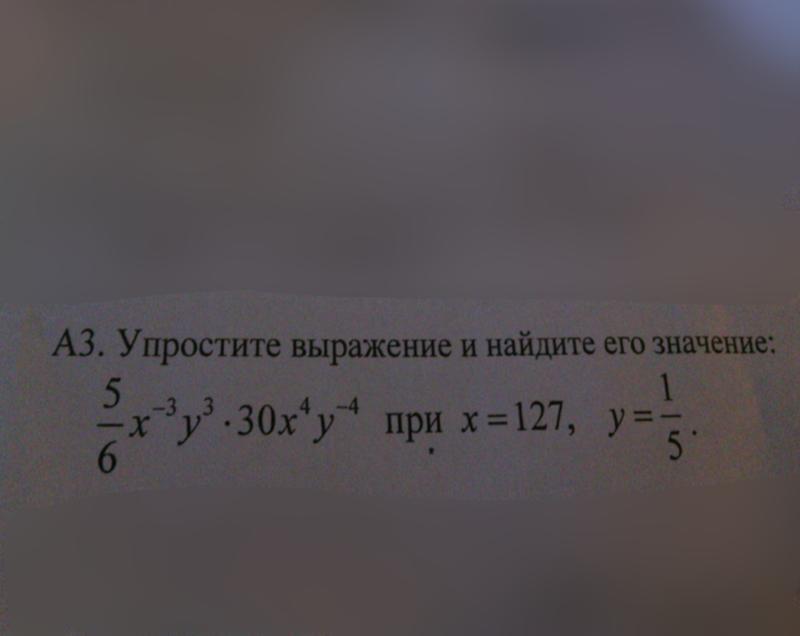 …
…

 2) Прибавление к многочлену нуля или нулевого многочлена не изменят его.
3) В многочлене можно приводить подобные члены.
2) Прибавление к многочлену нуля или нулевого многочлена не изменят его.
3) В многочлене можно приводить подобные члены.





 Упрощение в алгебре — математика — это весело
Упрощение в алгебре — математика — это весело Чтобы упростить выражения, мы объединяем все …
Чтобы упростить выражения, мы объединяем все … Одна из важных задач, которую мы выполняем в алгебре, — это упрощение. Вас часто просят положить что -нибудь…
Одна из важных задач, которую мы выполняем в алгебре, — это упрощение. Вас часто просят положить что -нибудь… 3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Это как сказать, что четыре яблока плюс три яблока равно семи яблокам. Но два яблока плюс шесть апельсинов не могут быть объединены и упрощены, потому что они не «подобны терминам». Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином. 92+3x-1[/latex]
3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Это как сказать, что четыре яблока плюс три яблока равно семи яблокам. Но два яблока плюс шесть апельсинов не могут быть объединены и упрощены, потому что они не «подобны терминам». Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином. 92+3x-1[/latex]
 Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] — это основание, а [latex]2[/latex] — это показатель степени — показатель степени определяет, сколько раз основание умножается само на себя.
Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] — это основание, а [latex]2[/latex] — это показатель степени — показатель степени определяет, сколько раз основание умножается само на себя. В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения.
В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения. Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке запутать ваше понимание этого!
Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке запутать ваше понимание этого!
 com Unabridged
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
com Unabridged
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022 |Washington Post
|Washington Post
 |DAILY BEAST
|DAILY BEAST д.) к более простой форме путем исключения общих множителей, перегруппировки терминов в одной переменной и т. д.
д.) к более простой форме путем исключения общих множителей, перегруппировки терминов в одной переменной и т. д. Примером упрощения является объяснение сложного математического понятия с использованием терминов, которые очень легко понять ребенку.
Примером упрощения является объяснение сложного математического понятия с использованием терминов, которые очень легко понять ребенку.

