Сумма (математика) | это… Что такое Сумма (математика)?
У этого термина существуют и другие значения, см. сумма.
Су́мма (лат. summa — итог, общее количество), результат сложения величин (чисел, функций, векторов, матриц и т. д.). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
а + b = b + aа + (b + с) = (а + b) + с(а + b) с = ас + bcс (а + b) = ca + cb
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы слагаемых множеств, взятые без повторений.
Содержание
|
Определенная сумма
Часто для краткости сумму n слагаемых ak, ak+1, …, aN обозначают заглавной греческой буквой Σ (сигма):
Это обозначение называют определённой (конечной) суммой по i от k до N.
Для удобства вместо иногда пишут , где — некоторое соотношение для , таким образом это конечная сумма всех , где
Свойства определённой суммы
Примеры
1. Сумма арифметической прогрессии:
2. Сумма геометрической прогрессии:
3.
Почему это так
4.
Почему это так
Доказательство:
5.
Почему это так
Доказательство:
- Стоит заметить, что при получаем , а это последовательность равенств следующего вида:
- Стоит заметить, что при получаем , а это последовательность равенств следующего вида:
Неопределённая сумма
Неопределённой суммой по называется такая функция , обозначаемая , что .
Формула Ньютона-Лейбница
Основная статья: Теорема Ньютона-Лейбница
Если найдена неопределённая сумма , то .
Этимология
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (S) первым ввёл Эйлер в 1755 году. Как вариант, использовалась греческая буква Сигма Σ. Позднее ввиду связи понятий суммирования и интегрирования, S также использовали для обозначения операции интегрирования.
Литература
Фихтенгольц Г.М. Курс дифференциального и интегрального исчесления. — седьмое. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
См. также
- Контрольная сумма
Использование функции СУММ для суммирования чисел в диапазоне
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Еще. ..Меньше
..Меньше
Для суммы чисел в диапазоне (группе ячеек) можно использовать простую формулу, но функцию СУММ проще использовать при работе с несколькими числами. Например, =СУММ(A2:A6) реже имеет ошибки при вводе, чем =A2+A3+A4+A5+A6.
Вот формула, использующая два диапазонаячеев: =СУММ(A2:A4;C2:C3) суммирует числа в диапазонах A2:A4 и C2:C3. Чтобы получить итоговую сумму в 39787, нажмите ввод.
Чтобы создать формулу:
-
Введите в ячейку =СУММ и открываю скобки (.
-
Чтобы ввести первый диапазон формул, который называется аргументом (частью данных, которую нужно выполнить), введите A2:A4 (или выберите ячейку A2 и перетащите ее через ячейку A6).

-
Введите запятую (,), чтобы отделить первый аргумент от следующего.
-
Введите второй аргумент C2:C3 (или перетащите его, чтобы выбрать ячейки).
-
Введите закрываюю скобки )и нажмите ввод.
Каждый аргумент может быть диапазоном, числом или ссылками на отдельные ячейки, разделенными запятой.
-
=СУММ(A2:A4;2429;10482)
org/ListItem»>
-
=СУММ(4823;12335;9718;C2:C3)
-
=СУММ(A2;A3;A4;2429;10482)
=СУММ(4823;A3:A4;C2:C3)
Совет: Если вам нужно свести столбцы или строки чисел рядом друг с другом, используйте авто сумму чисел.
Попробуйте попрактиковаться
Если вы хотите поиграть с образцом данных, воспользуйтесь некоторыми данными.
Чтобы узнать, как работает функция СУММ, скопируйте таблицу ниже в таблицу и вкопируйте ее в ячейку A1.
|
Данные |
||
|
-5 |
||
|
15 |
||
|
30 |
||
|
‘5 |
||
|
ИСТИНА |
||
|
Формула |
Описание |
Результат |
|
=СУММ(3;2) |
Прибавляет 3 и 2. |
5 |
|
=СУММ(«5»; 15; ИСТИНА) |
Прибавляет 5, 15 и 1. Текстовое значение «5» сначала переводится в число, а логическое значение ИСТИНА — в число 1. |
21 |
|
=СУММ(A2:A4) |
Суммы значений в ячейках A2-A4. |
40 |
|
=СУММ(A2:A4; 15) |
С суммой значений в ячейках A2–A4, а затем к результату прибавляет 15. |
55 |
|
=СУММ(A5;A6;2) |
Суммы значений в ячейках A5 и A6, а затем 2 к результату. Так как не числовые значения в ссылках не переводятся, значение в ячейке A5 (‘5) и значение в ячейке A6 (ИСТИНА) будут рассматриваться как текст, поэтому значения в этих ячейках игнорируются. |
2 |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Обозначение суммирования
|
Обозначения сигма и пи (обозначение суммирования и произведения) – MathMaine
Сигма (суммирование) Обозначение
Символ сигмы — заглавная буква греческого алфавита. Оно соответствует букве «S» в нашем алфавите и используется в математике для описания «суммирования», сложения или суммы нескольких терминов (подумайте о начальном звуке слова «сумма»: Sss igma = Sss мкм).
Символ сигмы можно использовать сам по себе для представления общей суммы… общей идеи суммы, неопределенного числа неуказанных терминов:
Но это не то, что можно оценить, чтобы получить конкретный ответ , так как нам не сказали, сколько членов включить в сумму, и нам не сказали, как определить значение каждого члена.
Более типичное использование обозначения сигма будет включать целое число ниже сигмы («номер начального члена») и целое число выше сигмы («номер конечного члена»). В приведенном ниже примере точные начальное и конечное числа не имеют большого значения, поскольку нас просят добавить одно и то же значение, два, несколько раз. Все, что имеет значение в этом случае, — это разница между начальным и конечным номерами термина… которая будет определять, сколько двоек нас просят добавить, по одной двойке для каждого номера термина.
В приведенном ниже примере точные начальное и конечное числа не имеют большого значения, поскольку нас просят добавить одно и то же значение, два, несколько раз. Все, что имеет значение в этом случае, — это разница между начальным и конечным номерами термина… которая будет определять, сколько двоек нас просят добавить, по одной двойке для каждого номера термина.
Сигма-нотация, или, как ее еще называют, нотация суммирования, обычно не стоит дополнительных чернил для описания простых сумм, таких как приведенная выше… умножение могло бы сделать это проще.
Сигма-нотация наиболее полезна, когда «номер термина» может использоваться каким-либо образом для вычисления каждого термина. Чтобы облегчить это, переменная обычно указывается под сигмой со знаком равенства между ней и номером начального члена. Если эта переменная присутствует в суммируемом выражении, то вместо переменной следует подставить текущий номер терма:
Обратите внимание, что можно иметь переменную ниже Sigma, но никогда не использовать ее. В таких случаях, как и в приведенном выше примере, который привел к связке двоек, добавляемый термин никогда не меняется:
В таких случаях, как и в приведенном выше примере, который привел к связке двоек, добавляемый термин никогда не меняется:
«Номер начального термина» не обязательно должен быть равен 1. Он может быть любым значением, включая 0. Для пример:
Это охватывает то, что вам нужно знать, чтобы начать работать с сигма-нотацией. Однако, поскольку сигма-нотация обычно имеет более сложные выражения после символа сигма, вот еще несколько примеров, чтобы дать вам представление о том, что возможно:
Обратите внимание, что последний пример выше иллюстрирует, что, используя свойство коммутативности сложения, сумму нескольких членов можно разбить на несколько сумм:
И, наконец, это обозначение может быть вложенный:
Самая правая сигма (аналогичная самой внутренней функции при работе с составными функциями) выше должна оцениваться первой. Как только это будет оценено, вы можете оценить следующую сигму слева. Круглые скобки также можно использовать, чтобы прояснить порядок оценки.
Круглые скобки также можно использовать, чтобы прояснить порядок оценки.
Пи (Продукт) Обозначение
Символ Пи — это заглавная буква греческого алфавита, называемая «Пи», и соответствует «Р» в нашем алфавите. Он используется в математике для представления произведения набора терминов (подумайте о начальном звуке слова «продукт»: Ppp i = Ppp roduct). Он используется так же, как описанный выше символ сигмы, за исключением того, что последующие члены умножаются, а не добавляются:
Резюме
Сигма (суммирование) и Пи (произведение) используются в математике для обозначения многократного сложения или умножения. Сигма-нотация обеспечивает компактный способ представления многих сумм и широко используется при работе с арифметическими или геометрическими рядами. Нотация Пи обеспечивает компактный способ представления многих продуктов.
Чтобы использовать их, вам понадобится выражение «закрытой формы» (которое позволяет вам описать значение каждого термина с помощью номера термина), описывающее все термины в сумме или произведении (точно так же, как вы часто делаете при работе с последовательностями и серии).

 также
также
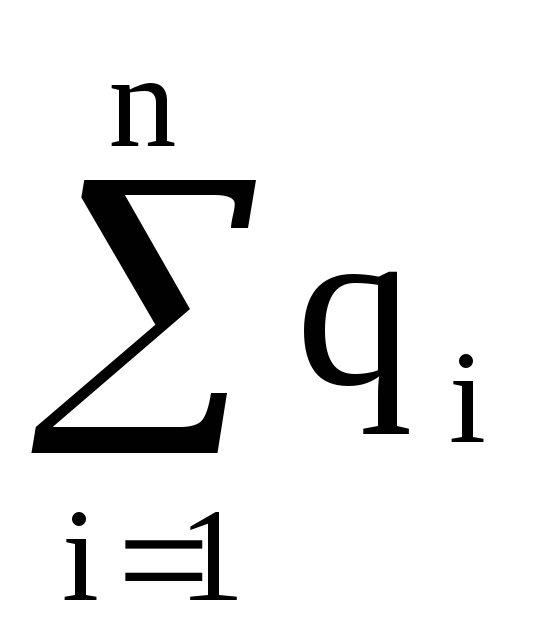

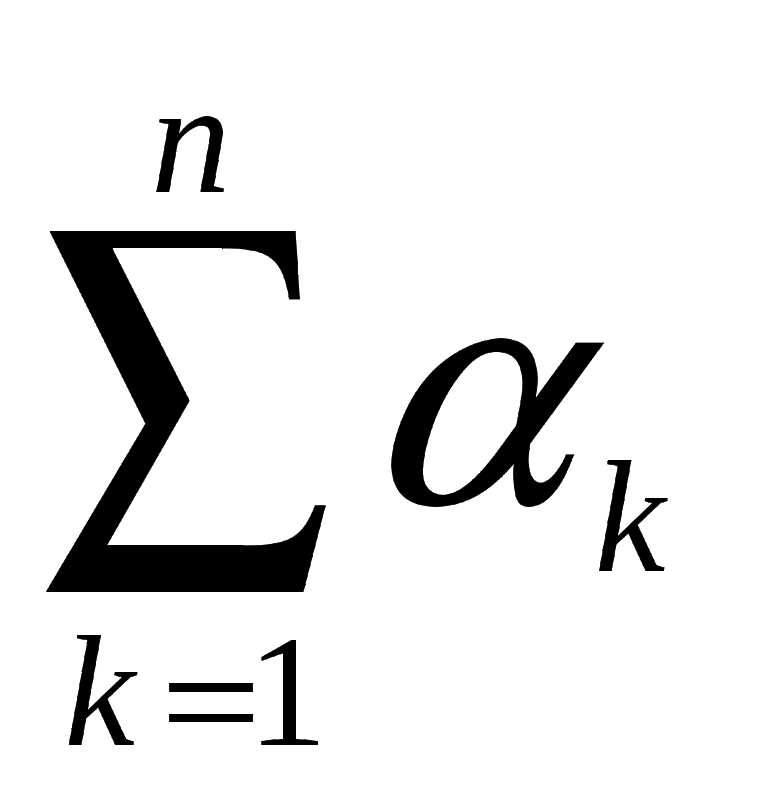
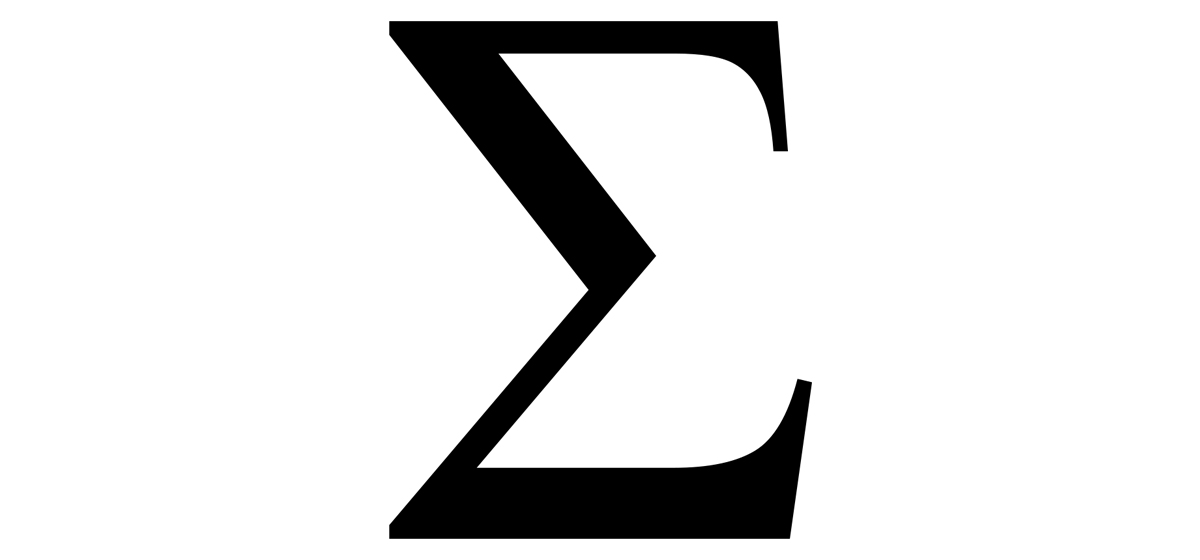 д. Следующее
формула означает суммирование весов четырех виноградин:
д. Следующее
формула означает суммирование весов четырех виноградин:
 Сумма перекрестных произведений.
Сумма перекрестных произведений.