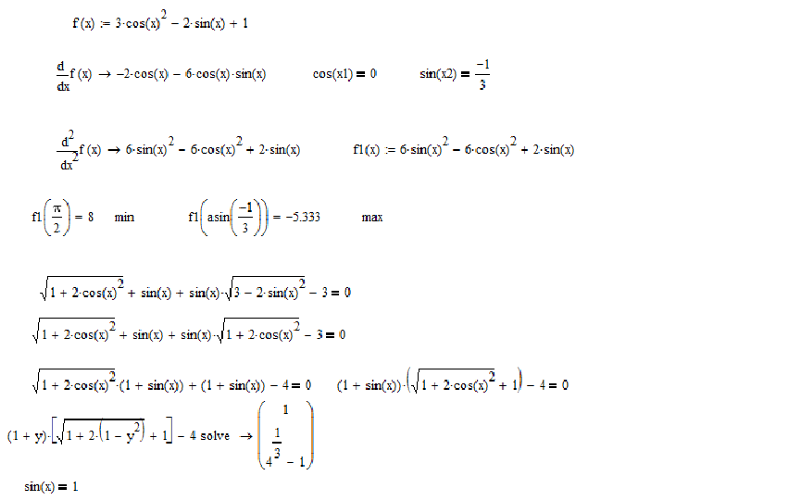Задавать вопрос
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 1к раз
$\begingroup$
Я хочу вычислить неопределенный интеграл 93(х)\sin(x)dx. $$
$\endgroup$
Решение | Можем ли мы упростить \cos 3\theta \sin 2\theta — \cos 4\theta \sin \theta? | Тригонометрия: составные углы
Выйти из полноэкранного режима
- Докажите, что \[\cos 3\theta \sin 2\theta — \cos 4\theta \sin \theta = \cos 2\тета \sin \тета.\]
Подход 1
Мы знаем \(\sin 2\theta=2\sin\theta\cos\theta\), поэтому левая часть становится
\[\начать{выравнивать*}
\cos 3\theta \sin 2\theta — \cos 4\theta \sin \theta
&{}= \cos 3\theta (2\sin\theta\cos\theta) — \cos 4\theta \sin \theta\\
&{}= \sin\theta(2\cos 3\theta\cos\theta — \cos 4\theta)
\конец{выравнивание*}\]
Теперь \(\cos3\theta\cos\theta\) появляется в расширении \(\cos 4\theta=\cos(3\theta+\theta)\), что дает
\[\начать{выравнивать*}
&\cos 3\theta \sin 2\theta — \cos 4\theta \sin \theta\\
&\qquad{}=\sin\theta(2\cos 3\theta\cos\theta — \cos 4\theta)\\
&\qquad{}=\sin\theta(2\cos 3\theta \cos\theta —
(\cos 3\тета\cos\тета-\sin3\тета\sin\тета))\\
&\qquad{}=\sin\theta(\cos 3\theta \cos\theta + \sin3\theta\sin\theta)\\
&\qquad{}=\sin\theta\cos(3\theta-\theta)\\
&\qquad{}=\sin\theta\cos 2\theta.
Подход 2
Используя тригонометрические разложения, которые мы знаем для \(\sin(P+Q), \sin(P-Q), \cos(P+Q)\) и \(\cos(P-Q)\), мы есть
\[\начать{выравнивать*} \sin P\cos Q &{}= \dfrac{1}{2}(\sin(P+Q)+\sin(PQ))\\ \cos P\sin Q &{}= \dfrac{1}{2}(\sin(P+Q)-\sin(PQ))\\ \cos P\cos Q &{}= \dfrac{1}{2}(\cos(P+Q)+\cos(PQ))\\ \sin P\sin Q &{}= -\dfrac{1}{2}(\cos(P+Q)-\cos(PQ)) \конец{выравнивание*}\]
Теперь положив \(A = P+Q\) и \(B = P-Q\), мы получим
\[\начать{выравнивать*} \sin A+\sin B &{}= 2\sin \frac{A+B}{2}\cos \frac{A-B}{2} \\ \sin A-\sin B &{}= 2\cos \frac{A+B}{2}\sin \frac{A-B}{2} \\ \cos A+\cos B &{}= 2\cos \frac{A+B}{2}\cos \frac{A-B}{2} \\ \cos A-\cos B &{}= -2\sin \frac{A+B}{2}\sin \frac{A-B}{2} \конец{выравнивание*}\]
Это дает
\[\начать{выравнивать*}
\cos 3\theta \sin 2\theta &{}- \cos 4\theta \sin \theta \\
&\quad{}=\dfrac{1}{2}(\sin 5\theta-\sin\theta-\sin 5\theta+\sin 3\theta)\\
&\quad{}=\dfrac{1}{2}(\sin 3\theta-\sin\theta)\\
&\quad{}=\cos 2\theta \sin \theta. \конец{выравнивание*}\]
\конец{выравнивание*}\]
- Исходя из отношений \[\начать{выравнивать*} \sin(A+B) &{}= \sin A \cos B + \cos A \sin B,\\ \cos(A+B) &{}= \cos A \cos B — \sin A \sin B, \конец{выравнивание*}\] получить выражение для \(\tan(A+B)\) через \(\tan A\) и \(\tan B\).
Мы знаем \(\tan\theta=\dfrac{\sin\theta}{\cos\theta}\), что дает
\[\начать{выравнивать*} \ tan (A + B) & {} = \ frac {\ sin (A + B)} {\ cos (A + B)} \\ &{}= \frac{\sin A\cos B + \cos A\sin B}{\cos A\cos B — \sin A\sin B}. \конец{выравнивание*}\]
Теперь мы делим числитель и знаменатель дроби на \(\cos A\cos B\), что дает
\[\начать{выравнивать*} \ tan (A + B) & {} = \ dfrac {\ dfrac {\ sin A} {\ cos A} + \ dfrac {\ sin B} {\ cos B}} {1 — \ dfrac {\ sin A \ грех B}{\cos A\cos B}} \\ &{}= \dfrac{\tan A + \tan B}{1 — \tan A\tan B} \конец{выравнивание*}\]
Не используя калькулятор или таблицы, покажите, что сумма трех острых углов, касательные которых равны \(\dfrac{2}{9}\), \(\dfrac{1}{4}\) и \ (\dfrac{1}{3}\) равно \(\dfrac{\pi}{4}\).
Назовите три угла \(A\), \(B\) и \(C\), так что \(\tan A = \dfrac{2}{9}\), \(\tan B = \ dfrac{1}{4}\) и \(\tan C = \dfrac{1}{3}\).
Затем \[\начать{выравнивать*} \tan(A+C) &{}= \frac{\tan A + \tan C}{1 — \tan A\tan C}\\ &= \ frac {\ frac {2} {9} + \ frac {1} {3}} {1 — \ frac {2} {9} \ frac {1} {3}} \\ &= \ гидроразрыва {(\ гидроразрыва {5} {9})}{(\frac{25}{27})}\\ &= \фракция{3}{5}. \конец{выравнивание*}\] Сейчас \[\начать{выравнивать*} \ tan (A + C + B) & {} = \ frac {\ tan (A + C) + \ tan B} {1 — \ tan (A + C) \ tan B} \\ &= \ frac {\ frac {3} {5} + \ frac {1} {4}} {1 — \ frac {3} {5} \ frac {1} {4}} \\ &= \frac{(\frac{17}{20})}{(\frac{17}{20})}\\ &= 1. \конец{выравнивание*}\]
Нам говорят, что \(A\), \(B\) и \(C\) являются острыми. Кроме того, поскольку \(\tan A\), \(\tan B\) и \(\tan C\) меньше, чем \(1\), углы \(A\), \(B\) и \(C\) находятся между \(0\) и \(\dfrac{\pi}{4}\). Следовательно, \(0 < A + B + C < \dfrac{3\pi}{4}\).