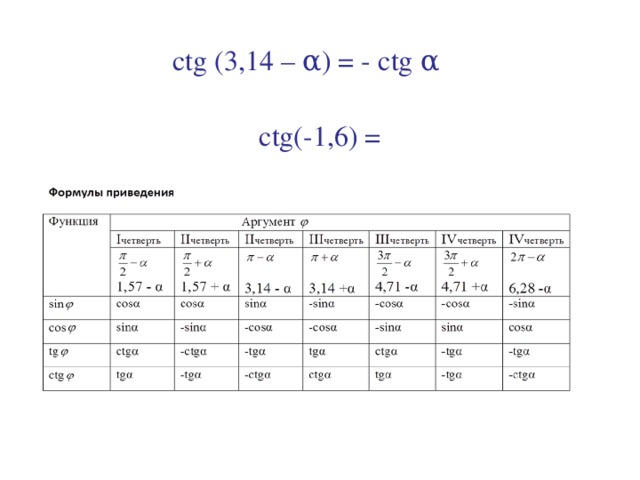
2+n-72)=1/(n+9)Интеграл косинуса
Неопределенный интеграл от косинуса cos (x) равен синусу. Для первоначальной косинуса к правой стороне добавляем постоянную Постоянную определяют с дополнительного условия на первоначальную.
График косинуса имеет вид
Само по себе определение интеграла косинуса достаточно простое. Но как только задают вычислить интеграл косинуса двойного угла, тройного или половины угла, сразу возникают трудности в половины студентов. Выведем формулу интегрирования для функции cos (k*x). Для применения табличной формулы интегрирования надо внести коэффициент под дифференциал, что может привести к изменению самого интеграл. Поэтому одновременно необходимо разделить на этот коэффициент.
.
Зная приведенную формулу, проинтегрировать косинус двойного угла сможет каждый школьник 10, 11 класса. Все что необходимо это подставить 2 или 3 в интеграл
и по индукции следующие интегралы
int(sin(k*x)=-1/k*cos(k*x).
Приведенная формула позволяет вычислить интеграл от косинуса половины угла
и интеграл от косинуса одной трети угла
В этих случаях коэффициент, стоящий при переменной в косинусе при интегрировании становится обратным значением перед синусом.
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус
Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование
Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл
Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл
Пример 5. Найти интеграл функции y= cos (x/6).
Решение: Проинтегрируем по приведенной выше формуле
Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.
Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса
Пример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования
Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1.
Решение: Находим первоначальную
С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
Находим определенный интеграл в указанных пределах
Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
Таким образом площадь необходимо искать на трех промежутках
Ось абсцисс можем записать функцией y = 0. Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = — cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy). Вычисляем площадь интегрированием в указаных пределах
Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
На этом знакомство с интегрированием косинуса завершается.
Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории «Интегрирование функций».
- Назад
- Вперёд
тригонометрия — Почему $\cos(i)>1$?
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 959 раз
$\begingroup$
Я всегда думал, что косинус колеблется только от $-1$ до $1$.
2$. Затем мы узнаем некоторое правило, согласно которому $f(x) \geq 0$ для всех $x$. Но подождите секунду, $f(i)$ отрицательно. Никакого скандала, поскольку $i$ — ненастоящее число. 9{-iz}}{2}$$
Когда вы подставляете комплексные числа в $\cos(z$), вы можете получить значения больше $1$ или меньше $-1$
$\endgroup$
6
$\begingroup$
Функция $\cos z$ принадлежит интервалу $\left[-1,1 \right]$, когда $z$ — действительное число, а не обязательно, когда $z$ — комплексное число. Примером этого является $\cos i > 1$, как вы правильно указали.
$\endgroup$
$\begingroup$
Подсказка
Используйте тождество $$\cos(x+iy)=\cos x\cosh y-i\sin x\sinh y$$
$\endgroup$
$\begingroup$
Вот что происходит визуально: кош по сути является косинусом с областью мнимых чисел, как я сказал в комментариях.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Функция арккосинуса
Функция арккосинусаФункция y = cos
-1 x = arccos x и ее график:Поскольку y = cos -1 x является обратной функцией y = cos x, функция y = cos -1 x тогда и только тогда, когда cos y = x . Но, поскольку y = cos x не является взаимно однозначным, его область определения должна быть ограничена, чтобы y = cos -1 x было функцией. Чтобы получить график y = cos -1 x, начните с графика y = cos x. | |
Ограничить область определения функции взаимно однозначной областью — обычно используется (выделено красным справа) для cos -1 x. Это оставляет диапазон ограниченной функции неизменным как [-1, 1]. | |
Отразите график через линию y = x, чтобы получить график
of y = cos -1 x (y = arccos x), черная кривая справа. Обратите внимание, что y = cos -1 x имеет домен [-1, 1] и диапазон . Он строго убывает на всей своей области определения. . | |
| Итак, когда вы попросите калькулятор построить график y = cos -1 x, вы получите график, показанный справа. (Окно просмотра [-2, 2] x [-0,5, 3,5].) |
Оценка y = cos
-1 x:Вычисление выражений cos -1 x следует той же процедуре, что и вычисление выражений sin -1 x — , вы должны знать домен и диапазон функции! Вот пример:
Пример 1: Оценка cos
-1 (-1/2)Если y = cos -1 (-1/2), то cos y = -1/2. Это уравнение имеет бесконечное число решений, но только одно из них () находится в пределах cos -1 х. Таким образом:
.
